Bewegte Felder

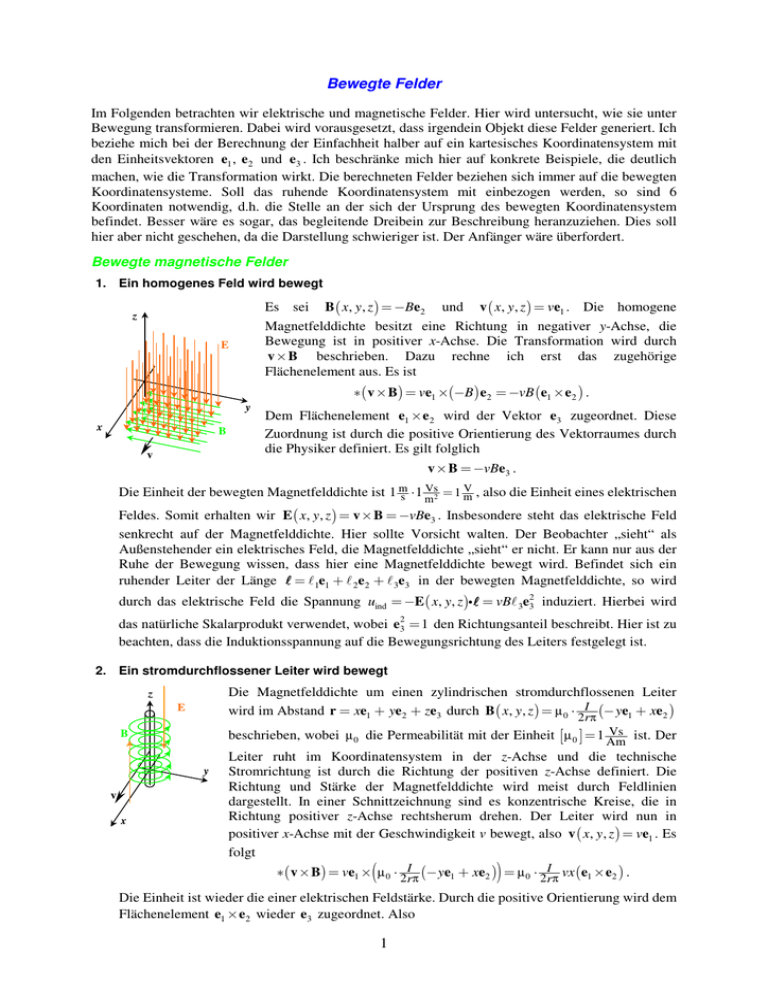
Bewegte Felder
Im Folgenden betrachten wir elektrische und magnetische Felder. Hier wird untersucht, wie sie unter
Bewegung transformieren. Dabei wird vorausgesetzt, dass irgendein Objekt diese Felder generiert. Ich
beziehe mich bei der Berechnung der Einfachheit halber auf ein kartesisches Koordinatensystem mit
den Einheitsvektoren e1 , e2 und e3 . Ich beschränke mich hier auf konkrete Beispiele, die deutlich
machen, wie die Transformation wirkt. Die berechneten Felder beziehen sich immer auf die bewegten
Koordinatensysteme. Soll das ruhende Koordinatensystem mit einbezogen werden, so sind 6
Koordinaten notwendig, d.h. die Stelle an der sich der Ursprung des bewegten Koordinatensystem
befindet. Besser wäre es sogar, das begleitende Dreibein zur Beschreibung heranzuziehen. Dies soll
hier aber nicht geschehen, da die Darstellung schwieriger ist. Der Anfänger wäre überfordert.
Bewegte magnetische Felder
1. Ein homogenes Feld wird bewegt
Es sei B ( x, y , z ) = −Be2 und v ( x, y , z ) = ve1 . Die homogene
Magnetfelddichte besitzt eine Richtung in negativer y-Achse, die
Bewegung ist in positiver x-Achse. Die Transformation wird durch
v × B beschrieben. Dazu rechne ich erst das zugehörige
Flächenelement aus. Es ist
z
E
∗ ( v × B) = ve1 ×(−B ) e 2 = −vB (e1 × e 2 ) .
y
x
B
v
Dem Flächenelement e1 × e 2 wird der Vektor e3 zugeordnet. Diese
Zuordnung ist durch die positive Orientierung des Vektorraumes durch
die Physiker definiert. Es gilt folglich
v × B = −vBe3 .
V , also die Einheit eines elektrischen
Die Einheit der bewegten Magnetfelddichte ist 1 ms ⋅1 Vs2 = 1 m
m
Feldes. Somit erhalten wir E ( x, y , z ) = v × B = −vBe3 . Insbesondere steht das elektrische Feld
senkrecht auf der Magnetfelddichte. Hier sollte Vorsicht walten. Der Beobachter „sieht“ als
Außenstehender ein elektrisches Feld, die Magnetfelddichte „sieht“ er nicht. Er kann nur aus der
Ruhe der Bewegung wissen, dass hier eine Magnetfelddichte bewegt wird. Befindet sich ein
ruhender Leiter der Länge ℓ = ℓ 1e1 + ℓ 2e2 + ℓ 3e3 in der bewegten Magnetfelddichte, so wird
durch das elektrische Feld die Spannung uind = −E ( x, y, z )iℓ = vBℓ 3e32 induziert. Hierbei wird
das natürliche Skalarprodukt verwendet, wobei e32 = 1 den Richtungsanteil beschreibt. Hier ist zu
beachten, dass die Induktionsspannung auf die Bewegungsrichtung des Leiters festgelegt ist.
2. Ein stromdurchflossener Leiter wird bewegt
Die Magnetfelddichte um einen zylindrischen stromdurchflossenen Leiter
wird im Abstand r = xe1 + ye2 + ze3 durch B ( x, y , z ) = µ 0 ⋅ 2Irπ (− ye1 + xe 2 )
z
E
Vs ist. Der
beschrieben, wobei µ 0 die Permeabilität mit der Einheit [ µ 0 ] = 1 Am
B
y
v
x
Leiter ruht im Koordinatensystem in der z-Achse und die technische
Stromrichtung ist durch die Richtung der positiven z-Achse definiert. Die
Richtung und Stärke der Magnetfelddichte wird meist durch Feldlinien
dargestellt. In einer Schnittzeichnung sind es konzentrische Kreise, die in
Richtung positiver z-Achse rechtsherum drehen. Der Leiter wird nun in
positiver x-Achse mit der Geschwindigkeit v bewegt, also v ( x, y , z ) = ve1 . Es
folgt
)
∗ ( v × B) = ve1 ×(µ 0 ⋅ 2rI π (− ye1 + xe2 ) = µ 0 ⋅ 2rI π vx (e1 × e2 ) .
Die Einheit ist wieder die einer elektrischen Feldstärke. Durch die positive Orientierung wird dem
Flächenelement e1 × e 2 wieder e3 zugeordnet. Also
1
E ( x, y , z ) = v × B = µ 0 ⋅ 2 Irπ vxe3 .
Der bewegte Leiter besitzt nun von außen betrachtet ein elektrisches Feld. Das reale E-Feld ist
schwierig darzustellen. In der Ebene x = 0 ist die E-Feldstärke null. In Bezug auf die
Bewegungsrichtung ist das E-Feld vor dem Leiter positiv und hinter dem Leiter negativ.
Ich habe hier eine vereinfachte Magnetfelddichte angenommen. Nach Biot-Savart ist die magnetische Felddichte etwas fassförmig. Der Leser berechne auch v ( x, y , z ) = −ve3 und vergleiche.
Bewegte elektrische Felder
3. Das bewegte Elektron
Das
im
Ursprung
ruhende
Elektron
wird
durch
E ( x, y , z ) = −e 3 ( x e1 + y e 2 + z e3 ) beschrieben. Mit v ( x, y , z ) = ve3 folgt
z
v
4 πε0r
E
( 4 −er ( x e + y e + z e ))
∗ ( v × E) = ve3 ×
B
y
1
3
πε0
2
3
= −ev 3 ( x e3 × e1 + y e3 × e 2 )
4πε0 r
= −ev 3 ( x e3 × e1 − y e 2 × e3 )
4πε0 r
x
Nun transformieren wir und erhalten
∗( v × E) = ev 3 (−x e2 + y e1 ) = ev 3 ( y e1 − x e2 ) .
4πε r
4πε r
0
0
As und der Permeabilität µ
Durch die Multiplikation mit der Permittivität ε 0 , [ ε 0 ] = 1 Vm
0
bekommen wir eine Magnetfelddichte
B ( x, y , z ) = µ 0 ε 0
Natürlich steht die magnetische Flussdichte senkrecht auf dem elektrischen
Feld. Der Vergleich mit dem stromdurchflossenen Leiter zeigt eine
Übereinstimmung mit der Richtung der Magnetfelddichte. Befindet sich
das Elektron in einem magnetischen Feld, so wird es in Richtung der
geringeren Feldstärke abgelenkt. Für das Proton hat das B-Feld die
entgegengesetzte Richtung. Da keine Tangentialbeschleunigung vorhanden
ist, zeigt der Beschleunigungsvektor an jeder Stelle auf einen gemeinsamen
Punkt. Dies ist der Mittelpunkt eines Kreises.
x
xxx
x
.... .
ev ( y e − x e ) = µ ev ( y e − x e ) .
1
2
0 4πr 3
1
2
4 πε0r3
v
4. Der bewegte geladene Leiter
z
B
Der geladene Leiter befinde sich in der z-Achse. Das elektrische Feld sei
E
Q
vereinfacht durch E ( x, y , z ) = 2πε rℓ ( xe1 + ye 2 ) dargestellt. Er werde in
0
Richtung der x-Achse mit der Geschwindigkeit v ( x, y , z ) = ve1 bewegt.
Wir erhalten
y
v
(
)
Q
∗ ( v × E) = v e1 × 2πε rℓ ( x e1 + y e2 )
0
Q
x
= 2πε rℓ vy ( e1 × e2 ).
0
Nach Transformation endlich
Q
v × E = 2πε rℓ vy e3 .
0
Q
Q
Die Magnetfelddichte ist folglich B ( x, y , z ) = µ 0 ε 0 2 πε rℓ vy e3 = µ 0 2πrℓ vy e3 .
0
Auch hier gilt das bereits unter 2. gesagte, so dass ich mich hier auf die zwei unterschiedlichen
Richtungen der magnetischen Felddichte beschränke.
Berechnen Sie auch v ( x, y , z ) = −ve3 ! Vergleiche!
2
Bewegte Planeten
Das im Ursprung ruhende Gravitationsfeld wird durch G ( x, y, z ) = −γ M3 ( x e1 + y e2 + z e3 )
r
beschrieben. Der Einfachheit halber bewege sich dieses Feld auf einer Kreisbahn. Dazu
verschieben wir den Planeten auf die Kreisbahn R (t ) = R (cos Rv t e1 + sin Rv t e 2 ) . Dann bewegt
v ( x, y , z , t ) = −v (sin Rv t e1 − cos Rv t e 2 ) . Das
sich der Planet mit der Geschwindigkeit
Gravitationsfeld bezüglich des Ursprungs wird nun durch
G ( x, y , z ) = −γ
M
x − R (t )
3
(( x − R cos( Rv t ))e + ( y − R sin( Rv t ))e
1
2
+ z e3
)
beschrieben. Hierbei ist x der Vektor, der auf den Punkt ( x, y , z ) zeigt (Ortsvektor).
Für das bewegte Gravitationsfeld folgt



v t ) e + ( y − R sin v t ) e + z e 
M
∗( v ×G) =−v (sin Rv t e1 − cos Rv t e2 )×−γ
(
x
−
R
cos
3 )
3(
R 1
R 2


x − R(t )


=γ
(( x cos Rv t − R cos
2
Mv
x − R(t )
3
)
v t + y sin v t − R sin2 v t e ×e
R
R
R 1 2
− z cos Rv t e2 ×e3 − z sin Rv t e3 ×e1
=γ
Mv
x − R(t )
3
)
(( x cos Rv t + y sin Rv t − R)e ×e − z cos Rv t e ×e − z sin Rv t e ×e )
1
2
2
3
3
1
Das neue bewegte Gravitationsfeld Γ ist folglich
Γ ( x, y , z ) = −γ
Mv
x − R (t )
3
( z cos Rv t e + z sin Rv t e + ( R − x cos Rv t − y sin Rv t) e ) .
1
2
3
Offen bleibt, um was für ein Feld es sich hier handelt.
Abschließende Bemerkung
Der geneigte Rezipient möge bitte beachten, dass es sich hier um reine Mathematik handelt. Es sollte
durch physikalische Messungen möglich sein, diese Ergebnisse zu überprüfen. Leider habe ich bis
heute keine derartigen Untersuchungen gefunden. Alle Formeln beruhen auf den newtonschen
Axiomen und, obwohl Coulomb in der Dynamik nicht anwendbar ist, auf dem coulombschen Gesetz.
Hier ist folglich noch ein richtiges Fundament zu erarbeiten. Zum Induktionsgesetz will ich noch
bemerken, dass bei der Bewegung des Leiters allen Elektronen ein Magnetfeld zugeschrieben werden
kann. Für den ruhenden Leiter im äußeren Magnetfeld existiert im Mittel über alle Elektronen das
resultierende Magnetfeld im Leiter nicht. Wird der Leiter bewegt, so werden die freien Elektronen
zusätzlich aus ihrer Bahn lokal auf Kreisbahnen gelenkt. Die gebundenen Elektronen werden in ihren
Orbitalen verschoben, also polarisiert. Mit anderen Worten: Die Leitungselektronen tragen nichts zur
Induktionsspannung bei.
In der modernen Fassung werden Differentialformen verwendet. Wir deuten D = ε 0 E und B = µ 0 H
als Zweiform, also
B ( x, y , z ) = B1dy ∧ dz + B2 dz ∧ dx + B3dx ∧ dy und D ( x, y , z ) = D1dy ∧ dz + D2 dz ∧ dx + D3dx ∧ dy .
Das Kreuzprodukt wird durch die Verjüngung E = ι v ( B) und H = ι v ( D) dargestellt. Zu beachten ist
die Definition der Bewegungsrichtung.
3