Kapitel 5 D ik d h t t Kö Dynamik ausgedehnter, starrer Körper

Kapitel 5
D
Dynamik
ik ausgedehnter,
d h t starrer
t
Kö
Körper
1
Volumen, Masse, Dichte des ausgedehnten starren Körpers
bisher betrachtet : Massenpunkte,
Massenpunkte ohne Ausdehnung
jetzt betrachtet : ausgedehnte Körper, aber (noch) nicht deformierbar
prinzipielles Vorgehen :
► Zerlegung des Körpers in Volumen-Elemente
► Summation über Volumenelemente
Volumen :
V = ∑ ΔVi
i
Masse :
M = ∑ Δmi
i
Di ht :
Dichte
Δmi
ρi =
ΔVi
2
N
Δmi
M =∑
ΔVi =∑ ρ i ΔVi
i =1 ΔVi
i =1
N
aus :
ergibt
ibt sich
i h für
fü infinitesimal
i fi it i l
kleine Volumenelementen :
V = lim
ΔVi →0
N →∞
∑ ΔV = ∫ dV
i
i =1
r
M = ∫ ρ (r ) dV
V
V
Anmerkung : Volumen-Elemente können in verschiedenen
Koordinaten-systemen berechnet werden
K
Kartesische
i h Koord.
K d
dV = dx
d dy
d dz
d
Zylinder-Koord
Zylinder-Koord.
dV = r dr dϕ dz
Kugel-Koord.
dV = r dr sin ϑ dϑ dϕ
2
3
Mathematische Zwischenbemerkung : Volumen-Integral in kartesischen Koord.
z2 = c
y2 = b
z1 = 0
y1 = 0
xx2 = a
2
= 0
xx11= 0
Ö Volumenelemente sind kleine Quader mit dV = dx dy dz
Ö
V = ∫ dV = ∫∫∫ dx dy dz
V
V
4
⎛ y 2 ⎡ x2 ⎤ ⎞
V = ∫ ⎜ ∫ ⎢ ∫ dx ⎥ dy ⎟ dz
⎜
⎟
⎢ x1 ⎦⎥ ⎠
z1 ⎝ y1 ⎣
z2
Auswertung
d IIntegrals
des
l :
Ö Beispiel : für das Volumen eines Quader ergibt sich aus dem Integral :
x2
y2
z2
x1
y1
z1
V = ∫ dx ∫ dy ∫ dz = ( z 2 − z1 )( y2 − y1 ) ( x2 − x1 ) = a b c
beachte : Sonderfall bei der Integration des Volumens eines Quaders in kartesischen
Koordinaten : Integrationsgrenzen sind konstant; im Allgemeinen hängen die
Integrationsgrenzen voneinander ab, z.b. z = z (x,y)
⎛ y 2 ⎡ x2
⎤ ⎞
M = ∫ ⎜ ∫ ⎢ ∫ ρ ( x, y, z ) dx ⎥ dy ⎟ dz
⎜
⎟
⎢
⎥
z1 ⎝ y1 ⎣ x1
⎦ ⎠
z2
Ö Masse :
Bei konstanter Dichte :
M = ρ 0 ∫ dV
V
5
Mathematische Zwischenbemerkung : Volumen-Integral in Zylinder-Koord.
dl1= dr
dl2 = r dϕ
dl3 = dz
Ö Volumenelemente sind kleine Ringsegmente mit dV = dr r dϕ dz
6
Auswertung
g
des Integrals :
⎛ ϕ 2 ⎡r2
⎞
⎤
V = ∫ ⎜ ∫ ⎢ ∫ r dr
d ⎥ dϕ ⎟ dz
d
⎜
⎟
z1 ⎝ ϕ1 ⎢
⎣ r1
⎦⎥
⎠
z2
Ö Beispiel : für das Volumen eines Zylinders ergibt sich aus dem Integral :
R
2π
h
2
R
2
V = ∫ r dr ∫ dϕ ∫ dz =
2π h = π R h
2
0
0
0
beachte : Sonderfall bei der Integration des Volumens eines Zylinders in ZylinderKoordinaten : Integrationsgrenzen sind konstant; im Allgemeinen hängen die
I t
Integrationsgrenzen
ti
voneinander
i d abb
7
Mathematische Zwischenbemerkung : Volumen-Integral in Kugel-Koord.
ähnlich wie beim Zylinder sind die VolumenVolumen
elemente in Kugelkoordinaten Ringsegmente;
allerdings ist der Radius des Rings abhängig von
d Höhe
der
Höh z bzw.
b dem
d Winkel
Wi k l ϑ
8
betrachte Schnitte in der x,z-Ebene (links) und der x,y-Ebene (rechts) :
dl2= r´ dϕ = r sinϑ dϕ
dl3= r dϑ
dl1= dr
d
9
Ö Volumenelemente dV = r2 dr sinϑ dϑ dϕ
Auswertung
A
t
des Integrals :
⎛ ⎡
⎞
⎤
V = ∫ ⎜ ∫ ⎢ ∫ r 2 dr ⎥ sin ϑ dϑ ⎟ dϕ
⎜ r
⎟
⎥
ϕ1 ⎝ ϑ1 ⎢
⎣1
⎦
⎠
ϕ 2 ϑ2 r2
Ö Beispiel : für das Volumen einer Kugel ergibt sich aus dem Integral :
π
2π
3
R
4
2
3
V = ∫ r dr
d ∫ sin
i ϑ dϑ ∫ dϕ =
⋅ 2 ⋅ 2π = π R
3
3
0
0
0
R
beachte : Sonderfall bei der Integration des Volumens einer Kugel in KugelKoordinaten : Integrationsgrenzen sind konstant; im Allgemeinen hängen die
Integrationsgrenzen voneinander ab
10
Massenschwerpunkt eines ausgedehnten Körpers
Summation über alle Massenelemente :
r
∑ ri Δmi
N
v
rS =
i =1
N
∑ Δm
i =1
r
∑ ri ρi ΔVi
N
=
i
i =1
N
∑ Δm
i =1
i
Ö für
fü infinitesimal
i fi it i l kleine
kl i Elemente
El
t :
r
1 r
1 r r
rS =
r dm
d =
r ρ (r ) dV
d
∫
∫
MV
MV
für konstante Dichte :
r ρ0 r
1 r
rS =
r dV = ∫ r dV
∫
MV
VV
11
Bewegung (Rotation) eines ausgedehnten, starren Körpers
Allgemeine Aussagen :
► die Bewegung eines starren Körpers lässt sich stets zerlegen in Translation
des Schwerpunktes und Rotation des Körpers (im Bezug auf den Schwerpunkt)
Ö vollständige
g Beschreibungg der Bewegung
g g erfordert Angabe
g
von :
r
Bahnkurve Schwerpunkt : rS (t ) = {xS (t ), y S (t ), z S (t )}
r
Variation Kreisfrequenz/Drehachse : ω (t ) = {ω x (t ), ω y (t ), ω z (t )}
beachte : Betrag und Richtung des Vektors ω können variieren !
Ö 6 Koordinaten Ö 6 Freiheitsgrade der Bewegung des starren Körpers
bei Fixierungg des Schwerpunkts
p
bleiben 3 Freiheitsgrade
g
bei zusätzlicher Fixierung der Drehachse bleibt ein Freiheitsgrad (Rotationswinkel)
12
Kräfte am starren Körper
F1
betrachte Kraft , die an einem
freien, starren Körper angreift
FH1
S
i
ri,s
i
z
rs
O
FH2
(
) (
r
r 1 r
r
1 r
Drehmoment : D =
ri , S × F1 − ri , S × FH 2
2
2
)
x
r
r
r
r ⎛ F1 FH 2 ⎞
⎟ ≡ DS
= ri , S × ⎜⎜ −
⎟
2
2
⎝
⎠
betrachte Kraft F1, die am Volumenelement dVi des Körpers angreift; wir „zerlegen
zerlegen“ die Kraft F1
in ein Kräftepaar F1,FH2 sowie eine Kraft FH1; die Beträge der Kräfte sind gleich; die Kräfte FH1
und FH2 greifen im Schwerpunkt an; F1 und FH2 wirken wie die Kräfte an einer Balkenwaage mit
Mitt l kt im
Mittelpunkt
i Vektor
V kt riS Ö Rotation;
R t ti
di Kraft
die
K ft FH1 bewirkt
b i kt offensichtlich
ff i htli h keine
k i Rotation
R t ti (da
(d am
anderen Ende der gedachten Balkenwaage die gleiche Kraft F1 in die gleiche Richtung zieht),
13
sondern verschiebt den Schwerpunkt des Körper Ö Translation
Drehmomente, verursacht durch die Schwerkraft
r
r r
Drehmoment in dmi : Di = ri × g dm
d i
Ö gesamtes Drehmoment :
r
D =
r r
r r r
∑ ri × g dmi → ∫ r × g ρ (r ) dV
i
z
r dmi
ri
SP
x
V
r
r
r r
r
r
Ö D = g × ∫ r ρ (r ) dV = g × ∫ r dm
V
1
mit der Definition r
rS =
des Schwerpunkts :
M
V
r r
F = g dmi
r
∫ r dm
V
r
r r
folgt : D = M g × rS = 0
r
da wir bei der Lagerung im SP zu Beginn gewählt hatten : rS = 0
d h bei Lagerung im Schwerpunkt heben sich alle Drehmomente auf
d.h.
Ödie Lage des Körpers ist stabil
14
Trägheitsmoment
►Dynamik der Drehbewegung wird wesentlich bestimmt durch die Verteilung der
Masse Ö Körper mit gleichen Gesamt-Massen, aber unterschiedlicher Masse/DichteVerteilung zeigen unterschiedliche Dynamik Ö Definition des Trägheitsmomentes
betrachte die kinetische Energie
eines Massenelements dmi :
es sei :
mit :
uundd :
r
ω || zẑ
Ekin ,i
dmi
ri,z
ri
ω
r r r
vi = ω × ri
r r
r
r
ri = ri , x + ri , y + ri , z
und dem Abstand zur Drehachse :
Ö
z
y
ri,y
ri,⊥
ri,x
ix
r r
r
r⊥ = ri , x + ri , y
x
r
r
r 2
1
= Δmi [ ω × (ri , z + ri ,⊥ )]
2
15
da :
Ö
r
r
ri ,z || ω
Ekin ,i
r
r
Ö ri , z × ω = 0
r2 1
r
1
2
2
= Δmi (ri ,⊥ × ω ) = Δmi ri ,⊥ ω
2
2
d.h. die Energie hängt lediglich vom senkrechten Abstand zur Drehachse ab
Integration über alle
Massenelemente liefert :
Ekin = Erot =
ω2
2
∫
ri 2,⊥ dm RotationsE
Energie
i
V
äquivalent zur kinetischen Energie der Translationsbewegung Ekin = ½mv2
definieren wir (als Entsprechung zur Masse m) das Trägheitsmoment :
beachte : Trägheitmoment I wird bestimmt durch die
Abstandsverteilung der Massen um Drehachse
I = ∫ ri 2,⊥ dm
V
Ö Rotationsenergie
R t ti
i :
Erot
1
= I ω2
2
16
Drehimpuls ausgedehnter starrer Körper
r
r r
für einen Massenp
Massenpunkt
nkt gilt : L = m r × v
r
r r
Ö für einzelne Massenelemente : Li = Δmi ri × vi
r
r r r
oder : Li = Δmi ri × ω × ri
r r r r
mit : r × ω × r || ω
2
L
=
Δ
m
r
Ö i
i i ,⊥ ω
r r
ω×r
r
r
L = ∑ Li = ∑ Δmi ri 2,⊥ ω → ω ∫ r⊥2 dm
i
i
L=Iω
Ö Rotationsenergie
R t ti
i :
ω
mit dem senkrechten Anteil von r bzgl. der Drehachse
Ö gesamter Drehimpuls :
Ö
r
V
Trägheitsmoment
Erot
2
1
L
= I ω2 =
2
2I
17
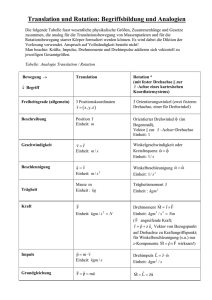
Vergleich der physikalischen Größen bei Translation und Rotation
Translation
Rotation
Ort x
Winkel ϕ
Geschwindigkeit v = dx/dt
Winkelgeschwindigkeit ω = dϕ/dt
Beschleunigung a = d2x/dt2
Winkelbeschleunigung d2ϕ/dt2
Masse m
Trägheitsmoment I
Impuls p
Drehimpuls L
Kraft F
Drehmoment D
18
Translation
Rotation
2
2
kin. Energie :
Ekin
1
p
2
= mv =
2
2m
Erot
1
L
2
= Iω =
2
2I
Impuls/Drehimpuls :
r
r
p = mv
r
r
L = Iω
Kraft/Drehmoment :
r
r
r&
&
F = ma = m x
r&
r&
r&
&
D = L = Iω = Iϕ
r&
r
&
m x = −D x
r&
r
&
I ϕ = −Dϕ
Bewegungsgleichung
B
l i h
(bei der Schwingung) :
19
Drehimpuls und Drehmoment bei variierender Massenverteilung
betrachte die Drehbewegung
g g eines starren Körpers,
p , bei dem sich während der Drehungg
die Massenverteilung ändert (nicht aber die Gesamt-Masse; ohne Einfluß äußerer
Kräfte), z.B. Eiskunstläufer bei Pirouette, Drehstuhl,…
r
ω
r
ω
ÖÄnderung der Massenverteilung führt zu Änderung des Trägheitsmoments
aber : Drehimpuls bleibt konstant (da keine äußeren Drehmomente wirken)
aus :
L = I ω = const.
folgt, z.B. bei Verkleinerung von I Ö Erhöhung der Rotationsgeschwindigkeit ω
20
Anmerkung : Zur Energiebilanz beim Drehstuhlversuch
Hanteln ausgestreckt
a sgestreckt : I1 , ω1
Hanteln angezogen : I2 < I1 , ω2 > ω1
vergleiche Energien :
L2
Erot ,1 =
2 I1
< Erot , 2
L2
=
2 I2
Frage : Woher kommt die Energie ?!
https://lp.uni-goettingen.de/get/text/676
r2
r1
Arbeit gegen Zentrifugalkraft :
W (r1 , r2 )
r r r2
2
= − ∫ FZF dr = ∫ m ω (r ) r dr
r2
r1
r1
21
I (r1 )
r12
= ω1 2
mit : ω (r ) = ω1
I (r )
r
Ö
W (r1 , r2 )
(gilt exakt für
(g
f Punktmassen))
r2
r
= m ω I (r1 ) ∫ 2 dr
I (r )
r1
2 2
1
r2
r2
1
= ω m r ∫ 2 4 dr = ω m r ∫ 3 dr
m r
r
r1
r1
2
1
3
4
1
r
2
1
4
1
2
2
⎡
⎤
⎛
⎞
⎛
⎞
1
1
1
r
r
2
2
4
1
1
= ω1 m r1 ⎢ 2 − 2 ⎥ = ... = I (r1 )ω1 ⎜⎜ 2 − 1⎟⎟ = Erot ,1 ⎜⎜ 2 − 1⎟⎟
2
⎣ r2 r1 ⎦
⎝ r2
⎝ r2
⎠
⎠
⎛ I1 ⎞
⎟
mit Masse m erweitert : W (r1 , r2 ) = Erot ,1 ⎜
−
1
⎜I
⎟<0
⎝ 2 ⎠
d.h. bei Bewegung von r1 nach r2 > r1 wird Energie benötigt,
bei der umgekehrten Bewegung von r2 nach r1 wird Energie gewonnen
22
Der Steiner‘sche Satz
► Der Steiner
Steiner‘sche
sche Satz beschreibt die Relation zwischen dem Trägheitsmoment IA
bezogen auf beliebige Achse A und dem Trägheitsmoment IS bezogen auf eine zu A
parallele Achse S durch den Schwerpunkt Ö aus Kenntnis von IS lässt sich mittels des
Steiner‘schen Satzes IA berechnen
r2
r r2
es gilt : I A = ∫ R dm = ∫ (r + a ) dm
V
r2
r r
r2
Ö I A = ∫ r dm + 2a ∫ r dm + ∫ a dm
V
r
R
r
SP r
V
V
r
a
V
= IS + a2M
aus Definition des Schwerpunkts :
r
r
∫ r dm = M rS = 0
V
A
S
I A = IS + M a
2
da der Schwerpunkt als Ursprung gewählt wurde
Steiner‘scher Satz
23
Rollbewegungen
betrachte einen rollenden Zylinder
auf einer schiefen Ebene :
Drehmoment :
D = I ϕ&& = I ω&
(äquivalent zu F = m &x& )
wirksames Drehmoment durch Schwerkraft :
D = M g r sin α
Trägheitsmoment
T
ä h it
t bzgl.
b l des
d Auflagepunktes
A fl
kt A
(nach Steiner‘schem Satz) :
Ö Bewegungsgleichung Rotation :
Ö es folgt für die Translationsbewegung des Schwerpunkts :
I = IS + M r
(
2
M g r sin α = I S + M r
2
) ω&
M g r sin α
a = v& = r ω& =
IS + M r2
2
24
g sin α
oder ((ein wenigg umgeschrieben)
g
): a=
IS
1+
M r2
Öje größer Trägheitsmoment, umso kleiner die Translationsbeschleunigung
oder : je grösser die Rotationsenergie, umso kleiner die Translationsenergie
Ö Körper mit gleicher Gesamtmasse, aber unterschiedlichem Trägheitsmoment
rollen unterschiedlich schnell die schiefe Ebene herunter
alternative Herleitung :
betrachte die Energie-Erhaltung :
E pot = Erot + Ekin = M g s sin α
(wenn der Körper die Strecke s auf der schiefen Ebene zurückgelegt hat)
mit :
Ekin
1
= M v2
2
und :
Erott
2
1
1
v
2
= Iω = I 2
2
2 r
Ö je grösser das Trägheitsmoment, umso größer ist die Rotationsenergie
Ö umso kleiner die verfügbare Translationsenergie
(d.h. die erreichte Endgeschwindigkeit)
25
Rollbewegungen : Das Maxwell‘sche Rad
r r r
r r
Drehmoment : D = r × F = M r × g
Trägheitsmoment für Drehung um Abrollpunkt :
1
2
2
I = IS + M r = M R + M r
2
2
Berechnung der Translations-Beschleunigung aus :
v = rω
Ö
a = v& = r ω& = r ϕ&&
r
r
die Bewegung des Maxwell-Rades stellt eine
Schwingung in der Winkelkoordinate dar;
Ö Rückstellmoment :
D = I ϕ&&
Ö
D
ϕ&& =
I
v
F
26
Einsetzen in den Ausdruck für die Beschleunigung liefert :
D
r 2M g
1
a=r =
= ... = g
≡ gα
2
1
R
I
2
2
M R +M r
1+ 2
2
2r
Ö die Fallbeschleunigung g wird also um den Faktor α herabgesetzt,
so dass man die Beschleunigung a im Experiment gut beobachten kann.
betrachte Energie-Erhaltung :
ΔE pot = M g h = Etrans (h) + Erot (h)
d.h. nach Fallstrecke h hat sich die Energie in Translation und Rotation aufgeteilt
2
1
2r
2
Ö v = v(h )
es ergibt sich : ΔEtrans ( h) = M v = M g h 2
2
2
R + 2r
2
1
R
2
ΔErot (h) = I ω = M g h 2
2
R + 2r2
Öder größte Bruchteil wird in Rotation umgewandelt
Ö
ω = ω (h )
27
Bewegungsgleichung der Rotation
betrachte Drehimpuls eines Massenpunkts i in einem System von Massen :
r r
r
r
r
2 r
Li = ri ,⊥ × pi = Δmi (ri ,⊥ × vi ) = Δmi ri ,⊥ ω
(
)
r
r&
r
r&
r r
Ö Li = Δmi ri , ⊥ × vi = ri × Fi ,t = Di
ω
pi
ri,⊥
r
2 r
Vergleich der beiden Gleichungen liefert : Di = Δmi ri ,⊥ ω&
r
r& 2
r&
2 r
&
Summe über Drehmomente D =
∑ Δmi ri,⊥ ω → ω ∫ r⊥ dm = ω I
(bzw. Massenpunkte) :
Ö
r
r&
r&
&
D = Iω = I ϕ
i
r
r&
&
äquivalent zu : F = m r
1⎛D⎞ 2
Lösung für D = const. : ϕ (t ) = ⎜ ⎟ t + ω t + ϕ 0
2⎝ I ⎠
äquivalent zu linearer, beschleunigter Bewegung in x
28
Drehschwingungen um feste Achse
Annahme : Rückstellmoment sei proportional
zur Auslenkung aus der Ruhelage
vergleiche Hook‘sches Gesetz
der linearen Bewegung :
Ö Bewegungsgleichung :
F = −D x
D = − Dr ϕ
Ri ht
Richtmoment
t Dr
I 0 ϕ&& = − Dr ϕ
mit dem Trägheitsmoment I0 des Drehtisches
Ö
Dr
2
&
&
ϕ = − ϕ ≡ α ϕ
I0
Lö
Lösung
der
d Schwingungs-Gleichung
S h i
Gl i h
:
ϕ (t ) = ϕ 0 sin (α t )
mit Amplitude ϕ0 und Eigenfrequenz α
29
Schwingungsdauer :
1
2π
I0
T0 =
=
= 2π
ν
α
Dr
Ö bei bekanntem Rückstellmoment Dr kann aus Messung der Schwingungsdauer T0 das
Trägheitsmoment I0 berechnet werden; oder : bei bekanntem Trägheitsmoment I0 des leeren
Drehtisches kann aus Messung von T0 das Rückstellmoment Dr berechnet werden; wird eine
unbekannte Masse I1 auf den Drehtisch gelegt (Ö gesamtes Trägheitsmoment I0+I1), kann aus
Messung von T1 und zuvor bestimmten Dr das unbekannte Trägheitsmoment I1 berechnet werden
nach
h:
I 0 + I1
T1 = 2π
Dr
30
Hauptachsen für Trägheitsmomente
betrachte einen Körper mit Rotationsachse ω durch den Schwerpunkt;
das Trägheitsmoment hängt von der Richtung der Drehachse ab
ω
ωinter
ωmin
i
z
y
x
ωmax
wir werden im Folgenden finden : es
gibt eine Achse ωmax (bzw. ωmin) bzgl.
d
derer
d
das
T ä h it
Trägheitsmoment
t maximal
i l
(bzw. minimal) wird; für eine beliebige
Achse ωmax, die senkrecht auf ωmax und
ωmin steht, liegt das Trägheitmoment
zwischen Imax und Imin; die Achsen ωmax,
ωmin stehen
t h senkrecht
k ht aufeinander;
f i d
31
Mathematische Zwischenbemerkung : Wichtige Vektorbeziehungen
(relevant für die folgende Diskussion)
(
r r r r r r r
D = A× B × C = A× B × C
)
(
r r r
r
D ⊥ A, B × C
Ö
)
Annahme : B und C spannen eine Ebene (x,y)
(x y) auf
aus :
r
xˆ || B ⊥
r
yˆ || C ⊥
(
(
r r
B×C
r r
B×C
)
)
Ö
(
r r
zˆ || B × C
Ö D muss in der (x
(x,y)
y)-Ebene
Ebene liegen Ö
Rechnung zeigt :
)
r
r
r
D = λB B + λC C
( ) ( )
r r r rr r
r r r r
D = A × B × C = AC B − AB C
32
Allgemeines zum Trägheitsmoment
Beitrag eines Massenelements dmi zum Drehimpuls Li :
r
r r
r r
r
dLi = dmi (ri × vi ) = dmi [ri × (ω × ri )]
r
A
Umformung mit der zuvor
hergeleiteten Vektor-Relation liefert :
[
r r
B C
[
r
r r r
2 r
dLi = dmi ri ω − (ri ω ) ri
]
]
r
rr r r
2 r
Ö Gesamtdrehimpuls : L = r ω − (r ω ) r ρ (r ) dV
∫
in ausführlicher
Schreibweise :
r
r
r r
2 r
L = ∫ r ω ρ (r ) dV − ∫ (x ω x + y ω y + z ω z ) r ρ (r ) dV
…daraus lassen sich die Komponenten Lx, Ly, Lz direkt berechnen
33
es folgt für die x-Kpt. :
Ö
Lx = ω x
∫ (r
2
[
]
Lx = ∫ r 2ω x − (x ω x + y ω y + z ω z ) x ρ dV
)
− x ρ dV − ω y ∫ xy ρ dV − ω z ∫ xz ρ dV
2
die Struktur der Gleichung
suggeriert die Form :
Lx = ω x I xx + ω y I xy + ω z I xz
I xx =
Vergleich der
Koeffizienten ergibt :
I xy =
I xxz =
∫ (r − x ) ρ dV
− ∫ xyy ρ dV = I
− ∫ xz ρ dV = I
2
2
yx
zxx
…entsprechende
entsprechende Gleichungen ergeben sich für Ly, Lz bzw.
bzw Iyy. Izz, Iyz
34
zusammengefasst
erhält man :
Lx = I xx ω x + I xy ω y + I xz ω z
Ly = I yx ω x + I yy ω y + I yz ω z
Lz = I zx ω x + I zy ω y + I zz ω z
Ö in Matrixform :
r ~r
L=Iω
beachte : I ist eine Matrix
mit dem Trägheitstensor I
⎛ I xx
~ ⎜
I = ⎜ I yx
⎜I
⎝ zx
I xy
I yy
I zy
I xz ⎞
⎟
I yz ⎟
I zz ⎟⎠
Ö bei beliebiger Drehachse tragen alle Trägheitsmomente Ijk zu Drehimpuls bei
Anmerkung:
r ~ r
A=M B
beschreibt Transformation von Vektor B
durch Matrix M in Vektor A
35
Mathematische Zwischenbemerkung : Abbildung mittels eines Tensors (Matrix)
speziell :
⎛ a '1 ⎞ ⎛ 1 0 0 ⎞ ⎛ a1 ⎞
⎜ ⎟ ⎜
⎟⎜ ⎟
⎜ a '2 ⎟ = ⎜ 0 1 0 ⎟ ⎜ a2 ⎟
⎜ a' ⎟ ⎜ 0 0 1 ⎟ ⎜ a ⎟
⎝ 3⎠ ⎝
⎠⎝ 3 ⎠
speziell :
⎛ a '1 ⎞ ⎛ b 0 0 ⎞ ⎛ a1 ⎞
⎜ ⎟ ⎜
⎟⎜ ⎟
⎜ a '2 ⎟ = ⎜ 0 b 0 ⎟ ⎜ a2 ⎟
⎜ a' ⎟ ⎜ 0 0 b ⎟ ⎜ a ⎟
⎝ 3⎠ ⎝
⎠⎝ 3 ⎠
allgemein :
⎛ a'1 ⎞ ⎛ M xx
⎜ ⎟ ⎜
⎜ a'2 ⎟ = ⎜ M yx
⎜ a' ⎟ ⎜ M
⎝ 3 ⎠ ⎝ zx
M xy
M yy
M zy
r r
a' = a
Identität
Streckung
M xz ⎞ ⎛ a1 ⎞
⎟⎜ ⎟
M yz ⎟ ⎜ a2 ⎟
⎟
M zz ⎠ ⎜⎝ a3 ⎟⎠
r
r
a' = b a
Drehung & Streckung
36
Lx = I xx ω x + I xy ω y + I xz ω z
z
L
Ly = I yx ω x + I yy ω y + I yz ω z
ω
Lz = I zx ω x + I zy ω y + I zz ω z
y
Ö die
di Beziehung
B i h
zeigt,
i dass
d i.d.R.
idR
L und ω nicht parallel zueinander sind
Frage : wann liegt L parallel zu ω ?
Lösung : z.B.
dann gilt :
x
alle Nichtdiagonal-Elemente Iik = 0 (i ≠ k)
und
d Di
Diagonal-Elemente
l El
Ixx = Iyy = Izz = I
Ö Körper muss offensichtlich Symmetrie besitzen
r
r
L = Iω
mit dem skalaren Wert I
37
Anmerkung zum Trägheits-Tensor :
⎛ I xx
~ ⎜
I = ⎜ I yx
⎜I
⎝ zx
I xy
I yy
I zy
I xz ⎞
⎟
I yz ⎟
I zz ⎟⎠
gibt Zusammenhang an zwischen Drehimpuls L und
Winkelgeschwindigkeit ω für gegebenen Körper in
gegebenen
b
K di
Koordinatensystem
KS (x,y,z)
(
)
Ö Drehung des Koordinatensystems ändert die Werte im Tensor
g : math. Darstellungg einer Matrix hängt
g von Wahl der Einheitsvektoren ab
vgl.
Ö es gibt ein Koordinatensystem KS‘ (x‘,y‘,z‘),
in der der Trägheits-Tensor diagonal wird :
Ö in KS
KS‘ gilt dann :
⎛ I x'x'
~ ⎜
I =⎜ 0
⎜ 0
⎝
0
I y'y'
0
0 ⎞
⎟
0 ⎟
I z ' z ' ⎟⎠
Lx ' = I x ' x ' ω x '
Ly ' = I y ' y ' ω y '
Lz ' = I z ' z ' ω z '
38
► eine Transformation T, die Einheitsvektoren in KS so nach KS‘ überführt,
dass der Trägheits-Tensor diagonal wird, heißt Hauptachsentransformation
KS
→ KS '
T
Ö
⎛ I xx
⎜
⎜ I yx
⎜I
⎝ zx
I xy
I yy
I zy
I xz ⎞
⎛ I x'x'
⎟
⎜
I yz ⎟ → ⎜ 0
T
⎟
⎜ 0
I zz ⎠
⎝
0
I y'y'
0
0 ⎞
⎟
0 ⎟
I z ' z ' ⎟⎠
mathematische Analyse ergibt :
► die Hauptachsen sind Symmetrie-Achsen des Körpers
► bzgl. der Hauptachsen wird der Trägheitstensor diagonal
Ö jede
j d Komponente
K
Li des
d D
Drehimpulses
hi
l in
i KS‘ iist ddann
proportional zur Komponente ωi der Winkelgeschwindigkeit :
Li = I ii ωi
39
Beispiel : Symmetrieachsen (Hauptachsen) eines Quaders
z'
z
y'
y
x
x'
40
Trägheitsellipsoid
Rotationsenergie bei
beliebiger Drehung :
r r r r
1
1
2
Δmi vi = Δmi (ω × ri )(ω × ri )
2
2
wir nutzen die Beziehung :
mit :
Ö
(
)(
)
( )
r r r r
rr
2 2
A × B A × B = A B − AB
( )
rr 2
2 2
2
2 2
2
AB = A B sin ϑ = A B 1 − cos ϑ
(
[
r 2 r2 r r 2
1
1
2
Δmi vi = Δmi ω ri − (ω ri )
2
2
2
)
]
Integration über alle Massenelemente liefert die gesamte Rotationsenergie :
Erot
1
=
2
[
]
r2
r 2 r2 r r 2
ω
∫ ω r − (ω r ) dm = 2
r2
1
∫ r dm − 2
rr 2
∫ (ω r ) dm
41
Beträge der einzelnen Komponenten ausgeschrieben :
Erot =
(ω
2
x
+ ω y2 + ω z2
2
)
r2
1
∫ r dm − 2
∫ (ω x + ω
x
y + ω z z ) dm
2
y
aus-muliplizieren und sortieren der Terme liefert :
Erot =
ω
2
x
2
∫ (r
2
)
− x 2 dm +
ω y2
2
∫ (r
2
)
− y 2 dm +
− ω xω y ∫ xy dm − ω xω z ∫ xz dm − ω yω z
ω z2
2
∫ (r
2
)
− z 2 dm
∫ yz dm
wir identifizieren die Elemente Ijk des Trägheitstensors
g
und schreiben :
Erot =
ω
2
x
2
I xx +
+ ω xω y I xy
ω
2
y
2
I yy +
ω
2
z
I zz
2
+ ω xω z I xz + ω yω z I yz
42
betrachte :
Erot =
ω
2
x
2
I xx +
+ ω xω y I xy
formal lässt sich die
Gleichung schreiben als :
mit
i :
ω = (ω x , ω y , ω Z )
rT
Erot
ω y2
2
I yy +
ω z2
I zz
2
+ ω xω z I xz + ω yω z I yz
1 rT ~ r
= ω Iω
2
⎛ I xx
~ ⎜
; I = ⎜ I yx
⎜I
⎝ zx
I xy
I yy
I zy
I xz ⎞
⎛ ωx ⎞
⎟
r ⎜ ⎟
I yz ⎟ ; ω = ⎜ ω y ⎟
⎟
⎜ω ⎟
I zz ⎠
⎝ Z⎠
Ö i.a.
i tragen
t
alle
ll Trägheitsmomente
T ä h it
t Ijk zur Rotationsenergie
R t ti
i bei
b i
43
es sei eine beliebige Drehachse ω gewählt; die Richtung der Drehachse ist
durch Winkel α,β,γ bzgl. der x,y,z-Achsen festgelegt
Ö Komponenten der
Winkelgesch indigkeit :
Winkelgeschwindigkeit
z
ω
γ
ω x = ω cos α
ω y = ω cos β
y
β
α
ω z = ω cos γ
x
Ö eingesetzt
i
in
i die
di Formel
F
l für
fü die
di Rotationsenergie
R i
i
Erot =
ω
2
x
2
I xx +
+ ω xω y I xy
ω
2
y
2
I yy +
ω
2
z
I zz
2
+ ω xω z I xz + ω yω z I yz
44
(ω cos α )
2
Erott =
(ω cos β )
2
I xx +
2
2
+ (ω cos α )(ω cos β ) I xy
(ω cos γ )
2
I yy +
2
I zz
+ (ω cos α )(ω cos γ ) I xz
+ (ω cos β )(ω cos γ )z I yz
liefert durch Vergleich mit :
Erot
1
= I ω (α , β , γ )ω 2
2
das Trägheitsmoment bzgl.
bzgl der Achse ω,
ω in Abhängigkeit von α,β,γ
αβγ:
I ω (α , β , γ ) = I xx cos 2 α + I yy cos 2 β + I zz cos 2 γ
+ 2 I xy cos α cos β + 2 I xz cos α cos γ + 2 I yz cos β cos γ
beachte : Iω(α,β,γ) ist eine skalare Größe
45
z.B. Spezialfälle :
⎛π π ⎞
I ω1 ⎜ , ,0 ⎟ = I zz
⎝2 2 ⎠
⎛π π ⎞
I ω2 ⎜ ,0, ⎟ = I yy
2⎠
⎝2
⎛ π π⎞
I ω3 ⎜ 0, , ⎟ = I xx
⎝ 2 2⎠
⎛π π π ⎞ 1
(I xx + I yy )
I ω4 ⎜ , , ⎟ =
2
⎝4 4 2⎠
z
ω1
y
ω2
ω4
ω3
x
Anmerkung : bei Ausrichtung der Drehachse in ei-Richtung ist nur Iii relevant
Ö man legt das Koordinatensystem (KS) günstigerweise zunächst so,
d di
dass
die Drehachse
D h h mit
i der
d Richtung
Ri h
einer
i Achse
A h des
d KS übereinstimmt
b i i
beachte : bei Einwirkung von Drehmomenten kann sich Richtung der Drehachse ändern !
46
► Richtungen (α,β,γ), unter denen Iω(α,β,γ) Extremwerte annimmt,
heißen Hauptträgheitsachsen
► die zugehörigen Trägheitsmomente heißen Hauptträgheitsmomente
⎛ I xx
⎜
~
I HA = ⎜ 0
⎜ 0
⎝
wir
i hatten
h tt bereits
b it früher
f üh gesehen
h :
► der Trägheitstensor in der Basis
d H
der
Hauptträgheitsachsen
tt ä h it h
ist
i t diagonal
di
l:
0
I yy
0
0⎞
⎟
0⎟
I zz ⎟⎠
d.h. es gilt für alle Nicht-Diagonalelemente : Ixy = Iyz = Izx = 0
eingesetzt in die Formel für Iω(α,β,γ) ergibt sich :
I HA (α , β , γ ) = I xx cos α + I yy cos β + I zz cos γ
2
2
2
TrägheitsT
ä h i
Ellipsoid
Trägheitsmoment für Drehung um Achse ω, die definiert ist über Winkel
((α,β,γ)
,β,γ) bzgl.
g Hauptträgheitsachsen
p g
Ö Iω((α,β,γ)
,β,γ) enthält keine Terme Ijk (j ≠ k))
47
die Rotationsenergie ergibt sich in der Basis der Hauptachsen zu :
Erot
(
1
1
2
= I HA ω = I xxω 2 cos 2 α + I yyω 2 cos 2 β + I zzω 2 cos 2 γ
2
2
1
2
2
2
= I xxω x + I yyω y + I zzω z
2
(
)
)
Ö Bereiche konstanter Rotationsenergie bei Variation der Komponenten ωx,y,z
(bzw der Winkel α,β,γ)
(bzw.
α β γ) sind definiert durch :
Erot
(
1
≡ const. = I xxω x2 + I yyω y2 + I zzω z2
2
)
TrägheitsTrägheits
Ellipsoid
dies ist offensichtlich die Gleichung der Oberfläche einer Ellipse,
g in zwei Dimensionen : R2 = ax2+ byy2
in den Variablen ωx,y,z
x y z ; vgl.
Spezialfall : Ixx = Iyy = Izz = I :
Ö
Erot
(
1
≡ const. = I ω x2 + ω y2 + ω z2
2
)
Ö Gleichung einer Kugel
48
Mathematische Zwischenbemerkung : Hauptachsentransformation
Bestimmung der Hauptachsentransformation :
⎛ I xx
⎜
⎜ I yx
⎜I
⎝ zx
I xy
I yy
I zy
I xz ⎞
⎛ I x'x'
⎟
⎜
I yz ⎟ → ⎜ 0
T
⎜ 0
I zz ⎟⎠
⎝
0 ⎞
⎟
0 ⎟
I z ' z ' ⎟⎠
0
I y'y'
0
wir suchen die Einheitsvektoren in einem Koordinatensystem KS‘, so dass die
Trägheitsmatrix (Tensor) in diesem Koordinatensystem Diagonalform hat
Ö Suche
S h nach
h Ei
Eigenwerten undd Eigenvektoren
Ei
k
einer
i
Matrix
M i
Eigenwerte
g
((Hauptträgheitsmomente)
p g
)
ergeben sich aus der Eigenwertgleichung :
r
~r
I eH = I H eH
(
)
~
~ r
Ö I − I H E eH = 0
(
)
~
~
Ö det I − I H E = 0
49
⎛ I xx − I H
⎜
Ö det ⎜ I yx
⎜ I
zx
⎝
I xy
I yy − I H
I zy
⎞
⎟
⎟=0
⎟
I zz − I H ⎠
I xz
I yz
ÖPolynom 3.
3 Grades Ö 3 Lösungen für IH
Ö Hauptträgheitsmomente Ix‘x‘ , Iy‘y‘ , Iz‘z‘
A
Anmerkung
k
: meist
i t Benennung
B
der
d Hauptträgheitsmomente
H tt ä h it
t mit
it Ia , Ib , Ic
Die drei Eigenvektoren (Hauptträgheitsachsen)
ergeben sich nach Einsetzen der drei Lösungen für
IH in die Eigenwertgleichung Ö 3 Gleichungen für
3 Vektorkomponenten
V kt k
t jedes
j d Eigenvektors
Ei
kt
r
~r
I e H , a = I a eH , a
r
~r
I eH ,b = I b eH ,b
r
~r
I eH , c = I c eH , c
50
Benennung der Hauptträgheitsachsen (a,b,c) :
Konvention :
Ia ≤ Ib ≤ Ic
unter Bezug auf die Hauptachsen wird :
I HA (α , β , γ ) = I a cos 2 α + I b cos 2 β + I c cos 2 γ
⎛ La ⎞ ⎛ I aωa ⎞
r ⎜ ⎟ ⎜
⎟
Ö Drehimpuls : L = ⎜ Lb ⎟ = ⎜ I bωb ⎟
⎜L ⎟ ⎜I ω ⎟
⎝ c⎠ ⎝ c c⎠
51
für die Energie ergibt sich :
Ö
Erot
Erot
(
1
2
2
2
= I aωa + I bωb + I cωc
2
L2a
L2b
L2c
=
+
+
2I a 2Ib 2I c
)
Rotationsenergie
asymmetrischer Kreisel : Ia ≠ Ib ≠ Ic
symmetrischer Kreisel : Ia = Ib oder Ib = Ic oder Ia = Ic
beachte : jeder rotations-symmetrische Körper ist ein symmetrischer Kreisel
aber : nicht jeder symmetrische Kreisel muss Rotationssymmetrie besitzen
(z.B. Würfel ist symmetrischer Kreisel, besitzt aber keine Rotationssymmetrie)
Spezialfall : Ia = Ib = Ic = I Ö
S hä i h Kreisel
Sphärischer
K i l
Erot
r2
1 2
L
2
2
=
La + Lb + Lc =
2I
2I
(
)
52
Beispiele : Asymmetrische Kreisel
Quader mit a = b > c
es gilt für den Quader :
Ia < Ib < Ic
auch
h iim dreiatomigen,
d i t i
nicht-linearen Molekül gilt :
Ia ≠ Ib ≠ Ic
53
Beispiele : Symmetrische Kreisel
Quader mit a = b > c
prolater
l t Kreisel
K i l
oblater
bl t Kreisel
K i l
Ia < Ib = Ic
Ia = Ib < Ic
54
Erot
(a)
L2a
L2b
L2c
=
+
+
2I a 2Ib 2I c
Trägheitsellipsoid
g
p
(b)
(a) Trägheitsellipsoid für den prolaten Kreisel. Das Trägheitsellipsoid ist ein lang gestrecktes
Rotationsellipsoid, dessen Symmetrieachse z länger ist als sein Durchmesser. (b)
Trägheitsellipsoid für den oblaten Kreisel.
Kreisel Das Trägheitsellipsoid ist ein gestauchtes
gesta chtes
Rotationsellipsoid. Anmerkung : für einen sphärischen Kreisel ist das Trägheitsellipsoid eine
55
Kugel, d.h. Trägheitsmoment und Rotationsenergie sind für jede Rotations-Richtung gleich
Beispiel : Hantelmodell eines linearen, zweiatomigen Molekül
c
b
a
Hauptachsen
Ib = Ic = I Ö sym. Kreisel
und : Ia << Ib,c
Ö
Erot ,a
2
a
L2b ,c
L
=
>>
= Erot ,b ,c
2I a
2I
Ö man braucht
b
h viel
i l (thermische)
(h
i h ) Energie,
E
i um Rotation
R i um Achse
A h a anzuregen
Ö Rotation um a ist bei nicht extrem hohen Temperaturen „eingefroren“
Ö es wird kein Drehimpuls bzgl
bzgl. der Achse a angeregt Ö La → 0
Ö
Erot
(
1 2
2
≈
Lb + Lc
2I
)
r2
L
≈
2I
Rotation eines zweiatomigen Moleküls
wird
i d durch
d h Ib = Ic = I und
d
Gesamtdrehimpuls L beschrieben
56
Rotation um freie Achsen
bisher betrachtet : Rotation um fest fixierte Drehachse
jetzt : Rotation um eine freie (d.h. nicht im Körper fixierte) Achse
► experimentell zeigt sich,
sich dass Rotation um die Achsen des kleinsten und größten
Trägheitsmoments stabil ist, während bei Rotation um andere Achsen kleinste
Störungen zu Instabilitäten (d.h. Torkel-Bewegungen, Umkippen der Achse) führen
(a)
(b)
(c)
Betrachte Rotation eines Quaders (asym. Kreisel), der an Faden aufgehängt ist; (a) stabile Rotation um
Achse größten Trägheitsmoments Ia; (b) instabile Rotation um Achse des mittleren Trägheitsmoments Ib ; (c)
57
Rotation (b) springt um in sehr stabile Rotation um Achse mit dem größten Trägheitsmoment Ic
Eine geschlossene Kette hängt an
einem Faden und wird zur Rotation
gebracht. Durch die Zentrifugalkraft
weitet sie sich zu einem Kreis auf, der
sich dann horizontal stellt,
stellt weil
dadurch die Rotation um die Achse
des
größten
Trägheitsmomentes
erfolgt und damit die Rotationsenergie
bei vorgegebenem Drehimpuls L
minimal wird. Auch hier fällt die
Rotationsachse
nicht
mit
der
Fadenrichtung zusammen.
ω
► Körper hat Tendenz zu Rotation um
Achse mit größtem Trägheitsmoment
FZF
Ö Rotationsenergie Erot ∼1/I wird minimal
kleinste Störungen führen dazu, dass
der Körper (z.B. durch Zentrifugalkräfte) in diese Lage getrieben wird
FZF
58
Euler‘sche Gleichungen
wenn Drehimpuls
p und Drehachse nicht p
parallel sind,,
dann ist die Bewegung des Körpers kompliziert
betrachte Bewegung in raumfesten
Koordinatensystem R :
r
r ⎛ dL ⎞
D = ⎜⎜ ⎟⎟
⎝ dt ⎠ R
das Koordinatensystem
y
K,, das durch Hauptachsen
p
des Körpers
p gebildet
g
wird,,
rotiert mit ω gegenüber dem raumfesten System R
r
r
⎛ dL ⎞
⎛ dL ⎞
r r
⎟ =⎜ ⎟ − ω×L
Ö ⎜⎜
⎟
⎜ dt ⎟
dt
⎝ ⎠K ⎝ ⎠R
(
r
r ⎛ dL ⎞
r r
⎟ + ω×L
Ö D = ⎜⎜
⎟
dt
⎝ ⎠K
(
)
)
59
betrachte z.B. Komponente Da des Drehmoments im Bezug auf Hauptachsen :
r
⎛ dL ⎞
r r
dI aωa ⎞
⎛
Da = ⎜⎜ ⎟⎟ + ω × L a = ⎜
⎟ + (ωb Lc − ωc Lb )
⎝ dt ⎠
⎝ dt ⎠ a
(
)
= I a ω& a + ωcωb (I c − I b )
ähnliche Gleichungen ergeben sich für Db und Dc
Ö
Da = I a ω& a + ωcωb (I c − I b )
Db = I b ω& b + ωaωc (I a − I c )
Dc = I c ω& c + ωbωa (I b − I a )
Euler sche
Euler‘sche
Gleichungen
► die
di Euler‘schen
E l ‘ h
Gl i h
Gleichungen
b h ib
beschreiben
di Variation
die
V i ti
d Rotation
der
R t ti
(Richtung und Geschwindigkeit) einer beliebigen Drehbewegung bei Wirkung
eines externen Drehmoments D (bei kräftefreier Bewegung ist D = 0); die
Beschreibung erfolgt im Koordinatensystem der Hauptachsen
60
Beispiel : Kräftefreier, sphärischer Kreisel
mit :
Da = Db = Dc = 0
und :
Ia = Ib = Ic = I
0 = I a ω& a + ωcωb (I c − I b ) = I ω& a
Ö 0 = I b ω& b + ω aωc (I a − I c ) = I ω& b
0 = I c ω& c + ωbωa (I b − I a ) = I ω& c
Ö die Drehachse bleibt in Richtung und Geschwindigkeit gleich
(keine zeitliche Veränderung der ωa,b,c)
beachte : für einen asymmetrischen Kreisel entstehen 3 gekoppelte DifferentialGleichungen für ωa,b,c
a b c Ö komplizierte Variation der Rotation
61
Beispiel : Wackelsteine
► die Rotation eines beliebig
g geformten
g
Körpers
p kann äußerst kompliziert
p
sein
(wie auch schon die Komplexität der Euler‘schen Gleichungen zeigt)
z b beim keltischen Wackelstein
z.b.
Der keltische Wackelstein besteht aus einem zehn bis zwanzig Zentimeter
langen, an der Unterseite ellipsoid geformten Stück Stein, Holz, Plastik
oder anderem Material. Dreht man einen auf der abgerundeten Seite
liegenden Wackelstein auf einer ebenen Unterlage, so zeigt er je nach
Drehrichtung ein unterschiedliches Verhalten: In einer Richtung dreht
sich
i h der
d Wackelstein
W k l i stabil,
bil bis
bi er durch
d h Reibung
R ib
zum Stehen
S h kommt.
k
I
In
der anderen Drehrichtung wird der Wackelstein jedoch rasch langsamer,
wobei er entlang der Längsachse zu wackeln anfängt. Nachdem die
D h
Drehung
k
komplett
l tt in
i eine
i Wackelschwingung
W k l h i
üb
übergegangen
i t fängt
ist,
fä t
der Wackelstein an, entgegengesetzt seiner ursprünglichen Drehrichtung
zu rotieren. Erklärung des Verhaltens (nur qualitativ) : Die Masse eines
Wackelsteins ist ungleich verteilt,
verteilt was durch Formgebung,
Formgebung oder
eingelassene/aufgesetzte Gewichte erreicht wird. Die entstehende
Unwucht sorgt für die Wackelbewegung. Während jeder Schwingung
kippt der Wackelstein leicht in Richtung seines Übergewichts,
Übergewichts so dass
eine Drehung in seine Vorzugsrichtung stattfindet.
62
Dynamik des kräftefreien, symmetrischen Kreisels
der sym.
sym Kreisel weist drei relevante Achsen/Richtungen auf :
Richtung des Drehimpulses L, momentane Drehachse ω, Figurenachse c
► kein
k i äußeres
ä ß
Drehmoment
D h
t (D = 0) Ö dL/dt = 0 Ö Vektor
V kt L ist
i t raumfest
f t
► wenn c die Symmetrieachse ist, dann ist Ia = Ib
► wenn ω in Richtung der HauptHaupt und Figuren-Achse
Figuren Achse c liegt,
liegt gilt :
⎛ La ⎞ ⎛ I aωa ⎞ ⎛ 0 ⎞
r ⎜ ⎟ ⎜
⎟ ⎜
⎟
L = ⎜ Lb ⎟ = ⎜ I bωb ⎟ = ⎜ 0 ⎟
⎜L ⎟ ⎜ I ω ⎟ ⎜I ω ⎟
⎝ c⎠ ⎝ c c⎠ ⎝ c c⎠
r
Ö L || cˆ
Ö stabile
t bil Rotation
R t ti um raumfeste
f t Achse
A h
(da Achse c räumlich stabil ist)
b ht : im
beachte
i allgemeinen
ll
i
Fall
F ll ist
i t L nicht
i ht parallel
ll l zu ω
(z.B. wenn alle ωi ≠ 0 und nicht alle Ia,b,c gleich sind)
63
Einwirkung eines Kraftstosses : Nutation
r r r
L || ω || c
es seii anfangs:
f
Schlag gegen Figurenachse c
mit Kraftstoß F⋅dt || x-Achse
z
ω = (ωx, 0,
0 ωz )
L = (Lx, 0, Lz )
L
Lz
Li = Ii ωi
ωz
r r r
dL = r × F dt
r
r : von Ursprung zu Schlagstelle
r
Ö dL || yˆ
r r
r
Ö L ' = L + dL
r r
mit : Lz ' = Lz da : dL ⊥ L
ω
L´
F
dL ωx
y
Lx
x
Ö Kraftstoß ändert Richtung der Figurenachse in x-Richtung
aber : Kraftstoß bewirkt Änderung
g dL in y
y–Richtung
g
Ö Drehimpuls L‘ liegt nicht mehr in xz-Ebene (Figurenachse hingegen schon)
Ö Drehimpuls und Figurenachse (bzw. Drehachse) sind nicht mehr parallel 64
Frage : Wie läuft Bewegung nach dem Schlag weiter ab ?
nach dem Schlag:
g Drehimpuls
p L’ nicht mehr p
parallel zu ω bzw. c
aber : Drehimpuls L‘ ist wieder zeitlich konstant (da Erhaltungsgröße)
z´= c
z L´
ωz
ω
L´
L
ωc
ω
Drehung des Koordinatensystems bis Drehimpuls L‘
in z´x´-Ebene
´ ´ Eb
l
liegt
:
y
dL ωx
L´c
L
x
y´
L´⊥
Momentaufnahme
:
r
ω⊥
x´
c || zˆ '
65
wir betrachten jetzt die Komponenten L´c (d.h. L´ ⇈ c) und L´⊥ (d.h. L´ ⊥ c)
Ö die Drehimpulskomponenten
beschreiben Komponenten der Rotation :
r r
Lc ' || ωc
r r
; L⊥ ' || ω⊥
Drehungen entsprechend L´c und L´⊥
müssen so koordiniert ablaufen, dass gilt :
z´
L´c
ωc
L´
ω
r r
r
Lc '+ L⊥ ' = L ' = const.
y´
L´⊥ ω⊥
L
x´
66
Versuche, das korrekte Verhalten von L´⊥ und L´c zu „erraten“ :
betrachte Drehung von L´c,
während L´⊥ erhalten bliebe
→ Vektor L´ wäre nicht erhalten
betrachte Drehung von L
L´⊥,
während L´c erhalten bliebe
→ Vektor L
L´ wäre nicht erhalten
z´
L´c
L´
L´
L´
y´
L´⊥
x´
67
Versuche, das korrekte Verhalten von L´⊥ und L´c zu „erraten“ :
betrachte synchrone Drehung von L
L´c und L
L´⊥,
so daß Vektor L‘ erhalten bleibt
die Spitzen des Drehimpuls-Vektors L´c
(bzw. Drehachse c) und des DrehimpulsV kt
Vektors
L´⊥ (bzw.
L
(b
D h h
Drehachse
ω))
beschreiben synchron durchlaufene
Kreise zu deren Zentrum L
Kreise,
L´ zeigt
Ö Drehimpuls-Vektor L‘ bleibt erhalten
zz´
L´c
L
L´
Ö (momentane) Drehachse ω
und Figurenachse c
nutieren
ti
um Drehimpuls
D hi
l L
y´
y
L´⊥
x´
68
Ö (momentane) Drehachse ω
und Figurenachse c
nutieren um Drehimpuls L
L´
beachte : unmittelbar sichtbar im Experiment
ist nur die Nutation der Figurenachse, nicht
d momentanen
der
t
D h h
Drehachse
g des Vektors ω ((d.h. die
beachte : die Länge
Rotationsgeschwindigkeit) bleibt bei der
Nutation erhalten Ö Energieerhaltung
z´
L´c
L´
ω
y´
x´
69
Einwirkung eines äußeren Drehmoments : Präzession
► Präzession : Reaktion des Kreisels auf externes Drehmoment,
Drehmoment
z.B. Lagerung außerhalb Schwerpunkt Ö Drehmoment durch Gewichtskraft
Präzession
P
ä
i : Drehimpuls-Vektor
D hi
l V kt L ändert
ä d t
Richtung; Betrag |L| bleibt aber konstant
W. Pauli und N. Bohr beobachten einen
präzedierenden Kreisel (bei der Eröffnung des
Instituts ffür Theoretische Physik
y in Lund,, 1952))
70
wir betrachten den Fall :
r
r : von Ursprung
zum Schwerpunkt
Ö
r r
L || c
r r
r || c
r r r r
r
D = r × F = r × Mg wirkt ständig
r r
Ö ständige Änderung
des Drehimpulses
p
: dL ∝ D ≠ 0
r r r r r r
dL ⊥ r ; dL ⊥ F ; dL ⊥ L
Ö Richtungsänderung
von des
d D
Drehimpulses
hi
l L
Ö Bewegung von L auf Kreis : Präzession
z
L
S
r
y
dL
x
F
71
r r
r
D = r × Mg
dϕ
z
D = Mgr sin α
r r
r r
dL = D dt ⊥ r , g
r
dL = L' dϕ = L sin
i α dϕ
Ö
α
dL
y
r
F
beachte : ωP ≠ Kreiselfrequenz ωK
D Mgr sin α Mgr
ωP = =
=
L'
L sin
i α
I ωK
dL
S
D = L& = L' dϕ& = L ' ω P
mit Präzessionsfrequenz ωP
Ö
L
dϕ
dL
x
L sin α
PräzessionsFrequenz
72
Beispiel : Präzession der Erdachse
Die Erde hat keine exakte Kugelform, sondern
p
g des Erdellipsoids
p
einen
durch die Abplattung
„Äquatorwulst“ von 21 km. Dadurch bewirken
die Gezeitenkräfte von Mond und Sonne ein
Drehmoment
Drehmoment,
welches
die
Erdachse
aufzurichten versucht und zur Präzession der
Erdachse führt (lunisolare Präzession). Für
einen
i
vollen
ll
K l l f benötigt
Kegelumlauf
b öti t die
di
Erdachse ca. 25.750 Jahre (Platonisches Jahr).
Die Erdpräzession (d.h. Variation der Richtung
der Erdachse) kann man z.B. in der scheinbaren
Wanderung von Fix-Sternen (z.B. NordPolarstern)) beobachten.
http://www.greier-greiner.at/hc/praezession.htm
73
Beispiel : Präzession in der Quantenmechanik (Ausblick)
Kern
El kt
Elektron 1
1
Elektron 2
Elektron 2
► Atomkern besitzt Eigen-Drehimpuls (Kernspin) I
► Elektronen
El kt
besitzen
b it
Bahn-Drehimpuls
B h D hi
l L undd Eigen-Drehimpuls
Ei
D hi
l (Spin)
(S i ) S
* Drehbewegung
g g ggeladener Teilchen bewirken Ströme Ö magnetische
g
Momente
* andererseits erzeugen Drehbewegungen (bzw. Ströme) auch Magnetfelder
Ö Magnetfelder
M
tf ld undd magnetische
ti h Momente
M
t wechselwirken
h l i k miteinander
it i d
Ö verschiedene Drehimpulse wechselwirken miteinander Ö Präzession
(messbar als Verschiebungen/Aufspaltungen von Orbital-Energien bzw.
bzw Übergängen)
74
Beispiel : Kreiseldynamik am Fahrrad
…ermöglicht
ermöglicht z.B.
z B Steuern eines Fahrrads durch Gewichtsverlagerung
Schwerpunkt
Kraft F = -mg
F
r r
r || F
r
Ö D=0
r
Ö L = const.
75
r
F
r
F
r r r
r
D = r × F ≠ 0 Ö dL ≠ 0
Ö Drehimpuls L ändert Richtung
Ö Verdrehung des Rades Ö Kurve
76
Beispiel : Kardanische Aufhängung
Kreisel
L
► Figurenachse des Kreisels kann in beliebige Richtung gedreht werden; der
p
des Kreisels befindet immer in der Mitte des Kardan-Rahmens
Schwerpunkt
Ö 3D-Aufhängung im Schwerpunkt Ö Kräftefreie Lagerung (egal, welche
Orientierung die Figurenachse des Kreisels in der Aufhängung hat)
77
Beispiel : Kreisel-Kompass
wir betrachten zunächst einen voll kardanisch aufgehängten Kreisel, d.h. die Drehachse
kann sich in drei Dimensionen beliebig einstellen; der Kreisel befinde sich am Äquator;
Ä
Blick längs der Drehachse des Kreisels in Richtung auf den Nordpol; da der Kreisel
kardanisch aufgehängt ist,
ist dreht sich die Plattform mit der Erde Ö kräftefrei
D hi
Drehimpuls
l L
L
L
N
L
N
T = 0 Std
T = 3 Std
T = 6 Std
78
wir fixieren jetzt die Lagerung des Kreisels in einer Richtung/Dimension, so dass die
Verkippung der Kreiselplattform um eine Achse || Erdoberfläche nicht mehr möglich ist
Fixierung einer
Drehachse
Drehmoment D durch
V ki
Verkippung
d Plattform
der
Pl f
Ebene parallel zur
E d b flä h
Erdoberfläche
Fixierung
Achse der Verkippung
parallel zu L → D = 0
L
L
dL = D dt
L + dL
D dt Ö dL Ö Präzession von L
N
D = 0 sobald L⇈Erdachse A
L richtet sich parallel zu A aus
L zeigt immer nach Norden
Ö Kreisel-Kompass
79
Früher Kreisel-Kompass, zerlegt
Moderner Kreiselkompass (Schnitt)
Der Erfinder des Kreiselkompass
H. Anschütz-Kämpfe mit einem
unbekannten Herrn beim Segeln
80