Physik I - htw saar

2.3.5
Dynamik der Drehbewegung
2.3.5.1
Drehimpuls
Drehimpuls
Betrachte einen Massepunkt m mit Geschwindigkeit ~v auf irgendeiner Bahn (es muss keine
Kreisbahn sein); dabei ist ~r der Ort der Massepunkts, betrachtet von einem bestimmten Koordinatenursprung aus.
~ bezüglich dieses Koordinatenursprungs definiert als
Dann ist der Drehimpuls L
~ = m · ~r × ~v = ~r × p~
L
(2.190)
Achtung: Eine Bewegung mit konstantem Drehimpuls muss nicht unbedingt eine Kreisbewegung sein!
Anschauliche Erklärung: wenn ein Beobachter, der am Koordinatenursprung steht, den Kopf drehen
müsste, um den Massepunkt zu verfolgen, dann ist der Drehimpuls ungleich Null!
Drehimpuls bei Kreisbewegung eines Massepunkts
Wenn sich ein Massepunkt auf einer Kreisbahn um den Koordinatenursprung befindet, dann ist
~ = m · ~r × ~v = m · ~r × (~ω × ~r)
L
= m ((~r · ~r) ω
~ − (~r · ω
~ ) ~r)
2
~
L = mr ω
~
(2.191)
Für einen starren Körper mit Trägheitsmoment J (s.u.) gilt
~ =J ω
L
~
Momentane Winkelgeschwindigkeit
Für eine beliebige Bewegung eines Massepunkts lässt sich umgekehrt diemomentane Winkelgeschwindigkeit ω
~ um den Koordinatenursprung angeben:
ω
~ =
~
L
m r2
(2.192)
Anschauliche Erklärung: das ist die Winkelgeschwindigkeit, mit der der Beobachter, der am Koordinatenursprung steht, den Kopf drehen müsste, um den Massepunkt zu verfolgen.
Impuls und Drehimpuls
• Translationsbewegung: der Wert des Impulses p~
p~ = m · ~v
hängt ab von der Geschwindigkeit des Inertialsystems, in dem die Bewegung beschrieben
wird.
~
• Rotationsbewegung: der Wert des Drehimpulses L
~ = m r2 ω
L
~
~ = J ·ω
bzw. L
~
hängt ab von der Geschwindigkeit und der Lage des Koordinatenursprungs (gedachter
Drehpunkt) des Inertialsystems, in dem die Bewegung beschrieben wird.
2-63
2.3.5.2
Drehmoment
Drehmoment
(Vergleich: Die zeitliche Änderung des Impulses ist die Kraft)
~ benötigt:
Zur Änderung des Drehimpulses eines Körpers wird ein Drehmoment M
~
dL
~
=M
dt
(2.193)
Zusammenhang mit Kraft F~ und Abstand ~r vom Drehpunkt:
~
d
dL
=
(~r × p~)
dt
dt
d~r
d~p
=
× p~ + ~r ×
dt
dt
~
= ~v × p~ +~r × F
| {z }
0
~
dL
~ = ~r × F~
=M
(2.194)
dt
Für ein System von Massepunkten bzw. einen starren Körper bedeutet das: die zeitliche Änderung des Drehimpulses ist gleich dem Drehmoment der äußeren Kräfte auf den Körper.
Beispiele aus der Biomechanik
In dem in Abbildung 2.41 gezeigten Beispiel der Hüftgelenke bewirken die Komponenten F~2
der Stützkraft Drehmomente um die Drehpunkte der Oberschenkel A bzw. A’, die zum Spreizen
der Beine führen würden, wenn keine Muskelkräfte dagegen wirken würden. Die Komponenten
F~1 der Gewichtskraft des Rumpfes hingegen bewirken Drehmomente um die Punkte B bzw. B’,
die schlimmstenfalls zum Knochenbruch (Oberschenkelhalsbruch) führen können.
~ 0 des Rumpfes wird durch zwei halb so große Stützkräfte
Abbildung 2.41: (links:) Die Gewichtskraft G
in A und A’ aufgehoben. (rechts:) Die über die Beine übertragenen Stützkräfte F~3 bewirken am Oberschenkelhals eine Druck- und eine Drehmomentbelastung. [Kamke-Walcher]
2-64
Abbildung 2.42: Kaumuskulatur, -kräfte und -drehmomente (schematisch) [Kamke-Walcher]
Drehimpulserhaltungssatz
Wenn auf ein System von Massepunkten bzw. einen starren Körper keine äußeren Drehmomente wirken, d.h. wenn die Vektorsumme der äußeren Drehmomente Null ist, dann bleibt der
(Gesamt-)Drehimpuls nach Betrag und Richtung konstant.
~ =0
M
⇔
~ = const
L
(2.195)
Insbesondere wird der Körper nicht in Drehung versetzt, wenn er vorher in Ruhe war.
Hebelgesetz
Als „Hebelgesetz“ wird der Drehimpulserhaltungssatzes mit zwei Drehmomenten, verursacht
durch zwei Kräfte, die an entgegengesetzten Seiten des Drehpunktes angreifen bezeichnet.
~ =0
M
⇔
~r1 × F~1 + ~r2 × F~2 = 0
(2.196)
Die beiden Drehmomente würden dann einzeln entgegensetzte Drehbewegungen verursachen,
zusammen bleibt das System in Ruhe.
„Kraft × Kraftarm = Last × Lastarm“ (wenn nur die Beträge betrachtet werden); die wesentliche Anwendung liegt darin, dass sich eine große Kraftwirkung („Last“) bei geeigneter Wahl
der Hebelarme auch durch eine kleine Muskel- oder Motorkraft („Kraft“) erzeugen lässt.
Balkenwaage
Bei einer Balkenwaage mit zwei Massen m1 und m2 auf einem horizontalen Balken in Abständen r1 und r2 auf entgegengesetzten Seiten des Drehpunkts gilt dann
~ = ~r1 × F~1 + ~r2 × F~2
M
= (r1 · (+~ex )) × (m1 · g · ~ey ) + (r2 · (−~ex )) × (m2 · g · ~ey )
= (m1 · r1 − m2 · r2 ) g · ~ez
~ =0
damit ist die Bedingung für das Gleichgewicht M
m1 r1 = m2 r2
2-65
(2.197)
2.3.5.3
Starrer Körper
Ein starrer Körper ist ein System von Massepunkten (bzw. eine Dichteverteilung) mit festen
Abständen. Er besitzt
• 3 Translationsfreiheitsgrade (3 Koordinaten von ~v ): Bewegung des Schwerpunktes in den
3 Raumrichtungen
• 3 Rotationsfreiheitsgrade (3 Koordinaten von ω
~ ): Rotation um eine beliebig orientierte
Rotationsachse durch den Schwerpunkt.
Wirkung von Kräften auf einen starren Körper
Äußere Kräfte können an einem starren Körper an verschiedenen Punkten angreifen.
• Translation: die Summe aller äußeren Kräfte ändert den Gesamtimpuls, d.h. die Bewegung des Schwerpunkts.
• Rotation: die Summe der Drehmomente der äußeren Kräfte hängt von der Lage der Angriffspunkte ab.
Kräftepaar
Als Kräftepaar werden zwei entgegengesetzt gleiche Kräfte F~1 und F~2 bezeichnet, die an Orten
~r1 und ~r2 an dem starren Körper angreifen:
F~1 = −F~2
F~1 + F~2 = 0,
(2.198)
Das Kräftepaar ändert also den Gesamtimpuls nicht. Das Drehmoment beträgt
~ = ~r1 × F~1 + ~r2 × F~2 = (~r1 − ~r2 ) × F~1 ,
M
(2.199)
es hängt also nur vom Abstand (~r1 − ~r2 ) zwischen der Angriffspunkten ab, unabhängig von
deren Lage relativ zum Koordinatenursprung oder zum Schwerpunkt.
Ist der Abstandsvektor (~r1 − ~r2 ) parallel zur Richtung der Kräfte, dann wirkt kein Drehmoment!
Statisches Gleichgewicht
Ein (unbewegter) starrer Körper ist im statischen Gleichgewicht wenn
• die Summe aller an ihm angreifenden äußeren Kräfte Null ist
X
F~a = 0
und
• die Summe aller an ihm angreifenden äußeren Drehmomente Null ist.
X
~a = 0
M
(2.200a)
(2.200b)
Auffinden des Schwerpunkts
Wo muß eine einzelne Kraft F~ an einem starren Körper angreifen und wie groß muß sie sein,
damit der starre Körper im statischen Gleichgewicht ist?
Die äußeren Kräfte sind die Gewichtskräfte mi~g der einzelnen Massepunkte und die Kraft F~ :
• Summe der Kräfte muss Null sein
F~ +
N
X
mi~g = 0
i=1
2-66
⇒
F~ = −mges~g
(2.201a)
• Summe der Drehmomente muss Null sein: unbekannter Angriffspunkt ~rx
~rx × F~ +
N
X
~ri × mi~g = 0
(2.201b)
i=1
Die weitere Rechnung ergibt (mges wieder eingesetzt)
!
!
N
N
X
X
~ri × mi~g − ~rx ×
mi ~g = 0
i=1
"
N
X
i=1
!
N
X
−
mi~ri
i=1
!
#
mi ~rx × ~g = 0
i=1
N
X
!
N
X
−
mi~ri
i=1
!
mi ~rx = 0
i=1
N
X
mi~ri
i=1
N
X
~rx =
(2.202)
mi
i=1
Dies entspricht der Definition des Schwerpunkts: (Gleichung 2.124)
Ein starrer Körper ist im statischen Gleichgewicht, wenn er im Schwerpunkt unterstützt bzw.
aufgehängt wird.
Dichteverteilungen
Ein realer starrer Körper ist meist keine Anordnung einzelner Massepunkte, sondern „massiv“
mit einer räumlichen Verteilung der Massendichte %(~r).
Ein infinitesimales Volumenelement dV am Ort ~r hat dann die Masse
dm = %(~r)dV
Die Gesamtmasse ist das Volumenintegral der Dichte über den ganzen Körper
Z
m = %(~r)dV
(2.203)
(2.204)
Der Ort des Schwerpunkts ist
Z
~r%(~r)dV
~rs = Z
(2.205)
%(~r)dV
2-67
Eigendrehimpuls und Bahndrehimpuls
~
Äußere Drehmomente ändern den Gesamtdrehimpuls L
~ =
L
N
X
mi~ri × ~vi
i=1
Der Ort ~ri eines jeden Massepunkts i lässt sich zerlegen in
(~ri − ~rs )
| {z }
~ri =
+
Ort der Masse i relativ zum Schwerpunkt
Damit ist dann
~ =
L
N
X
mi (~ri − ~rs ) × ~vi +
(2.206)
Ort des Schwerpunkts
N
X
i=1
~rs
|{z}
mi~rs × ~vi
(2.207)
i=1
{z
|
}
{z
|
Drehung um den Schwerpunkt
Rest?
}
Der hintere Term lässt sich folgendermaßen umformen
N
X
mi~rs × ~vi = ~rs ×
X
= ~rs ×
X
i=1
mi~vi
i=1
p~i
i=1
= ~rs × p~ges
Das ist das Vektorprodukt aus dem Ortsvektor des Schwerpunkts und dem Gesamtimpuls, d.h.
dem Impuls des Schwerpunkts: also der Drehimpuls des Schwerpunkts. Damit ist der Gesamtdrehimpuls bezüglich irgendeines Koordinatenursprungs
~ =
L
N
X
mi (~ri − ~rs ) × ~vi
+
~rs × p~ges
(2.208)
i=1
|
{z
Gesamtdrehimpuls der
Drehung um den
Schwerpunkt
(Eigendrehimpuls)
}
| {z }
Drehimpuls des
Schwerpunkts um den
Koordinatenursprung
(Bahndrehimpuls)
oder abgekürzt
~ =L
~S + L
~B
L
(2.209)
Beispiel: bei der Bewegung der Erde im Weltraum beschreibt der Bahndrehimpuls die Bahn der
Erde um die Sonne (Koordinatenursprung), der Eigendrehimpuls die Drehung der Erde um ihre
eigene Achse.
2-68
Freie Rotation
Die meisten bis hierhin betrachteten Kreisbewegungen sind „freie Rotationen“, d.h. es wird
nicht (mechanisch) erzwungen, dass die Drehung um eine bestimmte Drehachse erfolgt. (Ausnahme: Hebelgesetz).
Drehung eines starren Körpers um eine Achse
Wenn sich ein starrer Körper mit der Winkelgeschwindigkeit ω = | ω
~ | um eine vorgegebene
Achse (die Richtung von ω
~ ) dreht, dann beschreibt jeder Massepunkt i des starren Körpers eine
Kreisbahn mit (unterschiedlichem) Radius ri um einen Punkt auf dieser Achse mit der gleichen Winkelgeschwindigkeit ω. Sein Drehimpuls bezüglich des Mittelpunkts seiner Kreisbahn
beträgt (vgl. Gl. 2.191)
~ i = mi r2 ω
L
(2.210)
i ~
Die Summe aller dieser Drehimpulse ist allerdings nicht der Gesamtdrehimpuls, da ein solcher
sich immer auf einen gemeinsamen Ursprung bezieht.
Beispiel: Drehung einer symmetrischen Hantel um eine schiefe Achse
Man betrachte eine symmetische Hantel, d.h. zwei gleiche Massen m1 = m2 = m an Orten
~r1 = −~r2 , gemessen relativ zum Schwerpunkt des Systems, die sich um eine Achse durch den
Schwerpunkt, nicht aber durch die beiden Massen dreht. Dann drehen sich beide Massen auf
zwei unterschiedlichen Kreisbahnen.
Der Gesamtdrehimpuls um den Schwerpunkt beträgt
~ =L
~1 + L
~ 2 = m1~r1 × ~v1 + m2~r2 × ~v2
L
wegen der Symmetrie
~ = m~r1 × ~v1 + m(−~r1 ) × (−~v1 )
L
~ = 2L
~ 1 = 2m~r1 × ~v1
L
(2.211)
Dieser Vektor steht senkrecht auf der Ebene aus ~r1 und ~v1 ! Der Ortsvektor ~r1 lässt sich in zwei
Komponenten ~r1 = ~r⊥ + ~rk zerlegen:
• ~r⊥ senkrecht zur Achse (~ω · ~r⊥ = 0): Radius der Kreisbahn bzw. Abstand zur Achse
• ~rk parallel zur Achse (~ω × ~rk = 0): Lage des Kreismittelpunktes auf der Achse
Die Bahngeschwindigkeiten sind dann
~vi = ω × ~ri = ω × ~r⊥
~1 =
L
=
=
=
=
weil ω × ~rk = 0
m ~r⊥ + ~rk × (~ω × ~r⊥ )
m ω
~ ~r⊥ + ~rk · ~r⊥ − ~r⊥ ~r⊥ + ~rk · ω
~
m ω
~ [~r · ~r ] − ~r ~rk · ω
~
⊥2 ⊥ ⊥ m ω
~ r⊥ − ~r⊥ rk ω
2
m r⊥
ω
~ − m ωrk ~r⊥
| {z }
| {z }
konstant k ω
~
(2.212)
(2.213)
dreht sich k ~r⊥
Der Drehimpulsvektor ist nicht parallel zur Drehachse sondern er dreht sich selbst um diese
Achse!
2-69
Unwucht
Damit sich der Drehimpulsvektor dauernd ändert, ist ein Drehmoment nötig:1
~
~ = dL = ω
~ = −2m ω~rk (~ω × ~r⊥ )
M
~ ×L
(2.214)
dt
ansonsten würde sich die Hantel um eine ihrer „natürlichen“ Achsen (s.u.) drehen. Dieses Drehmoment wird – entsprechend einer Zwangskraft – von den Lagern einer realen mechanischen
Achse aufgebracht werden und kann – entsprechend „Kraft = Gegenkraft“ – auch zu einer Abnutzung der Lager führen.
Im mitbewegten Koordinatensystem: Fliehkraft
Betrachtet man die beiden Massen in einem mitrotierenden Koordinatensystem, so erfährt jede
der beiden Massen eine Zentrifugalkraft
F~z = m ω 2~r⊥,i
(2.215)
Diese Zentrifugalkräfte bewirken – mit der hier unbewegten Hantelstange als Hebel – ein Drehmoment um den Lagerpunkt an der Drehachse (vgl. Gl. 2.214)
M = 2m ω 2 r⊥ rk
(2.216)
Die durch dieses Drehmoment bewirkte Drehung würde – so lange nicht durch die Achslagerung verhindert – die Hantelstange senkrecht zur Drehachse ausrichten, so dass beiden Massen
auf dem gleichen Kreis rotieren würden.
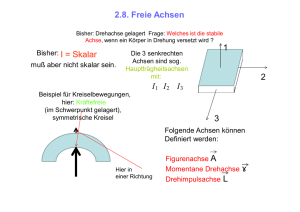
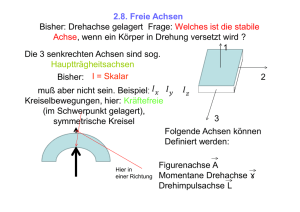
Hauptachsen
Jeder starre Körper besitzt drei ausgezeichnete Drehachsen durch den Schwerpunkt die als
Hauptachsen oder freie Achsen bezeichnet werden.
• Es liegt dann der Drehimpulsvektor parallel zur Drehachse, d.h. parallel zum Winkelgeschwindigkeitsvektor
~ k ω
L
~
~ = Ji ω
L
~
•
•
•
•
(2.217)
Ji ist das Hauptträgheitsmoment für die i-te Hauptachse
Es wirken dann keine Drehmomente, die eine Veränderung der Drehachse zu bewirken
suchen.
Eine solche Drehung ist also stabil und muss nicht durch Zwangskräfte (Achslager) erzwungen werden.
Die Hauptachsen sind häufig auch die Symmetrieachsen des Körpers
Durch „Auswuchten“ (Anbringen zusätzlicher kleiner Massen) versucht man zu erreichen, dass eine gewünschte Drehachse auch eine Hauptachse ist.
1
die Drehung eines beliebigen Vektors um den Winkelgeschwindigkeitsvektor ω
~ kann durch ein solches Vektorprodukt beschrieben werden, vgl. Gl. 2.49, ansonsten berechne man die Ableitung von Gl. 2.213 und vergleiche
~
das Ergebnis mit ω
~ ×L
2-70
Trägheitstensor
Für beliebige Lage der Drehachse ω
~ ist der Drehimpulsvektor eines Massepunktes i
~ = m · ~ri × ~vi
L
= m · ~ri × (~ω × ~ri )
= m · ri2 · ω
~ − (~ω · ~ri ) ~ri
(2.218)
In Koordinaten, Beispiel z-Komponente
Lz = m x2i + yi2 + zi2 ωz − (ωx xi + ωy yi + ωz zi ) zi
= m x2i + yi2 ωz − xi zi ωx + yi zi ωy
Der Drehimpulsvektor eines starren Körpers bei beliebiger Lage der Drehachse ω
~ ist
~ = J~ω
L
mit dem Trägheitstensor (Matrix) J


 
 2
ωx
yi + zi2 −xi yi
−xi zi
X
~ =
L
mi  −yi xi x2i + zi2 −yi zi   ωy 
i
ωz
−zi xi
−zi yi x2i + yi2
{z
}
|
(2.219)
(2.220)
Trägheitstensor J
z.B. die z-Komponente
Lz =
X
mi −zi xi ωx − xi yi ωy + x2i + yi2 ωz
i
Hauptachsentransformation
Die drei Hauptträgheitsachsen (1, 2, 3)stehen senkrecht aufeinander und bilden selbst ein Koordinatensystem mit den Einheitsvektoren ~e1 , ~e2 , ~e3 in Richtung der Hauptachsen. Durch Drehungen lässt sich das ursprüngliche Koordinatensystem (x, y, z) mit dem Schwerpunkt als Nullpunkt in dieses Koordinatensystem transformieren. Der Winkelgeschwindigkeitsvektor besteht
dann aus den Komponenten in Richtung der Hauptachsen
ω
~ = ω1~e1 + ω2~e2 + ω3~e3
(2.221)
Der Trägheitstensor hat in diesem Koordinatensystem die besonders einfache Form einer Diagonalmatrix:


J1 0 0
~ =  0 J2 0  ω
L
~
(2.222)
0 0 J3
(vgl. Gl. 2.217)
• Sind die Trägheitsmomente von zwei Hauptträgheitsachsen gleich, dann sind alle möglichen Drehachsen durch den Schwerpunkt, die in der Ebene dieser beiden Achsen liegen,
ebenfalls Hauptträgheitsachsen. (z.B. Zylinder oder Hohlzylinder)
• Sind alle Trägheitsmomente gleich, dann sind alle möglichen Drehachsen durch den
Schwerpunkt Hauptträgheitsachsen. Der Trägheitstensor ist dann eine Einheitsmatrix,
multipliziert mit diesem Trägheitsmoment. (z.B. Würfel, Kugel oder Kugelschale)
Siehe Tabelle 2.1
2-71
1
m(ra2 + ri2 )
2
1
m ra2 + ri2 + 13 l2
4
Hohlzylinder
Jx =
Jy = Jz =
dünnwandiger Hohlzylinder
Jx = mr2
Jy = Jz = 41 m 2r2 + 13 l2
Vollzylinder
Jx =
Jy = Jz =
1
mr2
2
1
mr2
4
dünne Scheibe (l r)
Jx =
Jy = Jz =
1
mr2
2
1
mr2
4
dünner Stab (l r)
unabhängig von der
Form des Querschnitts
Jx =
Jy = Jz =
1
mr2
2
1
ml2
12
dünner Ring
Jx = mr2
Jy = Jz = 21 mr2
Kugel, massiv
Jx = Jy = Jz =
2
mr2
5
dünne Kugelschale
Jx = Jy = Jz =
2
mr2
3
Quader
Jx =
Jy =
Jz =
+
1
ml2
12
1
m (b2 + h2 )
12
1
m (l2 + h2 )
12
1
m (l2 + b2 )
12
Tabelle 2.1: Hauptträgheitsmomente, (Abbildungen aus [Hering, Martin, Stohrer])
2-72
Trägheitsmoment bezüglich einer festen Drehachse
Bei der Rotation um eine fest vorgegebene Achse betrachtet man häufig nur die Drehimpulskomponente parallel zu dieser Achse (und ignoriert ggf. die Unwucht). Wie bereits in Gl. 2.213
gezeigt, hat für einen einzelnen Massepunkt m die Drehimpulskomponente parallel zur Achse
den Wert
2
~ k = mr⊥
L
·ω
~
(2.223)
dabei ist r⊥ der Abstand zur Achse. Es lässt sich damit das Trägheitsmoment bezüglich dieser
Achse definieren
Z
N
X
2
2
J=
mi r⊥,i bzw. J =
%(~r)r⊥
dV
(2.224)
V
i=1
Die Bewegungsgleichung für die Winkelbeschleunigung α
~ um die Drehachse lautet in dieser
Situation
~ = J ·α
M
~
(2.225)
Steinerscher Satz
Führt eine Drehachse nicht durch den Schwerpunkt, so setzt sich der Drehimpuls aus dem Ei~ S (Drehimpuls des starren Körpers um den Schwerpunkt) und dem Bahndregendrehimpuls L
~
himpuls LB (Drehimpuls des Schwerpunkts um die tatsächliche Drehachse) zusammen.
~ =L
~S + L
~B
L
~ S wird durch das Trägheitsmoment JS bezüglich einer Drehachse beDer Eigendrehimpuls L
stimmt, die durch den Schwerpunkt und parallel zu der tatsächlichen Drehachse verläuft. Ist
diese Achse eine Hauptachse, dann ist dies das entsprechende Hauptträgheitsmoment, anderenfalls ist es über den Trägheitstensor zu berechnen.
~ S = JS · ω
L
~
(2.226a)
~ B wird durch den Abstand r⊥,S des Schwerpunkts von der tatsächlichen
Der Bahndrehimpuls L
Drehachse bestimmt.
2
~ B = m · r⊥,S
L
·ω
~
(2.226b)
Das gesamte Trägheitsmoment ist damit (Steinerscher Satz)
2
J = JS + m · r⊥,S
(2.227)
Der Nutzen dieses Satzes liegt darin, dass sich so nicht nur die Trägheitsmomente bei Verschiebung der Drehachse, sondern auch die Trägheitsmomente von aus einfachen Formen (Quadern,
Kugeln etc., siehe Tabelle 2.1) zusammengesetzten Körpern leichter berechnen lassen.
2-73
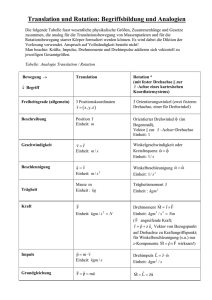
2.3.5.4
Gegenüberstellung Translation und Rotation
Translation
Rotation
Weg
Winkel
~s, d~s
Geschwindigkeit
d~s
~v =
dt
Beschleunigung
d~v
d2~s
~a =
= 2
dt
dt
Masse m, Gesamtmasse
Z
X
M=
mi = %(~r)dV
m
ϕ
~ , d~
ϕ
Winkelgeschwindigkeit
d~
ϕ
ω
~ =
dt
Winkelbeschleunigung
d~ω
d2 ϕ
~
α
~=
= 2
dt
dt
Massenträgheitsmoment
Z
X
2
J=
mi ri = r2 %(~r)dV
m/s
m/s2
kg
i
rad
rad/s
rad/s2
kgm2
i
kgm/s
Drehimpuls
~ = m~r × ~v = J~ω
p~ = m~v
= Ns
L
MassenmittelpunktX
eines Systems
Körpers
Z oder eines starren
Z
Xvon Massen
mi~ri
mi~ri
~r%(~r)dV
~r%(~r)dV
i
~rs = X
= i
= Z
=
M
M
mi
%(~r)dV
Impuls
kgm2 /s
= Nms
i
Gesamtimpuls lässt sich darstellen als Impuls
Gesamtdrehimpuls lässt sich darstellen als
des Schwerpunktes, d.h. wie wenn die Gesamtmasse im Ort des Schwerpunkts konzentriert
wäre. Die Summe der Einzelimpulse relativ
zum Schwerpunkt ist Null.
Drehimpuls des Schwerpunkts um den
gewählten Ursprung (Bahndrehimpuls)+
Drehimpuls des Systems um Schwerpunkt
Kraft
Drehmoment
d~p
F~ = m~a =
dt
Impulserhaltungssatz
kgm/s2 = N
~
dL
~ = ~r × F~ ; M
~ = Jα
M
~=
dt
Drehimpulserhaltungssatz
Nm
Summe der äußeren Kräfte
= Änderung des Gesamtimpulses
innere Kräfte ändern nicht den Impuls des
Schwerpunktes sondern nur die Einzelimpulse
Summe der Drehmomente der äußeren Kräfte
= Änderung des Gesamtdrehimpulses
innere Kräfte ändern Gesamtdrehimpuls nicht
Arbeit
Arbeit
~ =M
~ · d~
dW = M
ϕ
kinetische Energie
rot
Ekin
= 12 Jω 2
Leistung
dW
~ ·ω
P =
=M
~
dt
dW = F~ · d~s
kinetische Energie
trans
Ekin
= 12 mv 2
Leistung
dW
P =
= F~ · ~v
dt
Nm = J
J
J/s = W
Nm = J
J
J/s = W
Tabelle 2.2: Gegenüberstellung der Größen zur Beschreibung von Translations- und Rotationsbewegungen
2-74