Zusammenfassung Inflation und die Fisher Gleichung Geldtheorie

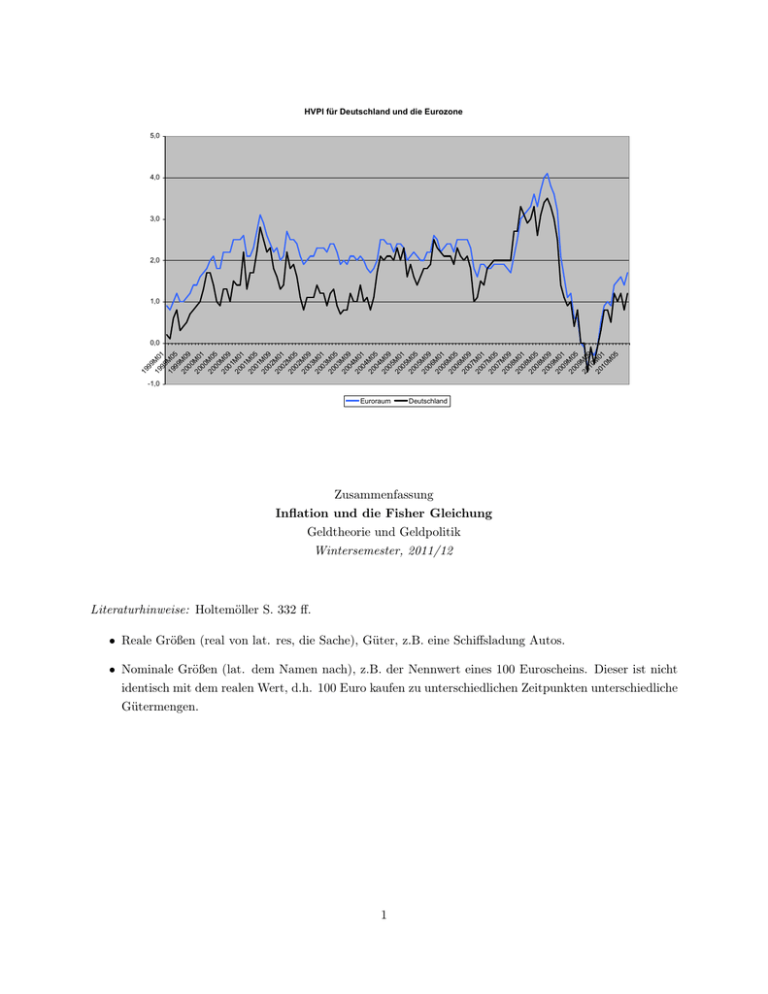
HVPI für Deutschland und die Eurozone
5,0
4,0
3,0
2,0
1,0
19
99
1 9 M0
99 1
1 9 M0
99 5
2 0 M0
00 9
2 0 M0
00 1
2 0 M0
00 5
2 0 M0
01 9
2 0 M0
01 1
2 0 M0
01 5
2 0 M0
02 9
2 0 M0
02 1
2 0 M0
02 5
2 0 M0
03 9
2 0 M0
03 1
2 0 M0
03 5
2 0 M0
04 9
2 0 M0
04 1
2 0 M0
04 5
2 0 M0
05 9
2 0 M0
05 1
2 0 M0
05 5
2 0 M0
06 9
2 0 M0
06 1
2 0 M0
06 5
2 0 M0
07 9
2 0 M0
07 1
2 0 M0
07 5
2 0 M0
08 9
2 0 M0
08 1
2 0 M0
08 5
2 0 M0
09 9
2 0 M0
09 1
2 0 M0
09 5
2 0 M0
10 9
2 0 M0
10 1
M
05
0,0
-1,0
Euroraum
Deutschland
Zusammenfassung
Inflation und die Fisher Gleichung
Geldtheorie und Geldpolitik
Wintersemester, 2011/12
Literaturhinweise: Holtemöller S. 332 ff.
• Reale Größen (real von lat. res, die Sache), Güter, z.B. eine Schiffsladung Autos.
• Nominale Größen (lat. dem Namen nach), z.B. der Nennwert eines 100 Euroscheins. Dieser ist nicht
identisch mit dem realen Wert, d.h. 100 Euro kaufen zu unterschiedlichen Zeitpunkten unterschiedliche
Gütermengen.
1
Vom Verbraucher subjektiv wahrgenommene Inflation in der Eurozone
80,00
70,00
60,00
50,00
40,00
30,00
20,00
10,00
Ja
n
9
M 9
ai
Se 99
p
9
Ja 9
n
00
M
ai
Se 00
p
0
Ja 0
n
01
M
ai
Se 01
p
0
Ja 1
n
0
M 2
ai
Se 02
p
0
Ja 2
n
0
M 3
ai
Se 03
p
0
Ja 3
n
0
M 4
ai
Se 04
p
0
Ja 4
n
0
M 5
ai
Se 05
p
0
Ja 5
n
0
M 6
ai
Se 06
p
0
Ja 6
n
07
M
ai
Se 07
p
0
Ja 7
n
08
M
ai
Se 08
p
0
Ja 8
n
09
M
ai
Se 09
p
0
Ja 9
n
10
M
ai
Se 10
p
10
0,00
-10,00
Figure 1: Quelle: Europäische Kommission. Die subjektive Wahrnehmung der Veränderung des Preisniveaus
in den vergangenen 12 Monaten durch die Verbraucher wird jeden Monat von der europäischen Kommission
in einer qualitativen Umfrage ermittelt. Dargestellt ist der saisonbereinigte Saldo zwischen den Anteilen der
positiven Antworten (”Die Preisniveaus ist im letzten jahr stark/mässig gestiegen”) und negativen Antworten
(”Die Preisniveaus ist im letzten Jahr in etwa gleich geblieben/gefallen”).
1
Die Inflationsrate
Inflation (von lat. das ”Aufschwellen”) bezeichnet den über mehrere Perioden andauernden Anstieg aller
Preise. Inflation wird mit Hilfe Preisindizes gemessen. Mathematisch ist die Inflationsrate π eine
Verhältniszahl. Die Inflationsrate als Wachstumsrate des Preisniveaus P ist definiert als
πt =
Pt − Pt−1
Pt
• zurückgestaute Inflation
• importierte Inflation
• Hyperinflation
• gefühlte Inflation
2
1.1
Die Messung von Inflation - Indexkonzepte
Ein Warenkorb ist ein Bündel in dem i = 1, ..., n Güter q-mal enhalten sind. pit ist der Preis des Gutes i
zum Zeitpunkt t.
Ein Preisindex P misst den nominalen Preis eines Warenkorbes in Periode t = ... − 2, −1, 0, 1, 2, ... im
Verhältnis zu den Preisen eines Basisjahres 0.
Ein Mengenindex Q vergleicht die nominellen Werte alternativer Warenkörbe zu den Preisen eines
Basisjahres .
Das Indexkonzept von Laspeyres
Pn
L
i=1 pit qi0
P0t
= Pn
i=1 pi0 qi0
Pn
i=1 pi0 qit
P
QL
=
0t
n
i=1 pi0 qi0
Pn
P
i=1 pit qit
P0t
= Pn
i=1 pi0 qit
Pn
i=1 pit qit
QP
0t = Pn
i=1 pit qi0
Das Indexkonzept von Paasche
Die Konzepte führen zu unterschiedlichen Ergebnissen - gibt es einen idealen Index?
1.2
Gütekriterien für Indizes nach Irving Fisher
Nach Irving Fisher sollte ein Preisindex drei Kriterien erfüllen
1. Proportionalität: Der Preisindex sollte die Veränderung der Preise proportional wiedergeben ”Wenn die Preise um 5% steigen sollte auch der Index um 5% steigen.”
2. Invarianz gegenüber dem Basisjahr: Die gemessene Preisveränderung sollte unabhängig vom
zugrundeliegenden Zeitpunkt sein.
3. Faktorinvarianz: Preis- und Mengenindizes müssen zum gleichen Ergebnis führen.
Beispiel:
Jahr 0
Jahr 1
Gut
Menge
Preis
Umsatz
Gut
Menge
Preis
Umsatz
1
40
1,50
60
1
30
2
60
2
4
30
120
2
3
50
150
3
20
2
40
3
40
2,10
84
3
Invarianz gegenüber dem Zeitpunkt der Messung
Laspeyres Index
Pn
qi,0 pi,1
80 + 200 + 42
L
P0,1
= Pi=1
=
= 1, 46
n
q
p
60
+ 120 + 40
i=1 i,0 i,0
Pn
qi,1 pi,0
45 + 90 + 80
L
P1,0
= Pi=1
=
= 0, 73
n
q
p
60
+ 150 + 84
i=1 i,1 i,1
L
1
P0,1
P1,0
=1
muss gelten, sofern der Index Zeitinvariant die Veränderung des Preisniveaus misst, aber
1, 46 6= 1, 367 =
1
0, 73
dies gilt auch für den Paasche Index.
1.3
Fisher’s Idealindex
Irving Fisher schlug als idealen Index einen geometriscchen Mittelwert aus Laspeyres und Paasche Index
vor
F
P0,1
=
q
L PP
P0,1
0,1
F
P1,0
=
q
L PP
P1,0
1,0
F
F
für Fisher’s Idealindex gilt P0,1
P1,0
= 1.
1.4
Kettenpreisindizes
Ein Kettenpreisindex ermittelt für jede Periode den Preis des Warenkorbes aus der Vorperiode zu aktuellen
Preisen (Laspeyres) oder wieviel der Warenkorb der laufenden Periode in der Vorperiode gekostet hat
(Paasche). D.h. ein Kettenpreisindex legt von Periode zu Periode einen anderen Warenkorb zugrunde.
Diese Methodik erlaubt es Änderungen im Konsumverhalten zu berücksichtigen.
1.5
Substitutionseffekte - ein Index für ein konstantes Nutzenniveau
• Substitution: Haushalte reagieren auf Veränderungen der Preise mit einer Anpassung der nachgefragten
Menge.
• Veränderungen der Preise führen zu Veränderungen in der Zusammensetzung des Warenkorbs und
damit des Nutzens.
Beispiel: Wir betrachten ein einfaches Modell mit zwei Gütern A, B und einen gegebenen Budget W .
Gegeben die Nutzenfunktion
U = U (qA , qB )
UA , UB > 0, UAA , UBB < 0
und das Budget
W = pA qA + pB qB
4
6
in t = 1 verändert sich das Preisniveau
6
-
Sofern die Preise der Güter mit unterschiedlichen Raten steigen müssen wir zwischen Einkommens- und
Substitutionseffekten Unterscheiden.
• Durch Parallelverschiebung können Punkte konstanten Nutzens zwischen den verschiedenen Zeitpunkten (mit unterschiedlichen Preisen) transferiert und verglichen werden.
• Q0 bezeichnet das in t = 0 erreichte Nutzenniveau, Q̄0 bezeichnet das gleiche Nutzenniveau in t = 1.
• Es lassen sich die Mindestausgaben herleiten die zur Erreichung eines konstanten Nutzenniveaus erforderlich sind.
• Zwei-Güter Fall, die Steigung der Budgetgerade entspricht dem dem Preisverhältnis der Güter.
Wir unterscheiden zwischen inferioren Gütern (Nachfrage wächst langsamer als das Einkommen) und
superioren Gütern (Nachfrage wächst schneller als das Einkommen). Eine unterschätzung (überschätzung)
der Substitutionseffekte führt zu zu einer Überzeichnung (Unterschätzung) der Preissteigerung für den
betrachtetetn Warenkorb.
Preisindex eines konstanten Nutzenniveaus
N
P0,1
(u0 ) =
pA,1 q̄A,1 + pB,1 q̄B,1
pA,0 qA,0 + pB,0 qB,0
5
wobei q̄A,1 , q̄B,1 auf der ”alten Indifferenzkurve” liegt und dem von Substitutions- und Einkommenseffekten
veränderte Güterbündel entspricht das den Nutzen aus t = 0 ”konserviert”. Das Mindestbutget in neuen
Preisen das zur Erreichung des Nutzenniveaus aus t = 0 erforderlich ist
W̄1 = pA,1 q̄a,1 + pB,1 q̄B,1
1.6
Vergleich mit den Indizes von Laspeyres und Paasche
6
-
N
P0,1
(u0 ) =
pA,1 q̄A,1 + pB,1 q̄B,1
pA,0 qA,0 + pB,0 qB,0
vs.
L
P0,1
=
pA,1 qA,0 + pB,1 qB,0
pA,0 qA,0 + pB,0 qB,0
• Laspeyres überzeichnet die Inflation
• Substitutionseffekt, die Tendenz zu günstigeren Gütern, wird nicht berücksichtigt - konstanter Warenkorb.
6
-
N
P0,1
(u0 ) =
pA,1 q̄A,1 + pB,1 q̄B,1
pA,0 qA,0 + pB,0 qB,0
N
P0,1
(u1 ) =
pA,1 qA,1 + pB,1 qB,1
pA,0 q̄A,0 + pB,0 q̄B,0
• Paasche unterzeichnet die Inflation.
6
vs
P
P0,1
=
pA,1 qA,1 + pB,1 qB,1
pA,0 qA,1 + pB,0 qB,1