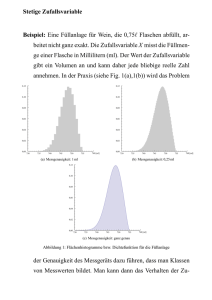
Stetige Verteilungen(16.09.2004) - Professuren für Statistik und

Kapitel 3
Stetige Verteilungen
3.1 Rechteckverteilung
Für die Rechteckverteilung benutzen wir die Notation U (a; b). Der Buchstabe U rührt von der
englischen Bezeichnung Uniform her. Wir wollen aber nicht Gleichverteilung oder gleichmäßige Verteilung sagen, um keine Verwechslungen mit gleicher Verteilung zu provozieren.
Statt gleicher Verteilung werden wir identische Verteilung sagen. Wir schreiben
X U (a; b) ;
wenn eine Zufallsvariable X eine Rechteckverteilung besitzt. Dabei sind a und b zwei Parameter, für die a < b gelten muss.
Definition 3.1 Die Dichtefunktion der Rechteckverteilung ist gegeben durch:
(
fX (x) =
1
b a
0
für a x b
sonst :
Der Verlauf der Dichtefunktion (siehe Abbildung 3.1) entspricht einem Rechteck über dem
Intervall [a; b℄.
Die Standardform der Rechteckverteilung oder Standardrechteckverteilung U (0; 1), die große
Bedeutung bei der Erzeugung von Zufallszahlen hat, hat die Parameter a = 0 und b = 1.
Satz 3.1 Die Verteilungsfunktion der Rechteckverteilung ist:
8
>
<
0
:
1
FX (t) = >
t a
b a
für
für
für
23
t<a
atb
t>b:
24
KAPITEL 3. STETIGE VERTEILUNGEN
1/(b-a)
a
b
Abbildung 3.1: Dichtefunktion der Rechteckverteilung
Beweis:
8
>
>
>
<
Zt
FX (t) =
für
t
R
1 dx
b
a a
fX (x)dx = >
1
t<a
für a t b
für t > b :
0
>
>
:
=
1
t a
b a
}
Abbildung 3.2 zeigt die Verteilungsfunktion. Es handelt sich also um eine Gerade mit der
Steigung 1=(b a).
Wir wollen jetzt den Erwartungswert und die Varianz einer Rechteckverteilung bestimmen.
Satz 3.2 Sei X eine Zufallsvariable mit einer Rechteckverteilung mit den Parametern a
und b. Dann gilt
EX =
b+a
2
und
V arX =
a
Z
(b a)2
:
12
Beweis:
EX =
1
Z
1
"
=
EX 2
=
b
Z
a
x2
xfX (x)dx =
x2
2b
b
1
1
#
a
b
a
=
"
Z
1
b
x 0 dx + x
1 b2
2 b
1 x3
dx =
a
b a3
a
a2
a
#
b
a
=
=
1
b a
b+a
:
2
1
Z
dx + x 0 dx
b
1 b3 a3 1 2
= (a + ab + b2 ) :
3 b a
3
3.1. RECHTECKVERTEILUNG
25
Nach Satz 2.2 gilt dann
a+b 2
1 2
2
2
2
V arX = EX (EX ) = (a + ab + b )
3
2
2
2
2
2
2
4(a + ab + b ) 3(a + 2ab + b ) a 2ab + b2
=
=
12
12
2
(b a)
=
:
12
!
}
1
a
b
Abbildung 3.2: Verteilungsfunktion der Rechteckverteilung
Für Anwendungen wichtig ist das folgende Resultat:
Satz 3.3 Sei X eine Zufallsvariable mit einer streng monotonen Verteilungsfunktion
FX (x). Die Zufallsvariable
U = FX (X )
ist dann verteilt wie U (0; 1),d.h.
U
U (0; 1) :
Beweis:
Die Verteilungsfunktion von U ist
FU (u) = P (fU ug) = P (fFX (X ) ug) = P (fFX 1(FX (X )) FX 1 (u)g)
= P (fX FX 1 (u)g) = FX (FX 1 (u)) = u
0u1:
Dies ist die Verteilungsfunktion einer U (0; 1) Zufallsvariablen. Im vorletzten Schritt wurde
die Definition der Verteilungsfunktion von X (FX (t) = P (fX tg)) benutzt.
}
Anschaulich kann man sich den obigen Sachverhalt wie folgt vorstellen. Abbildung 3.3 zeigt
die Verteilungsfunktion FX (x). Von den auf der x-Achse angedeuteten Realisationen der
26
KAPITEL 3. STETIGE VERTEILUNGEN
Zufallsvariablen X geht man dann in Pfeilrichtung zu den entsprechenden Werten der Verteilungsfunktion, die man an der u-Achse abliest. Dies sind dann die Realisationen der Zufallsvariablen U .
1.0
0.8
u
0.6
0.4
0.2
0.0
-4
-2
0
x
2
4
Abbildung 3.3: Zur Konstruktion der Zufallsvariablen U
Angewendet wird der Satz wie folgt:
Wenn wir eine Verteilung FX (x) für die Daten x1 ; x2 ; :::; xn postulieren, dann müssen u1
FX (x1 ); u2 = FX (x2 ); :::; un = FX (xn ) U (0; 1)-verteilt sein.
=
Wir können dies z.B. durch graphische Darstellungen (wie Histogramm) oder durch andere statistische Verfahren überprüfen. Ein Histogramm sollte etwa so aussehen, wie das in
Abbildung 3.4 dargestellte Histogramm.
2.0
1.5
1.0
0.5
0.0
0.0
0.2
0.4
0.6
0.8
1.0
x
Abbildung 3.4: Histogramm der u1 ; u2 ; :::; un (n = 100)
Das Histogramm in Abbildung 3.4 wurde mit folgenden R-Befehlen erzeugt:
u<-runif(100) # erzeugt 100 U(0,1)-Zufallszahlen
hist(u, probability=T) # zeichnet Histogramm
Stellt man sich die empirische Verteilungsfunktion der u1 ; u2 ; : : : ; un graphisch dar, so sollte
sich ungefähr eine Gerade mit der Steigung 1 wie in Abbildung 3.5 ergeben. Die Abbildung
3.5 wurde mit den folgenden R-Befehlen erzeugt.
3.1. RECHTECKVERTEILUNG
27
u<-sort(runif(100)) # erzeugt und sortiert 100 U(0,1)-ZZ
y<-(1:100)/100 # bildet Folge 1/100, 2/100, ..., 100/100
plot(u, y, type="s", ylab="F n") # plottet emp. Vertfkt.
abline(0,1) # zeichnet Diagonale
1.0
Fn(u)
0.8
0.6
0.4
0.2
0.0
0.0
0.2
0.4
0.6
0.8
1.0
u
Abbildung 3.5: Empirische Verteilungsfunktion der u1 ; u2 ; :::; un (n = 100)
Beispiel 3.1 (Verteilung des P-Wertes unter der Nullhypothese) Sei X die Prüfgröße in einem
Hypothesentest. Die Verteilungsfunktion der Prüfgröße unter der Nullhypothese sei FX . Der P-Wert
bei einem einseitigen Hypothesentest ist dann
FX (X )
oder
1 FX (X ) ;
je nachdem, ob der Ablehnungsbereich links oder rechts liegt. Der P-Wert ist eine Zufallsvariable. Es
folgt aus Satz 3.3, dass der P-Wert unter der Nullhypothese eine U (0; 1)-Verteilung besitzt. Häufig
ist die exakte Verteilung einer Prüfgröße nicht bekannt. Man kann dann meistens nur eine asymptotische Verteilung der Prüfgröße unter der Nullhypothese angeben. In Böker (1996) und Böker und
Dannenberg (1995, 1996) werden eine Reihe von graphischen Verfahren betrachtet, mit denen man
überprüfen kann, wie gut diese Approximation ist. Dazu werden Prüfgrößen unter der Nullhypothese simuliert und die P-Werte mit Hilfe der asymptotischen Verteilung berechnet. Diese P-Werte
sollten sich verhalten wie Realisationen U (0; 1)-verteilter Zufallsvariablen. Man kann insbesondere
überprüfen, ob die Prüfgrößen gewisse gewünschte Signifikanzniveaus einhalten können.
Der folgende Satz ist gewissermaßen die Umkehrung des vorangehenden Satzes.
Satz 3.4 Sei
U
U (0; 1)
und F (x) eine streng monotone Verteilungsfunktion. Dann hat die Zufallsvariable
X = F 1 (U )
die Verteilungsfunktion F (x).
28
KAPITEL 3. STETIGE VERTEILUNGEN
Beweis:
P (fX xg) = P (fF 1(U ) xg) = P (fF (F 1(U )) F (x)g)
= P (fU F (x)g) = FU (F (x)) = F (x) :
Im letzten Schritt, wurde benutzt, dass
der Stelle F (x), also gleich F (x) ist.
P (fU
F (x)g) die Verteilungsfunktion von U an
}
Der Inhalt dieses Satzes wird durch Abbildung 3.6 veranschaulicht. Dort ist wieder die Verteilungsfunktion F (x) dargestellt. Jetzt geht man jedoch den umgekehrten Weg. Man geht
von Realisationen der Rechteckverteilung U (0; 1) auf der Ordinate, der u-Achse, aus, geht
dann in Pfeilrichtung zur Verteilungsfunktion FX (x) und bestimmt dann auf der Abszisse
den zugehörigen x-Wert.
1.0
0.8
u
0.6
0.4
0.2
0.0
-4
-2
0
x
2
4
Abbildung 3.6: Zur Konstruktion der Zufallsvariablen X mit Verteilungsfunktion F (x)
Der Satz 3.4 findet Anwendung bei der Erzeugung von Zufallszahlen mit der Verteilungsfunktion F (x).
Es ist leicht U (0; 1)-Zufallszahlen, besser sollte man Pseudo-Zufallszahlen sagen, zu
erzeugen. Das sind Zahlen, die sich, ,,wenigstens annähernd” so verhalten wie ,,echte”
Realisationen U (0; 1)-verteilter Zufallsvariablen. Jeder Rechner hat solch ein Verfahren implementiert. Dabei wird häufig die lineare Kongruenz-Methode benutzt. Seien
u1 ; u2 ; : : : ; un
auf diese Weise gegeben.
Man bilde
x1 = F 1 (u1 ); x2 = F 1 (u2); : : : ; xn = F 1 (un ) :
Dann verhalten sich x1 ; x2 ; : : : ; xn wie Realisationen von Zufallsvariablen mit der Verteilungsfunktion F (x).
Beispiel 3.2 (Erzeugung exponentialverteilter Zufallsvariablen) Es sollen (Pseudo)-Zufallszahlen
erzeugt werden, die sich verhalten wie ,,echte” Realisationen exponentialverteilter Zufallsvariablen.
Die Verteilungsfunktion der Exponentialverteilung mit dem Parameter ( > 0) ist
F (x) = 1
e x :
3.2. NORMALVERTEILUNG
29
Um die Umkehrfunktion F 1 zu bestimmen, setzen wir
u=1
e x :
Diese Gleichung ist nach x aufzulösen:
x=
Speziell für = 1 ist
log(1 u)= = F 1 (u) :
x=
log (1 u) :
(3.1)
In der folgenden Tabelle stehen einige Werte von u, die mit dem R-Befehl
runif(5)
erzeugt wurden. Die x-Werte wurden nach Gleichung (3.1) erzeugt.
u
x
0.42
0.54
0.31
0.37
0.87
2.04
0.17
0.19
0.69
1.17
R-Befehle zur Rechteckverteilung
dunif(x, min=0, max=1) berechnet die Dichtefunktion der Rechteckverteilung
an der Stelle x, wobei x ein Vektor ist. Defaultmäßig (min=0, max=1) wird die
Dichte der Standardrechteckverteilung berechnet. Durch Veränderung der optionalen
Argumente min und max kann die Dichtefunktion für beliebige Parameter a und b
berechnet werden.
punif(q, min=0, max=1) berechnet die Verteilungsfunktion der Rechteckverteilung mit den Parametern a =min und b =max an der Stelle q, wobei q ein Vektor
ist.
qunif(p, min=0, max=1) berechnet die Umkehrfunktion der Verteilungsfunktion der Rechteckverteilung mit den Parametern a =min und b =max an der Stelle p,
wobei p ein Vektor von Wahrscheinlichkeiten, also Zahlen zwischen 0 und 1, ist.
runif(n, min=0, max=1) erzeugt
vall [0; 1℄.
n rechteckverteilte Zufallszahlen im Inter-
3.2 Normalverteilung
Definition 3.2 Die Dichtefunktion der Normalverteilung ist gegeben durch
fX (x) =
p 1 2e
2
(x )2 =22
für
1<x<1:
Dabei sind und 2 Parameter, für die gelten muss
1<<1
und
2 > 0 :
30
KAPITEL 3. STETIGE VERTEILUNGEN
Man schreibt dafür
Für = 0 und 2
X N (; 2 ) :
= 1 erhält man die Standardnormalverteilung, deren Dichte durch
fX (x) =
p1 e
2
gegeben ist. Man schreibt dann
x2 =2
1<x<1
für
X N (0; 1) :
Abbildung 3.7 zeigt die Dichtefunktion der Standardnormalverteilung.
0.5
f(x)
0.4
0.3
0.2
0.1
0.0
-4
-2
0
2
4
6
8
10
x
Abbildung 3.7: Dichtefunktion der Standardnormalverteilung
Über den Verlauf der Dichtefunktion (siehe Abbildung 3.7) kann man sagen: Die Dichtefunktion hat ihr Maximum an der Stelle , sie ist symmetrisch um eine senkrechte Achse
bei und hat Wendepunkte an den Stellen und + . Der Parameter ist ein Lageparameter. Eine Veränderung von bei konstantem bewirkt nur eine Verschiebung der
Dichtefunktion (siehe Abbildung 3.8).
0.5
f(x)
0.4
0.3
0.2
0.1
0.0
-4
-2
0
2
4
6
8
10
x
Abbildung 3.8: Dichtefunktion der N(3,1)-Verteilung
3.2. NORMALVERTEILUNG
31
0.5
f(x)
0.4
0.3
0.2
0.1
0.0
-4
-2
0
2
4
6
8
10
x
Abbildung 3.9: Dichtefunktion der N(3,4)-Verteilung
Dagegen ist 2 ein Streuungsparameter. Mit wachsendem 2 wird die Kurve flacher und
breiter (siehe Abbildung 3.9).
Die Verteilungsfunktion der Standardnormalverteilung ist
FX (x) = (x) =
x
Z
1
f (z )dz =
x
Z
1
p1 e
2
z 2 =2 dz
:
Abbildung 3.10 zeigt den Verlauf der Verteilungsfunktion der Standardnormalverteilung.
Diese Verteilungsfunktion ist nicht durch eine elementare Funktion darstellbar. Für die Standardnormalverteilung (N (0; 1)) ist die Verteilungsfunktion tabelliert. Das ist wegen des folgenden Satzes ausreichend:
Satz 3.5 Ist X verteilt wie N (; 2 ), so ist
Z=
X
verteilt wie N (0; 1).
N (; 2) und Z N (0; 1):
P (fa < X < b g)
Als Folgerung aus diesem Satz ergibt sich, wenn X
P (fa < X < bg) =
(
a X b = P
<
<
(
)!
a b = P
<Z<
!
b a = ;
)!
32
KAPITEL 3. STETIGE VERTEILUNGEN
wobei = FZ die Verteilungsfunktion der Standardnormalverteilung sei, die aus der Tabelle
abgelesen werden kann. Manche Tabellen enthalten jedoch (z ) nur für z 0. Dann hat man
zu beachten, dass aus Symmetriegründen (siehe Abbildung 3.7 oder 3.10) gilt
( z ) = 1 (z ) :
1.0
F(x)
0.8
0.6
0.4
0.2
0.0
-4
-2
0
x
2
4
Abbildung 3.10: Verteilungsfunktion der Standardnormalverteilung
Zwischen den Verteilungsfunktionen der N (; 2 )- und N (0; 1)-Verteilung besteht der folgende Zusammenhang, den wir beweisen wollen, da diese Beweismethode auch in anderen
Situationen nützlich sein kann.
Satz 3.6 Die Verteilungsfunktion FX einer N (; 2 )-Verteilung ist
FX (x) = x 1<x<1;
wobei die Verteilungsfunktion der Standardnormalverteilung bezeichne.
Beweis:
Die Verteilungsfunktion der N (; 2 )-Verteilung ist
FX (x) =
x
Z
1
p 1 2e
2
Wir substituieren
z=
Dann ist
dz 1
=
dt Dabei ändern sich die Grenzen wie folgt:
(t )2 =22 dt
(t )
:
oder
dt = dz :
:
3.2. NORMALVERTEILUNG
Wenn t =
Wenn t = x, ist z
33
1, ist z = 1 :
=
x :
Damit ist
FX (x) =
Beispiel 3.3 Sei X
x Z
1
p1 e
2
z 2 =2 dz
x =
:
}
N (10; 32 ). Die zugehörige Dichtefunktion ist in Abbildung 3.11 dargestellt.
0.3
f(x)
0.2
0.1
0.0
0
5
10
x
15
20
Abbildung 3.11: Dichtefunktion der N(10,9)-Verteilung
Die Verteilungsfunktion ist dann
FX (x) = x
10 :
3
Die Wahrscheinlichkeit P (13 X 16), die in Abbildung 3.12 als Fläche unterhalb der Dichtefunktion zwischen 13 und 16 dargestellt ist, berechnet sich dann zu:
16
10
13
10
P (f13 X 16g) = FX (16) FX (13) = 3
3
= (2) (1) = 0:977 0:841 = 0:136 :
Satz 3.7 Für eine normalverteilte Zufallsvariable X
EX = und
N (; 2) gilt
V ar(X ) = 2 :
34
KAPITEL 3. STETIGE VERTEILUNGEN
0.3
f(x)
0.2
0.1
0.0
0
5
Abbildung 3.12: P (f13 < X
10
x
15
20
< 16g) als Fläche unterhalb der Dichtefunktion
Beweis:
1
Z
E (X ) =
1
1
e
2 2
xp
(x )2 =22 dx
:
Wir verwenden wieder die Substitution
z=
Dann ist
x :
dz 1
=
dx x = z + oder
dx = dz :
Dabei ändern sich die Grenzen wie folgt.
1, ist z = 1 :
Wenn x = 1, ist z = 1 :
Wenn x =
Damit folgt:
E (X ) =
1
Z
1
Z1
1
(z + ) p 2 e
2
1
=
z p e
2
1
|
z 2 =2 dz
z 2 =2 dz +
{z
0
}
1
=
1
(z + ) p e
2
1
1
p e
2
1
Z
1
Z
z 2 =2 dz
=
1
Z
1
|
z 2 =2 dz
p1 e
2
{z
1
z 2 =2 dz
=:
}
Das erste Integral in der zweiten Zeile ist Null, da der Integrand punktsymmetrisch zum
Ursprung ist, z.B. ergibt sich für
z= 1:
z = +1 :
( 1) p12 e
(+1) p12 e
( 1)2 =2
(1)2 =2
:
3.2. NORMALVERTEILUNG
35
Es gilt also
g (z ) = g ( z ) ;
wenn wir den Integranden, dessen Graph in Abbildung 3.13 dargestellt ist, mit g bezeichnen.
0.4
g(z)
0.2
0.0
-0.2
-0.4
-4
-2
0
z
2
4
2
Abbildung 3.13: Graph der Funktion z p12 e z =2 für =1
Bei der Bestimmung der Varianz verwenden wir wieder die gleiche Substitution wie oben.
Zur Berechnung des Integrals in der zweiten Zeile verwenden wir die Regel der partiellen
Integration, die hier zur Erinnerung noch einmal aufgeschrieben sei:
b
Z
a
V ar(X ) =
=
1
Z
1
2
(x
b
0
v (x)w (x)dx = v (x)w(x)
a
)2
1
p 1 2e
2
1
z zp e
2
1
Z
(x )2 =22 dx
z 2 =2 dz
"
=
2
|
=
b
Z
a
1
Z
1
pz e
2
0
v (x)w(x)dx :
z22 p
z 2 =2
{z
0
1
e
2 2
1
#
1}
+ 2
(3.2)
z 2 =2 dz
1
Z
|
1
p1 e
2
{z
1
z 2 =2 dz
= 2
}
Bei der partiellen Integration wurde
v(z) = z =) v0(z) = 1
w0(z) = z p12 e z =2 =) w(z) =
2
p1 e z2 =2
2
benutzt.
}
Die große Bedeutung der Normalverteilung beruht auf folgenden Tatsachen:
a) Viele Phänomene sind normalverteilt: z.B. in der Finanzwissenschaft, Astronomie,
Ökonometrie, Biologie usw.
36
KAPITEL 3. STETIGE VERTEILUNGEN
b) Aufgrund des folgenden Satzes kann man viele Zufallsvariablen durch eine Normalverteilung approximieren.
Satz 3.8 (Zentraler Grenzwertsatz) Die Zufallsvariablen X1 ; X2 ; :::; Xn seien
unabhängig und identisch verteilt mit EXi = und V arXi = 2 < 1. Sei
n
P
X n = n1 Xi . Dann ist
i=1
X n p _ N (0; 1) :
= n
Das Zeichen _ bedeutet, die entsprechende Zufallsvariable ist asymptotisch verteilt
wie N (0; 1). Man beachte
E Xn = und V arX n = 2 =n :
Der standardisierte Mittelwert ist asymptotisch standardnormalverteilt. Wenn n groß
n durch eine Normalverteilung approximiert werden.
wird, kann die Verteilung von X
3
3
n= 5
2
n = 10
2
1
1
0
0
0
1
2
3
0
Mittelwerte
1
2
3
Mittelwerte
3
3
n = 20
2
n = 50
2
1
1
0
0
0
1
2
Mittelwerte
3
0
1
2
3
Mittelwerte
Abbildung 3.14: Histogramme von je 1 000 Mittelwerten in Stichproben der Größe
5; 10; 20; 50 aus einer exponentialverteilten Grundgesamtheit
n =
Abbildung 3.14 veranschaulicht den zentralen Grenzwertsatz. Dort sind die Mittelwerte von je 1 000 Stichproben der Größen n = 5; 10; 20; 50 in einem Histogramm
dargestellt. Je größer der Stichprobenumfang, desto mehr nähert sich die Form des
Histogramms der Dichtefunktion einer Normalverteilung an.
3.2. NORMALVERTEILUNG
37
c) Oft ist eine Variable die Summe unterschiedlicher Zufallseinflüsse. In solchen Fällen
ist die Normalverteilung häufig ein gutes Modell.
d) Die theoretischen Eigenschaften sind einfach zu bestimmen. Daher ist die Theorie der
Normalverteilung sehr weit entwickelt.
e) Die Normalverteilung hat viele angenehme Eigenschaften. So sind Linearkombinationen und insbesondere Summen unabhängiger normalverteilter Zufallsvariablen wieder
normalverteilt.
f) Abgesehen von einigen Ausnahmen sind Maximum-Likelihood-Schätzer von Parametern asymptotisch normalverteilt. Man benutzt dann diese Eigenschaft bei der Konstruktion von Konfidenzintervallen.
g) Die Normalverteilung tritt im Zusammenhang mit sogenannten Wiener-Prozessen auf.
Ein Wiener-Prozess ist ein stochastischer Prozess X (t); t 0 mit stetiger Zeit, d.h. für
jedes t gibt es eine Zufallsvariable X (t). Eine der Annahmen des Wiener-Prozesses ist,
dass die Zuwächse X (t) X (s) für s < t normalverteilt sind. Wiener-Prozesse fanden zunächst Anwendung in der Physik, wo die Bewegung eines kleinen Teilchens
beschrieben wurde, das einer großen Anzahl kleiner Stöße ausgesetzt ist. In diesem
Zusammenhang spricht man von einer Brownschen Bewegung. Wiener-Prozesse werden aber auch als Modell für Aktienkurse angewendet und wurden z.B. bei der Herleitung der Black-Scholes-Formel verwendet, deren Erfinder 1997 mit dem Nobelpreis
für Wirtschaftswissenschaften ausgezeichnet wurden.
Aufgrund ihrer angenehmen Eigenschaften und der weit entwickelten Theorie wird die Annahme einer Normalverteilung in vielen statistischen Verfahren, wie Varianzanalyse, Regressionsanalyse, Zeitreihenanalyse, Diskriminanzanalyse usw. verwendet. Ein weiterer Vorteil
ist es, dass die unter der Annahme der Normalverteilung entwickelten Test- und Schätzverfahren relativ unempfindlich gegenüber Abweichungen von dieser Annahme sind. Man sagt,
dass solche Verfahren robust sind. So kommt es z.B. beim t-Test zur Prüfung der Hypothese,
dass der Erwartungswert einen bestimmten Wert besitzt, nicht so sehr darauf an, dass die
einzelnen Beobachtungen einer Normalverteilung entstammen, sondern mehr, dass der Mittelwert normalverteilt ist, was aufgrund des zentralen Grenzwertsatzes zumindest für große
n gewährleistet ist.
R-Befehle zur Normalverteilung
dnorm(x, mean=0, sd=1) berechnet die Dichtefunktion der Normalverteilung
an der Stelle x, wobei x ein Vektor ist. Defaultmäßig (mean=0, sd=1) wird die
Dichte der Standardnormalverteilung berechnet. Durch Veränderung der optionalen
Argumente mean und sd kann die Dichtefunktion für beliebige Parameter und 2
berechnet werden. Dabei ist zu beachten, dass sd die Standardabweichung, also die
Quadratwurzel aus der Varianz 2 ist. Der Erwartungswert ist durch mean anzugeben.
pnorm(q, mean=0, sd=1) berechnet die Verteilungsfunktion der Normalverteilung mit dem Erwartungswert =mean und der Standardabweichung sd an der Stelle
q, wobei q ein Vektor ist. Standardmäßig wird P (X q ) berechnet. Mit dem zusätzlichen Argument lower.tail=F wird die Wahrscheinlichkeit P (X > q ) berechnet.
38
KAPITEL 3. STETIGE VERTEILUNGEN
qnorm(p, mean=0, sd=1) berechnet die Umkehrfunktion der Verteilungsfunktion der Normalverteilung mit dem Erwartungswert =mean und der Standardabweichung sd an der Stelle p, wobei p ein Vektor von Wahrscheinlichkeiten, also Zahlen
zwischen 0 und 1, ist. Auch hier kann das Argument lower.tail verwendet werden.
rnorm(n, mean=0, sd=1)] erzeugt n normalverteilte Zufallszahlen mit dem
Erwartungswert =mean und der Standardabweichung sd.
3.3 Gammaverteilung
Definition 3.3 Die Gammafunktion ist für 1
Z
( ) =
Für = 1 ergibt sich
(1) =
0
1
Z
0
> 0 definiert durch das Integral
t 1 e t dt :
(3.3)
e t dt = 1 :
Wir wenden für > 1 auf das Integral in Gleichung (3.3) die Regel der partiellen Integration
(siehe Gleichung (3.2)) an. Dabei setzen wir
v (t) = t
und
=)
1
w0(t) = e
t
v 0 (t) = (
=)
1)t
2
w(t) = e t :
Damit folgt
( ) = t 1 e t j1
0
|
{z
0
Das bedeutet
1
0
Z
}
0
(
1
1)t 2 e t dtA
( ) = (
= (
1
Z
1) t 2 e t dt :
0
|
1) (
{z
( 1)
}
1) :
Daraus folgt für natürliche Zahlen:
(1)
(2)
(3)
(4)
..
.
=
=
=
=
1
1 (1) = 1 1 = 1 = 1!
2 (2) = 2 1 = 2 = 2!
3 (3) = 3 2 1 = 6 = 3!
(n) = (n
1) (n 1) = (n
1)(n 2) : : : 2 1 = (n
1)!
3.3. GAMMAVERTEILUNG
39
Satz 3.9 Für natürliche Zahlen n gilt:
(n) = (n
1)!
Die Gammafunktion kann mit der R-Funktion
gamma(x)
berechnet werden. Sie ist in Abbildung 3.15 dargestellt.
Gammafunktion
20
Γ(ν)
15
10
5
0
0
1
2
ν
3
4
5
Abbildung 3.15: Der Graph der Gammafunktion
Definition 3.4 Die Dichtefunktion der Gammaverteilung ist gegeben durch
8
<
fX (x) = :
x 1 e
( )
0
x
x0
sonst :
Dabei sind und Parameter, für die gelten muss
> 0 und > 0 :
Wir schreiben
X G( ; ) ;
wenn eine Zufallsvariable X eine Gammaverteilung besitzt.
(3.4)
40
KAPITEL 3. STETIGE VERTEILUNGEN
Wir wollen nachweisen, dass durch Gleichung (3.7) tatsächlich eine Dichtefunktion definiert
wird, d.h. dass das Integral
1 1 x
x e
Z
0
( )
1
1 Z 1
dx =
x e
( ) 0
x dx
1
1 Z
=
(x) 1 e
( ) 0
x dx
(3.5)
( ) ergeben.
den Wert 1 hat, d.h. das ganz rechts stehende Integral muss
Wir verwenden die Substitution
=)
t = x
dt = dx :
Die Grenzen ändern sich wie folgt:
Wenn x = 0, ist t = 0 :
Wenn x = 1, ist t = 1 :
Damit ergibt sich für das obige Integral in Gleichung (3.5)
1
1 Z 1 t
t e dt = 1 :
( ) 0
|
{z
( )
}
}
Einen wichtigen Spezialfall der Gammaverteilung erhalten wir, wenn der Parameter
Wert 1 hat. Dann ist
1 x1 1 e
fX (x) =
(1)
x
= e
x
für
den
x0:
Dies ist die Dichte einer Exponentialverteilung mit dem Parameter , d.h.
G(1; ) Exp() :
(3.6)
Wir werden die Exponentialverteilung später in Abschnitt 3.5 behandeln.
Satz 3.10 Es gelte
Dann gilt
X G( ; ) :
EX = =
und
V arX = =2 :
Die Abhängigkeit der Dichtefunktion von den Parametern
dungen 3.16 - 3.19 entnehmen.
und können Sie den Abbil-
3.3. GAMMAVERTEILUNG
41
1.0
0.5
f(x)
0.8
0.6
1
1.5
0.4
2
0.2
0.0
0
5
10
15
x
Abbildung 3.16: Dichtefunktionen der Gammaverteilung mit 2
= 1 und = 0:5; 1; 1:5 und
1.0
0.8
f(x)
0.5
0.6
0.4
1
1.5
0.2
2
0.0
0
5
10
15
x
Abbildung 3.17: Dichtefunktionen der Gammaverteilung mit
und 2
= 1=2 und = 0:5; 1; 1:5
Man entnimmt diesen Abbildungen, dass der Parameter für die Gestalt oder die Form der
Dichtefunktion verantwortlich ist. In der englischen Literatur sagt man, dass ein ‘shape’Parameter ist, während ein ‘scale’-Parameter ist, d.h. bestimmt die Skala oder die Breite
der Dichtefunktion.
R-Befehle zur Gammaverteilung:
Beachten Sie bitte, dass der scale-Parameter in R in unserer Bezeichnungsweise das Inverse
des Parameters ist, d.h. R verwendet die Dichtefunktion der Gammaverteilung in der Form:
8
<
fX (x) = :
xa a 1 e x=b x 0
b (a)
0
sonst :
(3.7)
Dabei ist a = und b = 1=.
dgamma(x, shape,scale=1) berechnet die Dichtefunktion der Gammaverteilung mit den Parametern = 1 und =shape an der Stelle x. Dabei kann x ein
Vektor sein.
42
KAPITEL 3. STETIGE VERTEILUNGEN
1.0
f(x)
0.8
1
0.6
0.4
0.2
0.5
0.25
0.0
0
5
10
15
x
Abbildung 3.18: Dichtefunktionen der Gammaverteilung mit = 1 und = 1; 0:5 und 0:25
1.0
f(x)
0.8
0.6
1
0.4
0.2
0.5
0.25
0.0
0
5
10
15
x
Abbildung 3.19: Dichtefunktionen der Gammaverteilung mit
0:25
= 1:5 und = 1; 0:5 und
pgamma(q, shape,scale=1) berechnet die Verteilungsfunktion der Gammaverteilung mit den Parametern = 1 und =shape an der Stelle q . Dabei kann
q ein Vektor sein.
qgamma(p, shape,scale=1) berechnet die Umkehrfunktion der Verteilungsfunktion der Gammaverteilung mit den Parametern = 1 und =shape an der Stelle p. Dabei muss p ein Vektor von Wahrscheinlichkeiten, d.h. von Zahlen zwischen 0
und 1 sein.
rgamma(n, shape,scale=1) erzeugt
Parametern = 1 und =shape.
n gammaverteilte Zufallszahlen mit den
Anwendungen der Gammaverteilung
a) Wir betrachten einen Poissonprozess. Das ist eine Folge von zufälligen Punkten (Ereignissen) auf der positiven reellen Zahlenachse, unter der man sich häufig die Zeit
vorstellt. Bedingungen unter denen, eine solche zufällige Folge von Punkten ein Poissonprozess ist, werden an anderer Stelle betrachtet (siehe S. 51). Die Wartezeit (siehe
3.3. GAMMAVERTEILUNG
43
Abbildung 3.20) bis zum -ten ( muss eine ganze Zahl sein) Ereignis eines Poissonprozesses ist G( ; )-verteilt.
W G( ; )
b) Die Gammaverteilung der Wartezeiten bis zum -ten Ereignis eines Poissonprozesses
folgt aus dem folgenden Resultat. Die Zeiten zwischen Ereignissen eines Poissonprozesses sind nämlich unabhängig und identisch exponentialverteilt.
Satz 3.11 Wenn X1 ; X2 ; :::; X unabhängig und identisch exponentialverteilt
sind, d.h. Xi Exp(), ist
X
i=1
Xi G( ; ) :
Poissonprozess
W1
W2
W3
Zeit
Abbildung 3.20: Wartezeiten bei einem Poissonprozess
Beispiel 3.4 Sie haben eine Netzkarte und eine Ersatzkarte. Die Lebensdauern der einzelnen
Karten seien exponentialverteilt mit Parameter = 1=500 Tage. Wir suchen eine Antwort
auf die Frage: Wie groß ist die Wahrscheinlichkeit, dass Sie in einem Jahr keine zusätzliche
Netzkarte brauchen, d.h. dass die Netzkarte und die Ersatzkarte zusammen für mindestens 1
Jahr reichen?
Sei X1 die Lebensdauer der Netzkarte.
Sei X2 die Lebensdauer der Ersatzkarte.
Die Lebensdauer beider Karten zusammen ist
X
= X1 + X2 ;
und die gesuchte Wahrscheinlichkeit ist
P (fX > 365g) :
44
KAPITEL 3. STETIGE VERTEILUNGEN
Aufgrund unserer Annahmen über die Verteilungen von X1 und X2 und des Satzes 3.11 gilt
X
G(2; 1=500) :
Abbildung 3.21 zeigt die Dichtefunktion von X und die gesuchte Wahrscheinlichkeit als schraffierte Fläche unterhalb der Dichtefunktion. Sie können diese Wahrscheinlichkeit mit dem RBefehl
1-pgamma (365, 2, 500)
oder
pgamma(365,2,500,lower.tail=F)
berechnen.
Es gilt
P (fX > 365g) = 0:8337 :
c) Für ganzzahliges
bezeichnet.
wird die Gammaverteilung (G( ; )) auch als Erlangverteilung
8
7
10 000*f(x)
6
5
4
3
2
P({X>365})
1
0
0
Abbildung 3.21: P (fX
1000
2000
3000
4000
5000
x
> 365g) als Fläche unterhalb der Dichtefunktion
3.4 Chiquadratverteilung
Die aus der Grundvorlesung bekannte Chiquadratverteilung ist ein Spezialfall der Gammaverteilung.
Satz 3.12 Die Gammaverteilung mit den Parametern = n=2 und = 1=2 stimmt mit
der 2 -Verteilung mit dem Parameter n überein. Dabei ist n eine positive ganze Zahl.
3.4. CHIQUADRATVERTEILUNG
45
Die 2 -Verteilung hat einen Parameter n. Wir schreiben
X 2n oder X 2 (n) ;
wenn X eine 2 -Verteilung mit dem Parameter n besitzt und sagen: X hat eine 2 -Verteilung
mit n Freiheitsgraden.
Die Dichtefunktion der 2 -Verteilung mit n Freiheitsgraden ist
8
>
<
f (x) = >
:
xn=2 1 e x=2 x 0
2n=2 (n=2)
0
sonst :
Aus Satz 3.10 erhalten wir sofort:
Satz 3.13 Sei
Dann gilt
X 2n :
EX = n
und
V arX = 2n :
Beweis:
Nach Satz 3.12 gilt
2n G(n=2; 1=2) :
Erwartungswert und Varianz einer Gammaverteilung waren in Satz 3.10 angegeben. Mit
= n=2 und = 1=2 folgt
EX =
und
V arX =
n=2
=
=n
1=2
n=2
=
= 2n :
2 (1=2)2
Die Abbildungen 3.22 - 3.24 zeigen einige Dichtefunktionen der 2 -Verteilung mit wachsender Anzahl der Freiheitsgrade. Beachten Sie bei diesen Abbildungen die unterschiedlichen
Achsenskalierungen. Ab n = 3 Freiheitsgraden hat die 2 -Verteilung eine ganz typische
Form, die sich mit wachsenden Freiheitsgraden der Normalverteilung annähert, dabei verschiebt sich die Kurve weiter nach rechts. Für n = 2 Freiheitsgrade stimmt die 2 -Verteilung
mit der Exponentialverteilung mit dem Parameter = 1=2 überein (siehe Satz 3.12 und Gleichung (3.6)).
Anwendungen der 2 -Verteilung:
Die 2 -Verteilung tritt häufig als Verteilung von Prüfgrößen bei Hypothesentests auf.
Die Prüfgröße
nS 2
02
46
KAPITEL 3. STETIGE VERTEILUNGEN
1.0
0.8
f(x)
1
0.6
0.4
2
0.2
3
4
0.0
0
5
10
15
x
Abbildung 3.22: Dichtefunktionen der 2 -Verteilung
0.10
10
15
0.08
f(x)
20
0.06
30
0.04
0.02
0.0
0
20
40
60
x
Abbildung 3.23: Dichtefunktionen der 2 -Verteilung
zur Prüfung der Hypothese 2 = 02 , dass die Varianz in einer Grundgesamtheit einen
ganz bestimmten Wert 02 hat, ist 2 -verteilt mit n 1 Freiheitsgraden. Dabei ist
S2
n
1X
=
(X
n i=1 i
X )2
die geschätzte Varianz und n der Stichprobenumfang. Die Verteilung gilt exakt unter
der Normalverteilungsannahme, andernfalls nur approximativ.
Die Prüfgröße im Anpassungstest von Pearson ist asymptotisch 2 -verteilt. Geprüft
wird die Hypothese, dass Zufallsvariablen eine ganz bestimmte Verteilung besitzen
(z.B. U (0; 1) oder N (0; 1)) oder einer bestimmten Verteilungsfamilie angehören (z.B.
Gammaverteilung oder Normalverteilung).
Die Prüfgröße im Unabhängigkeitstest bei Kontingenztafeln ist als Spezialfall des Anpassungstests ebenfalls asymptotisch 2 -verteilt.
Summen von Quadraten von unabhängigen N (0; 1)-verteilten Zufallsvariablen sind
2 -verteilt. Solche Summen von Quadraten treten in der Varianzanalyse häufig auf und
3.5. EXPONENTIALVERTEILUNG
47
0.06
30
40
50
60
f(x)
0.04
0.02
0.0
0
20
40
60
80
100
x
Abbildung 3.24: Dichtefunktionen der 2 -Verteilung
bilden Zähler und Nenner von F -Prüfgrößen, die Ihnen in den Vorlesungen Lineare
Modelle und Ökonometrie begegnen werden. Solche Quotienten führen dann zu einer
F -Verteilung. Wir werden an späterer Stelle darauf zurückkommen (S. 85).
R-Befehle zur Chiquadratverteilung:
dchisq(x, df) berechnet die Dichtefunktion der Chiquadratverteilung mit dem
Parameter n =df an der Stelle x. Dabei kann x ein Vektor sein.
pchisq(q, df, ncp=0) berechnet die Verteilungsfunktion der Chiquadratverteilung mit dem Parameter n =df an der Stelle q . Dabei kann q ein Vektor sein. Mit
dem optionalen Argument ncp wird der Nichtzentralitätsparameter festgelegt. Wir behandeln hier die zentrale Chiquadratverteilung, für die ncp=0 ist.
qchisq(p, df) berechnet die Umkehrfunktion der Verteilungsfunktion der Chiquadratverteilung mit dem Parameter n =df an der Stelle p. Dabei muss p ein Vektor
von Wahrscheinlichkeiten, d.h. von Zahlen zwischen 0 und 1 sein.
rchisq(n, df) erzeugt
n =df.
n chiquadratverteilte Zufallszahlen mit dem Parameter
3.5 Exponentialverteilung
Definition 3.5 Die Dichtefunktion der Exponentialverteilung ist gegeben durch
(
f (x) =
e
0
x
0x<1
sonst :
Dabei ist ein Parameter, für den gelten muss
>0:
48
KAPITEL 3. STETIGE VERTEILUNGEN
Wir schreiben
X Exp() ;
wenn eine Zufallsvariable X eine Exponentialverteilung mit dem Parameter besitzt.
In einer alternativen Darstellung, die Sie in der Literatur finden werden, wird anstelle des
Parameters der Parameter = 1= verwendet. In dieser Darstellung ist dann die Dichtefunktion
(
1 x=
e
f (x) =
0
0x<1
sonst :
Es sei daran erinnert, dass die Exponentialverteilung ein Spezialfall der Gammaverteilung
ist. Eine Gammaverteilung mit dem Parameter = 1 ist eine Exponentialverteilung.
Exp() G(1; )
Abbildung 3.25 zeigt einige Dichtefunktionen in Abhängigkeit vom Parameter .
2.0
1.5
f(x)
2
1.0
0.5
1
0.5
0.0
0
1
2
3
4
5
x
Abbildung 3.25: Dichtefunktionen der Exponentialverteilung in Abhängigkeit von Die Dichtefunktionen sind monoton fallend, nehmen an der Stelle 0 den Wert des Parameters
an.
1.0
0.8
2
F(x)
1
0.5
0.6
0.4
0.2
0.0
0
1
2
3
4
5
x
Abbildung 3.26: Verteilungsfunktionen der Exponentialverteilung in Abhängigkeit von 3.5. EXPONENTIALVERTEILUNG
49
Satz 3.14 Die Verteilungsfunktion der Exponentialverteilung mit dem Parameter ist
(
0
1 e
F (t) =
t<0
t0:
für
für
t
Beweis:
Für t 0 ist
F (t) =
=
Z
0
t
f (x)dx =
e
t
Z
0
t
x dx
e
t
+1=1 e
= e
x t
0
:
}
In der alternativen Darstellung gilt:
(
F (t) =
0
1 e
t=
für
für
t<0
t0
Abbildung 3.26 zeigt einige Verteilungsfunktionen der Exponentialverteilung in Abhängigkeit des Parameters .
Obwohl wir Erwartungswert und Varianz der Exponentialverteilung aus denen der Gammaverteilung mit dem Parameter = 1 ableiten könnten, wollen wir beide hier explizit
berechnen.
Satz 3.15 Es gelte
X Exp() :
Dann gilt
EX =
Beweis:
EX =
1
1
Z
1
und
V arX =
xfX (x)dx =
1
Z
0
xe
1
:
2
x dx
Wir verwenden die Regel der partiellen Integration (siehe Gleichung (3.2) und setzen dabei
v(x) = x =) v0(x) = 1
w0(x) = e x =) w(x) = e
x
50
KAPITEL 3. STETIGE VERTEILUNGEN
Damit gilt
EX =
1
xe x 0
{z
}
=0
|
1
1Z
=
e
0
|
Dabei wurde benutzt, dass
1
Z
0
x dx
{z
lim xe
=
x )dx
1
:
}
=1
x!1
( e
x
=0
und dass das Integral über eine Dichtefunktion 1 ergibt.
Durch zweimalige Anwendung der partiellen Integration erhält man
EX 2
=
1
Z
0
x2 e
x dx
= 2=2
und damit nach Satz 2.2
V arX = EX 2
(EX )2 = 2=2
(1=)2 = 1=2
}
In der alternativen Darstellung gilt
EX = und
V arX = 2 :
Anwendungen der Exponentialverteilung:
a) Die Exponentialverteilung ist ein nützliches Modell für die Lebensdauer von Teilen,
die nicht wesentlich ,,altern”, wie elektronische Komponenten oder Fensterscheiben.
In diesem Zusammenhang ist die Exponentialverteilung durch die folgende Eigenschaft charakterisiert:
Satz 3.16 (Markoffsche Eigenschaft) Sei X die Lebensdauer eines Teiles. Die
Zufallsvariable X ist genau dann exponentialverteilt, wenn für alle x und x0
P (fX > x + x0 gjfX > x0 g) = P (fX > xg)
(3.8)
gilt.
Dieser Satz besagt, dass man Individuen (Teilen), deren Lebensdauer einer Exponentialverteilung folgt, ihr Alter nicht anmerkt. Gleichung (3.8) bedeutet, dass die bedingte
Wahrscheinlichkeit, den Zeitpunkt x + x0 zu überleben, wenn man weiß, dass der
Zeitpunkt x0 bereits überlebt wurde, genau so groß ist wie die Wahrscheinlichkeit, den
3.5. EXPONENTIALVERTEILUNG
51
Zeitpunkt x (von 0 ausgehend) zu überleben. Das bisher erreichte Alter des Individuums hat also keinen Einfluss auf die weiteren Überlebenswahrscheinlichkeiten, z.B.
gilt
P (fX > (3 + 2) JahregjfX > 2 Jahreg) = P (fX > 3 Jahreg) :
Das bedeutet die Wahrscheinlichkeit
P (fEin zwei Jahre altes Teil hält sich noch drei weitere Jahre g)
ist gleich der Wahrscheinlichkeit
P (fEin neues Teil hält sich drei Jahre g) :
Die Exponentialverteilung ist also eine Verteilung ohne Gedächtnis.
Auch Gegenstände, die sich wenig verändern, z. B. Teller, haben eine exponentialverteilte Lebensdauer.
b) Die Zeitintervalle zwischen Ereignissen eines Poissonprozesses sind exponentialverteilt. Typischerweise sind dies die folgenden Ereignisse: Unfälle, Nachfrage bestimmter Produkte, Stürme, Fluten, Telefonanrufe, radioaktiver Zerfall, usw..
Wir wollen die für einen Poissonprozess charakteristischen Eigenschaften in der folgenden Definition zusammenfassen.
Definition 3.6 Ein Poissonprozess liegt vor, wenn die folgenden Eigenschaften
erfüllt sind
i) Die Wahrscheinlichkeit, dass ein Ereignis in einem Intervall der Länge t
vorkommt, ist t, wobei eine Konstante ist.
ii) Die Wahrscheinlichkeit, dass zwei oder mehr Ereignisse in einem Intervall
der Länge t vorkommen, ist klein im Vergleich zu t.
lim
t!0
P (f2 oder mehr Ereignisse in tg)
=0
P (f1 Ereignis in tg)
iii) Die Ereignisse treten unabhängig auf.
Satz 3.17 Die Zeit zwischen zwei Ereignissen in einem Poissonprozess ist exponentialverteilt mit dem Parameter .
Beweis:
Betrachten Sie die Abbildung 3.27. Dort sind zwei Ereignisse durch das Zeichen
dargestellt.
52
KAPITEL 3. STETIGE VERTEILUNGEN
| | | | | | | | | | | | | | | | | | | | |
123
n
X
Abbildung 3.27: Zeitintervall zwischen zwei Ereignissen in einem Poissonprozess
Sei X das Zeitintervall zwischen diesen beiden Ereignissen. Die Zeitachse ist in kleine Intervalle der Länge t aufgeteilt. Die Anzahl der Teilintervalle zwischen diesen
beiden Ereignissen sei n. Wir müssen zeigen, dass die Verteilungsfunktion von X die
einer Exponentialverteilung ist (siehe Satz 3.14). Äquivalent dazu ist der Nachweis,
dass P (fX > xg), diese Funktion bezeichnet man auch als Überlebenszeitfunktion,
gegeben ist durch
P (fX > xg) =
(
0
e
x<0
x0
für
x für
Für x > 0 gilt
P (fX > xg) = P (fkein Ereignis in Intervall 1 und
kein Ereignis in Intervall 2 und
..
.
g)
P (fkein Ereignis in Intervall 1g) P (fkein Ereignis in Intervall 2g) kein Ereignis in Intervall n
=
..
.
P (fkein Ereignis in Intervall ng)
= (1
t) (1 t) : : : (1 t)}
|
{z
= (1
t)n
n
= (1 t)x=t :
Nun gilt (siehe z.B. Sydsæter und Hammond (2003), Formel (6.11.4) oder (7.10.1))
lim (1 t)x=t = e
t!0
x
:
Damit gilt für x > 0
F (x) = P (fX xg) = 1 P (fX > xg) = 1 e
x
:
}
R-Befehle zur Exponentialverteilung:
dexp(x, rate=1) berechnet die Dichtefunktion der Exponentialverteilung mit dem
Parameter =rate=1 an der Stelle x. Dabei kann x ein Vektor sein.
3.6. BETAVERTEILUNG
53
pexp(q, rate=1) berechnet die Verteilungsfunktion der Exponentialverteilung
mit dem Parameter =rate an der Stelle q . Dabei kann q ein Vektor sein.
qexp(p, rate=1) berechnet die Umkehrfunktion der Verteilungsfunktion der Exponentialverteilung mit dem Parameter =rate an der Stelle p. Dabei muss p ein
Vektor von Wahrscheinlichkeiten, d.h. von Zahlen zwischen 0 und 1 sein.
rexp(n, rate=1) erzeugt n exponentialverteilte Zufallszahlen mit dem Parameter
=rate.
3.6 Betaverteilung
Definition 3.7 Die Betafunktion ist definiert durch
B (; ) =
=
Z1
0
t 1 (1 t) 1 dt
>0 >0
() ( )
:
( + )
Es gibt eine R-Funktion beta(a,b), die die Betafunktion nach der obigen Formel berechnet.
Definition 3.8 Die Dichtefunktion der Betaverteilung ist gegeben durch
(
fX (x) =
x 1 (1 x)
B (; )
0
1
0x1
sonst :
Die Betaverteilung hat zwei Parameter, für die gelten muss
>0
und
>0:
Wir schreiben
X Be(; ) ;
wenn X eine Betaverteilung mit den Parametern und besitzt.
Die Verteilungsfunktion ist für 0 < x < 1 gleich
x
1 Z 1
FX (x) =
t (1 t) 1 dt :
B (; ) 0
54
KAPITEL 3. STETIGE VERTEILUNGEN
Das Integral auf der rechten Seite der obigen Gleichung ist auch als unvollständiger Betafunktions-Quotient (,,incomplete beta function ratio”) bekannt. Wir werden die Verteilungsfunktion bei Bedarf mit R berechnen (siehe unten).
Satz 3.18 Die Zufallsvariable X sei betaverteilt mit den Parametern und . Dann gilt
E (X ) =
+
V arX =
und
( + )2 ( + + 1)
:
Beweis:
Im folgenden Beweis benutzen wir den Zusammenhang zwischen der Betafunktion und der
Gammafunktion (siehe Definition 3.7).
EX =
Z1
0
xf (x)dx =
Z1
0
( + 1) ( )
( + 1 + )
=
+
=
EX 2
=
Z1
0
x2 f (x)dx
=
Z1
0
x
x
x) 1
B ( + 1; )
dx =
B (; )
B (; )
( + )
() ( + )
=
() ( )
() ( + )( + )
1+1 (1
x) 1
B ( + 2; )
dx =
B (; )
B (; )
( + )
( + 1) () ( + )
=
() ( )
() ( + )( + 1 + )( + )
1+2 (1
( + 2) ( )
=
( + 2 + )
( + 1)
=
( + 1 + )( + )
Mit Satz 2.2 folgt
( + 1)
2
2
2
V arX = EX (EX ) =
( + 1 + )( + )
+
2
( + 1)( + ) ( + 1 + )
=
( + 1 + )( + )2
3 + 2 + 2 + 3 2 2 =
=
:
( + )2 ( + + 1)
( + )2 ( + + 1)
!
}
Abbildung 3.28 zeigt einige Dichtefunktionen der Betaverteilung. Diese Abbildung macht
deutlich, wie verschieden die Gestalt der Dichtefunktion in Abhängigkeit der beiden Parameter sein kann. Für = 1 und = 1 ergibt sich als Spezialfall die Rechteckverteilung
3.6. BETAVERTEILUNG
55
3
3
3
0.5, 3
1, 3
3
2, 3
3, 3
2
2
2
2
1
1
1
1
0
0.0
0.5
1.0
3
0
0.0
0.5
1.0
3
0
0.0
0.5
1.0
3
0.5, 2
1, 2
0
0.0
3, 2
2
2
2
1
1
1
1
0.5
1.0
3
0
0.0
0.5
1.0
3
0
0.0
0.5
1.0
3
0.5, 1
1, 1
0
0.0
2, 1
2
2
1
1
1
1
1.0
3
0
0.0
0.5
1.0
3
0
0.0
0.5
1.0
3
0.5, 0.5
1, 0.5
0
0.0
2, 0.5
2
2
1
1
1
1
1.0
0
0.0
0.5
1.0
0
0.0
1.0
3, 0.5
2
0.5
0.5
3
2
0
0.0
1.0
3, 1
2
0.5
0.5
3
2
0
0.0
1.0
3
2, 2
2
0
0.0
0.5
0.5
1.0
0
0.0
0.5
1.0
Abbildung 3.28: Dichtefunktionen der Betaverteilung
U (0; 1). Für = ist die Dichtefunktion symmetrisch zu einer senkrechten Achse durch
x = 0:5. Vertauscht man und , so wird die Dichtefunktion an der gleichen Achse gespiegelt.
Die Betaverteilung kann auch in Abhängigkeit von den Parametern und dargestellt werden, wobei
= E (X )
und
=
1
:
+
Da die Betaverteilung nur Werte im Intervall [0; 1℄ annehmen kann, gilt
0<<1
und
>0:
Da E (X ) = =( + ) ist, gilt
=
+
und
=
1
:
+
> 0 und > 0 sind,
56
KAPITEL 3. STETIGE VERTEILUNGEN
Umgekehrt gilt:
= =
und
= (1 )= :
Mit diesen neuen Parametern gilt
E (X ) = Var(X ) = (1
und
)=(1 + ) :
Der Parameter ist ein Formparameter. Er bestimmt die Gestalt der Dichtefunktion.
Abbildung 3.29 zeigt Dichtefunktionen der Betaverteilung in Abhängigkeit von diesen Parametern.
3
3
0.33 , 0.1
3
0.33 , 0.33
3
0.33 , 0.5
2
2
2
2
1
1
1
1
0
0.0
3
0.5
1.0
0
0.0
3
0.4 , 0.1
0.5
1.0
0
0.0
3
0.4 , 0.33
0.5
1.0
0
0.0
3
0.4 , 0.5
2
2
2
2
1
1
1
1
0
0.0
3
0.5
1.0
0
0.0
3
0.5 , 0.1
0.5
1.0
0
0.0
3
0.5 , 0.33
0.5
1.0
0
0.0
3
0.5 , 0.5
2
2
2
2
1
1
1
1
0
0.0
3
0.5
1.0
0
0.0
3
0.67 , 0.1
0.5
1.0
0
0.0
3
0.67 , 0.33
0.5
1.0
0
0.0
3
0.67 , 0.5
2
2
2
2
1
1
1
1
0
0.0
0.5
1.0
0
0.0
0.5
1.0
0
0.0
0.5
1.0
0
0.0
0.33 , 0.67
0.5
1.0
0.4 , 0.67
0.5
1.0
0.5 , 0.67
0.5
1.0
0.67 , 0.67
0.5
1.0
Abbildung 3.29: Dichtefunktionen der Betaverteilung als Funktion von und Anstelle des Parameters wird auch der Parameter
'=
1
=
++1 +1
3.6. BETAVERTEILUNG
57
betrachtet. Für diesen Parameter gilt 0 < ' < 1. Es ist dann
= (1 ')='
und
= (1 )(1 ')=' :
Mit den Parametern und ' gilt
E (X ) = Var(X ) = (1
und
)' :
Abbildung 3.30 zeigt Dichtefunktionen der Betaverteilung in Abhängigkeit von den Parametern und '.
3
3
0.33 , 0.1
3
0.33 , 0.25
3
0.33 , 0.33
2
2
2
2
1
1
1
1
0
0.0
3
0.5
1.0
0
0.0
3
0.4 , 0.1
0.5
1.0
0
0.0
3
0.4 , 0.25
0.5
1.0
0
0.0
3
0.4 , 0.33
2
2
2
2
1
1
1
1
0
0.0
3
0.5
1.0
0
0.0
3
0.5 , 0.1
0.5
1.0
0
0.0
3
0.5 , 0.25
0.5
1.0
0
0.0
3
0.5 , 0.33
2
2
2
2
1
1
1
1
0
0.0
3
0.5
1.0
0
0.0
3
0.67 , 0.1
0.5
1.0
0
0.0
3
0.67 , 0.25
0.5
1.0
0
0.0
3
0.67 , 0.33
2
2
2
2
1
1
1
1
0
0.0
0.5
1.0
0
0.0
0.5
1.0
0
0.0
0.5
1.0
0
0.0
0.33 , 0.5
0.5
1.0
0.4 , 0.5
0.5
1.0
0.5 , 0.5
0.5
1.0
0.67 , 0.5
0.5
1.0
Abbildung 3.30: Dichtefunktionen der Betaverteilung als Funktion von und '
58
KAPITEL 3. STETIGE VERTEILUNGEN
Anwendungen der Betaverteilung
a) Aufgrund der großen Flexibilität der Gestalt der Dichtefunktion ist die Betaverteilung
sehr gut geeignet für stetige Zufallsvariablen, die nur Werte im Intervall (0; 1) annehmen, z.B. als Modell für Anteile.
b) Wir werden die Betaverteilung als Modell für die Apriori-Verteilung des Parameters einer Bernoulli-Verteilung verwenden (siehe S. 192). Die Betaverteilung wird sich als
konjugierte Verteilung (siehe Beispiel 10.7) der Binomialverteilung erweisen, und wir
werden sie zur Konstruktion der Beta-Binomialverteilung verwenden (siehe S. 176).
c) In der ,,Normalverteilungstheorie” erhält man die Betaverteilung als Verteilung von
V 2 = X12 =(X12 + X22 ) ;
wobei X12 ; X22 unabhängige 2 -verteilte Zufallsvariablen sind mit den Parametern n1
und n2 . Es gilt dann
V 2 Be(n1 =2; n2 =2) :
Da die 2 -Verteilung ein Spezialfall der Gammaverteilung ist, folgt dieses Resultat
aus dem folgenden allgemeineren: Wenn X1 und X2 eine Gammaverteilung mit identischem Parameter und 1 bzw. 2 besitzen, so gilt:
X1
X1 + X2
Be(1; 2 ) :
d) Die Zufallsvariable X besitze eine F -Verteilung (siehe Definition 5.2) mit 1 und 2
Freiheitsgraden, dann gilt:
1 X
2 + 1 X
Be(1 =2; 2=2) :
e) Für = = 1=2 ergibt sich als Spezialfall die Arcus-Sinus-Verteilung, die in der
Theorie der ,,random walks” Anwendung findet. Erfüllen die Parameter + = 1
(jedoch 6= 1=2), so spricht man auch von einer verallgemeinerten Arcus-SinusVerteilung.
f) Seien U1 ; U2 ; : : : Un unabhängig und identisch U (0; 1)-verteilt. Ordnet man die Realisationen u1 ; u2 ; : : : ; un der Größe nach, so dass
u(1) u(2) u(3) : : : u(n) ;
so nennt man die durch diese Umordnung neu entstehenden Zufallsvariablen
U(i) ; i = 1; 2; : : : ; n
die i-ten Ordnungsstatistiken, die ganz allgemein bei der Konstruktion verteilungsfreier Verfahren Anwendung finden. Unter der obigen Annahme der Rechteckverteilung
für Ui gilt
U(i) Be(i; n i + 1) :
3.6. BETAVERTEILUNG
59
R-Befehle zur Betaverteilung:
dbeta(x, shape1, shape2) berechnet die Dichtefunktion der Betaverteilung
mit den Parametern =shape1 und =shape2 an der Stelle x. Dabei kann x ein
Vektor sein.
pbeta(q, shape1, shape2) berechnet die Verteilungsfunktion der Betaverteilung mit den Parametern =shape1 und =shape2 an der Stelle q . Dabei kann q
ein Vektor sein.
qbeta(p, shape1, shape2) berechnet die Umkehrfunktion der Verteilungsfunktion der Betaverteilung mit den Parametern =shape1 und =shape2 an der
Stelle p. Dabei muss p ein Vektor von Wahrscheinlichkeiten, d.h. von Zahlen zwischen
0 und 1 sein.
rbeta(n, shape1, shape2) erzeugt n betaverteilte Zufallszahlen mit den Parametern =shape1 und =shape2.