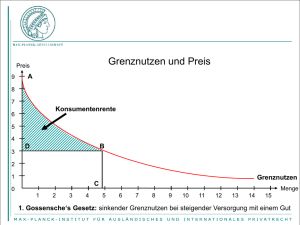
Aufgabe 22 - Administracja SGH

Aufgabe 22
• Die Aussage ist nicht richtig.
• Richtig ist: „Die Produktionsfunktion zeigt, welche
Produktmengen mit gegebenen Inputmengen maximal
produziert werden können.“
38
Aufgabe 23
23 a.
W
23 b.
Schnittpunkt der beiden
Kurven:
Wendepunkt der
Gesamtertragskurve
M Maximum des
Gesamtertrages
Q Durchschnittsertrag =
Grenzertrag
(Fahrstrahl = Tangente)
DE=
Durchschnittsertrag =
GE= Grenzertrag=
∆
∆
•
•
•
Durchschnittertrag ist (i)
maximal und (ii) gleich dem
Grenzertrag
Links vom Schnittpunkt: GE>DE
→DE↑
Rechts vom Schnittpunkt:
GE<DE → DE↓
23 c.
39
Aufgabe 24 a
• GRTS gibt an, um wie viele Einheiten der Produktionsfaktor v2 erhöht (gesenkt) werden muss, wenn bei
gleicher Ausbringungsmenge x der Faktoreinsatz v1 "um
eine Einheit" reduziert (erhöht) wird.
• Sie entspricht der Steigung einer Isoquanten im Punkt
(v1,v2).
i. Vollständige Substitute: GRTS = konstant
ii. Vollständige Komplementäre: GRTS = 0
40
Aufgabe 24 b und c
• Aufgabe 24b
– Produktionsfunktion
–
=−
,
=
= ∙
=
∙
∙
∙
∙
∙
⁄
= ∙
=
∙
⁄
∙
.
=
• Aufgabe 24c
– Minimalkostenkombination:
– (1)
"
#
= ⇒
=2∙
,
=−
=
=
!
!
einsetzen in die Kostenfunktion:
– 200 = 2 ∙ + 4 ∙ ⇒ 200 = 2 ∙ 2 ∙ + 4 ∙ = 8 ∙
– K= 25 einsetzen in (1): - = ,.
⇒ optimale Faktorkombination: K=25; A=50
⇒ * = +,
41
Aufgabe 25
• Skalenerträge beschreiben, wie sich der Output bei einer
gleichmäßigen Erhöhung der Inputs verändert.
• Sie können auch an der Kostenfunktion bestimmt werden,
da diese aus der Produktionsfunktion abgeleitet ist.
– Konstante Skalenerträge (constant returns to scale)
Eine Verdoppelung des Output führt zu einer Verdoppelung der Kosten
→ Durchschnittskosten bleiben konstant und sind identisch mit den
Grenzkosten; beide Kurven verlaufen horizontal.
– Zunehmende Skalenerträge (economies of scale)
Bei steigendem Output sinken die gesamten Durchschnittskosten.
– Abnehmende Skalenerträge (diseconomies of scale)
Mit steigendem Output erhöhen sich die gesamten Durchschnittskosten.
42
Skalenerträge anhand der Produktionsfunktion (I)
konstante Skalenerträge
zunehmende Skalenerträge
43
Skalenerträge anhand der Produktionsfunktion (II)
Abnehmende Erträge:
Der Abstand zwischen
den Isoquanten nimmt
zu.
44
Skalenerträge und Kostenfunktion
Skalenerträge
zunehmende konstante
abnehmende
Erlösfunktion
GE>DE
GE = DE
GE<DE
Kostenfunktion
GK<DK
GK=DK
GK>DK
GE = Grenzertrag,
DE= Durchschnittsertrag
GK= Grenzkosten,
DK= Durchschnittskosten
45
Aufgabe 26
• Kostenfunktion
• 26 a
0
=3
– Grenzkosten (GK)=
− 450
=9
– Durchschnittskosten (DK)=
#
#
+ 22500
− 900 + 22500
=3
#
− 450 + 22500
• 26b
– 1. Schnittpunkt von GK- und DK-Kurve bestimmen: GK=DK
• 9
• 6
#
− 900 + 22500 = 3
#
− 450 = 0 ⇒ x=75
#
− 450 + 22500
– 2. Bestimmung des Minimums der DK-Kurve. Dazu DK-Funktion
nach x ableiten und gleich null setzen.
•
6
= 6 − 450 = 0 ⇒ x=75
– Damit ein Minimum vorliegt, muß die 2. Ableitung der DK-Funktion
>0 sein: DK‘‘=6 > 0
⇒ Bei der Menge x=75 hat die DK-Kurve tatsächlich ihr Minimum.
46
Aufgabe 27
• Damit Grenzkosten- und die Angebotskurve eines
Unternehmens identisch sind, muß gelten:
1. Auf dem Markt, auf dem das Unternehmen operiert, herrscht
vollständiger Wettbewerb (homogenes Polypol), so daß es
sich als Mengenanpasser verhalten muß.
2. Das Unternehmen hat das Ziel der Gewinnmaximierung.
47
Aufgabe 28 a und b
a. gewinnmaximierende Produktionsmenge
– Gewinnmaximierungsregel bei vollständigem Wettbewerb: Preis
= Grenzkosten →7 =
– GK =
= 1000 + 250 ; p = 3.000
– 1000 + 250 = 3000 →
=8
b. Umsatz, Kosten, Gewinn
– Umsatz U = p*x= 3.000*8= 24.000
– Fixkosten : = 6.000(ablesen aus der Kostenfunktion!)
– Variable Kosten < = 1.000 + 125 # = 1.000 ∙ 8 + 125 ∙ 8# =
16.000
– Gesamtkosten = : + < = 6.000 + 16.000 = 22.000
– Gewinn = Umsatz – Kosten = 24.000 – 22.000 = 2.000
48
Aufgabe 28 c
• Langfristig sollte das Unternehmen seine Gesamtkosten
= : + < decken können.
• Kurzfristig kann das Unternehmen weiter anbieten,
solange p > > < bzw. Umsatz (U) > < . Ist p >> < (U>
< )kann das Unternehmen mit dem sich ergebenden
Betrag einen Teil der Fixkosten decken. In der BWL
spricht man vom Deckungsbeitrag.
• Ist p< > < (U< < )wird das Unternehmen die Produktion
ganz einstellen.
• Hier ist p >> < (3.000>2.000) bzw. U > < (24.000 >
16.000 → 8.000 bleiben zur Deckung der Fixkosten), d.h.
die Produktion kann kurzfristig weitergeführt werden.
49
Abbildung zu Aufgabe 28c:
Die kurzfristige Angebotskurve der Unternehmung bei vollständiger
Konkurrenz
Kosten
Bei P > DK macht
die Unternehmung
Gewinne.
kurzfristige
Angebotskurve
GK
DK
Bei P > DVK wird
die Unternehmung
kurzfristig weiter
betrieben.
Bei P < DVK
wird der
Betrieb
eingestellt.
DVK
0
2012 © Schäffer-Poeschel Verlag für Wirtschaft • Steuern • Recht • GmbH www.sp-dozenten.de
Menge
50
Institut für Wirtschaftswissenschaft. Universität Erlangen-Nürnberg.
50
Aufgabe 29
a. Bei vollständigem Wettbewerb gilt Preis = Grenzkosten,
d.h. da p = 0,30 € → GK = 0,30 €.
b. Eine Branche befindet sich langfristig im
Gleichgewicht wenn der Preis gleich dem Minimum
der gesamten Durchschnittskosten entspricht (@ = A*).
– Hier liegen die DK = 0,20 € unter dem Marktpreis von p = 0,30 €.
Deshalb kann sich die Branche nicht im langfristigen
Gleichgewicht befinden.
– Da die Unternehmen in dieser Situation kurzfristig Gewinne
machen, kommt es zu Markteintritten anderer Unternehmen.
51
Aufgabe 30 a.
• Im langfristigen Gleichgewicht ist der Preis für Gold
gleich dem Minimum der gesamten Durchschnittskosten
der Goldproduktion (@ = A*).
• Die einzelnen Anbieter von Gold machen demzufolge
weder Gewinn noch Verlust.
52
Aufgabe 30 b.
• Kurzfristig bewirkt die gestiegene Nachfrage nach Gold
von D1 auf D2 zunächst einen Anstieg des Preise auf P2,
von dem die einzelnen Goldminen profitieren.
• Die gewinnmaximale Produktionsmenge einer Goldmine
steigt. Da der Marktpreis über den durchschnittlichen
Gesamtkosten des Goldabbaus liegt, erzielt die
einzelnen Goldmine einen Gewinn.
53
Aufgabe 30 c.
• Langfristig locken die Gewinne neue Goldsucher an
(Markteintritte), deren zusätzliche Goldproduktion das
Angebot erhöht und den Preis wieder auf das Minimum
der Durchschnittskosten, also auf P1, sinken läßt.
• Dauerhaft erhöht hat sich nur die Goldproduktion.
• Im langfristigen Gleichgewicht macht kein Unternehmen
Gewinn.
54
Aufgabe 31
• Die einzelbetriebliche Nachfragekurve nach einem
Produktionsfaktor entspricht der Wertgrenzproduktkurve
– Wertgrenzprodukt (WGP) =p ∙
<
a. Wenn p steigt, steigt WGP → Faktornachfragekurve
verschiebt sich nach rechts.
b. Der substitutive Produktionsfaktor wird den billigeren
Produktionsfaktor ersetzt. Dessen Nachfrage steigt →
Faktornachfragekurve verschiebt sich nach rechts.
c. Durch technischen Fortschritt steigt das Grenzprodukt
→ Faktornachfragekurve verschiebt sich nach rechts.
<
55
Aufgabe 32
• Bei vollständigem Wettbewerb entspricht bei einem Unternehmen, das seinen Gewinn maximiert, die Entlohnung
des Produktionsfaktors Arbeit (Lohn) dem Wertgrenzprodukt (WGP).
• Die Kosten einer zusätzlichen Arbeitskraft müssen demzufolge über der Verkauf des Endproduktes verdient werden.
• Der zusätzliche Verkaufserlös (Grenzerlös bzw. –umsatz)
einer weiteren verkauften Einheit ist der Preis.
• Steigen die Preise auf dem Gütermarkt, kann der
Arbeitseinsatz mehr kosten und folglich kann Arbeit höher
entlohnt. Sinkt dagegen der Absatzpreis, so muß der
Arbeitseinsatz auch weniger kosten und der Lohnsatzfällt.
56
Aufgabe 33 a
57
Aufgabe 33 b
Da WGP = Faktorpreis (Lohnsatz) gelten muss, sollte Patrick zwei
Arbeiter beschäftigen.
58
Aufgabe 33 c
c) Neuer optimaler Punkt:
Patrick sollte jetzt 4 Arbeiter
beschäftigen.
59
Aufgabe 34 a-b.
• 34a. Vollkommener Markt
– Sachliche Gleichartigkeit der Güter
(keine Qualitätsunterschiede)
– Keine persönlichen Präferenzen
– Keine räumliche Differenzierung
Homogenitätsbedingung
– Keine zeitliche Differenzierung
– Vollständige Markttransparenz
(Alle Marktteilnehmer sind stets vollständig über
Marktverhältnisse informiert)
• 34b. unvollkommener Markt : Mindestens eine diese
Bedingungen ist nicht erfüllt.
60
Aufgabe 34 c
i.
Vollständiger Wettbewerb
1. Zahl und Größe der Marktteilnehmer:
− Sehr große Zahl von kleinen Anbietern und Nachfragern (Polypol)
2. Vollkommener Markt:
• Keine sachlichen, persönlichen, räumlichen und zeitlichen Präferenzen
(Homogenität)
• Völlige Markttransparenz
• Unendliche Reaktionsgeschwindigkeit
• Freier Marktzutritt und Marktaustritt
ii. Nur Mengenanpasser
iii. Monopolist: Preis- oder Mengenfixierung
61
Aufgabe 34 d (I)
• Referenzmaß, das in der Realität kaum anzutreffen
ist
– Homogenitätsbedingungen sind i.d.R. nicht erfüllt und deren
Erfüllung ist auch nicht unbedingt wünschenswert, da sonst
eintöniges Güterangebot.
– Völlige Markttransparenz ist nicht gegeben, weil Wirtschaftssubjekte keine vollkommene Information haben (können)
– i.d.R. keine unendliche Anpassungsgeschwindigkeit
„Nirwana-Ansatz“ (Demsetz, 1969)
62
Aufgabe 34 d (II)
• Problematisches Verständnis von Wettbewerb
– Wichtige Aktionsparameter, die in der Realität von großer
Bedeutung sind, wie Preise, Qualität oder Reklame stehen in
diesem Modell für die Unternehmer nicht zur Verfügung.
– De facto fehlen damit die Anreize zu unternehmerischem Handeln,
insbesondere zu Innovationen.
− „Vollkommener Wettbewerb bedeutet tatsächlich das Fehlen aller
wettbewerblichen Tätigkeiten“ (Hayek, 1948/76, S. 128).
− „Schlafmützenkonkurrenz“ (F.A. Lutz)
− In der Realität ist Wettbewerb aber ein dynamischer Prozess, der
durch die Handlungen der Unternehmer am Leben erhalten wird
und zu ständigen Veränderungen führt.
63
Aufgabe 34 d (III)
• Problematische normative Schlußfolgerungen, wenn
vollständiger Wettbewerb das Leitbild für die Wirtschaftspolitik ist:
– Verglichen wird die Realität mit einem (unrealistischen)
Idealzustand.
– Die Realität ist bei einem solchen Vergleich notwendigerweise
immer „unvollkommen“.
– Dies wird dann häufig als „Marktversagen“ bezeichnet.
– Zur Beseitigung des Marktversagens werden staatliche Eingriffe
empfohlen, um möglichst nahe an den Idealzustand zu kommen.
→ Gefahr ständiger staatlicher Eingriffe, vor allem in die
Marktstruktur, aber nicht selten auch ins Marktergebnis.
→ Solche Interventionen haben in der Regel unerwartete Neben- und
Folgeeffekte („Kobra-Effekte“).
64
Aufgabe 34 d (IV)
• Der Versuch der Wirtschaftspolitik, die Realität dem Ideal
des vollständigen Wettbewerbs anzugleichen ist
„Anmaßung von Wissen“ (Pretence of knowledge) (F.A.
von Hayek, 1974)
– Grund: Aus den Annahmen des Modell folgt, daß ein außenstehender Beobachter (Ökonom) die Gleichgewichtspreise und optimale
Produktionsmengen objektiv bestimmen könne.
– In der Realität ist dies wegen der dynamischen Natur des
Wettbewerbs aber nicht möglich. Alle Parameter, die das Modell
als konstant annimmt, verändern sich ständig.
– Wettbewerb ist deshalb ein offener Prozeß, d.h. die Ergebnisse
des Wettbewerbs können nicht vorhergesagt werden.
65
Aufgabe 35 a
• Gewinnmaximierungsbedingung des Monopolisten:
Grenzumsatz (GU) = Grenzkosten (GK)
• C = 7 ∙ = 20 − ∙ = 20 − #
•
•
C=
D
=2+
= 20 − 2
#→
=
=2 • 20 − 2 = 2 →E = ,einsetzen in:
• 7 = 20 − →F = G,
66
Aufgabe 35 b und c
b. Umsatz, Kosten und Gewinn
– C = 7 ∙ = 5 ∙ 15 = 75
–
= 2 + # = 2 + 5² = 27
–
= C − = 60 − 27 = 48
c. Verhalten als Mengenanpasser
–
–
–
–
–
–
Gewinnmaximierungsbedingung: p = GK (Nachfrage = Angebot)
20 − = 2 ↑→ = 6, 66
einsetzen in p = 20 − = 20 − 6, 66 = 13, 33
C = 7 ∙ = 13, 33 ∙ 6, 66 = 88,89
= 2 + # = 2 + 6, 66² = 46,44
= C − = 88,89 − 46,44 = 42, 45
• Polypol- und Monopollösung in eine Zeichnung! (siehe
nächste Folie)
67
Aufgabe 35 c: Zeichnung
Monopol- und Polypolpreisbildung
68
Aufgabe 36a
• Lösen mithilfe der Amoroso-Robinson-Relation:
G
F G−
= LMNOPQRSTNO
K
• Gegeben ist jeweils die Relation Preis zu GK, also
U
V
• Damit kann man die Amoroso-Robinson-Relation nach
der Preiselastizität der Nachfrage auflösen: W = X
Y
i.
ii.
U
V
=
U
V
=
[\
\\
0
#
= →W =
^\
\\
= →W =
_
[
=3
]
`
a
= 2,25
69
Aufgabe 36b
• Lösen mithilfe der Amoroso-Robinson-Relation:
G
F G−
= LMNOPQRSTNO
K
• Wenn W = 1, müssen in beiden Fällen die GK = 0 sein.
U
V
• Tatsächlich kann die Relation Preis zu GK
nicht
bestimmt werden, weil durch 0 nicht dividiert werden
kann.
70
Aufgabe 37 (I)
(1) Richtig.
• Bei zunehmenden Skalenerträgen sind Grenzkosten >
Durchschnittskosten
• Bietet er in diesem Bereich gemäß der Regel p=GK an, erleidet er
Verluste.
(2) Die GK-Kurve ist nur in dem Bereich mit der Angebotskurve
identisch, in dem die GK-Kurve oberhalb der DK-Kurve liegt.
Würde der Anbieter im Teil der GK-Kurve anbieten, der unterhalb der DK-Kurve liegt, würde der Anbieter einen Verlust
machen.
(3) Nein.
– Monopolisten setzen den Preis nach der Gewinnmaximierungsregel
Grenzumsatz = Grenzkosten.
– Würde er den höchst möglichen Preis verlangen, bedeutet dies, daß er im
Schnittpunkt der Nachfragekurve mit der Preisachse operieren würde. Hier
wäre der Umsatz aber 0 und es ergäbe sich einen Verlust in Höhe der fixen
Kosten (variablen Kosten wären 0, da x=0)
71
Aufgabe 37 (II)
(4) Die Gewinnmaximierungsbedingung des Monopolisten,
dargestellt mithilfe der Amoroso-Robinson-Relation
7 1−
=
zeigt, daß W > 1 sein muß, also
b
elastisch sein muß, da nur dann p>0 und GK > 0, also
positiv sind.
–
1−
b
=
V
U
>0→1−
b
>0→1>
b
→ K > G
72
Aufgabe 38a (I)
• Gewinnmaximierungsbedingung eines Monopolisten bei
Preisdiskriminierung: GU1=GK=GK2
• Gewinnmaximale Menge und Preis auf Markt 1
– 7=8−
– C =7∙ = 8−
–
C=
D
=8−2 ;
=8 −
#
= 4→ 8 − 2 = 4 → E = +
– Einsetzen in: F = 8 − = 8 − 2 = d
– Gewinn (G) = Umsatz (U) – Kosten (K)
• C=7∙
= 6 ∙ 2 = 12
•
=4⇒
=
=4 =4∙2= 8
• L = 12 − 8 = e
– Preiselastizität der Nachfrage W
–
U
= −1 → W
,U
f
#
,U
=
U
∙
U
= −1 ∙ = −3
73
Aufgabe 38a (II)
• Gewinnmaximale Menge und Preis auf Markt 2
– 7 = 16 −
– C = 7 ∙ = 16 −
–
C=
D
= 16 −
= 16 − 2 ;
#
= 4→ 16 − 2 = 4 → E = d
– Einsetzen in: F = 16 − = 16 − 6 = G.
– Gewinn (G) = Umsatz (U) – Kosten (K)
• C=7∙
= 10 ∙ 6 = 60
•
=4⇒
=
= 4 = 4 ∙ 6 = 24
• L = 60 − 24 = gd
– Preiselastizität der Nachfrage W
–
U
= −1 → W
,U
= −1 ∙
\
f
,U
=
U
∙
U
= −1,67
• Gesamtgewinn = Gewinn Markt 1 + Gewinn Markt 2 =
4+36 = 40
• Da auf Markt 2 Preiselastizität der Nachfrage geringer ist, kann
74
dort ein höherer Preis verlangt werden.
Graphische Lösung zu 38 a
75
Aufgabe 38b
• Angenommen der Monopolist verlangt auf beiden
Märkten p = 6 €
• Gewinn auf Markt 1
– p = 6 einsetzen in 7 = 8 −
– C = 7 ∙ = 6 ∙ 2 = 12
–
=4 =4∙2=8
– G = U – K= 12 – 8 = 4
→E=+
• Gewinn auf Markt 2
– p = 6 einsetzen in 7 = 16 −
– C = 7 ∙ = 6 ∙ 10 = 60
–
= 4 = 4 ∙ 10 = 40
– G = U – K= 60 – 40 = 20
→ E = G.
• Gesamtgewinn= 4+20=24 ist kleiner als bei
verschiedenen Preisen auf beiden Märkten (dort G=40).
76
Aufgabe 38 c
• Preisdiskriminierung 3. Grades
• Voraussetzungen:
– Der Markt kann in zwei Gruppen eingeteilt werden, wobei jede
Gruppe eine eigene Nachfragefunktion hat, d.h. unterschiedliche
Preiselastizitäten der Nachfrage.
– Arbitragegeschäfte müssen ausgeschlossen werden.
77
Aufgabe 38 d (I)
• Preisdiskriminierung ersten Grades
– Der Monopolist würde von jedem einzelnen Kunden den maximalen
Preis verlangen, den dieser bereit wäre zu bezahlen
(→ vollkommene Preisdifferenzierung)
Quelle: Pindyck & Rubenfeld (2009, S. 514).
78
Aufgabe 38 d (II)
Preisdiskriminierung zweiten Grades
Bei der Preisdiskriminierung zweiten Grades handelt es sich um die Diskriminierung
nach der konsumierten Menge – bzw. die Einteilung in Blöcke oder Pakete.
Beispiele:
•
•
Quelle: Pindyck & Rubenfeld (2009, S. 515).
Mengenrabatt
Paketpreisbildung
(Elektrizitäts-,
Gas- oder
Wasserwerke)
79
Aufgabe 39 a
• Monopson
– Ziel: Maximierung des Gewinns beim Einsatz des
Produktionsfaktors v: Gewinn = Umsatz – Kosten → max!
• Zur Unterscheidung vom Monopol werden die Kosten beim Monopson
häufig als Ausgaben bezeichnet: Gewinn = Umsatz – Ausgaben → max
–
V
<
=
D
<
– C=7∙
−
<
=0→
k →
hi
hj
hi
hj
=7∙
=
<
hhj
=Wertgrenzprodukt (WGP)
– l m = 16 − k (ist in der Aufgabe bereits angegeben!)
– Ausgaben = Faktorpreis * Faktormenge = 4 + k ∙ k = 4k + k #
–
hhj
= 4 + 2k, gleichsetzen mit WGP
– 16 − k = 4 + 2k→j = e
– Einsetzen in n = 4 + k→ o = p
80
Aufgabe 39 b
• Vollständiger Wettbewerb („Polypson“)
– Ziel: Maximierung des Gewinns beim Einsatz des
Produktionsfaktors v: Gewinn = Umsatz – Kosten → max!
– Gewinnmaximierungsregel: WGP = Faktorpreis
(⇒Faktornachfrage = Faktorangebot)
• Faktornachfrage: l m = 16 − k (ist in der Aufgabe angegeben!)
• Faktorangebot = Faktorpreis = q= 4 + v
– 16 − k = 4 + k→j = d
– Einsetzen in n = 4 + k→ o = G.
81
Aufgabe 39 b
82
Aufgabe 40
Bezeichnung
Ursache
Empirische Relevanz
Ressourcenmonopol
Einer Unternehmung allein
gehört eine für die Produktion wichtige Ressource
(Schlüsselressource).
selten
staatliche legitimierte
oder geschütztes
Monopol
Regierungen erlauben nur
einer Unternehmung, in
einem Bereich tätig zu sein
Häufigste Form!
(z.B. Deutsche Bahn,
Post, Schornsteinfeger,
Patente)
(„reines“ natürliches)
Monopol
Technologische bzw. unter- Selten von langfristiger
nehmerische Überlegenheit Dauer (z.B. Intel,
Microsoft?)
natürliches Monopol
Zunehmende
Skalenerträge
Versorgungsunternehmen
Unternehmenszusammenschlüsse
Skalenerträge, geringere
Transaktionskosten
Führt selten zu dauerhaften Monopolstellungen
83
Aufgabe 41
• Ökonomische Eintrittsbarrieren:
– hoher Kapitalbedarf für den Markteintritt (z.B. Bau einer
Eisenbahnlinie),
– Preisdiskriminierung, Preisunterbietung,
– Werbung,
– vertikale Bindungen.
• Staatliche (rechtliche) Eintrittsbarrieren:
–
–
–
–
–
Investitions-, Neugründungs- oder Niederlassungsverbote,
Zünfte im Mittelalter,
Befähigungsnachweise,
Importbeschränkungen.
Patente, Copyright
• Frage: Welche Eintrittsbarrieren sind legitim und
welche bedenklich?
84
Aufgabe 42 a (I)
• Es wird weniger angeboten zu einem höheren Preis. Ressourcen
bleiben ungenutzt.
• Konsumentenrente wird geringer, da ein Teil davon der Monopolist
abschöpft. Gleichzeitig sinkt die Gesamtrente, weil nicht alle
vorteilhaften Transaktionen durchgeführt werden
85
Aufgabe 42 a (II)
Diagramm (a) zeigt eine vollkommen wettbewerbliche Industrie: Output ist QC und der Marktpreis PC ist gleich den
Grenzkosten MC. Weil der Preis genau den durchschnittlichen Kosten des Produzenten entspricht, gibt es keine
Produzentenrente. Die Gesamtrente ist daher identisch mit der Konsumentenrente (schattierte Fläche).
Diagramm (b) zeigt eine monopolistische Industrie: der Monopolist verringert die Outputmenge auf QM und
verlangt einen Preis von PM. Die Konsumentenrente (die blaue Fläche) hat sich verkleinert, weil ein Teil von ihr
als Monopolgewinn abgeschöpft wird (die grüne Fläche). Die Gesamtrente sinkt: Der Nettowohlfahrtsverlust
86
(die orangefarbene Fläche) stellt den Wert der gegenseitig vorteilhaften Transaktionen
dar, die aufgrund
86
des Monopolverhaltens nicht zustande kommen.
Aufgabe 42 b (I)
• Wettbewerbsverständnis
– Statisch: Vergleich von Ergebnissen in einem Endzustand
• Einwand: Wettbewerb ist aber ein dynamischer, ergebnisoffener
Prozess → ständige Veränderungen →Vergleiche können nur
Momentaufnahmen sein
– Teleologisch: Mit Wettbewerb soll ein definierter optimaler Zustand
(Pareto-Optimum) erzielt werden.
• Einwand: Wettbewerb hat kein Ziel an sich.
• Wissensproblem:
– Wettbewerb ist ein Entdeckungsverfahren (Hayek, 1968) zur
Generierung des wirtschaftsrelevanten Wissens.
– Da die Ergebnisse dieses Entdeckungsprozesses von niemanden
antizipiert werden können, können sie auch nicht diktiert werden.
– „Jeder Versuch, einen (monopolistischen) Anbieter dazu
anzuhalten, so zu handeln, „als ob“ Wettbewerb bestünde, ist
absurd…“, (Hayek (1979/81), weil Anmaßung von Wissen.
87
Aufgabe 42 b (II)
• Monopolregulierung ist ein Eingriff in die
Handlungsfreiheit
– Ohne staatliche Eintrittsbarrieren gibt es eigentlich keine beständigen
Monopolstellungen.
– Kommt es dennoch zu einer lang andauernden Monopolstellung, kann diese
nur auf überlegenes Unternehmertum zurückgeführt werden. Das
Unternehmen bietet billiger und besser an als potentielle Kunden, sonst wäre
diese ja in den Markt eingetreten.
– [I]t would “be absurd to punish the possessor [of superior skills] for doing
better than anyone else by insisting that he should do as well as he can”
(Hayek, 1990: 72).
88
Aufgabe 43
• Das Unternehmen macht Verluste bei Preisfestsetzung auf dem
Niveau der Grenzkosten
– Grund: Bei sinkenden Durchschnittskosten, sind die Grenzkosten immer
niedriger als die durchschnittlichen Gesamtkosten.
• Negative Anreize für den Unternehmen zu Innovationen und
Kostensenkung, weil Regierung dann eine Preissenkung verlangt.
• Wissensproblem, insbesondere bei der Schätzung der Kosten- und
Nachfragefunktionen des Unternehmens, da diese sich bei sich
entwickelnden Marktbedingungen ändern. Bei Ertragsratenregulierung
Probleme bei der Bewertung des Kapitalstocks und der Festlegung
einer „fairen“ (was ist das?) Ertragsrate.
• Da das natürliche Monopol nicht aufgrund staatlicher Eintrittsbarrieren, sondern den spezifischen Produktionsbedingungen geschuldet
ist, wäre jede Regulierung ein Eingriff in die Handlungsfreiheit des
Unternehmers seinen Preis so zu setzen, wie es die
Marktbedingungen erlauben
89
Aufgabe 44 (I)
• Das Gefangenendilemma zeigt, warum Kooperation
selbst dann schwer fällt, wenn sie für beide Seiten
Vorteile bringt.
• Für Oligopolisten stellt sich stets die Frage, wie die
Konkurrenten auf Aktionen reagieren. Versuchen die
Oligopolisten sich abzusprechen, um ein Kartell zu
bilden und so also wie ein Monopolist zu agieren, stellt
sich die Frage, ob die Kartellvereinbarung eingehalten
wird.
90
Aufgabe 44 (II)
• Das Monopolergebnis zu realisieren ist für die
Oligopolisten genauso rational wie das Schweigen der
Gefangenen. Für jeden einzelnen besteht jedoch ein
Anreiz zur Vertragsverletzung.
• So wie das Eigeninteresse (Vermeidung einer Haftstrafe)
die Gefangenen in das Gefangendilemma und zum
Geständnis treibt, so macht es das Eigeninteresse für
die Oligopolisten (Erhöhung des Gewinns durch den
Verkauf zusätzlicher Produktionsmengen) schwer, die
Kooperation beizubehalten und durch eine niedrigere
Produktionsmenge laut Absprache gemeinsam hohe
Preise und hohe Gewinne zu erzielen.
91
Aufgabe 45a
• Gegeben sind:
– Marktnachfrage 7 = 120 − 2 , wobei 7 = 7( + # ) →
7 = 120 − 2 − 2 #
– Produktionskosten für beide Duoplisten = K = 20x
• Gewinnmaximum: Grenzumsatz=Grenzkosten
• Unternehmen 1:
– C =7∙
–
C =
uD
u
– 120 − 4
= 120 − 2
= 120 − 4
−2
#
−2
#
− 2 #;
∙
= 120
−2 ² −2 #
= 20
= 20
G
+
– EG = +, − E+ → Reaktionsfunktion von Unternehmen 1
• Aufgrund der Symmetrie beider Unternehmen gilt für
auch für Unternehmen 2:
G
+
– E+ = +, − EG → Reaktionsfunktion von Unternehmen 2
– (oder gleiche Berechnung wie für Unternehmen 1)
92
Aufgabe 45a und 5
• Abb. zu 45a
• Abb. zu 45b
93
Aufgabe 45b
• Durch Einsetzen in die Reaktionsfunktion von
Unternehmen 1 erhält man die Gleichgewichtsmenge
des 1 und entsprechend auch für 2:
– x = 25 − (25 − x ) → EG = Gd, dd; E+ = Gd, dd
#
#
• Gleichgewichtspreis:
– F = 120 − 2
−2
#
= 120 − 2 ∙ 16,66 − 2 ∙ 16,66 = ,g, gg
• Gewinn:
–
= 7 ∙ − 20 ∙ = 555,67
– Aufgrund der Symmetrie gilt auch:
#
=7∙
#
− 20 ∙
#=
555,67
94
Aufgabe 45c Stackelberg-Lösung (I)
•
Gegeben:
– Marktnachfrage 7 = 120 − 2 → 7 = 120 − 2
– Grenzkosten für beide Duoplisten = GK = 20
•
−2
#
Das Unternehmen 1 setzt die Produktionsmenge als
erstes fest, danach das Unternehmen 2
–
Unternehmen 1 setzt in die Marktnachfragefunktion die
G
Reaktionsfunktion von Unternehmen 2 (E+ = +, − EG ) ein:
+
7 = 120 − 2
•
ixSyTPiG = 7 ∙
•
–
G
+
− 2 G, − EG = 120 − 2
•
C = 70 − 2
= w. − EG
= 70
− 50 + x = w. − EG
− ²
= GK = 20 →EG = +,
einsetzen in Reaktionsfunktionsfunktion des 2: z + = 25 − 25 =
#
G+, ,
• Marktpreis F = 120 − 2 ∙ 25 − 2 ∙ 12,5 = e,
95
Aufgabe 45c (II)
• Gewinn des Unternehmens 1:
= 7 − 20 ∙ = 45 ∙
25 − 20 ∙ 25 = 625
• Gewinn des Unternehmens 2: # = 7 # − 20 ∙ # = 45 ∙
12,5 − 20 ∙ 12,5 = 312,50
• Unternehmen 1 produziert doppelt soviel und macht
doppelt so viel Gewinn
• Das vorliegende Modell ist das Stackelberg-Modell bzw.
-Lösung.
• Aus der Sicht der Konsumenten ist die StackelbergLösung angenehmer als die Cournotsche Zwei-DrittelLösung, weil:
– Marktpreis ist niedriger: 45 statt 53,33 €
– Gesamtangebot ist größer: 37,5 statt 33,33 Einheiten
96
Aufgabe 46
a. Jedes einzelne OPEC-Land stand vor der Entscheidung,
entweder die eigene Produktionsmenge zu kürzen oder über
eine Steigerung der eigenen Produktionsmenge einen
größeren Gewinn zu erzielen. Einige OPEC-Staaten erlagen
dem Anreiz des höheren Gewinns und erhöhten ihre
Produktionsmenge (bzw. senkten sie nicht). Das vermehrte
Angebot führte zu einem Preisverfall.
b. Der Anteil den Nicht-OPEC-Länder an der gesamten
Ölförderung ist relativ klein. Eine Kürzung der Produktion
durch diese Länder hätte deshalb nur eine geringe
Preisreaktion zur Folge. Die Nicht-OPEC-Länder sind
deutlich besser gestellt, wenn sich die OPEC-Länder auf
Produktionskürzungen einigen und dadurch der Ölpreis
deutlich ansteigt, während sie ihre Fördermengen
unverändert lassen (oder sogar erhöhen).
97
Aufgabe 47 a und b
a. Im Polypol gilt die Gewinnmaximierungsregel Preis = Grenzkosten.
→GK=1000→p=1000 bei x = 12.000 Stück.
b. Gewinnmaximierungsregel im Monopol: Grenzerlös = Grenzkosten
• Der Gewinn ist maximal bei p= 7.000 und x=6.000
Preis (€)
Menge
(Stück)
Umsatz (€)
Kosten (€)
Gewinn (€)
8.000
5.000
40.000.000
5.000.000
35.000.000
7.000
6.000
42.000.000
6.000.000
36.000.000
6.000
7.000
42.000.000
7.000.000
35.000.000
5.000
8.000
40.000.000
8.000.000
32.000.000
4.000
9.000
36.000.000
9.000.000
27.000.000
3.000
10.000
30.000.000
10.000.000
20.000.000
2.000
11.000
22.000.000
11.000.000
11.000.000
1.000
12.000
12.000.000
12.000.000
0
98
Aufgabe 47 c (I)
• Wenn beide Länder ein Kartell bilden, so realisiert sich
die Monopollösung, also p = 7.000 € und x = 6.000
Stück.
• Wenn die Produktionsmenge gleichmäßig aufgeteilt wird,
produziert Südafrika 3.000 Diamanten. Es erzielt dann
ein Gewinn von 18 Mio. €
– Umsatz = 7 ∙ = 7.000 ∙ 3.000 = 21.000.000
– Kosten = 1.000 ∙ = 1.000 ∙ 3.000 = 3.000.000
• Wenn Südafrika seine Produktion um 1.000 auf 4.000
Diamanten erhöht und Rußland weiterhin 3.000
Diamanten ergibt sich folgende Veränderung:
– Gesamtmenge auf dem Markt = 4.000+3.000=7.000 Stück
– Lt. Tabelle in b.) ist der dazugehörige Preis p = 6.000 €
99
Aufgabe 47 c (II) und d
– Umsatz = 7 ∙ = 6.000 ∙ 4.000 = 24.000.000
– Kosten = 1.000 ∙ = 1.000 ∙ 4.000 = 4.000.000
– Gewinn Südafrika: 20.000 €
• Kartellabsprachen bleiben oft erfolglos, weil es für die
Beteiligten von Vorteil ist, die eigene Produktionsmenge
zu erhöhen. Halten sich die anderen Beteiligten an die
Absprache, so realisiert derjenige, der die Absprache
bricht (hier c. Südafrika), einen höheren Gewinn.
100
Aufgabe 48 a
• Gewinnmaximierungsregel im Monopol: Grenzumsatz
(GU) = Grenzkosten (GK)
– C=7∙
–
C=
– >
= 32 −
D
∙
= 32 −
=
= 8
#
= 32 − 2
=8=
→
– 32 − 2 = 8 →E = G+einsetzen in:
– 7 = 32 − →F = +.
– L = 7 ∙ − > ∙ = 20 ∙ 12 − 8 ∙ 12 = Gee
• Aufgabe 48 b – d: siehe Word-Datei
101
1
Aufgabe 48
b.) Cournot-Modell
Annahme bzgl. Zahl der Anbieter: Nur 2 Anbieter = Duopol.
Verhaltensannahme: Die beiden Anbieter betreiben autonome Mengenstrategie, d.h. der
einzelne Anbieter nimmt an, daß er durch Veränderungen seiner Angebotsmenge keine Reaktion seines Rivalen in der laufenden Periode hervorruft.
Bei Cournot-Oligopol hängt der Gewinn eines Duopolisten vom Preis, der Absatzmenge und
seinen Kosten ab. Der Preis ist in diesem Modell für beide gleich und hängt von den Angebotsmengen beider Anbieter ab, also p = p ( x1 + x2 ) .
Verlauf des Anpassungsprozesses
Periode 2
Anbieter 1 agiert in dieser Periode nicht. Er bietet nach wie vor die Menge der Vorperiode
x1 = 12 an (ermittelt in a.). Anbieter 2 betrachtet die Menge x1 = 12 als Datum und bestimmt seine Angebotsmenge anhand seiner Reaktionsfunktion. Diese muß zunächst ermittelt
werden.
Ermittlung der Reaktionsfunktion
Es wird angenommen, daß der Anbieter seinen Gewinn maximieren will. Der Gewinn hängt
jedoch nicht nur vom Preis, den Kosten und seiner eigenen Angebotsmenge, sondern auch
von der Angebotsmenge seines Konkurrenten ab, so daß die Marktnachfragefunktion wie
folgt umgeschrieben werden muß: p = 32 − ( x1 + x 2 ). Die konkrete Marktnachfragefunktion des Anbieter 2 lautet p 2 = (32 − x1 ) − x2 = 32 − x1 − x2 .
Seine Gewinnmaximierungsregel ist GU 2 = GK .
Der Umsatz U 2 = p 2 x 2 = (32 − x1 − x2 ) ⋅ x2 .
U 2 = 32 x2 − x1 x2 − x22
Durch Bildung der ersten Ableitung nach x 2 erhält man den Grenzumsatz:
GU 2 =
dU 2
= 32 − x1 − 2 x2
dx2
Gleichsetzen mit den Grenzkosten GK = 8 ergibt
32 − x1 − 2 x2 = 8 .
2
Löst man diese Gleichung nach x 2 auf, erhält man die Reaktionsfunktion des Anbieters 2:
x2 = 12 −
1
x1 .
2
Setzt man für x1 = 12 , bekommt man die Menge, die Anbieter 2 in dieser Periode auf den
Markt bringt, nämlich x 2 = 6 .
Die gesamte angebotene Menge in Periode 2 ist
x = x1 + x2 = 12 + 6 = 18 ,
und der dazugehörige Marktpreis
p = 32 − ( x1 + x2 ) = 32 − 18 = 14 .
Der Gewinn des Anbieter 1 errechnet sich wie folgt:
G1 = p ⋅ x1 − DK ⋅ x1
G1 = 14 ⋅ 12 − 8 ⋅ 12 = 72 .
Der Gewinn des Anbieter 2 errechnet sich entsprechend:
G2 = p ⋅ x2 − DK ⋅ x2
G2 = 14 ⋅ 6 − 8 ⋅ 6 = 36 .
Periode 3
In dieser Periode agiert Anbieter 2 nicht. Dieser bietet die Menge der Vorperiode x 2 = 6 an.
Anbieter 1 betrachtet die Menge x 2 = 6 als Datum und bestimmt seine Angebotsmenge anhand seiner Reaktionsfunktion. Diese ermittelt sich analog zu der des Anbieter 2 und lautet
x1 = 12 −
1
x2 . Setzt man für x2 = 6 , bekommt man die Menge, die Anbieter 1 in dieser
2
Periode auf den Markt bringt, nämlich x1 = 9 .
Die gesamte angebotene Menge in Periode 3 ist
x = x1 + x2 = 9 + 6 = 15 ,
der dazugehörige Marktpreis
p = 32 − ( x1 + x2 ) = 32 − 15 = 17 .
Der Gewinn des Anbieter 1 ist:
G1 = p ⋅ x1 − DK ⋅ x1
G1 = 17 ⋅ 9 − 8 ⋅ 9 = 81 .
3
und der Gewinn des Anbieter 2:
G2 = p ⋅ x2 − DK ⋅ x2
G2 = 17 ⋅ 6 − 8 ⋅ 6 = 54 .
Berechnung der Gleichgewichtssituation
Ausgangspunkt sind die Reaktionsfunktionen
(1)
x1 = 12 −
1
x2 und
2
(2)
x2 = 12 −
1
x1 .
2
Durch Einsetzen von (2) in (1) erhält man
x1 = 12 −
1 
1

⋅ 12 − ⋅ x1  .
2 
2

Ausmultiplizieren und auflösen nach x1 ergibt x1 = 8 . Einsetzen in (2) ergibt x 2 = 8 . Die
gesamte angebotene Menge im Gleichgewicht ist
x = x1 + x2 = 8 + 8 = 16 .
Durch Einsetzen in p = 32 − ( x1 + x 2 ) erhält man den Marktpreis im Gleichgewicht
p = 32 − 16 = 16 .
Der Gewinn des Anbieter 1 im Gleichgewicht ist:
G1 = p ⋅ x1 − DK ⋅ x1
G1 = 16 ⋅ 8 − 8 ⋅ 8 = 64 .
Der Gewinn des Anbieter 2 im Gleichgewicht ist:
G2 = p ⋅ x2 − DK ⋅ x2
G2 = 16 ⋅ 8 − 8 ⋅ 8 = 64 .
4
c.) Kooperationslösung (Kartell)
Jeder Anbieter bietet die Hälfte der Monopolmenge an. Die Monopolmenge ist x M = 12
(vgl. a.), folglich bietet jeder Anbieter die Menge xi =
xM 12
= = 6 an (i = 1 = Anbieter 1; i
2
2
= 2 =Anbieter 2).
Der dazugehörige Preis erhält man durch einsetzen von xi = 6 in die Marktnachfragefunktion p = 32 − ( x1 + x 2 ) = 32 − (6 + 6 ) = 20 .
Der Gewinn eines jeden Oligopolisten errechnet sich wie folgt.
Gi = p ⋅ xi − DK ⋅ xi
Gi = 20 ⋅ 6 − 8 ⋅ 6 = 72 .
Anreiz, die Kartellvereinbarung zu brechen (am Beispiel des Anbieter 1):
Gefragt wird, welche Menge Anbieter 1 anbieten würde, wenn Anbieter 2 nicht reagiert und
die Angebotsmenge der Kooperationslösung die Ausgangslage ist. M.a.W.: Anbieter 1 setzt in
seine Reaktionsfunktion für x 2 die Angebotsmenge der Kooperationslösung ein:
x1 = 12 −
1
1
1
x2 = 12 − xi = 12 − ⋅ 6 = 9 .
2
2
2
Die gesamte angebotene Menge ist
x = x1 + x2 = 9 + 6 = 15 ,
der dazugehörige Marktpreis
p = 32 − ( x1 + x2 ) = 32 − 15 = 17 .
Der Gewinn des Anbieter 1 ist:
G1 = p ⋅ x1 − DK ⋅ x1
G1 = 17 ⋅ 9 − 8 ⋅ 9 = 81
und der Gewinn des Anbieter 2
G2 = p ⋅ x2 − DK ⋅ x2
G2 = 17 ⋅ 6 − 8 ⋅ 6 = 54 .
Für den Anbieter 1 hat sich der Gewinn von 72 auf 81 erhöht. Er hat deshalb einen Anreiz, die
Kooperation zu brechen.
5
d.) Stackelberg-Lösung (Asymmetrielösung)
Ein Anbieter, z.B. Anbieter 1, macht sich das Wissen zunutze, daß Anbieter 2 sich stets auf
dem ihm verbleibenden Raum à la Cournot einrichtet. Er bezieht die Unabhängigkeitsposition, in dem er sein Angebot auf den Markt wirft, an das sich der zweite Duopolist gemäß seiner Reaktionsfunktion x 2 = 12 −
1
x1 anpaßt. Diese Funktion wird in die Nachfragefunktion
2
des Anbieter 1 p1 = 32 − x1 − x2 eingesetzt.
1 

p1 = 32 − x1 − 12 − x1 
2 

p1 = 32 − x1 − 12 +
p1 = 20 −
1
x1
2
1
x1 .
2
Bildet man die Gewinngleichung des 1, so ergibt sich
G1 = p1 ⋅ x1 − DK ⋅ x1
1 

G1 =  20 − x1  ⋅ x1 − 8 ⋅ x1
2 

G1 = 20 x1 −
1 2
x1 − 8 x1 .
2
Um den maximalen Gewinn des Anbieter 1 zu ermitteln, muß dessen Gewinngleichung nach
x1 abgeleitet und gleich Null gesetzt werden.
dG1
= 20 − x1 − 8 = 0
dx1
Die gewinnmaximale Menge des 1 ist x1 = 12 . Setzt man die in die Reaktionsfunktion des 2
x2 = 12 −
1
x1 ein, erhält man die angebotene Menge des 2 x2 = 6 . Der Marktpreis ergibt
2
sich, in dem man x1 = 12 und x 2 = 6 in die Marktnachfragefunktion p = 32 − x1 − x 2
einsetzt, also p = 14.
Der Gewinn des Anbieter 1 ist:
G1 = p ⋅ x1 − DK ⋅ x1
G1 = 14 ⋅ 12 − 8 ⋅ 12 = 72
und der Gewinn des Anbieter 2
6
G2 = p ⋅ x2 − DK ⋅ x2
G2 = 14 ⋅ 6 − 8 ⋅ 6 = 36 .
Bowleysche Lösung
Beide Anbieter beziehen die Unabhängigkeitsposition, d.h. jeder Anbieter nimmt die Reaktionsfunktion des jeweils anderen in sein Kalkül auf. Jeder bietet deshalb x1 = x2 = 12 an. Die
gesamte angebotene Menge ist dann x = x1 + x2 = 12 + 12 = 24 .
Der dazugehörige Marktpreis beträgt
p = 32 − ( x1 + x2 ) = 32 − 24 = 8 .
Der Gewinn des Anbieter 1 und 2 ist:
Gi = p ⋅ xi − DK ⋅ xi
Gi = 8 ⋅ 12 − 8 ⋅ 12 = 0 .