4.2 Sinusförmige Wechselgrößen

FH Giessen-Friedberg
StudiumPlus
Grundlagen der Elektrotechnik
Wechselstromtechnik
4
Wechselstromtechnik
4.1
Wechselgrößen
Dipl.-Ing. (FH) M. Beuler
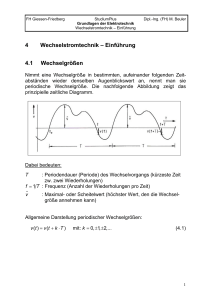
Nimmt eine Wechselgröße in bestimmten aufeinander folgenden Zeitabständen wieder denselben Augenblickswert an, nennt man sie
periodische Wechselgröße.
Allgemeine Darstellung periodischer Wechselgrößen:
v (t ) = v (t + k ⋅ T )
4.2
mit: k = 0, ±1, ±2,...
(4.1)
Sinusförmige Wechselgrößen
Sinusförmige Wechselgrößen ändern sich zeitlich sinusförmig:
v (t ) = v$ ⋅ sin(ωt + ϕ )
(4.2)
1
FH Giessen-Friedberg
4.3
StudiumPlus
Grundlagen der Elektrotechnik
Wechselstromtechnik
Dipl.-Ing. (FH) M. Beuler
Klassifikation von Wechselgrößen
Arithmetischer Mittelwert – Gleichanteil der Größe:
T
v=
1
T
∫ v (t ) ⋅ dt
(4.3)
0
Gleichrichtwert:
T
v =
1
T
∫ v (t ) ⋅ dt
(4.4)
0
Beispiel: Brückengleichrichter
u =
2 $
⋅u
π
Effektivwert:
Unter dem Effektivwert (quadratischer Mittelwert) einer Wechselgröße
versteht man den Wert, der die gleiche Leistung am gleichen Ohmschen
Widerstand R erbringt wie eine ebenso große Gleichgröße.
T
Veff =
1
T
∫ [v (t )]
2
⋅ dt
(4.5)
0
2
Veff
2
v$
=
2
⇒
Veff
v$
=
2
(4.6)
2
FH Giessen-Friedberg
StudiumPlus
Grundlagen der Elektrotechnik
Wechselstromtechnik
Dipl.-Ing. (FH) M. Beuler
4.4 Darstellung von sinusförmigen Wechselgrößen durch
Zeiger
Sinusförmige Wechselspannungen und Wechselströme lassen sich als
sog. rotierende Zeiger darstellen, d.h. die Sinusschwingung wird im
Zeigerdiagramm durch einen mit der Kreisfrequenz ω im
Gegenuhrzeigersinn um den Nullpunkt rotierenden Zeiger der Länge v$
beschrieben.
Transformation einer sinusförmigen Zeitfunktion in einen rotierenden
Zeiger:
Die Projektion des rotierenden Zeigers v (t ) auf die imaginäre Achse ist
der Augenblickswert v (t ) der sinusförmigen Wechselgröße. Die
sinusförmige Wechselgröße v (t ) wird somit in eine entsprechende
komplexe Zeitfunktion v (t ) eindeutig abgebildet (sog. Transformation ins
Komplexe).
3
FH Giessen-Friedberg
StudiumPlus
Grundlagen der Elektrotechnik
Wechselstromtechnik
Dipl.-Ing. (FH) M. Beuler
4.5 Komplexer Widerstand und komplexer Leitwert
Komplexer Widerstand (Impedanz):
Unter dem komplexen Widerstand versteht man das Verhältnis zwischen
den komplexen Momentanwerten von Spannung und Strom. Er ist gleich
dem Verhältnis der komplexen Amplituden.
Z=
u$ j (ϕu −ϕi )
⋅e
= Z ⋅ e jϕ
$i
(4.11)
Z = Z ⋅ e jϕ = Z ⋅ cos(ϕ ) + j ⋅ Z ⋅ sin(ϕ ) = R + jX
Z = R2 + X 2
;
ϕ = arctan ( X R )
(4.12)
(4.13)
Z nennt man Scheinwiderstand, R den Wirk- und X den Blindwiderstand.
Widerstandsdreieck für die Reihenschaltung eines Wirkwiderstandes mit
einem induktiven (a) bzw. kapazitiven Blindwiderstand (b):
jX c
Z = R + jX c
4
FH Giessen-Friedberg
StudiumPlus
Grundlagen der Elektrotechnik
Wechselstromtechnik
Dipl.-Ing. (FH) M. Beuler
Komplexer Leitwert (Admittanz):
Der komplexe Leitwert Y ist der Kehrwert des komplexen Widerstandes.
Y =
1
1
I
= =
= Y ⋅ e − jϕ
jϕ
U Z Z ⋅e
(4.14)
Y = Y ⋅ e − jϕ = Y ⋅ cos(ϕ ) − j ⋅ Y ⋅ sin(ϕ ) = G + jB
Y = G2 + B2
;
(4.15)
ϕ = arctan ( B G )
(4.16)
Y nennt man Scheinleitwert, G den Wirk- und B den Blindleitwert.
Parallelschaltung eines Wirkleitwertes mit einem kapazitiven (a) bzw.
induktiven Blindleitwert (b):
jBL
Y = G + jBL
Beispiel 4.1:
Die Reihenschaltung eines Wirkwiderstandes mit RR=100Ω und eines
induktiven Blindwiderstandes mit XL,R=200Ω soll in eine äquivalente
Parallelschaltung mit RP und XL,P umgerechnet werden.
5
FH Giessen-Friedberg
StudiumPlus
Grundlagen der Elektrotechnik
Wechselstromtechnik
Dipl.-Ing. (FH) M. Beuler
4.6 Ohmscher, kapazitiver und induktiver Widerstand im
Wechselstromkreis
Ohmscher Widerstand:
Bei einem Ohmschen Widerstand gibt es zwischen Spannung und Strom
keine Phasenverschiebung. Im Zeigerdiagramm liegen Stromzeiger I und
Spannungszeiger U in gleicher Richtung.
u$ = R ⋅ $i
bzw.
U = R ⋅I
(4.18)
ϕu = ϕi
(4.19)
Linien- und Zeigerdiagramm des Ohmschen Widerstandes:
Kapazitiver Widerstand:
Der kapazitive (Blind-)Widerstand –XC als Quotient der Amplituden von
Spannung und Strom ist gleich dem Kehrwert des Produktes ω·C, also
frequenzabhängig. Der Strom durch die Kapazität C eilt der Spannung
um π/2 voraus.
1
u$
− XC =
=
ωC $i
$i = ωC ⋅ u$
(4.20)
bzw.
ϕ = ϕu − ϕi = −
π
2
I = ωC ⋅ U
bzw.
ϕi = ϕu +
(4.21)
π
2
(4.22)
6
FH Giessen-Friedberg
StudiumPlus
Grundlagen der Elektrotechnik
Wechselstromtechnik
Dipl.-Ing. (FH) M. Beuler
Linien- und Zeigerdiagramm des kapazitiven Widerstandes:
Induktiver Widerstand:
Der induktive (Blind-)Widerstand XL als Quotient der Amplituden von
Spannung und Strom ist gleich dem Produkt ω·L, also ebenfalls
frequenzabhängig. Die Spannung an der Induktivität L eilt dem Strom um
π/2 voraus.
u$
X L = ωL =
$i
u$ = ωL ⋅ $i
(4.23)
bzw.
ϕ = ϕu − ϕi =
π
2
U = ωL ⋅ I
bzw.
ϕu = ϕi +
(4.24)
π
2
(4.25)
Linien- und Zeigerdiagramm des induktiven Widerstandes:
7
FH Giessen-Friedberg
StudiumPlus
Grundlagen der Elektrotechnik
Wechselstromtechnik
Dipl.-Ing. (FH) M. Beuler
4.7 Leistung im Wechselstromkreis
In einem Gleichstromkreis ist die Leistung zeitlich konstant, weil die
Spannung und der Strom zeitlich konstant sind:
P = U ⋅I
In Wechselstromkreisen sind Spannung und Strom sinusförmige
Größen, d.h. auch das Produkt – die Augenblicksleistung – ist zeitlich
veränderlich:
p = u ⋅ i = u$ ⋅ sin (ωt + ϕu ) ⋅ $i ⋅ sin (ωt + ϕi ) = pw + pB
(4.26)
Die Augenblicksleistung setzt sich aus zwei Komponenten zusammen:
• Leistungskomponente, die mit 2ω pulsiert, dabei aber ihr Vorzeichen nicht wechselt. Die durch sie beschriebene Leistung fließt
also in einer Richtung und kann somit als dauernde Energieentnahme bzw. -aufnahme, d.h. als irreversible Leistungsumwandlung, gedeutet werden. Sie wird als Wirkleistung pw bezeichnet.
• Leistungskomponente, die mit 2ω um die Nulllinie pendelt, d.h. ihr
Vorzeichen periodisch wechselt. Das bedeutet, dass sich auch die
Richtung des Leistungsflusses periodisch umkehrt. Es wird in dem
Verbraucher lediglich Energie gespeichert, die dann wieder
abgegeben wird. Im Mittel wird dem Verbraucher von dieser
Leistungskomponente keine Energie zugeführt. Man spricht von
der Blindleistung pB.
pw =
u$ ⋅ $i
⋅ cos (ϕu − ϕi ) ⋅ 1 − cos 2 (ωt + ϕu )  
2
pB = −
u$ ⋅ $i
⋅ sin (ϕu − ϕi ) ⋅ sin 2 (ωt + ϕu ) 
2
(4.27)
(4.28)
8
FH Giessen-Friedberg
StudiumPlus
Grundlagen der Elektrotechnik
Wechselstromtechnik
Dipl.-Ing. (FH) M. Beuler
Scheinleistung:
Die Scheinleistung PS ist die Leistung, die scheinbar zur Verfügung steht,
wenn man z.B. mit einem Messgerät getrennt zuerst die Spannung und
dann den Strom misst (Effektivwerte), also die Phasenlage nicht
berücksichtigt. Die Scheinleistung lässt sich auch über das Leistungsdreieck ermitteln.
PS =
u$ ⋅ $i
= Ueff ⋅ Ieff = Pw2 + PB2
2
(4.31)
PS
PB
α
PW
Wirk-, Blind- und Scheinleistung am komplexen Widerstand (nur
Impedanz):
• Die Wirkleistung Pw ist ein Maß für die im Ohmschen Widerstand
umgesetzte Leistung.
• Die Blindleistung PB ist ein Maß für die gespeicherte Leistung.
• Die Scheinleistung PS ist ein Maß für die gesamte Leistung, d.h.
die im Ohmschen Widerstand umgesetzte und die in den induktiven und kapazitiven Widerständen gespeicherte Leistung.
I
Rr
jX r
UR
UX
Z ges = Rr + jX r
U
Pw = 21 ⋅ I ⋅ Re {Z ges }
(4.32)
PB = 21 ⋅ I ⋅ Im {Z ges }
(4.33)
2
2
9
FH Giessen-Friedberg
induktiver Widerstand:
StudiumPlus
Grundlagen der Elektrotechnik
Wechselstromtechnik
PB = 12 ⋅ I ⋅ ω Lr
2
kapazitiver Widerstand: PB = − 12 ⋅ I ⋅
2
Dipl.-Ing. (FH) M. Beuler
mit: X r = ω Lr
1
ω Cr
mit: X r = −
1
ω Cr
U = Z ges ⋅ I = Rr2 + X r2 ⋅ I
⇒ PS =
U ⋅I 1
2
= 2 ⋅ I ⋅ Rr2 + X r2
2
induktiver Widerstand:
PS = 12 ⋅ I ⋅ Rr2 + ω 2 L2r
2
kapazitiver Widerstand: PS = 12 ⋅ I ⋅ Rr2 +
2
1
ω Cr2
2
10