Lineare Programmierung - Lehrstuhl Informatik 1

Einführung in die Lineare Programmierung
Berthold Vöcking
Lehrstuhl Informatik I
Algorithmen & Komplexität
RWTH Aachen
30. Juli 2008
Inhaltsverzeichnis
1 Lineare Programme
3
1.1
Die kanonische Form . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.2
Geometrische Interpretation . . . . . . . . . . . . . . . . . . . . . .
5
1.3
Die algebraische Gleichungsform . . . . . . . . . . . . . . . . . . . .
8
1.4
Basislösungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
2 Das Simplexverfahren
12
2.1
Geometrische Beschreibung . . . . . . . . . . . . . . . . . . . . . .
12
2.2
Durchführung der Pivotschritte . . . . . . . . . . . . . . . . . . . . .
13
2.2.1
Erläuterung eines Pivotschrittes . . . . . . . . . . . . . . . .
13
2.2.2
Beispielrechung mit Simplextableau . . . . . . . . . . . . . .
16
2.2.3
Komplexität einzelner Pivotschritte . . . . . . . . . . . . . .
17
2.3
Berechnung der initialen Basislösung . . . . . . . . . . . . . . . . .
19
2.4
Besondere Aspekte degenerierter LPs . . . . . . . . . . . . . . . . .
19
2.4.1
Blands Pivotregel . . . . . . . . . . . . . . . . . . . . . . . .
20
2.4.2
Perturbierung . . . . . . . . . . . . . . . . . . . . . . . . . .
20
2.4.3
Symbolische Perturbierung . . . . . . . . . . . . . . . . . . .
23
Laufzeit der Simplexmethode . . . . . . . . . . . . . . . . . . . . . .
24
2.5
1
3 Die Ellipsoidmethode
3.1
27
Zulässigkeitstest versus Optimieren . . . . . . . . . . . . . . . . . .
27
3.1.1
Beweis von Lemma 3.1 . . . . . . . . . . . . . . . . . . . . .
29
3.1.2
Beweis von Lemma 3.2 . . . . . . . . . . . . . . . . . . . . .
31
3.2
Beschreibung der Ellipsoidmethode . . . . . . . . . . . . . . . . . .
32
3.3
Skizze der Laufzeitanalyse . . . . . . . . . . . . . . . . . . . . . . .
34
3.4
Zusammenfassung . . . . . . . . . . . . . . . . . . . . . . . . . . .
37
4 Dualität
39
4.1
Primale und duale LPs . . . . . . . . . . . . . . . . . . . . . . . . .
39
4.2
Das starke Dualitätsprinzip . . . . . . . . . . . . . . . . . . . . . . .
42
4.3
Zwei prominente Beispiele . . . . . . . . . . . . . . . . . . . . . . .
44
5 Aspekte der Ganzzahligkeit
46
5.1
Ganzzahlige lineare Programme . . . . . . . . . . . . . . . . . . . .
46
5.2
Totale Unimodularität . . . . . . . . . . . . . . . . . . . . . . . . . .
47
6 Hilfreiche Literatur
51
2
Kapitel 1
Lineare Programme
1.1 Die kanonische Form
Ein Lineares Programm (LP) in kanonischer Form besteht aus d Variablen mit Wertebereich R, einer linearen Zielfunktion und m + d linearen Nebenbedingungen (Constraints). Für i = 1, . . . , m und j = 1, . . . , d seien cj , bi und aij reelle Zahlen. Gesucht
ist eine Belegung der Variablen x1 , . . . , xd , so dass die Zielfunktion
d
X
cj xj
j=1
maximiert wird unter den Nebenbedingungen
d
X
j=1
aij xj ≤ bi
(für i = 1, . . . , m)
xj ≥ 0
(für j = 1, . . . , d) .
Letztere Bedingungen heißen Nicht-Negativitätsbedingungen. Setze x = (xj ), c =
(cj ), b = (bi ) und A = (aij ). Kurzgefasst, lässt sich ein derartiges LP dann wie folgt
schreiben.
Maximiere cT x unter Ax ≤ b, x ≥ 0.
LPs in anderer Form können einfach in die kanonische Form gebracht werden:
• Ein Minimierungsproblem kann in ein Maximierungsproblem transformiert werden durch einen Vorzeichenwechsel in der Zielfunktion, d.h. cT x wird zu −cT x.
3
• Eine Gleichung aT x = b wird ersetzt durch zwei Ungleichungen aT x ≤ b und
aT x ≥ b.
• Eine Ungleichung aT x ≥ b kann durch eine Ungleichung −aT x ≤ −b ersetzt
werden.
• Eine möglicherweise negative Variable x ∈ R wird ersetzt durch den Ausdruck
x0 − x00 für zwei Variablen x0 ≥ 0 und x00 ≥ 0.
Elementares Beispiel. Gegeben seien 1000 qm Gartenfläche, davon 600 qm für Anbau von Blumen geeignet. Der Erlös pro qm Blumen sei 100 Euro, der Erlös pro qm
Gemüse 50 Euro. Bestimme eine Verteilung der Anbauflächen, die den Erlös maximiert. Das LP für dieses Problem lautet
Maximiere 100x1 + 50x2
unter den Nebenbedingungen
x1 + x2 ≤ 1000
x1 ≤ 600
x1 , x2 ≥ 0
Kurzgefasst, lautet das LP:
1000
1 1 x1
x1
, x ≥ 0.
≤
unter
Maximiere (100, 50)
600
1 0 x2
x2
Beispiel: Flussproblem. Gegeben sei ein Flussnetzwerk G = (V, E, q, s, c) mit
Quelle q, Senke s und Kapazitätsfunktion c. Seien A(v) und E(v) die Ausgangs- bzw.
Eingangskanten zum Knoten v ∈ V . Sei xe der Fluss auf Kante e ∈ E. Das entsprechende LP ist:
X
Maximiere
xe
e∈A(q)
unter den Nebenbedingungen
X
xe =
e∈A(v)
X
xe
e∈E(v)
xe ≤ c(e)
xe ≥ 0
∀v ∈ V \ {q, s}
∀e ∈ E
∀e ∈ E
4
Beispiel: Relaxiertes Rucksackproblem. Bei diesem Problem handelt es sich um
eine Variante des bekannten Rucksackproblem mit teilbaren Objekten. Gegeben seien
d Objekte mit Gewicht gi und Nutzen vi , 1 ≤ i ≤ d, sowie eine Gewichtsschranke G.
Sei xi der Bruchteil von Objekt i, den wir einpacken. Die Zielfunktion lautet:
Maximiere
d
X
vi xi
i=1
Die Nebenbedingungen sind:
d
X
i=1
gi xi ≤ G
xi ≤ 1
xi ≥ 0
1≤i≤d
1≤i≤d
1.2 Geometrische Interpretation
Der Lösungsraum von LPs lässt sich geometrisch darstellen.
• Eine Variablenbelegung x = (x1 , . . . , xd )T entspricht einem Punkt im d-dimensionalen Raum Rd .
• Jede Nebenbedingung ai x ≤ bi bzw. ai x ≥ bi definiert einen Halbraum. Die
Grenze dieses Halbraumes ist die Hyperebene ai x = bi . Der Halbraum besteht
aus den Punkten auf einer Seite dieser Hyperebene.
• Die Schnittmenge der Halbräume über alle Nebenbedingungen ist der Raum der
zulässigen Lösungen. Ein LP wird als zulässig bezeichnet, wenn der Raum der
zulässigen Lösungen nicht leer ist.
• Schnittmengen aus Halbräumen bilden ein sogenanntes Polyhedron. Der Raum
der zulässigen Lösungen ist somit ein Polyhedron und wird auch als Lösungspolyhedron bezeichnet.
Behauptung 1.1 (Konvexität des Lösungsraums) Die durch ein Polyhedron P beschriebene Punktmenge ist konvex, d.h., für jedes Punktepaar x, y ∈ P sind auch alle
Punkte auf der Verbindungslinie
`(x, y) = {λx + (1 − λ)y | λ ∈ [0, 1]}
zwischen x und y in P enthalten.
5
Beweis: Ein Polyhedron ist die Schnittmenge von Halbräumen. Jeder einzelne dieser
Halbräume ist konvex. Wir müssen also nur zeigen, dass die Schnittmenge von zwei
konvexen Mengen A und B ebenfalls konvex ist.
• Seien x, y ∈ A ∩ B.
• Dann sind x, y ∈ A, so dass `(x, y) ⊆ A.
• Zudem sind x, y ∈ B, so dass `(x, y) ⊆ B.
• Also ist `(x, y) ⊆ A ∩ B und somit ist A ∩ B konvex.
2
Aus der Konvexität lässt sich folgern, dass ein lokales Optimum auch gleichzeitig ein
globales Optimum ist, d.h., wenn x ein zulässiger Punkt ist, der die Zielfunktion nicht
global maximiert, dann gibt es in der unmittelbaren Umgebung von x einen zulässigen
Punkt y, der einen besseren Zielwert als x erreicht.
Behauptung 1.2 (lokales Optimum = globales Optimum) Zu x ∈ P gebe es z ∈ P
mit cT z > cT x. Dann existiert für jedes > 0 ein Punkt y ∈ P mit ||x − y|| ≤ und
cT y > cT x.
Beweis: Da P konvex ist, liegt die Verbindungslinie `(x, z) zwischen x und z in P.
Wähle einen beliebigen Punkt y ∈ `(x, z), y 6= x, ||x − y|| ≤ . Aus der Definition
von `(x, z) ergibt sich, es gibt ein λ > 0, so dass y = λx + (1 − λ)z. Somit folgt
cT y =
=
>
=
cT (λx + (1 − λ)z)
λcT x + (1 − λ)cT z
λcT x + (1 − λ)cT x
cT x .
2
Wenn also ein nicht-optimaler Lösungspunkt x ∈ P vorliegt, können wir den Lösungswert kontinuierlich verbessern, indem wir uns kontinuierlich in die Richtung einer beliebigen besseren Lösung z ∈ P bewegen.
Unterräume und ihre Bedeutung. Eine Hyperebene im Rd wird durch eine Gleichung
α1 x1 + α2 x2 + · · · αn xd = β
6
beschrieben, d.h. nur jeweils d − 1 der d Variablen können frei gewählt werden und
legen den Wert der verbleibenden Variable fest. Der durch eine Hyperebene beschriebene affine Unterraum hat deshalb die Dimension d − 1. Der Unterraum, der durch die
Schnittmenge von k vielen linear unabhängigen Hyperebenen entsteht, hat entsprechend die Dimension d − k.
Falls sich mehr als d der Nebenbedingungen in einem Punkt schneiden, so sagen wir
das LP ist degeneriert. Wir werden an einigen Stellen die Annahme treffen, dass das
LP nicht degeniert ist. Dadurch vereinfachen sich unsere Beschreibungen in vielerlei Hinsicht. Später werden wir zeigen, wie man ein degeneriertes LP in ein nichtdegeneriertes LP transformieren kann, ohne dabei die Zusammensetzung der optimalen Lösung zu verändern.
Die Oberfläche“ eines Polyhedrons besteht aus sogenannten Facetten“, die wie folgt
”
”
definiert sind. Sei P ein Polyhedron und H eine Hyperebene, so dass P vollständig in
einem der beiden durch H definierten Halbräume enthalten ist. Sei f = H ∩ P. Falls
f 6= ∅, so ist f eine Facette von P. Facetten können von unterschiedlicher Dimension
sein.
• Eine d − 1 dimensionale Facette wird als Face bezeichnet. Ist P beispielsweise
drei-dimensional, so entspricht ein Face einer Seitenfläche von P.
• Eine Kante entsteht aus dem Schnitt von d−1 vielen Hyperebenen und entspricht
einer ein-dimensionalen Facette.
• Ein Knoten wird durch den Schnitt von d Hyperebenen definiert und entspricht
einer Facette der Dimension 0.
Zwei Knoten des Polyhedrons, die durch eine Kante verbunden sind, werden als benachbart bezeichnet. Wir beobachten, dass benachbarte Knoten sich genau bezüglich
einer Hyperebene unterscheiden. Wenn P unbeschränkt ist, gibt es Kanten mit nur
einem oder sogar keinem Endpunkt. Diese Kanten werden als unbeschränkte Kanten
bezeichnet.
Die Zielfunktion cT x gibt eine Richtung im Rd an. Den Richtungsvektor c können
wir z.B. in Form eines am Ursprung startenden, durch den Punkt c führenden Strahls
visualisieren. Ein LP dessen Zielwert cT x durch die Nebenbedingungen nach oben beschränkt ist, wird als beschränktes LP bezeichnet. Andernfalls ist das LP unbeschränkt.
Das Lösungspolyhedron P eines beschränkten LPs muss nur in Richtung des Zielvektors c beschränkt sein. In andere Richtungen (z.B. in Richung −c) kann P durchaus
unbeschränkt sein. Falls ein Polyhedron in alle Richtungen beschränkt ist, d.h. es gibt
eine Kugel, die das Polyhedron umschließt, so wird es auch als Polytop bezeichnet.
7
Geometrische Bestimmung des Optimums. Wir betrachten ein beschränktes LP in
kanonischer Form mit Zielfunktion cT x und Lösungspolyhedron P.
• Sei H eine Hyperebene, die zum Richtungsvektor c orthogonal ist. Wegen der
Orthogonalität gibt es einen Wert t ∈ R mit der Eigenschaft H = {x ∈ Rd |cT x =
t}. Alle Punkte auf H haben also den gleichen Zielwert t.
• H sei so gewählt, dass H ∩ P =
6 ∅. Wir stellen uns nun vor, wir verschieben H
unter Einhaltung dieser Invariante soweit wie möglich parallel in Richtung des
Vektors c. Sei H∗ die so erhaltene Hyperebene.
• Sei nun x∗ ein beliebiger Punkt aus H∗ ∩ P. x∗ ist eine optimale Lösung des
LPs.
Wir beobachten, H∗ ∩ P ist eine Facette von P. Jede Facette enthält mindestens einen
Knoten von P, und somit gibt es mindestens einen optimalen Knoten, also einen Knoten, der den optimalen Zielwert annimmt.
Beobachtung 1.3 Das Optimum eines zulässigen und beschränkten LPs wird an einem Knoten des Lösungpolyhedrons angenommen.
2
Wir möchten darauf hinweisen, dass das hier beschriebene geometrische Verfahren
zur Bestimmung des Optimums nur der Veranschaulichung dient. Es bleibt unklar, wie
man dieses Verfahren effizient für höherdimensionale LPs auf dem Rechner umsetzen
kann.
1.3 Die algebraische Gleichungsform
Um das Lösungspolyhedron und seine Facetten auf dem Rechner abbilden zu können,
benötigen wir eine geeignete Repräsentationsform. Dazu wechseln wir von der kanonischen Form in die folgende Gleichungsform:
Maximiere cT x unter Ax = b, x ≥ 0.
Die Anzahl der Variablen bezeichnen wir mit n, die Anzahl der Nebenbedingungen
(ohne die Nichtnegativitätsbedingungen) mit m. Die Zeilen von A seien linear unabhängig, ansonsten könnten wir Zeilen entfernen, ohne das Gleichungssystem zu
verändern. Somit gilt rang(A) = m ≤ n.
8
x2
x1
Abbildung 1.1: Lösungspolyhedron P beschrieben durch die Nebenbedingungen x1 ≤
4, x2 ≤ 2, −x1 + x2 ≤ 1.
LPs in der kanonischen Form können durch Hinzufügen von Schlupfvariablen in die
Gleichungsform überführt werden: Aus der iten Nebenbedingung in Ungleichungsform
d
X
αij xj ≤ bi
j=1
entstehen die Nebenbedingungen
d
X
αij xj + si = bi
j=1
und si ≥ 0 ,
wobei si eine sogenannte Schlupfvariable ist. Falls wir in der kanonischen Form d
Variablen haben, so hat die zugehörige Gleichungsform n = m+d Variablen. Beachte,
für die Matrix A eines aus der kanonischen Form hergeleiteten LPs in Gleichungsform
gilt zwangsläufig rang(A) = m, weil das Hinzügen der Schlupfvariablen dafür sorgt,
dass die Zeilen von A linear unabhängig sind.
Beispiel. Wir geben ein Beispiel für die Transformation von der kanonischen in die
Gleichungsform. Seien x und y nicht-negative Variablen und das Lösungspolyhedron
P sei durch die Nebenbedingungen x1 ≤ 4, x2 ≤ 2, −x1 + x2 ≤ 1 beschrieben.
Abbildung 1.1 zeigt dieses Polyhedron. Für jede Bedingung fügen wir eine nichtnegative Schlupfvariable hinzu und erhalten die Gleichungen x1 +x3 = 4, x2 +x4 = 2,
−x1 + x2 + x5 = 1. Der Lösungsraum P 0 ist jetzt eine Teilmenge des R5≥0 . Es gibt eine
bijektive Abbildung zwischen den Punkten in P und P 0 . Beispielsweise entspricht der
Punkt (1, 2) dem Punkt (1, 2, 3, 0, 0). Dazu lösen wir einfach das Gleichungssystem
9
nach den Schlupfvariablen auf.
x3 = 4 − x1
x4 = 2 − x2
x5 = 1 + x1 − x2
Beachte der Punkt (1, 2) ist ein Knoten von P: Die beiden Hyperebenen zu den Nebenbedingungen x2 ≤ 2 und −x1 +x2 ≤ 1 schneiden sich in diesem Punkt. Deshalb haben
die Schlupfvariablen x4 und x5 , die zu diesen beiden Nebenbedingungen gehören den
Wert 0.
1.4 Basislösungen
Wir gehen von einem LP in Gleichungsform aus. Sei B eine geordnete Auswahl
von k ≥ 1 Spalten der m × n Matrix A. Dann bezeichne AB die Teilmatrix von
A, die nur aus den Spalten in B besteht. Mit B(i) (1 ≤ i ≤ k) bezeichnen wir
den Index der iten Spalte in B, d.h. AB entsteht aus der Konkatenation der Spalten
AB(1) , AB(2) , . . . , AB(k) . Zu jeder Spalte aus A ist eine Variable und ein Koeffizient
der Zielfunktion assoziiert. Die Teilvektoren aus denjenigen Variablen und Koeffizienten, die zu den Spalten in B assoziiert sind, werden mit xB bzw. cB bezeichnet.
Sei nun B eine Spaltenauswahl der Kardinalität m. B wird dann als Basis von A
bezeichnet, wenn die Vektoren in B linear unabhängig sind. In diesem Fall ist AB
invertierbar. Mit N bezeichnen wir diejenigen Spalten von A, die nicht in B enthalten
sind. Wir schreiben das Gleichungssystem Ax = b wie folgt um.
AB xB + AN xN = b .
(1.1)
Wenn wir nun xN = 0 setzen, hat das verbleibende Gleichungssystem AB xB = b
−1
eine eindeutige Lösung, nämlich xB = A−1
B b. Die Lösung (xB , xN ) = (AB b, 0) wird
Basislösung zur Basis B genannt. Der Zielfunktionswert dieser Lösung ist cTB A−1
B b.
In der kanonischen Form entsprechen die Basislösungen den Schnittpunkten von d Nebenbedingungshyperebenen. Dies kann man wie folgt einsehen. In einer Basislösung
haben mindestens n − m = d Variablen den Wert 0. Bei diesen Variablen handelt es
sich entweder um Schlupfvariablen, deren zugehörige Nebenbedingung mit Gleichheit
erfüllt ist, oder um Variablen aus der kanonischen Form, deren Nichtnegativitätsbedingung mit Gleichheit erfüllt ist. Somit sind also d Nebenbedingungen aus dem LP in kanonischer Form mit Gleichheit erfüllt, so dass die Basislösung dem Schnittpunkt der
zugehörigen Hyperebenen entspricht. Die Basislösung ist zulässig, falls auch die m
Basisvariablen nicht-negative Werte haben. In diesem Fall entspricht die Basislösung
10
einem Knoten des Lösungspolyhedrons der kanonischen Form. Falls eine der Basisvariablen den Wert Null annimmt schneiden sich mehr als d Hyperebenen in einem
Punkt und das zugrundeliegende LP ist degeneriert.
Beobachtung 1.4 Die Knoten des Lösungspolyhedrons zur kanonischen Form entsprechen den zulässigen Basislösungen in der Gleichungsform. Diese Basislösungen
sind dadurch gekennzeichnet, dass alle Variablen nicht-negative Werte annehmen. Ist
das LP nicht-degeneriert, so sind die Werte der Basisvariablen strikt positiv.
2
11
Kapitel 2
Das Simplexverfahren
Das Simplexverfahren wurde 1951 von Dantzig vorgestellt. Es ist das in der Praxis
wohl erfolgreichste Verfahren zur Lösung von LPs. Wir beginnen zunächst mit einer intuitiven, geometrischen Beschreibung des Verfahrens basierend auf der kanonischen Form. Anschließend wechseln wir zum Zwecke der formalen Beschreibung in
die Gleichungsform.
2.1 Geometrische Beschreibung
Gegeben sei ein nicht-degeneriertes, möglicherweise unbeschränktes LP mit Lösungspolyhedron P. Die Simplexmethode entspricht einer lokalen Suche auf den Knoten
des Lösungspolyhedrons: Von einem beliebigen Knoten ausgehend wird nach einem
Nachbarknoten mit besserem Zielwert gesucht, und von dort die Suche fortgesetzt, bis
kein Nachbarknoten mit besserem Zielwert mehr existiert. Die Korrektheit der Simplexmethode basiert darauf, dass von jedem nicht-optimalen Knoten eine Kante ausgeht entlang derer sich der Zielwert erhöht, eine sogenannte verbessernde Kante. Diese
Eigenschaft müssen wir noch formal nachweisen. Die Schritte des Simplexverfahrens
können wie folgt zusammengefasst werden.
1. Bestimme einen beliebigen Knoten v von P.
2. Falls es keine verbessernde Kante inzident zu v gibt, dann ist v optimal, stopp.
3. Folge einer beliebigen verbessernden Kante e von v. Falls e unbeschränkt ist so
ist das LP unbeschränkt, stopp.
4. Sei u der andere Endpunkt von e. Setze v = u. Gehe zurück zu Schritt 2.
12
Der Wechsel von einem Knoten zum anderem wird als Pivotschritt bezeichnet. Wir
beschreiben im folgenden zunächst ausführlich, wie man diese Pivotschritte auf dem
Rechner realisiert. Dazu werden die Knoten in Form von Basislösungen abgebildet.
Erst nach der Erörterung der Pivotschritte erläutern wir, wie man die initiale Basislösung in Schritt 1 des Simplexverfahrens berechnet. Bei unserer Beschreibung gehen wir von einem nicht-degenerierten LP aus. Im Anschluss werden wir zeigen, wie
man degenerierte LPs auf geeignete Art und Weise in nicht-degenerierte LPs transformieren kann. Als letztes erörtern wir die Laufzeit des Simplexverfahrens.
2.2 Durchführung der Pivotschritte
Wir gehen nun davon aus, dass das LP in der Gleichungsform vorliegt. Wir vernachlässigen zunächst die Frage, wie wir eine zulässige Basislösung bestimmen können, und
nehmen an, dass eine zulässige Basis B bekannt ist. Wir nutzen aus, dass die Basismatrix AB invertierbar ist. Wenn wir die Terme im Gleichungssystem Ax = b von links
mit A−1
B multiplizieren, erhalten wir das äquivalente Gleichungssystem Âx = b̂ mit
−1
−1
Â = A−1
B A und b̂ = AB b. Für die Basismatrix dieses Systems gilt ÂB = AB AB =
Em , wobei Em der m × m Einheitsmatrix entspricht. Wenn eine zulässige Basis bekannt ist, können wir also das Gleichungssystem derart transformieren, dass die Basismatrix der Einheitsmatrix entspricht.
2.2.1 Erläuterung eines Pivotschrittes
Wir gehen jetzt davon aus, dass das Gleichungssystem zu Beginn eines Pivotschritts
in der Form Âx = b̂ vorliegt, wobei die Basismatrix ÂB der Einheitsmatrix Em entspricht. Unter dieser Annahme vereinfacht sich das Gleichungssystem (1.1) zu
xB + ÂN xN = b̂ .
Wir lösen nach xB auf und erhalten
xB = b̂ − ÂN xN .
(2.1)
In der Basislösung zu B gilt xN = 0, so dass sich xB = b̂ ergibt. Der Zielfunktionswert der Basislösung zu B ist somit cTB b̂. Wenn wir von der Basislösung abweichen
indem wir den Vektor xN verändern ergeben sich die Basisvariablen xB wie in Gleichung (2.1) beschrieben. Die Basisvariablen können somit als Funktion der Nichtbasisvariablen aufgefasst werden. Ebenso können wir den Zielfunktionswert als Funktion
13
von xN beschreiben.
cT x = cTB xB + cTN xN
= cTB (b̂ − ÂN xN ) + cTN xN
= cTB b̂ + (cTN − cTB ÂN )xN .
(2.2)
Der Vektor cTN −cTB ÂN wird als Vektor der reduzierten Kosten bezeichnet. Er enthält für
jede Nichtbasisvariable einen Eintrag der beschreibt, wie sich der Zielfunktionswert in
Abhängigkeit von dieser Variable verändert. Der Vektor der reduzierten Kosten liefert
ein einfaches Kriterium um festzustellen, ob eine zulässige Basislösung optimal ist.
Satz 2.1 (Optimalitätskriterium) Falls der Vektor der reduzierten Kosten zu einer
Basis B keinen positiven Eintrag enthält, so ist B optimal.
Beweis: Es gelte cTN − cTB ÂN ≤ 0. Wähle eine beliebige zulässige Lösung x0 . Wegen
der Zulässigkeit von x0 gilt x0 ≥ 0 also insbesondere auch x0N ≥ 0. Aus Gleichung 2.2
ergibt sich nun
cT x0 = cTB b̂ + (cTN − cTB ÂN ) x0N ≤ cTB b̂ .
{z
} |{z}
|
≤0
≥0
Letzterer Wert ist aber der Zielfunktionswert der Basislösung zu B. Dieser Zielfunktionswert ist somit nicht kleiner als der Zielfunktionswert jeder anderen zulässigen
Lösung. In anderern Worten, die Basislösung zu B ist optimal.
2
Wenn das Optimalitätskriterium erfüllt ist, so terminiert das Simplexverfahren. Ansonsten suchen wir eine Basislösung B 0 , die sich in genau einer Spalte von B unterscheidet und einen besseren Zielwert aufweist. B 0 kann wie folgt konstruiert werden.
Sei xj eine der Nichtbasisvariablen mit positiven reduzierten Kosten, d.h.
cj −
m
X
cB(k) âk,j > 0 .
k=1
Wir zeigen, wie wir (ausgehend von der Basislösung zu B) den Zielfunktionswert
erhöhen können, indem wir den Wert der Variable xj verändern. Die Werte aller anderen Nichtbasisvariablen bleiben unverändert. Wenn wir den Wert der Variable xj
(ausgehend von 0) kontinuierlich erhöhen, so erhöht sich wegen Gleichung (2.2) auch
der Zielfunktionswert kontinuierlich. Allerdings verändern sich die Werte der Basisvariablen ebenfalls kontinuierlich wie in Gleichung (2.1) beschrieben: Es gilt
X
âik xk = b̂i − âij xj ,
(2.3)
xB(i) = b̂i −
k∈N
14
weil wir die Variablen xk , k ∈ N \ {j}, auf Null fixiert haben. Wenn xj wächst,
nehmen einige Basisvariablen möglicherweise negative Werte an, und die Lösung wird
unzulässig. Wir gehen jedoch davon aus, dass das LP nicht-degeneriert ist, so dass alle
Basisvariablen in der Basislösung strikt positive Werte haben (Behauptung 1.4). Somit
kann der Wert von xj zumindest um einen kleinen, positiven Betrag erhöht werden,
bevor eine der Basisvariablen einen negativen Wert annimmt. Es können die folgenden
Fälle auftreten.
1. Für alle i ∈ {1, . . . , m} gilt âij ≤ 0. In diesem Fall kann der Wert von xj beliebig erhöht werden, ohne dass die durch Gleichung (2.1) beschriebene Lösung
unzulässig wird. Das Simplexverfahren terminiert mit der Feststellung, dass das
LP unbeschränkt ist.
2. Es gibt mindestens ein i ∈ {1, . . . , m}, für das gilt âij > 0. Wähle
)
(
b̂k i = argmin1≤k≤m
âkj > 0 .
âkj Wenn wir die Variable xj = âb̂iji setzen, ergibt sich, wie aus Gleichung (2.3)
folgt, eine zulässige Lösung, in der die Variable xB(i) den Wert 0 annimmt und
alle anderen Basisvariablen nicht-negative Werte haben. Diese Lösung entspricht
der Basislösung zur Basis B 0 , die wir aus B erhalten, wenn wir die Basisspalte
ÂB(i) durch die Nichtbasisspalte Âj ersetzen.
Schritt 2 ist der eigentliche Pivotschritt. Die Spalte Âj wird als Eingangspivotspalte bezeichnet, weil sie in die Basis aufgenommen wird, und die Spalte ÂB(i) ist die
sogenannte Ausgangspivotspalte, weil sie aus der Basis verdrängt wird. Dieser Vorgang hat die folgende geometrische Interpretation: In der kanonischen Form ist nach
dem Erhöhen der Variable xj die mit dieser Variable assoziierte Nebenbedingung nicht
mehr mit Gleichheit erfüllt, dafür aber jetzt die zu xB(i) gehörende Nebenbedingung.
Wir sind somit von dem durch B beschriebenen Knoten entlang einer verbessernden
Kante zu einem benachbarten Knoten gewechselt, der der Basis B 0 entspricht.
Zu Beginn der Beschreibung des Pivotschritts haben wir angenommen, dass das Gleichungssystem Âx = b̂ derartig vorliegt, dass die Basismatrix ÂB der Einheitsmatrix
Em entspricht. Wir schließen die Beschreibung des Pivotschrittes, indem wir zeigen,
wie das Gleichungssystem durch elementare Zeilenoperationen so umgeformt werden
kann, dass nach der Transformation die Basismatrix zur neuen Basis B 0 wiederum als
Einheitsmatrix vorliegt. Wir gehen zweistufig vor.
1. Die Zeile (Âi , b̂i ) des Gleichungssystems wird mit 1/âij multipliziert. Nach dieser Operation gilt âij = 1.
15
2. Für k 6= i, falls âkj 6= 0, addieren wir die in Schritt 1 erzeugte Zeile multipliziert
mit −âkj zur Zeile (âk , bk ) hinzu. Nach dieser Operation gilt âkj = 0.
Nach dieser Transformationen sind die Voraussetzungen für den nächsten Pivotschritt
gegeben.
2.2.2 Beispielrechung mit Simplextableau
Wir setzen das Beispiel aus Abschnitt 1.3 fort. Die Nebenbedingungen sind x1 + x3 =
4, x2 + x4 = 2, −x1 + x2 + x5 = 1, x ≥ 0. Die Zielfunktion sei −x1 + 2x2 . Betrachte
die Basis B = (A3 , A4 , A5 ). Glücklicherweise gilt ohne jegliche Umformung AB =
E3 und die Basis ist zulässig, da die zugehörige Basislösung xB = b nicht-negativ
ist. Deshalb können wir das Simplexverfahren mit der Basis B starten, ohne initiale
Umformungen vornehmen zu müssen. Wir setzen Â = A und b̂ = b und speichern die
zugehörigen Einträge in einem Tableau ab. Die Spalten von Â bezeichnen wir dabei
mit Â1 , . . . , Â5 .
b̂
4
2
1
Â1
1
0
−1
Â2
0
1
1
Â3
1
0
0
Â4
0
1
0
Â5
0
0
1
Die reduzierten Kosten von Spalte 2 sind c2 − cB · Â2 = 2, denn c2 = 2 und cB =
(cB(1) , cB(2) , cB(3) ) = (c3 , c4 , c5 ) = (0, 0, 0). Wir können somit Spalte Â2 als Eingangspivotspalte wählen. Der Term b̂i /âi2 , âi2 > 0, wird minimiert für i = 3. Damit ist
die Spalte ÂB(3) = Â5 die eindeutig bestimmte Ausgangspivotspalte. Der Pivotschritt
tauscht also die Basisspalte Â5 gegen die Spalte Â2 aus. Das Gleichungssystem wird
wie folgt transformiert. Wir dividieren die 3. Zeile zunächst durch â32 = 1. Dann addieren wir diese Zeile multipliziert mit −â12 = 0 zur ersten Zeile und multipliziert mit
−â22 = −1 zur zweite Zeile. Das neue Gleichungssystem ergibt sich wie folgt.
b̂
4
1
1
Â1
1
1
−1
Â2
0
0
1
Â3
1
0
0
Â4
0
1
0
Â5
0
−1
1
Die neue Basis ist B = (Â3 , Â4 , Â2 ). Somit gilt cB = (0, 0, 2). Die reduzierten Kosten
von Spalte 1 sind c1 − cB Â1 = (−1) − 2 · (−1) = 1 > 0. Spalte Â1 ist somit eine
geeignete Eingangspivotspalte. Der Term b̂i /âi1 , âi1 > 0, wird minimiert für i = 2.
Damit ist ÂB(2) = Â4 die Ausgangspivotspalte. Wir tauschen somit die Basisspalte Â4
gegen die Spalte Â1 aus. Wir dividieren die Zeile 2 durch â21 = 1. Dann addieren wir
16
die so entstandene Zeile multipliziert mit −â11 = −1 zu Zeile 1 und multipliziert mit
−â31 = 1 zu Zeile 3. Wir erhalten das folgende Gleichungssystem.
b̂
3
1
2
Â1
0
1
0
Â2
0
0
1
Â3
1
0
0
Â4
−1
1
1
Â5
1
−1
0
Die Basis ist jetzt B = (Â3 , Â1 , Â2 ). Es gilt cB = (0, −1, 2). Beide Nichtbasisspalten Â4 und Â5 haben jetzt negative reduzierte Kosten. Das Verfahren terminiert. Als
optimale Basislösung ergibt sich x1 = 1, x2 = 2, x3 = 3, x4 = 0, x5 = 0.
Es ist interessant zu verfolgen, welchen Verlauf das Simplexverfahren in Bezug auf die
geometrische Darstellung in Abbildung 1.1 nimmt. Die initiale Basislösung (Â3 , Â4 , Â5 )
entspricht dem Punkt (0, 0). Die nächste besuchte Basislösung (Â3 , Â4 , Â2 ) entspricht
dem Punkt (0, 1). Das Verfahren terminiert mit der Basislösung (Â3 , Â1 , Â2 ), die dem
Punkt (1, 2) entspricht.
2.2.3 Komplexität einzelner Pivotschritte
Die Bestimmung der Eingangs- und Ausgangsspalten in einem Pivotschritt sowie die
anschließende Transformation des Gleichungssystems kann mit O(nm) algebraischen
Rechenoperationen auf rationalen Zahlen durchgeführt werden. Wir gehen davon aus,
dass die Koeffizienten in der Zielfunktion und den Nebenbedingungen ganzzahlig sind.
In den einzelnen Pivotschritten können jedoch bedingt durch die Multiplikation der
Zeilen des Gleichungssystems, durch die wir die Basismatrix in die Einheitsmatrix
transformieren, rationale Zahlen entstehen, die nicht ganzzahlig sind. Wir repräsentieren diese Zahlen in Form von Brüchen mit binär kodierten ganzzahligen Nennern und
Zählern. Dabei gehen wir davon aus, dass Nenner und Zähler minimal gewählt sind,
d.h. nicht weiter gekürzt werden können. Das können wir erreichen, indem wir auf alle Zwischenergebnisse den Euklidischen Algorithmus anwenden. Die Größe der dabei
entstehenden Nenner und Zähler können wir wie folgt beschränken.
Lemma 2.2 Bezeiche α den größten absoluten Wert über alle (ganzzahligen) Eingabezahlen eines LPs in Gleichungsform.
a) Sei β der größte absolute Wert über alle (gekürzten) Zähler und Nenner der
−1
−1
0
Zahlen in den Matrizen Â = A−1
B A, A = AB und dem Vektor b̂ = AB b. Es
m
gilt β ≤ (αm) .
b) Sei γ der größte absolute Wert über die (gekürzten) Zähler und Nenner der Zielfunktionswerte cT x über alle Basislösungen x. Es gilt γ ≤ (αm)m+1 .
17
Beweis: Sei M eine invertierbare k ×k-Matrix und b ein k-Vektor. Sei x die eindeutig
bestimmte Lösung zum Gleichungssystem Mx = b, also x = M −1 b. Dann besagt die
Cramersche Regel, dass für jedes i ∈ {1, . . . , k} gilt
xi =
det(M1 , . . . , Mi−1 , b, Mi+1 , . . . , Mk )
,
det(M)
wobei Mi die ite Spalte von M bezeichne. Die Zahlen in M und b seien nun ganze
Zahlen mit Absolutwert höchstens α. Die Determinante einer k × k Matrix ist definiert
als Summe von k! Produkten von jeweils k Matrixeinträgen. Die beiden betrachteten
Determinanten sind deshalb ganzzahlig und ihre Absolutwerte sind durch k! αk ≤
(αk)k nach oben beschränkt.
Die obere Schranke für β ergibt sich nun wie folgt. Aus den obigen Überlegungen
folgt sofort, dass die Nenner und Zähler in b̂ durch (αm)m nach oben beschränkt sind,
denn b̂ = A−1
B b ist die eindeutig bestimmte Lösung zum Gleichungssystem AB x = b.
Die obere Schranke für die Nenner und Zähler in b̂ lässt sich offensichtlich auf jeden
Vektor v̂ der Form v̂ = A−1
B v übertragen, falls die Koeffizienten in v ganzzahlig sind
und ihr Absolutwert durch α beschränkt ist. Entsprechend gilt dieselbe obere Schranke
−1
0
auch für die Nenner und Zähler der Zahlen in Â = A−1
B A und A = AB Em .
Zuletzt zeigen wir die obere Schranke für γ. Gemäß der Cramerschen Regel können
wir jede Basislösung x so darstellen, dass die Bruchdarstellungen der Zahlen x1 , . . . , xm
denselben Nenner haben, dessen Absolutwert durch β nach oben beschränkt ist, und
auch die Absolutwerte aller Zähler sind durch β nach oben beschränkt. Ferner sind die
Absolutwerte der ganzzahligen Koeffizienten im Zielfunktionsvektor c durch α beschränkt. Entsprechend läßt sich der Term cT x durch einen Bruch darstellen, dessen
Nenner durch β ≤ (αm)m und dessen Zähler durch αβm ≤ (αm)m+1 absolut nach
oben beschränkt ist.
2
Die Absolutwerte der Zähler und Nenner können durch die in den Pivotschritten durchgeführten Zeilenoperationen dramatisch anwachsen. Für die Komplexität der Rechenoperationen sind aber nicht die Absolutwerte dieser Zahlen entscheidend sondern ihre
binäre Kodierungslänge. Bezeichne ` die maximale Kodierungslänge einer einzelnen
Eingabezahl. Dann gilt ` = Θ(log α). Die in der Rechnung entstehenden Zahlen haben
somit Länge höchstens O(log((αm)m+1 )) = O(m(log m + log α)) = O(m log m +
m`). Damit sind die Kodierungslängen dieser Zahlen polynomiell in der Eingabelänge
des LPs beschränkt.
Satz 2.3 Die Laufzeit jedes einzelnen Pivotschrittes ist polynomiell beschränkt in der
Eingabelänge des LPs.
18
2.3 Berechnung der initialen Basislösung
Bisher haben wir beschrieben, wie man eine optimale Lösung berechnet, wenn bereits
eine zulässige Basislösung vorliegt. Wir müssen noch zeigen, wie die erste zulässige
Basislösung berechnet werden kann. Der Raum der zulässigen Lösungen sei beschrieben durch das System Ax = b, x ≥ 0. O.B.d.A. gelte b ≥ 0; ansonsten multipliziere
die nicht dieser Annahme entsprechenden Zeilen mit -1.
Zur Berechnung einer zulässigen Basislösung ignorieren wir die gegebene Zielfunktion und ersetzen sie durch eine neue Hilfszielfunktion. Diese Zielfunktion ist definiert
über einer Menge von Hilfsvariablen h1 , P
. . . , hm ≥ 0 — jeweils eine Hilfsvariable pro
Zeile von A. Die i-te Nebenbedingung N
j=1 aij xj = bi , 1 ≤ i ≤ m, wird ersetzt
durch
N
X
aij xj + hi = bi .
j=1
Die neue Zielfunktion lautet
Minimiere h1 + h2 + · · · + hm .
Für dieses HilfsLP gibt es eine offensichtliche zulässige Basislösung, nämlich x = 0,
h = b ≥ 0. Ausgehend von dieser Basislösung können wir nun die Hilfszielfunktion durch Anwendung von Pivotschritten minimieren. Die berechnete Lösung genügt
einem der beiden folgenden Fälle.
1. Die optimale Lösung für das HilfsLP hat einen positiven Zielfunktionswert.
Dann gibt es keine Lösung mit h1 = h2 = · · · = hm = 0. Es folgt, dass
das eigentliche LP keine zulässige Lösung hat.
2. Der berechnete Zielfunktionswert des HilfsLP ist 0. In der berechneten Basislösung des HilfsLP gilt somit h1 = h2 = · · · = hm = 0. Damit ist diese
Basislösung auch zulässig für das eigentliche LP.
Die Berechnung der optimalen Lösung mit Hilfe des Simplexalgorithmus besteht also
aus zwei sehr ähnlichen Phasen. In Phase 1 berechnen wir mit Hilfe von Pivotschritten eine zulässige Basislösung. In Phase 2 berechnen wir dann ausgehend von einer
zulässigen Lösung mit Hilfe von Pivotschritten eine optimale Lösung.
2.4 Besondere Aspekte degenerierter LPs
In einem nicht-degenerierten LP verbessert sich der Wert der aktuellen Basislösung
von Schritt zu Schritt. Da es nur endliche viele Basislösungen gibt, ist damit die Ter19
minierung des Simplexverfahrens sichergestellt. In einem degenerierten LP kann es
vorkommen, dass in einem Pivotschritt eine oder mehrere Basisvariablen den Wert 0
haben. Durch Austausch einer Basisspalte, die zu einer solchen Variable gehört, erhöht
sich der Zielfunktionswert nicht. In der geometrischen Darstellung zur kanonischen
Form mit d Variablen entspricht dieses dem Fall, dass sich mehr als d Hyperebenen
in einem Punkt treffen. Dadurch werden mehrere Basislösungen auf denselben Punkt
abgebildet, so dass sich durch einen Wechsel von einer Basislösung zur anderen der
Zielfunktionswert nicht erhöht.
2.4.1 Blands Pivotregel
Zyklisches Verhalten des Simplexalgorithmus kann durch die folgende Pivotregel von
Bland verhindert werden: Wähle beide Pivotspalten, also die Eingangsspalte Aj und
die Ausgangsspalte AB(i) , mit möglichst kleinem Index, also so, dass zunächst der
Index j und dann der Index B(i) minimal unter den in Abschitt 2.2 beschriebenen
Bedingungen gewählt wird. Für den Beweis, dass diese Regel Zyklen verhindert, verweisen wir auf die Literatur.
Blands Pivotregel ist einfach umzusetzen, hat aber den Nachteil, dass sie die Auswahl
der Eingangspivotspalte festlegt. Gemäß unserer bisherigen Beschreibung konnte jede
Nichtbasisspalte mit positiven reduzierten Kosten als Eingangsspalte gewählt werden.
Einige Heuristiken versuchen diese Freiheit zu nutzen, indem sie beispielsweise die
Spalte mit den größten reduzierten Kosten als Eingangsspalte wählen. Das bedeutet
sie verbessern die Basislösung entlang derjenigen ausgehenden Kante im Lösungspolyhedron, die die größte Steigung bezüglich der Zielfunktion aufweist. Im folgenden
werden wir einen allgemeinen Ansatz zur Vermeidung von Zyklen beschreiben, der
die Wahl der Eingangspivotspalte freilässt und nur die Ausgangspivotspalte festlegt.
Beachte, dass die Wahl der Ausgangspivotspalte in einem nicht-degenerierten LP im
Gegensatz zur Wahl der Eingangspivotspalte ohnehin keine Freiheitsgrade aufweist.
2.4.2 Perturbierung
Wir perturbieren (stören) ein gegebenes LP leicht um degenerierte Knoten, also Schnittpunkte von mehr als n Nebenbedingungshyperebenen aufzuheben. Die Perturbierung
ist so gering, dass eine Basislösung, die für das perturbierte LP optimal ist, auch für
das ursprüngliche LP optimal ist. In der geometrischen Darstellung können wir degenerierte Knoten dadurch aufheben, dass wir jede der Hyperebenen etwas parallel
verschieben. Das entspricht dem Aufaddieren eines kleinen Wertes zum Vektor b. Die
Idee ist es also, ein möglicherweise degeneriertes LP in ein nicht-degeneriertes LP zu
transformieren und dadurch die Terminierung des Simplexverfahrens zu garantieren.
20
Bezeichne LP ein lineares Programm dem das Gleichungssystem Ax = b (oder alternativ Ax ≤ b) zugrundeliegt. Bezeichne LP (), > 0, dasjenige LP in dem wir den
Vektor b durch den Vektor b + ~ ersetzen, wobei


 2 


~ =  ..  .
 . 
m
Wir werden so klein wählen, dass zwar die degenerierten Knoten aufgehoben werden,
aber die optimale Basis bzw. zumindest eine der optimalen Basen erhalten bleiben.
Beachte, für kleines > 0 gilt gilt 2 · · · m . Wir merken an, dass es
zur Aufhebung von degenerierten Knoten nicht ausreicht, alle Nebenbedingungen um
denselben Betrag zu verschieben.
Satz 2.4 Es gibt ein δ > 0, so dass für jedes ∈ (0, δ) gilt:
a) LP () ist nicht-degeneriert.
b) Jede zulässige Basis für LP () ist auch zulässig für LP .
c) Jede optimale Basis für LP () ist auch optimal für LP .
Beweis: Zunächst beweisen wir Aussage a). Sei B eine Basis. In der Basislösung zu
B für LP () ist
−1
xB = A−1
) = A−1
.
B (b + ~
B b + AB ~
Aus dieser Gleichung extrahieren wir den Wert für eine einzelne Basisvariable xi .
−1
0
Bezeichne b̂ = A−1
B b und A = AB . Es gilt
xi = b̂i +
m
X
a0ij j .
j=1
Wir beobachten, dass der Wert von xi durch ein Polynom in beschrieben wird. Dieses
Polynom ist
m
X
a0ij sj .
pB,i (s) = b̂i +
j=1
Da die Matrix A0 invertierbar ist, gibt es mindestens einen Index j mit a0ij 6= 0. Falls
pB,i eine positive Nullstelle hat, so bezeichne δB,i die kleinste positive Nullstelle, sonst
sei δB,i = ∞. Setze nun
δ = min{δB,i | B ist Basis mit Basisvariable xi } .
21
Für < δ gilt nun pB,i () 6= 0 und zwar für jede Basis B und jede Basisvariable
xi . Das bedeutet alle Basisvariablen in LP () haben Werte ungleich Null. Damit ist
Aussage a) bewiesen.
Wir wenden uns nun Aussage b) zu. Sei x∗ die Basislösung zu einer zulässigen Basis B
von LP (). Es gilt x∗ ≥ 0. Weil LP () nicht degeneriert ist, gilt für die Basisvariablen
sogar
m
X
∗
xi = b̂i +
a0ij j > 0 .
j=1
Wir behaupten: Es gilt b̂i ≥ 0. Da xB = b̂ die Basislösung zu B bezüglich LP ist,
folgt aus dieser Behauptung, dass B auch zulässig für LP ist, und damit wäre Aussage
b) gezeigt. Zum Zwecke des Widerspruchs, gelte b̂i < 0. Wir betrachten das Polynom
pB,i . Aus b̂i < 0 folgt pB,i (0) < 0. Andererseits gilt pB,i () > 0. Aus dem Zwischenwertsatz für stetige Funktionen folgt somit, dass es ein s ∈ (0, ) ⊂ (0, δB,i ) gibt, für
das gilt pB,i (s) = 0. Die kleinste positive Nullstelle dieses Polynoms ist jedoch δB,i .
Ein Widerspruch. Damit ist Aussage b) bewiesen.
Als letztes beweisen wir Aussage c). Eine optimale Basis ist dadurch gekennzeichnet,
dass sie zulässig ist und der Vektor der reduzierten Kosten keinen positiven Eintrag
enthält (Satz 2.1). Der Vektor der reduzierten Kosten für LP und LP () ist jedoch
gleich. Also folgt c) unmittelbar aus b).
2
Wie klein müssen wir den Parameter wählen, damit die im Satz beschriebenen Eigenschaften gelten? – Dem Beweis für a) entnehmen wir, dass es hinreichend ist, kleiner als die kleinste positive Nullstelle eines Polynoms der Form
p(s) =
m
X
βi si
i=0
mit mindestens einem nicht-nullwertigem Koeffizienten zu wählen. Die Koeffizienten
−1
0
von p sind dabei rationale Zahlen aus dem Vektor b̂ = A−1
B b und der Matrix A = AB .
Seien die Absolutwerte der Zähler und Nenner dieser Koeffizienten durch β nach oben
beschränkt, d.h. β erfüllt für alle nicht-nullwertigen Koeffizienten die Ungleichungen
β ≥ |βi | und β ≥ |β1i| . Zur Vereinfachung der Notation machen wir o.B.d.A. die
folgenden Annahmen.
• Es gelte β0 6= 0. (Ansonsten dividiere das Polynom solange durch s bis der
Koeffizient vor dem Term s0 nicht-nullwertig ist. Diese Divisionen haben keinen
Einfluss auf die Nullstellen.)
• Es gilt β0 > 0. (Ansonsten multipliziere das Polynom mit −1. Auch diese Multiplikation hat keinen Einfluss auf die Nullstellen des Polynoms.)
22
Für jedes δ ∈ (0, 2β1 2 ] gilt nun
m
X
βi δ i |p(δ)| = i=0
≥ β0 −
m
X
i=1
m
X
|βi |δ i
i
1
β
2β 2
i=1
m i
1
1X 1
≥
> 0 .
−
β β i=1 2
| {z }
1
−
≥
β
<1
Somit ist die kleinste positive Nullstelle von p größer als 2β1 2 . Damit können wir
= 2β1 2 setzen. Wenn wir die in Lemma 2.2 bewiesenen oberere Schranken für die
Absolutwerte der Nenner und Zähler der Zahlen im Simplextableau berücksichtigen,
so gilt β ≤ (αm)m , wobei α der größte Absolutwert über alle Eingabezahlen ist.
Damit genügt es = 12 (αm)−2m zu setzen, um die in Satz 2.4 beschriebenen Eigenschaften zu garantieren. Beachte, durch die Perturbierung wächst die Eingabelänge.
Dieses Wachstum ist aber polynomiell beschränkt: Sei ` eine obere Schranke für die
binäre Länge der Eingabezahlen. Dann genügen O(m(` + log m)) Bits zur Darstellung
von und somit O(m2 (` + log m)) Bits zur Darstellung von bi + i für 1 ≤ i ≤ m.
Bemerkung 2.5 Sei α der Absolutwert des größten Nenners bzw. Zählers der Eingabezahlen von LP . Die Aussagen in Satz 2.4 gelten für = 21 (αm)−2m . Die Eingabelänge von LP () ist damit polynomiell in der Eingabelänge von LP beschränkt.
2.4.3 Symbolische Perturbierung
Der offensichtliche Nachteil der oben beschriebenen Perturbierung ist, dass sehr
klein gewählt werden muss, um die in Satz 2.4 genannten Eigenschaften zu erzielen.
Dadurch vergrößert sich die Eingabelänge zwar nur polynomiell aber dennoch derartig signifikant, dass sich die Perturbierung spürbar auf die Laufzeit auswirkt. Wir beschreiben jetzt einen Weg, der es ermöglicht, die Pertubierung implizit durchzuführen,
ohne die Eingabe zu manipulieren. Der Trick ist, dass wir den Parameter durch einen
symbolischen Wert repräsentieren.
Wir betrachten einen Pivotschritt zu einer Basis B. Wie zuvor verwenden wir die Be−1
−1
zeichnungen A0 = A−1
B , Â = AB A und b̂ = AB b. Sei j der Index der Eingangspivot23
spalte.1 Sei B(i) der Index der gewählten Ausgangspivotspalte. Die in Abschnitt 2.2
beschriebenen Auswahlregeln bestimmen den Index i wie folgt.
)
(
P
0 t a
b̂k + m
t=1 kt
i = argmin1≤k≤m
âkj > 0
âkj
pB,k () = argmin1≤k≤m
âkj > 0 .
âkj Für = 0 gibt es möglicherweise mehrere Indizes, die dieses Minimum liefern. Für
jeden Parameter ∈ (0, δ) gibt es jedoch genau einen solchen Index, denn sonst wäre
LP () degeneriert.2 Zur Bestimmung der Ausgangspivotspalte wählen wir den Index
pB,k () âkj > 0 .
i = lim argmin1≤k≤m
→0
âkj Beachte, die Terme, über die das Minimum bestimmt wird, sind Polynome in . Für
→ 0 kann das kleinste dieser Polynome durch Koeffizientenvergleich bestimmt werden: Den Vergleich zwischen zwei Polynomen entscheidet jeweils der Koeffizient mit
kleinstem Grad in dem sich die Polynome unterscheiden. Der zusätzliche Aufwand zur
Durchführung dieser Pivotregel besteht also im Wesentlichen darin, zusätzlich zum Pivottableau auch die Umkehrmatrix A0 = A−1
B von Schritt zu Schritt mitzuführen, um
im Falle eines Unentschiedens zwischen zwei Ausgangsspalten eine eindeutige Wahl
treffen zu können.3
2.5 Laufzeit der Simplexmethode
Wir haben gesehen, dass sich die einzelnen Pivotschritte effizient durchführen lassen.
Die Anzahl der Pivotschritte ist jedoch problematisch. Der folgende Satz zeigt, dass
die Anzahl der Pivotschritte exponentiell in der Anzahl der Variablen und Nebenbedingungen sein kann, ohne dass man dabei in der Eingabe auf Zahlen großer Kodierungslänge zurückgreifen muss. Dieses Ergebnis wurde gezeigt von Klee und Minty
(1972).
Satz 2.6 Für jedes n, gibt es ein LP in kanonischer Form mit n Variablen und 2n ganzzahligen Koeffizienten mit Absolutwert höchstens 4, so dass der Simplex-Algorithmus
2n − 1 Pivotschritte benötigt.
1
Die Wahl der Eingangspivotspalte wird durch die Perturbierung nicht beeinflusst. Warum?
Tatsächlich folgt aus der Nicht-Degeneriertheit dieser LPs sogar, dass für alle ∈ (0, δ) derselbe
Spaltenindex selektiert wird. Warum?
3
Wenn wir davon ausgehen, dass die initiale Basismatrix der Einheitsmatrix entspricht, so liegt die
Matrix A0 zu Beginn jedes Pivotschrittes bereits im Tableau vor. Welche Spalten im Tableau entsprechen
den Spalten dieser Matrix?
2
24
Wir beschränken uns darauf die Beweisidee zu beschreiben. Um eine derartige Beispielinstanz zu konstruieren, benötigen wir zunächst ein LP mit exponentiel vielen
Basislösungen, denn die Anzahl der Basislösungen ist eine offensichtliche oberere
Schranke für die Anzahl der Iterationen des Simplexalgorithmus. Wir betrachten ein
LP mit der Zielfunktion
Maximiere x1
unter den Nebenbedingungen
0 ≤ xi ≤ 1
für 1 ≤ i ≤ n. Das Lösungspolyhedron dieses LPs entspricht dem n dimensionalen
Hypercube. Die Knoten des Hypercubes, also die Basislösungen des LPs, entsprechen
den Punkten aus der Menge {0, 1}n. Das LP hat also 2n Basislösungen.
Behauptung 2.7 Es gibt einen Hamiltonpfad auf den 2n Knoten des Hypercubes, auf
dem sich der Zielfunktionswert nicht verschlechtert.
Beweis: Der bekannte Gray-Code ist dadurch gekennzeichnet ist, dass er die Bitstrings aus {0, 1}n in einer deartigen Reihenfolge aufzählt, dass sich zwei nacheinander aufgezählte Strings nur in einem Bit unterscheiden, so dass die entsprechenden
Knoten auf dem Hypercube benachbart sind. Der Gray-Code definiert somit einem
Hamiltonpfad auf dem Hypercube. Die Zielfunktionwerte auf diesem Pfad verringern
sich nicht, da der Gray-Code zunächst die Knoten aufzählt, die mit einer 0 beginnen
und dann die Knoten, die mit einer 1 beginnen.
2
Um eine exponentielle Anzahl Schritte für den Simplexalgorithmus zu erreichen, benötigen wir jedoch einen Pfad, auf dem sich der Zielfunktswert nicht nur nicht verschlechtert sondern sogar von Knoten zu Knoten verbessert. Dies erreicht man, wenn man den
Hypercube durch den sogenannten Klee-Minty-Cube ersetzt, der einem perturbierten
Hypercube entspricht. Für > 0 definieren wir die folgenden Nebenbedingungen.
≤ x1 ≤ 1 ,
xj−1 ≤ xj ≤ 1 − xj−1 ,
Für → 0 konvergiert das durch diese Ungleichungen beschriebene Ungleichungssystem gegen den Hypercube. Auf diesem Polyhedron hat der oben beschriebene Hamiltopfad ansteigende Zielfunktionswerte. Die Konstruktion funktioniert für ≤ 14 . Auf
den Beweis dieser Eigenschaft verzichten wir hier. Wenn wir = 14 setzen und alle
Nebenbedingungen mit 4 multiplizieren erhalten wir ein LP mit ganzzahligen Koeffizienten wie im Satz beschrieben.
Die Konstruktion von Klee-Minty geht nicht nur von einer Worst-Case-Eingabe sondern auch von einer Worst-Case-Pivotentscheidung aus. Tatsächlich lassen sich derartige Beispiele auch für zahlreiche bekannte Pivotregeln wie z.B. Blands Pivotregel
25
finden. Die Frage, ob es eine Pivotregel mit polynomieller Laufzeit gibt, ist ungeklärt.
√
Bisher konnte man nur für randomisierte Pivotregeln eine Laufzeit von mO( n) nachweisen; unabhängig gezeigt von einerseits Kalai (1992) und andererseits Matousek,
Sharir und Welzl (1992). Es ist sogar unklar, ob es überhaupt einen Weg polynomieller Länge zum Optimum gibt, also ob der Durchmesser des Graphs eines Polyhedrons
sich polynomiell in der Anzahl seiner Facetten (Nebenbedingungen) und der Dimension beschränken lässt. Eine optimistische aber weder bewiesene noch widerlegte Behauptung von Hirsch (1957) lautet: Der Durchmesser eines n-dimensionalen Polytops
mit m Facetten ist höchstens m − n. Das beste bekannte bewiesene Ergebnis ist eine
obere Schranke in Höhe von mlog2 n+2 für den Durchmesser gezeigt durch Kalai und
Kleitman (1992).
Im Gegensatz zu den obigen theoretischen Überlegungen zur Worst-Case-Laufzeit des
Simplexverfahrens stehen die praktischen Erfahrungen mit diesem Verfahren: Viele
in der Praxis auftretenden LPs lassen sich tatsächlich effizient mit dieser Methode
lösen. Dies wird untermauert durch theoretische Untersuchungen die zufällig erzeugte Eingabeinstanzen untersuchen. Borgwardt (1977) untersucht beispielsweise LPs bei
denen die Koeffizienten der Nebenbedingungsmatrix A uniform zufällig generiert werden. Über die Relevanz eines derartigen Eingabemodells bezüglich der in der Praxis
vorkommenden LPs lässt sich streiten. Spielman und Teng (2001) präsentieren ein
raffinierteres probabilistisches Eingabemodell. In ihrer sogenannten geglätteten Analyse (Smoothed Analysis) erzeugt zunächst ein Gegner die Nebenbedingungsmatrix
und dann werden die Einträge dieser Matrix durch eine leichte zufällige Perturbierung
verändert. Intuitiv startet die geglättete Analyse also mit einer Worst-Case-Eingabe,
zu der ein leichtes Gauß’sches Rauschen hinzuaddiert wird. Auch für dieses semizufällige Eingabemodell lässt sich die Laufzeit des Simplex-Algorithmus polynomiell
beschränken.
26
Kapitel 3
Die Ellipsoidmethode
Wir werden in diesem Abschnitt einen Algorithmus zur Lösung von LPs kennenlernen,
der auch im Worst-Case eine polynomielle Laufzeit garantiert. Es handelt sich dabei
um die sogenannte Ellipsoidmethode, die zur Lösung nichtlinearer Optimierungsprobleme entwickelt wurde. Im Jahre 1979 entdeckte der russische Mathematiker Leonid
Khachiyan, dass diese Methode auch zur Lösung von LPs eingesetzt werden kann und
das die Laufzeit dieser Methode für LPs polynomiell in der Eingabelänge beschränkt
werden kann. In praktischen Anwendungen beobachtet man jedoch, dass die Ellipsoidmethode dem Simplexverfahren in der Regel deutlich unterlegen ist.
3.1 Zulässigkeitstest versus Optimieren
Eigentlich handelt es sich bei der Ellipsoidmethode lediglich um ein Verfahren, das
für ein lineares Ungleichungssystem LI (linear inequalities) der Form Ax ≤ b in polynomieller Zeit entscheidet, ob LI zulässig ist, also ob es eine Lösung gibt, die alle
Ungleichungen erfüllt. Das folgende Lemma besagt jedoch, dass das Optimieren eines
LPs auf das Entscheiden, ob es überhaupt eine Lösung gibt, die alle Nebenbedingungen erfüllt, reduziert werden kann.
Lemma 3.1 Existiert ein polynomieller Algorithmus, der entscheidet, ob ein System
von linearen Ungleichungen eine Lösung besitzt, so existiert auch ein polynomieller
Algorithmus zur Lösung von LPs.
Die wesentliche Idee wie man das Optimieren von LPs auf einen Zulässigkeitstest reduziert, lässt sich wie folgt zusammenfassen: Wenn das vorliegende LP beschränkt und
zulässig ist, dann ist der optimale Zielfunktionswert z eindeutig dadurch bestimmt,
27
dass z der größtmöglichste Wert ist, für den das LP auch dann noch zulässig bleibt,
wenn wir die Nebenbedingung cT x ≥ z hinzufügen. Wir können deshalb den optimalen Zielfunktionswert mittels einer Binärsuche finden, in der wir Zulässigkeitstests für
verschiedene z-Werte durchführen. Für den Start der Binärsuche benötigt man untere und obere Schranken für den kleinst- und größtmöglichen Zielfunktionswert eines
zulässigen und beschränkten LPs mit Eingabelänge L (in binärer Kodierung). Es gilt
−2poly(L) ≤ z ≤ 2poly(L) . Die Binärsuche konvergiert gegen den optimalen Zielfunktionswert. Um den optimalen Zielfunktionswert bis auf einen additiven Fehler von δ zu
erreichen benötigt die Binärsuche O(log(2poly(L) /δ)) = poly(L)+O(log(1/δ)) Schritte. Für δ = 2−poly(L) ergibt sich somit eine Laufzeit, die polynomiell in L ist. Jetzt
muss man noch zeigen, wie man die optimale Lösung effizient bestimmen kann, wenn
man den optimalen Zielfunktionswert bis auf einen additiven kleinen Fehler kennt.
Der Schlüssel hierzu ist, dass alle nicht-optimalen Basislösungen eines LPs der Eingabelänge L einen Zielfunktionswert haben, der um die Größenordnung 2−poly(L) geringer ist, als der optimale Zielfunktionswert. Eine Basislösung, die diese Bedingung
erfüllt (und somit optimal ist) kann nun durch geschicktes Lösen von polynomiell vielen Gleichungssystem erreicht werden. Die Details dieser Reduktion von Optimierung
auf Zulässigkeitstest werden in Abschnitt 3.1 beschrieben.
Als Konsequenz aus Lemma 3.1 müssen wir nun nur noch zeigen, wie man lineare
Ungleichungssystem effizient auf ihre Zulässigkeit testet. Bevor wir uns der eigentlichen Methode zuwenden, präsentieren wir einige Schritte zur Vereinfachung der Ungleichungssysteme, die unter anderem dafür sorgen, dass das Ungleichungssystem beschränkt und der Lösungsraum nicht zu klein ist, es sei denn, der Lösungsraum ist
leer.
Lemma 3.2 Ein lineares Ungleichungssystem LI der Eingabelänge L kann in polynomieller Zeit in ein lineares Ungleichungssystem LI ∗ mit den folgenden Eigenschaften
transformiert werden.
a) LI ∗ hat genau dann eine Lösung, wenn LI eine Lösung hat.
b) Der Lösungsraum von LI ∗ ist in einer Kugel um den Ursprung mit Radius höchs2
tens 2O(L ) enthalten.
c) Wenn der Lösungsraum von LI ∗ nicht leer ist, so enthält er eine Kugel mit Ra4
dius mindestens 2−O(L ) .
d) Die Eingabelänge von LI ∗ ist beschränkt durch O(L2 ).
Die Details dieser Transformation werden in Abschnitt 3.2 beschrieben.
28
3.1.1 Beweis von Lemma 3.1
Es sei ein Algorithmus A gegeben, der für ein gegebenes System linearer Ungleichungen in polynomieller Zeit entscheidet, ob es eine Lösung gibt, die alle Ungleichungen
erfüllt. O.B.d.A. sei ein LP in der Gleichungsform max cT x, Ax = b, x ≥ 0 gegeben.
Wie üblich bezeichne m die Anzahl der Nebenbedingungen, n die Anzahl der Variablen und α den größten Absolutwert über alle Zähler und Nenner der Eingabezahlen.
Wir benötigen das folgende Lemma.
Lemma 3.3 Seien x und y zwei Basislösungen mit cT x 6= cT y, dann gilt |cT x−cT y| ≥
(αm)−2(m+1) .
Beweis: Aus Lemma 2.2 b) folgt, dass die Absolutwerte der Zähler und Nenner in
cT x und cT y durch (αm)m+1 nach oben beschränkt sind. Seien a, b, c, d derartig beschränkte ganze Zahlen. Dann gilt
a c ad − bc 1
≥ 1 ≥
.
− = b d
bd
|bd|
(αm)2(m+1)
2
Wir werden A nun als Black-Box einsetzen, um eine optimale Lösung für das betrachtete LP zu berechnen:
1. Wir beginnen damit, zu prüfen, ob das gegebene LP überhaupt eine gültige
Lösung besitzt. Dazu rufen wir A mit den Ungleichungen Ax ≤ b, Ax ≥ b
und x ≥ 0 auf. Gibt es keine gültige Lösung, so brechen wir an dieser Stelle ab.
2. Nun testen wir, ob das LP unbeschränkt ist. Aus Lemma 2.2 folgt, dass der Zielfunktionswert cT x für eine beliebige Basislösung x durch (αm)m+1 nach oben
beschränkt ist. Wir rufen A nun mit den Ungleichungen Ax ≤ b, Ax ≥ b,
x ≥ 0 und cT x ≥ (αm)m+1 + 1 auf. Die binäre Kodierungslänge des Terms
(αm)m+1 + 1 ist O(m log(αm)) = O(L2 ). Somit ist die Größe des Ungleichungssystems polynomiell in der Eingabelänge des LPs beschränkt. Hat dieses
Ungleichungssystem eine Lösung, so ist das LP offenbar unbeschränkt, da jedes beschränkte LP eine optimale Basislösung mit Zielfunktionswert höchstens
(αm)m+1 hat.
3. Wir wissen nun, dass es eine optimale Basislösung x∗ gibt, und versuchen den
Zielfunktionswert cT x∗ bis auf ein sehr kleines Intervall einzugrenzen. Dieses
Intervall soll die Länge δ = (αm)−2(m+1) haben, also höchstens so groß sein,
wie der in Lemma 3.3 beschriebene minimale Abstand zwischen den Zielfunktionswerten zweier Basislösungen. Insbesondere suchen wir eine ganze Zahl K,
so dass gilt δK ≤ cT x∗ < δ(K + 1).
29
Wir bestimmen K durch eine Binärsuche, in der wir A mit den Ungleichungen
Ax ≤ b, Ax ≥ b, x ≥ 0 und cT x ≥ δK mit verschiedenen Werten für K aufrufen. Wir haben in Schritt 2 gesehen, dass |cT x∗ | ≤ (αm)m+1 gilt, somit wissen
wir, die gesuchte ganze Zahl K erfüllt die Ungleichung |K| ≤ (αm)m+1 /δ =
(αm)3(m+1) . Die Binärsuche benötigt also nur
O log (αm)3(m+1) = O(m log m + m log α) = O(L2 )
Aufrufe von A . Also kann die gesuchte ganze Zahl K in polynomieller Zeit
berechnet werden.
4. Aus δK ≤ cT x∗ < δ(K+1) für δ = (αm)−2(m+1) in Verbindung mit Lemma 3.3
folgt nun, dass jede Basislösung x, die die Ungleichungen
Ax ≤ b, Ax ≥ b, x ≥ 0, cT x ≥ δK
erfüllt, den gleichen Wert wie x∗ hat, also optimal ist. Das bedeutet, wir müssen
nur noch eine beliebige Basislösung finden, die diese Ungleichungen erfüllt.
Um eine solche Basislösung zu finden, genügt es, zu ermitteln, welche Variablen
in ihr auf 0 gesetzt sind. Zu diesem Zweck überprüfen wir nun iterativ, ob für
die Indizes k = 1, . . . , n die folgenden Ungleichungen erfüllbar sind:
A ≤ b, A ≥ b, x ≥ 0, cT x ≥ δK
und xk ≤ 0
und xj ≤ 0 für j ∈ S(k).
Dabei bezeichne S(k) die Menge derjenigen Indizes kleiner als k für die die
entsprechenden Ungleichungen erfüllbar waren.
Liefert beispielsweise der Aufruf von A für k = 1 ein positives Ergebnis zurück,
so wissen wir, dass es eine Lösung mit x1 = 0 gibt, die die Ungleichungen (4)
erfüllt. Somit gibt es auch eine Basislösung mit x1 = 0, die diese Bedingungen
erfüllt. Eine solche suchen wir dann mit den folgenden Aufrufen von A . Es
wird am Ende höchstens m Indizes geben, die nicht in S(n + 1) enthalten sind,
da jede Basislösung höchstens m Einträge ungleich Null enthält. Ist das lineare
Programm nicht degeneriert, so gibt es exakt m Indizes, die nicht in S(n +
1) liegen, wir können dann die dazugehörigen Spalten als Basis B wählen und
erhalten die Basislösung wie üblich durch die Gleichung xB = A−1
B b.
Enthält S(n + 1) weniger als m Indizes, so bilden diese zwar keine Basis, definieren wir jedoch auch in diesem Fall B als die Menge der Spalten, die nicht
in S(n + 1) enthalten sind, so besitzt das Gleichungssystem xB = A−1
B b eine
Lösung mit positiven Variablen, weil wir bereits wissen, dass es eine gültige Basislösung gibt, die die Ungleichungen (4) erfüllt und in der alle Variablen aus
S(n + 1) auf Null gesetzt sind.
Offensichtlich ist auch dieser Schritt in polynomieller Zeit durchführbar.
30
3.1.2 Beweis von Lemma 3.2
LI werde durch das Gleichungssystem Ax ≤ b beschrieben. Bezeichne m die Anzahl
der Nebenbedingungen in LI, n die Anzahl der Variablen und α den größten Absolutwert über alle Eingabezahlen. Wir gehen in zwei Transformationsschritten vor:
1. Wir fügen zu LI zunächst die Nebenbedingungen xi ≤ (αm)m und xi ≥
−(αm)m für 1 ≤ i ≤ n hinzu. Das erhaltene Ungleichungssystem A0 x ≤ b0 bezeichnen wir mit LI 0 . Die Anzahl der Nebenbedingungen in LI 0 ist m0 = m+2n.
Die Absolutwerte der Zahlen in LI 0 sind durch α0 = (αm)m beschränkt.
2. Wir perturbieren LI 0 wie in Abschnitt 2.4.2 beschrieben, d.h. wir ersetzen den
0
Vektor b0 durch den Vektor b0 + ~ für ~ = (1 , 2 , . . . , m )T mit = 21 (α0m0 )−2m .
Das so erhaltenen Ungleichungssystem nennen wir LI ∗ .
In Schritt 1 wächst die Eingablänge nur um einen polynomiellen Faktor, da die Länge
der einzelnen Eingabezahlen nach der Transformation durch
O(log α0 ) = O(log(αm)2m )) = O(m log m + m log α) = O(L2 )
beschränkt ist. Aus Bemerkung 2.5 folgt, dass die Eingabelänge durch die Perturbierung in Schritt 2 ebenfalls nur um einen polynomiellen Faktor anwächst. Eigenschaft
d) ist somit gewährleistet.
Aussage a) kann wie folgt gezeigt werden. Alle betrachteten Ungleichungssysteme
haben genau dann eine zulässige Lösung, wenn sie eine zulässige Basislösung haben.
Wenn LI eine zulässige Basislösung x hat, so folgt aus Lemma 2.2, dass |xi | ≤ (αm)m
für 1 ≤ i ≤ n. Also ist x auch zulässig für LI 0 und damit auch für LI ∗ . Wenn LI keine
zulässige Basislösung hat, so hat offensichtlich auch LI 0 keine zulässige Basislösung.
Jetzt folgt aus Satz 2.4b) zusammen mit Bemerkung 2.5, dass auch LI ∗ keine zulässige
Basislösung hat. Damit ist a) gezeigt.
Als nächstes beweisen wir Aussage b). Nach dem ersten Transformationsschritt ist der
Lösungsraum in dem durch die Ungleichungen |xi | ≤ (αm)m (1 ≤ i ≤ m) beschriebenen Hyperwürfel eingeschlossen. Durch die Perturbierung in Schritt 2 vergrößert
sich der Lösungsraum leicht, ist aber immer noch im Hyperwürfel |xi | ≤ (αm)m + 1
enthalten. Dieser Hyperwürfel ist in einer Kugel mit Radius
√
2
n((αm)m + 1) = 2O(log n+m log m+m log α) = 2O(L )
um den Ursprung eingeschlossen. Damit ist auch Eigenschaft b) nachgewiesen.
Eigenschaft c) ist eine Konsequenz der Perturbierung. Betrachte die ite Nebenbedingung a0i x ≤ bi aus LP 0 und ihre perturbierte Variante a0i x ≤ bi + i aus LP ∗ für ein
31
beliebiges i ∈ {1, . . . , m0 }. Der Abstand zwischen den beiden Hyperebenen a0i x = bi
1
i
0 0 −2m0
,
und a0i x = bi + i beträgt mindestens √n·α
0 . Wir substituieren = 2 (α m )
0
0
m
0
m = m + 2n, α = (αm) sowie i ≤ m und erhalten eine untere Schranke für
den Abstand der Hyperebenen in Höhe von
√
1
i
√
≥
0
m
2(m+n)
n·α
(2((αm) (m + n))
)i · n · (αm)2m
2
= 2−O(m(m+n)
4
= 2−O(L )
log(αm))
Wenn nun der Lösungsraum von LI ∗ nicht leer ist, so folgt aus a), dass auch der
Lösungsraum von LI nicht leer ist und somit auch LI 0 einen zulässigen Punkt x
enthält. Für diesen Punkt gilt a0i x ≤ bi . Der Abstand von x zur Hyperebene a0i x = bi +i
ist somit mindestens so groß wie der Abstand zwischen den beiden oben betrachteten
4
Hyperebenen, also mindestens 2−O(L ) . Da dieser Abstand zu jeder Nebenbedingungs4
hyperebene von LI ∗ eingehalten wird, gibt es eine Kugel mit Radius 2−O(L ) um x, die
keine dieser Hyperebenen schneidet. Da x zulässig ist, ist diese Kugel somit, wie in
Aussage c) behauptet, im Lösungspolyhedron von LI ∗ enthalten. Damit ist Lemma 3.2
bewiesen.
3.2 Beschreibung der Ellipsoidmethode
Gegeben sei nun eine Menge von linearen Ungleichungen Ax ≤ b und es bezeichne
S ⊆ Rn die Menge der zulässigen Lösungen. Es soll entschieden werden, ob S leer
ist oder nicht. Dabei sei ferner eine Zahl u ∈ R gegeben, so dass S eine Teilmenge
der Kugel um den Ursprung mit Radius u ist, und eine weitere Zahl l ∈ R mit der
Bedeutung, dass entweder S = ∅ oder S eine Kugel mit Radius l enthält. Die Parameter u und l können wir aus Lemma 3.2 ableiten. Man transformiert dazu das gegebene
System linearer Ungleichungen LI in ein System LI ∗ mit den gewünschten Eigenschaften, das genau dann eine Lösung besitzt, wenn LI eine besitzt. Aus dem Lemma
2
4
ergibt sich u = 2O(L ) und l = 2O(−L ) , wobei L die Eingabelänge des ursprünglichen
Ungleichungssystems LI ist.
Die Idee hinter der Ellipsoidmethode ist es den Lösungsraum S in immer kleinere Ellipsoide einzuschließen, bis schließlich ein Ellipsoid erreicht ist, der S so eng
umschließt, dass sein Mittelpunkt in die Menge S fallen muss, es sei denn S ist
leer. Ein Ellipsoid ist ein geometrisches Gebilde, dass durch affine Transformationen wie Verschiebungen, Drehungen, Spiegelungen, Streckungen aus einer Kugel entsteht. Formal kann man jedes mögliche Ellipsoid beschreiben, indem man von einer
n-dimensionalen Einheitskugel mit dem Ursprung als Mittelpunkt ausgeht, und eine
umkehrbare affine Abbildung angibt, die die Kugel in den Ellipsoid überführt. Unter
32
der n-dimensionalen Einheitskugel Sn verstehen wir dabei die Menge
Sn = x ∈ Rn | xT x ≤ 1 .
Die affine Abbildung ist von der folgenden Form: Sei t ∈ Rn ein Vektor und Q eine
invertierbare n×n-Matrix. Ein Punkt x ∈ Rn wird dann auf den Punkt T (x) = t+Q·x
abgebildet. Der aus Sn durch die affine Transformation T entstehende Ellipsoid entspricht der Punktmenge T (Sn ). Die Matrix Q beschreibt dabei affine Transformationen
wie Streckungen, Spiegelungen und Drehungen der Kugel und der Vektor t beschreibt
eine Verschiebung des Mittelpunktes.
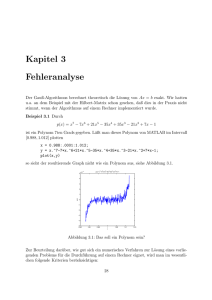
Die Ellipsoidmethode besteht nun aus den folgenden Schritten:
1. Wähle den initialen Ellipsoid E als eine Kugel um den Ursprung mit Radius u.
Gemäß unseren Annahmen ist nach diesem Schritt S in E enthalten.
2. Falls das Volumen von E kleiner als das Volumen der Kugel mit Radius l ist,
terminiere mit der Ausgabe S = ∅“.
”
3. Es sei z der Mittelpunkt von E. Wir testen, ob z ∈ S, d.h. ob z alle Nebenbedingungen erfüllt. Im positiven Fall terminiere mit der Ausgabe S 6= ∅“.
”
4. Ansonsten können wir wie folgt einen abgeschlossenen Halbraum H identifizieren, der S enthält und auf dessen Rand sich z befindet. Dazu wählen wir
zunächst eine Ungleichung aus, die vom Mittelpunkt z nicht erfüllt wird. Diese
Ungleichung beschreibt eine Hyperebene, durch die der Raum so in zwei Hälften
geteilt wird, dass z in der einen Hälfte liegt und S in der anderen. Verschieben
wir diese Hyperebene parallel so, dass sie durch z verläuft, so erhalten wir den
gewünschten Halbraum H.
Es bezeichne E-halbe den Schnitt von E mit dem Halbraum H. Die Fläche von
E-halbe ist nur noch halb so groß wie die von E und es gilt S ⊆ E-halbe.
Allerdings ist E-halbe keine Ellipse mehr, siehe Abbildung 3.1. Wir möchten
S aber wiederum durch eine Ellipse umschließen. Deshalb berechnen wir nun
die kleinste Ellipse E 0 die E-halbe enthält. Wir setzen E auf E 0 und fahren mit
Schritt 2 fort.
Wir fassen zusammen: Von Iteration zu Iteration berechnen wir einen neuen Ellipsoiden E unter Einhaltung der Invariante:
E enthält S.
(3.1)
Das Verfahren bricht ab, sobald der Mittelpunkt des Ellipsoids ein zulässiger Punkt
ist oder wenn das Volumen von E kleiner als das Volumen der Kugel mit Radius l
ist. Im ersteren Fall gilt offensichtlich S 6= ∅ und die Methode arbeitet korrekt. Im
33
H
E
E’
z
E−halbe
Abbildung 3.1: Veranschaulichung von Schritt 4 der Ellipsoidmethode
letzteren Fall folgt aus der Invariante, dass das Volumen von S ebenfalls kleiner als
das Volumen der Kugel mit Radius l ist. Gemäß unserer Voraussetzung umschließt S
aber eine Kugel mit Radius l, es sei denn S = ∅. Es folgt S = ∅ und damit arbeitet die
Ellipsoidmethode auch in diesem Fall korrekt. Damit ist die partielle Korrektheit der
Methode nachgewiesen. Um zu beweisen, dass die Methode terminiert und zwar nach
nur polynomiell vielen Iterationen, werden wir im nächsten Abschnitt nachweisen,
dass das Volumen des Ellipsoids von Iteration zu Iteration signifikant abnimmt.
3.3 Skizze der Laufzeitanalyse
Wir werden die Laufzeitanalyse nur skizzieren. Von zentraler Bedeutung ist das folgende Lemma.
Lemma 3.4 Für den in Schritt 4 berechneten Ellipsoid E 0 gilt
vol(E 0 ) ≤
vol(E)
.
21/2(n+1)
Beweis: Wir werden dieses Lemma nur für den zwei-dimensionalen Fall, also für den
Fall n = 2, nachweisen. In diesem Fall entspricht der Ellipsoid einer Ellipse und sein
Volumen ist die Fläche dieser Ellipse.
Um das Lemma zu beweisen, müssen wir uns Schritt 4 noch einmal näher anschauen. Wie berechnen wir eine möglichst kleine Ellipse E 0 , die den Schnitt von E -halbe
und H enthält? – Wir betrachten dazu zunächst eine besonders einfache Situation und
34
E’
(0,1)
(−1,0)
c
E
(0,−1)
Abbildung 3.2: Schritt 4 im beschriebenen Spezialfall
gehen davon aus, dass E ein Kreis mit Radius 1 um den Ursprung ist und dass H der
Halbraum der Punkte mit negativer x-Koordinate ist, und werden später zeigen, wie
man den allgemeinen Fall auf diese spezielle Situation zurückführen kann. Betrachtet man Abbildung 3.2, so scheint es eine gute Idee zu sein, E 0 als eine Ellipse zu
wählen, deren Achsen parallel zu den Koordinatenachsen verlaufen und deren Mittelpunkt auf der negativen x-Achse liegt. Ferner sollte der Rand der Ellipse durch die
Punkte (−1, 0), (0, 1) und (0, −1) verlaufen. Somit gilt für geeignete Werte a, b, c ∈ R
E 0 = (x, y) ∈ R2 | ((x − c)/a)2 + (y/b)2 ≤ 1 .
Es gilt −1 ≤ c ≤ 0 und a und b entsprechen den Längen der Achsen von E 0 . Deshalb
gilt a > 0 und b > 0. Die Länge a der horizontalen Achse beträgt offenbar 1 + c,
also gilt a = 1 + c und wegen 2a ≥ 1 muss − 21 ≤ c ≤ 0 gelten. Da der Punkt
(0, 1) auf dem√Rand von E 0 liegt, muss (c/(1 + c))2 + (1/b)2 = 1 gelten und somit
b = (1 + c)/ 1 + 2c. Nun hängt die Ellipse
E 0 nur noch vom Parameter c ab. Die
√
0
2
Fläche von E beträgt πab = π(1 + c) / 1 + 2c. Eine leichte Rechnung ergibt, dass
diese Fläche für c = − 31 minimiert wird. Mit diesem Wert für c ergibt sich eine Ellipse
mit Mittelpunkt (− 31 , 0) und Achsen der Länge a = 32 und b = √23 . Wir behaupten,
dass diese Ellipse tatsächlich E -halbe umschließt. Sei dazu ein beliebiger Punkt (x, y)
35
mit x2 + y 2 ≤ 1 und x ≤ 0, also ein beliebiger Punkt aus E -halbe gegeben. Dann gilt
2
1
9
3
(x − c)2 y 2
x+
+ 2 =
+ y2
2
a
b
4
3
4
1 3 2
6 2 3
x + y2
x + x+ +
=
4
2
4 4
3 2 3
≤
x + x + 1 ≤ 1,
2
2
wobei die letzte Ungleichung aus x2 + x ≤ 0 für −1 ≤ x ≤ 0 folgt.
0
π( 32 )2 /
q
Die Fläche von E ist π. Die Fläche der oben berechneten Ellipse E beträgt
Somit gilt
√
( 23 )2
4 3
area(E 0 )
= q =
= 0.76 . . . < 0.89 . . . = 2−1/6 = 2−1/2(n+1) .
area(E)
9
1
1
.
3
3
Es verbleibt nun noch die Frage, wie wir mit beliebigen Ellipsen verfahren. Um auch
in diesem Fall E 0 berechnen zu können, führen wir die folgenden Schritte durch:
1. Verschiebe den Raum so, dass z im Koordinatenursprung liegt.
2. Drehe das Koordinatensystem so, dass die Achsen parallel zu den Achsen von
E verlaufen.
3. Skaliere die x- und y-Koordinaten so, dass E zu einem Kreis mit Radius 1 wird.
4. Der Rand von H ist nun eine Gerade, die durch den Ursprung verläuft. Drehe
das Koordinatensystem nun so, dass die Gerade der y-Achse entspricht.
5. Nun sind wir in dem gerade behandelten Spezialfall und können E 0 berechnen.
6. Wir wenden auf E 0 die Schritte 1 bis 4 in umgekehrter Reihenfolge an.
Nur in Schritt 3 wird das Volumen von E bzw. E 0 verändert. Skalierungen des Koordinatensystems haben jedoch die schöne Eigenschaft, dass sie zwar das Volumen bzw.
die Fläche verändern, nicht jedoch das Verhältnis zweier Volumina bzw. Flächen. Das
bedeutet, dass die Schranke, die wir für das Verhältnis der Flächen von E und E 0 im
Spezialfall hergeleitet haben, übertragen werden kann.
Damit ist Lemma 3.4 für n = 2 nachgewiesen. Die Analyse für allgemeines n ist nicht
wesentlich schwieriger nur technische aufwendiger.
2
Aus dem obigen Lemma ergibt sich nun die folgende obere Schranke für die Anzahl
der Iterationen der Ellipsoidmethode. Der erste Ellipsoid ist eine Kugel mit Radius u =
36
2
2O(L ) . Der vorletzte berechnete Ellipsoid hat mindestens das Volumen einer Kugel
4
mit Radius l = 2O(−L ) . Das Volumen hat also zwischen der ersten und der vorletzten
Iteration höchstens um den Faktor ( ul )n abgenommen. Aus Lemma 3.4 folgt, dass das
Volumen des Ellipsoids in jeder Iteration mindestens um den Faktor 21/2(n+1) abnimmt.
Wenn T die Anzahl der Iterationen ist, ergibt sich somit
u n
.
2(T −1)/2(n+1) ≤
l
Durch Auflösen nach T ergibt sich
u
T ≤ 2n(n + 1) log2
+ 1 = O(n2 L4 ) .
l
Damit erhalten wir den folgenden Satz.
Satz 3.5 Die Ellipsoidmethode terminiert nach O(n2 L4 ) Iterationen.
2
An dieser Stelle möchten wir anmerken, dass wir uns hier nicht bemüht haben eine
möglichst genaue Laufzeitabschätzung für die Ellipsoidmethode zu erhalten, sondern
wir wollten auf möglichst prägnante Art und Weise die Ideen präsentieren, die zur polynomiellen Laufzeitschranke für die Ellipsoidmethode führen. Man kann tatsächlich
zeigen, dass nur O(n2L) Iterationen zum Entscheiden der Zulässigkeit eines Ungleichungssystems ausreichen.
Um aus dem obigen Satz eine polynomielle Laufzeitschranke abzuleiten, muss noch
gezeigt werden, dass die einzelnen Iterationen in polynomieller Zeit durchgeführt werden kann. Das schwierige Problem, das dabei auftritt, ist die numerische Stabilität
der Methode. Um nämlich den Mittelpunkt der neuen Ellipse E 0 und die Länge ihrer
Achsen zu berechnen, müssen Wurzeln gezogen werden. Das bedeutet insbesondere,
dass die Zahlen sogar irrational werden können. Um das zu verhindern, müssen die
Zwischenergebnisse gerundet werden. Durch das Runden könnten aber wichtige Eigenschaften der Ellipsoidmethode verloren gehen, beispielsweise könnte es passieren,
dass die Ellipsoide nicht mehr um einen konstanten Faktor schrumpfen. Man kann jedoch zeigen, dass die Ellipsoidmethode weiterhin funktioniert, wenn man jede Zahl so
rundet, dass sie nur noch aus polynomiell vielen Bits besteht. Dann kann auch jeder
Iterationsschritt in polynomieller Zeit durchgeführt werden.
3.4 Zusammenfassung
Wir haben gezeigt, dass LPs mit einer polynomiellen Anzahl von Aufrufen der Ellipsoidmethode, die jeweils polynomiell viele Iterationen benötigen, gelöst werden
können. Da auch die einzelnen Iterationen eine polynomielle Laufzeitschranke haben,
ergibt sich der folgende Satz.
37
Satz 3.6 Lineare Programme können durch die Ellipsoidmethode in polynomieller
Zeit gelöst werden.
Die Ellipsoidmethode garantiert somit im Gegensatz zur Simplexmethode eine polynomielle Worst-Case-Laufzeit. Für einen Großteil der in der Praxis vorkommenden LPs
ist die Ellipsoidmethode jedoch der Simplexmethode unterlegen, weshalb die Simplexmethode immer noch die am weitesten in der Praxis verbreitete Methode zur Lösung
von LPs ist.
Die Ellipsoidmethode hat noch weitere Fähigkeiten, die wir bisher noch nicht angesprochen haben. Man kann sie zur effizienten Lösung von Problemen verwenden, deren Lösungspolyhedron durch eine exponentielle Anzahl von Facetten bzw. Nebenbedingungen definiert ist, die nicht explizit in der Eingabe definiert sind. Voraussetzung dafür ist ein sogenanntes Separation-Oracle, das es erlaubt, für einen unzulässigen Punkt in polynomieller Zeit eine verletzte Nebenbedingung zu benennen. Dieses
Separation-Oracle wird in der Ellipsoidmethode eingesetzt, um den Ellipsoid E -halbe
zu berechnen, wie wir es in Abschnitt 3.2 beschrieben haben. Wenn ein derartiges
Separation-Oracle für ein Problem gegeben ist, kann das Problem in polynomieller
Zeit durch die Ellipsoidmethode gelöst werden. Für weitergehende Informationen verweisen wir auf die Literatur.
38
Kapitel 4
Dualität
Zum Problem des Maximalen Flusses gibt es ein korrespondierendes Problem, nämlich
das Problem des Minimalen Schnittes. Beide Problem haben denselben Zielfunktionswert. Das eine Problem ist das duale Problem“ des anderen Problems. In die”
sem Kapitel werden wir sehen, dass diese Art von Dualität kein besonderes Phänomen von Flussproblemen ist, sondern dass es zu jedem Maximierungs-LP ein duales
Minimierungs-LP mit demselben Zielfunktionswert gibt und umgekehrt. LP-Dualität
ist der Schlüssel zur eleganten Lösung vieler Optimierungsprobleme. Beispielsweise
folgt die Korrektheit der bekannten Ford-Fulkerson-Methode für Flussprobleme aus
der Dualität zwischen maximalen Flüssen und minimalen Schnitten.
4.1 Primale und duale LPs
Betrachte das folgende LP in kanonischer Form, das wir als primales LP bezeichnen.
Maximiere 5x1 + 7x2
unter den Nebenbedingungen
x1 + 4x2 ≤ 4
x1 + x2 ≤ 2
x1 , x2 ≥ 0 .
Es gibt eine einfache Möglichkeit um eine obere Schranke für den Zielwert zu erhalten.
Wir multiplizieren die erste Bedingung mit 4 und addieren sie zur zweiten Bedingung.
Wir erhalten
5x1 + 17x2 ≤ 18 .
Hieraus können wir folgern, dass der Zielfunktionswert des LPs durch den Wert 18
nach oben beschränkt ist, denn es gilt 5x1 + 7x2 ≤ 5x1 + 17x2 ≤ 18. Alternativ
39
können wir die erste Bedingung auch mit 2 und die zweite mit 3 multiplizieren. Das
ergibt
5x1 + 11x2 ≤ 14 ,
und wir erhalten eine bessere obere Schranke für das primale LP, nämlich den Wert 14.
An dieser Stelle beobachten wir, dass wir obere Schranken für das primale LP herleiten
können, indem wir die erste und zweite Nebenbedingung mit nicht-negativen Faktoren
y1 bzw. y2 multiplizieren, die die Eigenschaften y1 + y2 ≥ 5 und 4y1 + y2 ≥ 7 erfüllen.
Für welche Faktoren y1 und y2 erhalten wir die beste untere Schranke, die wir auf diese
Art und Weise ableiten können? – Diese Frage führt zu dem folgenden Minimierungsproblem, das nach der besten oberen Schranke sucht, die nach den obigen Prinzipien
abgeleitet werden kann.
Minimiere 4y1 + 2y2
unter den Bedingungen
y1 + y2 ≥ 5
4y1 + y2 ≥ 7
y1 , y2 ≥ 0 .
Dies ist das duale LP zum obigen primalen LP. Die folgende Definition verallgemeinert
dieses Prinzip.
Definition 4.1 Wir betrachten das folgende LP in der kanonischen Form
Maximiere cT x unter Ax ≤ b, x ∈ Rd≥0 .
Die Anzahl der Nebenbedingungen (ohne die Nichtnegativitätsbedingungen) sei m.
Dieses LP bezeichnen wir als primales LP. Das zugehörige duale LP ist definiert als
Minimiere y T b unter y T A ≥ cT , y ∈ Rm
≥0 .
oder äquivalent
Minimiere bT y unter AT y ≥ c, y ∈ Rm
≥0 .
Anschaulich gesprochen werden aus den Nebenbedingungen des primalen LPs die Variablen des dualen LPs und aus den Variablen des primalen LPs die Nebenbedingungen des dualen LPs. Wenn das primale LP nicht in kanonischer Form vorliegt, können
wir das duale LP herleiten, indem wir zunächst das primale LP in die kanonische Form
bringen und dann das duale LP aus dieser Form ableiten. Auf diese Art und Weise ergeben sich verschiedene Regeln für LPs mit Variablen und Nebenbedingungen, die nicht
der kanonischen Form genügen. Aus einer Nebenbedingung in Gleichungsform wird
beispielsweise eine Variable ohne Nichtnegativitätsbedingung; und aus einer Variable
ohne Nicht-Negativitätsbedingung eine Nebenbedingung in Gleichungsform. Da wir
aus Abschnitt 1.1 wissen, wie man ein beliebiges LP in die kanonische Form bringt,
können wir es uns sparen, alle diese Sonderfälle aufzuzählen, und wir konzentrieren
uns auf LPs in kanonischer Form.
Wir beweisen zunächst einige einfache Eigenschaften von primalen und dualen LPs.
40
Satz 4.2 Das duale LP des dualen LPs ist das primale LP.
Beweis: Gegeben sei das duale LP mit d Nebenbedingungen wie in Definition 4.1
beschrieben:
Minimiere bT y unter AT y ≥ c, y ∈ Rm
≥0 .
Zunächst müssen wir das LP in die kanonische Form bringen, um die in der Definition
beschriebenen Regeln für die Bildung des dualen LPs anwenden zu können. Dazu
multiplizieren wir die Zielfunktion und die Nebenbedingung mit -1. Dadurch liegt das
duale LP nun in kanonischer Form vor.
Maximiere −bT y unter −AT y ≤ −c, y ∈ Rm
≥0 .
Das duale dieses LPs lautet
Minimiere −cT x unter −Ax ≥ −b, x ∈ Rd≥0 .
Wir schreiben nun das duale des dualen LPs um, indem wir Zielfunktion und Nebenbedingungen wiederum mit -1 multiplizieren. Dadurch ergibt sich das primale LP.
Maximiere cT x unter Ax ≤ b, x ∈ Rm
≥0 .
2
Unsere Idee war es, das duale LP zur Berechnung möglichst guter oberer Schranken
für das primale LP zu verwenden. Dies wird im folgenden Satz konkretisiert.
Satz 4.3 (Schwaches Dualitätsprinzip) Sei x eine zulässige Lösung für das primale
LP und y eine zulässige Lösung für das duale LP wie in Definition 4.1 beschrieben. Es
gilt y T b ≥ cT x.
Beweis: Wegen der Zulässigkeit von x und y gilt einerseits x ≥ 0 und andererseits
y T A ≥ cT . Es folgt
cT x ≤ y T Ax .
Die Zulässigkeit der beiden Lösungen liefert außerdem y ≥ 0 und Ax ≤ b, so dass
folgt
y T Ax ≤ y T b .
Aus diesen beiden Ungleichungen ergibt sich der Satz nun unmittelbar.
41
2
4.2 Das starke Dualitätsprinzip
Wir untersuchen das Beispiel aus dem vorherigen Abschnitt genauer. Die optimale
Lösung für das primale LP ist x∗ = ( 43 , 32 ). Der maximale Zielfunktionswert ist also
5 · 34 + 7 · 23 = 34
. Die optimale Lösung für das duale LP ist y ∗ = ( 32 , 13
). Der minimale
3
3
34
Zielfunktionswert ist somit 4 · 32 + 2 · 13
=
.
Das
duale
LP
gibt
also
nicht nur eine
3
3
obere Schranke für das primale LP, sondern die beiden LPs haben denselben optimalen
Zielfunktionswert. Der folgende Satz zeigt, dass dies kein Zufall ist.
Satz 4.4 (Starkes Dualitätsprinzip) Sei x∗ eine optimale Lösung für das primale LP
und y ∗ eine optimale Lösung für das duale LP wie in Definition 4.1 beschrieben. Es
gilt y ∗T b = cT x∗ .
Beweis: Wir zeigen, wie man zu einer geeignet gewählten optimalen primalen Lösung
x∗ eine zulässige duale Lösung y ∗ mit demselben Zielfunktionswert konstruieren kann.
Aus dem schwachen Dualitätsprinzip folgt dann, dass y ∗ eine optimale Lösung des
dualen LPs sein muss.
Als ersten Schritt transformieren wir das primale LP durch Hinzufügen von Schlupfvariablen s1 , . . . , sm in die Gleichungsform.
Maximiere cT x unter Ax + Em s = b, x ∈ Rd≥0 , s ∈ Rm
≥0 .
Sei B eine Basis mit nicht-positiven reduzierten Kosten. Aus Satz 2.1 folgt, dass B
eine optimale Basis ist. Diese Basis entspricht einer Auswahl von m der m + d Spalten
der Matrix (A, Em ). Die Anzahl der Basisspalten aus A bezeichnen wir mit m1 , und
die Anzahl der Basisspalten aus Em mit m2 = m − m1 . O.B.d.A. nehmen wir an,
dass die Basisspalten B(1), . . . , B(m1 ) den ersten m1 Spalten aus der Matrix (A, Em )
entsprechen und die Basisspalten B(m1 + 1), . . . , B(m) den letzten m2 Spalten aus
dieser Matrix. (Ansonsten ordne die Spalten und Zeilen der Matrix entsprechend um,
ohne das Gleichungssystem zu verändern.) Auf diese Art und Weise können wir das
Gleichungssystem (A, Em , b) in die folgenden Teilkomponenten mit den jeweils angegebenen Anzahlen von Zeilen und Spalten zerlegen:
m1
m2
cTB
cTN
A11
A12
Em1
0 b1
A21
A22
0 Em2 b2
m1 d − m1 m1 m2
In dieser Notation lautet das primale LP
Maximiere cTB xB + cTN xN
42
unter den Nebenbedingungen
A11 xB + A12 xN + Em1 sN = b1 ,
A21 xB + A22 xN + Em2 sB = b2
d−m1
m2
1
1
für die Variablen xB ∈ Rm
, sN ∈ Rm
≥0 , xN ∈ R≥0
≥0 und sB ∈ R≥0 . Der Zielfunktionswert der Basislösung x∗ zur Basis B ist somit cT x∗ = cTB x∗B = cTB A−1
11 b1 , weil die
Nichtbasisvariablen in der Basislösung den Wert 0 annehmen. Wir sind nun am Vektor
der reduzierten Kosten interessiert. Dazu beschreiben wir zunächst die Basisvariablen
xB und dann die Zielfunktion cT x in Abhängigkeit von den Nichtbasisvariablen. Aus
dem obigen Gleichungssystem ergibt sich
xB = A−1
11 (b1 − A12 xN − sN ) .
Für die Zielfunktion erhalten wir somit
T
cT x = cTB A−1
11 (b1 − A12 xN − sN ) + cN xN
T
T −1
T −1
= cTB A−1
11 b1 + (cN − cB A11 A12 )xN − cB A11 sN .
Die Nichtbasisvariablen xN haben somit die reduzierten Kosten cTN − cTB A−1
11 A12 , und
die Nichbasisvariablen sN haben die reduzierten Kosten −cTB A−1
.
Wir
haben
B so
11
gewählt, dass diese Kosten nicht positiv sind. Somit folgt
T
cTB A−1
11 A12 ≥ cN ,
cTB A−1
≥ 0 .
11
(4.1)
(4.2)
In der oben eingeführten Notation lautet das duale LP:
T
b2
Minimiere yBT b1 + yN
unter den Nebenbedingungen
T
yBT A11 + yN
A21 ≥ cTB ,
T
yBT A12 + yN
A22 ≥ cTN
m2
1
für die Variablen yB ∈ Rm
≥0 und yN ∈ R≥0 . Wir konstruieren nun die gesuchte
Lösung y ∗ , die zulässig für das duale LP ist und denselben Zielfunktionswert wie
∗
x∗ hat. Wir behaupten, diese Lösung lautet yN
= 0 und yB∗T = cTB A−1
11 . Wir prüfen
zunächst die Zulässigkeit dieser Lösung.
• Der Wert für y ∗T ist genau so gewählt, dass die erste Nebenbedingung yBT A11 +
T
yN
A21 ≥ cTB exakt erfüllt ist.
• Die Gültigkeit der zweiten Nebenbedingung folgt aus Ungleichung (4.1), denn
∗T
T
yB∗T A12 + yN
A22 = yB∗T A12 = cTB A−1
11 A12 ≥ cN .
43
• Ungleichung (4.2) liefert die Nicht-Negativitätsbedingungen.
Als letztes beweisen wir, dass die Zielfunktionswerte der beiden Lösungen übereinstimmen. Es gilt
T ∗
T ∗
y ∗T b = yB∗T b1 = cTB A−1
11 b1 = cB xB = c x .
2
Zur Konstruktion im obigen Beweis können wir noch einige interessante Beobachtungen machen.
• Wir haben nicht nur gezeigt, dass die Zielfunktionswerte der optimalen primalen und dualen Lösung übereinstimmen, sondern auch, wie aus einer optimalen primalen Basislösung in polynomieller Zeit eine optimale duale Basislösung
konstruiert werden kann. Der aufwendigste Schritt ist dabei die Berechnung der
3
3
Matrix A−1
11 , die mit O(min{m , d }) Operationen berechnet werden kann. Aus
Symmetriegründen kann natürlich auch eine optimale primale Basislösung in
polynomieller Zeit aus einer optimalen dualen Basislösung konstruiert werden.
• Die dualen Basisvariablen yB∗ gehören genau zu denjenigen primalen Nebenbedingungen, in denen die Schlupfvariablen sN auftauchen. Diese Schlupfvariablen nehmen in der optimalen dualen Basislösung den Wert Null an. Das bedeutet, die Basisvariablen zur optimalen dualen Basis gehören zu primalen Nebenbedingungen, die in der optimalen primalen Basislösung exakt erfüllt sind.
In Analogie gilt, dass auch die Basisvariablen zu einer optimalen primalen Basislösung zu dualen Nebenbedingungen gehören, die in der optimalen dualen
Basislösung exakt erfüllt sind. Tatsächlich sind die primale und die duale Lösung
genau dann optimal, wenn diese Bedingungen erfüllt ist. Diese Eigenschaft bezeichnet man als complementary slackness.
4.3 Zwei prominente Beispiele
Wir stellen ein alternatives LP für das Problem des maximalen Flusses vor. Gegeben
sei ein Netzwerk G = (V, E) mit Quelle q und Senke s und Kantenkapazitäten c :
E → R≥0 . Sei P die Menge aller einfachen Pfade von der Quelle zur Senke. Für jeden
Pfad P ∈ P haben wir eine Variable xP . Das primale LP lautet:
P
Maximiere P ∈P xP
44
unter den Nebenbedingungen
X
P 3e
xP ≤ c(e)
∀e ∈ E
xP ≥ 0
∀P ∈ P
Das duale LP lautet
P
Minimiere
unter den Nebenbedingungen
X
e∈P
e∈E
c(e)ye
ye ≥ 1
∀P ∈ P
ye ≥ 0
∀e ∈ E
Für dieses duale LP kann man basierend auf Eigenschaften der Adjazenzmatrix (vgl.
Kapitel 5) die folgenden Besonderheit zeigen: Es gibt immer eine ganzzahlige optimale Basislösung. Der Wertebereich der Variablen kann somit auf {0, 1} eingeschränkt
werden. Wenn wir dieses Wissen voraussetzen, erkennen wir im dualen LP das MinCut-Problem in der folgenden Formulierung wieder: Bestimme eine minimale Anzahl Kanten, so dass die Löschung dieser Kanten alle Wege zwischen Quelle und Ziel
zerstört.
Das relaxierte Maximum-Matching-Problem auf einem Graphen G = (V, E) hat das
folgende primale LP.
P
Maximiere e∈E xe
unter den Nebenbedingungen
X
e3v
xe ≤ 1
∀v ∈ V
xe ≥ 0
∀e ∈ E
Das duale LP lautet
Minimiere
unter den Nebenbedingungen
X
v∈e
P
v∈V
yv
yv ≥ 1
∀e ∈ E
yv ≥ 0
∀v ∈ V
Wir beobachten, dass dieses LP dem relaxierten Vertex-Cover-Problem entspricht.
Auch diese beiden LPs haben ganzzahlige optimale Basislösungen, allerdings nur auf
bipartiten Graphen. Somit sind bipartites Matching und Vertex Cover auf bipartiten
Graphen duale Probleme.
45
Kapitel 5
Aspekte der Ganzzahligkeit
5.1 Ganzzahlige lineare Programme
Ganzzahlige lineare Programme (ILPs = Integer Linear Programs) haben fast dieselbe
Form wie lineare Programme. Der einzige aber wesentliche Unterschied ist, dass nur
ganzzahlige Lösungen zulässig sind. Wir präsentieren im folgenden zwei Beispiele für
ILPs in denen der Lösungsraum der Variablen tatsächlich auf die Werte 0 und 1 beschränkt ist. Es handelt sich deshalb um sogenannte binäre Programme, ein Spezialfall
von ILPs.
Beispiel: Rucksackproblem. Gegeben seien n Objekte mit Gewicht gi und Nutzen
vi , 1 ≤ i ≤ n, sowie eine Gewichtsschranke G. Gesucht ist eine Teilmenge der Objekte, die den Nutzen unter Einhaltung der Gewichtsschranke maximiert. Dieses Problem
kann wie folgt als ILP formuliert werden.
Maximiere
n
X
vi xi
i=1
unter den Nebenbedingungen
n
X
i=1
gi xi ≤ G ,
∀i ∈ {1, . . . , n} : xi ∈ {0, 1} .
Beispiel: gewichtetes Matchingproblem. Gegeben sei ein Graph G = (V, E) mit
Kantengewichten we , e ∈ E. Gesucht ist ein Matching M, das die Summe der Ge46
wichte maximiert. Dieses Problem hat die folgende ILP-Formulierung.
X
Maximiere
we xe
e∈E
unter den Nebenbedingungen
∀v ∈ V :
∀e ∈ E :
X
e∈E:v∈e
xe ≤ 1 ,
xe ∈ {0, 1} .
Wir stellen fest, durch die Forderung einer ganzzahligen Lösung kann ein Optimierungsproblem, wie im Fall des Rucksackproblems, NP-hart werden. Dies kann durchaus als typisch angesehen werden. In einigen Fällen ist jedoch auch die ganzzahlige
Variante eines Problems effizient lösbar, wie etwa im Fall des Matchingproblems. Es
gibt keine allgemeingültige Antwort, welche derjenigen Problem, die als ILPs kodiert
werden können, algorithmisch schwierig oder einfach sind. Im folgenden Abschnitt
werden wir jedoch eine Klasse von Problemen identifizieren, die deshalb effizient
gelöst werden können, weil ihre ILP- und LP-Formulierungen dieselben Lösungen
liefern.
5.2 Totale Unimodularität
In diesem Abschnitt gehen wir grundsätzlich davon aus, dass alle Eingabezahlen der
betrachteten LPs ganzzahlig sind. Einige LPs haben eine besondere Eigenschaft: Das
Simplexverfahren und auch die Ellipsoidmethode berechnen immer optimale Lösungen, die ganzzahlig sind. Beispielsweise weisen Flussprobleme dieses wirklich erstaunliche Phänomen auf, dem wir in diesem Abschnitt genauer nachgehen wollen.
Definition 5.1 Eine ganzzahlige quadratische Matrix wird als unimodular bezeichnet,
wenn ihre Determinante den Wert 1 oder -1 hat. Eine ganzzahlige Matrix A wird als
total unimodular bezeichnet, wenn jede quadratische, reguläre Teilmatrix von A unimodular ist.
Satz 5.2 Betrachte ein LP in Gleichungsform Ax = b. Ist A total unimodular, so sind
alle Basislösungen dieses LPs ganzzahlig.
Beweis: Sei B eine Basis von A. Die Basislösung zu B wird durch die Gleichung
AB xB = b beschrieben. Die Matrix AB ist dabei eine quadratische Teilmatrix von
47
A, die durch die Spalten in B gebildet wird. Somit ist AB unimodular.1 Gemäß der
Cramerschen Regel gilt
xB(i) =
det(AB(1) , . . . , AB(i−1) , b, AB(i+1) , . . . , AB(k) )
.
det(AB )
Die Determinante im Zähler ist ganzzahlig, und die Determinante im Nenner hat den
Wert 1 oder −1, da AB unimodular ist.
2
Satz 5.3 Betrachte ein LP in kanonischer Form Ax ≤ b. Ist A total unimodular, so
sind alle Basislösungen dieses LPs ganzzahlig.
Beweis: Die Anzahl der Zeilen in A sei m. Nach Hinzufügen von Schlupfvariablen erhalten wir ein LP in Gleichungsform mit Nebenbedingungsmatrix (A|Em ). Um Satz 1
anwenden zu können, müssen wir zeigen, dass die Matrix (A|Em ) total unimodular
ist. Sei nun C eine beliebige quadratische, reguläre Teilmatrix von (A|Em ). Durch
geeignete Permutation der Zeilen von C erhalten wir eine Matrix der Form
M 0
0
C =
,
∗ Ek
wobei
• Ek der k × k–Einheitsmatrix entspricht,
• 0 die (m − k) × k–Nullmatrix bezeichnet, und
• M eine (m − k) × (m − k)–Teilmatrix von A mit möglicherweise vertauschten
Zeilen ist.
Es gilt |det(C)| = |det(C 0 )| = |det(M)| = 1, da M unimodular ist. Somit ist jede
reguläre Teilmatrix C von (A|Em ) unimodular und damit ist (A|Em ) total unimodular.
2
Wir untersuchen nun welche Arten von Anwendung total unimodulare Nebenbedingungsmatrizen aufweisen. Zunächst starten wir mit relativ abstrakten Eigenschaften,
die wir dann konkretisieren.
1
Da wir die Basis als geordnete Auswahl von Spalten definiert haben, tauchen in der Matrix AB die
Spalten möglicherweise in einer anderen Reihenfolge auf als in der Matrix A. Dies hat jedoch keine
Auswirkungen auf die Unimodularität, denn das Vertauschen zweier Spalten oder auch Zeilen dreht
lediglich das Vorzeichen der Determinante.
48
Satz 5.4 Eine ganzzahlige Matrix A mit Einträgen aus {−1, 0, 1} ist total unimodular,
wenn nicht mehr als zwei nicht-nullwertige Einträge pro Spalte vorliegen, und wenn
die Zeilen in zwei Mengen I1 und I2 eingeteilt werden können, die die folgenden Bedingungen erfüllen:
a) Falls eine Spalte zwei Einträge mit demselben Vorzeichen enthält, so sind die
entsprechenden Zeilen unterschiedlichen Mengen zugeordnet.
b) Falls eine Spalte zwei Einträge mit unterschiedlichem Vorzeichen enthält, so sind
die entsprechenden Zeilen derselben Menge zugeordnet.
Beweis: Der Satz folgt durch Induktion über die Größe der Teilmatrizen. Jede reguläre 1 × 1–Teilmatrix ist offensichtlich unimodular. Es gelte nun, dass jede reguläre
(k − 1) × (k − 1)–Teilmatrix unimodular ist. Sei C eine k × k–Teilmatrix. Wir müssen
zeigen, dass C entweder nicht regulär oder unimodular ist. Wir unterscheiden drei
Fälle.
1) Wenn C eine Spalte mit ausschließlich null-wertigen Einträgen enthält, so ist C
nicht regulär.
2) Wenn C eine Spalte hat, die nur einen nicht-nullwertigen Eintrag enthält, so
können wir die Determinante nach dieser Spalte entwickeln. Das bedeutet, abgesehen vom Vorzeichen entspricht die Determinante der (k − 1) × (k − 1)–
Teilmatrix von C, die wir erhalten, wenn wir die Zeile und Spalte des betrachteten nicht-nullwertigen Eintrags entfernen.
3) Wenn C nun zwei nicht-nullwertige Einträge in jeder Spalte enthält, so folgt aus
den Bedingungen a) und b), dass für jede Spalte j die folgende Gleichung gilt.
X
X
aij .
aij =
i∈I2
i∈I1
Wenn wir also die Zeilenvektoren aus I1 aufaddieren und die aus I2 subtrahieren,
so erhalten wir einen Zeilenvektor mit Wert Null, d.h. die Zeilen sind nicht linear
unabhängig und C ist somit nicht regulär.
2
Die Inzidenzmatrix eines Graphen enthält für jede Kante des Graphen eine Spalte und
für jeden Knoten eine Zeile. Bei einem gerichteten Graphen enthält jede Spalte genau
zwei Einträge, die ungleich 0 sind, nämlich +1 in der Zeile des Knotens, an dem
die Kante endet, und −1 in der Zeile des Knoten, an dem die Kante beginnt. Die
Inzidenzmatrix eines ungerichteten Graphen enthält nur Nullen und Einsen. In jeder
49
Spalte stehen genau zwei Einsen, nämlich in den Zeilen, die zu Knoten gehören, die
zu der entsprechenden Kante inzident sind.
Die Inzidenzmatrix eines gerichteten Graphen erfüllt die Bedingungen a) und b) des
obigen Satzes, wenn wir alle Zeilen der Menge I1 zuordnen. Die Inzidenzmatrix eines
ungerichteten bipartiten Graphen G = (U ∪ V, E) erfült die Bedinungen, wenn wir
die Zeilen für die Knoten in U der Menge I1 und die Zeilen für die Knoten in V der
Menge I2 zuordnen.
Korollar 5.5 Ein LP in Standardform oder in kanonischer Form hat nur ganzzahlige
Basislösungen, falls die Nebenbedingungsmatrix (oder ihre Transponierte)
• der Inzidenzmatrix eines gerichteten Graphen oder
• der Inzidenzmatrix eines bipartiten ungerichteten Graphen
entspricht.
Aus dem Korollar folgt, dass die (relaxierten) LP-Formulierungen der folgenden Probleme ganzzahlige optimale Lösungen haben.
• maximaler Fluss
• kürzester Weg
• gewichtetes bipartites Matching
• bipartites Vertex-Cover
Insbesondere folgt deshalb, dass die Dualität von Vertex-Cover und Matching auf bipartiten Graphen nicht nur für die relaxierten, nicht-ganzzahligen Varianten der Probleme gilt.
Das folgende Beispiel zeigt, dass die obigen Aussagen sich nicht auf die Inzidenzmatrizen beliebiger ungerichteter Graphen verallgemeinern lassen. Wir betrachten das
(ungewichtete) Matchingproblem auf einem Graphen aus drei Knoten und drei Kanten
mit der Inzidenzmatrix


1 1 0
 0 1 1  .
1 0 1
Die Determinante dieser Matrix ist 2. Der zugehörige Graph entspricht einem Dreieck. Jedes (ganzzahlige) Matching enthält höchstens eine Kante. Im optimalen nichtganzzahligen Matching ist jede Kante e mit Wert xe = 21 enthalten. Die Lösung des
relaxierten LPs ist also 32 .
50
Kapitel 6
Hilfreiche Literatur
• B. Korte, J. Vygen. Combinatorial Optimization: Theory and Algorithms, 2nd
Edition, Springer, 2002.
• E. Lawler. Combinatorial Optimization: Networks and Matroids. Dover Publications, 1976.
• C. Papadimitriou und K. Steiglitz. Combinatorial Optimization: Algorithms and
Complexity. Prentice Hall, 1982.
• A. Schrijver. Combinatorial Optimization: Polyhedra and Efficiency. Springer,
2003.
51