Achterbahn Ein Fahrzeug ohne eigenen Antrieb startet auf der

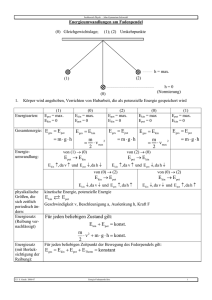
Achterbahn
Ein Fahrzeug ohne eigenen Antrieb startet auf der abgebildeten Bahn von dem
Punkt (1) und fährt reibungsfrei über den Punkt (2) zum Punkt (3).
a) Warum bewegt sich das Fahrzeug?
Lösungsidee Lösung
b) Welche Energien wirken bei der Fahrt?
Lösungsidee Lösung
c) Wie groß sind diese Energien in den gekennzeichneten
Lösungsidee Lösung
Punkten?
d) Wie groß ist die Höhe, die das Fahrzeug in Punkt (3)
Lösungsidee Lösung
erreicht?
e) Wie lange bewegt sich das Fahrzeug?
Lösungsidee Lösung
f) Angenommen, der Startpunkt (Punkt (1)) hätte eine
Lösungsidee Lösung
Höhe h1 = 20 m und das Fahrzeug eine Masse m = 1 t.
Berechnen Sie die Beträge der Energien, die Höhe h2
sowie die Geschwindigkeit v im Punkt(3)?
Abbildung 1: Achterbahn, mit dem Wagen in Punkt (1)
Energie und Bewegung, Achterbahn
1
Lösungsidee a) :
Das Fahrzeug befindet sich anfangs in Ruhe und seine Geschwindigkeit
vergrößert sich auf dem Weg zum Punkt 2. Es handelt sich also um eine
beschleunigte Bewegung. Sie müssen jetzt noch herausfinden, welche Kraft
diese Beschleunigung verursacht. Tipp: Die Bewegung geht nach unten.
zurück zur Aufgabe
Energie und Bewegung, Achterbahn
Lösung
2
Lösungsidee b) :
Es gibt zwei Energieformen die hier auftreten. Zum Einen befindet sich das
Fahrzeug in einer sich verändernden Höhe über dem Erdboden. Zum Anderen
hat das Fahrzeug eine sich verändernde Geschwindigkeit.
zurück zur Aufgabe
Energie und Bewegung, Achterbahn
Lösung
3
Lösungsidee c) :
Sie müssen sich überlegen, welchen Betrag die Höhe und die Geschwindigkeit
in den drei Punkten haben. Wenn Sie dann noch einen der drei
Erhaltungssätze berücksichtigen, können Sie die Energiebeträge in den drei
Punkten bestimmen.
zurück zur Aufgabe
Energie und Bewegung, Achterbahn
Lösung
4
Lösungsidee d) :
Der in c) angewendete Erhaltungssatz erlaubt den direkten Vergleich der
Energien in den drei Punkten.
zurück zur Aufgabe
Energie und Bewegung, Achterbahn
Lösung
5
Lösungsidee e) :
In der Aufgabe wird von einer reibungsfreien Fahrt ausgegangen und Sie
haben in c) alle Energien bestimmt. Wo könnte die Energie noch hingehen,
ohne den in c) benutzten Erhaltungssatz zu verletzen?
zurück zur Aufgabe
Energie und Bewegung, Achterbahn
Lösung
6
Lösungsidee f) :
Setzen Sie für die Höhe h1 die 20 m ein und berechnen damit nacheinander
die Energien in den drei Punkten.
zurück zur Aufgabe
Energie und Bewegung, Achterbahn
Lösung
7
Lösung a) :
Auf das Fahrzeug wirkt die Gravitationskraft Fg = m · g, die das Fahrzeug zur
Erde hin beschleunigt.
zurück zur Aufgabe
Energie und Bewegung, Achterbahn
8
Lösung b) :
Die auftretenden Energien sind die potentielle Energie Epot und die kinetische
Energie Ekin.
zurück zur Aufgabe
Energie und Bewegung, Achterbahn
9
Lösung c) :
Für die potentielle Energie gilt: Epot = m·g·h
Und für die kinetische Energie: Ekin = ½ m·v²
Beide Energien sind über die Energieerhaltung miteinander verbunden. Da die
Energie immer konstant sein muss, gilt für jeden Punkt auf der Bahn:
E=E pot E kin=konst.
Die potentielle Energie kann für jeden Punkt auf der Bahn bestimmt werden,
wir brauchen nur h zu messen.
Punkt (1): Die Geschwindigkeit v ist noch 0 also gilt:
h=h 1 ⇒ E pot =m⋅g⋅h 1
v =0⇒ E kin=0
⇒ E  Punkt 1=E pot E kin =m⋅g⋅h1
Punkt (2): Hier ist die Höhe h = 0. Wegen der Energieerhaltung muss die
potentielle Energie aus Punkt (1) im Punkt (3) vollständig in kinetische
Energie umgewandelt werden:
h  Punkt 2=0⇒ E pot =0
1
⇒ E  Punkt 2=m⋅g⋅h 1=E pot  E kin= ⋅m⋅v 2
2
Punkt (3):Die Geschwindigkeit v ist 0. Aus der Energieerhaltung folgt, das die
kinetische Energie vollständig in potentielle Energie umgewandelt wurde:
v =0 ⇒ E kin =0
⇒ E pot =m⋅g⋅h
⇒ E  Punkt 3=m⋅g⋅h1=E pot E kin=m⋅g⋅h
Die Energie „pendelt“ sozusagen zwischen der kinetischen und potentiellen
Energie hin und her.
zurück zur Aufgabe
Energie und Bewegung, Achterbahn
10
Lösung d) :
Die Berechnung der Energie in Punkt (3) ergibt
E  Punkt 3=m⋅g⋅h1=E pot E kin=m⋅g⋅h
⇒ h=h1
Das bedeutet, dass der Punkt (3) die gleiche Höhe hat wie der Punkt (1).
zurück zur Aufgabe
Energie und Bewegung, Achterbahn
11
Lösung e) :
Im Punkt (3) ist die Geschwindigkeit 0. Die Gravitation beschleunigt
anschließend wieder Richtung Punkt (2): Die Bewegung wiederholt sich
unendlich lange, da immer nur potentielle in kinetische Energie und
umgekehrt verwandelt wird.
Nur wenn wir Reibung mit berücksichtigen, wird die Bewegung irgendwann
aufhören, da ein Teil der kinetischen Energie in Wärme umgewandelt wird. Die
Wärme kann jedoch weder in potentielle noch in kinetische Energie
zurückverwandelt werden.
zurück zur Aufgabe
Energie und Bewegung, Achterbahn
12
Lösung f) :
Gegeben: h1 = 20 m
Gesucht: Energieformen, h2
Ansatz:
Betrachten der einzelnen Punkte.
Punkt (1):
E=E pot E kin=E pot 0=m⋅g⋅h1=1 t⋅9,81
m
⋅20 m=196,2 kJ
s2
Punkt (2):
1
E=E pot E kin=0E kin= ⋅m⋅v 2=196,2 kJ
2
v=
 
E kin
196,2 kJ
m
=
=19,8
1
1
s
⋅m
⋅1000 kg
2
2
Punkt (3):
E=E pot E kin =E pot 0=196,2 kJ=m⋅g⋅h 2
¿
h 2=
E pot
196,2 kJ
=
=20 m
m⋅g
m
1 t⋅9,81 2
s
Ergebnis: h2 = 20 m
zurück zur Aufgabe
Energie und Bewegung, Achterbahn
13