Musterlösung zur Klausur “Elektrische und Magnetische Felder” vom

Musterlösung zur Klausur
“Elektrische und Magnetische Felder” vom 01.09.2011
Lösungsskizze zu Aufgabe 1
• 1.1
Für zeitharmonische Vorgänge gilt:
∂
→ jω
∂t
Damit gilt für die Maxwell-Gleichungen im Vakuum:
~ =0
∇·E
~
~ = −jω B
∇×E
~ =0
∇·B
1
~
~ = jω0 E
∇×B
µ0
(1)
(2)
(3)
(4)
• 1.2
~ aufgelöst werden:
Gleichung (2) kann nach B
~
~ =− 1 ∇×E
B
jω
Anschließend wird dieser Ausdruck in Gleichung (4) eingesetzt:
−
1
~ = jω0 µ0 E
~
∇×∇×E
jω
Auswerten der doppelten Rotation ergibt
~ − ∇2 E
~ = ω 2 0 µ0 E
~
∇ ∇·E
Für die Divergenz des elektrischen Feldes gilt Gleichung (1). Daraus ergibt
sich
~
~ = ω 2 0 µ0 E
−∇2 E
Dies ist die Wellengleichung des elektrischen Feldes in Koordinaten freier
Form. In kartesischen Koordinaten gilt für die Wellengleichung:
2
∂
∂2
∂2 ~
~ =0
E + ω 2 0 µ0 E
+
+
∂x2
∂y 2
∂z 2
1
• 1.3
Für die y-Komponente des elektrischen Feldes gilt in Ausbreitungsrichtung
~ = E (x, y)e−jkz ~ey
E
y
y
• 1.4
Nun muss E y (x, y) bestimmt werden. Dazu ist die Wellengleichung zu
lösen:
2
∂2
∂
2
+ 2 − k E y (x, y)e−jkz = ω 2 0 µ0 E y (x, y)e−jkz
∂x2
∂y
Nun wird für E y (x, y) ein Seperationsansatz gewählt
E y (x, y) = X(x)Y (y)
Eingesetzt in die Wellengleichung und Kürzen ergibt
2
1 d2 Y (y)
ω
1 d2 X(x)
2
+
+
−k =0
X(x) dx2
Y (y) dy 2
c2
Die einzelnen Summanden müssen somit konstant sein. Für den x-abhängigen Summand gilt:
1 d2 X(x)
= −kx2
X(x) dx2
Wir erhalten also die Differentialgleichung
d2 X(x)
+ kx2 X(x) = 0
dx2
Für diese Differentialgleichung kann die allgemeine Lösung angegeben werden:
X(x) = c1 cos(kx x) + c2 sin(kx x)
Aus den Randbedingungen folgt:
X(0) = X(a) = 0
Daraus kann die allgemeine Lösung für den x-abhängigen Teil weiter spezifiziert werden. Die Konstante c1 wird zu 0 und es gilt:
c2 sin(kx a) = 0
2
Die triviale Lösung für c2 = 0 soll nicht weiter betrachtet werden und für
kx muss gelten:
mπ
kxm =
a
Damit folgt für X(x)
X(x) = c2 sin(kx x)
Die Differentialgleichung für den y-abhängigen Teil wird analog gelöst und
man erhält wieder als allgemeine Lösung:
Y (y) = c3 cos(ky y) + c4 sin(ky y)
Aus den Randbedingungen folgt:
Y 0 (0) = Y 0 (b) = 0
Damit erschließt sich die Konstante c4 zu 0. Es gilt die Konstante ky zu
bestimmen:
c3 sin(ky b) = 0
Daraus folgt für ky :
kyn =
nπ
b
Für Y (y) gilt somit:
Y (y) = c3 cos(ky y)
Insgesamt folgt damit für E y (x, y):
E y (x, y) = X(x)Y (y)
= c2 c3 sin(kx x) cos(ky y)
= Emn sin(kx x) cos(ky y)
Die y-Komponente des zweifachen Phasors des elektrischen Feldes kann
somit zusammenfassend geschrieben werden als:
~ = Emn sin(kx x) cos(ky y)e−jkz ~ey
E
y
• 1.5
Für eine ausbreitungsfähige Welle muss gelten: k ∈ R
Für die Wellenzahl gilt
r
ω2
− kx2 − ky2
k=±
c2
3
Da k reell sein muss, folgt für den Radikand:
ω2
− kx2 − ky2 > 0
c2
Aufgelöst nach ω 2 ergibt das schließlich
ω 2 > c2 (kx2 + ky2 )
• 1.6
Es gilt für kx1
kx1 =
π
a
Für ky0 folglich
ky0 = 0
Und für ω = 1Ghz eingesetzt in die Gleichung aus Aufgabe 1.5 folgt:
a>
c
2 · 1Ghz
Ausgerechnet ergibt das
a > 0.15m
4
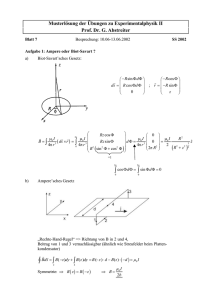
Lösungsskizze zu Aufgabe 2
• 2.1
Qa
Qi
ri
rm
ra
eps1
eps2
• 2.2 Es gilt die Maxwellsche-Gleichung
~ =ρ
∇·D
Integriert man auf beiden Seiten über das Volumen der Anordung folgt
somit
Z
Z
~ dv =
∇·D
ρ dv
V
V
Wendet man den Satz von Gauß an folgt
Z
~ · df~ = Q
D
∂V
Aufgrund des radialsymmetrischen Aufbaus und der Ladung −Q an der
inneren Elektrode folgt:
Z
Dr e~r · df~ = −Q
∂V
Das differentielle Flächenelement muss in Kugelkoordinaten in e~r -Richtung
gewählt werden
Z
Z
2π
0
π
0
Dr r2 sin(ϑ)dϑdϕ = −Q
Ausführen der Integration und umformen nach Dr ergibt
Dr = −
5
Q
4πr2
Insgesamt ergibt sich für die elektrische Verschiebungsdichte
Q
~
D(r)
=−
e~r
4πr2
Für lineare Medien gilt
~ = εE
~
D
Daraus folgt für das elektrische Feld:
Q
~
e~r
E(r)
=−
4πεr2
• 2.3
~ = 0:
Für das elektrische Feld gilt aufgrund ∇ × E
~ = −∇φ
E
Betraglich gilt in Kugelkoordinaten
Er = −
∂φ
∂r
Im Bereich ri < r < ra gilt demnach für das Potential
Z r
Q
dr0
φ(r) =
02
4πεr
rr
Berechnet man das Integral, erhält man somit
Q 1
1
φ(r) =
−
4πε ri
r
Das Potential φa an der Stelle ra lautet dann
1
Q 1
−
φa = φ(ra ) =
4πε ri
ra
• 2.4
Es gilt für die unterschiedlichen Dielektrika
Q
4πε1 r2
Q
=−
4πε2 r2
Er1 = −
Er2
6
Das Potential lässt sich dann analog zu Aufgabe 2.3 berechnen
Z r
Q
dr0
φ1 (r) =
02
ri 4πε1 r
Q
1
1
=
+ c1
−
4πε1 ri
r
Z
r
Q
dr0
02
4πε
r
2
rm
Q
1
1
=
+ c2
−
4πε2 rm
r
φ2 (r) =
Über die Randbedingung φ1 (ri ) = 0 und φ2 (rm ) = φm lassen sich die
Konstanten bestimmen. Daraus ergeben sich die Potentiale
1
1
Q
−
φ1 (r) =
4πε1 ri
r
Q
1
1
φ2 (r) =
+ φm
−
4πε2 rm
r
Für das Potential an der Stelle r = ra gilt
Q
1
1
φa = φ2 (ra ) =
+ φm
−
4πε2 rm
ra
Das Potential an der Stelle r = rm ist stetig
φ1 (rm ) = φ2 (rm )
Es ergibt sich somit für das Potential φm
φm
Q
1
1
= φ1 (rm ) =
−
4πε1 ri
rm
Nun muss das Verhältnis φφma bestimmt werden. Für φa und φm werden
die bekannten Terme eingesetzt. Es ergibt sich
rm
−1
ε1
φa
=
− 1 ri rm
ε2
φm
1 − ra
Für die in der Aufgabenstellung gegebenen Werte ergibt sich somit
ε1
=2
ε2
7
Lösungsskizze zu Aufgabe 3
3.1 Flächenladungsdichte:
ρF (~r) =
Z
Fläche
σδ (3) (~r − ~rF ) d2 rF
mit


R cos ϕ
~rF =  R sin ϕ 
0
d2~rF = R dϕ dR ~ez
~r = r ~ez
(Zylinderkoordinaten in ~eR Richtung)
(F lächenelement in ~ez)
(Auf punkte des P otentials auf der
z − Achse)
Couloumb-Intergral:
Z Z R0 Z 2π
1
1
dV 0 R dϕ dR
σδ (3) (~r − r~F ) 0
Φ(z) =
4π0 V 0
|~r − ~rF )|
0
mit Ausblendeigenschaften:
Z R0 Z 2π
R
σ
dϕ dR
→ Φ(z) =
0
4π0 0
|~r − ~rF )|
0
Z R0
R
σ
√
dR
=
2
20 0
R + z2
Substitution:
R2 + z 2 = t
σ
Φ(z) =
20
q
2
2
R0 + z − |z|
3.2 → analog zu 3.1 aber mit anderen Radien
Bereich 1: 0 ≤ R ≤ R1 ; σ = −σ
Bereich 2: R1 ≤ R ≤ R0 ; σ = σ
q
σ
( R12 + z 2 − |z|)
Φ1 (z) = −
20
q
q
σ
( R02 + z 2 − R12 + z 2 )
Φ2 (z) =
20
!
r
r
R02
R12
σ
|z|
+1−2
+1+1
Φ(z) = Φ1 + Φ2 =
20
z2
z2
q
q
σ
( R02 + z 2 − 2 R12 + z 2 + |z|)
=
20
3.3
σ
(R0 − 2R1 ) = 0
20
R1
1
=
R0
2
Φ(0) =
8
3.4
R02
1,
z2
und
R12
1
z2
⇒
Φ(z) ≈
σ
(R0 − 2R1 + |z|)
20
3.5
p
p
σ
|z|( δ0 + 1 − 2 δ1 + 1 + 1)
20
p
1
δi + 1 ≈ 1 + δi , i ∈ {0, 1}
δi 1 ⇒
2
∞
X
1 (n)
Φ(z) =
Φ (z0 )(z − z0 )n
n!
n=0
Φ(z) =
mit
⇒ Φ(z) ≈
σ 21 R02 − R12
20
|z|
3.6 Benutze zur Hilfe Ergebnisse aus 3.4 und 3.5
3.4 für Bereich um 0
3.5 für z → ∞
φ
σ(R0 −2R1 )
2
0
R1
R0
z
Lösungsskizze zu Aufgabe 4
4.1 Idee: Vom ganzen Kreis πR2 werden folgende Teilflächen subtrahiert, so
dass die schraffierte Flächen F (x) bleibt:
πR2
2
p
(R − x) R2 − (R − x)2
2
2
2 arcsin
R
R−x
πR2
R
2πR
oberer Halbkreis
2 Dreiecke mit der Grundseite
und der Höhe (R − x)
p
R2 − (R − x)2
2 Kreissegmente mit Anteile R arcsin
am vollen Kreisumfang πR2
9
R−x
R
4.2 x = vx t in F(x) einsetzen:
p
πR2
− (R − vx t) R2 − (R − vx t)2 − R2 arcsin
F (t) =
2
Z
~ df~ = BF (t)
ψ(t) =
B
R − vx t
R
F (t)
4.3
dψ
dt
p
dF (t)
= −B
= −2Bvx R2 − (R − vx t)2
dt
Uind = −
Uind
4.4
|
| BU0 vind
xR
2.0
1.5
1.0
0.5
0.5
1.0
4.5 Lentz’sche Regel → Gegenuhrzeigersinn
10
1.5
2.0
t
R/vx