14. Mechanische Schwingungen und Wellen zu a) Das y(t

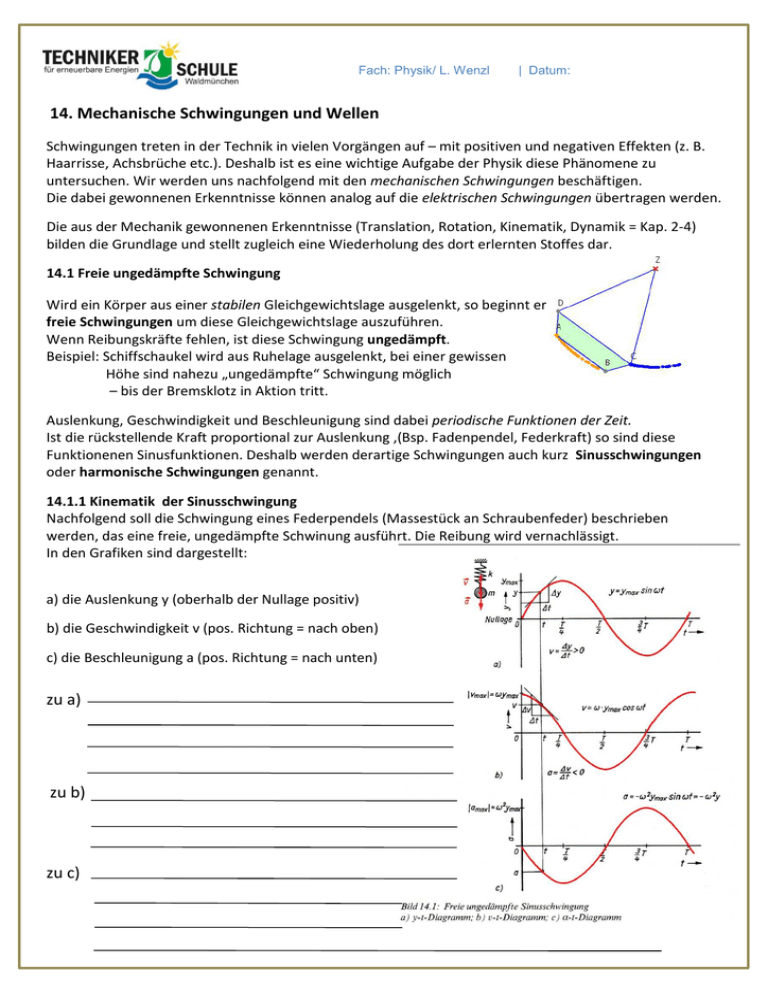
Fach: Physik/ L. Wenzl
| Datum:
14. Mechanische Schwingungen und Wellen
Schwingungen treten in der Technik in vielen Vorgängen auf – mit positiven und negativen Effekten (z. B.
Haarrisse, Achsbrüche etc.). Deshalb ist es eine wichtige Aufgabe der Physik diese Phänomene zu
untersuchen. Wir werden uns nachfolgend mit den mechanischen Schwingungen beschäftigen.
Die dabei gewonnenen Erkenntnisse können analog auf die elektrischen Schwingungen übertragen werden.
Die aus der Mechanik gewonnenen Erkenntnisse (Translation, Rotation, Kinematik, Dynamik = Kap. 2-4)
bilden die Grundlage und stellt zugleich eine Wiederholung des dort erlernten Stoffes dar.
14.1 Freie ungedämpfte Schwingung
Wird ein Körper aus einer stabilen Gleichgewichtslage ausgelenkt, so beginnt er
freie Schwingungen um diese Gleichgewichtslage auszuführen.
Wenn Reibungskräfte fehlen, ist diese Schwingung ungedämpft.
Beispiel: Schiffschaukel wird aus Ruhelage ausgelenkt, bei einer gewissen
Höhe sind nahezu „ungedämpfte“ Schwingung möglich
– bis der Bremsklotz in Aktion tritt.
Auslenkung, Geschwindigkeit und Beschleunigung sind dabei periodische Funktionen der Zeit.
Ist die rückstellende Kraft proportional zur Auslenkung ‚(Bsp. Fadenpendel, Federkraft) so sind diese
Funktionenen Sinusfunktionen. Deshalb werden derartige Schwingungen auch kurz Sinusschwingungen
oder harmonische Schwingungen genannt.
14.1.1 Kinematik der Sinusschwingung
Nachfolgend soll die Schwingung eines Federpendels (Massestück an Schraubenfeder) beschrieben
werden, das eine freie, ungedämpfte Schwinung ausführt. Die Reibung wird vernachlässigt.
In den Grafiken sind dargestellt:
a) die Auslenkung y (oberhalb der Nullage positiv)
b) die Geschwindigkeit v (pos. Richtung = nach oben)
c) die Beschleunigung a (pos. Richtung = nach unten)
zu a) Das y(t)-Diagramm stellt eine Sinuskurve dar,
er schwingt harmonisch um die Nulllage.
Da sich die Schwingung kontinuierlich wiederholt handelt es sich um einer periodische Schwingung
zu b) Das v(t)-Diagramm stellt eine Cosinuskurve dar,
Im Nulldurchgang hat der Körper die größte
Geschwindigkeit, an den Umkehrpunkten ist diese
„Null“ (kurzzeitiger Stillstand)
zu c) Das a(t)-Diagramm stellt eine invertierte Sinuskurve
dar. An den Umkehrpunkten liegt die größte
Beschleunigung vor, da ja die Feder „auf
Spannung ist. Im Nulldurchgang verursacht die Feder keine Beschleunigung.
Fach: Physik/ L. Wenzl
| Datum:
14. Mechanische Schwingungen und Wellen
Schwingungen treten in der Technik in vielen Vorgängen auf – mit positiven und negativen Effekten (z. B.
Haarrisse, Achsbrüche etc.). Deshalb ist es eine wichtige Aufgabe der Physik diese Phänomene zu
untersuchen. Wir werden uns nachfolgend mit den mechanischen Schwingungen beschäftigen.
Die dabei gewonnenen Erkenntnisse können analog auf die elektrischen Schwingungen übertragen werden.
Die aus der Mechanik gewonnenen Erkenntnisse (Translation, Rotation, Kinematik, Dynamik = Kap. 2-4)
bilden die Grundlage und stellt zugleich eine Wiederholung des dort erlernten Stoffes dar.
14.1 Freie ungedämpfte Schwingung
Wird ein Körper aus einer stabilen Gleichgewichtslage ausgelenkt, so beginnt er
freie Schwingungen um diese Gleichgewichtslage auszuführen.
Wenn Reibungskräfte fehlen, ist diese Schwingung ungedämpft.
Beispiel: Schiffschaukel wird aus Ruhelage ausgelenkt, bei einer gewissen
Höhe sind nahezu „ungedämpfte“ Schwingung möglich
– bis der Bremsklotz in Aktion tritt.
Auslenkung, Geschwindigkeit und Beschleunigung sind dabei periodische Funktionen der Zeit.
Ist die rückstellende Kraft proportional zur Auslenkung ‚(Bsp. Fadenpendel, Federkraft) so sind diese
Funktionenen Sinusfunktionen. Deshalb werden derartige Schwingungen auch kurz Sinusschwingungen
oder harmonische Schwingungen genannt.
14.1.1 Kinematik der Sinusschwingung
Nachfolgend soll die Schwingung eines Federpendels (Massestück an Schraubenfeder) beschrieben
werden, das eine freie, ungedämpfte Schwinung ausführt. Die Reibung wird vernachlässigt.
In den Grafiken sind dargestellt:
a) die Auslenkung y (oberhalb der Nullage positiv)
b) die Geschwindigkeit v (pos. Richtung = nach oben)
c) die Beschleunigung a (pos. Richtung = nach unten)
zu a) Das y(t)-Diagramm stellt eine Sinuskurve dar,
er schwingt harmonisch um die Nulllage.
Da sich die Schwingung kontinuierlich wiederholt handelt es sich um einer periodische Schwingung
zu b) Das v(t)-Diagramm stellt eine Cosinuskurve dar,
Im Nulldurchgang hat der Körper die größte
Geschwindigkeit, an den Umkehrpunkten ist diese
„Null“ (kurzzeitiger Stillstand)
zu c) Das a(t)-Diagramm stellt eine invertierte Sinuskurve
dar. An den Umkehrpunkten liegt die größte
Beschleunigung vor, da ja die Feder „auf
Spannung ist. Im Nulldurchgang verursacht die Feder keine Beschleunigung.
Fach: Physik/ L. Wenzl
| Datum:
Begriffe zur freien Schwingung:
Schwingungdauer T (Periodendauer) = Zeitspanne für eine volle Schwingung
Man erhält geneuere Ergebnisse für T, wenn man die Anzahl z der Schwingungen zählt und parallel dazu
die benötigte Zeitspanne ∆t misst.
∆t
T=
∆t = Zeitspanne für z Schwingungen
z = Anzahl der gezählten Schwingungen
[T] = 1 s
z
Frequenz f = Anzahl der Schwingungen, die in einer Sekunde absolviert werden
(z. B. Netzspannung -> 50 Hz)
1
f=
z
=
∆t
T
[f] = 1/s = 1 Hz (Hertz)
Kreisfrequenz ω = Multiplikation der Frequen f mit dem Faktor 2π (6,28 rad). Gibt an,
(omega)
welchen Winkel (in Bogenmaß,rad) ein rotierender Zeiger in 1s
überstreichen würde.
ω = 2 *π * f
[ω] = 1/s
Diese Größen und die nachfolgenden Formen finden auch in der Beschreibung und Berechnung
elektrotechnischer Signale Anwendung.
Auslenkung:
Mit der Amplitude (= maximale Auslenkung) ŷ und der Kreisfrequenz ω lässt sich die jeweilige Auslenkung (Augenblickswert)
eines Schwingungsvorganges berechnen.
y = ŷ * sinω
ωt
Beispiel: Sie zählen innerhalb von 10,0s eine Anzahl von 15 Schwingungen.
Der schwingende Körper hat eine maximale Auslenkung von 1,00 m.
Berechnen Sie T, f, ω.
An welcher Position befindet sich der nach 3,30 s und nach 5,20s ?
Geg.:
Ges.:
Fach: Physik/ L. Wenzl
| Datum:
14.1.2 Dynamik der Sinusschwingung
Aus der –soeben erfolgten- kinematischen Beschreibung von Schwingungbewegungen geht nicht hervor,
wodurch Frequenz und Amplitude von Schwingungen bestimmt werden.
Um dies zu beantworten, müssen die Kräfte und Energien eines schwingenden Systems untersucht
werden.
Aus dem Grundgesetz der Dynamik und dem Hookschen Gesetz ergibt sich die Aussage:
F = m*a und FRück = - D*y -> gleichsetzen: m*a = -D*y -> a = -(D/m)*y (I)
Nicht hergeleitet wird folgender Zusammenhang: a = -ω2 .y (II)
Gleichsetzen von (I) und (II) ergibt: -ω2 . y = -(D/m)*y -> ω2 = D/m
ω = √(D/m)
1
ω = √(D/m)
fo =
* √(D/m)
2π
Erkenntnis: Die Frequnz der Sinusschwingung hängt nur von den Eigenschaften des Systems
(hier Masse und Federkonstante) ab. Sie hängt dagegen nicht von der
Auslenkung des Systems ab.
Man nennt die Frequenz fo „Eigenfrequenz“ des Schwingungssystem (Oszillators)
Bedeutung: Wenn man ein schwinungsfähiges System (z. B. Federpendel, Schiffschaukel)
mehr auslenkt, so bewegt sich der Körper mit höherer Geschwindigkeit v,
jedoch bleibt die Frequenz –unabhängig von der Auslenkung- stets konstant.
Beispiel:
Geg.:
Das abgebildete Federpendel besitzt eine Masse m = 300 g.
Die Federkonstante D der Schraubenfeder beträgt 1,00 N/cm
Berechnen Sie die Eigenfrequenz des Pendels.
Ges.:
Fach: Physik/ L. Wenzl
| Datum:
14.1.3 Mathematisches Pendel
Ein mathematisches Pendel besteht idealisiert aus einem
puntkförmigen Körper der Masse m an einem masselosen Faden
der Länge l.
Die Herleitung ergibt für diese Pendel folgende Eigenfrequenz:
Daraus ergibt sich, dass die Frequen allein von der Länge (sofern man von „irdischen“ Verhältnissen
ausgeht) abhängt. Die Masse spielt keine Rolle.
So würden z. B. beim Schiffschaukeln zwei Gondeln gleich schnell pendeln, obwohl die eine mit schweren
Erwachsenen, die andere mit leichten Kindern besetzt ist. Hierbei muss jedoch davon ausgegangen
werden, dass zum Zeitpunkt der Beobachtung kein Kraftaufwand („Anschieben“) erfolgen darf, weil ja
ansonsten Energie in das System eingebracht wird.
Beschreiben Sie mit eigenen Worten, wie sich bei diesem Pendel der Energieerhaltungssatz zeigt:
Das ausgelekte Pendel hat seine maximale Lageenergie (Potentielle Energie).
Beim Loslassen wird es aufgrund der Erdanziehung beschleunigt –> Es gewinnt kinetische
Energie.
Jedoch verliert es auch an Höhe -> Potentielle Energie geht verloren.
Beim Nulldurchgang hat es seine maximale kinetische Energie, die sich jedoch wegen des
Ausschlags zur anderen Seite kontinuierlich in Potentielle Energie umwandelt.
Beispiel 1: Das oben abgebildete Fadenpendel hat ein Länge l = 0,500 m
Berechnen Sie die Eigenfrequenz des Pendels.
Geg.:
Ges.:
Beispiel 2: Ein Fadenpendel schwingt mit einer Frequen von 2,00 Hz. Welche Länge hat der Faden?
Geg.:
Ges.: