9 Multipol-Entwicklung Für eine axial symmetrische

9
Multipol-Entwicklung
Im vorigen Kapitel haben wir gesehen, dass die Lösungen der Laplace-Gleichung bei axialer Symmetrie
in einer Entwicklung nach Legendre-Polynomen dargestellt werden können,
∞ X
Bl
l
Al r + l+1 Pl (cos ϑ).
φ(r, ϑ) =
r
l=0
In dieser Vorlesung werden wir, dass sich die Lösungen der Poisson-Gleichung ebenfalls in obiger
Form darstellen lassen. In diesem Fall geben die Koeffizienten Auskunft über die Symmetrie der
Ladungsverteilung.
Betrachte die erzeugende Funktion der Legendre-Polynome,
∞
g(x, t) = √
für |t| < 1.
X
1
=
Pl (x) tl
1 − 2xt + t2
l=0
1
nach Multipolen:
|r − r 0 |

∞ l

1 X r0


Pl (cos γ)

 r
r
1
l=0
=
∞
|r − r 0 | 
1 X r l


Pl (cos γ)

 r0
r0
Dies definiert eine Entwicklung von
(r > r 0 )
,
0
(r < r )
l=0
wobei γ = 6 (r, r0 ) der Winkel zwischen r und r 0 ist, d.h.
cos γ = cos ϑ cos ϑ0 + sin ϑ sin ϑ0 cos(ϕ − ϕ0 ).
Die obige Entwicklung kann zusammenfassend als
l
∞ 1 X r<
1
Pl (cos γ)
=
|r − r 0 |
r>
r>
l=0
geschrieben werden, wobei r> = max(r, r0 ) und r< = min(r, r0 ).
Betrachte nun die Lösung der
Poisson-Gleichung
φ(r, ϑ)
Für eine
im freien Raum,
=
1
4π0
Z
=
1
4π0
Z
=
∞ Z
1
1 X
dV 0 l+1 (r< )l Pl (cos γ) ρ(r 0 )
4π0
r
>
l=0
dV 0
dV 0
ρ(r 0 )
|r − r 0 |
∞
X
(r< )l
Pl (cos γ)
l+1
r>
l=0
(1)
axial symmetrische Ladungsverteilung,
ρ(r 0 ) = ρ(r, ϑ)
hängt das Potential nicht vom Azimuthalwinkel ϕ ab. Außerhalb der Ladungsverteilung gilt dann
∞ Bl
1 X
l
Al r + l+1 Pl (cos ϑ).
φ(r, ϑ) =
4π0
r
l=0
Betrachte nun speziell das Potential weit entfernt von allen Ladungen. Dann
ist r > r0 , d.h. r = r> und r0 = r< . Damit das Potential im Unendlichen endlich bleibt, muß
Al = 0 für l > 0.
⇒ φ(r, ϑ) = φ∞ +
∞
1 X Bl
Pl (cos ϑ).
4π0
rl+1
l=0
Durch Vergleich mit der
tials
Multipol-Entwicklung des elektrostatischen Potenφ(r, ϑ) =
Z
∞
1 X 1
dV 0 (r0 )l Pl (cos γ) ρ(r0 , ϑ0 )
4π0
rl+1
l=0
findet man die Koeffizienten Bl .
Die Entwicklungskoeffizienten
Z
dV 0 (r0 )l Pl (cos γ) ρ(r0 , ϑ0 )
hängen noch vom Winkel ϑ ab.
Demgegenüber sind die Bl unabhängig von ϑ. Zu ihrer Bestimmung bedient man sich daher des
folgenden Tricks:
Man berechnet das Potential auf der z-Achse. Dort ist ϑ = 0 und entsprechend γ = ϑ0 .
Z
⇒ Bl Pl (cos ϑ = 1) = Bl = dV 0 (r0 )l Pl (cos ϑ0 ) ρ(r0 , ϑ0 )
{z
}
|
1
Die Bl sind die (zylindrischen) Multipol-Koeffizienten des elektrostatischen Potentials im Außenraum
der Ladungen.
Damit ist das Potential
bekannt,
im ganzen Raum außerhalb der Ladungsverteilung
φ(r, ϑ) =
∞
1 X
Pl (cos ϑ)
Bl
.
4π0
rl+1
l=0
Beispiel:homogen
geladener Ring
Ein homogen geladener Ring liege parallel zur xy-Ebene und sein Mittelpunkt im Abstand b (entlang
z) vom Koordinatenursprung. Die Ladungsverteilung ist also in Zylinderkoordinaten durch
ρ(r) =
q
δ(r − a)δ(z − b)
2πa
gegeben.
Für einen Punkt r = rez auf der z-Achse ist der Abstand zu jedem Punkt auf dem Ring durch
q
d = r2 + r02 − 2rr0 cos α
mit
r02 = b2 + a2
gegeben. Hier ist α der Winkel zwischen der z-Achse und dem Verbindungsvektor r 0 vom Ursprung
zu einem beliebigen Punkt des Rings.
Da dieser Abstand nicht vom Azimuthalwinkel abhängt, ist das Potential im Punkt r durch
Z
1
1 q
q
φ(r, ϑ = 0) =
dφ =
4π0
2πd
4π0 d
gegeben.
Wegen d = |r − r 0 | gilt die Multipolentwicklung
φ(r, 0) =
∞
l
q X r<
Pl (cos α).
l+1
4π0
r
l=0 >
Hieraus kann man die Entwicklungskoeffizienten al und bl ablesen:
Für r < r0 erhält man bl = 0 und al = Pl (cos α)/r0l+1 . Dahingegen gilt für r > r0 , daß al = 0 und
bl = r0l Pl (cos α).
Die Multipol-Entwicklung ist eine Entwicklung nach:
l
1
1. Potenzen von
r
2. spezifischen Winkelcharakteristika
monopole
dipole
quadrupole
octupole
q
q
-q
q
monopole
-q
-q
q
dipole
quadrupole
Die Multipol-Momente hängen im Allgemeinen von der Wahl des Ursprungs des Koordinatensystems
ab. Verschwinden hingegen alle Multipol-Momente für l < l0 , so ist das l-te Multipol-Moment von
der Wahl des Ursprungs unabhängig. Im Einzelnen:
Das Dipol-Moment (l = 1) ist von der Wahl des Koordinatenursprungs unabhängig, wenn die Gesamtladung verschwindet.
Das Quadrupol-Moment (l = 2) ist von der Wahl des Koordinatenursprungs unabhängig, wenn sowohl
die Gesamtladung als auch das Dipol-Moment verschwinden.
9.1
Elektrischer Dipol, Multipol-Entwicklung in kartesischen Koordinaten
Die Multipol-Entwicklung charakterisiert das Potentials in weiter Entfernung von der Ladungsverteilung.
Je höher das Multipol-Moment, um so schneller fällt der entsprechende Beitrag zum Potential in
großer Entfernung ab (∝ r −(l+1) ). Gemäß unserer Vorstellung, daß das Potential einer Ladungsverteilung
in großer Ferne dem einer Punktladung ähnelt, gibt das l = 0-Multipol-Moment (Monopol) die
Gesamtladung der Ladungsverteilung an,
Z
B0 = dV ρ(r) = Q.
9.2
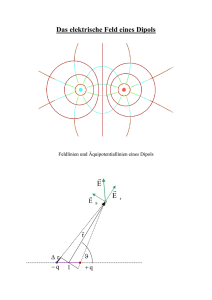
Elektrischer Dipol
Der l = 1-Beitrag zum Potential
Vl=1 =
1 1
4π0 r2
Z
dV 0 r0 cos γρ(r0 ) = Vdip
wird als Dipol-Potential bezeichnet.
Mit
r0 cos γ = er · r 0
läßt sich das Dipol-Potential als
Vdip =
schreiben, wobei das
Dipolmoment
1 p·r
4π0 r2
einer Ladungsanordnung durch
Z
p = dV 0 r 0 ρ(r 0 )
gegeben ist.
Bei axialsymmetrischen Problemen ist es ausreichend die Projektion der Multipol-Momente auf die
z-Achse zu kennen. Dementsprechend bezeichnet
Z
B2 = dV 0 (r0 )2 [3 cos2 ϑ0 − 1]
das
Quadrupol-Moment
der Ladungsanordnung.
Als erstes Beispiel haben Sie bereits kennengelernt, daß die Influenzladung auf der Oberfläche einer
Kugel im homogenen elektrischen Feld das Dipolmoment
p = 4π0 E0 R3 eE0
besitzt.
Dies läßt sich nun leicht überprüfen:
Ist das homogene elektrische Feld in z-Richtung gerichtet, so hat die induzierte Ladung die Form
σ = 30 E0 cos ϑ.
Das Dipolmoment lautet also:
Z
dV 0 r 0 ρ(r 0 ) = dV 0 r 0 30 E0 cos ϑ0 δ(r − R)


Z
sin ϑ cos ϕ
=
dV r  sin ϑ sin ϕ  30 E0 cos ϑδ(r − R)
cos ϑ
p =
Z
(2)
(3)
Integration über ϕ ⇒ x- und y-Komponenten verschwinden.
z-Komponente:
pz = 30 E0
Z
2
2
3
dV r cos ϑδ(r − R)r sin ϑdrdϑdϕ = 30 E0 R 2π
Z
1
x2 dx = E0 R3 4π0 .
−1
Alle höheren Multipol-Momente verschwinden. Daher erzeugt diese Ladungsverteilung im Außenraum
der Kugel einen idealen Dipol.
Der Begriff des Multipols leitet sich anschaulich daraus her, daß zur Erzeugung der jeweiligen Potentialkomponenten mehrere Punktladungen nötig sind. Zur Erzeugung des Dipolpotentials benötigt
man zwei, zur Erzeugung des Quadrupolpotentials vier Punktladungen.
Der physikalische Dipol besteht aus zwei Punktladungen mit entgegengesetzt gleichgroßen
Ladungen, die sich in einem Abstand a voneinander befinden. Die Ladungsdichte dieser Anordnung
lautet also:
1
1
ρ(r) = q(δ(r − aez ) − δ(r + aez )).
2
2
Damit besitzt die Anordnung ein Dipolmoment
p = qaez .
Die Ladungsverteilung kann also auch als
ρ(r) =
p
1
1
(δ(r − aez ) − δ(r + aez ))
a
2
2
geschrieben werden.
Einen idealen
Ladungen:
Dipol
erhält man im Grenzfall verschwindenden Abstands zwischen den beiden
∂
1
1
p
(δ(r − aez ) − δ(r + aez )) = −p δ(r) = −(p · ∇)δ(r)
a→0 a
2
2
∂z
Berechnet man für diese Ladungsverteilung das elektrostatische Potential, so ergibt sich
Z
Z
(p · ∇0 )δ(r0 )
1
1
1
0
=
dV
dV 0 δ(r 0 )(p · ∇0 )
φ(r) = −
4π0
|r − r0 |
4π0
|r − r 0 |
Z
1
1
1
1
=−
(p · ∇)
= −
dV 0 δ(r 0 )(p · ∇)
4π0
|r − r 0 |
4π0
r
1 p·r
=
.
4π0 r3
ρ(r) = lim
(4)
(5)
(6)
(1. Schritt: partielle Integration; 2. Schritt: Vertauschung der Ableitung nach r 0 und r wegen der
Symmetrie von |r − r 0 |)
Das Potential des idealen Dipols hat also nur eine Dipolkomponente.
Demgegenüber besitzt der physikalische
ungeradem l). Beispielsweise:
Z
Z
1
B3 = dV r3 (5 cos3 ϑ − 3 cos ϑ)ρ(r) = q dV
2
9.3
Dipol höhere Multipol-Momente (allerdings nur solche mit
a3
a3
1
1
(5z 3 − 3r2 z)δ(x)δ(y)[δ(z − a/2) − δ(z + a/2)] = q[5 − 3 ] = qa3
2
8
8
4
Multipol-Entwicklung in kartesischen Koordinaten
Bei der Herleitung der Multipol-Entwicklung in Kugelkoordinaten ist uns die Entwicklung nach Potenzen von 1r in gewisser Weise “glücklich in den Schoß gefallen”. In kartesischen Koordinaten ist eine
solche Entwicklung etwas mühsamer. Rufen wir uns ins Gedächtnis, daß es sich um eine Entwicklung
für r r0 handelt, so ist klar, daß wir in kartesischen Koordinaten eine Taylor-Entwicklung
des Potentials vornehmen müssen.
Die Taylor-Entwicklung einer Funktion in einer Variablen läßt sich als
∞
X
1
d
d
2 00
( )n f (x) = exp( )f (x)
f (x + ) = f (x) + f (x) + f (x) + . . . =
2!
n!
dx
dx
n=0
0
schreiben, wobei der letzte Schritt in gewisser Weise symbolischen Charakter hat und durch die
vorherigen Ausdrücke definiert ist.
Die Taylor-Entwicklung einer Funktion, die von den drei (Raum-)Koordinaten x, y und z abhängt,
ergibt sich dann entsprechend zu
∂
∂
∂
∂
)f (x, y + 2 , z + 3 ) = exp(1 ) exp(2 ) exp(3 )f (x, y, z)
∂x
∂x
∂y
∂z
∞
X
1
( · ∇)n f (x, y, z)
= exp( · ∇)f (x, y, z) =
n!
n=0
f (x + 1 , y + 2 , z + 3 ) = exp(1
(7)
(8)
Dann ergibt sich für |r − r 0 |−1 die Taylor-Entwicklung
1
|r − r 0 |
=
=
=
∞
X
1
1
(−r0 · ∇)n
n!
r
n=0
(9)
1
1
1
1
+ (−r0 · ∇) + (r 0 · ∇)2 + . . .
r
r 2!
r 1 3(r · r0 )2
(r0 )2
1 r · r0
+ 3 +
− 3 +...
r
r
2
r5
r
(10)
(11)
Im letzten Schritt wurde benutzt, daß
∇
1
1
= −n n+1 ∇r.
rn
r
Somit erhält man für das Potential
Z
Z
Z
Z
1
r
1 1
1
1
ρ(r 0 )
0
0
0 2
0 2 2
0
0 0
0
0
φ(r) =
·
r
)
+
ρ(r
)
+
)
−
(r
)
r
ρ(r
)
+....
=
·
dV
r
dV
ρ(r
dV
3(r
dV 0
4π0
|r − r 0 |
4π0 r
r3
2 r5
Man erkennt in dieser Entwicklung leicht das Monopol-Moment
Z
Q = dV ρ(r)
sowie das Dipol-Moment
p=
Z
dV rρ(r)
wieder.
Mit der Umformung
3(r · r0 ) − r2 (r0 )2 =
X
i,j
x0i x0j (3xi xj − r2 δij ) =
X
i,j
(x0i x0j −
(r0 )2
δij )(3xi xj − r2 δij )
3
erhält man die Entwicklung des Potentials in den ersten 3 Multipol-Momenten in kartesischen Koordinaten,



1  Q r · p 1 X 3xi xj − r2 δij
,
+ 3 +
Q
φ(r) =
ij

4π0  r
r
6 i,j
r5
mit dem
Quadrupoltensor
Qij =
Z
dV 0 (3x0i x0j − (r0 )2 δij )ρ(r 0 ).
(Bei der obigen Umformung wurde benutzt, daß
X
i,j
δij (3xi xj − r2 δij ) =
X
i
(3xi xi − r2 ) = 0.)
Der Quadrupoltensor ist symmetrisch, d.h. Qij = Qji und seine Spur verschwindet,
Dementsprechend hat der Quadrupoltensor fünf unabhängige Matrixelemente.
Bei axialsymmetrischen Ladungsverteilungen gilt
Z
Z
2
dV x ρ(r) = dV y 2 ρ(r).
Dem entsprechend ist Qxx = Qyy . Wegen der verschwindenden Spur von Q gilt dann
Qzz = −2Qxx = −2Qyy .
Außerdem erhält man für die Außerdiagonal-Elemente (i 6= j)
Z
Z
dV xyρ(r) = 0 = dV xi xj ρ(r).
P
i
Qii = 0.
Also
Qij = 0 für i 6= j.
Damit ist der Quadrupoltensor diagonal und hat nur ein einziges unabhängiges Matrixelement.
Für Qzz erhält man
Qzz =
Z
dV (3z 2 − r2 )ρ(r) =
Z
dV r2 (3 cos ϑ − 1)ρ(r) = B2 .
Die zz-Komponente des Quadrupoltensors stimmt also bei axialsymmetrischen Ladungsverteilungen
mit dem sphärischen Quadrupolmoment überein.
Bei kugelsymmetrischen Ladungsverteilungen verschwindet der Quadrupoltensor, denn dann gilt
Z
Z
Z
Z
1
dV r2 ρ(r).
dV z 2 ρ(r) = dV x2 ρ(r) = dV y 2 ρ(r) =
3
Es ist offensichtlich, daß die Entwicklung des Potentials nach höheren Multipol-Momenten in kartesischen Koordinaten sehr mühsam wird.
9.4
Wechselwirkung einer Ladungsverteilung mit einem äußeren
Feld
Die Multipol-Entwicklung ist sehr nützlich für die Berechnung der Energie einer Ladungsverteilung mit
einem äußeren Feld φex (r). Für die folgenden Betrachtungen nehmen wir an, daß die Ladungsanordnung stationär ist, sich also unter dem Einfluß des äußeren Feldes nicht ändert.
Beispiele hierfür sind etwa: ein Dipol im Feld eines anderen Dipols oder die Nukleonen im Feld der
Elektronen.
Die Energie einer solchen Anordnung ist dann
Z
W = dV 0 ρ(r 0 )φex (r 0 ) + innere Energie,
wobei hier unter “innerer Energie” diejenige Energie verstanden werden soll, die zum Aufbau der
Ladungsverteilung nötig war.
Der Einfachheit halber legen wir den Koordinatenursprung ins Zentrum der Ladungsverteilung und
nehmen an, daß das externe Potential am Ort der Ladungsverteilung nur wenig variiert.
Eine Taylor-Entwicklung des externen Potentials um den Koordinatenursprung liefert dann
1
φex (r 0 ) = φex (0) + (r 0 · ∇)φex (r)|r=0 + (r 0 · ∇)2 φex (r)|r=0 + . . . .
2
Wir weiterhin an, daß das äußere Feld am Ort der Ladungverteilung quellenfrei ist,
∆φex (r) = 0(im Ladungsbereich).
Dann gilt:
X
1
∂ ∂
1
∂ ∂
− (r0 )2 δij
φex (r).
(r 0 · ∇)2 φex (r) = (r 0 · ∇)2 − (r0 )2 ∆ φex (r) ==
x0i x0j
3
∂x
∂x
3
∂x
∂x
i
j
i
j
i,j
Setzt man dies in den Ausdruck für die Energie ein, so erhält man
W
R
R
= [ dV 0 ρ(r 0 )]φex (0) + [ dV 0 ρ(r 0 )r 0 ] · ∇φex (r)|r=0
=
Qφex (0)
=
Monopol-WW
−
p · E ex (0)
Dipol-WW
+
−
1
6
P
R
0
0
0 0
0 2
i,j [ dV ρ(r ){3xi xj − (r ) δij }]
P
∂Ei 1
Q
ij
i,j
6
∂xj r=0
Quadrupol-WW
∂φex (r) ∂xi ∂xj r=0
+ ...
+ ...
Analog ergibt sich für die Kraft auf eine Ladungsverteilung
Z
Z
ex 0
0
0
F =
dV ρ(r )E (r ) = dV 0 ρ(r 0 ) [E ex (0) + (r · ∇)E ex (r)|r=0 + . . .]
= QE ex (0) + (p · ∇)E(r)|r=0 + . . .
Hier gibt der erste Term die Kraft auf die Gesamtladung der Ladungsverteilung an. Der zweite Term
gibt zu erkennen, daß auf einen Dipol nur dann eine Kraft ausgeübt wird, wenn das elektrische Feld
inhomogen ist.
Analog erhält man das Drehmoment das auf die Ladungsverteilung wirkt zu
Z
Z
N =
dV 0 r 0 × ρ(r 0 )E ex (r 0 ) = dV 0 ρ(r 0 )r 0 × [E ex (0) + . . .]
= p × E ex (0) + . . .
d.h. das elektrische Feld wirkt auf das Dipolmoment ein Drehmoment aus.