Mechanik starrer Körper

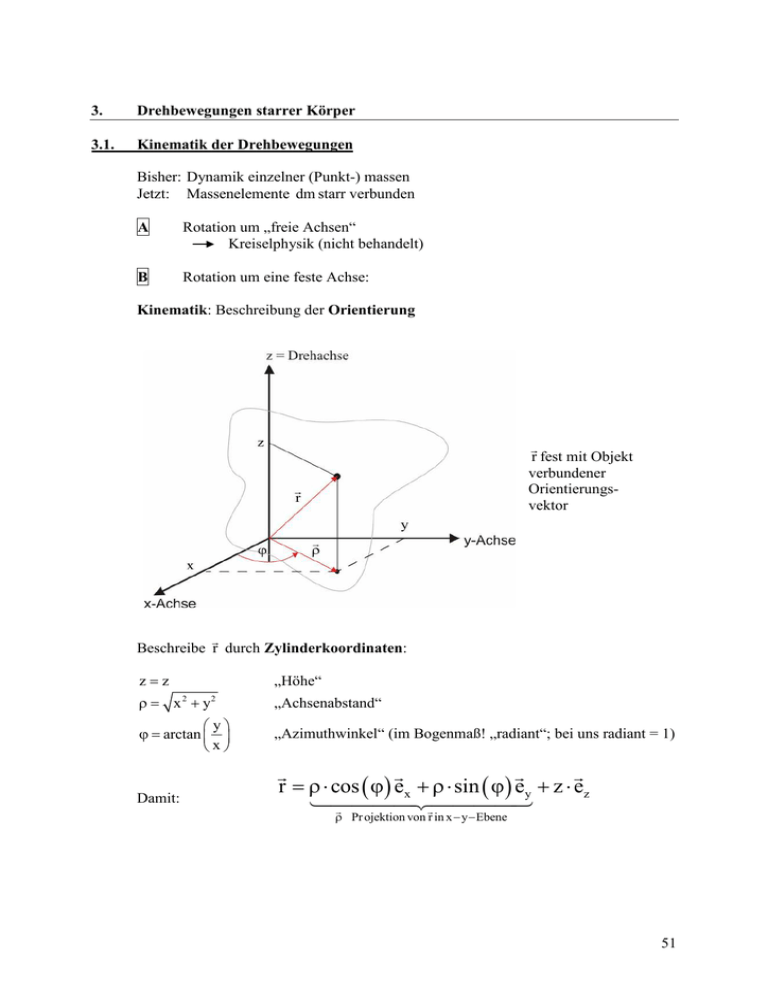
3.
Drehbewegungen starrer Körper
3.1.
Kinematik der Drehbewegungen
Bisher: Dynamik einzelner (Punkt-) massen
Jetzt: Massenelemente dm starr verbunden
A
Rotation um „freie Achsen“
Kreiselphysik (nicht behandelt)
B
Rotation um eine feste Achse:
Kinematik: Beschreibung der Orientierung
r fest mit Objekt
verbundener
Orientierungsvektor
Beschreibe r durch Zylinderkoordinaten:
z=z
„Höhe“
ρ= x +y
2
2
y
ϕ = arctan  
x
Damit:
„Achsenabstand“
„Azimuthwinkel“ (im Bogenmaß! „radiant“; bei uns radiant = 1)
r = ρ ⋅ cos ( ϕ ) ex + ρ ⋅ sin ( ϕ ) ey + z ⋅ ez
ρ Pr ojektion von r in x − y − Ebene
51
Rotation um z-Achse:
ρ = const.; z = const.; ϕ = ϕ ( t )
(immer möglich: z = 0 ; ab jetzt angenommen)
Definition:
ϕ ( t ) = ϕ ( t ) ⋅ ez heißt Orientierungswinkel (-Vektor)
Damit Bewegung beschreibbar:
Def.:
dϕ
ɺ ez = ω⋅ ez
ω = ϕɺ =
= ϕ⋅
dt
heißt „Winkelgeschwindigkeit“,
[ ω] =
1
s
ɺ =ϕ
ɺɺ = ω⋅
ɺ ez = ϕ
ɺɺ ⋅ ez = α ⋅ ez
α=ω
heißt „Winkelbeschleunigung“,
Beachte:
[α] =
1
s2
Vektorcharakter erlaubt ganz allgemein (auch in „Kreiselphysik“ !)
Achsenorientierung (bei uns immer ez ) und Drehrichtung
(durch V.Z. der Skalarkomponenten) zu beschreiben !
Beispiele:
(aus Blickrichtung
entgegen der
z -Achse)
schneller werdende Linksdrehung:
langsamer werdende Linksdrehung:
langsamer werdende Rechtsdrehung:
usw.
ω > 0, α > 0
ω > 0, α < 0
ω < 0, α > 0
Die gleichförmige Drehbewegung
α ( t ) = 0 ⇒ ω ( t ) = ω⋅ ez = const.
⇒ ϕ ( t ) = ϕ0 + ω⋅ t ⋅ ez
Anfangswinkel
für t = 0
+ für links rum
- für rechts rum
Bahnkurven in kartesischen Koordinaten:
ρ ( t ) = ( x, y )( t ) = ( ρ ⋅ cos ( ωt + ϕ0 ) , ρ ⋅ sin ( ωt + ϕ0 ) )
v ( t ) = ρɺ = ( −ωρ ⋅ sin ( ωt + ϕ0 ) , ωρ ⋅ cos ( ωt + ϕ0 ) )
a ( t ) = vɺ = ( −ω2ρ ⋅ cos ( ωt + ϕ0 ) , −ω2ρ ⋅ sin ( ωt + ϕ0 ) )
52
und daraus, als Vektorgleichung:
a ( t ) = −ω2ρ ( t )
Das gilt allgemein für jeden Punkt des Körpers (mit ρ und ϕ0 angepasst )!
Frequenz und Winkelgeschwindigkeit
Definition:
ω:
Winkelgeschwindigkeit oder Kreisfrequenz
2π
:
Periodendauer
ω
1 ω
1
ν= =
: Frequenz
[ ν] = = 1Hz
T 2π
s
T=
“Hertz“
Beispiel:
Motor mit 6000 Umdrehungen pro Minute (rpm,
revolutions per minute):
1
s = 10 ms
100
ν = 100 Hz
T=
ω = 624s −1
53
3.2.
Dynamik der Drehbewegungen
Betrachte K.S. mit Ursprung irgendwo in der Drehachse und r als Vektor zu
beliebigem Massenelement dm des rotierenden
Körpers.
⇒ r ( t ) gekrümmte Bahnkurve (siehe 2.5.) mit Krümmungsradius K = ρ
Bahngeschwindigkeit:
ds ρdϕ
v(t) = =
= ρ ⋅ ω( t )
dt
dt
(kein Vektor; > 0 für links rum ; < 0 für rechts rum)
⇒ Radialbeschleunigung
v2 ( t )
ar ( t ) =
e−ρ = ρ ⋅ ω2 ( t ) e−ρ
… ist Abstand ⋅ Winkelgeschwindigkeit 2 .
ρ
Tangentialbeschleunigung
dv
ɺ ev = ρ ⋅ α ( t ) ⋅ ev …ist Abstand ⋅ Winkelbeschleunigung.
at (t) =
ev = ρ ⋅ ω⋅
dt
Gesamtkraft auf Massenelement dm
dF = dm ⋅ a ( t ) = dm ( a r ( t ) + a t ( t ) )
wird i.a. durch elastische Kräfte der Nachbar-Volumenelemente ausgeübt !
⇒ elastische Verformung ! (kommt später)
A
at = 0
Beispiele:
1.)
Masse m an Feder, gleichförmige Drehbewegung (Schleuder)
ω ( t ) = const.
⇒ a r = ρ ⋅ ω2 , a t = 0
F = m ⋅ a r = m ⋅ ρ ⋅ ω2 ⋅ e−ρ
sichtbar an Federdehnung (s.u.) !
2.)
Auto mit konstanter Geschwindigkeit um Kurve mit
Krümmungsradius K :
v2
F = m ⋅ a r = m ⋅ ⋅ e− K
K
sichtbar durch elastische Verformung der Reifen !
Bei gleichförmiger Drehbewegung greift nur diese Radialkraft am Objekt an und heißt
Zentripetalkraft FZ.P. (auf Drehachse/Krümmungskreiszentrum hin gerichtet.)
Bei der Beschreibung der Dynamik in einem mitbewegten, d.h. mit a = a r selbst
beschleunigten Bezugssystem tritt demgegenüber eine auf alle Objekte wirkende
Trägheitskraft Fa = − m ⋅ a auf. Das gilt allgemein für alle beschleunigten
Bezugssysteme (z.B. auch anfahrender oder bremsender Fahrstuhl). Hier heißt diese
Trägheitskraft
„Zentrifugalkraft“ FZ.F. = − ma r = −FZ.P. (von Drehachse/Krümmungskreiszentrum
weg gerichtet.)
54
⇒
FZ.F. ist im mit bewegten (beschleunigten!) Bezugssystem ohne Kontakt wirkend, also
wie eine der Masse proportionale Feldkraft und „entlarvt“ das beschleunigte
Bezugssystem !
Beachte Analogie zur Gravitationskraft: Fγ ∼ m und auch kontaktfrei wirkend.
Einstein, allgemeine Relativitätstheorie: Fγ und FZ.F. sind äquivalent !
B
ɺ (t) ≠ 0
a t ( t ) ≠ 0 , also a t = ρ ⋅α ( t ) = ρ ⋅ ω
Draufsicht auf Drehachse = z -Achse
Fr = F ⋅ cos β
„Radialkomponente“
⇒ elastisch
kompensiert
Ft = F ⋅ sin β
„Tangentialkomponente“
mit Wirkung ∼ ρ
M = ρ ⋅ F ⋅ sin ( β ) ⋅ ez
ist das von F verursachte Drehmoment und bewirkt a t
Ft
„ M = Achsenabstand ⋅ Tangentialkraft“
Auch anders lesbar:
M = ρ ⋅ sin ( β ) ⋅ F ⋅ ez
mit ρeff = „Lot von Drehachse auf Kraft-Wirkungslinie L“
ρeff
„ M = Kraft ⋅ effektiver Hebelarm“
Vektoriell:
M = ρ× F
bewirkt
α = const ⋅ M
?
Beachte:
M ist (bzgl. 0 -Punkt auf Drehachse) eigentlich nur die
z -(Vektor-)Komponente M z von
M ges = r × F = ( ρ ⋅ eρ + z ⋅ ez ) × F = ρ× F + z ⋅ ez × F = M z + M ⊥
55
M ⊥ bewirkt bei freier Drehung (Kreiselphysik) zusätzliche
Winkelbeschleunigungen um x - und y -Achse (Achse „kippt“), wird
aber bei fester Drehachse durch elastische Kräfte im Drehachsenlager
kompensiert. Das ist durch „Auswuchten“ auch minimierbar!
Versuch: Schwerpunktsbestimmung durch Pendelaufhängung
Rotationsenergie und Trägheitsmoment
Rotationsenergie = kinetische Energie aller Massenelemente
1
1
dK rot = ⋅ ( dm ) ⋅ v 2 = ⋅ρ2 ⋅ ω2 ⋅ dm
2
2
⇒ Aufsummieren mit dm = D ( ρ ) dV
(ACHTUNG: Dichte jetzt D (früher ρ ) !!)
1
K rot = ⋅
2
∫
ρ2 ⋅ D ( ρ ) dV ⋅ ω2
Körper
Trägheitsmoment J, [ J ]= kg ⋅m 2
Also: Rotationsenergie ist
analog wie bei Translation:
1
⋅ J ⋅ ω2
2
1
= ⋅ m ⋅ v2
2
K rot =
K
Das Trägheitsmoment eines Körpers bezüglich einer Drehachse ist die
achsenabstandsquadratgewichtete Summe aller seiner Massenelemente.
Beachte:
Hängt von Lage der Rotationsachse ab (s.u., Satz von Steiner) !
Grundgleichung für Rotation starrer Körper
analog zu
F = m ⋅ a = m ⋅ vɺ = pɺ
ɺ = Lɺ ,
M = J ⋅α = J⋅ω
gilt:
alles Vektoren z !
56
Trägheitsmomente homogener ( D ( r ) = konst. ), symmetrischer Körper
Beispiel Zylinder:
J=
∫
ρ2 ⋅ D ( ρ ) dV
Körper
⇒ Nutze Zylinderkoordinaten und summiere
über Scheiben mit Ringsektoren
(„Baumringe“)
dV = dρ ⋅ρdϕ⋅ dz
„Ringdicke“ „Ringhöhe“
2π
R
H
R
J = ∫ dρ ∫ dϕ∫ dz ρ ⋅ρ ⋅ D ( ρ )  = 2π ⋅ H ⋅ ∫ ρ ⋅ρ2 ⋅ D ( ρ ) dρ
2
0
0
0
0
R
= ∫ ρ ⋅ D ( ρ ) ⋅ H ⋅ 2π ⋅ρ dρ
2
0
Gewichtung
für D = konst.
=
R
2π ⋅ H ⋅ D ⋅ ∫ ρ3 dρ
0
Zylindermantel −
volumen
R
 ρ4 
1
R2
4
2
= 2π ⋅ H ⋅ D ⋅   = π ⋅ H ⋅ D ⋅ R = π ⋅ R ⋅ H ⋅ D ⋅
2
 4 0 2
M Zylinder
=
1
M Zylinder ⋅ R 2
2
Vergleiche dünner Hohlzylinder mit gleicher Masse:
J Hohlzylinder = 1⋅ M Zylinder ⋅ R 2
doppelt so groß !
Projektion: Trägheitsmomente symmetrischer Körper
57
FAZIT: Struktur immer gleich:
Trägheitsmoment = Geometriefaktor x Masse x Ausdehnungsparameter 2:
J = f ⋅ m ⋅ R2
Versuche: Rollen auf schiefer Ebene
Ziel:
Berechnung der Beschleunigung a = a ⋅ ex des Schwerpunkts längs der Ebene.
Kräfte:
Insgesamt greifen drei Kräfte an dem rollenden Objekt an:
Fγ = − m ⋅ g ⋅ cos ( α ) ey + m ⋅ g ⋅ sin ( α ) ex ,
ist die Gravitationskraft, die von der Erde ausgeübt auf das Objekt wirkt.
FN = FN ⋅ ey = + m ⋅ g ⋅ cos ( α ) ey ist die elastische Normalkraft, die von der Unterlage im
rechten Winkel zur Kontaktfläche auf das Objekt ausgeübt wird. Sie stellt sich
so ein, dass Fγ + FN keine Normalkomponente besitzt. Das muss deswegen so
sein, weil auch die Beschleunigung und damit die Gesamtkraft keine
Normalkomponenten besitzen und die noch fehlende dritte Kraft (s.u.) eine
reine Tangentialkraft ist. Fγ und FN addieren sich also gerade zu einer reinen
Tangentialkraft Ft = m ⋅ g ⋅ sin ( α ) ex .
FR = − FR ⋅ ex ist die elastische Tangentialkraft (Scherkraft), die von der Unterlage in der
Kontaktfläche antiparallel zur Schwerpunktsgeschwindigkeit auf das Objekt
ausgeübt wird. Sie stellt sich so ein, dass gerade die Rollbedingung erfüllt ist
Wirkung der Kräfte: FR = − FR ⋅ ex bewirkt die Winkelbeschleunigung α um den
Schwerpunkt(i) herum mit dem Drehmoment
M = ρ× FR = − R ⋅ e y × ( − FR ⋅ ex ) = FR ⋅ R ⋅ e− z = J ⋅ α
FR
(*)
J
(**)
α=R
Fγ + FN + FR = Ft + FR = m ⋅ g ⋅ sin ( α ) ex − FR ex = m ⋅ a ⋅ ex
ist die Gesamtkraft auf das Objekt und bewirkt die Beschleunigung a
des Schwerpunkts.
Wenn, wie hier, die Drehachse eines Körpers selbst beschleunigt wird, darf die Grundgleichung M = J ⋅ α nur
mit Bezug auf den Schwerpunkt bzw. eine Achse durch den Schwerpunkt ausgewertet werden!
(i)
58
Rollbedingung:
v = R ⋅ ω und a = R ⋅ α ; Einsetzen für α aus (*):
F
a = R ⋅ α = R 2 R also:
J
J
FR = 2 a
R
Einsetzen in (**):
m ⋅ a ⋅ ex = m ⋅ g ⋅ sin ( α ) ex −
J
⋅ a ⋅ ex
R2
J 

 m + 2  ⋅ a = m ⋅ g ⋅ sin ( α ) oder nach Kürzen von m:
R 

g ⋅ sin ( α ) g ⋅ sin ( α )
=
.
a=
(1 + f )
1 + mRJ 2
(
)
Man Beachte: 1.) Die Beschleunigung hängt (wie beim freien Fall) nicht von der Masse ab
2.) J=0 und damit f=0 (unendlich leicht rollende Masse) entspricht der
Gleitbewegung
3.)Durch das Rollen wird die Trägheit effektiv um den Faktor 1 + f erhöht:
Je weiter außen die Masse bei einem rollenden Objekt angeordnet ist, desto größer
Trägheitsmoment, Geometriefaktor f und Gesamtträgheit bei der Rollbewegung!
Geometriefaktor für eine Auswahl symmetrischer Körper
1+
1
*
f
KÖRPER
f
Hohlzylinder (Reifen, ∞ dünn)
1
Hohlkugel (Wand ∞ dünn)
2/3
2,5
Vollzylinder
1/2
3
Vollkugel
2/5
3,5
2
* Kritischer Gefällekoeffizient für Haftung beim Rollen (s. u.)
Trägheitsmomente allgemeiner Körper, Steiner’scher Satz
Trägheitsmoment hängt von Lage der Drehachse im Objekt ab, d.h. J nur sinnvoll
bzgl. Drehachse !
Projektion: Steiner’scher Satz
Der Steiner’sche Satz:
Das Trägheitsmoment eines Körpers bezüglich der Drehung um eine Achse, von welcher der
Schwerpunkt des Körpers einen Abstand b besitzt, ist die Summe aus dem Trägheitsmoment
des Körpers bezüglich einer in den Schwerpunkt verschobenen parallelen Drehachse und dem
Trägheitsmoment mb2, welches dem mit der gesamten Masse m des Körpers gewichteten
Schwerpunkt bezüglich der betrachteten Drehachse entspricht.
59
Anwendung: Alternative Beschreibung des Rollvorganges als kontinuierliches Kippen um den
Kontaktpunkt (K.P.):
Berechne Winkelbeschleunigung α = a / R für die Drehbewegung um den Kontaktpunkt
herum. Bezüglich der Drehachse durch diesen Kontaktpunkt gilt nach dem Steinerschen Satz
für das Drehmoment JK.P. :
J K.P. = J + mR 2 und damit
α=
Re− y × Fγ
R ⋅ mg ⋅ sin (θ )
M
und damit
=
=
J K.P. J + MR 2 f ⋅ mR 2 + mR 2
mR 2 ⋅ g ⋅ sin (θ ) g ⋅ sin (θ )
a = αR =
=
wie oben.
f ⋅ mR 2 + mR 2
f +1
4.
Statik
4.1
Elastizität
Elastizität:
A
Verteilung von Kräften auf Volumenelemente von Körpern durch
elastische Verformung.
Dehnung
∆L 1 F
= ⋅
L
E A
Dehnung
(mechanische) Spannung
E: (Der) Elastizitätsmodul
(„Young’s modulus“)
[ E ] = 
F N
= 2 = Pa "Pascal"
 A  m
60
Beispiele:
N
m2
200
70
13
3
E /109
Stahl
Alu
Holz
Kunststoff
B
G /109
N
m2
77
26
-
Scherung
∆x 1 F
= ⋅
L G A
Scherung
G: (Der) Schubmodul …
Makroskopisch übersetzbar in „Federkonstante“
Hook’sches Gesetz:
F = −D ⋅ ∆x
Bei technischen Federn:
[ D] =
N
m
Rückstellkraft mittels Torsion = Scherung !
61
z.B.:
Autofederung:
D≈
Labor-Kraftmesser:
F=
m
s 2 = 10000 N
0, 25m
m
250kg ⋅10
1N
N
= 100
cm
m
Beachte:
1.)
2.)
Mechanisch übertragene (=elastische) Kräfte sind im Prinzip sind stets durch
Verformung „sichtbar“.
Mikroskopische Ursache für elastische Kräfte: Störung der Balance aus
anziehenden und abstoßenden Coulombkräften zwischen Festkörper-Atomen:
Newton III:
4.2
F1,2 = − F2,1
bleibt deswegen aber auch für elastische Kräfte
gültig !
Die Gleichgewichtsbedingungen
1.)
Kräftebalance
Die an einem Objekt angreifenden Kräfte addieren sich vektoriell zu 0 ,
also F = ∑ Fi = 0 .
i
⇒ a=
2.)
F
=0
m
Objekt bleibt in Ruhe oder in gleichförmiger Bewegung
Drehmomentbalance
Die Drehmomente aller an einem Objekt angreifenden Kräfte addieren sich
zu 0 , also M = ∑ M i =∑ ρi × Fi = 0 .
i
i
M
=0
J
Objekt bleibt in Ruhe oder gleichförmiger Rotation
⇒ α=
Beachte:
Wenn 1.) gilt ist 2.) unabhängig vom Bezugspunkt für die
Drehmomente; denn dann gilt bei Verschiebung − r0 des Bezugspunktes
zur Auswertung des Gesamtdrehmoments:
M 0 = ∑ ( r0 + ρi ) Fi = r0 × ∑ Fi + ∑ ρi × Fi = M
i
i
i
!
0
Das Ergebnis ist also durch die Verschiebung des Bezugspunktes nicht
verändert worden!
62
Kräftegleichgewicht
Beispiel: (Masseloser) Flaschenzug
Elastische Kraft Fel in jedem Seilquerschnitt gleich
Gleichgewicht Fges = 0 :
⇒ n ⋅ Fel = m ⋅ g
⇒ Fich = Fel =
m⋅g
„Haltekraft = Gewicht / Anzahl Rollen“
n
Beachte:
1.)
Kraft auf Aufhängung F↓ ,ges =
n +1
⋅ mg = ( n + 1) ⋅ Fel
n
(größer als bei elastischer Aufhängung der Masse)
2.)
Arbeit bei Hub h:
W = Fel ⋅ ∆x Seil = Fel ⋅ ( n ⋅ h ) =
m⋅g
(n ⋅ h) = m ⋅ g ⋅ h ;
n
kein Gewinn
63
4.3
Reibungskräfte
In der Realität sind Reibungskräfte unvermeidlich !
Reibung unterdrückt / bremst Relativbewegungen.
Unterscheide:
A
Festkörperreibung (Coulomb-Reibung)
Haften:
FH Haftkraft
FH,max = µ H ⋅ FN
v
S
Fγ
−FH / G
FN
maximale Haftkraft =
maximale Kraft bis Bewegung
einsetzt
⇒ µ H Haftreibungszahl
(Gleichförmiges) Gleiten:
FG
Gleitkraft bei Bewegung
( ≈ unabhängig von v)
FH / G
Normalkraft FN meist − Fγ = − mg
FG = µG ⋅ FN
⇒ µ G Gleitreibungszahl
i.a.: µ G < µ H !
ähnlich: „Rollreibung“
FH , FG am Körper angreifende Scherkräfte;
FN am Körper angreifende elastische Kraft von der Unterlage
− FN Gewichtskraft des Körpers auf die Unterlage
Versuch: Haften und Gleiten eines Quaders
Beispiel: Rollbewegung, Seite 58 f:
Bedingung, damit Körper tatsächlich rollt, und nicht gleitet: FR < µ H ⋅ FN , also FR / FN < µ H :
m ⋅ g ⋅ sin ( α ) ⋅ 1+f f
tan ( α )
FR
m⋅a ⋅f
=
=
=
< µ . Damit setzt die Rollbewegung nur
FN m ⋅ g ⋅ cos ( α )
m ⋅ g ⋅ cos ( α )
(1 + 1/ f ) H
ein, falls das Gefälle tan ( α ) der Ebene unterhalb eines kritischen Wertes bleibt, nämlich
solange gilt:
tan ( α ) < (1 + 1f ) ⋅µ H
Beispiel: Rollbedingung für µ H = 0, 3
⇒
; andernfalls gleitet der Körper anstatt zu rollen!
Hohlzylinder : tan α < 0,3 ⋅ 2 = 60%
Vollkugel : tan α < 0,3 ⋅ 3,5 = 105%
64
B
Viskose Reibung (Stokessche Reibung)
⇒ Bewegung in einem Medium
FR = − k ⋅ v k = Reibungskoeffizient, hängt von Körper und Medium ab;
i.a. ∼ ’Größe’ (später)
Kräfte- und Drehgleichgewicht
Beispiel: Mensch auf Leiter an glatter Wand
Kräfte:
∑F
∑F
x
= 0 ⇒ Fel = FR
y
= 0 ⇒ FN = ( m1 + m 2 ) ⋅ g
Drehmomente: Wähle Kontaktpunkt Leiter – Boden als Referenzpunkt.
M z,l = + m1 ⋅ g ⋅ρ1 + m 2 ⋅ g ⋅ρ2
„linksdrehend“
M z,r = − Fel ⋅ h
„rechtsdrehend“
Drehgleichgewicht:
M z,l + M z,r = 0 oder M z,l = M z,r ⇒ Fel =
m1 ⋅ρ1 + m 2 ⋅ρ2
⋅g
h
Bedingung, damit Leiter hält:
65
⇔ FR < FR ,max = µ H FN
FR Fel
=
< µH
Schwerpunkt bzgl. Kontaktpunkt
FN FN
m ⋅ρ + m 2 ⋅ρ2 1 Sx
⇔ 1 1
⋅ =
< µH
m1 + m 2
h h
⇔
Beispiel:
Schwerpunktbestimmung durch Pendelaufhängung
⇒ Resultat:
Drehmoment M = Fγ × ρ ≠ 0
ɺ
ɺ ≠0
⇒L = J⋅ω
Rotation, Pendelbewegung
⇒ klingt ab bis M = 0 ⇒ Gleichgewicht erreicht
⇔ ρ Fγ
⇒ Schwerpunkt in vertikaler Ebene durch Drehachse
⇒ Schwerpunktbestimmung durch Schnittpunkt zweier Lote möglich!
Beachte:
1.) Der Schwerpunkt liegt immer in allen Spiegelebenen eines Objektes
Beweis:
Sz =
∫
links
o.b.d.A. Spiegelebene = y-z-Ebene :
x ⋅ D ( x ) dV +
∫
x ⋅ D ( x ) dV
weil D(x ) = D( − x )
=
rechts
∫ ( −x + x ) ⋅ D ( x ) dV = 0
rechts
2.) Die Schwerpunktbildung ist iteriertbar.
Beweis:
o.b.d.A. Spiegelebene = y-z-Ebene :


∫V r ⋅ D ( r ) dV
M1S1 + M 2S2
1
=
⋅  M1 1
+ M2
M1 + M 2
M1 + M 2 

∫V D ( r ) dV

1

∫ r ⋅ D ( r ) dV 
1
=
⋅ ∫ r ⋅ D ( r ) dV = Sges.
 M +M
1
2 V1 ∪ V2
∫V D ( r ) dV 
2

V2
66