Aufgabe B 1 Wahlteil 2016 – Aufgabe B 1

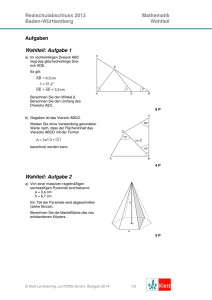
Wahlteil 2016 – Aufgabe B 1
1
2
Aufgabe B 1.1
Abiturprüfung Mathematik 2016
Baden-Württemberg
Allgemeinbildende Gymnasien
Wahlteil
Analytische Geometrie / Stochastik
Aufgabe B 1.1 und B 1.2 - Lösungen
[email protected]
In einem Koordinatensystem beschreiben
die Punkte 15 0 0 , 15 20 0 , und
0 20 6 Eckpunkte der rechteckigen
Nutzfläche einer Tribüne
(alle Koordinatenangaben in Meter).
Die
-Ebene stellt den Erdboden dar.
Die Eckpunkte der Dachfläche liegen
vertikal über den Eckpunkten der
Nutzfläche. Die Dachfläche liegt in der
durch :
− 3 = −27 beschriebenen
Ebene (siehe Abbildung).
1
1 1
www.elearning-freiburg.de
Wahlteil 2016 – Aufgabe B 1
Wahlteil 2016 – Aufgabe B 1
3
4
a) Bestimmen Sie eine Koordinatengleichung der Ebene, in der die
Nutzfläche liegt.
Berechnen Sie den Neigungswinkel der Nutzfläche gegen den Erdboden.
Ermitteln Sie den Inhalt der Nutzfläche.
(4 VP)
b) Aus Sicherheitsgründen muss die senkrecht zum Boden verlaufende
Rückwand zwischen der Nutzfläche und der Dachfläche mindestens
2,5 m hoch sein.
Überprüfen Sie, ob diese Bedingung erfüllt ist.
Zur Installation von Lautsprechern wird eine 5,2 m lange, senkrecht zum
Erdboden verlaufende Stütze montiert. Ihre Enden werden an der Kante
und am Dach der Tribüne fixiert.
Berechnen Sie die Koordinaten des Punktes auf der Kante
, in dem das
untere Ende der Stütze fixiert wird.
(4 VP)
Wahlteil 2016 – Aufgabe B 1
15 0 0
15 20 0
0 20 6
5
0
= −20
0
−15
=
0
6
Wahlteil 2016 – Aufgabe B 1
6
Lösung a)
Mit dem Kreuzprodukt
×
lässt sich aus den beiden Richtungsvektoren
ein Normalenvektor bestimmen:
Koordinatengleichung der Ebene in der die
Tribüne liegt
Mit Hilfe der Punkte , und
die beiden Richtungsvektoren
bestimmen:
0
−20
0
0
−20
0
kann man
und
0
15
15
0 − 20 = −20
0
0
0
0
15
−15
= 20 − 20 =
0
6
0
6
=
Wahlteil 2016 – Aufgabe B 1
−15
0
6
−15
0
6
×
−20 ⋅ 6
= 0 ⋅ −15
0⋅0
−
0⋅0
0⋅6
−20 ⋅ −15
=
−20 ⋅ 6
0
20 ⋅ −15
Da es bei einem Normalenvektor nicht auf die Länge ankommt, teilen wir
2
zunächst durch −20 und anschließend durch 3 und erhalten: = 0 .
5
2
= 0
5
15 0 0
7
:2
+5
Wahlteil 2016 – Aufgabe B 1
8
Mit dem Normalenvektor lässt sich nun eine Koordinatengleichung der Ebene
aufstellen, nämlich : 2 + 5 = mit einem noch unbekannten .
Da wir aber wissen, dass beispielsweise der Punkt in der Ebene liegt,
können wir einsetzen und erhalten 2 ⋅ 15 + 5 ⋅ 0 = 30 = .
Damit haben wir die Ebenengleichung komplett.
Ergebnis: Eine Koordinatengleichung der Ebene in der die Tribüne liegt lautet
: 2 + 5 = 30.
Neigungswinkel von
bezüglich des Erdbodens
Für den Winkel zwischen zwei Ebenen verwendet man die Winkelformel
cos
sind.
=
|!" ⋅!# |
!" ⋅|!# |
wobei
In unserem Fall ist
und
die Normalenvektoren der beiden Ebenen
2
= 0 der Normalenvektor der Ebene .
5
Ein Normalenvektor für die Bodenfläche (die
Es gilt
und
0
= 0 .
1
= 2 + 5 = 29
-Ebene) ist z.B.
⋅
= 2 ⋅ 0 + 0 ⋅ 0 + 5 ⋅ 1 = 5 sowie
= 1.
= 30
Wahlteil 2016 – Aufgabe B 1
= 29
=1
⋅
=5
9
15 0 0
15 20 0
0 20 6
Wahlteil 2016 – Aufgabe B 1
10
Einsetzen in die Winkelformel cos
cos
=
%
&
=
|!" ⋅!# |
!" ⋅|!# |
Inhalt der Nutzfläche
liefert
An den Koordinaten der Punkte , und kann
man erkennen, dass die Tribüne rechtwinklig ist.
Wir haben also lediglich die Fläche eines Rechtecks
zu berechnen.
0
15
15
= 20 − 0 = 20 , d.h.
= 20.
Es gilt
0
0
0
0
15
−15
Weiterhin gilt
= 20 − 20 =
0 ,
6
0
6
≈ 0,92848.
Mit dem GTR (siehe Abbildung rechts) erhält man daraus
den Neigungswinkel ≈ 21,8°.
Ergebnis: Die Tribüne ist um etwa 21,8° gegen den Boden geneigt.
Hinweis: Vergessen Sie nicht, den GTR in den Modus DEGREE umzuschalten!
d.h.
Wahlteil 2016 – Aufgabe B 1
−15
+ 6 = 261.
Wahlteil 2016 – Aufgabe B 1
:
−3
0 20 6
= −27
12
Der Flächeninhalt des Rechtecks ist somit gegeben durch:
= 20 ⋅ 261 ≈ 323,1
Ergebnis: Die Tribüne hat eine Nutzfläche von etwa 323 m².
Lösung b)
+
Werden die Sicherheitsbestimmungen
eingehalten?
Wir formulieren die Frage einfach um:
.
11
= 20
= 261
=
≥ 2,5?
1
1 1
Liegt die Dachfläche mindestens 2,5 m über
dem hinteren Rand der Tribüne?
Der Punkt + der Dachfläche liegt senkrecht über dem Punkt .
Somit hat + dieselbe - und dieselbe -Koordinate wie .
Wir setzen daher die - und die -Koordinate von in die Ebenengleichung
ein und bestimmen daraus die Höhenkoordinate des Punktes + und
damit die des Dachs.
Es folgt 0 − 3
= −27 also
= 9.
Wahlteil 2016 – Aufgabe B 1
:
−3
0 20 6
= −27
13
Wahlteil 2016 – Aufgabe B 1
:
15 20 0
0 20 6
− 3 = −27
14
Der Punkt + hat die Koordinaten + 0 20 9 .
Verankerungspunkt der Stütze
Das Dach liegt drei Meter über der Nutzfläche, d.h. die Rückwand zwischen
der Nutzfläche und des Dachs ist überall 3 m hoch.
Wir konstruieren uns eine zum Dach (genauer gesagt zur Ebene ) parallele
Hilfsebene /, die genau 5,2 m unterhalb des Dachs liegt.
Danach bestimmen wir eine Geradengleichung für die Gerade 0, auf der die
Kante
liegt.
Ergebnis: Die Sicherheitsbestimmung, die eine Mindesthöhe der Rückwand
von 2,5 m verlangt, wird eingehalten.
Stütze
5,2 m
Schließlich bestimmen wir den Schnitt von 0 mit / und erhalten so den
Verankerungspunkt 1.
/
1
:
−3
= −27
Wahlteil 2016 – Aufgabe B 1
15
Wahlteil 2016 – Aufgabe B 1
/:
−3
15 20 0
0 20 6
= −11,4
16
Schritt 1: Konstruktion der Hilfsebene 2
Schritt 2: Aufstellen der Geradengleichung für die Kante 56
Da / parallel zu sein soll, können wir den Normalenvektor von für /
verwenden.
Wir können also /:
− 3 = mit einem noch unbekannten ansetzen.
Die Gerade 0, auf der die Kante
liegt ist gegeben durch
0: 7 = 8 + 9 ⋅
15
−15
Durch Einsetzen erhält man 0: 7 = 20 + 9 ⋅ 0 .
0
6
Nun suchen wir uns einen beliebigen Punkt 3 auf der Ebene , indem wir z.B.
=
= 0 setzen und aus der Ebenengleichung von
bestimmen.
Wir erhalten 0 − 3 = −27 also = 9. Somit ist 3 0 0 9 ein Punkt auf .
Der Punkt 3‘ 0 0 3,8 , der 5,2 m unter 3 liegt muss damit ein Punkt der
Hilfsebene / sein. Wenn wir die Koordinaten von 3‘ in / einsetzen erhalten
wir und damit die komplette Gleichung von /.
Es folgt 0 − 3 ⋅ 3,8 = −11,4 =
und damit /:
−3
= −11,4.
Schritt 3: Schnitt von : mit 2
Ein Punkt auf 0 hat die Koordinaten 15 − 159 20 69 . Diese setzen wir ein
in / und erhalten:
15 − 159 − 189 = −11,4 ⇔ 15 − 339 = −11,4
⇔ −339 = −26,4 ⇔ 9 = 0,8
Wahlteil 2016 – Aufgabe B 1
15
−15
0: 7 = 20 + 9 ⋅ 0
0
6
9 = 0,8
17
Wahlteil 2016 – Aufgabe B 1
18
Schritt 4: Ermittlung der Koordinaten des Verankerungspunktes <
3
15
−15
= 20 .
Einsetzen von 9 = 0,8 in 0 liefert 20 + 0,8 ⋅ 0
4,8
0
6
Aufgabe B 1.2
Bei einem Spiel wird ein idealer Würfel verwendet, dessen Netz in der
Abbildung dargestellt ist.
Ergebnis: Der Verankerungspunkt 1 der Stütze hat die Koordinaten
1(3 20 4,8).
a) Der Würfel wird 2-mal geworfen.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Augensumme der
beiden Würfe 3 beträgt.
Nun wird der Würfel 12-mal geworfen.
Berechnen Sie die Wahrscheinlichkeit dafür, dass er mindestens 4-mal die
Augenzahl 2 zeigt.
Wahlteil 2016 – Aufgabe B 1
Wahlteil 2016 – Aufgabe B 1
19
20
Die Beschriftung des Würfels soll so geändert werden, dass man bei
12-mailgem Werfen des Würfels mit mindestens 99 % Wahrscheinlichkeit
mindestens 4-mal die Augenzahl 3 erhält.
Auf wie vielen Seiten muss dann die Augenzahl 3 mindestens stehen?
(4 VP)
b) Ein Spieler hat die Vermutung, dass der ursprüngliche Würfel zu oft die
Augenzahl 3 zeigt. Die Nullhypothese
/? : „Die Wahrscheinlichkeit für die Augenzahl 3 beträgt höchstens .“
@
soll durch eine Stichprobe mit 100 Würfen auf einem Signifikanzniveau
von 1 % getestet werden.
Formulieren Sie die dazugehörige Entscheidungsregel in Worten.
(3 VP)
Lösung a)
Wahrscheinlichkeit für Augensumme B
Die Wahrscheinlichkeiten bei einem Wurf sind folgende:
3( C0D EFGH 1) = = , 3( C0D EFGH 2) = = und
@
@
3( C0D EFGH 3) = .
@
Bei zweimaligem Würfeln kann die Augensumme 3 nur durch die
Kombination (1,2) oder (2,1) zustande kommen. Da beide Kombinationen
dieselbe Wahrscheinlichkeit haben gilt
1 1 1
3 C0D 9CIID 3 = 2 ⋅ 3 1,2 = 2 ⋅ ⋅ = ≈ 33,3%
2 3 3
Ergebnis: Die Ausgensumme 3 wird mit einer Wahrscheinlichkeit von etwa
33% geworfen.
3( C0D EFGH 2) =
Wahlteil 2016 – Aufgabe B 1
21
1
3
Wahlteil 2016 – Aufgabe B 1
22
Wahrscheinlichkeit für mindestens J-mal Augenzahl K bei LK Würfen
Anzahl der Seitenflächen mit einer B
Bei diese Art von Versuch handelt es sich um ein Bernoulli-Experiment,
genauer gesagt um eine Bernoulli-Kette der Länge 12.
Die „Trefferwahrscheinlichkeit“, also die Wahrscheinlichkeit für Augenzahl 2
ist M = .
Die Anzahl der Würfe werde repräsentiert durch die Zufallsvariable N.
Zu bestimmen ist also 3 N ≥ 4 .
Gemäß den Rechenregeln ist 3 N ≥ 4 = 1 − 3 N ≤ 3 .
Die rechte Seite der Gleichung können Sie mit dem GTR
berechnen, indem Sie 1-binomcdf(12,1/3,3) eingeben
(die Funktion binomcdf erhalten Sie über 2ND distr).
Sie erhalten das folgende
12mal Werfen, mindestens 4mal Augenzahl 3 mit eine WS von min. 99%.
Wir haben eine unbekannte Anzahl F an Seiten mit Augenzahl 3, daher ist
P
die „Trefferwahrscheinlichkeit“ M = .
@
Das formale ausrechnen der gesuchten Wahrscheinlichkeit wäre sehr
kompliziert. Ein einfacherer Weg besteht darin, die verschiedenen Werte für
F auszuprobieren und mit dem GTR nachzurechnen.
Versuch 1 z.B. mit F = 3, also M = = :
@
Wir bestimmen 3 N ≥ 4 = 1 − 3 N ≤ 3 mit dem GTR und erhalten nach
Eingabe von 1-binomcdf(12,1/2,3) den Wert 0,927 < 0,99.
Ergebnis: Die Wahrscheinlichkeit für mindestens 4-mal Augenzahl 2 bei
12 Würfen beträgt 0,6069 also etwa 61%.
Wahlteil 2016 – Aufgabe B 1
23
Wahlteil 2016 – Aufgabe B 1
24
R
@
Versuch 2 mit F = 4, also M = = :
Lösung b)
Eingabe von 1-binomcdf(12,2/3,3) liefert den Wert 0,996 > 0,99.
Entscheidungsregel
Ergebnis:
Die Augenzahl 3 muss auf mindestens 4 Seiten vorliegen, damit man bei
12maligem Würfeln mit einer Mindestwahrscheinlichkeit von 99% eine 3
wirft.
Wir haben folgende Eckdaten:
/? : M ≤ , Stichprobenumfang
@
= 100, Signifikanzniveau = 1 % = 0,01.
Wir haben einen rechtsseitigen Test, denn wenn die Augenzahl 3 öfter als
„erwartet“ erscheint, dann muss /? abgelehnt werden.
Der Ablehnungsbereich hat folglich die Gestalt T, … , 100 .
Unsere Aufgabe besteht also darin, einen konkreten Wert für T zu
bestimmen. Wie üblich bezeichnen wir die Anzahl der Dreien mit der
Zufallsvariablen N.
Gesucht ist also ein kleinstmögliches T, so dass 3 N ≥ T ≤ 0,01 gilt.
Wahlteil 2016 – Aufgabe B 1
Wahlteil 2016 – Aufgabe B 1
25
26
Leider lässt sich 3 N ≥ T nicht direkt mit dem GTR berechnen.
W(X[Z\ )
Daher formen wir um:
3 N ≥ T ≤ 0,01 ⟺ 1 − 3 N ≤ T − 1 ≤ 0,01
Ergebnis:
W(XYZ)
T
Geben Sie im Y-Editor Ihres GTR bei Y1 den Ausdruck
1-binomcdf(100,1/6,X-1) ein und lassen Sie sich mit 2ND Table
die Wertetabelle anzeigen, siehe rechts.
Hier lesen Sie ab 3 N ≥ 26 ≈ 0,011 > 0,01
bzw. 3 N ≥ 27 ≈ 0,006 < 0,01, d.h. für T = 27 liegen wir erstmals unter
dem Signifikanzniveau.
Bei 27 oder mehr Dreien muss die Nullhypothese abgelehnt werden.
Entscheidungsregel => siehe nächste Folie.
Die Entscheidungsregel lautet:
Wenn in einer Stichprobe von 100 Würfen 27 oder mehr Dreien beobachtet
werden, so muss die Nullhypothese bei einer Irrtumswahrscheinlichkeit von
höchstens 0,6% (was kleiner als die Forderung von 1% ist) abgelehnt
werden.
Erscheint die 3 weniger als 27 Mal, so kann die Nullhypothese angenommen
werden.