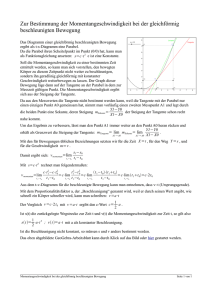
zweiseitig

Analysis 1
Jürgen Pöschel
Erste Rohfassung März 2005
6
Inhaltsverzeichnis
1
2
3
4
5
Einige Grundlagen
1-A Aussagen .
1-B
Mengen . .
1-C
Relationen .
1-D Funktionen
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
5
6
9
13
Die reellen Zahlen
2-A Körperaxiome . . . . . . . .
2-B Ordnungsaxiome . . . . . .
2-C Vollständigkeitsaxiom . . . .
2-D Die erweiterte Zahlengerade
2-E
Intervalle . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
17
18
21
24
29
30
Die natürlichen, ganzen, und rationalen Zahlen
3-A Die natürlichen Zahlen . . . . . . . . . . . . . . . . . . . . . . .
3-B Die ganzen und die rationalen Zahlen . . . . . . . . . . . . . . .
3-C
Abzählbarkeit und Mächtigkeit . . . . . . . . . . . . . . . . . . .
33
33
41
44
Die komplexen Zahlen
4-A Vorüberlegungen . . . . . . . . . .
4-B
Konstruktion der komplexen Zahlen
4-C
Einige elementare Eigenschaften . .
4-D Fundamentalsatz der Algebra . . . .
.
.
.
.
51
52
53
54
57
.
.
.
.
.
.
59
60
66
71
76
77
83
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Folgen
5-A Metrische und normierte Räume
5-B
Häufungspunkt und Grenzwert .
5-C Grenzwertsätze . . . . . . . . .
5-D Einige wichtige Grenzwerte . . .
5-E
Existenzsätze . . . . . . . . . .
5-F
Uneigentliche Konvergenz . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Reihen
6-A Konvergenz . . . .
6-B Konvergenzkriterien
6-C Cauchyprodukte . .
6-D Potenzreihen . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
87
. 87
. 93
. 99
. 101
7
Funktionen
7-A Funktionsgrenzwerte . . . . . . . . . . . . . . . . . . . . . . . .
7-B Grenzwertsätze . . . . . . . . . . . . . . . . . . . . . . . . . . .
7-C Uneigentliche Grenzwerte . . . . . . . . . . . . . . . . . . . . .
107
108
112
115
8
Stetigkeit
8-A Stetige Funktionen . . . . . . . . . . .
8-B Zwischenwertsatz und Umkehrfunktion
8-C Offene und abgeschlossene Mengen . .
8-D Kompaktheit . . . . . . . . . . . . . . .
8-E
Stetigkeit und Kompaktheit . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
117
117
122
126
134
136
Differenziation in einer Variablen
9-A Definitionen und Rechenregeln . . . .
9-B Extrema und Mittelwertsatz . . . . . .
9-C Höhere Ableitungen . . . . . . . . . .
9-D Taylorpolynom und Taylorreihe . . . .
9-E
Summenfunktionen von Potenzreihen
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
143
143
151
155
158
164
10 Spezielle Funktionen
10-A Die Exponentialfunktion . . . . . . . . .
10-B Der Logarithmus und allgemeine Potenzen
10-C Sinus und Cosinus . . . . . . . . . . . . .
10-D Weitere trigonometrische Funktionen . . .
10-E Exp, Sin und Cos im Komplexen . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
167
167
170
173
178
181
11 Ergänzungen
11-A Das Gegenbeispiel von Cauchy
11-B Die Regel von l’Hopital . . . .
11-C Konvexität . . . . . . . . . . .
11-D Ungleichungen . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
187
187
188
193
197
9
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1-B
Mengen
1-B
1
6
Mengen
»Definition« (Cantor 1895) Eine Menge ist eine Zusammenfassung M von bestimmten, wohlunterschiedenen Objekten unserer Anschauung oder unseres Denkens (welche die Elemente von M genannt werden) zu einem Ganzen. Einige Grundlagen
Extensionsprinzip Eine Menge ist eindeutig bestimmt durch die in ihr enthaltenen
Elemente. 1-A
Aussagen
Teilmengen
Prinzipien
Prinzip vom ausgeschlossenen Dritten Eine Aussage ist entweder wahr oder falsch. Prinzip vom ausgeschlossenen Widerspruch Eine Aussage ist nicht gleichzeitig
wahr und falsch. A und B Mengen:
A B , x 2 A ) x 2 B:
Damit
A D B , A B ^ B A:
Leere Menge
Logische Verknüpfungen
A ^ B,
»A und B «
∅ D fg
Disjunktion:
A _ B,
»A oder B «
ist Teilmenge jeder Menge.
Implikation:
A ) B,
»wenn A , so B «
Äquivalenz:
A , B,
»A genau dann, wenn B «
Konjunktion:
Charakterisierung durch Eigenschaften
M D fx W A.x/g
Sätze
oder bezogen auf Grundmenge X :
Distributivgesetz Für Aussagen A; B; C gilt:
M D fx 2 X W A.x/g X;
A ^ .B _ C / , .A ^ B/ _ .A ^ C /;
A _ .B ^ C / , .A _ B/ ^ .A _ C /:
Sätze von de Morgan Für Aussagen A und B gilt:
:.A _ B/ , :A ^ :B;
:.A ^ B/ , :A _ :B:
wobei A.x/ eine Aussageform.
Mengenoperationen
Vereinigung:
Durchschnitt:
Differenz:
A [ B D fx W x 2 A _ x 2 B g
A \ B D fx W x 2 A ^ x 2 B g
A B D fx W x 2 A ^ x … B g
Komplement in A:
CA B D A B ,
falls B A
7
Mengen
1-B
1-B
Mengen
Einschub: Quantoren
Gilt
A \ B D ∅;
Generalisator oder Allquantor
8x 2 X W P .x/»für alle x 2 X gilt P .x/«
so heißen A und B disjunkt. Andernfalls treffen sich die Mengen:
A B , A \ B ¤ ∅:
Partikularisator oder Existenzquantor
9x 2 X W P .x/»für ein x 2 X gilt P .x/«
Sätze
»ein« im Sinne von »wenigstens ein«. Damit
\
˚
A D x W 8 2 I W x 2 A ;
Distributivgesetz Für Mengen A; B; C gilt:
A \ .B [ C / D .A \ B/ [ .A \ C /;
A [ .B \ C / D .A [ B/ \ .A [ C /:
2I
[
˚
A D x W 9 2 I W x 2 A :
2I
Sätze von de Morgan Für Teilmengen A; B einer Menge M gilt:
CM .A [ B/ D CM A \ CM B;
CM .A \ B/ D CM A [ CM B:
Mengenfamilien
Negation:
: 8x 2 X W P .x/ , 9x 2 X W :P .x/
: 9x 2 X W P .x/ , 8x 2 X W :P .x/
Noch ein Symbol:
Sei I eine beliebige Indexmenge.
9!x 2 X W P .x/»für genau ein x 2 X gilt P .x/«
.A /2I
Übung:
heißt Familie oder System von Mengen A .
Durchschnitt
\
˚
A D x W x 2 A für alle 2 I
2I
Vereinigung
[
, 9x 2 X W .P .x/ ^ .8y 2 X W .P .y/ ) y D x//:
Kartesisches Produkt
˚
A D x W x 2 A für ein 2 I
2I
Sätze von de Morgan Für eine Familie .A /2I von Teilmengen einer Menge M
gilt:
[
\
A D
CM A ;
CM
2I
CM
9!x 2 X W P .x/
\
2I
2I
A D
[
2I
CM A :
A B D f.a; b/ W a 2 A ^ b 2 B g
Elemente sind geordnete Paare .a; b/:
.a; b/ D .u; v/ , a D u ^ b D v:
Potenzmenge
Potenzmenge einer Menge M :
P .M / D fA W A M g:
8
9
Relationen
1-C
1-C
Relationen
10
die sogenannte Diagonale in X , die Gleichheitsrelation:
Russelsche Antinomie
a X b , .a; b/ 2 X , a D b:
Das Objekt
R D fM W M … M g
kann keine Menge sein, da weder R 2 R noch R … R wahr sein können.
G
Uns interessieren vor allem Relationen sogenannte Äquivalenzrelationen und Ordnungsrelationen. Dazu zuerst einige Grundbegriffe.
Definition Eine Relation R in A heißt
reflexiv, falls
1-C
Relationen
symmetrisch, falls
transitiv, falls
In unserer Vorstellung stellt eine Relation zwischen zwei Elementen einer Menge A
eine Art »Beziehung« dar. Die Gesamtheit dieser »Beziehungen« ist dann eine Menge von Paaren aus Elementen von A. Um Relationen mathematisch zu betrachten,
sind solche semantischen Konnotationen eher hinderlich. Statt dessen betrachtet man
jede Teilmenge aus A A als Beschreibung einer Relation.
Definition Eine Relation in einer Menge A ist eine Teilmenge von A A . Ist R A A eine solche Teilmenge, so schreibt man
a R b , .a; b/ 2 R:
Das Symbol R verwenden wir, um Assoziationen mit vertrauten Relationen zu vermeiden.
1F
A D f1; 2; 3; 4; 5; 6g,
Eine mögliche Interpretation dieser Relation ist
a T b , 1 < a < b 6 ^ a teilt b:
G
Sei G die Menge aller Geraden in der euklidischen Ebene,
P D f.a; b/ 2 G G W a und b sind parallelg
antisymmetrisch, falls
a R b ^ b R a ) a D b,
jeweils für alle a; b; c 2 A. Äquivalenzrelationen
Äquivalenzrelationen stellen eine Verallgemeinerung der Gleichheitsbeziehung dar.
Definition Eine reflexive, symmetrische und transitive Relation auf A heißt Äquivalenzrelation in A, generisch bezeichnet mit . Ist eine Äquivalenzrelation auf A, so heißt
Œa D fb 2 A W b ag
heißt Restklassenmenge modulo von A.
4 F X und P sind Äquivalenzrelationen, ihre Restklassen sind zum einen alle
Ein-Punkt-Mengen
Œx D fx g X;
Dann ist
a P b , .a; b/ 2 P , a k b:
3F
a R b ) b R a,
a R b ^ b R c ) a R c,
die Äquivalenzklasse oder Restklasse von a , und jedes Element b 2 Œa heißt ein
Repräsentant von Œa . Die Menge
˚
Œa W a 2 A DW A=
T D f.2; 4/; .2; 6/; .3; 6/g A A:
2F
a R a,
G
Ist X eine beliebige, nichtleere Menge, so definiert
X D f.x; x/ W x 2 X g;
zum anderen
Œg D fh 2 G W h k gg
die Scharen paralleler Geraden. G
11
Relationen
1-C
Das Charakteristische an einer Äquivalenzrelation ist, dass sie eine Zerlegung der
Grundmenge in Klassen von Elementen bewirkt, die man bezüglich dieser Relation
identifizieren möchte.
Definition Eine Zerlegung einer Menge A ist eine Familie .A /2I von nichtleeren, disjunkten Teilmengen von A, deren Vereinigung A ist. Es gilt also
(i) A ¤ ∅
für alle 2 I ,
(ii) A \ A D ∅ für alle ¤ in I ,
S
(iii)
2I A D A .
Satz
Ist eine Äquivalenzrelation auf A, so ist A= eine Zerlegung von A . ///// Auf Grund der Reflexivität ist a 2 Œa für alle a 2 A . Somit ist keine
Restklasse leer, und es gilt
[
[
Œa fag D A:
a2A
a2A
1-D
Relationen
Ordnungsrelationen
Definition Eine reflexive, transitive und antisymmetrische Relation auf A heißt
Ordnung oder Ordnungsrelation auf A, generisch bezeichnet mit . Ist eine Ordnung auf A, so heißt das Paar .A; / eine geordnete Menge. Es
muss allerdings nicht zwischen allen Elementen eine Ordnungsrelation bestehen. Ist
dies der Fall, spricht man von einer totalen Ordnung.
Definition Eine geordnete Menge .A; / heißt total geordnet, falls für alle a; b 2
A entweder a b oder b a gilt. 5 F Die Potenzmenge P .X / einer nichtleeren Menge X ist durch die Inklusionsrelation geordnet, welche man auch als natürliche Ordnung bezeichnet. Sie ist
aber nicht total geordnet, falls X mehr als ein Element hat. G
6 F Die rationalen Zahlen sind durch die Kleiner-Gleich-Relation total geordnet. G
Weitere Bezeichnungen sind:
a b W, b a;
Bleibt zu zeigen, dass verschiedene Klassen disjunkt sind. Dies ist äquivalent
mit
a b W, a b ^ a ¤ b;
a b W, b a:
Œa Œb ) Œa D Œb:
Gilt Œa Œb , so gibt es ein c 2 Œa \ Œb . Ist dann d 2 Œa, so gilt also d a ,
c a und c b , also auch
d a;
a c;
c b:
Folglich ist auch d b , also d 2 Œb . Damit ist Œa Œb gezeigt. Aus
Symmetriegründen gilt dann aber auch Œb Œa , und das war zu zeigen. /////
Diese Notation wird allerdings nicht strikt durchgehalten. Die Inklusionsrelation
A B ist üblicherweise gleichbedeutend mit A B , schließt also auch die Gleichheit ein. Soll diese ausgeschlossen werden, schreibt man A B .
Satz Ist .A; / eine total geordnete Menge, so gilt für je zwei Elemente a; b 2 A
genau eine der Aussagen
a b;
Es gilt übrigens auch die Umkehrung des letzten Satzes. Da wir ihn nicht benötigen, überlassen wir den Beweis als Übung.
Satz Jede Zerlegung von A ist die Restklassenmenge genau einer Äquivalenzrelation auf A. Äquivalenzrelationen und Zerlegungen sind also zwei verschiedene Erscheinungsformen ein- und derselben Sache.
12
/////
7F
a D b;
a b:
Das ist klar. /////
Ist .A; / eine total geordnete Menge, so wird auf A A durch
.a; u/ .b; v/ , a < b _ a D b ^ u v
eine totale Ordnung definiert, die sogenannte lexikographische Ordnung. G
13
Funktionen
1-D
1-D
Funktionen
1-D
Funktionen
sind gleich dann und nur dann, wenn
A D U;
Umgangssprachliche Definition Unter einer Funktion oder Abbildung f von einer Menge A nach einer Menge B versteht man eine »Vorschrift«, die jedem Element a 2 A genau ein Element b 2 B »zuordnet«, geschrieben
f W A ! B;
14
a 7! b D f .a/:
B D V;
und f .a/ D g.a/
für alle a 2 A:
Einige Begriffe
Eine Abbildung f W A ! B heißt
Dieses zugeordnete Element b heißt der Funktionswert von f an der Stelle a,
oder auch der Bildpunkt des Urbildes a unter f .
(i) injektiv oder eineindeutig, wenn jedes Bild höchstens ein Urbild besitzt:
Man nennt A den Definitionsbereich und B den Wertebereich von f . Dieser ist
genau zu unterscheiden von der Bildmenge von f
(ii) surjektiv, wenn ihre Bildmenge gleich ihrem Wertebereich ist: zu jedem b 2
B existiert ein a 2 A mit b D f .a/,
f .a/ D f .b/ ) a D b;
a; b 2 A;
(iii) bijektiv, wenn sie injektiv und surjektiv ist.
im.f / WD f .A/
WD fb 2 B W b D f .a/ für ein a 2 Ag B;
also der Menge aller Werte, die f auf A auch tatsächlich annimmt.
Andere Bezeichnungen: Transformation, in unendlich dimensionalen Räumen
Funktional oder Operator, und ganz allgemein Morphismus.
Die Menge
˚
G D .a; b/ 2 A B W b D f .a/ A B
heißt Graph von f . Dieser definiert eine funktionale Relation zwischen A und B ,
also eine Teilmenge G von A B mit
.a; b/ 2 G ^ .a; c/ 2 G
)
Ist f W A ! B bijektiv, so ist ihre Umkehrfunktion oder Umkehrabbildung
f 1 W B ! A;
b 7! a D f 1 .b/
dadurch erklärt, dass a D f 1 .b/ das eindeutige Element in A mit f .a/ D b ist.
Sind f W A ! B und gW B ! C zwei Funktionen, so ist ihre Komposition oder
Hintereinanderausführung erklärt:
g B f W A ! C;
a 7! g.f .a//;
gelesen »g nach f « oder auch »g Kringel f «.
b D c:
Spezielle Funktionen: Tupel, Folgen, Operationen
und
fag B \ G ¤ ∅;
a 2 A:
Das bedeutet nichts anderes, als dass jedem Element von A durch G genau ein
Element aus B zugeordnet ist.
Mengentheoretische Definition Eine Funktion oder Abbildung f W A ! B ist
gegeben durch eine funktionale Relation G zwischen den Mengen A und B . Eine Funktion ist ein Objekt, das aus einem Definitionsbereich, einem Wertebereich, und einer Zuordnungsvorschrift besteht.
Zwei Funktionen
f W A ! B;
gW U ! V
Tupel
Eine Funktion
f W f1; : : : ; ng ! X
ist vollständig beschrieben durch ihre n Funktionswerte
xk D f .k/;
1 k n:
Diese werden kurz in Form eines n-Tupels .x1 ; : : : ; xn / angegeben; xk heißt die
k-te Koordinate des Tupels.
n-Tupel können also aufgefaßt werden als Funktionen auf f1; : : : ng. Dementsprechend gilt:
.x1 ; : : : ; xn / D .y1 ; : : : ; yn / , xk D yk ;
1 k n:
15
Funktionen
1-D
Das n-fache kartesische Produkt einer Menge X ist die Menge aller n-Tupel mit
Koordinaten in X :
X n WD f.x1 ; : : : ; xn / W xk 2 X; 1 k ng
Folgen
Eine Funktion
fW N!X
ist vollständig beschrieben durch ihre Funktionswerte xn D f .n/ für n D 0; 1; ; : : : .
Diese werden in Form einer Folge
.x0 ; x1 ; : : : / D .xn /n0 D .xn /
angegeben.
Folgen können also aufgefaßt werden als Funktionen mit Definitionsbereich N .
Operationen
Eine Funktion
W X X ! X;
die jedem Paar .a; b/ in X X ein Element c in X zuordnet, kann aufgefasst werden als eine binäre Operation oder zweistellige Verknüpfung auf X . Schreibweise:
c D a b WD .a; b/:
Definition Eine binäre Operation auf einer Menge X heißt
(i) kommutativ, falls a b D b a ,
(ii) assoziativ, falls .a b/ c D a .b c/,
für alle a; b; c 2 X . Bemerkung. Ist eine Operation nicht kommutativ, so bedeutet das nicht, dass
a b ¤ b a für alle a und b gilt. Es genügt ein einziges Beispiel dieser Art. 1-D
Funktionen
16
2-A
2-A
2
Die reellen Zahlen
Körperaxiome
18
Körperaxiome
Zunächst einmal bilden die reellen Zahlen einen Körper, also eine Menge, in der
zwei Operationen erklärt sind, die üblicherweise als Addition und Multiplikation
bezeichnet werden.
Definition Eine Menge K mit zwei binären Operationen C und , genannt Addition und Multiplikation, heißt Körper, wenn gilt:
Die reellen Zahlen bilden das Fundament der gesamten Analysis. Es ist daher sinnvoll, sich zunächst Klarheit über dieses Fundament zu verschaffen.
Wir werden dieses Fundament in axiomatischer Weise beschreiben. Wir werden
also angeben, welche grundlegenden Eigenschaften die reellen Zahlen haben sollen,
aus denen wir dann alles Weitere ableiten werden. Wir werden dagegen nicht sagen,
was die reellen Zahlen »eigentlich sind«, oder wie man sie, ausgehend von den natürlichen Zahlen, konstruieren kann. Dies ist langwierig und etwas mühsam, und für
den Anfänger auch nicht sonderlich erhellend.
Die Quintessenz dieses Kapitels ist die folgende Aussage.
(A-1)
Die Addition ist assoziativ und kommutativ.
(A-2)
Es gibt ein Element 0 2 K , genannt neutrales Element der Addition, so
dass
x C 0 D x;
(A-3)
Zu jedem x 2 K existiert ein Element y 2 K , genannt additiv Inverses zu
x , so dass x C y D 0.
(M-1)
Die Multiplikation ist assoziativ und kommutativ.
(M-2)
Es gibt ein Element 1 2 K verschieden von 0, genannt neutrales Element
der Multiplikation, so dass
Satz Die reellen Zahlen bilden einen ordnungsvollständigen, angeordneten Körper, der mit R bezeichnet wird. Dies sind eigentlich drei Aussagen:
x 1 D x;
3. Und er ist in einem gewissen Sinne vollständig.
Darüberhinaus charakterisieren diese Eigenschaften die reellen Zahlen »bis auf Isomorphie« eindeutig.
Was dies alles bedeutet, werden wir in den nächsten Abschnitten erklären.
x 2 K:
(M-3)
Zu jedem x 2 K , x ¤ 0, existiert ein Element y 2 K , genannt multiplikativ Inverses zu x , so dass x y D 1.
(D)
Es gilt das Distributivgesetz:
1. Die reellen Zahlen bilden einen Körper K .
2. Dieser Körper K besitzt außerdem eine Ordnung.
x 2 K:
x .y C z/ D .x y/ C .x z/;
x; y; z 2 K:
Genauer ist ein Körper ein Tripel .K; C; /, bestehend aus einer Menge K mit
zwei Operationen C und mit den oben genannten Eigenschaften. Sind aber diese
Operationen klar, spricht man einfach von dem Körper K .
Um Klammern zu sparen, vereinbart man, dass »Punktoperationen« stärker binden als »Strichoperationen«. Auch schreibt man meistens xy für x y . Das Distributivgesetz lautet dann
x.y C z/ D xy C xz:
Bemerkung. Aus den Axiomen folgt, dass die neutralen und die inversen Elemente eindeutig sind. Dies muss also nicht explizit gefordert werden. ///// Ist 0Q ein weiteres neutrales Element, so ist mit (A-2) sowohl für 0 als
auch für 0Q und (A-1)
19
Körperaxiome
2-A
0Q D 0Q C 0 D 0 C 0Q D 0:
yQ D yQ C .x C y/ D y C .x C y/
Q D y C 0 D y:
Entsprechend argumentiert man für die Multiplikation. /////
Man schreibt x für das eindeutig bestimmte additiv Inverse zu x , und
1
D 1=x D x 1
x
für sein eindeutig bestimmtes multiplikativ Inverses, falls x ¤ 0. Ferner setzt man
x y WD x C .
y/
20
In einem Körper gilt:
(i) .
x/ D x ,
(ii) .x 1 /1 D x;
x ¤ 0,
(iii) 0 x D 0,
(iv) .
1/ x D x ,
(v) x .y z/ D x y x z ,
(vi) x y D 0 ) x D 0 _ y D 0. ///// (i) Aus x C .
x/ D 0 folgt auch, dass x das additive Inverse zu x
ist. Also x D .
x/ auf Grund der vereinbarten Notation.
(ii) Analog zu (i).
(iii) Es ist 0 D 0 C 0, und mit dem Distributivgesetz
0 x D .0 C 0/ x D 0 x C 0 x:
und
x
1
x=y WD WD x D xy 1 ;
y
y
y ¤ 0:
Dann ist .x; y/ 7! x y eine Operation auf K , genannt Subtraktion. Dagegen ist
.x; y/ 7! x=y eine Operation nicht auf K , sondern auf
K D K f0g;
genannt Division, da ja die Division durch 0 nicht erklärt ist.
Mit diesen Vereinbarungen erhalten wir die vertrauten Lösungen der Gleichungen
a C x D b und ax D b .
In einem Körper K besitzt
(i) a C x D b die eindeutige Lösung x D b a,
(ii) ax D b für a ¤ 0 die eindeutige Lösung x D b=a. 1F
Körperaxiome
Satz
Ist nun yQ neben y ein weiteres Inverses zu x , so folgt aus x C y D 0 und
x C yQ D 0 und der Assoziativität und Kommutativität der Addition
Satz
2-A
Der kleinste Körper ist B D f0; 1g , wenn man
1C1D0
setzt und ansonsten wie üblich addiert und multipliziert. G
2 F Die Menge Q der rationalen Zahlen mit der üblichen Addition und Multiplikation bildet einen Körper, desgleichen die Menge C der komplexen Zahlen. G
Es folgen einige elementare Rechenregeln in Körpern, die für die reellen Zahlen
wohlvertraut sind.
Subtraktion von 0 x ergibt 0 D 0 x .
(iv) Mit (iii) ist
0 D 0 x D .1 C .
1// x D 1 x C .
1/ x D x C .
1/ x:
Also ist .
1/ x das additiv Inverse zu x , was die Behauptung ist.
(v) Mit (iv) erhält man
x.y z/ D x.y C .
1/ z/
D xy C .
1/ xz
D xy C .
xz/
D xy xz:
(vi) Sei xy D 0. Ist x D 0, so sind wir fertig. Ist x ¤ 0, so können wir
die Gleichung mit x 1 multiplizieren, und mit (iii) folgt y D 0 . /////
Mit (i) und (iv) folgt übrigens
.
1/ .
1/ D .
1/ D 1:
Wir werden diese Regeln im Folgenden verwenden, ohne explizit auf den Satz zu
verweisen.
Wir haben hiermit – etwas mühsam – Dinge bewiesen, die wir über die reellen
Zahlen »immer schon« wussten. Der Satz gilt aber in jedem beliebigen Körper, also
auch dann, wenn dessen Elemente mit reellen Zahlen keine Ähnlichkeit haben, und
› C‹ und › ‹ etwas völlig anderes bedeuten. Darin liegt die Stärke der axiomatischen
21
Ordnungsaxiome
2-B
2-B
22
negativ, falls x < 0. Methode: Haben wir erst einmal die Körperaxiome verifiziert, so gelten auch sofort
eine Fülle weiterer Sätze.
3F
Ordnungsaxiome
In jedem Körper gelten die Regeln des Bruchrechnens, wie zum Beispiel
Es folgen einige elementare Rechenregeln für angeordnete Körper, die für die
reellen Zahlen ebenfalls wohlvertraut sind.
c
ad C bc
a
C D
;
falls bd ¤ 0:
G
b
d
bd
///// Mit den bisher etablierten Rechenregeln gilt ja
2.1
.ab 1 C cd 1 /bd D ab 1 bd C cd 1 bd D ad C bc:
Somit ist
Satz In einem angeordneten Körper K gilt:
(i) x > y ) x y > 0,
(ii) x > y ^ u > v ) x C u > y C v ,
(iii) a > 0 ^ x > y ) ax > ay ,
(iv) x > 0 ) x < 0,
ab 1 C cd 1 D .ad C bc/.bd/1 :
/////
x < 0 ) x > 0,
(v) x > 0 ^ y < 0 ) xy < 0,
x < 0 ^ y < 0 ) xy > 0,
(vi) a < 0 ^ x > y ) ax < ay ,
(vii) x ¤ 0 ) x 2 > 0. 2-B
Ordnungsaxiome
Insbesondere folgt aus (vii) mit x D 1:
Reelle Zahlen kann man nicht nur addieren und multiplizieren, man kann sie auch
hinsichtlich ihrer Größe vergleichen. Diese Anordnung der reellen Zahlen ist mit den
Rechenoperatioen im folgenden Sinn verträglich.
Definition Ein Körper K heißt angeordnet, wenn es eine totale Ordnung auf K
gibt, für die gilt:
(O-1)
x < y ) x C z < y C z,
(O-2)
0 < x ^ 0 < y ) 0 < x y. Hier definiert man analog zu Abschnitt 1-C
x < y W, x y ^ x ¤ y;
sowie entsprechend x y und x > y . Es gilt dann insbesondere auch hier:
Satz Für je zwei Elemente x und y eines angeordneten Körpers K gilt genau
eine der Relationen
x < y;
x D y;
x > y:
Bezeichnungen Ein Element x 2 K heißt
positiv, falls x > 0,
nichtnegativ, falls x 0,
nichtpositiv, falls x 0,
1 > 0;
was wir a priori nicht wussten.
///// (i) ^ (ii) folgen mit ein- und zweimaliger Anwendung von (O-1).
(iii) Mit (i) ist x y > 0, und mit (O-2) folgt a.x y/ D ax ay > 0,
also auch ax > ay mit (O-1).
(iv) Ist x > 0, so ist jedenfalls x ¤ 0. Wäre x > 0, so folgt mit (ii)
auch x C .
x/ > 0, was Unfug ist. Also ist x < 0. Entsprechend für
x < 0.
(v) Mit (iv) ist y > 0, also mit (O-2) xy D x .
y/ > 0 und somit
xy < 0 wieder mit (iv). Analog der zweite Fall.
(vi) Mit x y > 0 wegen (i) ist dann a.x y/ D ax ay < 0 wegen (v),
also ax < ay mit (O-1).
(vii) Dies folgt mit (ii) für x > 0 und (vi) für x < 0. /////
Wir werden auch diese Regeln im Folgenden verwenden, ohne explizit auf den
Satz zu verweisen.
4 F Der kleinste Körper B D f0; 1g kann nicht angeordnet werden, denn einerseits gilt 1 > 0, aber andererseits 1 C 1 D 0 6> 0. G
5 F Ebensowenig kann der Körper C der komplexen Zahlen angeordnet werden,
denn es ist i ¤ 0, aber sowohl i > 0 wie auch i < 0 führen zu dem Widerspruch
1 D i2 > 0 . G
23
Ordnungsaxiome
2-C
In einem angeordneten Körper ist der absolute Betrag jxj eines Elementes definiert durch
(
x für x 0;
jxj WD
x für x < 0:
2.2
2-C
2-C
2.3
jxj x ,
(ii) jxj D 0 , x D 0,
(iii) jxyj D jxj jyj,
(iv) jx C yj jxj C jyj
/////
(Dreiecksungleichung). Wir beweisen nur die letzte Behauptung. Ist x C y 0, so ist
jx C yj D x C y jxj C jyj
mit (i). Ist aber x C y < 0 , so erhalten wir
jx C yj D .x C y/ D .
x/ C .
y/ jxj C jyj
ebenfalls mit (i). /////
Die Berechtigung der Bezeichnung »Dreiecksungleichung« wird sich erst im
Kontext der komplexen Zahlen erhellen. Sie gilt auch dort, auch wenn C nicht angeordnet ist.
Korollar In einem angeordneten Körper gilt auch die »umgekehrte Dreiecksungleichung«
ˇ
ˇ
jx yj ˇjxj jyjˇ:
///// Aus x D y C .x y/ und y D x C .y x/ folgt mit Hilfe der
Dreiecksungleichung
jxj jyj C jx yj;
jyj jxj C jy xj;
und damit jx yj jxj jyj jx yj. Das ergibt die Behauptung. /////
24
Vollständigkeitsaxiom
Bisher haben wir über die reellen Zahlen nichts gesagt, was nicht auch für die rationalen Zahlen gilt – sowohl Q als auch R sind angeordnete Körper. Die rationalen
Zahlen haben aber den entscheidenden Nachteil, dass es von ihnen »nicht genug
gibt«.
Satz Für die Betragsfunktion j j gilt:
(i) jxj D j
xj 0,
Vollständigkeitsaxiom
Satz Es gibt keine rationale Zahl r mit r 2 D 2. ///// Der klassische Beweis erfolgt indirekt. Angenommen, es gibt solch eine rationale Zahl r D p=q , wobei wir p und q als teilerfremd annehmen
dürfen. Aus
r 2 D p 2 =q 2 D 2 , p 2 D 2q 2
folgt, dass p 2 und deshalb auch p durch 2 teilbar ist. Es ist also p D 2m
mit einer gewissen ganzen Zahl m. Dann aber ist
.2m/2 D 2q 2 , q 2 D 2m2 :
Also ist auch q durch 2 teilbar. Das ist aber ein Widerspruch zu der Annahme,
dass p und q teilerfremd sind. /////
Es besteht somit die Notwendigkeit, die rationalen Zahlen zu vervollständigen,
indem man, salopp gesagt, »deren Löcher ausfüllt«. Dies kann auf mannigfache
und recht unterschiedliche Weise geschehen, beispielsweise mit Hilfe von CauchyFolgen oder Dezimaldarstellungen.
Hier wollen wir jedoch nur das Ergebnis solcher Konstruktionen – also die Vollständigkeit der reellen Zahlen – axiomatisch beschreiben. Auch dies kann auf verschiedenen Wegen geschehen, beispielsweise mit Hilfe von Intervallschachtelungen,
Dedekindschen Schnitten oder der Existenz von Suprema. Wir wählen den letzten
Weg, da die Existenz von Suprema ohnehin ein wiederkehrendes Thema ist.
Supremum und Infimum
Sei K eine total geordnete Menge – die Körperaxiome werden im Folgenden nicht
benötigt. Eine nichtleere Teilmenge A K heißt nach oben beschränkt, wenn es
ein s 2 K gibt mit
x s;
x 2 A:
Man schreibt auch kürzer A s und nennt s eine obere Schranke von A.
25
Vollständigkeitsaxiom
2-C
Analog heißt A nach unten beschränkt, wenn es ein s 2 K mit s A gibt. Ein
solches s heißt untere Schranke von A . Ist A nach oben und unten beschränkt, so
heißt A beschränkt.
Besitzt A eine obere Schranke, so gibt es unter allen oberen Schranken höchstens
eine kleinste obere Schranke, da K total geordnet ist. Es muss aber in K keine solche kleinste Schranke geben, wie wir am Beispiel der rationalen Zahlen noch zeigen
werden. Die Existenz einer kleinsten oberen Schranke ist also nicht selbstverständlich.
2-C
nicht leer. Also gibt es ein c 2 K mit A c B . Dies ist eine obere
Schranke von A, und es ist wegen wegen b B die kleinste aller oberen
Schranken. Also existiert c D sup A.
(ii) , (iii) Dies ergibt sich aus (i) , (ii) /////
Korollar Eine total geordnete Menge ist genau dann ordnungsvollständig, wenn
jede beschränkte Menge ein Supremum und ein Infimum besitzt. A sup A s
für jede obere Schranke s von A .
Der folgende Satz gibt zwei weitere Charakterisierungen der Ordnungsvollständigkeit. Für zwei nichtleere Teilmengen A und B schreibt man analog A B ,
wenn a b für alle a 2 A und b 2 B .
Satz
Wir bemerken noch, dass für zwei nichtleere Teilmengen A B immer gilt:
Jede nichtleere, nach oben beschränkte Teilmenge besitzt eine kleinste obere Schranke. Diese kleinste obere Schranke einer Teilmenge A wird Supremum von A genannt und mit sup A bezeichnet. Es gilt dann
A sup A inf B B:
Damit ist erklärt, was unter einem total geordneten, ordnungsvollständigen Körper zu verstehen ist. Wir zeigen nun, dass dies nicht der Körper der rationalen Zahlen
sein kann.
Satz
Betrachte die beiden Mengen
˚
˚
A D a 2 Q W a > 0; a2 < 2 ; B D b 2 Q W b > 0; b 2 > 2 :
Für a 2 A und b 2 B gilt
(i) K ist ordnungsvollständig.
a
b D
(ii) Zu je zwei nichtleeren Teilmengen A und B mit A B existiert ein Element
c 2 K mit A c B .
Diese größte untere Schranke von A wird Infimum von A genannt und mit inf A
bezeichnet. Es gilt also für jede untere Schranke s von A :
s inf A A:
///// (i) ) (ii) Seien A und B nicht leer mit A B . Mit c WD sup A ist
dann A c . Es ist aber auch c B , denn sonst fände sich in B noch eine
kleinere obere Schranke zu A. Also ist
A c B:
(ii) ) (i)
Ist A nach oben beschränkt, so ist
Der Körper der rationalen Zahlen ist nicht ordnungsvollständig. /////
In einer total geordneten Menge K sind die folgenden Aussagen äquivalent.
(iii) Jede nichtleere, nach unten beschränkte Teilmenge A besitzt eine größte untere Schranke. 26
B WD fb 2 K W A b g
Definition Eine total geordnete Menge heißt ordnungsvollständig, wenn gilt:
(V)
Vollständigkeitsaxiom
a2 b 2
< 0 , a < b;
aCb
somit ist A B . Wäre Q ordnungsvollständig, so gäbe es ein c 2 Q mit
(j)
A c B:
Wir zeigen, dass dann c 2 D 2. — Betrachte dazu
d WD c c2 2
2c C 2
D
2 Q:
cC2
cC2
Es ist d > 0 und
d2 2 D
2c 2 4
D r .c 2 2/;
.c C 2/2
rD
2
> 0:
.c C 2/2
Wäre nun c 2 2 > 0, so wäre 0 < d < c und d 2 2 > 0, also d 2 B , im
Widerspruch zu (j). Wäre aber c 2 2 < 2, so wäre c < d und d 2 2 < 2,
also d 2 A, ebenfalls im Widerspruch zu (j).
27
Vollständigkeitsaxiom
2-C
Also muss c 2 D 2 gelten. Dies ist aber ein Widerspruch zu Satz 2.3, somit
ist Q nicht ordnungsvollständig. /////
Es liegt in der Natur des Supremums und Infimums einer beschränkten Menge,
dass es innerhalb der Menge selbst beliebig gut approximiert werden kann. Diesen
einfachen, aber wichtigen Sachverhalt formulieren wir im folgenden Satz.
Dazu noch eine bequeme Notation. Ist eine Teilmenge A von R nach oben beschränkt, so ist sup A eine reelle Zahl, und wir schreiben
sup A < 1:
Andernfalls ist A nach oben unbeschränkt, wofür wir
2-C
Vollständigkeitsaxiom
Entsprechend heißt s minimales Element oder Minimum von A, falls
sA
^
s 2 A;
geschrieben min A. Dieses ist zugleich das Infimum dieser Menge: min A D inf A.
Beschränkte Mengen müssen jedoch weder ein Maximum noch ein Minimum
besitzen.
6 F Für A D fx 2 R W 0 < x < 1g ist inf A D 0 und sup A D 1. Da diese Punkte aber nicht zu A gehören, besitzt die Menge weder Minimum noch Maximum. G
7F
Für die Menge A D f2n W n 2 Ng ist
1 D 20 D sup A D max A;
sup A D 1
schreiben. Analoges gilt für die Schreibweisen inf A > 1 und inf A D 1 .
Damit ist natürlich in keiner Weise insinuiert, dass 1 oder 1 reelle Zahlen sind.
Der folgende Satz gilt für beschränkte wie unbeschränkte Mengen.
2.4
28
0 D inf A;
aber ein Minimum existiert nicht. G
8 F Jede endliche Teilmenge von R besitzt ein Minimum und ein Maximum. Dies
beweist man mit vollständiger Induktion. G
Annäherungssatz Sei A R nicht leer und x 2 R . Dann gilt:
(i) Ist x < sup A, so existiert ein a 2 A mit x < a.
(ii) Ist inf A < x , so existiert ein a 2 A mit a < x . In Worten: Jede reelle Zahl unterhalb von sup A wird durch ein Element in A
übertroffen, und jede reelle Zahl oberhalb von inf A wird durch ein Element von A
unterboten.
///// Existiert zu x < sup A kein solches a 2 A , so wäre A x . Im
Fall sup A D 1 ist dies ein Widerspruch zur Unbeschränktheit von A , im
anderen Fall zur Eigenschaft von sup A , die kleinste obere Schranke zu sein.
Entsprechend die zweite Behauptung. /////
Schlussbemerkung
Der folgende Satz beschreibt, in welchem Sinne es »bis auf Isomorphie« nur einen
ordnungsvollständigen, angeordneten Körper gibt.
Satz Ist .R0 ; C0 ; 0 ; 0 / neben .R; C; ; / ein weiterer ordnungsvollständiger,
angeordneter Körper, so existiert eine bijektive Abbildung
˚ W R ! R0
mit folgenden Eigenschaften:
(i) ˚.x C y/ D ˚.x/ C0 ˚.y/,
(ii) ˚.x y/ D ˚.x/ 0 ˚.y/,
Maximum und Minimum
Ist eine obere Schranke s einer Menge A zugleich ein Element von A , gilt also
As
^
s 2 A;
so spricht man von einem maximalen Element oder einem Maximum von A , geschrieben max A . In einer total geordneten Menge ist das Maximum eindeutig, und
es ist notwendigerweise zugleich das Supremum:
max A D sup A:
(iii) x y ) ˚.x/ 0 ˚.y/ ,
jeweils für alle x; y 2 R . Man sagt, ˚ respektiert die Operationen und die Anordnung in R und R0 . Zum
Beispiel impliziert dies ˚.0/ D 00 : Es ist
˚.x/ D ˚.x C 0/ D ˚.x/ C0 ˚.0/;
also auch
x 0 D x 0 C0 ˚.0/;
x 0 2 R0 ;
x 2 R;
29
Die erweiterte Zahlengerade
2-D
da ˚ bijektiv ist. Somit ist ˚.0/ das eindeutige neutrale Element 00 der Addition in
R0 .
Damit ist natürlich noch nichts über die Existenz der reellen Zahlen gesagt. Dies
erfordert eine Konstruktion, die, ausgehend von den natürlichen Zahlen N , den »Zahlenturm«
NZQRC
2-E
Intervalle
30
0
0
WD 0;
WD 0:
1
1
Alle diese Operationen sollen auch kommutativ sein. Nicht erklärt sind weiterhin
˙1
;
˙1
0 .˙1/;
0
;
0
˙1
:
0
N auch kein Körper.
Insbesondere ist R
aus ganzen, rationalen, reellen und schließlich komplexen Zahlen aufbaut. Dies werden wir, wie gesagt, hier nicht tun. Vielmehr werden wir im nächsten Kapitel die
natürlichen, ganzen und rationalen Zahlen in R »wiederentdecken«.
2-E
Intervalle
Die wichtigsten Teilmengen der reellen Zahlen sind die sogenannten Intervalle.
2-D
Die erweiterte Zahlengerade
Für das Weitere wollen wir die Verwendung des Symbols 1 noch auf eine feste
Grundlage stellen.
Definition Unter der erweiterten Zahlengerade versteht man die Menge
N WD R [ f
1g [ fC1g
R
x 2 R:
N eine total geordnete Menge. Dabei sind C1
Mit dieser Vereinbarung wird R
und 1 selbst keine reellen Zahlen. Die Bezeichnung C1 wird vor allem im
Kontext der komplexen Zahlen Bedeutung gewinnen, zur Unterscheidung von 1.
Im Kontext der reellen Zahlen schreiben wir im Folgenden kürzer 1.
N ausdehnen läßt, ist dies
Während sich die Ordnungsrelation ohne Mühe auf R
mit den Operationen nicht im vollen Umfang möglich. Doch die folgenden VereinN setzen wir
barungen sind sinnvoll. Für x 2 R
x C 1 WD 1;
x > 1;
x 1 WD 1;
x < 1:
Dagegen ist 1 1 nicht erklärt. Ferner setzen wir
(
(
1;
x>0
1; x > 0
x 1 WD
; x .
1/ WD
;
1; x < 0
1;
x<0
und
Die leere Menge ∅ R ist ein Intervall, denn die Voraussetzung, zwei Punkte
in ihr zu finden, ist schon nicht erfüllt. Ist I ein nichtleeres Intervall, so definieren
wir
a D inf I
zusammen mit der Vereinbarung
1 < x < C1;
Definition Ein Intervall ist eine Teilmenge der reellen Zahlen, die mit je zwei
Punkten auch alle dazwischen liegenden Punkte enthält. b D sup I
als dessen linken respektive rechten Endpunkt. Diese Punkte gehören zur erweiterten
N , und aus dem Annäherungssatz 2.4 und der Definition eines InterZahlengerade R
valles folgt, dass im Falle a < b das offene Intervall
.a; b/ WD fx 2 R W a < x < b g R
auf jeden Fall zu I gehört. Intervalle unterscheiden sich daher nur darin, welcher
ihrer Endpunkte zum Intervall selbst gehört. Tut er es nicht, kann er auch 1 bzw
1 sein.
Definition Ein nichtleeres Intervall I heißt links abgeschlossen, falls es seinen
linken Endpunkt enthält, andernfalls heißt es links offen. Entsprechend sind rechts
abgeschlossen und rechts offen erklärt. Es gibt somit vier Arten von Intervallen: das offene Intervall
.a; b/ D fx 2 R W a < x < b g;
1 a b 1;
mit der Vereinbarung .a; a/ D ∅, das abgeschlossene Intervall
Œa; b D fx 2 R W a x b g;
1 < a b < 1;
31
Intervalle
2-E
wobei Œa; a D fag , und die halboffenen Intervalle
.a; b D fx 2 R W a < x b g;
1 a b < 1;
Œa; b/ D fx 2 R W a x < b g;
1 < a b 1:
Dabei sind a D 1 und b D 1 genau dann zugelassen, wenn das betreffende
Intervallende offen ist. Daher sind alle diese Intervalle in R enthalten.
Bemerkung. Schreiben wir a D 1, so bedeutet das nicht, dass wir 1 als
reelle Zahl betrachten, sondern nur, dass wir für a das Symbol 1 einsetzen. 9F
a.
Jede Ein-Punkt-Menge fag R ist ein abgeschlossenes Intervall.
b.
R D .
1; 1/ ist ein offenes Intervall.
c.
R D R f0g ist kein Intervall. G
Den Annäherungssatz 2.4 können wir nun auch so formulieren: Ist M R nicht
leer, so ist
M \ .a; 1/ ¤ ∅
bzw
M \ .
1; a/ ¤ ∅
für alle a < sup M bzw inf M < a.
Zur Erinnerung: Eine Menge M R heißt beschränkt, wenn es reelle Zahlen
m und s gibt mit m M s .
Satz und Definition Ein nichtleeres Intervall I ist beschränkt genau dann, wenn
seine beiden Endpunkte endlich sind. In diesem Fall heißt
jI j WD sup I inf I:
die Länge des Intervalls I .
10 F Jedes von R verschiedene unbeschränkte Intervall ist von einer der Formen
.a; 1/;
mit a; b 2 R . G
Œa; 1/;
.
1; b/;
.
1; b
2-E
Intervalle
32
3-A
Die natürlichen Zahlen
34
///// Einerseits ist N N nach Voraussetzung. Andererseits ist auch N N wegen der Definition der natürlichen Zahlen. Also ist N D N . /////
3
Die natürlichen, ganzen, und rationalen
Zahlen
Vollständige Induktion
Der vorangehende Satz bildet die Grundlage des Beweisprinzips der vollständigen
Induktion. Die einfachste und am häufigsten gebrauchte Form ist die folgende.
Induktionsprinzip I Sei A.n/ eine Aussageform, für die gilt:
(i) A.0/ ist richtig.
3-A
Die natürlichen Zahlen
(ii) Ist A.n/ richtig, so ist auch A.n C 1/ richtig.
Das ist A.n/ für alle n 2 N richtig. Die natürlichen Zahlen sind von frühester Kindheit durch das Abzählen vertraut:
/////
1 D 1;
N D fn 2 N W A.n/ ist richtigg:
2 D 1 C 1;
3 D 2 C 1 D 1 C 1 C 1;
und so weiter . . . : von einer natürlichen Zahl gelangen wir zur nächsten, indem wir
1 addieren, ad infinitum. Um dieses »und so weiter« mathematisch zu präzisieren,
führen wir folgenden Begriff ein.
Definition Eine Teilmenge M von R heißt induktiv, wenn gilt:
(i) 0 2 M ,
(ii) Ist x 2 M , so ist auch x C 1 2 M . Bemerkung. In manchen Büchern wird statt 0 2 M auch 1 2 M gefordert.
Dies ist allein eine Frage der Praktikabilität und mathematisch unerheblich. 1F
Die Menge fm C n=3 W m; n 2 Ng ist induktiv, ebenso Z, Q und R . G
Der Durchschnitt einer Familie induktiver Mengen ist wieder eine induktive Menge. Die kleinste solche Menge erhält man, indem man über alle induktiven Teilmengen der reellen Zahlen schneidet. Dies charakterisiert die natürlichen Zahlen als Teilmenge der reellen Zahlen.
Definition Die Menge N der natürlichen Zahlen ist der Durchschnitt aller induktiven Teilmengen von R . 3.1
Satz Ist N eine induktive Teilmenge von N , so ist N D N . Sei
Dann ist 0 2 N wegen (i), und aus n 2 N folgt n C 1 2 N wegen (ii). Also
ist N eine induktive Teilmenge von N , somit N D N mit Satz 3.1. /////
Um einen Beweis mit Hilfe der vollständigen Induktion zu führen, ist also Folgendes zu tun.
(A) Induktionsanfang (IA): Zeige, A.0/ ist richtig.
(B) Induktionsschritt (IS):
Induktionsannahme: Nehme an, A.n/ ist richtig.
Induktionsschluss: Folgere daraus, dass auch A.n C 1/ richtig ist.
Dann ist die Aussage A.n/ für alle n 2 N richtig.
Beispiele hierfür werden in großer Zahl folgen, so im Beweis des nächsten Satzes,
in dem wir einige elementare Eigenschaften der natürlichen Zahlen zusammenstellen.
Satz
Für n; m 2 N gilt:
(i) n 0 .
(ii) n C m 2 N sowie nm 2 N .
(iii) Es ist entweder n D 0 oder n 1 2 N .
(iv) Ist n m, so ist n m 2 N .
(v) Ist n < m n C 1, so ist m D n C 1. 35
Die natürlichen Zahlen
3-A
3-A
Die natürlichen Zahlen
Es ist also zum Beispiel min N D 0 wegen (i), und zwischen n und n C 1 liegt
keine weitere natürliche Zahl wegen (v).
///// (i) Betrachte A.n/W n 0. IA: Es ist A.0/ richtig, denn 0 2 N . IS:
Ist nun A.n/ richtig, so ist also n 2 N . Dann ist auch n C 1 2 N , denn N
ist eine induktive Menge. Also ist auch A.n C 1/ richtig. Somit gilt A.n/ für
alle n 2 N .
(ii) Fixiere m 2 N und betrachte die Aussage
A.n/W n C m 2 N:
Ist r C1 < m, so ist dies ebenfalls eine zulässige Darstellung, also nC1 2 N .
Andernfalls ist r C 1 D m, und dann
n C 1 D km C m D .k C 1/m D .k C 1/m C 0:
Auch hier erhalten wir wieder eine zulässige Darstellung, also n C 1 2 N .
Damit ist der Satz mit vollständiger Induktion bewiesen. /////
Zusatz Die Darstellung (1) ist eindeutig. /////
IA: Es gilt A.0/, da ja m 2 N . IS: Gilt A.n/, so ist also n C m 2 N . Dann
ist auch .n C m/ C 1 D .n C 1/ C m 2 N , es gilt also auch A.n C 1/. Somit
gilt A.n/ für alle n 2 N . Da m 2 N beliebig war, ist die Aussage für alle n
und m in N bewiesen.
(iii) Betrachte hierzu
Falls k D kQ , so folgt sofort r D rQ . Andernfalls können wir k > kQ annehmen. Dann ist k kQ 1, und es folgt mit Satz 2.1
Q C r rQ m rQ 1;
.k k/m
IA: A.0/ ist sicher richtig. IS: Es gelte A.n/. Also n D 0 oder n 1 2 N .
Im ersten Fall ist dann .n C 1/ 1 D 0 2 N . Im zweiten Fall gilt ebenso
.n C 1/ 1 D .n 1/ C 1 2 N . Also ist auch A.n C 1/ richtig, und die
Aussage ist bewiesen.
(iv) und (v) übergehen wir. /////
Als ein weiteres Beispiel für die vollständige Induktion erwähnen wir die Grundlage des euklidischen Algorithmus, auch als Division mit Rest bekannt. Setze
ein Widerspruch. /////
Wir bemerken noch, dass die Induktion nicht immer bei 0 beginnen muss.
Induktionsprinzip II Sei A.n/ eine Aussageform, für die gilt:
(i) A.n0 / ist richtig für ein n0 2 N .
(ii) Ist A.n/ richtig für irgendein n n0 , so ist auch A.n C 1/ richtig.
Dann ist A.n/ für alle natürlichen Zahlen n n0 richtig. N D N f0g:
(1)
///// Setze N D fn 2 N W A.n C n0 / ist richtigg und argumentiere wie beim
Induktionsprinzip I. /////
Zu jedem n 2 N und m 2 N existieren ein k 2 N und ein r 2 N mit
n D km C r;
/////
r < m:
Fixiere m 1 , und betrachte
N D fn 2 N W n besitzt die Darstellung (1)g:
Dann ist 0 2 N , denn 0 D 0 m C 0 ist wegen 0 < m eine zulässige
Darstellung.
Sei nun n 2 N , also n D km C r für ein k 2 N ein und r 2 N mit
0 r < m. Dann ist
n C 1 D km C r C 1:
Sind n D km C r und n D kQ C rQ zwei solche Darstellungen, so ist
Q C r rQ D 0:
.k k/m
A.n/W n D 0 _ n 1 2 N:
Satz
36
2F
Man zeigt durch Induktion, dass 2n > n2 für alle n 2 N mit n 5. G
Satz vom Minimum
3.2
Satz vom Minimum Jede nichtleere Teilmenge der natürlichen Zahlen besitzt ein Minimum. ///// Sei M N nicht leer. Da die natürlichen Zahlen nach unten beschränkt sind, existiert s D inf M in R . Zu zeigen ist, dass s 2 M . Falls
nicht, so ist s < n für alle n 2 M , und nach Satz 2.4 existiert ein n 2 M
mit n < s C 1. Nach demselben Satz existiert dann sogar ein m 2 M mit
37
Die natürlichen Zahlen
3-A
s < m < n < s C 1 . Dann aber ist 0 < n m < 1 , was für eine natürliche
Zahl unmöglich ist. /////
Bemerkung. Aus diesem Satz folgt, dass es keine uninteressanten natürlichen
Zahlen gibt. 3-A
Auf dem Prinzip der vollständigen Induktion beruht auch das Prinzip der rekursiven
Definition einer Folge, also einer Funktion auf N . Zunächst einige Beispiele.
3F
m D pq;
p; q > 1:
Insbesondere ist dann p < m und q < m, somit besitzen p und q endliche
Primfaktorzerlegungen, und damit auch m – /////
Die Fakultät n! einer natürlichen Zahl n ist rekursiv definiert durch
0! WD 1;
n! WD n .n 1/!;
n 1:
Der Wert von n! wird also für n 1 durch Rückgriff auf den Wert der Funktion bei
n 1 erklärt. Nach endlich vielen Schritte ist n! auf 0! zurückgeführt. Man erhält
1! D 1 0! D 1;
2! D 2 1! D 2 1;
Bemerkung. Diese Zerlegung ist auch eindeutig bis auf die Reihenfolge der
Primfaktoren, siehe [AE, S. 40]. ///// Falls nicht, so existiert eine kleinste Zahl m 2, die sich nicht in
endlich viele Primfaktoren zerlegen lässt. Dann kann m selbst keine Primzahl
sein, denn diese wäre ja ihre eigene Primfaktorzerlegung. Also ist m eine
zusammengesetzte Zahl:
38
Rekursion
///// Angenommen, die Menge U D fn 2 N W n ist uninteressantg ist nicht
leer. Dann existiert m D min U , die kleinste uninteressante natürliche Zahl.
Das ist natürlich eine sehr interessante Zahl – /////
Satz und Anwendungsbeispiel Jede natürliche Zahl n 2 besitzt eine Zerlegung
in endlich viele Primfaktoren. Die natürlichen Zahlen
3! D 3 2! D 3 2 1;
:::
n! D n .n 1/ : : : 2 1:
G
Die Fakultät spielt eine wichtige Rolle bei vielen kombinatorischen Problemen
oder der binomischen Formel. Der Beweis des folgenden Satzes sei als Übung überlassen.
Satz Es gibt genau n! verschiedene Bijektionen der Menge f1; : : : ; ng auf sich
selbst. Anschaulich: Es gibt n! verschiedene Anordnungen, oder Permutationen, von n
verschiedenen Objekten.
4F
Die Fibonacchi-Folge
.fn /n0 D .0; 1; 1; 2; 3; 5; 8; 13; 21; : : : /
ist rekursiv erklärt durch
f0 D 0;
f1 D 1;
fn D fn1 C fn2 ;
n 2:
n
G
5 F In einem beliebigen Körper K sind die Potenzen a eines Elementes a erklärt durch
a0 WD 1;
an WD a an1 ;
n 1:
Mit Induktion beweist man die üblichen Potenzgesetze:
an am D anCm ;
.an /m D anm :
G
39
Die natürlichen Zahlen
3-A
3-A
Sei X eine beliebige Menge mit Operation C, die wir als Addition betrachten.
Sind a0 ; : : : ; an 2 X , so schreibt man deren Summe als
a0 C a1 C C an D
n
X
nC1
X
ak :
ak WD a0 ;
kD0
n1
X
ak C an ;
a0 a1 : : : an D
n 1:
n
Y
ak :
(ii)
(iii)
kD0
a0 C a1 C C an D
n
X
ak
kD0
kD0
lD0
kD1
kD0
bk :
kD0
ak kD0
a :
m
X
bl D
lD0
X
ak bl : 0kn
0lm
lD0
kD0
D
D0
n
X
D
lD0
ak kD0
Ebenso kann er über andere Intervalle der natürlichen Zahlen laufen:
(
q
X
X
0
für q < p;
ak WD
ak WD
a
C
C
a
für
q p:
p
q
kDp
pkq
Ditto für Produkte. n
X
.2k 1/ D n2 . G
6F
abk D a
n
X
///// Wir zeigen nur (iii) mit Induktion über n. Für n D 0 ist die Aussage
gleichbedeutend mit (ii). Ist die Gleichung richtig für ein n 0 und alle
m 0, so folgt
X
X
nC1
m
n
m
X
X
ak bl D
ak C anC1 bl
Bemerkung. Der »Laufindex« kann durch ein beliebiges anderes Zeichen ersetzt werden:
n
X
kD0
n
X
kD0
In der letzten Gleichung erstreckt sich die Doppelsumme über alle möglichen
Kombinationen der Indizes k und l mit den Vorgaben 0 k n und 0 l m.
Sie umfasst somit .n C 1/.m C 1/ Summanden. Wegen Satz 3.3 kommt es auf ihre
Reihenfolge nicht an, sie muss daher auch nicht näher spezifiziert werden.
unabhängig von der Reihenfolge der Summanden. Entsprechendes gilt für Produkte. al D
kD0
n
X
kD0
3.3
Satz Ist C eine assoziative und kommutative Operation auf X , so ist die
Summe
n
X
kD1
In einem Körper gilt:
n
n
n
X
X
X
ak C
bk D
.ak C bk /.
(i)
kD0
ak D
.2k 1/ C .2n C 1/ D n2 C 2n C 1 D .n C 1/2 ;
Satz
Entsprechend verfährt man mit Produkten:
n
X
n
X
was zu zeigen war. /////
kD0
ak WD
.2k 1/ D
kD1
Deren rekursive Definition ist
n
X
40
///// Für n D 0 ist die Gleichung richtig, wie auch für n D 1. Gilt sie für
irgendein n 0, so folgt damit
kD0
0
X
Die natürlichen Zahlen
X
0kn
0lm
m
X
bl C anC1
lD0
ak bl C
X
kDnC1
0lm
m
X
bl
lD0
a k bl D
X
ak bl :
/////
0knC1
0lm
Wir formulieren noch einen allgemeinen Satz, der die bisherigen Beispiele für
rekursive Definitionen auf eine feste mathematische Grundlage stellt. Für den Beweis
verweisen wir auf [AE, S. 43].
Satz
Sei X eine beliebige Menge, und für jedes n 2 N sei eine Abbildung
41
Die ganzen und die rationalen Zahlen
3-B
n W X n ! X
3-B
42
Definition
˚
Q WD m=n W m 2 Z ^ n 2 N
gegeben. Dann existiert zu jedem a 2 X eine Abbildung f W N ! X mit
(i) f .0/ D a ,
(ii) f .n/ D n .f .0/; : : : ; f .n 1//;
Die ganzen und die rationalen Zahlen
n 1. Das bedeutet: Mit dem Startwert a0 WD f .0/ D a sind sukzessive
a1 WD f .1/ D 1 .a0 /;
a2 WD f .2/ D 2 .a0 ; a1 /;
::
:
an WD f .n/ D n .a0 ; : : : ; an1 /
eindeutig erklärt. Die Abbildung n definiert den Folgenwert an als Funktion der
ersten n Folgenwerte a0 ; : : : ; an1 .
heißt Menge der rationalen Zahlen. Satz
Die Menge Q der rationalen Zahlen bildet einen angeordneten Körper. Wir übergehen den einfachen Beweis. Insbesondere ist also die Gleichung ax D
b mit a ¤ 0 in Q immer eindeutig lösbar, und zwar mit x D b=a.
Die Darstellung einer rationalen Zahl als Quotient ganzer Zahlen ist nicht eindeutig, vielmehr gilt
p=q D m=n , np D mq:
Die Anordnung der rationalen Zahlen lässt sich auf die Anordnung der ganzen Zahlen zurückführen:
p=q < r=s , ps < qr:
3-B
Die ganzen und die rationalen Zahlen
Die Gleichung n C x D m ist in N genau dann lösbar, wenn n m. Um sie auch
für n > m lösen zu können, müssen wir Zahlen n mit n 2 N einbeziehen.
Definition
Z D fn W n 2 N _ n 2 Ng D f: : : ; 2; 1; 0; 1; 2; : : :g
heißt Menge der ganzen Zahlen. Satz In der Menge Z der ganzen Zahlen gelten alle Axiome eines angeordneten
Körpers mit Ausnahme der Existenz eines multiplikativen Inversen. Man sagt, die ganzen Zahlen bilden einen Ring mit Eins. Insbesondere ist die
Gleichung n C x D m in Z immer eindeutig lösbar, und zwar mit x D m n .
Satz 3.2 vom Minimum gilt in Z in folgender Form. Der Beweis geht genauso.
Satz Jede nach unten beschränkte Menge ganzer Zahlen besitzt ein Minumum. Die Gleichung nx D m ist in Z genau dann lösbar, wenn m ein Vielfaches von
n ist. Um diese Einschränkung fallen lassen zu können, müssen wir alle Zahlen der
Form m=n betrachten.
Man überlegt sich, dass dies nicht von der Darstellung der rationalen Zahlen abhängt.
Das Prinzip des Archimedes
Jeder angeordnete Körper enthält mit 0 und 1 »automatisch« auch ein Abbild der
natürlichen Zahlen als monoton steigende Folge
0 < 1 < 2 D 1 C 1 < 3 D 2 C 1 < ::: :
Wir »wissen«, dass innerhalb der reellen Zahlen diese Folge jede vorgelegte Schranke übertrifft. Das gilt aber nicht in jedem angeordneten Körper, für ein Beispiel siehe
[Behrends I, S. 52]. Somit lässt sich diese Eigenschaft nicht aus den Axiomen eines
angeordneten Körpers ableiten!
Definition Ein angeordneter Körper K heißt archimedisch geordnet, wenn es zu
jedem x 2 K ein n 2 N gibt mit x < n . Weil diese Eigenschaft für die reellen Zahlen so selbstverständlich erscheint, wird
sie oft als Archimedisches Axiom postuliert. Wir erhalten diese Eigenschaft als Konsequenz der Vollständigkeit der reellen Zahlen.
Prinzip des Archimedes Die Menge der ganzen Zahlen ist in den reellen Zahlen
nach oben unbeschränkt. 43
Die ganzen und die rationalen Zahlen
3-B
3-C
///// Falls doch, so existiert s D sup Z in R . Da s 1 < s , existiert nach
dem Annäherungssatz 2.4 ein n 2 Z mit
a < m=n < bn;
und die rationale Zahl r D m=n hat die gewünschte Eigenschaft. /////
Wir bemerken noch, dass nach dem Prinzip von Archimedes zu jeder reellen Zahl
x genau eine ganze Zahl n existiert mit
Korollar 1 Zu jeder positiven reellen Zahl h und jeder reellen Zahl x existiert
genau eine ganze Zahl n mit .n 1/h x < nh. /////
Die Menge
44
Dann aber gibt es eine ganze Zahl m mit an < m < bn. Somit ist
s 1 < n s:
Aber dann ist s < n C 1 2 Z, also s doch keine obere Schranke von Z –
/////
Abzählbarkeit und Mächtigkeit
n x < n C 1;
die größte ganze Zahl kleiner oder gleich x . Diese wird üblicherweise mit Œx bezeichnet, gelesen Gaußklammer von x . Es ist also
fm 2 Z W x= h < mg Z
ΠW R ! Z;
x 7! Œx D max fn 2 Z W n x g:
ist wegen des vorangehenden Satzes nicht leer und nach unten beschränkt.
Somit besitzt sie ein minimales Element n, für das gilt:
n 1 x= h < n:
Wegen h > 0 ist dies äquivalent zur Behauptung. Die Eindeutigkeit von n
folgt aus der Eindeutigkeit des Infimums einer Menge. /////
Korollar 2
(i) Zu jeder reellen Zahl " > 0 existiert ein n 2 N mit
0 < 1=n < ":
(ii) Ist a 2 R und 0 a 1=n für alle n 2 N , so ist a D 0 . ///// (i) Nach dem Prinzip des Archimedes existiert eine ganze Zahl n mit
1 < n". Da hierbei n > 0 gelten muss, folgt die Behauptung.
(ii) a > 0 wäre ein Widerspruch zu (i). /////
Satz Zu zwei beliebigen reellen Zahlen a < b existiert immer eine rationale Zahl
r mit a < r < b . /////
mit
Es ist b a > 0. Somit existiert nach dem letzten Korollar ein n 2 N
0 < 1=n < b a;
oder
0 < an C 1 < bn:
3-C
Abzählbarkeit und Mächtigkeit
Wir wollen unter anderem die folgenden Fragen ansprechen:
Gibt es mehr rationale Zahlen als natürliche Zahlen?
Gibt es mehr reelle Zahlen als rationale Zahlen?
Gibt es Mengen, die »noch größer« sind als die Menge der reellen Zahlen?
Dazu definieren wir zuerst, wann wir zwei Mengen als »gleich groß« ansehen wollen.
Definition Zwei Mengen X und Y heißen gleichmächtig, symbolisch X Y ,
wenn es zwischen ihnen eine Bijektion gibt. Dies entspricht der intuitiven Vorstellung. Können wir die Elemente zweier Mengen paarweise zuordnen, ohne dass am Ende ein Element übrig bleibt, so betrachten
wir diese Mengen als gleich groß. Dazu müssen wir die Mengen nicht einmal abzählen.
Innerhalb einer beliebigen Menge von Mengen definiert eine Äquivalenzrelation, deren Klassen aus gleichmächtigen Mengen bestehen.
7F
Die Mengen fH, i, l, f, eg und f; ; ; ; g sind gleichmächtig. G
8 F Die Mengen N und 2N D f2n W n 2 Ng sind gleichmächtig, ebenso die Mengen N und Z. G
/////
Es ist N ! 2N , n 7! 2n eine Bijektion, ebenso
45
Abzählbarkeit und Mächtigkeit
(
N ! Z;
n 7!
n=2;
3-C
Diese nummeriert Z als Folge 0; 1; 1; 2; 2; 3; 3; : : : durch. /////
Für führen »Referenzmengen« für endliche Mengen ein. Es sei A0 D ∅ und
n 1:
Die Aussage M A0 soll gleichbedeutend sein mit M D ∅. Diese Mengen
sind tatsächlich nicht gleichmächtig und auch von N verschieden, wie die beiden
folgenden Sätze zeigen.
Satz
Abzählbarkeit und Mächtigkeit
m0 ; m1 ; m2 ; : : : ;
n gerade;
.n C 1/=2; n ungerade:
An D An1 [ fng D f1; : : : ; ng;
3-C
An1 Am1 :
Nach n 1 solchen Schritten gelangen wir zu A1 AmnC1 . Das ist aber
offensichtlich nur möglich, wenn m D n. /////
Satz Es ist An N für alle n 2 N . /////
Der Beweis ist ähnlich zum vorangehenden Beweis. /////
mn D .n/;
hinzuschreiben, so dass M D fmn W n 0g. Obendrein tritt jedes Folgenglied genau einmal auf.
Definition Die Anzahl oder Kardinalität einer Menge ist
(
n; falls M An ;
jM j WD
1 sonst:
Andere gebräuchliche Bezeichnungen sind
jM j D # M D card M D Anz.M /:
Es gilt An Am genau dann, wenn n D m. ///// Ist n D m , so sind die beiden Mengen gleich, also erst recht gleichmächtig. Sei also umgekehrt An Am , wobei wir noch 1 n m annehmen können. Dann existiert zwischen beiden Mengen eine Bijektion, die wir
noch so einrichten können, dass n 7! m. Deren Einschränkung auf An1 ist
dann auch eine Bijektion zwischen An1 und Am1 , es ist also
Die so definierte Anzahlfunktion macht keinen Unterschied zwischen »abzählbar
unendlich« und »überabzählbar«.
Abzählbare Mengen
Zunächst einige Beobachtungen zu abzählbaren Mengen. Dass Teilmengen abzählbarer Mengen wieder abzählbar sind, ist eigentlich nicht überraschend, trotzdem aber
beweisbedürftig. Zuerst betrachten wir die Menge N selbst.
Satz
Jede Teilmenge von N ist entweder endlich oder abzählbar unendlich. ///// Man zeigt durch Induktion über die obere Schranke, dass eine beschränkte Teilmenge A von N endlich ist. Ist also A nicht endlich, so ist A insbesondere unbeschränkt, und wir können eine Abbildung
W N ! A
Definition Eine Menge M heißt
(i) endlich, falls M An für ein n 2 N ,
(ii) abzählbar unendlich, falls M N ,
(iii) überabzählbar in allen anderen Fällen.
Sie heißt abzählbar, wenn sie endlich oder abzählbar unendlich ist. Bemerkung. Wegen des vorangehenden Satzes ist eine Menge nicht gleichzeitig
endlich und abzählbar unendlich. Die Definition ist also sinnvoll. Eine Bijektion W N ! M zwischen N und einer abzählbar unendlichen Menge
M können wir als »Durchnummerierung« aller Elemente von M auffassen. Sie
erlaubt es, alle Elemente in Form einer Folge
46
induktiv definieren durch
.0/ WD min A;
.m C 1/ WD min fn 2 A W n > .m/g:
Aus dieser Definition folgt
.m/ < .m C 1/;
m 0;
und damit wiederum durch Induktion
.m/ < .n/;
m < n:
Die Funktion ist somit streng monoton steigend und damit injektiv.
47
Abzählbarkeit und Mächtigkeit
3-C
3-C
Bleibt zu zeigen, dass surjektiv auf A ist. Zu beliebigen n0 2 A sollte
m0 WD min fm W .m/ n0 g
der richtige Kandidat sein. In der Tat ist einerseits
3.5
Korollar Das kartesische Produkt zweier, und allgemeiner endlich vieler
abzählbarer Mengen ist abzählbar. ///// Wir betrachten nur den Fall zweier abzählbar unendlicher Mengen. Es
sei also A N und B N . Dann aber ist A B N N , und die
Behauptung folgt aus dem vorangehenden Satz.
Das kartesische Produkt von mehr als zwei, aber endlich vielen abzählbaren
Mengen behandelt man mit Induktion über die Anzahl der Faktoren. /////
(für m0 D 0 entfällt die linke Ungleichung), alles andere widerspräche der
Definition von m0 . Andererseits ist aber auf Grund der strengen Monotonie
.m0 / D min fn 2 A W n > .m0 1/g n0 :
Da jede abzählbare Menge bijektiv auf N oder eine der Mengen An abgebildet
werden kann, folgt unmittelbar aus diesem Satz das entsprechende Result für beliebige abzählbare Mengen.
3.4
Bemerkung. Das kartesische Produkt abzählbar vieler abzählbarer Mengen ist
dagegen nicht mehr abzählbar. Satz
Korollar Jede Teilmenge einer abzählbaren Menge ist abzählbar. Die Menge Q der rationalen Zahlen ist abzählbar. ///// Jede rationale Zahl r 2 Q besitzt eine eindeutige teilerfremde Darstellung
Abzählbarkeit »vererbt« sich also auf Teilmengen – was nicht weiter überrascht.
Interessanter ist da schon die Frage, ob auch »abzählbar abzählbar = abzählbar«
gilt. Das ist in der Tat richtig.
rD
m
;
n
.m; n/ 2 Z N :
Dies definiert eine Bijektion zwischen Q und einer Teilmenge von Z N .
Letztere ist abzählbar wegen Korollar 3.5, also ist auch Q abzählbar wegen
Korollar 3.4. /////
Satz Die Menge N N ist abzählbar. ///// Wir führen den Beweis mit Hilfe einer Zeichnung. Dazu ordnen wir die
Elemente von N N in einem unendlichen Matrixschema an:
.0; 0/ .0; 1/ .0; 2/ .0; 3/
.1; 0/ .1; 1/ .1; 2/ .1; 3/
.2; 0/ .2; 1/ .2; 2/ .2; 3/
.3; 0/ .3; 1/ .3; 2/ .3; 3/
:
::
::
::
:
::
:
:
48
Dies liefert sicher eine Bijektion N ! N N . /////
.m0 1/ < n0 .m0 /
Also ist .m0 / D n0 . /////
Abzählbarkeit und Mächtigkeit
Überabzählbare Mengen
::
:
Wir wollen zunächst die Frage klären, ob es überhaupt überabzählbare Mengen gibt.
Der nächste Satz gibt eine positive Antwort.
Wir nummerieren das Schema durch, indem wir sukzessive die Diagonalen
durchnummerieren, deren Elemente .n; m/ die gleiche »Quersumme« n C m
haben. Die ersten Glieder dieser Folge sind
Also gibt es erst recht keine Bijektion, es gilt X P .X / für jede beliebige
Menge.
Insbesondere ist P .N/ überabzählbar, und jede der Mengen
.0; 0/;
Für keine Menge X gibt es eine Surjektion von X auf P .X /. N;
.1; 0/; .0; 1/;
P .N/;
P .P .N//;
P .P .P .N///;
:::
ist mächtiger als die vorangehenden.
.2; 0/; .1; 1/; .0; 2/;
.3; 0/; .2; 1/; .1; 2/; .0; 3/;
Satz
::: :
///// Für X D ∅ ist P .X / D f∅g . Da die Bildmenge einer auf der leeren
Menge definierten Abbildung ebenfalls leer ist, ist die Behauptung in diesem
49
Abzählbarkeit und Mächtigkeit
3-C
Fall richtig.
Sei also jetzt X ¤ ∅, und
und somit
A D fx 2 X W x … .x/g 2 P .X /:
Angenommen, es git ein 2 X mit ./ D A . Wäre 2 A , so bedeutete
dies … ./ D A. Wäre aber … A, so implizierte dies 2 ./ D A .
Das klappt also hinten und vorne nicht, und so gibt es kein 2 X mit ./ D
A. /////
Uns interessieren aber jetzt konkret die reellen Zahlen.
Die Menge R der reellen Zahlen ist überabzählbar. Angenommen, R ist abzählbar, es gibt also eine Nummerierung
x0 ; x1 ; x2 ; : : :
aller reellen Zahlen. Wir konstruieren dann eine weitere reelle Zahl , die
nicht dazu gehört.
Diese reelle Zahl konstruieren wir als Durchschnitt einer fallenden Folge von
Intervallen
In D Œan ; bn ;
50
a0 a1 an < bn b1 b0 ;
eine beliebige Abbildung. Um zu zeigen, dass nicht surjektiv ist, betrachten
wir die Teilmenge
/////
Abzählbarkeit und Mächtigkeit
Für die Randpunkte der so definierten Intervalle gilt dann
W X ! P .X /
Satz
3-C
n 0:
Das heißt,
I0 I1 I2 : : : ;
\
In D f g:
n0
Eine solche Folge wird als Intervallschachtelung bezeichnet.
Wir definieren diese Folge rekursiv. Als I0 wählen wir ein beliebiges Intervall
der Länge b0 a0 D 1 mit
I0 WD Œa0 ; b0 6 3 x0 :
Ist nun In1 für n 1 bereits konstruiert, so wählen wir In als linkes oder
rechtes Drittel von In1 so, dass auf jeden Fall
In WD Œan ; bn 6 3 xn :
Das ist sicher möglich. Außerdem ist automatisch In1 In .
A D fan W n 0g < B D fbn W n 0g:
Wegen der Ordnungsvollständigkeit von R existiert also eine reelle Zahl mit
A B:
Dann aber ist 2 In D Œan ; bn 6 3 xn für alle n 0 und deshalb sicherlich
¤ xn für alle n 0. /////
4-A
Vorüberlegungen
4-A
52
Vorüberlegungen
Angenommen, es gibt einen Erweiterungskörper K R und ein Element – oder
auch eine »Zahl« – i 2 K mit
4
Die komplexen Zahlen
i2 D 1:
Dann ist jedenfalls i … R . Ferner gehören auch alle Ausdrücke – oder »Zahlen« –
der Form
Wir haben bisher den »Zahlenturm«
NZQR
beschrieben. Von unten betrachtet, werden die ganzen Zahlen als Erweiterung der
natürlichen Zahlen eingeführt, oder »erfunden«, um uneingeschränkt die Gleichung
mCx Dn
innerhalb dieses Zahlensystems lösen zu können – und zwar mit x D n m. Die
rationalen Zahlen werden eingeführt, um uneingeschränkt die Gleichung
ax D b;
a ¤ 0;
innerhalb dieses Zahlensystems lösen zu können – und zwar mit x D b=a. Die rationalen Zahlen wurden schließlich zu dem angeordneten Körper der reellen Zahlen
vervollständigt, um unter anderem die quadratische Gleichung
x 2 D a;
a 0;
uneingeschränkt lösen zu können.
Mehr ist allerdings auch nicht zu erwarten! Denn in jedem angeordneten Körper
gilt ja x 2 0 . Mit anderen Worten, eine Gleichung wie x 2 D a < 0 ist in einem
angeordneten Körper unerfüllbar.
Trotzdem bleibt das Bedürfnis – und der Bedarf –, auch eine Gleichung wie
2
x D 1
zu lösen. Dies führt zur Erweiterung der reellen Zahlen zu den komplexen Zahlen,
und damit zu einer weiteren Stufe unserer Turmes
N Z Q R C:
Dieser Erweiterungskörper C kann dann natürlich nicht mehr angeordnet sein.
z WD x C iy;
x; y 2 R;
zu K . Dabei nennt man
Re z WD x;
Im z WD y
den Realteil respektive Imaginärteil von z .
Behauptung Real- und Imaginärteil von z D x C iy sind eindeutig bestimmt. Ist x C iy D u C iv , so folgt
/////
x u D i.v y/:
Ist v ¤ y , so können wir diese Gleichung weiter umformen zu
iD
x
u
:
v
y
Letztere ist aber eine reelle Zahl – ein Widerspruch. Also ist v D y , und dann
auch x D u . /////
Wir setzen jetzt
˚
C WD x C iy 2 K W x; y 2 R K:
Behauptung
C mit den von K ererbten Operationen ist ein Körper. Für z D x C iy und w D u C iv sind diese Operationen
z C w D .x C u/ C i.y C v/;
z w D .xw yv/ C i.xv C yw/;
denn z w D xw C ixv C iyw C i2 yv und i2 D 1.
///// Beweis der Behauptung Zum Beispiel sind 0Ci0 und 1Ci0 die Null
und die Eins in C . Ferner ist
53
Konstruktion der komplexen Zahlen
4-B
1
1
x iy
x iy
;
D
D
D 2
z
x C iy
.x C iy/.x iy/
x C y2
also
1
y
x
i 2
:
D 2
z
x C y2
x C y2
4-C
Einige elementare Eigenschaften
Bemerkung. Ganz ähnlich verfährt man bei der Konstruktion der ganzen Zahlen aus den natürlichen Zahlen, und der rationalen Zahlen aus den ganzen Zahlen.
Statt »Zahlen« betrachtet man in jedem Fall »Zahlenpaare« und definiert für diese
Operationen, die die gewünschten Operationen nachbilden. Dieser Körper ist eine Erweiterung von R in folgendem Sinn: Die Abbildung
W R ! K;
Dies ist ein wohldefiniertes Element in C für x 2 C y 2 ¤ 0 , also für z ¤ 0.
Auf diese Weise zeigt man: Sind z; w 2 C , dann auch
z C w; z; z w; z
1
2 C;
x 7! .x/ D .x; 0/
ist injektiv und »bettet« R in K »operationsverträglich« ein. Das heißt, es gilt
.x C y/ D .x/ C0 .y/;
Letzteres für z ¤ 0 . Die übrigen Körperaxiome sind leicht verifiziert. /////
Damit erkennen wir: Gibt es überhaupt einen Erweiterungskörper K von R mit
der gewünschten Eigenschaft, so enthält dieser immer den Körper C . Diesen Körper
nennt man den Körper der komplexen Zahlen und bezeichnet ihn mit C . – Bleibt nur
noch, diesen Körper explizit zu kontruieren.
54
.x y/ D .x/ 0 .y/:
Wir können deshalb R mit
.R/ D f.x; 0/ 2 K W x 2 Rg K
identifizieren und so in K wiederfinden.
Setzen wir jetzt noch
4-B
.1; 0/ DW 1;
Konstruktion der komplexen Zahlen
Wir konstruieren jetzt ein Modell der komplexen Zahlen. Denn alles bisher Gesagte
beruhte ja auf der Annahme der Existenz der komplexen Zahlen. Doch daraus folgt
ja keineswegs deren Existenz.
Setze K D f.x; y/ W x; y 2 Rg D R R und definiere
und schreiben im Folgenden wieder C und statt C0 und 0 , so wird
.x; y/ D .x; 0/ C .0; y/
Dx 1Cy i
DW x C iy
.x; y/ C0 .u; v/ WD .x C u; y C v/;
.x; y/ 0 .u; v/ WD .xu yv; xv C yu/:
Dann rechnet man unter anderem nach:
C0 und 0 sind assoziativ und kommutativ.
.0; 1/ DW i;
Dz
eine komplexe Zahl in vertrauter Schreibweise.
Mit anderen Worten: 1 D .1; 0/ und i D .0; 1/ sind Basisvektoren des zweidimensionalen reellen Vektorraumes K , und z D x C iy ist eine kompakte Schreibweise für deren Linearkombination mit Skalaren x und y .
Es gilt das Distributivgesetz.
.0; 0/ ist die »Null« bzgl C0 und .1; 0/ die »Eins« bzgl 0 .
Die inversen Elemente sind .x; y/ D .
x; y/ und
x
y
;
;
.x; y/ ¤ .0; 0/:
.x; y/1 D
x2 C y2 x2 C y2
Das Ergebnis lautet deshalb:
Satz
0
0
.K; C ; / ist ein Körper. 4-C
Einige elementare Eigenschaften
Von nun an schreiben wir wieder
C D fx C iy W x; y 2 Rg:
h Geometrische Veranschaulichungi
55
Einige elementare Eigenschaften
4-C
4-C
Die komplexe Konjugation
Für jedes z 2 C ist
z zN D x 2 C y 2 0
.x C iy/ D x iy;
die z auf die zu ihr komplex konjugierte Zahl .z/ DW zN abbildet. Geometrisch
handelt es sich um die Spiegelung der komplexen Ebene an der x-Achse. Es gilt
zN D ..z// D z;
eine nichtnegative reelle Zahl, und man definiert
q
p
jzjC WD z zN D x 2 C y 2
als den absoluten Betrag der komplexen Zahl z D x C iy . Es gilt
oder funktional ausgedrückt:
jzjC D jzjR ;
2 D B D idC :
denn
Solche Abbildungen heißen Involutionen. Sie sind zum Beispiel immer umkehrbar,
und es gilt 1 D .
Satz
Für komplexe Zahlen gilt:
(i) Re z D 12 .z C zN / ,
Im z D
1
.z
2i
zN /.
z 2 R;
p
x 2 D jxj;
z D x C i0:
Wir müssen daher nicht zwischen dem Betrag einer reellen und dem Betrag einer
komplexen Zahl unterscheiden und schreiben in Zukunft einfach j j.
Satz Für komplexe Zahlen gilt:
(i) jzj 0,
(iii) z1 C z2 D zN1 C zN2 .
(ii) jzj D 0 , z D 0,
(iv) z1 z2 D zN1 zN2 . (iii) jRe zj jzj;
Die letzten beiden Identitäten besagen, dass ein Automorphismus von C ist –
eine bijektive Abbildung also, die die Körperoperationen »respektiert«:
.z C w/ D .z/ C .w/;
jzjC D
4.1
(ii) z 2 R , zN D z .
/////
56
Der Betrag einer komplexen Zahl
Als komplexe Konjugation bezeichnet man die Abbildung
W C ! C;
Einige elementare Eigenschaften
.zw/ D .z/.w/:
Zum Beispiel ist
1
1
.z zN / D ..x C iy/ .x iy// D y D Im z;
2i
2i
und damit
z 2 R , Im z D 0 , z zN D 0 , z D zN :
Die übrigen Aussagen sind ebenso leicht zu beweisen. /////
jIm zj jzj,
(iv) jzwj D jzjjwj,
(v) jz C wj jzj C jwj
/////
(Dreiecksungleichung). (i)–(iii) sind klar. (iv) folgt aus
S D z zN w wN D jzj2 jwj2 :
jzwj2 D zw zw
Die Dreiecksungleichung (v) ergibt sich dann aus
N
jz C wj2 D .z C w/.Nz C w/
D z zN C z wN C w zN C zN wN
D jzj2 C 2 Re.z w/
N C jwj2 ;
und wegen jRe z wj
N jzjjwj
N D jzjjwj weiter
2
jz C wj2 jzj2 C 2jzjjwj C jwj2 D jzj C jwj :
Das ergibt die Behauptung. /////
57
Fundamentalsatz der Algebra
4-D
In der komplexen Ebene ist es nicht sinnvoll, Intervalle zu betrachten. Deren Rolle
übernehmen hier die Kreisscheiben.
Für a 2 C und r > 0 heißt
Dr .a/ WD fz 2 C W jz aj < r g
die offene Kreisscheibe um a vom Radius r , und
DN r .a/ WD fz 2 C W jz aj r g
die abgeschlossene Kreisscheibe um a vom Radius r . Insbesondere heißen
N WD DN 1 .0/
D
die offene und abgeschlossene Einheitskreisscheibe.
1F
Für a 2 R und r > 0 ist
Dr .a/ \ R D .a r; a C r /;
DN r .a/ \ R D Œa r; a C r ;
und D \ R D .
1; 1/. G
4-D
Fundamentalsatz der Algebra
Unser Ausgangspunkt war, eine Lösung für die Gleichung
x2 C 1 D 0
zu konstruieren. Tatsächlich haben wir damit viel mehr konstruiert:
Fundamentalsatz der Algebra Jede Gleichung
z n C an1 z n1 C C a1 z C a0 D 0
mit komplexen Koeffizienten a0 ; a1 ; : : : ; an1 und n 1 besitzt wenigstens eine
Lösung 2 C . /////
Fundamentalsatz der Algebra
58
besitzt keine Nullstelle in C . Dann ist
Kreisscheiben
D WD D1 .0/;
4-D
Angenommen, das Polynom
p.z/ D z n C an1 z n1 C C a1 z C a0
q.z/ D
1
p.z/
eine auf ganz C erklärte, analytische Funktion. Für diese Funktion gilt:
sup jq.z/j ! 0 für R ! 1:
jzjDR
Dann ist aber nach dem Satz von Liouville q das Nullpolynom – /////
Dieser Beweis ist an dieser Stelle natürlich unverständlich. Er soll nur illustrieren,
wie leicht sich wichtige Sätze herleiten lassen, wenn man nur über das richtige Werkzeug verfügt. Der Satz von Liouville wird üblicherweise in den ersten Wochen einer
Vorlesung über Funktionentheorie bewiesen, die sich, anders als der Name vermuten
läßt, ganz speziell mit differenzierbaren Funktionen von komplexen Zahlen befaßt.
5-A
Metrische und normierte Räume
60
Um zu untersuchen, ob die Glieder einer Folge in X sich einem bestimmten
Punkt nähern, ist es zweckmäßig, einen Begriff des Abstandes zwischen den Punkten
des Raumes X zu haben. Für Zahlenfolgen ist dies natürlicherweise der Betrag der
Differenz zweier Zahlen,
5
Folgen
»Abstand von x und y« D jx yj:
Es stellt sich aber heraus, dass für eine sinnvolle Abstandsmessung nur drei Eigenschaften erforderlich sind, und man für viele Belange von der konkreten Beschaffenheit des Abstandes absehen kann. Dies führt zum Begriff des metrischen Raumes.
Eine Folge in einer beliebigen, nichtleeren Menge X ist eine Aufzählung von Elementen dieser Menge. Formal ist eine solche Folge eine Funktion
xW N ! X;
die man am einfachsten durch Aufzählung ihrer Funktionswerte angibt, zum Beispiel
in der Form
.x1 ; x2 ; x3 ; : : : / D .xn /n2N D .xn /n1 D .xn /:
Dabei heißt
xn WD x.n/
das n-te Glied der Folge x .
Man spricht von Zahlenfolgen, genauer von reellen bzw komplexen Zahlenfolgen, wenn alle Folgenglieder reelle respektive komplexe Zahlen sind. Ferner spricht
von vektorwertigen Folgen, falls X D Rm . Diese werden vorläufig unsere wichtigsten Beispiele sein. Aber natürlich gibt es auch Folgen von Mengen, Funktionen,
Räumen . . . .
Die ersten Glieder einer Folge sind eigentlich uninteressant. Denn an einer Folge
interessiert ihr asymptotisches Verhalten, also die Frage, wie sie sich verhält, wenn n
gegen 1 strebt. Gibt es zum Beispiel einen Punkt in X , den man als den Grenzwert
der Folge bezeichnen könnte?
1F
Die reelle Zahlenfolge
.1=n2 /n1 D .1; 1=4; 1=9; : : : ; 1=n2 ; : : : /
scheint gegen 0 zu streben, denn die Folgenglieder sind positiv, werden aber immer
kleiner. Die reelle Folge
..
1/n /n1 D .
1; 1; 1; 1; 1; : : : /
dagegen hat sicher keinen Grenzwert, da sie ständig zwischen 1 und 1 ›oszilliert‹. G
5-A
Metrische und normierte Räume
Metrische Räume
Ein metrischer Raum ist eine Menge, in der mit Hilfe einer Metrik zwischen je zwei
Punkten in sinnvoller Weise ein Abstand erklärt ist.
Definition Eine Metrik oder Abstandsfunktion auf einer nichtleeren Menge X ist
eine Abbildung
d W X X ! R;
für die gilt:
(M-1) d.x; y/ 0,
und
(M-2) d.x; y/ D d.y; x/
d.x; y/ D 0 , x D y
(Definitheit),
(Symmetrie),
(M-3) d.x; z/ d.x; y/ C d.y; z/
(Dreiecksungleichung),
jeweils für alle x; y; z 2 X . Das Paar .X; d/ nennt man einen metrischen Raum. Wie in vielen ähnlichen
Fällen auch, spricht man einfach nur von dem metrischen Raum X , wenn die Metrik
aus dem Zusammenhang klar ist.
Bemerkung. Die Begriffe Raum und Punkt sind eigentlich nur Synonyme für
Menge und Element. Doch spricht man vor allem dann von einem Raum, wenn er
noch mit einer Struktur versehen ist:
Vektorraum ! lineare Struktur,
metrischer Raum ! Metrik,
normierter Raum ! Norm,
topologischer Raum ! Topologie
61
Metrische und normierte Räume
5-A
und viele andere . . . 2F
d.x; y/ WD jx yj
d.z; w/ WD jz wj D
Metrische und normierte Räume
p
.z w/.Nz w/:
N
5.1
Trennungssatz Zu je zwei verschiedenen Punkten a und b eines metrischen Raumes gibt es ein " > 0 derart, dass B" .a/ und B" .b/ disjunkt sind. Beide werden als natürliche Metriken bezeichnet. Die Dreiecksungleichungen haben
wir in Satz 2.2 und 4.1 nachgewiesen. G
3 F Eine Teilmenge Y eines metrischen Raumes .X; d/ wird in natürlicher Weise wiederum zu einem metrischer Raum, wenn man ihn mit der eingeschränkten
Metrik d jY Y versieht.
So ist jede Teilmenge von R oder C , wie zum Beispiel ein Intervall oder Q, mit
der eingeschränkten natürlichen Metrik ebenfalls ein metrischer Raum. G
4 F Sind .X1 ; d1 / und .X2 ; d2 / zwei metrische Räume, so wird deren kartesisches Produkt X D X1 X2 mittels der Produktmetrik
d.x; y/ D max fd.x1 ; y1 /; d.x2 ; y2 /g;
ebenfalls zu einem metrischen Raum .X; d/. G
/////
Ist a ¤ b , so ist " D d.a; b/=2 > 0. Gäbe es nun einen Punkt
c 2 B" .a/ \ B" .b/;
so wäre auf Grund der Dreiecksungleichung
d.a; b/ d.a; c/ C d.c; b/ < " C " D d.a; b/;
was offensichtlich Unfug ist. Also sind B" .a/ und B" .b/ disjunkt. /////
Mit Hilfe von Kugeln ist auch der Begriff der Beschränktheit erklärt.
Definition Eine Teilmenge eines metrischen Raumes X heißt beschränkt, wenn
sie in einer abgeschlossenen Kugel enthalten ist. Eine Folge in X heißt beschränkt,
wenn die Menge ihrer Folgenglieder beschränkt ist. Satz Eine Teilmenge M eines metrischen Raumes X ist beschränkt genau dann,
wenn es zu jedem Punkt a 2 X ein r 0 gibt, so dass M BN r .a/. Kugeln
Für a 2 X und r > 0 nennt man die Menge
///// ) Nach Definition ist M Bs .b/ für ein b 2 X und ein s 0.
Für jedes beliebige a 2 X gilt dann
Br .a/ WD fx 2 X W d.x; a/ < r g
M BN r .a/;
die offene Kugel vom Radius r um a , oder kurz die offene r -Kugel um a, und
BN r .a/ WD fx 2 E W d.x; a/ r g
r D s C d.a; b/;
denn auf Grund der Dreiecksungleichung gilt für jedes m 2 M
die abgeschlossene Kugel vom Radius r um a, oder kurz abgeschlossene r -Kugel
um a.
5F
62
Man darf allerdings nicht erwarten, dass diese Kugeln immer wie Kugeln aussehen – siehe Abbildung ??.
Wesentlich für uns ist, dass es um je zwei verschiedene Punkte eines metrischen
Raumes immer offene Kugeln gibt, die sich nicht treffen. Man sagt, man kann je
zwei verschiedene Punkte durch offene Kugeln trennen.
Auf R ist
eine Metrik, ebenso auf C
5-A
d.m; a/ d.m; b/ C d.a; b/ s C d.a; b/ D r:
(
Klar. /////
In R mit der natürlichen Metrik ist
Br .a/ D .a r; a C r /;
BN r .a/ D Œa r; a C r ;
in C mit der natürlichen Metrik ist
Br .a/ D Dr .a/ D fz 2 C W jz aj < r g:
G
Normierte Räume
Eine bedeutsame Klassen metrischer Räume bilden die normierten Räume. Dies sind
Vektorräume, die mit einer Norm versehen sind. Für uns von Bedeutung sind KVektorräume, wobei K für R oder C steht.
63
Metrische und normierte Räume
5-A
Definition Eine Norm auf einem K-Vektorraum E ist eine Abbildung
5-A
Metrische und normierte Räume
schen Norm ist gegeben durch
k kW E ! R;
jxj2 D hx;xi D
für die gilt:
(N-1) kxk 0,
n
X
jxi j2 ;
x 2 Rn :
iD1
und
(N-2) kxk D jjkxk
kxk D 0 , x D 0
(Definitheit),
Cauchy-Schwarz-Bunjakowski-Ungleichung Für x; y 2 Rn gilt
(positive Homogenität),
(N-3) kx C yk kxk C kyk
jhx;yij jxj jyj:
(Dreiecksungleichung),
für alle x; y 2 E und alle 2 K. /////
t D
0 hx;xi 2
x D .x1 ; : : : ; xn /;
h ; iW Rn Rn ! R;
hx;yi WD
hx;yi2
hx;yi2
hx;yi2
C
D hx;xi ;
hy;yi
hy;yi
hy;yi
also hx;yi2 hx;xihy;yi. Wurzelziehen ergibt die Behauptung. /////
5.2
Dreiecksungleichung Für die euklidische Norm auf dem Rn gilt
ja C bj jaj C jbj:
/////
Um die Dreiecksungleichung für die euklidische Norm zu verifizieren, führen wir
das Standard-Skalarprodukt auf dem Rn ein:
n
X
hx;yi
hy;yi
wählen. Einsetzen in die vorangehende Ungleichung ergibt dann
n
eine Norm, die euklidische Norm des R . Da diese für n D 1 und n D 2 mit
der reellen respektive komplexen Betragsnorm übereinstimmt, wenn wir C mit R2
identifizieren, wird diese auch natürliche Norm genannt.
Definitheit und positive Homogenität sind für die euklidische Norm sofort zu
verifizieren. Nicht so offensichtlich ist die Dreiecksungleichung, sie wird in Satz 5.2
nachgewiesen. G
Für alle reellen Zahlen t gilt
Da die behauptete Ungleichung sicher für y D 0 gilt, können wir y ¤ 0
annehmen, und dann
6 F Auf R wie auf C definiert der Betrag j j eine Norm, die sogenannte Betragsnorm. G
Auf Rn definiert
q
jxj WD jx1 j2 C C jxn j2 ;
0 hx C ty;x C tyi D hx;xi C 2thx;yi C t 2 hy;yi:
Das Paar .E; k k/ nennt man einen normierten Vektorraum oder kurz einen normierten Raum. Auch hier spricht man einfach von dem normierten Raum E , wenn
klar ist, welche Norm gemeint ist. Diese wird auch gern mit j j statt k k bezeichnet
– das spart zwei Striche . . .
7F
64
Es ist
ja C bj2 D ha C b;a C bi
D jaj2 C 2ha;bi C jbj2
jaj2 C 2jajjbj C jbj2 D .jaj C jbj/2 ;
xi yi :
iD1
wobei wir im vorletzten Schritt die Cauchy-Schwarz-Ungleichung verwendeten. Wurzelziehen ergibt die Behauptung. /////
Die wesentlichen Eigenschaften dieses Skalarproduktes sind
(S-1) hx;xi 0
(S-2) hx;yi D hy;xi
(Positivität),
8F
(Symmetrie),
(S-3) hx C y;zi D hx;zi C hy;zi
(Linearität),
für alle x; y; z 2 Rn und alle ; 2 R .
Wegen der Symmetrie ist das Skalarprodukt auch linear im zweiten Argument.
Man spricht daher von einer bilinearen Form. Der Zusammenhang mit der euklidi-
Weitere Normen auf dem Rn sind die zum Beispiel die Summennorm:
kxk1 D jx1 j C C jxn j;
und die Supremumsnorm:
˚
kxk1 D max jx1 j; : : : ; jxn j :
65
Metrische und normierte Räume
5-B
Die Beziehung zwischen diesen verschiedenen Normen auf dem Rn werden wir bald
untersuchen. G
Satz
Ein normierter Raum .E; k k/ wird durch die induzierte Metrik
d W E E ! RC ;
d.x; y/ D kx yk
/////
In einem normierten Raum ist der Abstand zwischen zwei Punkten x und y also
eine Funktion der Differenz x y . Er ändert sich nicht, wenn beide Punkte um
denselben Vektor verschoben werden, er ist somit translationsinvariant.
In einem normierten Raum E sind die r -Kugeln die Mengen
Br .a/ D fx 2 E W kx ak < r g;
BN r .a/ D fx 2 E W kx ak r g:
Die Beschränkheit einer Folge lässt sich wie folgt charakterisieren.
Satz Folgende Aussagen über eine Folge in einem normierten Raum E sind äquivalent.
(i) Die Folge .xn / ist beschränkt.
(ii) Es gibt ein r 0, so dass kxn k r für alle n.
(iii) Es ist sup fkxn k W n 1g < 1. Häufungspunkt und Grenzwert
unendlich ist; sie gilt für fast alle n , falls
kx yk C ky zk
D d.x; y/ C d.y; z/:
66
Wir betrachten nun Folgen in einem metrischen Raum .X; d/. Dazu vereinbaren wir
folgende Redeweise. Eine Aussage A gilt für unendlich viele natürliche Zahlen n –
bzw Glieder einer Folge – , falls
Wir verifizieren nur die Dreiecksungleichung:
d.x; z/ D kx zk
/////
5-B
Häufungspunkt und Grenzwert
fn 2 N W A.n/g
zu einem metrischen Raum .E; d /. /////
5-B
fn 2 N W :A.n/g
endlich ist. Anders gesagt: Ist die Menge fn 2 N W A.n/g unbeschränkt, so gilt die
Aussage A für unendlich viele n . Ist das Komplement dieser Menge sogar endlich,
so gilt A für fast alle n . Es ist klar, dass
»fast alle« ) »unendlich viele«
gilt, aber nicht die Umkehrung.
9 F »Fast alle natürlichen Zahlen sind gerade« ist eine falsche Aussage, denn »unendlich viele natürliche Zahlen sind ungerade« ist eine wahre Aussage. G
Wir brauchen noch den Begriff der Umgebung, der in formaler Weise ausdrückt,
dass wir uns in der Nähe eines Punktes befinden. Hier definieren wir ihn mit Hilfe von "-Kugeln, in der Topologie wird dieser Begriff noch wesentlich allgemeiner
gefasst.
Definition Eine Teilmenge U eines metrischen Raumes X heißt Umgebung des
Punktes a 2 X , falls sie eine offene "-Kugel um a enthält. Die Kugeln B" .a/ selbst
heißen "-Umgebungen des Punktes a. 10 F Jede abgeschlossene r -Kugel um a ist eine Umgebung von a. G
Leichte Übung. /////
Häufungspunkte
Definition Ein Punkt a 2 X heißt Häufungspunkt der Folge .xn / in X , falls in
jeder Umgebung von a unendlich viele Folgenglieder liegen. Aus dieser Definition ergibt sich sofort die folgende Charakterisierung von Häufungspunkten.
Satz
Die folgenden Aussagen sind äquivalent.
(i) a ist Häufungspunkt der Folge .xn / .
67
Häufungspunkt und Grenzwert
5-B
(ii) Zu jeder Umgebung U von a und jedem N 1 existiert ein n N mit
xn 2 U .
5-B
11 F
a. Die konstante Folge .x; x; x; : : : / besitzt genau einen Häufungspunkt,
nämlich x selbst.
b. Die reelle Zahlenfolge ..
1/n /n0 besitzt genau zwei Häufungspunkte,
nämlich 1 und 1 .
c. Die komplexe Zahlenfolge .in /n0 besitzt genau vier Häufungspunkte,
nämlich 1; i; 1; i.
d. Ist x D .xn / eine beliebige Abzählung von Q, also xW N ! Q eine
Bijektion, so ist die Menge der Häufungspunkte dieser Folge gerade R . G
lim xn D a ,
n!1
lim xn D a
n!1
oder
.n ! 1/;
oder auch kurz lim xn D a und xn ! a. Man sagt auch, .xn / konvergiert gegen a
(für n gegen unendlich).
Satz
In einem metrischen Raum .X; d / sind folgende Aussagen äquivalent.
(i) Die Folge .xn / konvergiert gegen a.
(ii) Zu jeder Umgebung U von a existiert ein N 1 so, dass xn 2 U für alle
nN.
(iii) Zu jedem " > 0 existiert ein N 1, so dass xn 2 B" .a/ für alle n N .
(iv) Die reelle Zahlenfolge .d.xn ; a// konvergiert in R gegen 0 . Für reelle Zahlenfolgen erhalten wir mit (iii) die klassische Charakterisierung des
8 jxn aj < ":
///// (i) , (ii) Liegen in jeder Umgebung U von a fast alle Folgenglieder, so muss es ein N geben, so dass xn 2 U für alle n N . Und
umgekehrt.
(ii) , (iii) Gilt (ii), so gilt dies insbesondere für jede "-Umgebung von a.
Umgekehrt enthält jede Umgebung U von a auch eine "-Umgebung B" .a/
von a. Gilt also (iii) für "-Umgebungen, dann auch für beliebige Umgebungen.
(iii) , (iv) Es ist
xn 2 B";X .a/ , d.xn ; a/ < " , d.xn ; a/ 2 B";R .0/;
wobei der zweite Index den Raum angibt, in dem die "-Kugel sich befindet.
Da bereits die Äquivalenz von (iii) mit (i) gezeigt ist, ist daher xn ! a in X
gleichbedeutend mit d.xn ; a/ ! 0 in R . /////
Da wir Folgen vorwiegend in normierten Räumen betrachten werden, formulieren wir diesen Satz noch einmal für diese Räume.
Satz
xn ! a
9
Bemerkung. In der Formulierung (iii) hängt die Schranke N natürlich von "
ab. Daher schreibt man auch gerne N ."/. Grenzwerte
Schreibweisen hierfür sind
8
">0 N 1 nN
Konvergierende Zahlenfolgen mit Grenzwert 0 werden auch Nullfolgen genannt.
///// Wir beweisen nur die letzte Aussage. Angenommen, die reelle Zahl a
ist kein Häufungspunkt der Abzählungsfolge. Dann existiert ein " > 0, so
dass in .a "; a C "/ kein Glied der Folge liegt. Das widerspricht aber der
Tatsache, dass in jedem offenen Intervall rationale Zahlen liegen. /////
Definition Eine Folge .xn / in einem metrischen Raum X heißt konvergent mit
Grenzwert a, falls jede Umgebung von a fast alle Folgenglieder enthält. 68
Grenzwertes:
(iii) Zu jedem " > 0 und jedem N 1 existiert ein n N mit xn 2 B" .a/. Wir übergehen den Beweis, da wir gleich einen sehr ähnlichen Satz für Grenzwerte beweisen.
Häufungspunkt und Grenzwert
In einem normierten Raum .E; k k/ sind folgende Aussagen äquivalent.
(i) Die Folge .xn / konvergiert gegen a.
(ii) Die Folge .xn a/ konvergiert in E gegen 0.
(iii) Die reelle Folge .kxn ak/ konvergiert in R gegen 0. /////
Folgt aus dem letzten Satz. /////
Hier noch ein sehr einfaches Beispiele. Zahllose weitere Beispiele folgen später
zwangsläufig.
12 F Die reelle Folge .1=n/n1 konvergiert gegen 0, ist also eine Nullfolge. G
///// Zu jedem " > 0 existiert nach dem Satz des Archimedes eine natürliche
Zahl N mit 1=N < ". Dann gilt aber auch
0<
1
1
< ";
n
N
n N;
69
Häufungspunkt und Grenzwert
5-B
also 1=n 2 B" .0/ für n N . Somit gilt 1=n ! 0 für n ! 1. /////
13 F Die Zahlenfolgen ..
1/n / und .in / konvergieren nicht, ebensowenig jede
Abzählung der rationalen Zahlen. G
Grundlegende Sätze
Eigentlich rechtfertigt erst dieser Satz, von dem Grenzwert einer konvergenten
Folge zu sprechen. Dagegen kann eine Folge sogar überabzählbar viele Häufungspunkte haben.
///// Sei a D lim xn und b ¤ a . Nach dem Trennungssatz 5.1 gibt es ein
" > 0 , so dass
B" .a/ \ B" .b/ D ∅:
Da fast alle Folgenglieder in B" .a/ liegen, können nur noch höchstens endlich viele in B" .b/ liegen. Also kann b kein Häufungspunkt und erst recht
kein Grenzwert der Folge .xn / sein. /////
Satz Eine konvergente Folge ist beschränkt. /////
Ist a D lim xn , so gibt es ein N 1 mit
xn 2 BN 1 .a/;
n N:
Mit
˚
r D max 1; d.x1 ; a/; : : : ; d.xn1 ; a/
gilt dann xn 2 BN r .a/ für alle n 1. /////
Teilfolgen
Aus einer Folge .xn / gewinnen wir eine Teilfolge, indem wir nur einen Teil der
Folgenglieder behalten,
.xn1 ; xn2 ; xn3 ; : : : /;
und die übrigen ignorieren.
Häufungspunkt und Grenzwert
70
Definition Ist x D .xn / eine Folge in X und ' W N ! N strikt wachsend, so heißt
x B 'W N ! E
eine Teilfolge von x , geschrieben .xnk / mit nk D '.k/. Die Abbildung ' selbst
heißt eine Auswahlfolge. Für Auswahlfolgen gilt
Satz Der Grenzwert einer konvergenten Folge ist eindeutig bestimmt, und er ist ihr
einziger Häufungspunkt. 5.3
5-B
n 1 < n2 < n3 < : : : ;
'.k/ k;
k 2 N;
wie man durch Induktion zeigt. Die Menge aller Auswahlfolgen, und damit die Menge aller möglichen Teilfolgen einer Folge, ist übrigens überabzählbar.
14 F Die Folge ..
1/n / besitzt die beiden Teilfolgen
..
1/2k /k0 D .1; 1; : : : /;
..
1/2kC1 /k0 D .
1; 1; : : : /;
und natürlich noch viele andere. G
Satz Ist .xn / konvergent, so auch jede Teilfolge von .xn /, und die Grenzwerte
stimmen überein. /////
Das sollte klar sein. /////
5.4
Satz Eine Folge .xn / besitzt a als Häufungspunkt genau dann, wenn es
eine Teilfolge von .xn / gibt, die gegen a konvergiert. ///// Gibt es eine solche Teilfolge .xnk / mit xnk ! a, so liegen in jeder
Umgebung von a fast alle Glieder der Teilfolge, also auch unendlich viele
Glieder der Originalfolge. Also ist a ein Häufungspunkt dieser Folge.
Sei umgekehrt a ein Häufungspunkt der Folge .xn /. Dann definieren wir
rekursiv eine Auswahlfolge .nk / durch n1 WD 1 und
˚
k 2:
nk WD min n 2 N W n > nk1 ^ xn 2 U1=k .a/ ;
Die Menge auf der rechten Seite ist nicht leer, da a ein Häufungspunkt ist.
Somit ist nach Satz 3.2 vom Minimum auch das Minimum definiert, und es
ist nk > nk1 . Wir erhalten eine Auswahlfolge n1 < n2 < : : : , und es bleibt
zu zeigen, dass xnk ! a. Nun, zu " > 0 existiert immer ein K 1 mit
1=K < ". Dann gilt auf Grund der Konstruktion für alle k K
xnk 2 U1=k .a/ U1=K .a/ U" .a/:
Somit gilt xnk ! a. /////
71
Grenzwertsätze
5-C
5-C
Grenzwertsätze
72
Bemerkung. Der letzte Satz besagt, dass der Raum c der konvergenten KFolgen einen linearen Vektorraum bildet, und
Grenzwertsätze
Ist auf einem metrischen Raum X eine Operation W X X ! X erklärt, so stellt
sich die Frage, ob diese mit der Grenzwertbildung ›kompatibel‹ ist, also vertauscht.
Sind .xn / und .yn / zwei konvergente Folgen in X , so ist es wünschenswert, dass
die Folge .xn yn / ebenfalls konvergiert und sich der Grenzwert in naheliegender
Weise aus den Grenzwerten der Operanden ergibt als
lim.xn yn / D .lim xn / .lim yn /:
Linearkombinationen
In einem Vektorraum haben wir die Möglichkeit, Linearkombinationen zu bilden.
5.5
Grenzwertsatz L Sind .xn / und .yn / zwei konvergente Folgen in einem
normierten Vektorraum, so ist auch jede Linearkombination .xn Cyn / konvergent,
und es gilt
lim .xn C yn / D lim xn C lim yn :
limW c ! K;
.xn / 7! lim xn
eine lineare Abbildung ist. Sie ist sicher surjektiv – man nehme konstante Folgen – ,
und ihr Kern ist
c0 WD f.xn / 2 c W lim xn D 0g
der Unterraum der Nullfolgen in K. Dies ist die Frage nach der Stetigkeit der Operation auf X . Zunächst betrachten
wir aber die wichtigsten Spezialfälle.
/////
5-C
Sei a D lim xn und b D lim yn , und
Multiplikation und Division
In K, also in R oder in C , haben wir auch die Möglichkeit der Multiplikation und
Division. Grundlage auch im Hinblick auf wesentlich allgemeinere Resultate ist hier
die folgende Beobachtung.
5.6
Satz Ist .xn / eine Nullfolge und .yn / eine beschränkte Folge in K – oder
umgekehrt – , so ist auch .xn yn / eine Nullfolge in K. /////
Ist .xn / eine Nullfolge und .yn / beschränkt, so ist
jyn j M;
n 1;
mit einem M > 0, und zu jedem " > 0 existiert ein N mit
L D 1 C jj C jj:
Zu " > 0 existieren ein Nx und ein Ny , so dass
jxn aj < "=L;
n Nx ;
jyn bj < "=L;
n Ny :
Also gilt für n max.Nx ; Ny / auf Grund der Dreiecksungleichung
j.xn C yn / .a C b/j
jjjxn aj C jjjyn bj < .jj C jj/"=L < ":
Somit ist .xn C yn / konvergent mit Grenzwert a C b . /////
Es ist notwendig anzunehmen, dass .xn / und .yn / konvergieren. Denn für eine
beliebige reelle Zahl a gilt ja
a D lim .n C .a n// D lim .xn C yn /
mit xn D n und yn D a n. Aber natürlich darf man hier den Grenzwertsatz nicht
anwenden.
jxn j < "=M;
n N:
Dann aber gilt
jxn yn 0j jxn jjyn j M jxn j < ";
n N:
Das aber bedeutet, dass xn yn ! 0. /////
Auf die Annahme der Beschränktheit einer der Folgen kann nicht verzichtet werden. Zum Beispiel entsteht aus der Nullfolge xn D 1=n und der unbeschränkten
Folge yn D n im Produkt xn yn D 1 keine Nullfolge.
5.7
Grenzwertsatz M Sind .xn / und .yn / zwei konvergente Folgen in K, so
ist auch .xn yn / konvergent in K, und es gilt
lim xn yn D lim xn lim yn :
/////
Mit a D lim xn und b D lim yn ist
xn yn ab D .xn a/yn C .yn b/a:
73
Grenzwertsätze
5-C
Wegen Satz 5.6 sind .xn a/yn und .yn b/a Nullfolgen. Also ist auch
xn yn ab eine Nullfolge. Das ergibt die Behauptung. /////
5-C
Grenzwertsätze
5.8
Satz Sind .xn / und .yn / konvergente reelle Folgen, und gilt xn yn für
unendlich viele n , so ist auch lim xn lim yn :
Es bleibt noch die Division zu behandeln.
///// Sei a D lim xn und b D lim yn . Dann gibt es zu jedem " > 0 wenigstens ein n mit
Grenzwertsatz D Konvergiert die Folge .xn / in K gegen einen nicht-verschwindenden Grenzwert, so sind fast alle Glieder von .xn / von Null verschieden, und es
gilt
lim
/////
1
1
D
:
xn
lim xn
xn 2 U" .a/;
und somit a b < 2". Da dies für alle " > 0 gilt, muss a b sein. /////
Also gilt auch jxn j > jaj=2 > 0 für fast alle n. Die zweite Behauptung folgt
wie im letzten Beweis aus
1
1
1
D .xn a/ xn a
xn a
und der Beschränkheit von 1=xn a. /////
Oft sind diese Sätze nicht unmittelbar anwendbar und erfordern eine geeignete
Vorbereitung der Terme. Wir geben zwei Beispiele, viele weitere ergeben sich später
zwangsläufig.
15 F Im Zähler und Nenner wird n3 gekürzt, um konvergente Folgen zu erhalten:
1 C n12 1 n1
11
1
.n2 C 1/.n 3/
D
! 3 D :
G
3
8
.2n C 1/3
2
1
2C n
16 F Zunächst wird mit
C
yn 2 U" .b/:
a " < xn yn < b C ";
jaj jxn j jxn aj < " D jaj=2:
p
xn yn ;
Daraus folgt
Ist a D lim xn ¤ 0 , so ist " D jaj=2 > 0, und für fast alle n gilt
p
74
Ganz wichtig: Dieser Satz gilt nicht mit ›< ‹ an Stelle von › ‹. Es ist zum Beispiel
1
1
< ;
n 1;
n
n
aber beide Folgen haben denselben Grenzwert 0. Eine strikte Ungleichung übersteht
einen Grenzübergang im Allgemeinen nicht.
5.9
Sandwich-Satz Sind .un / und .un / konvergente reelle Folgen mit gleichem
Grenzwert a, und ist .xn / eine reelle Folge mit
un xn vn ;
so ist auch .xn / konvergent mit Grenzwert a. /////
Zu jedem " > 0 gibt es ein N , so dass
an ; bn 2 U" .c/;
n N:
Da U" .c/ ein Intervall ist, folgt aus der Voraussetzung auch
erweitert und dann wie eben verfahren:
p
p
.n2 C 4n/ .n2 8n/
n2 C 4n n2 8n D p
p
n2 C 4n C n2 8n
12
12
Dp
!
D 6:
p
2
1 C 4=n C 1 8=n
n n0 ;
xn 2 U" .c/;
n max .n0 ; N /:
Da " > 0 beliebig war, folgt xn ! c . /////
G
Anordnung
Auf der reellen Geraden stellt sich noch die Frage der Vertauschbarkeit der Grenzwertbildung mit der Ordnungsrelation. Hier ist ein wichtiger Unterschied zwischen
› ‹ und ›< ‹ zu machen.
Ein einfacher, häufig auftretender Spezialfall ist der
5.10
mit
Nullfolgen-Satz Ist .ın / eine reelle Nullfolge und .xn / eine reelle Folge
jxn j ın ;
n n0 ;
so ist auch .xn / eine Nullfolge. 75
Grenzwertsätze
5-D
Konvergenz in Rm und C
xn D .x1;n ; : : : ; xm;n / 2 Rm :
5.11 Satz Eine Folge .xn / konvergiert in Rm gegen a D .a1 ; : : : ; am / genau
dann, wenn die Folgen .xi;n / für 1 i m in R gegen ai konvergieren. 17 F Für eine komplexe Zahl a mit jaj < 1 gilt
lim an D 0:
X
X ˇ
ˇ
ˇ
ˇ 2
ˇxk;n ak ˇ2 ˇxk;n ak ˇ ;
1km
G
///// Da der Fall a D 0 offensichtlich ist, nehmen wir q WD jaj 2 .0; 1/ an.
Wegen
jan j D jajn D q n
genügt es zu zeigen, dass q n eine Nullfolge bildet. Schreibe dazu
qD
Für 1 i m gilt
1km
und damit
1
;
1C"
"D
mit
1
q
> 0;
q
Aus der Bernoullischen Ungleichung folgt
qn D
1
1
:
.1 C "/n
1 C "n
Auf der rechten Seite steht eine Nullfolge, und die Behauptung folgt mit dem
Nullfolgen-Satz. /////
X ˇ
ˇ
ˇxk;n ak ˇ:
jxi;n ai j jxn aj 1km
Bemerkung. Wenn die komplexe Folge .an / überhaupt konvergiert, so gilt
Gilt xn ! a , so bildet jxn aj eine Nullfolge. Also bildet auch die linke
Seite eine Nullfolge, und es folgt xi;n ! ai für 1 i m. Gilt umgekehrt
xi;n ! ai für jedes i , so bildet die rechte Seite der Ungleichung nach dem
Nullfolgen-Satz eine Nullfolge. Also ist auch jxn aj eine Nullfolge, somit
xn ! a. /////
Spezialfall Eine komplexe Folge .zn / D .xn C iyn / konvergiert genau dann, wenn
die Folge ihrer Real- und Imaginärteile konvergiert, und es gilt
lim zn D a C ib , lim xn D a ^ lim yn D b:
76
Einige wichtige Grenzwerte
n!1
Dies ist tatsächlich der Fall. Die vektorwertige Folge .xn / konvergiert genau dann,
wenn sie komponentenweise konvergiert:
jxi;n ai j2 Einige wichtige Grenzwerte
5-D
Die Vermutung liegt nahe, statt speziell im Rm die Konvergenz einer Folge .xn /
zusammenhängt mit der Konvergenz der einzelnen Koordinaten von
/////
5-D
lim an D lim anC1 D a lim an
nach dem Grenzwertsatz M. Ist also lim an ¤ 0, so folgt sofort a D 1. Somit
konvergiert an nur für jaj < 1 oder a D 1. 18 F Für eine komplexe Zahl a mit jaj < 1 gilt sogar für jedes r 2 Z
lim nr an D 0:
n!1
G
///// Wie zuvor setzen wir q D jaj, und betrachten die Folge xn D nr q n
für 0 < q < 1. Es gilt
xnC1
nC1 r
1 r
D
q D 1C
q ! q < 1:
xn
n
n
Es gibt somit ein m 1, so dass
xnC1
1Cq
< WD
< 1;
xn
2
n m:
Für alle n m folgt hieraus
xn xn1
xmC1
::: xm nm xm :
xn D
xn1 xn2
xm
77
Existenzsätze
5-E
Da nach dem vorangehenden Beispiel die rechte Seite für n ! 1 gegen 0
konvergiert, ist nach dem Nullfolgen-Satz auch .xn / eine Nullfolge. Das war
zu zeigen. /////
19 F Für eine beliebige komplexe Zahl a gilt
an
D 0:
n!1 n!
1
jaj
;
n
2
n D 0; 1; : : : :
n!1
n
m
n
Y
Y
Y
jaj
jaj
jajn
D
n!
k
k
kDmC1
1
Dc
2
nm
1
! 0:
2
/////
Im nächsten Beispiel antizipieren wir die Definition der n-ten Wurzel einer positiven reellen Zahl a als diejenige eindeutige positive reelle Zahl, deren n-te Potenz
a ist – siehe Satz8.6.
p
20 F lim n n D 1. G
n!1
///// Für jedes " > 0 ist n=.1 C "/n nach Beispiel 18 eine Nullfolge. Also
gibt es ein N 1 mit
n
< 1;
n N:
.1 C "/n
Dies ist äquivalent mit
p
n
n < 1 C ";
n N:
p
Da natürlich auch 1 n n, folgt
p
n
n 2 U" .1/;
n N:
/////
5-E
n
X
1
;
k!
e D lim en :
Dann folgt für n > m
kD1
Tatsächlich ist es aber so, dass man den meisten Folgen nicht ansehen kann, welchen Grenzwert sie haben, auch wenn sie ›sehr konvergent aussehen‹, wie zum Beispiel die Folge
Sehr oft will man auch bestimmte reelle Zahlen als Grenzwert gewisser Folgen erst
definieren, wie zum Beispiel
n m:
kD1
78
kD0
Da a fest ist, gibt es ein m , so dass
/////
Existenzsätze
en D
G
lim
5-E
Existenzsätze
Bisher gehen wir davon aus, dass wir den Grenzwert einer konvergenten Folge auch
kennen. Dies kommt bereits in der Definition zum Ausdruck: Eine Folge ist konvergent, wenn sie gegen einen bestimmten Grenzwert konvergiert.
Es geht daher im Folgenden darum, nur durch Eigenschaften einer Folge selbst deren
Konvergenz und damit die Existenz eines Grenzwert festzustellen
Wir betrachten dazu zunächst reelle Folgen.
Monotone Folgen
Definition Eine reelle Folge .xn / heißt monoton wachsend oder monoton steigend,
falls
xn xnC1
für alle n. Sie heißt streng monoton wachsend oder strikt wachsend, falls sogar
xn < xnC1
für alle n. Analog sind monoton fallende und streng monoton fallende Folgen definiert. Schließlich heißt eine Folge (streng) monoton, wenn sie (streng) monoton
steigend oder fallend ist. Für die Konvergenz einer monotonen Folge gegen einen Grenzwert a schreibt
man auch
xn a;
xn a:
5.12 Satz von der monotonen Konvergenz Jede monotone und beschränkte reelle Folge .xn / ist konvergent, und es gilt
xn sup fxn W n 2 Ng;
xn inf fxn W n 2 Ng
für monoton steigende respektive monoton fallende Folgen. 79
Existenzsätze
5-E
///// Sei etwa .xn / monoton steigend. Da die Menge S D fxn W n 2 Ng
nach Voraussetzung beschränkt ist, existiert
s D sup S < 1:
xN 2 S \ .s "; 1/:
Das heißt, es ist s " < xN s . Wegen der Monotonie der Folge gilt dann
s " < xN xn s;
n N;
also xn 2 U" .s/ für n N . Da " beliebig war, konvergiert .xn / gegen
s . /////
Wir wissen bereits, dass jede konvergente Folge beschränkt ist. Bei monotonen
Folgen ist die Beschränktheit also auch hinreichend für die Konvergenz.
21 F Die Summen
n
X
1
1
1
1
D1C1C C
C C :
k!
2
23
n!
kD0
definieren eine Folge .en /, die sicher streng monoton steigt. Außerdem gilt
n
n1
1 12
1
1
en 1 C 1 C C C
D1C
3
2
2
1 12
n!1
n!1
n
X
kD0
1
DW
k!
1
X
kD0
1
:
k!
G
Der Satz von Bolzano-Weierstraß
Nicht jede reelle Folge ist monoton. Man kann aber den allgemeinen Fall auf diesen
zurückführen.
Satz
Jede reelle Folge .xn / enthält eine monotone Teilfolge. /////
80
Ist A unendlich, so definieren die Elemente von A eine Auswahlfolge .nk /,
für die gilt:
Dann ist .xnk / monoton fallend. Ist dagegen A endlich, so existiert n0 D
max A . Zu jedem n > n0 existiert dann ein m > n mit
xn xm , xn < xm :
Aus diesen Indizes können wir induktiv eine monoton steigende Teilfolge
.xnk / konstruieren. /////
Dieser Satz zusammen mit dem Satz von der monotonen Konvergenz führt direkt
zum ersten Satz von Bolzano-Weierstraß.
Satz Jede beschränkte reelle Folge besitzt eine konvergente Teilfolge und damit
auch einen Häufungspunkt. ///// Mit dem letzten Satz können wir aus einer beschränkten Folge eine
monotone Teilfolge auswählen. Diese ist natürlich auch beschränkt, also nach
Satz 5.12 konvergent. Der Grenzwert dieser Teilfolge ist nach Satz 5.4 ein
Häufungspunkt der Originalfolge. /////
Dies gilt auch in höheren Dimensionen.
Satz von Bolzano-Weierstraß Jede beschränkte reelle, komplexe, oder vektorwertige Folge besitzt eine konvergente Teilfolge und damit auch einen Häufungspunkt. für alle n. Also existiert
e D lim en D lim
Existenzsätze
xnk xnkC1 :
Nach dem Approximationssatz für Suprema existiert zu jedem " > 0 ein
en D
5-E
Betrachte die Menge
A D fn 2 N W xn xm für alle m ng:
Ein n gehört also zu A, wenn alle auf xn folgenden Glieder der Folge nicht
oberhalb von xn liegen.
///// Identifizieren wir C mit R2 , so genügt es, Folgen in Rm zu betrachten.
Der Fall m D 1 ist bereits gezeigt, zur vollständigen Induktion fehlt also nur
noch der Induktionsschritt.
Sei .xn / eine beschränkte Folge in RmC1 . Dann ist
M D sup fjxn j W n 0g < 1:
Wir schreiben RmC1 D Rm R und dementsprechend
x D .u; v/ 2 Rm R:
Aus der gegebenen Folge entstehen auf diese Weise zwei Folgen .un / in Rm
und .vn / in R . Beide sind wiederum beschränkt, denn für jedes n gilt
q
jun j C jvn j jun j2 C jvn j2 D jxn j M:
81
Existenzsätze
5-E
Nach Induktionsvoraussetzung besitzt nun .un / eine konvergente Teilfolge
.unk / mit Grenzwert u :
unk ! u:
Aus der entsprechenden Teilfolge .vnk / können wir eine weitere konvergente
Teilfolge .vnl / extrahieren, denn auch hier ist die Induktionsvoraussetzung
anwendbar:
vnl ! v:
Dann aber gilt für die wieder zusammengesetzte Folge:
Existenzsätze
82
Uns kommt es natürlich auf die Umkehrung dieses Satzes an. Diese gilt jedoch
nicht in jedem metrischen Raum. Zwei wesentliche Zwischenergebnisse gelten allerdings immer.
Lemma Jede Cauchy-Folge ist beschränkt. ///// In der Tat, zu " D 1 existiert ein N mit d.xn ; xm / < 1 für n; m N .
Insbesondere ist also mit a D xN
d.xn ; a/ 1;
n N:
Also gilt auch
xnl D .unl ; vnl / ! .u; v/ DW x:
Denn allgemein gilt
q
jxn xj D jun uj2 C jvn vj2 jun uj C jvn vj;
und entlang der Auswahlfolge n D nl konvergiert die rechte Seite gegen 0.
Also auch die linke Seite. /////
d.xn ; a/ max .1; d.x1 ; a/; : : : ; d.xN 1 ; a// < 1;
n 1:
/////
Lemma Besitzt eine Cauchy-Folge einen Häufungspunkt, so ist dieser der Grenzwert der Folge. ///// Sei a ein Häufungspunkt der Cauchy-Folge .xn / . Zu " > 0 existiert
dann ein N mit d.xn ; xm / < "=2 für alle n; m N , sowie ein i N mit
xi 2 U"=2 .a/:
Cauchy-Folgen
Die Frage, welche Eigenschaft eine Folge zu einer – möglicherweise – konvergenten
Folge macht, führt zum Begriff der Cauchy-Folge, auch Fundamentalfolge genannt.
Definition Eine Folge .xn / in einem metrischen Raum .X; d/ heißt Cauchy-Folge,
wenn es zu jedem " > 0 ein N gibt, so dass
d.xn ; xm / < ";
5-E
n; m N:
Dann aber gilt
d.xn ; a/ d.xn ; xi / C d.xi ; a/ < "=2 C "=2 D ";
n N:
Da " > 0 beliebig war, folgt xn ! a für n ! 1. /////
Insbesondere kann eine Cauchy-Folge höchstens einen Häufungspunkt haben. –
Nun der eigentliche Satz für die Räume R , C und Rm .
5.13 Satz Jede konvergente Folge in einem metrischen Raum ist eine CauchyFolge. Satz Jede reelle, komplexe, oder vektorwertige Cauchy-Folge besitzt einen Grenzwert. ///// Sei .xn / eine konvergente Folge und a ihr Grenzwert. Dann existiert
zu " > 0 ein N mit
///// Wir haben gezeigt, dass jede Cauchy-Folge beschränkt ist. Nach dem
Satz von Bolzano-Weierstraß besitzen beschränkte Folgen in R , C oder Rm
einen Häufungspunkt. Dieser ist aber nach dem eben bewiesenen Lemma der
Grenzwert der Cauchy-Folge. /////
d.xn ; a/ < "=2;
n N:
Für beliebige n; m N folgt mit der Dreiecksungleichung
d.xn ; xm / d.xn ; a/ C d.xm ; a/ < "=2 C "=2 D ":
Somit ist .xn / eine Cauchy-Folge. /////
Im Raum Q mit der natürlichen Metrik besitzt dagegen nicht jede Cauchy-Folge
einen
p Grenzwert, so zum Beispiel jene Folgen rationaler Zahlen nicht, die in R gegen
2 konvergieren. Es ist also eine Eigenschaft des zu Grunde liegenden Raumes,
ob Cauchy-Folgen konvergieren. Es sit im Grunde die gleiche Eigenschaft, die die
83
Uneigentliche Konvergenz
5-F
5-F
Uneigentliche Konvergenz
84
reellen von den rationalen Zahlen unterscheidet, weshalb man sie Vollständigkeit
nennt.
in jeder Umgebung von 1 unendlich viele Folgenglieder liegen.
Für 1 sind die Definitionen entsprechend. Die "-Umgebungen sind hier
Definition Ein metrischer Raum heißt vollständig, wenn jede Cauchy-Folge einen
Grenzwert besitzt. U" .
1/ WD .
1; 1="/;
p
n
22 F Es gilt lim
n! D 1. G
" > 0:
n!1
Besonders wichtig sind die vollständigen normierten Räume, weshalb sie einen
eigenen Namen haben und Banachräume genannt werden. Wir haben also gezeigt:
Die Räume R , C mit der Betragsnorm sowie Rm mit der euklidischen Norm sind
Banachräume.
Mit Satz 5.13 ergibt sich schließlich:
5.14 Cauchy-Kriterium In einem Banachraum konvergiert eine Folge genau
dann, wenn sie eine Cauchy-Folge ist. ///// Sei E > 0. Wegen E n =n! ! 0 nach Beispiel 19 gibt es ein N , so
dass
En
< 1;
n!
Dann aber ist
n N:
p
n
n! > E für n N . /////
Die grundlegenden Sätze über Folgen, die nur auf dem Umgebungsbegriff basieren, gelten auch hier. In Stichworten:
»Der Grenzwert ist eindeutig und der einzige Häufungspunkt.«
»Teilfolgen konvergenter Folgen haben denselben Grenzwert.«
5-F
Uneigentliche Konvergenz
In Abschnitt 2-D hatten wir die reelle Gerade R durch Hinzufügen der Punkte 1
N gemacht. Diese Punkte können wir auch
und 1 zur erweiterten Zahlengeraden R
als ›uneigentliche Grenzwerte‹ und ›uneigentliche Häufungspunkte‹ von reellen Folgen zuzulassen. Dazu genügt es, geeignete Umgebungen von 1 und 1 zu definieren.
Eine Teilmenge U in R heißt Umgebung von 1, wenn sie eine "-Umgebung
von 1 ,
U" .1/ WD .1="; 1/;
" > 0;
enthält.
Eine reelle Folge .xn / konvergiert gegen den uneigentlichen Grenzwert 1, oder
besitzt 1 als uneigentlichen Grenzwert, wenn in jeder Umgebung von 1 fast alle
Folgenglieder liegen. Äquivalent dazu ist die Forderung, dass zu jedem E > 0 ein
N existiert, so dass
xn > E;
n N:
lim xn D 1
.xn / c
bzw
.xn / c
eine Abkürzung für xn > c bzw xn c für fast alle n, wobei c 2 R .
5.15
Satz Für reelle Folgen .xn / und .yn / gilt:
(i) xn ! 1 ^ .yn / c ) xn C yn ! 1,
(ii) xn ! 1 ^ .yn / c > 0 ) xn yn ! 1,
(iii) jxn j ! 1 ) xn1 ! 0,
(iv) xn ! 0 ^ .xn / 0 ) xn1 ! 1. /////
mit
Zum Beispiel (i). Gilt xn ! 1 , so existiert zu jedem " > 0 ein N
xn > 1=" c;
Man schreibt
n!1
»Zu jedem Häufungspunkt existiert eine konvergente Teilfolge.«
Natürlich gilt nicht, dass eine uneigentlich konvergente Folge beschränkt ist!
Die Grenzwertsätze gelten nur in Auszügen. Sei
n N:
Dann aber gilt, eventuell mit einem größeren N , auch
bzw
xn ! 1 .n ! 1/:
Analog besitzt die reelle Folge .xn / den uneigentlichen Häufungspunkt 1, wenn
xn C yn xn C c > 1=";
n N:
Also gilt auch xn C yn ! 1. /////
85
Uneigentliche Konvergenz
5-F
Schließlich können wir noch zwei Existenzsätze allgemeiner formulieren.
Erweiterter Satz von der monotonen Konvergenz Jede reelle, monotone Folge
konvergiert gegen einen eigentlichen oder uneigentlichen Grenzwert. ///// Ist die Folge beschränkt, so kommt der Satz von der monotonen Konvergenz zur Anwendung. Andernfalls ist die Folge unbeschränkt. Wegen der
Monotonie hat sie dann den uneigentlichen Grenzwert 1 oder 1. /////
Erweiterter Satz von Bolzano-Weierstraß Jede reelle Folge besitzt einen eigentlichen oder uneigentlichen Häufungspunkt. 5-F
Uneigentliche Konvergenz
86
6-A
Konvergenz
88
s0 D a0 ;
6
sn D sn1 C an ;
n 1:
P1
Definition Die Reihe
nD0 an heißt konvergent, wenn die Folge ihrer Partialsummen .sn / konvergiert. Ihr eindeutig bestimmter Grenzwert s heißt Wert dieser
Reihe. Konvergiert die Folge der Partialsummen dagegen nicht, so heißt die Reihe
divergent. Reihen
Im Falle der Konvergenz haben wir also
1
X
Folgen besonderer Art sind »unendliche Summen«
1
X
n!1
n
X
ak :
kD0
Andere Schreibweisen sind
reeller oder komplexer Zahlen. Da man nicht sämtliche Glieder einer Folge .an /
»auf einmal« aufsummieren kann, steht eine solche Summe vielmehr für Folge der
Partialsummen
sn D
n
X
ak ;
n 0;
kD0
die man nun in gewohnter Weise untersuchen kann.
Solche Reihen lassen sich nicht nur aus reellen oder komplexen Zahlen bilden,
sondern aus Elementen jeden Raumes, in dem eine Addition erklärt ist. Wir werden
deshalb die Grundbegriffe von vornherein in Banachräumen erklären. Alle Beispiele
werden aber in R und C angesiedelt sein.
1
X
an
mit Glieder oder Summanden a0 ; a1 ; : : : in E . Die endlichen Summen
sn WD
n
X
ak ;
n 0;
kD0
heißen die n-ten Parialsummen dieser Reihe und sind induktiv erklärt durch
an D
X
an ;
n
n0
Bemerkung. Eigentlich ist zu unterscheiden zwischen der formalen Reihe
1
X
an ;
nD0
deren Konvergenz noch nicht feststeht und die auch divergieren kann, und der konvergenten Reihe
nD0
nD0
X
P
oder schlicht
an , wenn es nur um die Konvergenz an sich geht und es auf die
ersten Glieder der Reihe nicht ankommt. Die Summation einer Reihe kann natürlich
bei einem beliebigen Index, nicht nur bei 0 beginnen.
1
X
Sei E ein Banachraum mit Norm j j . Eine Reihe in E ist ein Ausdruck der Form
an D
nD0
Konvergenz
1
X
n!1
nD0
an D a0 C a1 C a2 C : : :
nD0
6-A
an D s D lim sn D lim
an D lim
n!1
n
X
ak :
kD0
Die formale Reihe steht also für die Folge ihrer Partialsummen, die konvergente Reihe für deren Grenzwert. Dieser Unterschied kommt in dieser, allgemein üblichen
Notation nicht zum Ausdruck. Nun die ersten Standardbeispiele.
1F
Bereits bekannt ist die Konvergenz der Reihe
1
X
1
D e:
n!
nD0
G
89
2F
Konvergenz
6-A
Die Partialsummen der Reihe
4F
nD1
sind monoton steigend, da ihre Summanden positiv sind. Außerdem gilt
kD1
Konvergenz
1
1C
k2
Die harmonische Reihe
X1
1
1
1
D C C C :::
n
1
2
3
n1
ist divergent. G
n
X
1
k.k 1/
kD2
n X
1
1
1
D1C
D 1 C 1 < 2:
k 1 k
n
/////
Es gilt
s2n sn D
kD2
Die Folge der Partialsummen ist also beschränkt. Wegen Satz 5.12 von der monoP
tonen Konvergenz ist also n1 1=n2 konvergent. Tatsächlich wusste bereits Euler,
dass
1
X
2
1
D
:
6
n2
zn;
z2C
nD0
besitzt für z ¤ 1 die Partialsummen
sn D 1 C z C : : : C z n D
Für jzj < 1 gilt jz j ! 0, siehe Beispiel 17 in Abschnitt 5-D. Somit folgt aus den
Grenzwertsätzen
1
X
1
zn;
D
1
z
jzj < 1:
nD0
/////
P
n
n
:
2
an konvergent, so bilden ihre Glieder an eine Null-
Konvergiert die Folge der Partialsummen, so folgt aus Grenzwertsatz L
lim an D lim .snC1 sn / D lim snC1 lim sn D 0:
///// Es ist ja
ˇ
ˇX
ˇ
ˇ m
ˇ D jsm sn1 j;
ˇ
a
k
ˇ
ˇ
kDn
es handelt sich also um nichts anderes als das Cauchy-Kriterium 5.14 für die
Folge .sn / der Partialsummen. /////
Für jzj 1 ist die Reihe wegen jz n j 0 dagegen wegen des folgenden Satzes
divergent. G
6.1
Satz Ist die Reihe
folge. s2n 1 C
kDn
1 z nC1
:
1
z
n
sn !
Daraus folgt durch Induktion
Wir formulieren nun das Cauchy-Kriterium speziell für Reihen.
P
6.2
Cauchy-Kriterium Die Reihe n an konvergiert in E genau dann, wenn
es zu jedem " > 0 ein N gibt, so dass
ˇ m
ˇ
ˇX ˇ
ˇ
ˇ
a
m n N:
k ˇ < ";
ˇ
Die formale geometrische Reihe
1
X
1
1
1
1
1
C
C C
n
D :
nC1
nC2
2n
2n
2
Somit konvergieren die Partialsummen nicht, die Reihe ist vielmehr divergent
mit dem uneigentlichen Grenzwert 1. /////
G
nD1
3F
90
Die Umkehrung gilt natürlich nicht, wie das folgende Standardbeispiel zeigt.
1
X
1
n2
n
X
6-A
/////
In einem Banachraum können wir mit konvergenten Reihen rechnen wie mit
»normalen« Elementen.
P
P
6.3
Satz Sind n an und n bn konvergente Reihen, so konvergiert auch die
P
Reihe n .an C bn / für ; 2 K, und es gilt
X
X
X
.an C bn / D an C bn :
n
/////
n
Nach Voraussetzung gilt
n
91
Konvergenz
sn D
n
X
ak ! s;
kD0
tn D
n
X
6-A
sn C tn D
.ak C bk /
kD0
folgt die Behauptung dann aus dem Grenzwertsatz A für Folgen:
sn C tn ! s C t:
/////
In einer endlichen Summe ist es kein Problem, die Reihenfolge der Summanden
beliebig zu ändern, wenn die Addition kommutativ ist – die Summe ändert sich nicht.
In einer unendlichen Reihe ist dies aber keineswegs immer so, dazu bedarf es einer
stärkeren Form der Konvergenz.
P
P
Definition Eine Reihe n an heißt absolut konvergent, wenn die Reihe n jan j
konvergiert. Eine konvergent, aber nicht absolut konvergent Reihe heißt dagegen bedingt konvergent.
P
n
an das Cauchy-Kriterium, wenn es
an ist gegeben durch eine Bijektion
Umordnungssatz für bedingt konvergente Reihen Ist eine reelle Reihe konvergent, aber nicht absolut konvergent, so existiert zu jeder reellen Zahl s eine Umordnung dieser Reihe, die gegen s konvergiert. Dies gilt sogar mit s D 1 und s D 1. – Wir beweisen diesen Satz hier nicht,
da wir ihn nicht benötigen.
P
///// Beweis des Umordnungssatzes Sei s D
n0 an , und W N ! N
eine Bijektion. Wegen der absoluten Konvergenz der Originalreihe existiert
zu jedem " > 0 ein N , so dass
m
X
jak j < ";
m n N:
kDn
Dann gilt mit n D N und m ! 1 auch
///// Wegen
ˇ
ˇ m
m
ˇX ˇ X
ˇ
ak ˇˇ jak j
ˇ
erfüllt
n
P
die zugehörige umgeordnete Reihe ist n a .n/ . Es treten also genau dieselben SumP
manden wie in n an auf, deren Reihenfolge ist aber möglicherweise sehr verschieden, insbesondere wenn fn W .n/ ¤ ng unendlich ist.
P
Umordnungssatz Ist die Reihe n an absolut konvergent, so ist es auch jede Umordnung dieser Reihe, und der Wert der Reihe ändert sich dabei nicht. Jede absolut konvergente Reihe ist auch konvergent. kDn
P
Dass dieser Satz nicht selbstverständlich ist, demonstriert der komplementäre
Satz über nicht-absolut konvergente Reihen.
Absolute Konvergenz
kDn
92
W N ! N;
kD0
n
X
Konvergenz
»leiden«. Eine Umordnung einer Reihe
bk ! t:
Mit
Satz
6-A
1
X
P
n
jak j ":
kDN
jan j erfüllt. /////
Die Glieder a0 ; : : : ; aN 1 treten in der umgeordneten Reihe
spätestens bis zu einem gewissen Index M auf, genauer
˚
M D max 1 .0/; : : : ; 1 .N 1/ :
Die Umkehrung gilt – natürlich – nicht. So konvergiert die alternierende harmonische Reihe
X .
1/nC1
1
1 1
D 1 C ˙ :::
n
2
3 4
n1
– siehe Beispiel 8 – , während die Reihe der Absolutbeträge nach Beispiel 4 divergiert.
Wir konkretisieren nun, dass absolut konvergente Reihen in beliebiger Reihenfolge aufsummiert werden können, ohne dass die Konvergenz oder der Wert der Reihe
(j)
P
n0
a .n/
Dann gilt für n N und m M
ˇ n
ˇ
m
1
X
X
ˇX
ˇ
ˇ
ˇ
a
a
jak j ";
k
.k/
ˇ
ˇ
kD0
kD0
kDN
denn in der Differenz heben sich die Glieder a0 ; : : : ; aN 1 auf, während jedes weitere Glied sich entweder ebenfalls aufhebt oder genau einmal stehen
93
Konvergenzkriterien
6-B
6-B
Konvergenzkriterien
m
X
bleibt. Durch Grenzübergang n ! 1 erhalten wir hieraus
ˇ1
ˇ ˇ
ˇ
m
m
X
X
ˇX
ˇ ˇ
ˇ
ˇ
ˇ D ˇs ˇ ":
a
a
a
k
.k/
.k/
ˇ
ˇ ˇ
ˇ
kD0
kD0
1
X
a .k/ D s D
kD0
kDn
1
X
kD0
Konvergenzkriterien
P
Ist n an eine Reihe in einem beliebigen Banachraum, so sind die Partialsummen
P
der Absolutreihe
n jan j monoton wachsend. Aus Satz 5.12 über die monotone
Konvergenz ergibt sich daher das einfachste aller Konvergenzkriterien.
P
6.4
Satz Die Reihe n an ist absolut konvergent genau dann, wenn die Folge
P
der Partialsummen der Reihe n jan j beschränkt ist. Damit reduziert sich die Frage der absoluten Konvergenz einer Reihe auf die
Frage der Konvergenz von Reihen mit reellen, nicht-negativen Gliedern. Diese lässt
sich wiederum oft reduzieren auf das Studium geeigneter »Majoranten«.
P
Eine reelle Reihe
m mit nicht-negativen Gliedern heißt Majorante einer
P n n
Banachraum-Reihe n an , wenn es ein N gibt, so dass
jan j mn ;
n N:
Gilt umgekehrt 0 mn jan j für n N , so spricht man von einer Minorante.
Majorantenkriterium Besitzt eine Reihe in einem Banachraum eine konvergente
Majorante, so ist die Reihe absolut konvergent. P
P
///// Sei n an die gegebene Reihe und n mn eine konvergente Majorante. Dann gilt jan j mn für n N , und für m n N folgt
kDn
1
X
mk < 1:
kDn
///// Denn wäre die Reihe absolut konvergent, so wäre es nach dem Majorantenkriterium auch ihre Minorante – . /////
5F
Die Reihe
X 1
n1
6-B
mk Minorantenkriterium Besitzt eine Reihe eine divergente Minorante, so ist die
Reihe nicht absolut konvergent. ak :
Um noch die absolute Konvergenz zu zeigen, genügt es, in (j) bei ak und
a.k/ die Beträge zu nehmen. Alles andere bleibt unverändert. /////
m
X
Also folgt die absolute Konvergenz aus dem vorangehenden Satz. /////
kD0
Dies gilt für alle m M . — Da zu jedem " > 0 ein solches M existiert,
folgt die Konvergenz der umgeordneten Reihe gegen s :
jak j 94
nr
D1C
1
1
C r C :::
2r
3
konvergiert für r 2 und divergiert für r 1, wobei reelle Exponenten in Abschnitt 10-B erklärt werden. G
/////
Wegen
0<
ist
P
1
1
2;
nr
n
n1
r 2;
1=n2 nach Beispiel 2 eine konvergente Majorante für r 2. Wegen
1
1
> 0;
r 1;
nr
n
P
ist n1 1=n nach Beispiel 4 eine divergente Minorante für r 1. /////
Die Wahl spezieller Majoranten führt zu besonders handlichen Konvergenzkriterien. Besonders praktisch sind das Wurzel- und das Quotientenkriterium, die auf der
geometrischen Reihe als Majorante beruhen.
Im Folgenden greifen wir auf die Definition der n-ten Wurzel einer reellen Zahl
vor, die erst in Satz 8.6 erfolgt. Die Ergebnisse dort sind aber unabhängig von diesem
Kapitel, so dass kein Zirkelschluss vorliegt.
P
Wurzelkriterium Sei
n an eine Reihe in einem Banachraum.
(i) Gibt es ein q 2 .0; 1/ und ein N , so dass
p
n
n N;
jan j q < 1;
so ist die Reihe absolut konvergent.
95
Konvergenzkriterien
(ii) Gilt
p
n
6-B
6-B
Konvergenzkriterien
(i) Gibt es ein q 2 .0; 1/ und ein N , so dass jan j > 0 für n N und
jan j 1
janC1 j
q < 1;
jan j
für unendlich viele n;
so ist die Reihe divergent.
(iii) Trifft weder (i) noch (ii) zu, so kann die Reihe konvergieren oder divergieren. (i)
(ii) Gilt
janC1 j
1;
jan j
n N;
jan j q ;
P n
und n q ist nach Beispiel 3 für q 2 .0; 1/ eine konvergente Majorante.
Also folgt die absolute Konvergenz mit dem Majorantenkriterium.
(ii) Da jan j 1 für unendlich viele n, kann an keine Nullfolge sein. Die
Reihe divergiert daher wegen Satz 6.1.
P
(iii) Für die Reihe n1 nr mit r 1 gilt
p
p r
p r
n
< 1;
lim n n
D 1;
jan j D n n
(iii) Trifft weder (i) noch (ii) zu, so kann die Reihe konvergieren oder divergieren. /////
siehe Beispiel 20 in Abschnitt 5-D. Daher sind weder (i) noch (ii) anwendbar.
Für r D 1 ist die Reihe divergent, für r 2 konvergent. Das Wurzelkriterium liefert somit keinen Aufschluss über das Konvergenzverhalten dieser
Reihe für verschiedene r . /////
Satz Die Reihe
exp z WD
n1
1
X
zn
z2
z3
D1CzC
C
C :::
n!
2
3!
nD0
konvergiert absolut für jedes z 2 C mit jzj < 1 und beliebiges r 2 N . G
Es gilt
q
p
p r
n
n
jan j D nr jzjn D n n jzj ! jzj;
n ! 1:
Ist jzj < 1, so existiert zu 0 < " < 1 jzj ein N , so dass
p
n
n N:
jan j < jzj C " DW q < 1;
Das Wurzelkriterium ist somit anwendbar. /////
Quotientenkriterium Sei
Für n N gilt also janC1 j qjan j, und mit Induktion
Als Anwendungsbeispiel des Quotientenkriteriums eine der wichtigsten Reihen.
6.5
Die Reihe
X
nr z n
(i)
c D q N jaN j:
jan j q nN jaN j D cq n ;
P
Mit q 2 .0; 1/ ist somit n cq n eine konvergente Majorante, und die absolute Konvergenz folgt mit dem Majorantenkriterium.
(ii) Für n N gilt dann jan j jan1 j jaN j > 0, die Reihenglieder bilden also keine Nullfolge.
(iii) Dies zeigt man mit demselben Beispiel wie beim Wurzelkriterium. /////
n!1
/////
n N;
so ist die Reihe divergent.
Aus der Voraussetzung folgt
n
6F
n N;
so ist die Reihe absolut konvergent.
Im Fall (iii) liefert das Quotientenkriterium somit keinen Aufschluss über das
Konvergenzverhalten der Reihe.
/////
96
P
n
an eine Reihe in einem Banachraum.
ist für jedes z 2 C absolut konvergent. ///// Wir können z ¤ 0 annehmen. Dann gilt
ˇ
ˇ
nC1
ˇ anC1 ˇ
n!
1
jzj
ˇ D jzj
ˇ
D
;
n 2jzj:
n
ˇ a ˇ
nC1
2
jzj .n C 1/!
n
Also ist das Quotientenkriterium für jedes z 2 C anwendbar. /////
In Beispiel 5 ist der Fall 1 < r < 2 noch offen geblieben. Dieser lässt sich auch
nicht mit dem Wurzel- oder Quotientenkriterium behandeln. Hier hilft das folgende
Kriterium.
97
Konvergenzkriterien
6-B
6-C
Verdichtungssatz Sei .an / eine monoton fallende, reelle Nullfolge. Dann sind die
beiden Reihen
X
X
an ;
2n a2n
n1
q D 21r < 1 , r > 1:
Sie ist übrigens auch divergent für
n0
q D 21r 1 , r 1:
1 a2 a2
1 a1 ;
2 a2 ;
4 a8 a5 C C a8 4 a4
n
und allgemein
mit an 0 für fast alle n.
2n a2nC1 a2n C1 C C a2nC1 2n a2n :
Leibniz-Kriterium Die alternierende Reihe
monoton fallend gegen Null konvergiert. Addieren wir diese Summen auf, erhalten wir
n
X
2k a2kC1 kD0
nC1
2X
ak kD2
n
X
/////
2k a2k :
nC1
X
2k a2k D a1 C 2
kD1
n
X
2k a2kC1
nC1
2X
1
ak Sn :
.SnC1 a1 / 2
X 1
Die Reihe
konvergiert für alle r > 1. G
nr
n1
Wir betrachten die verdichtete Reihe
nD0
2n 1
1
X
X
1
nr n
D
2
D
qn;
.2n /r
nD0
nD0
Da .an / monoton fällt, ist
und wegen an ! 0 ist das Cauchy-Kriterium anwendbar. /////
Daraus folgt, dass die Konvergenz der einen Reihe auch die Konvergenz der
anderen Reihe nach sich zieht. Desgleichen für die Divergenz. /////
1
X
konvergiert, falls .an /
kDn
kD2
/////
n
n .
1/ an
Also gilt für m n
ˇ
ˇX
ˇ
ˇ m
k
ˇ
.
1/ ak ˇˇ D jan anC1 C anC2 ˙ am j an ;
ˇ
kD0
und wir erhalten
7F
P
an anC1 C anC2 ˙ am
(
.an anC1 / C .anC2 anC3 / C C am 0;
D
an :
an .anC1 anC2 / : : :
kD0
Nennen wir die rechts stehende Summe Sn , so ist
SnC1 D a1 C
/////
Die bisherigen Konvergenzkriterien sichern die absolute Konvergenz, nicht aber
die bedingte Konvergenz. Da diese im Hinblick auf den Umordnungssatz sehr delikat
ist, erwähnen wir nur das einfachste Kriterium für sogenannte alternierende Reihen,
also Reihen der Form
X
.
1/n an
Auf Grund der Monotonie der an gilt:
2 a4 a3 C a C 4
98
Diese Reihe ist konvergent für
entweder beide konvergent oder beide divergent. /////
Konvergenzkriterien
q D 21r :
8F
Die alternierende harmonische Reihe
1
X
nD1
.
1/nC1
1
1
1 1
D 1 C C :::
n
2
3 4
konvergiert nach dem Leibniz-Kriterium. G
99
Cauchyprodukte
6-C
6-C
Cauchyprodukte
6-C
(j)
X
X
cn WD
ak bl D
1
X
ak bl WD
k;l0
1
X
nD0
cn D
ai bni ;
1 X
X
/////
lD0
Es ist
X
X
cn D
0nN
und deshalb
X
jak j jbl j C
0lN
X
jbl j C
l0
X
jak j 0kN
X
k0
jak j X
ak bl D
1 X
n
X
jcn j jbl j:
l>N=2
1
X
ak
kD0
1
X
bl :
lD0
X
jak jjbl j:
ai bni :
P
Die Konvergenz der Reihe n jcn j folgt, indem man auf der linken Seite von
(j) die Beträge der Reihenglieder betrachtet. /////
Eine wichtige Anwendung des Cauchyprodukt-Satzes ist die Funktionalgleichung
der in Satz 6.5 eingeführten exp-Funktion.
6.6
Funktionalgleichung der Exponentialfunktion Für a; b 2 C gilt
exp a exp b D exp.a C b/:
nD0 iD0
/////
0nN kClDn
ak bl D
jbl j
N=2<lN
kClDn
nD0 iD0
nD0 kClDn
X
X
Um auch noch die absolute Konvergenz des Cauchyproduktes nachzuweisen,
bemerken wir, dass
Im Falle von Potenzreihen – siehe nächster Abschnitt – läuft dies gerade darauf hinaus, Terme gleicher Ordnung zusammenzufassen.
P
P
Cauchyprodukt-Satz Sind die Reihen k ak und l bl absolut konvergent, so
ist deren Cauchyprodukt ebenfalls absolut konvergent, und es gilt
X
X
X
1
1
1 X
n
ak
bl D
ai bni :
kD0
cn D
nD0
und damit das Cauchyprodukt der beiden Reihen als
X
N=2<kN
X
P
P
Da die Reihen k ak und l bl absolut konvergieren, strebt dieser letzte
Term für N ! 1 gegen 0. Also strebt auch auch die linke Seite von (j)
P
gegen 0. Dies bedeutet aber, dass n cn konvergiert mit Grenzwert
iD0
kClDn
jak j k>N=2
Nicht zum Ausdruck kommt hierbei, in welcher Reihenfolge die rechte Summe gebildet wird.
Um dies festzulegen, definiert man die endlichen Summen
(1)
jak bl j:
0k;lN
kCl>N
X
jak bl j k;l0
n
X
lD0
0k;lN
kCl>N
Deren Produkt besteht formal aus der Summe aller möglichen Produkte ak bl ihrer
Glieder, symbolisch ausgedrückt als
X
X
X
ak bl D
ak bl :
l0
kD0
X
Ist k C l > N , so ist entweder k > N=2 oder l > N=2. Deshalb gilt weiter
l0
k0
100
ˇX
ˇ
N
N
X
X
ˇN
ˇ
ˇ
ˇ
c
a
b
n
k
l
ˇ
ˇ
nD0
Satz 6.3 behandelt den einfachen Fall der Linearkombination zweier konvergenter
Reihen. Das Produkt zweier reell- oder komplexwertiger Reihen erfordert dagegen
eine genauere Untersuchung.
Gegeben seien zwei reelle oder komplexe Reihen
X
X
ak ;
bl :
k0
Cauchyprodukte
X
0k;lN
kClN
ak bl ;
Das Cauchyprodukt der Reihen für exp a und exp b ist
exp a exp b D
1 X
X
ak bl
:
k! l!
nD0 kClDn
Weiter ist
101
Potenzreihen
6-D
n
X ak bl
X
ai b ni
D
k! l!
i ! .n i/!
D
1
n!
n
X
iD0
1
n!
ai b ni D .a C b/n
i !.n i /!
n!
auf Grund der binomischen Formel. Also ist
exp a exp b D
1
X
nD0
1
.a C b/n D exp.a C b/:
n!
Potenzreihen
102
für alle n. Für jzj < jz0 j ist dann
iD0
kClDn
6-D
/////
jzjn
jzj
< 1:
M n;
D
jz0 jn
jz0 j
P
P
Somit besitzt die Reihe n an z n die konvergente Majorante n M n . /////
jan z n j D jan z0n j
Im Umkehrschluss zieht die Divergenz in einem Punkt z0 ¤ 0 auch die Divergenz für alle z 2 C mit jzj > jz0 j nach sich. Dies führt zu folgendem Ergebnis.
P
6.7
Satz Zu jeder komplexen Potenzreihe n an z n existiert eine eindeutig bestimmte reelle Zahl r 2 Œ0; 1 , so dass die Reihe
für jzj < r absolut konvergiert,
6-D
Potenzreihen
Eine Reihe der Bauart
X
an z n
n0
mit z 2 C und Koeffizienten a0 ; a1 ; a2 ; 2 C heißt Potenzreihe, genauer komplexe
Potenzreihe. Verschwinden alle Koeffizienten jenseits von an , so handelt es sich
insbesondere um ein komplexes Polynom
a0 C a1 z C C an z n :
Potenzreihen sind also »Polynome unendlichen Grades«. Während Polynome immer
auf ganz C erklärt sind, muss dies bei Potenzreihen jedoch keineswegs so sein.
P
n
9 F Die exp-Reihe
n0 z =n! konvergiert für alle z 2 C , die geometrische
P
n
Reihe n0 z nur für alle z 2 D , siehe Satz 6.5 und Beispiel 3. G
P
Eine Potenzreihe n0 an z n konvergiert natürlich immer für z D 0. Konvergiert sie noch in einem weiteren Punkt, so gilt das folgende, auf den ersten Blick
überraschende Resultat.
P
Satz Konvergiert die Potenzreihe n an z n in einem Punkt z0 ¤ 0, so konvergiert
sie absolut für alle z 2 C mit jzj < jz0 j . ///// Wegen der Konvergenz in z0 bildet an z0n eine Nullfolge. Also existiert
eine Konstante M mit
jan z0n j M
für jzj > r divergiert, falls r < 1.
Diese reelle Zahl r heißt der Konvergenzradius, die Kreisscheibe fz 2 C W jzj < r g
P
der Konvergenzkreis der Potenzreihe n an z n . Bemerkung. Wir sprechen der Kürze halber von der »reellen Zahl r 2 Œ0; 1«,
auch wenn r D 1 zugelassen ist. ///// Sei K die Menge aller komplexen Zahlen, für die die gegebene Reihe
konvergiert. Wegen 0 2 K ist K nicht leer, und wir können
˚
r D sup jzj W z 2 K 2 Œ0; 1
definieren. Ist nun jzj < r , so existiert ein z0 2 K mit jzj < jz0 j, und
die absolute Konvergenz folgt aus dem vorangehenden Satz. Ist jzj > r , so
kann die Reihe nicht konvergieren, da dies der Definition von r widerspricht.
Damit ist die Existenz eines Konvergenzradius gezeigt. Seine Eindeutigkeit
ist offensichtlich. /////
Der Satz macht keine Aussage über das Verhalten der Potenzreihe auf dem Rand
des Konvergenzkreises, also für jzj D r , falls r < 1. Tatsächlich stehen fast alle
Möglichkeiten offen. Hier drei einfache Beispiele.
10 F Die Potenzreihe
X zn
nr
n1
besitzt für jedes r 0 den Konvergenzradius 1. Für r D 0 divergiert sie für alle z
mit jzj D 1 . Für r D 1 erhalten wir in z D 1 die divergente harmonische Reihe,
in z D 1 die konvergente alternierende harmonische Reihe. Für r > 1 schließlich
103
Potenzreihen
ist die Reihe für alle z mit jzj D 1 absolut konvergent, denn
konvergente Majorante. G
P
n1
6-D
1=nr ist eine
Limes Superior
Satz 6.7 sichert zwar für jede Potenzreihe die Existenz eines eindeutig bestimmten
Konvergenzradius, macht aber keinerlei Angaben, wie dieser aus deren Koeffizienten zu bestimmen ist. Zu diesem Zweck benötigen wir noch den Begriff des Limes
superior einer reellen Zahlenfolge.
Jede reelle Zahlenfolge .xn / besitzt auf Grund des Satzes von Bolzano-Weierstraß
mindestens einen eigentlichen order uneigentlichen Häufungspunkt. Die Menge aller
Häufungspunkte einer reellen Folge ist somit nicht leer und besitzt ein Supremum in
N . Daher ist folgende Definition sinnvoll.
R
Definition Der Limes superior einer reellen Zahlenfolge ist das Supremum aller
ihrer eigentlichen oder uneigentlichen Häufungspunkte. lim sup xn D lim xn :
n!1
Satz zum Limes superior Für den Limes superior einer reellen Folge .xn / gilt:
(i) Ist .xn / konvergent, so ist lim sup xn D lim xn .
(ii) .xn / ist nach oben unbeschränkt genau dann, wenn lim sup xn D 1.
(iii) Ist lim sup xn D x endlich, so existiert zu jedem " > 0 ein N , so dass
xn < x C ";
n N:
(iv) Ist lim sup xn D 1, so gilt lim xn D 1.
///// (i) Ist .xn / konvergent, so ist lim xn der einzige Häufungspunkt der
Folge, also auch ihr Limes superior.
(ii) .xn / ist nach oben unbeschränkt genau dann, wenn 1 uneigentlicher
Häufungspunkt ist. Das ist dann auch der größte Häufungspunkt der Folge.
(iii) Falls nicht, so gibt es ein " > 0 , so dass
xn x C "
Potenzreihen
104
(iv) Nach Voraussetzung ist 1 der einzige Häufungspunkt der Folge. Also wird jede vorgegebene Schranke von fast allen Folgengliedern unterboten.
Das bedeutet aber auch, dass lim xn D 1 gilt. /////
Entsprechendes gilt für den Limes inferior einer reellen Folge. Diesen werden
wir aber im Weiteren nicht benötigen.
P
6.8
Satz Für den Konvergenzradius der komplexen Potenzreihe n an z n gilt
die Hadamardsche Formel
rD
1
lim sup
:
p
n
jan j
p
///// Ist r D 0, so bildet n jan z n j für z ¤ 0 keine Nullfolge. Die Reihe
konvergiert also nur für z D 0, und der Satz ist bewiesen.
Ist r > 0, so ist für jzj < r
p
p
lim sup n jan z n j D jzj lim sup n jan j < 1:
Dies gilt auch für den Fall r D 1 . Also existiert ein q 2 .0; 1/ und ein N ,
so dass
p
n
n N:
jan z n j q < 1;
Bezeichnungen für den Limes superior sind
n!1
6-D
für unendlich viele n:
Diese xn müssen aber nach Bolzano-Weierstraß einen weiteren Häufungspunkt oberhalb von x besitzen, und x wäre nicht der größte Häufungspunkt.
Die Konvergenz der Reihe folgt damit aus dem Wurzelkriteriums.
Die Divergenz für jzj > r folgt analog. Wegen seiner Eindeutigkeit muss
daher r der Konvergenzradius der Reihe sein. /////
P
11 F Für n0 n! z n ist
p
n
lim sup n! D 1;
r D 0;
die Reihe konvergiert also nur für z D 0 und divergiert für alle z ¤ 0.
P
Für die geometrische Reihe n0 z n ist
p
n
r D 1:
lim sup 1 D 1;
Diese Reihe konvergiert absolut für jzj < 1, und divergiert für jzj 1, wie wir
bereits in Beispiel 3 festgestellt haben.
P
Für die exp-Reihe n0 z n =n! gilt
1
D 0;
lim sup p
n
n!
r D 1;
die Reihe konvergiert für alle z 2 C , wie wir ebenfalls bereits wissen. G
105
Potenzreihen
6-D
Rechenregeln
P
P
Rechenregeln für Potenzreihen Seien n an z n und n bn z n Potenzreihen mit
positiven Konvergenzradien ra und rb . Dann gilt
X
X
X
.an C bn /z n ;
an z n C
bn z n D
n0
X
n0
an z n n0
X
n0
bn z n D
n0
X X
n0
ani bi z n ;
0in
mindestens für alle z mit jzj < min .ra ; rb /. Bemerkung. Der Konvergenzradius raCb und rab der Summen- bzw Produktreihe ist also mindestens min .ra ; rb /, er kann aber sehr wohl größer sein. /////
Beide Reihen konvergieren absolut für
jzj < min .ra ; rb /:
Für diese z folgt der Satz also aus den entsprechenden Sätzen über Summen
und Produkte absolut konvergenter Reihen. /////
Bemerkung. Das Cauchyprodukt ist also gerade so definiert, dass jeweils alle
Terme gleicher Ordnung »gesammelt« werden. Mit der Notation von (1) ist
X cn D
ak z k bl z l
kClDn
D
X
kClDn
ak bl z kCl D z n
X
kClDn
ak bl :
6-D
Potenzreihen
106
7-A
Funktionsgrenzwerte
108
und analog UP " .
1/. Die Definition des Häufungspunktes bleibt unverändert. Man
nennt ˙1 uneigentliche Häufungspunkte, alle anderen Punkte dagegen auch eigentliche oder endliche Häufungspunkte.
7
1F
a. Die Menge f1; 2; 3g besitzt keine Häufungspunkte.
b. Die Menge der Häufungspunkte des offenen Intervalls .0; 1/ ist das abgeschlossene Intervall Œ0; 1.
c. Die Menge der eigentlichen Häufungspunkte von Q ist R .
d. N R besitzt den uneigentlichen Häufungspunkt 1. G
Funktionen
Wir wollen nun klären, was man unter dem Grenzwert einer Funktion f an einer
Stelle a versteht, geschrieben
Bemerkung. Ein Punkt a 2 A, der nicht Häufungspunkt von A ist, heißt isolierter Punkt von A. Für ihn gibt es also ein " > 0, so dass
U" .a/ \ A D fag:
lim f .x/ D b:
x!a
Wie im Fall der Konvergenz von Folgen studieren wir diese Frage im Kontext metrischer Räume.
Seien also .X; dX / und .Y; dY / metrische Räume, A X , und
Satz Ist a Häufungspunkt der Menge A, so liegen in jeder Umgebung von a unendlich viele Punkte von A. ///// Wir betrachtenden den Fall eines endlichen Häufungspunktes. Gilt die
Behauptung des Satzes nicht, so gibt es eine Umgebung U.a/ mit nur endlich
vielen Punkten in A. Dann aber ist
˚
" D min dX .x; a/ W x 2 UP .a/ > 0;
f W A ! Y:
Um überhaupt von einem Grenzwert der Funktion f im Punkt a sprechen zu können, muss dieser »von A aus« beliebig gut approximierbar sein, ohne dabei selbst zu
A gehören zu müssen. Dies führt zu dem Begriff des Häufungspunktes einer Menge.
Unter der punktierten " -Umgebung des Punktes a 2 X versteht man die Menge
da das Minimum endlich vieler positiver Zahlen positiv ist. Es gilt dann
UP " .a/ \ A D ∅:
UP " .a/ WD U" .a/ fag
Also ist a kein Häufungspunkt von A. /////
D fx 2 X W 0 < dX .x; a/ < "g:
Eine beliebige Teilmenge von X heißt punktierte Umgebung von a, wenn sie eine
punktierte "-Umgebung von a , nicht aber den Punkt a selbst enthält.
Definition Ein Punkt a heißt Häufungspunkt der Menge A X , wenn in jeder
punktierten "-Umgebung von a mindestens ein Punkt von A liegt. Funktionsgrenzwerte
Für das Folgende sei immer
f W A ! Y;
Formal ausgedrückt:
UP " .a/ \ A ¤ ∅;
7-A
" > 0:
Der Punkt a muss dabei nicht zu A gehören!
Auf der reellen Geraden wollen wir auch noch ˙1 als Häufungspunkte zulassen. Dazu definieren wir deren punktierte Umgebungen als
UP " .1/ WD U" .1/ D .1="; 1/;
mit A X , und a ein Häufungspunkt von A. Wir nehmen aber nicht a 2 A an.
Definition Die Funktion f W A ! Y besitzt für x ! a den Grenzwert b 2 Y ,
falls es zu jeder "-Umgebung U" .b/ eine punktierte ı-Umgebung UP ı .a/ gibt, so
dass
f .UP ı .a/ \ A/ U" .b/:
109
Funktionsgrenzwerte
7-A
7-A
Funktionsgrenzwerte
punktierten 1=n -Umgebung von a einen Punkt xn 2 A mit
Bezeichnungen für diesen Grenzwert sind
f .xn / … U" .b/:
lim f .x/ D b:
A3x!a
oder f .x/ ! b für A 3 x ! a. Ist der Definitionsbereich A aus dem Kontext klar,
so wird er auch weggelassen.
Zu jedem " > 0 existiert also ein ı > 0, so dass im Fall endlicher Punkte a und
b die Aussage
0 < dX .x; a/ < ı ^ x 2 A ) dY .f .x/; b/ < "
gilt, während zum Beispiel für a D 1
x > 1=ı ^ x 2 A ) dY .f .x/; b/ < "
Diese xn bilden eine Folge in Afag mit Grenzwert a, für die f .xn / sicher
nicht gegen b konvergiert. /////
Wir geben noch eine weitere Charakterisierung des Funktionsgrenzwertes.
Satz Sei a ein eigentlicher oder uneigentlicher Häufungspunkt der Menge A, und
f W A ! Y . Dann gilt:
(i)
7.1
Folgenkriterium Sei a ein Häufungspunkt von A X und f W A ! Y .
Dann gilt
lim f .x/ D b
x!a
lim f .x/ D b:
x!a
/////
2F
///// ) Es gelte limA3x!a f .x/ D b , und es sei .xn / eine beliebige
Folge in A fag . Zu jedem " > 0 existiert ein ı > 0 , so dass
Dies folgt direkt aus den Definitionen. /////
Für jede konstante Funktion c W X ! Y , x 7! c gilt
lim c D c:
lim id.x/ D lim x D a:
x!a
3F
Zu diesem ı existiert wiederum ein N , so dass
n N:
Da für jedes " > 0 solch ein N existiert, gilt limn!1 f .xn / D b .
( Dies beweisen wir indirekt. Gilt nicht limA3x!a f .x/ D b , so gibt es
ein " > 0 , »zu dem kein ı > 0 existiert«. Insbesondere gibt es dann in jeder
G
Die Gaußklammer
Œx D max fn 2 Z W n x g
besitzt einen Grenzwert in jedem Punkt a … Z:
lim Œx D Œa;
x!a
a … Z:
In jedem Punkt m 2 Z besitzt sie dagegen keinen Grenzwert, da
n N;
da xn ! a in A . Tatsächlich ist nach Annahme xn ¤ a für alle n. Also gilt
x!a
ΠW R ! R;
f .UP ı .a/ \ A/ U" .b/:
f .xn / 2 U" .b/;
x!a
genau dann, wenn für jede gegen a konvergierende Folge .xn / in A fag gilt:
xn 2 Uı .a/ \ A;
x!a
Für die Identitätsfunktion idW X ! X , x 7! x gilt
A3x!a
lim f .xn / D b:
lim f .x/ D b , lim dY .f .x/; b/ D 0.
x!a
(ii) Gilt dY .f .x/; b/ .x/ in einer punktierten Umgebung von a, und ist
lim .x/ D 0, so gilt
gilt. Für diese Definition ist es völlig unerheblich, ob und wie die Funktion im Punkt
a selbst definiert ist!
Funktionsgrenzwerte und Folgengrenzwerte sind auf folgende Weise miteinander
verknüpft.
n!1
110
lim Œm 1=n D m 1 ¤ m D lim Œm C 1=n:
n!1
4F
n!1
G
Für die Funktion f W R ! R , x 7! x sin x1 gilt
lim f .x/ D 0:
x!0
Hier existiert also ein Grenzwert in einem Punkt, in dem die Funktion nicht erklärt
worden ist. G
111
Funktionsgrenzwerte
/////
7-A
Bekanntlich ist jsin xj 1 für alle x . Also gilt
Grenzwertsätze
x2R :
lim
Ist also x 2 UP " .0/ , so ist jf .x/j jxj < " . Daraus folgt die Behauptung. /////
Die signum oder Vorzeichenfunktion ist definiert als
8
ˆ
ˆ
< 1; x > 0;
sgnW R ! R; sgn.x/ D
0; x D 0;
ˆ
:̂ 1; x < 0:
N3x!1
lim
7-B
Seien nun E und F normierte Räume mit Normen j jE und j jF . Sind
f W A ! F;
sgn.x/ D 1;
lim
.0;1/3x!0
x!0
Die Dirichlet-Funktion
ıW R ! R;
zwei Funktionen auf A E , so definiert man deren lineare Kombination f C g
punktweise durch
sgn.x/ D 1;
(
ı.x/ D
G
fgW A ! F;
1; x 2 Q;
lim
/////
1
D 0;
x
7.2
Grenzwertgleichungen Sei a ein eigentlicher oder uneigentlicher Häufungspunkt von A, und seien f; gW A ! F Funktionen mit
lim f .x/ D b;
x!a
lim exp x D 1;
x!1
lim exp x D 0:
x!1
X xn
1 C x;
n!
(iii)
n0
die dritte aus exp.
x/ D .exp x/1 und somit
Eine Folge .xn / in X ist gegen durch eine Funktion
xW N ! X;
n 7! x.n/ D xn :
(iv)
/////
lim g.x/ D c:
x!a
Dann gilt:
(ii)
x 0;
1
lim exp x D lim exp.
t/ D lim
D 0:
x!1
t !1
t !1 exp t
G
(i)
Die zweite Behauptung folgt aus
exp x D
.fg/.x/ D f .x/g.x/
erklärt. Entsprechend f =g , wenn g auf A nirgends verschwindet.
0; x … Q;
Einige uneigentliche Grenzwerte:
x!1
.f C g/.x/ D f .x/ C g.x/:
Sind die Funktionen reell- oder komplexwertig, also F D K, so ist auch
besitzt in keinem Punkt einen Grenzwert. G
8F
gW A ! F:
f C gW A ! F;
lim jsgn.x/j D 1 ¤ 0 D jsgn.0/j:
7F
n!1
Grenzwertsätze
sowie
6F
x.n/ D lim xn ;
wenn diese Grenzwerte existieren. G
Hier gilt zum Beispiel
.1;0/3x!0
112
Dann ist
jf .x/j D jxj jsin 1=xj jxj;
5F
7-B
lim jf .x/jF D jbjF ,
x!a
lim .f C g/.x/ D b C c
x!a
für
2 K,
lim .fg/.x/ D bc ,
x!a
lim .f =g/.x/ D b=c ,
x!a
falls c ¤ 0.
wobei die letzten beiden Aussagen für reell- oder komplexwertige Funktionen gelten. Bemerkung. In diesem Satz sind alle Grenzwerte eigentlich, also endlich, auch
wenn a D ˙1. 113
Grenzwertsätze
7-B
7-B
///// Wir beweisen zum Beispiel (iv) mit Hilfe des Folgenkriteriums. Sei
.xn / eine beliebige Folge in A fag mit xn ! a . Dann gilt also
lim f .xn / D b;
n!1
UP .a/ WD UPf .a/ \ UP g .a/
ist wiederum eine punktierte Umgebung von a. Für x 2 UP .a/ \ A gilt dann
n!1
Insbesondere gibt es zu " D jcj=2 > 0 ein N mit
f .x/ < b C " D c " < g.x/:
n N:
Mit der umgekehrten Dreiecksungleichung folgt daraus
jg.xn /jF > jcjF " D ";
lim
lim f .x/ D b;
lim g.f .x// D c:
A3x!a
g.y/ 2 U" .c/;
f .x/ 2 Uı .b/;
x!a
wenn diese Grenzwerte existieren.
x 2 UP .a/ \ A:
Ist nun f .x/ ¤ b für alle x in einer punktierten Umgebung von a so folgt,
bei hinreichend kleinem , aus diesen beiden Inklusionen auch
(ii) Gilt f .x/ h.x/ g.x/ für x in einer punktierten Umgebung von a und
g.f .x// 2 U" .c/:
lim f .x/ D b D lim g.x/;
x!a
Gibt es jedoch auch x 2 UP .a/ mit f .x/ D b , so ist mit Annahme (a) erst
Recht
so existiert auch limx!a h.x/ und ist gleich b .
(iii) Gilt
g.f .x// D g.b/ D c 2 U" .c/:
lim f .x/ D b < c D lim g.x/;
Also gilt in jedem Fall g.f .x// 2 U" .c/ für x 2 UP .a/ \ A. Das war zu
zeigen. /////
x!a
so existiert eine punktierte Umgebung UP .a/, so dass
///// Zum Beispiel (iii). Sei " D .c b/=2 > 0. Dann gibt es punktierte
Umgebungen UPf .a/ und UP g .a/ mit
f .UPf .a/ \ A/ U" .b/;
y 2 UP ı .b/ \ B:
Zu der nicht-punktierten Umgebung UP ı .b/ wiederum existiert ein > 0 mit
lim f .x/ lim g.x/;
x 2 UP .a/ \ A:
Gegeben " > 0, so gibt es ein ı > 0 mit
/////
(i) Gilt f .x/ g.x/ für x in einer punktierten Umgebung von a, so gilt auch
f .x/ < g.x/;
Hierbei ist natürlich angenommen, dass a Häufungspunkt von A und b Häufungspunkt von B ist.
Grenzwertungleichungen Sei a ein eigentlicher oder uneigentlicher Häufungspunkt von A , und seien die folgenden Funktionen auf A reellwertig.
x!a
B3y!b
und gilt (i) g.b/ D c oder (ii) f .x/ ¤ b für alle x in einer punktierten Umgebung
von a, so gilt auch
Da dies für jede Folge .xn / in Afag mit xn ! a gilt, folgt die Behauptung
wiederum mit dem Folgenkriterium. /////
x!a
lim g.y/ D c;
A3x!a
lim f .xn /
f .xn /
b
D
D :
g.xn
lim g.xn /
c
x!a
/////
Verkettung von Grenzwerten Besitzen die Funktionen f W A ! B und gW B !
C die Grenzwerte
n N:
Auf Grund des Grenzwertsatzes M gilt daher auch
n!1
114
Deren Durchschnitt
lim g.xn / D c:
jg.xn / cjF < ";
Grenzwertsätze
g.UP g .a/ \ A/ U" .b/:
9F
lim
x!1
/////
xn 1
D n. G
x
1
Für x ¤ 1 ist
n
x 1
D x n1 C x n2 C C x C 1:
x
1
115
Uneigentliche Grenzwerte
7-C
Auf der rechten Seite können wird die Grenzwertsätze für Addition und Multiplikation anwenden, und erhalten
xn 1
D lim x n1 C x n2 C C x C 1
x!1 x 1
x!1
D 1n1 C 1n2 C C 1 C 1 D n:
(iv)
/////
11 F
Es ist
exp z D
Xz
z
z
D1CzC
C
C :::;
n!
2!
3!
n
2
3
n0
und für z ¤ 0 somit
X zn
z
z2
exp z 1
D1C C
C ::: D 1 C
DW 1 C r .z/:
z
2!
3!
.n C 1/!
n1
Für jzj < 1 können wir abschätzen:
jr .z/j X jzjn
jzj=2
jzj
jzj:
D
D
2n
1 jzj=2
2 jzj
n1
Also gilt limz!0 r .z/ D 0, und daraus folgt die Behauptung. /////
7-C
Uneigentliche Grenzwerte
Die vorangehenden Sätze betreffen eigentliche Grenzwerte von Funktionen. Wie bei
den Grenzwertsätzen für reelle Zahlenfolgen wollen wir jetzt noch die Ergebnisse
erwähnen, die auch für uneigentliche Grenzwerte gelten.
Im folgenden Satz steht
g a c;
f a 0;
für g.x/ 0 bzw f .x/ > 0 für x in einer punktierten Umgebung von a.
Satz Sei a ein eigentlicher oder uneigentlicher Häufungspunkt von A , und seien
f und g reellwertige Funktionen auf A. Dann gilt:
lim f .x/ D 1 ^ g a c ) lim .f C g/.x/ D 1,
x!a
Uneigentliche Grenzwerte
116
lim f .x/ D 1 ^ g a c > 0 ) lim .fg/.x/ D 1;
x!a
x!a
lim jf .x/j D 1 ) lim 1=f .x/ D 0,
x!a
x!a
lim f .x/ D 0 ^ f a 0 ) lim 1=f .x/ D 1. x!a
x!a
///// Dies folgt aus Satz 5.15 und dem Folgenkriterium 7.1 für Funktionsgrenzwerte. /////
exp z 1
D 1: G
z!0
z
lim
/////
(i)
(ii)
(iii)
lim
10 F
7-C
x!a
1
D 1;
x
1
1
D lim D 1:
lim
t
.1;0/3x!0 x
.0;1/3t!0
lim
.0;1/3x!0
G
8-A
Stetige Funktionen
118
2 F Die Vorzeichenfunktion sgnW R ! R ist in 0 unstetig, in jedem anderen
Punkt stetig. G
3F
8
Stetigkeit
8-A
wobei q.x/ den kleinstmöglichen positiven Nenner aller Darstellungen der rationalen Zahl x als Quotient zweier ganzer Zahlen bezeichnet. Diese Funktion ist in allen
irrationalen Punkten stetig, in allen rationalen Punkten unstetig. G
Stetige Funktionen
Lokale Stetigkeit
Seien .X; dX / und .Y; dY / metrische Räume, und f W X ! Y .
Definition Die Funktion f W X ! Y heißt stetig im Punkt a 2 X , wenn es zu
jedem " > 0 ein ı > 0 gibt, so dass für alle x 2 X gilt:
dX .x; a/ < ı ) dY .f .x/; f .a// < ":
In der Sprache der Umgebungen: . . . , so dass gilt:
f .Uı .a// U" .f .a//:
Zur Erinnerung:
Uı .a/ D fx 2 X W dX .x; a/ < ıg X
ist immer eine Teilmenge von X , auch wenn X Teilmenge eines größeren metrischen Raumes ist.
Ist eine Funktion in a 2 X nicht stetig, so heißt sie unstetig im Punkt a.
1F
In einem isolierten Punkt ist jede Funktion stetig. G
///// Sei f W X ! Y . Ist a 2 X ein isolierter Punkt von X , so gibt es ein
ı > 0 mit
Bı .a/ D fag:
Dann ist aber trivialerweise für jedes " > 0
dY .f .x/; f .a// D 0 < "
für alle x 2 Bı .a/. /////
Die »modifizierte« Dirichletfunktion @W R ! R ist definiert durch
(
0;
x … Q;
@.x/ D
1=q.x/; x 2 Q;
8.1
Satz Die folgenden Aussagen über die Funktion f W X ! Y und a 2 X
sind äquivalent:
(i) f ist stetig im Punkt a.
(ii) Das Urbild jeder Umgebung von f .a/ enthält eine Umgebung von a.
(iii) Es gilt limx!a f .x/ D f .a/.
(iv) Für jede Folge .xn / in X mit xn ! a gilt auch f .xn / ! f .a/. Gemäß (iii) darf man also »f « und »lim« vertauschen, wenn f in a stetig ist:
lim f .x/ D f . lim x/ D f .a/:
x!a
x!a
Der Frage, unter welchen Voraussetzung man »lim« mit anderen Operationen vertauschen darf, werden wir immer wieder begegnen, zum Beispiel beim Studium von
Folgen von Funktionen.
/////
(i) ) (ii)
Ist V eine Umgebung von f .a/, so existiert ein " > 0 mit
U" .f .a// V:
Zu diesem " gibt es wegen der Stetigkeit von f in a ein ı > 0 mit
f .Uı .a// U" .f .a//:
Das aber bedeutet, dass
Uı .a/ f 1 .U" .f .a// f 1 .V /:
Also ist f 1 .V / eine Umgebung von a.
(ii) ) (iii) Sei " > 0. Das Urbild der Umgebung U" .f .a// ist eine Umgebung von a, enthält also eine ı-Umgebung Uı .a/ . Für dX .x; a/ < ı gilt
somit dY .f .x/; f .a// < ". Da zu jedem " > 0 ein solches ı > 0 existiert,
119
Stetige Funktionen
8-A
ist
lim f .x/ D f .a/:
x!a
(iii) ) (iv) Das ist der Inhalt von Satz 7.1.
(iv) ) (i) Angenommen, f ist nicht stetig in a. Dann gibt es ein "0 > 0,
und zu jedem n 1 ein xn 2 U1=n .a/ mit
8-A
Satz
dY .f .x/; f .y// LdX .x; y/ < Lı D
5 F Ist die Funktion f W X ! Y stetig und M X eine beliebige Teilmenge,
so ist auch die Einschränkung f jM W M ! Y stetig. G
6F
Die Wurzelfunktion ist auf Œ0; 1/ stetig. G
///// Betrachte zuerst den Punkt a D 0. Ist jx aj D jxj < ı WD "2 , so ist
ˇp
p ˇ p
ˇ x aˇ D x < ":
Die Definition der Stetigkeit im Punkt a D 0 ist also mit ı D "2 erfüllt. Die
übrigen Punkte betrachten wir in Beispiel 10 unten. /////
Eine große und wichtige Klasse stetiger Funktionen bilden die Lipschitz-stetigen
Funktionen.
Definition Eine Funktion f W X ! Y heißt Lipschitz-stetig auf X , oder einfach
Lipschitz, wenn es eine Konstante L 0 gibt, so dass
dY .f .x/; f .y// L dX .x; y/
für alle x; y 2 X . Eine solche Zahl L heißt Lipschitz- oder L-Konstante. L"
< ":
LC1
Da wir ı unabhängig vom betrachteten Punkt in X wählen können, folgt
daraus die Stetigkeit von f auf ganz X . /////
Globale Stetigkeit
4 F Auf jedem metrischen Raum X sind konstante Funktionen stetig, ebenso die
Identität idW X ! X . G
Jede Lipschitz-stetige Funktion ist stetig. ///// Zu gegebenen " > 0 wähle man ı D "=.L C 1/. Für alle x; y 2 X
mit dX .x; y/ < ı gilt dann
Wir erhalten eine Folge .xn / in X mit xn ! a, aber f .xn / f .a/. Dies
ist ein Widerspruch zur Annahme (iv). /////
Umgekehrt ist f auf X unstetig, wenn sie in wenigstens einem Punkt von X
unstetig ist. Ein ›schlechter‹ Punkt genügt also, um die Stetigkeit auf X zu ruinieren . . .
120
Mit L ist natürlich auch jede reelle Zahl L0 L eine Lipschitz-Konstante.
L-Konstanten sind also nicht eindeutig.
Auch wenn der Name es suggeriert, müssen wir doch noch nachweisen, dass
Lipschitz-Funktionen stetig sind.
dY .f .xn /; f .a// "0 :
Definition Die Funktion f W X ! Y heißt stetig auf X , oder kurz stetig, wenn
sie in jedem Punkt von X stetig ist. Stetige Funktionen
7 F Auf einem beliebigen metrischen Raum sind konstante Funktionen Lipschitz
mit L D 0, und die Identität ist Lipschitz mit L D 1. G
8F
Auf C sind die Abbildungen
z 7! Re z;
z 7! Im z;
z 7! zN
sämtlich Lipschitz mit L D 1. Zum Beispiel ist
ˇ
ˇ
ˇ z zN w wN ˇ jz wj C jNz wj
N
ˇ
D jz wj:
jIm z Im wj D ˇˇ
2i
2i ˇ
2
9F
Auf einem normierten Raum .E; k k/ ist die Norm
k kW E ! R;
x 7! kxk
Lipschitz mit L D 1. Dies ist gerade die umgekehrte Dreiecksungleichung:
G
jkxk kykj kx yk:
p
10 F Die Wurzelfunktion ist auf jedem Intervall Œa; 1/ mit a > 0 Lipschitz,
nicht aber auf Œ0; 1/. G
p
///// Wähle L D 1=2 a. Dann gilt für x ¤ y in Œa; 1/ die Abschätzung
ˇ
ˇ
ˇ ˇ
ˇ
ˇp
jx yj
ˇ x py ˇ D ˇ p x y
ˇ
/////
ˇ x C py ˇ pa C pa D Ljx yj:
G
121
Stetige Funktionen
8-A
Stetigkeitssätze
8-B
Zwischenwertsatz und Umkehrfunktion
Satz
8.2
Satz Seien f; gW X ! Y im Punkt a 2 X stetig. Ist Y ein normierter
Raum, so sind auch die Funktionen
f C g;
fg;
f =g
(falls g.a/ ¤ 0)
Wir betrachten nun die Verkettung von stetigen Abbildungen.
8.4
Satz Seien X; Y; Z metrische Räume. Ist f W X ! Y stetig auf X und
gW Y ! Z stetig auf Y , so ist auch die verkettete Funktion
in a stetig. ///// Dies folgt mit dem Stetigkeitskriterium von Satz 8.1 aus dem entsprechenden Satz 7.2 für Funktionsgrenzwerte. Betrachte zum Beispiel f =g . Nach
Voraussetzung gilt
lim f .x/ D f .a/;
x!a
gBfW X !Z
stetig auf X . ///// Ist a 2 X beliebig, und .xn / eine beliebige Folge in X mit Grenzwert
a, so ist wegen der Stetigkeit von f
lim g.x/ D g.a/ ¤ 0:
x!a
Nach Satz 7.2 gilt dann auch
lim f .xn / D f .a/ D b:
f .x/
f .a/
D
;
x!a g.x/
g.a/
n!1
lim
Da die Folge der yn D f .xn / in Y gegen b konvergiert, gilt weiter
und das ist die Behauptung. /////
lim g.yn / D g.b/ D c
n!1
Aus diesem Satz ergibt sich sofort die entsprechende »globale« Version.
wegen der Stetigkeit von g . Also gilt auch
8.3
Satz Seien f; gW X ! Y auf X stetig. Ist Y ein normierter Raum, so sind
auch die Funktionen
f C g;
lim g.f .xn // D lim g.yn / D c D g.f .a/:
n!1
f =g
(falls g ¤ 0 auf X )
auf X stetig. /////
n!1
/////
11 F Sei .E; k k/ ein normierter Raum. Ist f W X ! E stetig, so ist auch
kf k
kf kW X ! R;
für alle ; 2 K auf X stetig. Ist sogar Y D K, so sind auch die Funktionen
fg;
Jedes Polynom ist stetig auf C . ///// Wir können die Koeffizienten als konstante Funktionen und z als die
Identitätsfunktion auf C auffassen. Diese sind stetig auf C . Jedes Polynom
entsteht durch Addition und Multiplikation solcher Funktionen, dessen Stetigkeit folgt daher mit Satz 8.3. /////
kf k
für alle ; 2 K in a stetig. Ist sogar Y D K, so sind auch die Funktionen
122
x 7! kf .x/k
stetig. Denn dies ist die Verkettung der stetigen Funktion f mit der stetigen Normfunktion k kW E ! R . G
Wende den vorangegangenen Satz auf jeden Punkt a 2 X an. /////
h C.X; Y / ist Vektorraum, Algebrai
Eine wichtige Klasse stetiger Funktionen bilden die Polynome. Dies sind Funktionen pW C ! C der Gestalt
n
p.z/ D an z C an1 z
n1
C C a1 z C a0
mit Koeffizienten a0 ; : : : ; an 2 C . Ist an ¤ 0, so heißt n der Grad des Polynoms.
8-B
Zwischenwertsatz und Umkehrfunktion
In diesem Abschnitt betrachten wir einige fundamentale Eigenschaften stetiger, reellwertiger Funktionen auf einem Intervall I . Es ist also im Folgenden
f W I ! R:
123
Zwischenwertsatz und Umkehrfunktion
8-B
8-B
Zwischenwertsatz von Bolzano Sei f W Œa; b ! R stetig und f .a/ ¤ f .b/.
Dann existiert zu jeder reellen Zahl c zwischen f .a/ und f .b/ mindestens ein
2 .a; b/ mit f ./ D c . /////
Ohne Beschränkung der Allgemeinheit können wir annehmen, dass
f .a/ < c < f .b/:
Andernfalls gehen wir zu f und den Zwischenwert c über. Betrachte
A D fx 2 Œa; b W f .x/ < c g Œa; b:
Wenden wir den Satz von Bolzano auf die Einschränkung von f auf das abgeschlossene Intervall zwischen a und b an, so erhalten die Behauptung. /////
Bemerkung. Alle drei Versionen des Zwischenwertsatzes sind äquivalent. Das
heißt, aus jedem der drei Sätze lassen sich die beiden anderen Sätze ableiten. Beispiel und Satz Jedes reelle Polynom ungeraden Grades besitzt mindestens eine
reelle Nullstelle. /////
f ./ D lim f .xn / c:
lim p.x/ D 1;
n!1
///// Entweder ist f .a/ < 0 < f .b/ oder f .a/ > 0 > f .b/. In jedem Fall
können wir den Satz von Bolzano mit c D 0 anwenden. /////
Zwischenwertsatz für allgemeine Intervalle Sei I ein beliebiges Intervall und
f W I ! R stetig. Dann nimmt f jeden Wert zwischen infI f und supI f mindestens einmal an. Hierbei bedeutet zum Beispiel infI f D inf ff .x/ W x 2 I g.
/////
Sei infI f < c < supI f . Dann gibt es a 2 I und b 2 I mit
au ¤ 0;
mit reellen Koeffizienten definiert eine stetige Funktion pW R ! R . Wir können au D 1 annehmen, denn die Nullstellen von p bleiben unverändert, wenn
wir p mit a1
u multiplizieren. Dann aber gilt
und es gibt eine Folge .xn / in A mit xn ! . Da f stetig ist und f .xn / < c
für alle n gilt, folgt auf Grund von Satz 5.8
Spezialfall des Zwischenwertsatz Ist f W Œa; b ! R stetig und f .a/f .b/ < 0 ,
so besitzt f in .a; b/ mindestens eine Nullstelle. Ein Polynom
p.x/ D au x 2nC1 C a2n x 2n C C a1 x C a0 ;
D sup A b;
Der Zwischenwertsatz gilt nicht, wenn f nicht stetig, oder der Definitionsbereich
kein Intervall ist. Die Intervalleigenschaft haben wir stillschweigend für den Schluss
benutzt, dass D sup A zum Definitionsbereich von f gehört.
124
f .a/ < c < f .b/:
Diese Menge ist beschränkt und nicht leer, da a 2 A . Somit existiert
Zu zeigen bleibt, dass f ./ D c .
Es ist < b wegen c < f .b/. Wäre nun f ./ < c , so gäbe es auf Grund der
Stetigkeit von f auch noch ein 2 .; b/ mit f ./ < c , also auch 2 A .
Dies aber widerspricht der Definition von als Supremum von A . Also gilt
f ./ D c . /////
Zwischenwertsatz und Umkehrfunktion
x!1
lim p.x/ D 1:
x!1
Die Existenz einer Nullstelle folgt dann aus dem Zwischenwertsatz. /////
Der Satz ist – natürlich – falsch für Polynome geraden Grades. Das Polynom
x 2 C 1 beispielsweise besitzt keine reelle Nullstelle.
Eine zweite wichtige Konsequenz des Zwischenwertsatzes ist »topologischer«
Natur: Stetige Bilder von Intervallen sind wieder Intervalle.
Satz
Ist I ein Intervall und f W I ! R stetig, so ist auch f .I / ein Intervall. /////
Es ist
f .I / D ff .x/ W x 2 I g:
Gehören u < v zu f .I /, so nimmt f die Werte u und v an. Dann nimmt f
aber aus Stetigkeitsgründen auch alle dazwischen liegenden Werte an, es gilt
also auch Œu; v f .I / . Somit enthält f .I / mit je zwei Punkten auch alle
dazwischen liegenden Punkte, ist also per definitionem ein Intervall. /////
Umkehrfunktionen
8.5
Satz Sei I ein Intervall, und f W I ! R stetig und streng monoton steigend. Dann gilt:
(i) f .I / D I ist wieder ein Intervall.
125
Zwischenwertsatz und Umkehrfunktion
8-B
8-C
x n y n D .x y/.x n1 C C y n1 / > 0;
(ii) f W I ! I ist bijektiv.
(iii) Die Umkehrfunktion f 1 W I ! I ist ebenfalls stetig und streng monoton
steigend.
///// (i) Dies ist der vorangehende Satz.
(ii) Die Surjektivität ist Teil der Aussage von (i). Die Injektivität folgt aus
der strengen Monotonie: Ist s1 ≷ s2 , so ist auch f .s1 / ≷ f .s2 /. Also ist
f W I ! I bijektiv.
(iii) Wegen (ii) existiert die Umkehrfunktion f 1 W I ! I , und es ist
leicht zu verifizieren, dass f 1 ebenfalls streng monoton steigt. Zu zeigen
bleibt die Stetigkeit von f 1 .
Angenommen, f 1 ist in einem Punkt t0 2 I nicht stetig. Dann existiert
ein " > 0 und eine Folge .tn / in I mit
ˇ 1
ˇ
ˇf .tn / f 1 .t0 /ˇ ":
tn ! t0 ;
Mit sn D f 1 .tn / und tn D f .sn / ist dies gleichbedeutend mit
f .sn / ! f .s0 /:
Wegen der Monotonie von f ist die Folge .sn / in I beschränkt. Mit dem
Satz von Bolzano-Weierstraß kann man also eine Teilfolge .sni / auswählen,
die gegen einen Grenzwert sQ0 ¤ s0 konvergiert. Da f stetig ist, gilt
f .Qs0 / D lim f .sni / D lim f .sn / D f .s0 /:
i!1
n!1
Dies aber widerspricht der Injektivität von f . /////
Eine Anwendung dieses Satzes liefert uns die Existenz der n-ten Wurzeln als
stetige Funktionen auf Œ0; 1/.
8.6
Satz Für jedes n 1 besitzt die Funktion x 7! x n auf Œ0; 1/ eine streng
monoton steigende, stetige Umkehrfunktion, die sogenannte n-te Wurzelfunktion
p
Œ0; 1/ ! Œ0; 1/;
x 7! n x:
p
Für diese gilt limx!1 n x D 1. /////
Sei n 1 und I D Œ0; 1/ . Die Funktion
f W I ! I;
f .x/ D x n ;
ist stetig, da ein Polynom, und streng monoton steigend, da
126
x > y 0:
Schließlich gilt limx!1 f .x/ D 1, also f .I / D I . Alle Aussagen folgen
daher aus dem vorangehenden Satz. /////
Entsprechendes gilt für streng monoton fallende Funktionen. jsn s0 j ";
Offene und abgeschlossene Mengen
8-C
Offene und abgeschlossene Mengen
Offene Mengen
Für alles Weitere sei .X; d/ ein metrischer Raum.
Erinnerung: Für a 2 X und " > 0 bezeichnet
B" .a/ D fx 2 X W d.x; a/ < "g
die offene Kugel um a vom Radius ", oder auch die "-Umgebung von a .
Eine Menge U X heißt Umgebung von a, wenn sie eine "-Umgebung von a
enthält.
8.7
Definition Eine Menge A X heißt offen, oder genauer offen in X , wenn
sie mit jedem Punkt a auch eine Umgebung von a enthält. Eine äquivalente Formulierung ist: Eine Menge A X ist offen, wenn sie Umgebung jedes ihrer Punkte ist.
Zuvor schon hatten wir die Begriffe ›offenes Intervall‹ und ›offene Kugel‹ erklärt.
Die Beispiele werden zeigen, dass jene Verwendung des Begriffes ›offen‹ konsistent
ist mit der eben gegebenen Definition und sozusagen im Vorgriff geschah. Ein ›offenes Intervall‹ ist also ›offen‹ im Sinne der Definition 8.7.
12 F Jedes offene Intervall
.a; b/ R;
1 a < b 1
ist offen im Sinne der Definition 8.7. G
/////
Ist c 2 .a; b/, so wählte " D min fc a; b c; 1g. Dann gilt
B" .c/ D .c "; c C "/ .a; b/;
und dies schließt auch die Fälle a D 1 und b D 1 ein. /////
13 F In einem metrischer Raum .X; d/ sind die leere Menge ∅, der Raum X
selbst sowie jede offene Kugel Br .a/ mit r > 0 offen. G
127
Offene und abgeschlossene Mengen
8-C
8-C
Offene und abgeschlossene Mengen
///// Die leere Menge ∅ ist offen im Sinne der Definition 8.7, da deren
Voraussetzung nicht erfüllt ist. Der Raum X ist offen, da er Umgebung jedes
seiner Elemente ist. Betrachte schließlich Br .a/ mit r > 0 : Ist x 2 Br .a/,
so ist s D d.x; a/ < r , also
Dann gibt es zu jedem i ein "i > 0 derart, dass
B"i .a/ Oi ;
B" .a/ B"i .a/ Oi ;
Dann ist B" .x/ Br .a/, denn für beliebiges z 2 B" .x/ gilt auf Grund der
Dreiecksungleichung
also auch
B" .a/ d.z; a/ d.z; x/ C d.x; a/ < " C s D r;
somit auch z 2 Br .a/. /////
8.8
Satz In einem metrischen Raum X gilt:
(i) ∅ und X sind offen.
(ii) Die Vereinigung beliebig vieler offener Mengen ist offen.
(iii) Der Durchschnitt endlich vieler offener Mengen ist offen. ///// (i) Siehe Beispiel 13.
(ii) Sei .O /2I eine beliebige Familie offener Teilmengen von X . Ist
[
a2
O ;
2I
so ist also a 2 O für ein 2 I . Da die Menge O offen ist, enthält sie
auch eine Umgebung B" .a/ von a , und somit gilt
[
B" .a/ O O :
2I
Sei .Oi /1in eine endliche Familie offener Teilmengen von X , und
\
a2
Oi :
(iii)
1in
1 i n:
Mit " D min f"1 ; : : : ; "n g > 0 gilt dann auch
" D r s > 0:
Wichtig: Eine Menge ist nicht per se offen, oder wissenschaftlich ausgedrückt,
Offenheit ist keine intrinsische Eigenschaft, die sich innerhalb einer Menge selbst
erschließt. Es kommt vielmehr darauf an, in welchem Raum man sich befindet. So
ist zum Beispiel eine Strecke ohne ihre Endpunkte als Teilmenge der reellen Geraden
offen – dann handelt es sich um ein offenes Intervall –, als Teilmenge der euklidischen Ebene aber nicht. Daher sagt man in eventuell mehrdeutigen Fällen, die Menge
A ist offen in X .
Eine intrinsische Eigenschaft ist zum Beispiel die Kompaktheit einer Menge, die
wir im nächsten Abschnitt beschreiben.
128
\
Oi :
1 i n;
/////
1in
Bemerkung. Wesentlich für den Beweis von (iii) ist, dass das Minimum endlich
vieler positiver Zahlen wieder positiv ist. Dies gilt nicht für unendlich viele Zahlen,
und (iii) ist auch falsch für unendliche Durchschnitte. So ist in R
\
.
1=n; 1=n/ D f0g
n1
nicht offen. Abgeschlossene Mengen
Für A X sei Ac D CA D X A das Komplement von A in X .
Definition Eine Menge A X heißt abgeschlossen, oder abgeschlossen in X ,
wenn Ac offen in X ist. Beachte: ›Abgeschlossen‹ ist nicht gleichbedeutend mit ›nicht offen‹.
Satz
In einem metrischen Raum X gilt:
(i) ∅ und X sind abgeschlossen.
(ii) Der Durchschnitt beliebig vieler abgeschlossener Mengen ist abgeschlossen.
(iii) Die Vereinigung endlich vieler abgeschlossener Mengen ist abgeschlossen. ///// Dies folgt aus Satz 8.8 mit den Regeln von de Morgan. Sind zum Beispiel A1 ; : : : ; An abgeschlossene Teilmengen von X , so ist
.A1 [ [ An /c D Ac1 \ \ Acn
der Durchschnitt endlicher vieler offener Mengen Ac1 ; : : : ; Acn , also wiederum offen. Somit ist A1 [ [ An abgeschlossen. /////
129
Offene und abgeschlossene Mengen
8-C
Bemerkung. Aussage (iii) gilt nicht für unendliche Vereinigungen. So ist in R
[
Œ1=n; 1 1=n D .0; 1/
8-C
Offene und abgeschlossene Mengen
130
aller Häufungspunkte von A wird auch die abgeleitete Menge von A genannt.
Definition Die Menge
n1
A WD A [ A0 ;
offen, nicht abgeschlossen. 14 F Einpunktige Teilmengen, und allgemeiner endliche Teilmengen eines beliebigen metrischen Raumes sind abgeschlossen. G
bestehend aus allen Elementen und Häufungspunkten von A, heißt Abschluss der
Menge A . 15 F Die Intervalle
8.9
Œa; b;
Œa; 1/;
.
1; b
(i) A ist abgeschlossen.
(ii) A ist die kleinste abgeschlossene Menge in X , die A enthält. sind alle abgeschlossen, denn ihre Komplemente
.
1; a/ [ .b; 1/;
.
1; a/;
.b; 1/
sind jeweils offen. G
16 F Die Kugeln
˚
BN r .a/ D x 2 X W d.x; a/ r ;
Satz Für eine Teilmenge A eines metrischen Raumes X gilt:
r 0;
sind abgeschlossen. G
///// Wir zeigen, dass Komplement von BN r .a/ ist offen. Sei x … BN r .a/.
Dann ist
s D d.x; a/ > r;
also " D s r > 0. Für jedes z 2 B" .x/ gilt dann
d.z; a/ d.x; a/ d.x; z/ > s " D r;
also z … BN r .a/. Somit gilt
B" .x/ \ BN r .a/ D ∅ , B" .x/ BN r .a/c :
Also ist BN r .a/c offen. /////
Abschluss
Um abgeschlossene Mengen besser zu verstehen, erinnern wir an den Begriff des
Häufungspunktes: Ein Punkt a 2 X heißt Häufungspunkt der Menge A X , wenn
in jeder Umgebung von a mindestens ein von a verschiedener Punkt von A liegt.
Die Menge
A0 WD fx 2 X W x ist Häufungspunkt von Ag
Die erste Aussage rechtfertigt die Bezeichnung ›Abschluss‹ für die Menge A .
Die zweite Aussage bedeutet: Ist B X irgend eine abgeschlossene Obermenge
von A, so ist A B . Daraus folgt auch, dass
\˚
B X W A B, B abgeschlossen
A D
der Durchschnitt aller abgeschlossenen Obermengen von A ist.
/////
(i)
Sei x … A , also
x … A ^ x … A0 :
Da x kein Häufungspunkt von A ist, existiert eine punktierte "-Umgebung
BP " .x/, die keine Punkte von A enthält. Wegen x … A enthält sogar B" .x/
keine Punkte von A, und damit auch keine Häufungspunkte von A. Es ist
also
B" .x/ .A /c :
Da ein solches " für jedes x … A existiert, ist das Komplement von A
offen, und A selbst abgeschlossen.
(ii) Sei B eine abgeschlossene Obermenge von A:
A B ^ B abgeschlossen:
Wir zeigen, dass dann auch
A0 B:
Daraus folgt A D A [ A0 B , was die Behauptung ist.
Angenommen, es ist A0 š B . Dann existiert ein x 2 A0 mit x … B , also
x 2 B c . Da B c offen ist, gibt es auch ein " > 0 mit
131
Offene und abgeschlossene Mengen
8-C
B" .x/ B c :
Wegen B c Ac kann dann aber x kein Häufungspunkt von A sein. Also
ist A0 B . /////
Wir kommen nun zur Charakterisierung abgeschlossener Mengen.
8.10 Satz Für eine Teilmenge A eines metrischen Raumes X sind folgende Aussagen äquivalent.
(i) A ist abgeschlossen.
(ii) A D A.
(iii) A0 A
(iv) Jede Folge in A, die in X konvergiert, hat ihren Grenzwert in A . ///// (i) ) (ii) Einerseits ist A A . Ist andererseits A abgeschlossen,
so folgt aus (ii) des letzten Satzes auch A A . Also ist A D A .
(ii) ) (iii) Wegen A [ A0 D A folgt aus A D A natürlich A0 A.
(iii) ) (iv) Ist .xn / eine Folge in A, die in X gegen einen Grenzwert a
konvergiert, so ist a 2 A0 . Wegen A0 A ist also a 2 A .
(iv) ) (iii) Ist a 2 A0 , so existiert eine Folge .xn / in A mit xn ! a.
Somit ist nach Voraussetzung a 2 A . Also gilt A0 A .
(iii) ) (ii) Aus A0 A folgt natürlich auch A D A [ A0 A.
(ii) ) (i) Nach Satz 8.9 ist A abgeschlossen. /////
Offener Kern
Wir haben damit abgeschlossene Mengen für unsere Zwecke hinreichend charakterisiert. Da diese als Komplemente offener Mengen definiert sind, gibt es auch eine
entsprechende Charakterisierung offener Mengen.
Definition Sei A Teilmenge eines metrischen Raumes X . Ein Punkt a 2 A heißt
innerer Punkt von A, wenn A auch eine Umgebung von a enthält. Die Menge
AB D fa 2 A W a ist innerer Punkt von Ag
aller inneren Punkte von A, gelesen »A Null«, heißt offener Kern von A . Satz
Für eine Teilmenge A eines metrischen Raumes X gilt:
(i) AB ist offen.
(ii) AB ist die größte offene Teilmenge von A. 8-C
Offene und abgeschlossene Mengen
132
Die zweite Aussage bedeutet: Ist O A offen, so ist O AB . Daraus folgt
auch, dass
[˚
O A W O ist offen :
AB D
Die Menge AB kann durchaus leer sein!
///// (i) Ist x 2 AB , so enthält A eine Umgebung von x , und damit auch
eine offene Kugel B" .x/. Dann ist jeder Punkt von B" .x/ ein innerer Punkt
von A , also B" .x/ AB . Also ist AB offen.
(ii) Ist O A offen, so ist jeder Punkt von O offensichtlich ein innerer
Punkt von A. Also gilt O AB . /////
Satz Eine Teilmenge A eines metrischen Raumes X ist offen genau dann, wenn
A D AB . Mit anderen Worten: A ist offen, wenn jeder Punkt von A ein innerer Punkt von
A ist.
///// Ist A offen, so ist jeder Punkt von A auch innerer Punkt von A und
deshalb A D AB . Gilt umgekehrt A D AB , so ist A nach dem vorangehenden
Satz offen. /////
17 F Für I D Œa; b/ R ist
I B D .a; b/;
I D Œa; b:
Für A D I f0g R2 dagegen ist
AB D ∅;
A D Œa; b f0g:
G
18 F Ist X ein normierter Vektorraum und M D Br .a/ mit r > 0, so ist
M B D M;
M D BN r .a/:
G
Stetigkeit
Wir kommen nun zu dem grundlegenden Satz, der offene und abgeschlossene Mengen in Beziehung zu stetigen Abbildungen setzt.
Satz Sei f W X ! Y eine Abbildung zwischen den metrischen Räumen X und Y .
Dann sind äquivalent:
(i) f ist stetig.
(ii) f 1 .O/ ist offen in X für jede in Y offene Menge O .
133
Offene und abgeschlossene Mengen
8-C
8-D
Kompaktheit
f 1 .y/ D fx 2 X W f .x/ D y g;
(iii) f 1 .A/ ist abgeschlossen in X für jede in Y abgeschlossene Menge A . Zu (ii) sagt man auch, Urbilder offener Mengen sind offen, und zu (iii) entsprechend, Urbilder abgeschlossener Mengen sind abgeschlossen. Hierbei ist
f 1 W P .Y / ! P .X /;
f 1 .M / D fx 2 X W f .x/ 2 M g
eine Mengenabbildung, die für jede Abbildung f W X ! Y erklärt ist, nicht nur für
bijektive.
///// (i) ) (ii) Sei O offen in Y . Ist x 2 f 1 .O/, so existiert zu f .x/ 2
O auch eine offene Umgebung U in O . Gemäß Satz 8.1 enthält f 1 .U /
dann auch eine Umgebung von x . Da dies für jedes x 2 f 1 .U / gilt, ist
diese Menge offen.
(ii) ) (iii) Sei A Y abgeschlossen. Dann ist Ac offen in Y , und nach
Annahme auch f 1 .Ac / offen in X . Aus
f 1 .Ac / D .f 1 .A//c
folgt, dass f 1 .A/ abgeschlossen in X ist.
(iii) ) (i) Sei x 2 X und y D f .x/ 2 Y . Zu gegebenen " > 0 sei
O D B" .y/;
A D Oc:
134
y 2 Y;
eine abgeschlossene Teilmenge von X , da jede 1-Punkt-Menge fy g abgeschlossen
in Y ist. G
20 F Sei X ein metrischer Raum und f W X ! R stetig. Dann ist die Nullstellenmenge von f ,
X0 D fx 2 X W f .x/ D 0g;
abgeschlossen in X . Außerdem sind die Mengen
X c D fx 2 X W f .x/ c g;
c 2 R;
abgeschlossen in X , denn diese sind die Urbilder der abgeschlossenen Intervalle
.
1; c. G
21 F Ist .E; kk/ ein normierter Raum, so sind die Einheitskugel und die Einheitssphäre,
B D fx 2 X W kxk 1g;
S D fx 2 X W kxk D 1g;
abgeschlossen in E , denn diese sind die Urbilder der abgeschlossen Mengen Œ0; 1
bzw f1g unter der stetigen Abbildung kkW X ! R . G
Dann ist A abgeschlossen in Y , also auch f 1 .A/ abgeschlossen in X . Da
f 1 .A/ D f 1 .O c / D .f 1 .O//c
abgeschlossen ist und x nicht enthält, gibt es ein ı > 0 mit
Bı .x/ f 1 .O/ D f 1 .B".y//:
Da es zu jedem x 2 X und " > 0 solch ein ı > 0 gibt, ist f stetig. /////
Dieser Satz ist ›in beiden Richtungen‹ wichtig. Einerseits charakterisiert er Stetigkeit durch eine topologische Eigenschaft, indem nur Bezug auf offene Teilmengen genommen wird. Dies ermöglicht es, Stetigkeit in sogenannten topologischen
Räumen zu definieren, in denen keine Metrik zur Verfügung steht. Dies wird uns
allerdings im Rahmen der Analysis nicht beschäftigen.
Andererseits ermöglicht der Satz, komplizierte Mengen als offen oder abgeschlossen zu erkennen, in dem sie als Urbilder einfacher offener oder abgeschlossener Mengen unter stetigen Abbildungen dargestellt werden. In dieser Weise werden wir den
Satz vielfach anwenden.
19 F Seien X und Y metrische Räume, und f W X ! Y stetig. Dann ist jede
Faser
8-D
Kompaktheit
Definition Eine Teilmenge K eines metrischen Raumes X heißt kompakt, wenn
jede Folge in K eine in K konvergente Teilfolge besitzt. Wichtig: Die Teilfolge ist nicht nur konvergent, ihr Grenzwert liegt auch in K .
22 F Die leere Menge ∅ ist kompakt, wie auch jede endliche Teilmenge eines
beliebigen metrischen Raumes X ,
K X;
jKj < 1:
Denn eine beliebige Folge in K muss wenigstens einen Punkt unendlich oft enthalten. Die entsprechende Teilfolge ist konstant und somit konvergent in K . G
Diese Beispiele sind trivial. Interessantere Beispiele folgen gleich.
Satz
(i) Die Vereinigung endlich vieler kompakter Mengen ist wieder kompakt.
(ii) Jede abgeschlossene Teilmenge einer kompakten Menge ist kompakt. 135
Kompaktheit
/////
(i)
8-D
Seien K1 ; : : : ; Kn kompakte Teilmengen in X , und
K D K1 [ [ Kn :
Ist .xn / eine Folge in K , so muss wenigstens eine Menge Ki unendlich viele
Folgenglieder enthalten. Die aus diesen Gliedern gebildete Teilfolge ist dann
ganz in Ki enthalten, und enthält ihrerseits, da Ki kompakt ist, eine in Ki
konvergente Teilfolge. Diese zweite Teilfolge ist dann auch in der Obermenge
K konvergent. Somit ist K kompakt.
(ii) Sei A K eine abgeschlossene Teilmenge der kompakten Menge K .
Ist .xn / eine Folge in A, so auch in K . Sie besitzt somit eine in K konvergente Teilfolge. Deren Grenzwert ist aber ein Häufungspunkt der Folge .xn /
und gehört deshalb zu A, da A abgeschlossen ist. Also ist die konvergente
Teilfolge auch in A konvergent. /////
8-E
///// Sei K X kompakt. Ist x ein Häufungspunkt von K , so ist x Grenzwert einer Folge in K . Folglich gehört auch x zu K , da K kompakt ist. K
enthält somit alle seine Häufungspunkte, ist nach Satz 8.10 also auch abgeschlossen.
Angenommen nun, K ist nicht beschränkt. Sei x0 2 X ein beliebiger Punkt.
Dann existiert zu jedem n 1 ein Punkt
xn 2 K;
d.xn ; x0 / > n:
Die so gewonnene Folge .xn / in K besitzt keine konvergente Teilfolge. Denn
für jedes x 2 X ist dann
d.xn ; x/ d.xn ; x0 / d.x0 ; x/ 1;
n d.x0 ; x/ C 1;
somit kann x kein Häufungspunkt der Folge sein. /////
Die Frage stellt sich, ob umgekehrt jede abgeschlossene und beschränkte Menge
auch kompakt. Im Allgemeinen ist dies falsch, zum Beispiel in unendlich-dimensionalen Vektorräumen. In einem sehr wichtigen Fall ist dies jedoch richtig.
136
Zur Erinnerung: Die natürliche Metrik ist auf R und C gegeben durch die Betragsnorm, auf dem Rm durch die euklidische Norm. Wir werden allerdings im
nächsten Abschnitt zeigen, dass es auf die Norm nicht ankommt, da alle Normen
im Rm äquivalent sind.
///// ) Dies ist der vorangehende Satz.
( Sei K eine solche abgeschlossene und beschränkte Teilmenge, und .xn /
eine Folge in K . Nach dem Satz von Bolzano-weierstraß besitzt diese Folge
eine konvergente Teilfolge, da K beschränkt ist. Der Grenzwert dieser Folge gehört auch zu K , da K abgeschlossen ist. Also besitzt .xn / eine in K
konvergente Teilfolge, was zu zeigen war. /////
Die Hauptlast dieses Beweises liegt beim Satz von Bolzano-Weierstraß. Jener
Satz ist im Grunde eine Kompaktheitsaussage.
23 F Die kompakten Intervalle sind genau die abgeschlossenen Intervalle
Wir notieren jetzt zwei notwendige Eigenschaften einer kompakten Menge.
Satz Eine kompakte Teilmenge eines metrischen Raumes ist abgeschlossen und beschränkt. Stetigkeit und Kompaktheit
Œa; b;
1 < a b < 1:
Ferner sind die Einheitskugel B und die Einheitssphäre S im Rm kompakt. G
8-E
Stetigkeit und Kompaktheit
Seien .X; dX / und .Y; dY / weiterhin metrische Räume.
Satz
Ist f W X ! Y stetig und K X kompakt, so ist auch f .K/ kompakt. ///// Sei .yn / eine beliebige Folge in f .K/. Zu jedem n existiert dann mindestens ein xn 2 K mit
yn D f .xn /:
Die so gewonnene Folge .xn / liegt in der kompakten Menge K und hat daher
eine konvergente Teilfolge .xni / mit Grenzwert x 2 K . Da f stetig ist,
folgt
yni D f .xni / ! f .x / DW y 2 f .K/:
Somit besitzt .yn / eine in f .K/ konvergente Teilfolge. /////
m
Satz Eine Teilmenge von R , C oder R ist kompakt genau dann, wenn sie abgeschlossen und beschränkt in der natürlichen Metrik ist. 8.11 Satz von Minimum und Maximum Ist f W X ! R stetig und X kompakt, so existieren Punkte x ; x 2 X mit
137
Stetigkeit und Kompaktheit
f .x / f .x/ f .x /;
8-E
x 2 X;
X
f .x / D sup f:
X
Der Satz sagt also aus, dass auf einer kompakten Menge das Infimum und das
Supremum einer reellwertigen stetigen Funktion auch als Funktionswerte angenommen werden. Somit ist das Infimum auch ein Minimum, und das Supremum auch ein
Maximum. Man sagt daher, terminologisch nicht ganz korrekt: Eine stetige Funktion
nimmt auf einer kompakten Menge ihr Minimum und Maximum an.
///// Nach dem vorangehenden Satz ist f .X / kompakt in R , also insbesondere beschränkt. Also ist zum Beispiel
m WD inf f > 1:
X
Wie im vorangehenden Beweis können wir eine Folge .xn / in X wählen mit
f .xn / ! m:
Da X kompakt ist, besitzt diese Folge eine konvergente Teilfolge .xni / mit
xni ! x 2 K:
Da f stetig ist, folgt
f .x / D lim f .xni / D lim f .xn / D m:
Entsprechend argumentiert man für das Supremum. /////
Auf Stetigkeit und Kompaktheit kann in Satz 8.11 natürlich nicht verzichtet werden. – Wir geben nun zwei geometrische Anwendungsbeispiele dieses Satzes.
Abstand zu Mengen
Sei M eine beliebige, nichtleere Teilmenge eines metrischen Raumes .X; d/. Die
Abstandsfunktion zur Menge M ,
dM W X ! R;
ist punktweise definiert durch
˚
dM .x/ WD inf d.x; a/ W a 2 M :
Zum Beispiel ist dM .x/ D 0 für x 2 M .
Stetigkeit und Kompaktheit
138
Lemma Für jede nichtleere Menge M eines metrischen Raumes .X; d/ ist die
Funktion dM Lipschitz mit L-Konstante 1:
oder äquivalent dazu,
f .x / D inf f;
8-E
jdM .x/ dM .y/j d.x; y/;
/////
x; y 2 X:
Für beliebige x; y 2 X und alle a 2 M gilt
dM .x/ d.x; a/ d.x; y/ C d.y; a/:
Gehen wir auf der rechten Seite zum Infimum über a 2 M über, so folgt
dM .x/ d.x; y/ C dM .y/:
Aus Symmetriegründen gilt dann auch dM .y/ d.x; y/ C dM .x/ . Beides
zusammen ergibt die Behauptung. /////
Satz Ist M eine kompakte und nichtleere Teilmenge von X , so existiert zu jedem
x 2 X ein x 2 M mit
dM .x/ D d.x; x /:
Der Abstand wird also an wenigstens einer Stelle x in M auch realisiert. Dieser
Punkt hängt im Allgemeinen jedoch nicht stetig von x ab.
/////
Für jedes x 2 X ist die Funktion
ıx W M ! R;
ıx .a/ D d.x; a/
stetig auf M , und ihr Infimum ist gerade dM .x/. Da M kompakt ist, wird
dieses Infimum auch an wenigstens einer Stelle x angenommen. Es ist also
dM .x/ D inf ıx D d.x; x /:
M
/////
Den Abstand zwischen zwei Mengen N und M in X definieren wir als das
Infimum der Abstände aller Punkte in N zur Menge M :
˚
d.N; M / WD inf dM .a/ W a 2 N :
Satz Sind M und N kompakte, nichtleere Teilmengen von X , so existieren Punkte
x 2 M und y 2 N mit
d.N; M / D d.x ; y /:
˚
///// Ist N kompakt, so wird inf dM .a/ W a 2 N wegen der Stetigkeit von
dM an einem Punkt y 2 N angenommen. Es ist also
d.N; M / D dM .y /:
139
Stetigkeit und Kompaktheit
8-E
DA auch M kompakt ist, wird der Abstand von M zu y an einer Stelle
x 2 M angenommen. Es gilt also
d.N; M / D dM .y / D d.x ; y /:
/////
Dieser Satz gilt im Allgemeinen nicht, wenn N nicht kompakt ist.
Normen auf Rm
Wir zeigen nun, dass alle Normen auf dem Rm äquivalent sind. Dazu genügt es zu
zeigen: Jede Norm auf dem Rm ist äquivalent zur euklidischen Norm.
Sei also kk die euklidische Norm und N W Rm ! R eine beliebige weitere
Norm auf Rm . Es gilt also
(N-1) N .x/ 0,
und
N .x/ D 0 , x D 0,
(N-2) N .x/ D jjN .x/,
(N-3) N .x C y/ N .x/ C N .y/ ,
für alle x; y 2 Rm und 2 R .
Lemma Jede Norm auf dem Rm ist stetig, sogar Lipschitz bezüglich der euklidischen Norm. /////
Für jede Norm N gilt die umgekehrte Dreiecksungleichung
jN .x/ N .y/j N .x y/:
Gibt es nun ein L 0, so dass
N .x/ Lkxk;
x 2 Rm ;
so folgt hieraus weiter jN .x/ N .y/j Lkx yk, und wir sind fertig. Mit
x D .x1 ; : : : ; xm / D x1 e1 C C xm em folgt dies aber aus
N .x/ D N .x1 e1 C C m em /
jx1 jN .e1 / C C jxm jN .em /
max fjx1 j; : : : ; jxm jg .N .e1 / C C N .em //
kxk L
mit L D N .e1 / C C N .em /. /////
Satz
Jede Norm auf dem Rm ist äquivalent zur euklidischen Norm. 8-E
Stetigkeit und Kompaktheit
140
///// Sei N eine beliebige Norm auf Rm . Dann ist N stetig nach dem vorangehenden Lemma und nimmt daher auf der kompakten Einheitssphäre
˚
S D x 2 Rm W kxk D 1
ihr Infimum und Supremum an. Da N definit ist, kann dieses Infimum nicht
Null sein, denn der Nullvektor gehört nicht zu S . Somit existieren Konstanten
0 < a b mit
a N .x/ b;
x 2 S:
Für beliebiges 0 ¤ x 2 Rm folgt daraus mit Hilfe der positiven Homogenität
von N
(
kxk b
N .x/ D kxk N .x=kxk/
;
kxk a
da x=kxk 2 S . Dies gilt, bis auf den Zwischenschritt, auf für x D 0. Somit
haben wir gezeigt, dass
akxk N .x/ bkxk;
x 2 Rm
mit positiven Konstanten a b . Das war zu zeigen. /////
Damit ist gezeigt, dass zwei beliebige Normen auf dem Rm äquivalent sind. Topologisch bedeutet dies: Ist eine Menge offen bezüglich der einen Norm, so auch in
der anderen Norm. Man sagt, äquivalente Normen erzeugen dieselbe Topologie. Für
uns wichtig ist die folgende Konsequenz: Ist eine Funktion auf dem Rm stetig in
einer Norm, so auch in jeder anderen Norm.
Gleichmäßige Stetigkeit
Die Stetigkeit einer Funktion f W X ! Y ist, für einmal mit Quantoren ausgedrückt,
gleichbedeutend mit der Aussage
8 8 9
8 .dX .x; y/ < ı ) dY .f .x/; f .y// < "/:
x2X ">0 ı>0 y2X
Hierbei hängt die Wahl von ı im Allgemeinen nicht nur von ", sondern auch vom
betrachteten Punkt x in X ab. Ist dies nicht der Fall, spricht man von gleichmäßiger
Stetigkeit.
Definition Eine Funktion f W X ! Y heißt gleichmäßig stetig auf X , wenn es zu
jedem " > 0 ein ı > 0 gibt, so dass für alle x; y 2 X gilt:
dX .x; y/ < ı ) dY .f .x/; f .y// < ":
141
Stetigkeit und Kompaktheit
8-E
8
8 .dX .x; y/ < ı ) dY .f .x/; f .y// < "/:
24 F Ist f W X ! Y Lipschitz auf X , so ist f auch gleichmäßig stetig auf X . G
x; y 2 X:
Wählen wir zu " > 0 nun ı D "=.L C 1/ , so folgt aus dX .x; y/ < ı auch
dY .f .x/; f .y// LdX .x; y/ < Lı ";
x; y 2 X:
/////
Gleichmäßig stetige Funktionen sind offensichtlich stetig. Die Umkehrung gilt
allerdings nicht.
25 F Die Funktion x 7! x 1 ist nicht gleichmäßig stetig auf .0; 1/. G
/////
Für die Folge der Punkte xn D 1=n gilt
jxnC1 xn j D
1
! 0;
n.n C 1/
n ! 1;
aber
jf .xnC1 / f .xn /j D j.n C 1/ nj D 1;
n 1:
Zu " D 1 gibt es daher kein ı > 0 mit der erforderlichen Eigenschaft. /////
Gleichmäßige Stetigkeit bedeutet in gewisser Weise, dass eine Funktion nicht
»unendlich steil« wird. Eine Änderung des Arguments um ı bewirkt höchstens eine
Änderung des Funktionswertes um " an jeder Stelle des Definitionsbereiches. Dabei
kommt es allerdings nicht nur auf die Funktion, sondern auch den Definitionsbereich
an.
Satz Ist f W X ! Y stetig und K X kompakt, so ist die Einschränkung von f
auf K gleichmäßig stetig auf K . Ist insbesondere X selbst kompakt, so ist f W X ! Y gleichmäßig stetig.
///// Sei f W X ! Y stetig und K X kompakt und nicht leer. Angenommen, f ist auf K nicht gleichmäßig stetig. Dann existieren ein " > 0 , und
zu jedem
ın D 1=n;
n D 1; 2 : : : ;
zwei Punkte xn ¤ yn in K mit
dY .f .xn /; f .yn // " :
xni ! a 2 K:
Wegen dX .xn ; yn / < ın gilt dann aber auch yni ! a. Aus der Stetigkeit von
f folgt daraus
Es gibt also ein L 0, so dass
dY .f .x/; f .y// LdX .x; y/;
142
Da K kompakt ist, besitzt die Folge .xn / eine konvergente Teilfolge
">0 ı>0 x2X y2X
/////
Stetigkeit und Kompaktheit
dX .xn ; yn / < ın ;
Mit Quantoren ausgedrückt ist dies gleichbedeutend mit der Aussage:
8 9
8-E
dY .f .xni /; f .yni // dY .f .xni /; f .a// C dY .f .yni /; f .a//
" =4 C " =4
D " =2
für alle hinreichend großen i , ein offensichtlicher Widerspruch. /////
9-A
Definitionen und Rechenregeln
144
(i) f ist differenzierbar in t0 , und es ist f 0 .t0 / D a 2 E .
(ii) Es gibt eine im Punkt t0 stetige Funktion ' W I ! E mit '.t0 / D a, so dass
f .t/ D f .t0 / C '.t/.t t0 /;
9
Differenziation in einer Variablen
t 2 I:
(iii) Es gibt einen Vektor a 2 E und eine in t0 stetige Funktion "W I ! E mit
".t0 / D 0, so dass
f .t / D f .t0 / C a.t t0 / C ".t/.t t0 /:
9-A
(i) ) (ii) Wir definieren
(
.t t0 /1 .f .t/ f .t0 //;
'.t/ WD
a;
Definitionen und Rechenregeln
/////
Im Folgenden sei immer I R ein Intervall. Wir betrachten zunächst Funktionen
f W I ! E;
df
.t0 / D fP.t0 /:
dt
Der Punkt wird dann verwendet, wenn die unabhängige Variable als Zeit aufgefasst
wird.
Ist t0 ein Endpunkt des Intervalls in I , so handelt es sich in (1) um einen einseitigen Grenzwert, da t0 C h D t 2 I vorausgesetzt ist. Ist also beispielsweise
I D Œa; b, so ist f 0 .a/ durch einen rechtsseitigen Grenzwert definiert.
In der Definition der Ableitung wird nicht vorausgesetzt, dass die Funktion differenzierbar ist. Dies ist auch nicht nötig, wie wir gleich sehen werden.
f 0 .t0 / D Df .t0 / D
9.1
Satz Für eine Funktion f W I ! E und einen Punkt t0 2 I sind die folgenden Aussagen äquivalent.
t D t0 :
lim '.t / D a D '.t0 /:
Definition Eine Funktion f W I ! E heißt an der Stelle t0 2 I differenzierbar,
wenn der Grenzwert
1
f .t / f .t0 /
(1)
lim .f .t0 C h/ f .t0 // D lim
t
!t
t t0
h!0 h
0
Andere Bezeichnungen für diesen Grenzwert sind
t ¤ t0 ;
Die Differenzierbarkeit von f in t0 mit Ableitung f 0 .t0 / D a bedeutet dann
gerade, dass
mit Werten in einem normierten Raum E , die wir geometrisch als Kurven in E
auffassen können.
in E existiert. Dieser Grenzwert heißt erste Ableitung von f an der Stelle t0 und
wird mit f 0 .t0 / bezeichnet.
Die Funktion f heißt auf I differenzierbar, wenn sie in jedem Punkt von I
differenzierbar ist. t!t0
Also ist ' in t0 stetig.
(ii) ) (iii) Schreibe '.t / D a C ".t/, also ".t / D '.t / a.
(iii) ) (i) Aus (iii) folgt ja sofort
lim
t !t0
f .t/ f .t0 /
D lim .a C ".t// D a:
t !t0
t t0
/////
Aussage (ii) beinhaltet insbesondere die Stetigkeit von f in t0 .
Korollar Ist f W I ! E in t0 2 I differenzierbar, so ist f in t0 auch stetig. Die Umkehrung ist – natürlich – nicht richtig. Eine Funktion kann in einem Punkt
stetig sein, ohne dort auch differenzierbar zu sein. Das Standardbeispiel ist die Betragsfunktion
f W R ! R;
f .t/ D jt j:
Wegen
lim
t0
f .t / f .0/
t
f .t/ f .0/
t
D lim
D 1 ¤ lim
D lim D 1;
t 0 t
t 0
t0 t
t 0
t 0
konvergieren die Differenzenquotienten bei t0 D 0 nicht. Also ist j j in 0 nicht
differenzierbar.
145
Definitionen und Rechenregeln
9-A
Die Betragsfunktion ist nur in einem Punkt nicht differenzierbar. Tatsächlich gibt
es sogar stetige Funktionen f W R ! R , die in keinem einzigen Punkt differenzierbar
sind. hReferenzi
Von besonderer Bedeutung sind natürlich Funktionen mit Werten in Rm .
Satz Eine Funktion f W I ! R
ihrer Koordinatenfunktionen
fi W I ! R;
m
9-A
.f C g/0 .t0 / D f 0 .t0 / C g 0 .t0 /
.f =g/0 .t0 /
/////
mit
0
.t0 / D g .t0 /:
Der Ausdruck in eckigen Klammern ist stetig in t und hat in t0 den Wert
f .t0 / .t0 / C '.t0 /g.t0 / D f .t0 /g 0 .t0 / C f 0 .t0 /g.t0 /:
Wiederum mit Satz 9.1 folgt hieraus die Differenzierbarkeit von fg in t0 mit
der behaupteten Ableitung. — Die übrigen Aussagen werden entsprechend
bewiesen. /////
t 7! t
2F
in jedem Punkt differenzierbar, und es gilt
Für n 0 ist
.x n /0 D nx n1 ;
d
d
c D 0;
t D 1:
dt
dt
Allgemeiner ist jede Funktion
x 2 R;
auf Grund der Produktregel und einem Induktionsargument. Definieren wir für n 1
außerdem
f .t / D at C b;
a; b 2 R;
differenzierbar mit f 0 .t/ D a für alle t 2 R . G
Aus diesen einfachen Beispielen lassen sich mit dem folgenden Satz bereits eine
Vielzahl differenzierbarer Funktionen bilden.
9.2
Rechenregeln Sind die Funktionen f; gW I ! R in t0 2 I differenzierbar,
so sind es auch die Funktionen
f =g
.t /.t t0 /
C Œf .t0 / .t/ C '.t /g.t0 / C '.t/ .t /.t t0 / .t t0 /
t 7! c;
f g;
g.t/ D g.t0 / C
.fg/.t / D f .t0 /g.t0 /
sowie die Identitätsfunktion
f C g;
Daraus folgt beispielsweise
/////
Auf R ist jede konstante Funktion
f W R ! R;
(Quotientenregel):
Nach Satz 9.1 ist
'.t0 / D f .t0 /;
In den nächsten Abschnitten werden wir uns deshalb vor allem mit differenzierbaren, reellwertigen Funktionen beschäftigen.
t W R ! R;
f .t0 /g.t0 / f .t0 /g .t0 /
g.t0 /2
0
an auf
(Produktregel)
0
mit in t0 stetigen Funktionen ' und
///// Man wende Satz 5.11 über den Grenzwert von Folgen im R
den Differenzenquotienten
c W R ! R;
D
0
f .t / D f .t0 / C '.t/.t t0 /;
m
(Summenregel)
.f g/0 .t0 / D f 0 .t0 /g.t0 / C f .t0 /g 0 .t0 /
1 i m;
1
.f .t / f .t0 // 2 Rm :
t t0
146
und es gilt:
ist in t0 differenzierbar genau dann, wenn jede
in t0 differenzierbar ist, und es gilt
f 0 .t0 / D f10 .t0 /; : : : ; fm0 .t0 / :
1F
Definitionen und Rechenregeln
(falls g.t0 / ¤ 0);
1
;
x ¤ 0;
xn
so gilt auch in diesem Fall auf Grund der Quotientenregel
x n WD
.x n /0 D .
n/x n1 ;
3F
x ¤ 0:
Ein reelles Polynom p vom Grad n,
p.x/ D
n
X
kD0
ak x k ;
G
147
Definitionen und Rechenregeln
9-A
9-A
Definitionen und Rechenregeln
dz
dz dy
D
:
dx
dy dx
mit an ¤ 0, ist in jedem Punkt von R differenzierbar, und es ist
p 0 .x/ D
n
X
kak x k1 :
G
kD1
4 F Die Wurzelfunktion x 7!
es gilt
1
d p
xD p ;
dx
2 x
p
x ist in jedem Punkt x > 0 differenzierbar, und
Dies ist aber nur eine Merkregel! In keiner Weise darf man mit den Symbolen dx ,
dy , dz rechnen wie mit reellen Zahlen.
/////
p
mit in y0 stetigem
lim
x!x0
Für x D 0 und h > 0 sind die Differenzenquotienten divergent. /////
in x0 differenzierbar, und es gilt
0
0
x 2 I;
Der Ausdruck in eckigen Klammern ist stetig in x0 , mit Grenzwert
1
lim p
p D p :
h!0
2
x
xChC x
m
.y0 / D g .y0 /. Für y D f .x/ haben wir weiter
g.f .x// D g.f .x0 // C Π.f .x/ '.x/ .x x0 /:
1
9.3
Kettenregel Seien f W I ! R und gW J ! Rm Funktionen auf Intervallen
I und J , und es sei f .I / J . Ist f in x0 2 I und g in f .x0 / 2 J differenzierbar, so ist
und
y 2 J;
0
mit in x0 stetigem ' und '.x0 / D f 0 .x0 / . Ersetzen wir in der ersten Gleichung y durch f .x/, so erhalten wir y y0 D '.x/.x x0 / und damit
Für h ! 0 konvergiert der Differenzenquotient somit gegen
Neben den algebraischen Operationen gehören die Verkettung und die Umkehrung zu den ›Standardoperationen‹, die man mit Funktionen ausführt. Wie bei der
Stetigkeit müssen wir daher die Frage untersuchen, unter welchen Bedingungen die
Differenzierbarkeit bei diesen Operationen erhalten bleibt. Hierbei beschränken wir
uns auf reellwertige Funktionen.
.y/.y y0 /;
f .x/ D f .x0 / C '.x/.x x0 /;
Für x > 0 und 0 < jhj < x ist
p
xCh
x
1
h
1
D p
p Dp
p :
h
h xChC x
xChC x
gBfW I !R
Sei y0 D f .x0 / 2 J . Mit Satz 9.1 ist
g.y/ D g.y0 / C
x > 0:
In x D 0 ist die Wurzelfunktion jedoch nicht differenzierbar. G
/////
148
.f .x/ '.x/ D
.y0 /'.x0 / D g 0 .y0 /f 0 .x0 /:
Mit Satz 9.1 folgt daraus die Behauptung. /////
5F
Die Funktion f W R ! R mit
p
f .x/ D 1 C x 2
ist in jedem Punkt differenzierbar, und es gilt
1
x
f 0 .x/ D p
2x D p
:
2 1 C x2
1 C x2
G
Zur ›Grundausstattung‹ der Differenzialrechnung gehört auch die Ableitung der
Umkehrfunktion. Zur Erinnerung: Ist f W I ! R stetig, so ist f .I / D I wiederum
ein Intervall, und
f W I ! I
0
.g B f / .x0 / D g .f .x0 //f .x0 /:
Man sagt, man erhält .g B f /0 .x0 / als
äußere Ableitung bei f .x0 / innere Ableitung bei x0 :
Mit y D f .x/ und z D g.y/ schreibt sich dies einprägsam als
ist bijektiv genau dann, wenn f streng monoton ist. In diesem Fall existiert die
Umkehrfunktion
f 1 W I ! I;
und diese ist wiederum stetig.
149
Definitionen und Rechenregeln
9-A
9.4
Ableitung der Umkehrfunktion Sei f W I ! I stetig und bijektiv. Ist f
in x0 differenzierbar mit Ableitung f 0 .x0 / ¤ 0, so ist auch die Umkehrfunktion
9-B
g 0 .f .x0 // D
/////
y D f .x/
Nach Satz 9.1 ist
f .x/ D f .x0 / C '.x/.x x0 /;
differenzierbar und umkehrbar, mit Umkehrfunktion g , so ist
x 2 I;
mit einer in x0 stetigen Funktion ' mit '.x0 / D f 0 .x0 /. Wegen f 0 .x0 / ¤ 0
gibt es daher ein ı > 0, so dass
x 2 Iı WD .x0 ı; x0 C ı/ \ I:
'.x/ ¤ 0;
Für x 2 Iı gilt daher auch
x D x0 C
y D f .x/ , x D g.y/;
y 2 f .Iı /:
Nach Satz 8.5 ist g stetig auf I , insbesondere also in y0 , und ' ist stetig
in x0 D g.y0 / und dort nicht Null. Somit ist 1=' B g stetig in y0 , und mit
Satz 9.1 folgt die Differenzierbarkeit von g in y0 mit
1
1
1
g .y0 / D
D 0
D 0
:
'.g.y0 /
f .g.y0 //
f .x0 /
/////
Die Gleichung für die Ableitung der Umkehrfunktion gewinnt man übrigens
leicht mit Hilfe der Kettenregel. Für g D f 1 ist ja
x 2 I:
Differentiation nach x liefert
1 D g 0 .f .x0 / f 0 .x0 /:
Die Funktion
f .x/ D x 2 ;
ist strikt wachsend und differenzierbar mit Ableitung
f 0 .x/ D 2x > 0;
und insbesondere y0 D f .x0 /, ist dies gleichbedeutend mit
0
falls f 0 .x/ ¤ 0. Nun kommt es ›nur noch‹ darauf an, auf der linken Seite x durch
g.y/ zu ersetzen, also die linke Seite ›durch y auszudrücken‹, um die Ableitung von
g.y/ als Funktion von y zu erhalten.
f W Œ0; 1/ ! Œ0; 1/;
Mit den Bezeichnungen für die Umkehrfunktion g , also
1
g.y/ D g.y0 / C
.y y0 /;
'.g.y//
1
D g 0 .f .x// D g 0 .y/;
f 0 .x/
6F
f .x/ f .x0 /
:
'.x/
x D g.f .x//;
1
:
f 0 .x0 /
Dies ist allerdings kein Ersatz für den vorangegangenen Beweis. Um die Kettenregel
anwenden zu dürfen, müssen wir bereits wissen, dass g differenzierbar ist!
Praktisch wendet man Satz 9.4 folgendermaßen an. Ist
in y0 D f .x0 / differenzierbar, und es gilt
1
:
f 0 .x0 /
150
Ist f 0 .x0 / ¤ 0, so folgt hieraus
g D f 1 W I ! I
g 0 .y0 / D
Definitionen und Rechenregeln
x > 0:
Die Umkehrfunktion
gW Œ0; 1/ ! Œ0; 1/;
g.y/ D
p
y;
ist deshalb in jedem Punkt y D f .x/ D x 2 mit x > 0 differenzierbar. Für die
Ableitung finden wir
g 0 .y/ D
1
1
1
D
D p :
f 0 .x/
2x
2 y
Dies stimmt zum Glück mit Beispiel 4 überein. G
151
9-B
Extrema und Mittelwertsatz
9-B
Extrema und Mittelwertsatz
In diesem Abschnitt betrachten wir Funktionen
f W I ! R;
also reellwertige Funktionen auf einem Intervall I R .
Extrema
Definition Die Funktion f W I ! R besitzt an der Stelle x0 2 I ein lokales
Maximum bzw ein lokales Minimum, wenn es eine Umgebung Bı .x0 / gibt, so dass
(2)
f .x0 / f .x/
bzw
f .x0 / f .x/
für alle x 2 I \ Bı .x0 /. Lokale Minima und Maxima werden auch gemeinsam als Extrema bezeichnet.
Punkte, an denen ein lokales Extremum vorliegt, werden Extremalstellen genannt,
genauer Minimal- und Maximalstellen.
Weiter spricht man von einem strikten Extremum, wenn in (2) die strikte Ungleichung für x ¤ x0 gilt. Man spricht von einem globalen Extremum, wenn (2) nicht
nur lokal, sondern für alle x 2 I gilt, und von einem strikten globalen Extremum,
wenn sogar
f .x0 / > f .x/
bzw
f .x0 / < f .x/
für alle x 2 I fx0 g gilt.
Satz (Fermat) Besitzt f W I ! R in einem inneren Punkt x0 von I ein lokales
Extremum, und ist f im Punkt x0 differenzierbar, so gilt
f 0 .x0 / D 0:
///// Sei x0 zum Beispiel eine innere Minimalstelle. Dann gibt es ein ı > 0,
so dass .x0 ı; x0 C ı/ I und
f .x/ f .x0 /;
Somit gilt auch
f .x0 C h/ f .x0 /
h
jx x0 j < ı:
(
0;
0 < h < ı;
0; ı < h < 0:
Der Grenzwert für h ! 0 existiert, da f in x0 differenzierbar ist, und die
Grenzübergänge h 0 und h 0 ergeben
9-B
Extrema und Mittelwertsatz
152
f 0 .x0 / 0 f 0 .x0 /:
Also ist f 0 .x0 / D 0. /////
Definition Ist f W I ! R in x0 differenzierbar und f 0 .x0 / D 0, so heißt x0 ein
stationärer oder kritischer Punkt von f . Der Satz von Fermat besagt also: Eine Extremstelle im Innern ist notwendigerweise ein kritischer Punkt, wenn die Funktion dort differenzierbar ist.
Beide Voraussetzungen des Satzes – Lage der Extremstelle im Innern und Differenzierbarkeit – sind notwendig. In einer Extremstelle am Rand muss die Ableitung
keineswegs verschwinden. Und an einer Extremstelle im Innern muss eine Funktion
nicht differenzierbar sein, also auch keine horizontale Tangente besitzen.
Es gilt auch nicht die Umkehrung. Ein kritischer Punkt, im Innern oder am Rande,
ist nicht notwendigerweise eine Extremalstelle.
hBilderi
Die absoluten Extrema einer differenzierbaren Funktion lassen sich nun im Prinzip leicht bestimmen.
Satz Sei f W Œa; b ! R stetig und auf .a; b/ differenzierbar. Sind x1 ; : : : ; xs die
kritischen Punkte von f in .a; b/, so gilt
max f D max ff .a/; f .x1 /; : : : ; f .xs /; f .b/g:
Œa;b
Entsprechendes gilt für minŒa;b f . ///// Da Œa; b kompakt ist, nimmt f nach Satz 8.11 sein Supremum in einem Punkt xN 2 Œa; b an. Ist xN kein Randpunkt, so ist xN ein innerer Punkt,
nach dem Satz von Fermat also einer der kritischen Punkte x1 ; : : : ; xs . Andernfalls ist xN einer der Randpunkte a und b . Das Supremum tritt also auf
jeden Fall unter den Werten f .a/; f .x1 /; : : : ; f .xs /; f .b/ auf. /////
Mittelwertsätze
9.5
Satz von Rolle Sei f W Œa; b ! R stetig und auf .a; b/ differenzierbar. Ist
dann f .a/ D f .b/, so existiert in .a; b/ ein kritischer Punkt. ///// Ist f konstant, so ist jeder Punkt in Œa; b ein kritischer Punkt. Ist f
nicht konstant, so existiert nach dem Satz vom Infimum und Supremum im
Innern ein Extremum. Da f im Innern auch differenzierbar ist, liegt nach
dem Satz von Fermat dort auch ein kritischer Punkt. /////
153
Extrema und Mittelwertsatz
9-B
Bemerkung. Der Satz von Rolle gilt natürlich erst recht, wenn f auf ganz Œa; b
differenzierbar ist. Es ist aber sinnvoll, hier und im Folgenden nur die Differenzierbarkeit auf .a; b/ zu verlangen, den häufigen Fall von Funktionen wie in Bild 00
zu erfassen, die in den Endpunkten des Intervalls stetig, aber nicht differenzierbar
sind. Und sowieso stellt ein Mathematiker nicht gerne Bedingungen, die er gar nicht
benötigt . . . 9-B
f 0 .x/ 0 (bzw 0);
/////
Definiere ' durch
'.x/ D f .x/ .x a/;
D
f .b/ f .a/
:
b
a
Dann ist ' ebenfalls auf Œa; b stetig, auf .a; b/ differenzierbar, und es ist
'.b/ D f .b/ .b a/ D f .a/ D '.a/:
Nach dem Satz von Rolle besitzt ' einen kritischen Punkt 2 .a; b/. Aus
0 D ' 0 ./ D f 0 ./ folgt dann die Behauptung. /////
Bemerkung. Der Satz von Rolle ist offensichtlich ein Spezialfall des Mittelwertsatzes. Diesen haben wir aber gerade mit dem Satz von Rolle bewiesen. Beide Sätze
sind somit äquivalent. Variante des Mittelwertsatz Ist f auf dem abgeschlossenen Intervall mit den
Endpunkten x und x C h stetig und im Innern differenzierbar, so existiert ein 2
.0; 1/ mit
f .x C h/ f .x/ D f 0 .x C h/ h:
Dies folgt unmittelbar aus dem vorangehenden Satz. Der Vorteil dieser Formulierung ist, dass sie gleichermaßen für h > 0 und h < 0 gilt.
Nun ziehen wir einige Folgerungen aus den Mittelwertsätzen.
9.6
Satz Sei f W Œa; b ! R stetig und auf .a; b/ differenzierbar.
(i) f ist konstant auf Œa; b genau dann, wenn
f 0 .x/ 0;
x 2 .a; b/:
x 2 .a; b/:
(iii) f ist Lipschitz auf Œa; b mit L-Konstante L genau dann, wenn
jf 0 .x/j L;
x 2 .a; b/:
///// Nach dem Mittelwertsatz existiert zu zwei beliebigen Punkten u; v in
Œa; b ein in .a; b/ mit
(j)
154
(ii) f ist monoton steigend (bzw fallend) auf Œa; b genau dann, wenn
Mittelwertsatz Ist f W Œa; b ! R stetig und auf .a; b/ differenzierbar, so existiert
ein Punkt 2 .a; b/ mit
f .b/ f .a/ D f 0 ./.b a/:
Extrema und Mittelwertsatz
f .v/ f .u/ D f 0 ./.v u/:
(i) Verschwindet f 0 überall, so ist also f .u/ D f .v/. Umgekehrt hat natürlich jede konstante Funktion eine verschwindende Ableitung.
(ii) Ist f 0 .x/ 0 für alle x 2 .a; b/, so folgt für u < v in Œa; b aus (j)
auch f .v/ f .u/ 0. Somit ist f monoton wachsend.
Ist umgekehrt f monoton wachsend, so gilt für jedes x 2 .a; b/ und 0 <
h<b
x
f .x C h/ f .x/
0;
h
also auch
f .x C h/ f .x/
f 0 .x/ D lim
0:
h
h0
(iii)
Ist f Lipschitz mit L-Konstante L , so gilt
jf .x C h/ f .x/j Lh
für x 2 .a; b/ und 0 < h < b x . Also folgt
ˇ
ˇ
ˇ f .x C h/ f .x/ ˇ
ˇ L:
jf 0 .x/j D lim ˇˇ
ˇ
h
h0
Umgekehrt, ist jf 0 .x/j L für alle x 2 .a; b/, so erhalten wir mit (j)
jf .v/ f .u/j D jf 0 ./jjv uj Ljv uj:
Also ist f Lipschitz mit L-Konstante L. /////
Für die Charakterisierung der strengen Monotonie genügt uns das folgende hinreichende, aber nicht notwendige Kriterium.
9.7
Satz Sei f W Œa; b ! R stetig und auf .a; b/ differenzierbar. Ist f 0 > 0
auf .a; b/ mit Ausnahme endlich vieler stationärer Punkte, so ist f streng monoton
steigend. 155
Höhere Ableitungen
9-C
///// Auf jeden Fall ist f auf Grund des letzten Satzes monoton steigend.
Wäre nun f .u/ D f .v/ für zwei u < v in Œa; b, so wäre f konstant auf
Œu; v und hätte unendlich viele stationäre Punkte. /////
9-C
Höhere Ableitungen
156
Jede dieser Inklusionen ist eine echte Inklusion.
Wie im Falle der ersten Ableitung haben wir zu untersuchen, wie sich die höheren
Ableitungen mit den wichtigsten Operationen vertragen. Wegen
.˛f C ˇg/0 D ˛f 0 C ˇg 0
Ein analoges Resultat gilt natürlich für streng monoton fallende Funktionen.
ist induktiv klar, dass jede Linearkombination von C r -Funktionen wieder eine C r Funktion ist. Also gilt der folgende Satz.
9-C
Höhere Ableitungen
9.8
Sei I R ein Intervall, und f W I ! R eine reellwertige Funktion. Ist f auf I
differenzierbar, so ist
f 0 W I ! R;
wiederum eine Funktion auf I mit Werten in R . Somit kann man die Frage stellen,
ob f 0 wiederum in einzelnen Punkten oder auf ganz I differenzierbar ist. Ist dies
der Fall, erhält man die zweite Ableitung
f 00 WD .f 0 /0 W I ! R
der Funktion f .
So kann man fortfahren, so lange es die Funktion zulässt. Induktiv erklärt man
die höheren Ableitungen von f durch
wobei f
.0/
(3)
.fg/.r / D
r
X
r s
f .r s/ g .s/ :
sD0
///// Für r D 0 ist dies Satz 8.3, und für r D 1 die Produktregel von Satz
9.2. Wir können daher induktiv annehmen, dass der Satz für r 1 bereits
bewiesen ist. Sind nun f und g r C 1-mal differenzierbar, so ist jede der
rechts in (3) auftretenden Funktionen wenigstens noch einmal differenzierbar.
Die Produktregel ist somit anwendbar und ergibt
r 1:
.fg/.r C1/ D
WD f . Insbesondere ist also
f .1/ D f 0 ;
Als nächstes betrachten wir das Produkt von Funktionen.
9.9
Satz Sind f; gW I ! R r -mal (stetig) differenzierbar auf I , so ist es auch
deren Produkt fgW I ! R , und es gilt die Leibnizsche Formel
t 7! f 0 .t/
f .r / WD .f .r 1/ /0 ;
Satz Jeder Raum C r .I / mit r 0 bildet einen reellen Vektorraum. r
X
r .r sC1/ .s/
g C f .r s/ g .sC1/
f
s
sD0
f .2/ D f 00 :
0
D
.r /
auf I
Man sagt, f ist r -mal auf I differenzierbar, r 1, wenn f; f ; : : : ; f
existieren. Ist außerdem f .r / stetig auf I , so heißt f r -mal stetig differenzierbar
auf I . Die Klasse dieser Funktionen wird mit
r
X
r s
f .r C1s/ g .s/ C
sD0
rX
C1
tD1
D f .r C1/ g .0/ C
r
X
r s
C
r
t 1
f .r C1t/ g .t /
.r C1s/ .s/
g C f .0/ g .r C1/ :
f
r
s1
sD1
C r .I /
bezeichnet, und man sagt, f 2 C r .I / ist von der Klasse C r , oder kurz, f ist C r .
Schließlich definiert man noch
\
C r .I /;
C 1 .I / WD
r 0
die Klasse der unendlich oft differenzierbaren Funktionen I ! R . Man erhält so
eine Hierarchie oder Skala von Funktionenräumen
C 1 .I / C r C1 .I / C r .I / C 1 .I / C 0 .I /:
Mit
r
r
r C1
C
D
s
s
1
s
folgt dann
.fg/.r C1/ D
rX
C1
r C1
s
f .r C1s/ g .s/ :
sD0
Sind nun alle Ableitungen von f und g auch noch stetig, so ist es offensichtlich auch der in dieser Gleichung rechts stehende Ausdruck. /////
157
Höhere Ableitungen
9-C
9-D
Taylorpolynom und Taylorreihe
Einen Vektorraum, in dem auch ein mit der Addition verträgliches Produkt erklärt
ist, nennt man eine Algebra. Somit können wir Satz 9.8 verbessern.
7F
Differenziert man die erste Ableitung
g0 D
Korollar Jeder Raum C r .I / mit r 0 bildet eine reelle Algebra. Wir untersuchen nun noch die Komposition und die Umkehrung von Funktionen
im Hinblick auf höhere Ableitungen.
.g B f /0 D g 0 B f f 0 :
Sind f und g als r C 1-mal differenzierbar vorausgesetzt, so ist g 0 r -mal
differenzierbar, nach Induktionsannahme also auch g 0 B f r -mal differenzierbar. Da auch f 0 r -mal differenzierbar ist, ist nach dem vorangegangenen Satz
9.9 auch g 0 B f f 0 r -mal differenzierbar. Also ist g B f selbst r C 1-mal
differenzierbar. – Die Stetigkeitsaussage folgt analog. /////
1
D .f 0 B g/1
f0Bg
einer Umkehrfunktion, so erhält man als zweite Ableitung
g 00 D .
1/.f 0 B g/2 f 00 B g g 0
Satz Sind f W I ! R und gW J ! R r -mal (stetig) differenzierbar, und gilt
f .I / J , so ist auch g B f W I ! R r -mal (stetig) differenzierbar auf I . ///// Für r D 0 ist dies Satz 8.4, und für r D 1 ist dies die Kettenregel 9.3.
Wir können daher induktiv annehmen, dass der Satz für ein r 1 gilt. Dann
gilt nach der Kettenregel
158
D .
1/.f 0 B g/3 f 00 B g
D
f 00 B g
:
.f 0 B g/3
G
Die wesentlichen Ergebnisse dieses Abschnitts können wir so zusammenfassen:
f; g 2 C r ) fg; f B g 2 C r ;
sowie
f 2 C r ^ f 0 ≷ 0 ) f 1 2 C r :
9-D
Taylorpolynom und Taylorreihe
9.10 Satz Sei r 1. Ist f W I ! R r -mal stetig differenzierbar auf I , und
verschwindet f 0 nirgends auf I , so ist f umkehrbar, und die Umkehrfunktion g D
f 1 ist ebenfalls r -mal stetig differenzierbar auf f .I /. Die Differenzierbarkeit einer Funktion f W I ! R in einem Punkt x0 2 I ist äquivalent zu ihrer lokale Approximierbarkeit durch eine lineare Funktion: es gilt
///// Da f 0 auf I stetig ist und nirgends verschwindet, hat f 0 festes Vorzeichen auf I . Nach Satz 9.7 ist daher f streng monoton und umkehrbar.
Die Umkehrfunktion g D f 1 ist nach Satz 9.4 außerdem auf I D f .I /
differenzierbar, da ja f 0 nirgends verschwindet, und es gilt
mit einer in x0 stetigen und dort verschwindenden Funktion ". Analog kann man
auch die Stetigkeit in x0 charakterisieren als die lokale Approximierbarkeit durch
eine konstante Funktionen:
g0 D
1
:
f Bg
0
Definieren wir die Funktion h durch h.t / D 1=t für t ¤ 0 , so stellt sich
g0 D h B f 0 B g
als Komposition dar von drei r 1-mal stetig differenzierbaren Funktionen.
Nach dem vorangegangen Satz ist somit g 0 r 1-mal stetig differenzierbar.
Das ergibt die Behauptung. /////
f .x/ D f .x0 / C f 0 .x0 /.x x0 / C ".x/.x x0 /
f .x/ D f .x0 / C ".x/:
Wir wollen jetzt die Frage untersuchen, ob und wie sich eine Funktion in der
Umgebung eines Punktes durch Polynome höherer Ordnung approximieren lässt.
Um eine Idee von der Gestalt einer solchen Approximation zu gewinnen, nehmen
wir zuerst an, f sei selbst ein Polynom vom Grad n , und x0 ein beliebiger Punkt
in R . Da auf Grund der binomischen Formel
x k D .x0 C .x x0 //k D x0k C C .x x0 /k ;
können wir f in der Form
159
Taylorpolynom und Taylorreihe
n
X
f .x/ D
9-D
ak .x x0 /k
kD0
schreiben. Dann ist natürlich f .x0 / D a0 , und wegen
f .k/ .x/ D n.n 1/ : : : .n k C 1/an .x x0 /nk C C k !ak
gilt allgemeiner
f .k/ .x0 / D k !ak ;
k D 0; : : : ; n:
Im Falle eines Polynoms f vom Grad n gilt somit die Identität
f .x/ D
n
X
1 .k/
f .x0 /.x x0 /k :
k!
kD0
Ist f kein Polynom, aber n-mal differenzierbar, so ist die rechte Seite nach wie
vor definiert. Es liegt daher nahe, dieses Polynom als n-te Approximation an die
Funktion f aufzufassen.
Definition Ist f n-mal differenzierbar auf I und x0 2 I , so heißt
Tn;x0 f .x/ D
n
X
kD0
f .k/ .x0 /
.x x0 /k
k!
das n-te Taylorpolynom von f an der Stelle x0 . Sind f und x0 aus dem Zusammenhang klar, schreibt man auch kurz Tn für
Tn;x0 f . Mit x D x0 C h schreibt sich dieses in der Form
Tn .x/ D Tn;x0 f .x/
D
n
X
kD0
f W .
1; 1/ ! R;
Definition Ist f n-mal differenzierbar auf I und Tn;x0 f das n-te Taylorpolynom
von f an der Stelle x0 in I , so heißt
Rn;x0 f D f Tn;x0 f
das n-te Restglied von f an der Stelle x0 . In kürzerer Notation:
Rn D Rn;x0 f D f Tn;x0 f D f Tn :
Für dieses Restglied gibt zahlreiche Darstellungen, zum Teil auch mit Hilfe von Integralen. Die folgende ist eine der am häufigsten verwendete.
Restgliedformel von Lagrange Sei f n C 1-mal differenzierbar auf I . Dann gibt
es zu beliebigen Punkten x0 und x D x0 C h in I ein 2 .0; 1/ , so dass
Rn;x0 f .x0 C h/ D
p
1 C x:
Mit .x r /0 D r x r 1 für r 2 Q erhält man
1
1
;
p
2 1Cx
1
f .nC1/ .x0 C h/ hnC1 :
.n C 1/!
1
1
f 00 .x/ D p
:
4 1 C x3
Mit anderen Worten, es gilt
C
f .x/ D
160
Die ersten und zweiten Taylorpolynome von f bei x0 D 0 sind dann
x
T1 .x/ D f .0/ C f 0 .0/x D 1 C ;
2
1 00
x x2
2
:
G
T2 .x/ D T1 .x/ C f .0/x D 1 C 2
2
8
Für sich genommen ist das Taylorpolynom recht bedeutungslos, wenn man nicht
weiß, wie gut es die gegebene Funktion approximiert. Es kommt also darauf an, den
Approximationsfehler zu kontrollieren.
f .k/ .x0 / k
h
k!
Betrachte
f 0 .x/ D
Taylorpolynom und Taylorreihe
f .x0 C h/ D f .x0 / C f 0 .x0 /h C C
1
1
D f .x0 / C f 0 .x0 /h C f 00 .x0 /h2 C C f .n/ .x0 /hn :
2
n!
8F
9-D
1 .n/
f .x0 /hn
n!
1
f .nC1/ .x0 C h/ hnC1
.n C 1/!
mit einem 2 .0; 1/. Das Restglied in dieser Darstellung entspricht dem n C 1-ten
Term des Taylorpolynoms, nur wird es an einer Zwischenstelle x0 C
h ausgewertet.
///// Der Beweis ist nicht sehr intuitiv, benötigt dafür aber nur den üblichen
Mittelwertsatz. Sei oBdA x0 < x . Für x0 u x setzen wir
'.u/ WD f .x/ f .u/ f 0 .u/.x u/ : : :
.x u/nC1 :
.n C 1/!
1 .n/
f .u/.x u/n
n!
161
Taylorpolynom und Taylorreihe
9-D
9-D
Taylorpolynom und Taylorreihe
Dann ist '.x/ D 0, und wir können noch so wählen, dass auch '.x0 / D 0.
Nach dem Satz von Rolle existiert dann ein 2 .x0 ; x/ mit
Tx0 .x/ WD
die Taylorreihe von f bei x0 . Gilt
Eine kurze Rechnung zeigt aber, dass
f .x/ D Tx0 .x/
1 .nC1/
.u/.x u/n C .x u/n :
f
n!
n!
für alle x in einer Umgebung von x0 in I , so heißt f um x0 in seine Taylorreihe
entwickelbar. Aus ' 0 ./ D 0 folgt deshalb
D f .nC1/ ./:
9F
1
X
1 .k/
f .x0 /.x x0 /k
k!
kD0
' 0 ./ D 0:
' 0 .u/ D 162
Es gilt f .x/ D Tx0 f .x/ genau dann, wenn
Dies zusammen mit u D x0 ergibt die Behauptung. /////
p
In Beispiel 8, mit f .x/ D 1 C x und x0 D 0 , erhalten wir
lim Rn;x0 f .x/ D 0;
n!1
denn im Falle der Konvergenz der Taylorreihe im Punkt x gilt
3
1
:
f .x/ D p
8 1 C x5
000
f .x/ Tx0 f .x/ D lim .f .x/ Tn;x0 f .x// D lim Rn;x0 f .x/:
n!1
Für beispielsweise jxj 1=2 gilt
ˇ
p
ˇ
1
1
ˇ
p
D 2:
p
ˇ
1Cx
1 C x xD1=2
Die Konvergenz der Taylorreihe selbst dagegen bedeutet keineswegs, dass der Wert
der Reihe mit dem Funktionswert an dieser Stelle übereinstimmt. In Abschnitt 11-A
werden wir Cauchy’s Beispiel einer Funktion 2 C 1 .R/ beschreiben, für die gilt:
Für das Restglied nach Lagrange gilt deshalb für jj 1=2 die Abschätzung
p
2
1 ˇˇ 000 ˇˇ 1 3 p 5
f ./ 2 D
:
3!
6 8
4
T0 0;
p
1 ˇˇ 000 ˇˇ
2 3
f ./ jx x0 j3 jxj ;
3!
4
jxj 1=2:
.x/ ¤ 0 , x ¤ 0:
G
9.11
Satz Sei f 2 C 1 .I /. Gibt es Konstanten M > 0 und R > 0 , so dass
1 ˇˇ .n/ ˇˇ
f .x/ MRn
n!
Taylorreihe
Ist f in einer Umgebung von x0 beliebig oft differenzierbar, so können wir die
Reihe
Tx0 f .x/ D
aber
Die Taylorreihe dieser Funktion konvergiert also mühelos auf der reellen Geraden,
hat aber dort mit der Funktion selbst nichts zu tun.
Somit sind Kriterien wichtig, unter welchen Umständen C 1 -Funktionen durch
ihre Taylorreihen dargestellt werden.
Somit folgt aus der Lagrangeschen Restgliedformel:
jf .x/ T2;0 f .x/j n!1
1
X
f .k/ .x0 /
.x x0 /k ;
k!
kD0
bilden, die zumindest für x D x0 gegen den Grenzwert f .x0 / konvergiert.
Definition Für f 2 C 1 .I / und x0 2 I heißt
für alle x 2 I und n 0, so gilt
f .x/ D Tx0 f .x/
für alle x0 ; x 2 I mit jx x0 j < 1=R. ///// Sei x0 ; x 2 I mit jx x0 j < 1=R. Für das Restglied nach Lagrange
erhalten wir mit einem zwischen x0 und x
163
Taylorpolynom und Taylorreihe
ˇ
ˇ
ˇRn;x f .x/ˇ D
0
9-E
ˇ
ˇ
1
ˇ .nC1/ ˇ
./ˇjx x0 jnC1
ˇf
.n C 1/!
MRnC1 jx x0 jnC1
D M nC1
ˇ
ˇ
mit D jx x0 j R < 1. Somit gilt ˇRn;x0 f .x/ˇ ! 0 für n ! 1. /////
Wir formulieren noch eine nützliche Variante des letztes Satzes. Die Voraussetzung ist stärker, dafür aber auch die Folgerung.
9.12
Satz Sei f 2 C 1 .I /. Gibt es Konstanten M > 0 und R > 0 , so dass
ˇ .n/ ˇ
ˇf .x/ˇ MRn
für alle x 2 I und n 0, so gilt f .x/ D Tx0 f .x/ für alle x0 ; x 2 I . ///// Für das Restglied nach Lagrange erhalten wir analog zum letzten Beweis
ˇ
ˇ
ˇ
ˇ
1
ˇ .nC1/ ˇ
ˇRn;x f .x/ˇ D
./ˇjx x0 jnC1
ˇf
0
.n C 1/!
MRnC1
jx x0 jnC1
.n C 1/!
M nC1
D
;
D jx x0 j R:
.n C 1/!
Für beliebiges konvergiert die rechte Seite für n ! 1 gegen Null. /////
Funktionen f 2 C 1 .I / , die sich in jedem Punkt in I in ihre Taylorreihe entwickeln lassen, heißen reell analytisch, und die Klasse dieser Funktionen wird mit
C ! .I / bezeichnet. Wie bereits bemerkt, wird nicht jede C 1 -Funktion durch ihre
Taylorreihe dargestellt, es gilt also
C ! .I / C 1 .I /:
9-E
9-E
Summenfunktionen von Potenzreihen
164
Summenfunktionen von Potenzreihen
Mit Hilfe der Taylorreihe können geeignete Funktionen als Potenzreihe dargestellt
werden. Das klärt aber noch nicht die Frage, wie es sich mit Potenzreihen selbst
verhält! Zu klären ist noch, ob eine Potenzreihe mit positivem Konvergenzradius in
ihrem Konvergenzkreis eine stetige, differenzierbare, oder sogar analytische Funktion definiert.
Besitzt eine Potenzreihe
X
an .x x0 /n
n0
positiven Konvergenzradius r > 0, so definiert der Wert der Reihe für alle x in
Br .x0 / punktweise eine Funktion, die wir als die Summenfunktion der Potenzreihe
bezeichnen wollen.
Differenziationssatz Die Summenfunktion einer Potenzreihe ist auf dem gesamten
Konvergenzkreis stetig und differenzierbar, und es gilt
X
d X
an .x x0 /n D
nan .x x0 /n1 ;
dx
n0
n1
wobei die abgeleitete Reihe denselben Konvergenzradius wie die ursprüngliche Reihe besitzt. Man erhält also die Ableitung einer Potenzreihe durch gliedweise Differenziation, wobei der Konvergenzradius nicht beeinträchtigt nicht. Man kann daher diesen
Vorgang iterieren, und erhält das folgende Ergebnis.
Satz Die Summenfunktion einer Potenzreihe ist auf dem gesamten Konvergenzkreis
beliebig oft differenzierbar, und es gilt
k X
X
d
n!
an .x x0 /n D
an .x x0 /nk ;
dx
.n k/!
n0
nk
wobei alle abgeleiteten Reihen denselben Konvergenzradius wie die ursprüngliche
Reihe besitzt. 9.13 Satz Jede Potenzreihe ist innerhalb ihres Konvergenzkreises die Taylorreihe
ihrer Summenfunktion. Identitätssatz für Potenzreihen Die Summenfunktionen f und g zweier Potenz-
165
Summenfunktionen von Potenzreihen
9-E
reihen seien auf einem gemeinsamen Kreis K D Br .x0 / definiert. Gilt dann
f .xn / D g.xn /;
n 0;
für eine Folge unterschiedlicher Punkte xn mit Häufungspunkt x0 , so gilt f D g
auf ganz K , und die definierenden Potenzreihen sind identisch. 9-E
Summenfunktionen von Potenzreihen
166
10-A
Die Exponentialfunktion
168
Satz 9.12 überall gegen f . Also gilt
f .x/ D T0 f .x/ D .x/:
Damit ist auch die Eindeutigkeit gezeigt. /////
10
10-A
10.1
Spezielle Funktionen
Bemerkung. Wir haben hier die Theorie der Potenzreihen verwendet, um die
Existenz und Eindeutigkeit von Lösungen gewisser Differenzialgleichungen zu zeigen. Später werden wir eine wesentlich allgemeinere und flexiblere Theorie kennenlernen, die eindeutige Lösungen garantiert, auch wenn diese nicht analytisch
sind. Die Exponentialfunktion
Satz Es gibt genau eine differenzierbare Funktion W R ! R mit
0 D ;
.0/ D 1:
Definition Die in Satz 10.1 eindeutig definierte Funktion heißt Exponentialfunktion und wird mit ›exp‹ bezeichnet. Es gilt somit
Diese ist reell analytisch und besitzt bei 0 die auf ganz R konvergierende Potenzreihenentwicklung
(1)
1
X
xn
x2
.x/ D
D1CxC
C :::
n!
2!
:
nD0
///// Um die Existenz nachzuweisen, definieren wir durch (1). Die Potenzreihe konvergiert für alle x 2 R und definiert nach Satz 9.13 eine reell
analytische Funktion. Durch gliedweises Differenzieren finden wir
0 .x/ D
1
X
nD1
n1
n
x
n!
D
1
X
nD1
n1
x
D
.n 1/!
1
X
nD0
n
x
D .x/:
n!
Außerdem ist .0/ D 1.
Um die Eindeutigkeit nachzuweisen, sei f irgendeine differenzierbare Funktion auf R mit den gleichen Eigenschaften wie . Dann ist f jedenfalls
unendlich oft differenzierbar, mit
f .n/ D f;
f .n/ .0/ D f .0/ D 1;
n 0:
Die Taylorreihe dieser Funktion bei 0 ist demnach
T0 f D
1
1
X
f .n/ .0/ n X x n
x D
:
n!
n!
nD0
.n/
nD0
D f auch alle Ableitungen von f auf jedem kompakDa wegen f
ten Intervall gleichmäßig beschränkt sind, konvergiert die Taylorreihe nach
exp0 x D exp x;
exp 0 D 1:
Wir müssen allerdings noch untersuchen, was diese Funktionen mit der üblichen Exponenziation zu tun hat. Zunächst jedoch formulieren wir die wichtigsten
Eigenschaften von exp. Dabei machen wir von der Potenzreihendarstellung kaum
Gebrauch, vielmehr nutzen wir die Charakterisierung von exp durch die Differenzialgleichung.
10.2
Satz Für alle x; y 2 R gilt
(i) exp.
x/ exp x D 1,
(ii) exp x > 0,
(iii) exp.x C y/ D exp x exp y . /////
(i)
Wegen
.exp.
x/ exp x/0 D exp.
x/ exp x C exp.
x/ exp x D 0
ist die Funktionexp.
x/ exp x konstant, also gleich ihrem Wert 1 bei x D 0.
(ii) Wegen (i) hat exp keine reelle Nullstelle, wechselt also nicht das Vorzeichen. Aus exp 0 D 1 > 0 folgt daher die Behauptung.
(iii) Dies wurde bereits in Satz 6.6 gezeigt. Für einen unabhängigen Beweis
fixiere y 2 R , und betrachte die Funktion mit
.x/ D
exp.x C y/
:
exp y
Dann ist .0/ D 1 und
169
Die Exponentialfunktion
0 .x/ D
10-A
exp.x C y/
D .x/:
exp y
170
Für m D 1 und n 1 ist, mit n Summanden bzw Faktoren,
exp.n/ D exp.1 C C 1/ D exp.1/ : : : exp.1/ D e e D en :
(j)
Für m D 1 und n 1 folgt dann mit Satz 10.2
Für jedes n 0 gilt
lim x n exp x D 1;
lim x n exp x D 0:
x!1
x!1
exp.n/ D
exp.1=m/m D exp.m=m/ D exp.1/ D e;
Aus der Potenzreihendarstellung folgt für jedes n 0
x nC1
exp x ;
.n C 1/!
somit ist nach Definition der m-ten Wurzel
x 0:
exp.1=m/ D e1=m :
Bildet man nun von beiden Seiten die n-te Potenz, folgt die allgemeine Aussage. /////
Also folgt
lim x n exp x lim
x!1
nC1
x!1
1
1
D n D en :
exp.
n/
e
Für n D 1 und m 1 gilt dann analog zu (j)
Man sagt, die Exponentialfunktion strebt für x ! 1 schneller gegen 1 als
jede Potenz von x , und für x ! 1 schneller gegen 0 als jede Potenz von 1=x .
/////
Der Logarithmus und allgemeine Potenzen
/////
Also ist mit Satz 10.1 .x/ D exp x , und das ist die Behauptung. /////
Satz
10-B
1 x
D 1;
x n .n C 1/!
Für jedes x 2 Q gilt also ex D exp.x/ . Dies rechtfertigt die folgende Definition.
Definition Für alle x 2 R ist
sowie
.
1/n
D 0:
lim x n exp x D lim .
x/n exp.
x/ D lim n
x!1
x!1
x!1 x
exp x
/////
Aus den beiden letzten Sätzen ergibt sich insbesondere folgendes Bild der expFunktion.
Satz Die Exponentialfunktion exp ist streng monoton steigend und bildet R bijektiv auf .0; 1/ ab. ex WD exp.x/ D
1
X
xn
:
n!
nD0
Es gilt dann unter anderem
exCy D ex ey ;
wie es sich für eine Exponentialfunktion gehört.
Bereits früher hatten wir Eulersche Zahl definiert als
e D exp 1 D
1
X
1
:
n!
10-B
nD0
Der Logarithmus und allgemeine Potenzen
Potenzen von e haben wir bisher nur für rationale Exponenten n=m erklärt durch
n
en=m WD e1=m ;
Die Exponentialfunktion bildet die reelle Achse streng monoton steigend auf das
Intervall .0; 1/ ab. Also besitzt sie nach Satz 8.5 eine Umkehrfunktion.
wobei e1=m die nach Satz 8.6 eindeutig bestimmte, positive m-te Wurzel von e bezeichnet. Wir zeigen nun, das dies mit exp.n=m/ übereinstimmt.
Definition Die Umkehrfunktion der Exponentialfunktion heißt Logarithmusfunktion und wird mit ›log‹ bezeichnet. 10.3
Satz Für n 2 Z und m 2 N gilt
n=m
exp.n=m/ D e
:
Es ist also
log D exp1 W .0; 1/ ! R:
171
Der Logarithmus und allgemeine Potenzen
10-B
10-B
Es gilt unter Anderem log 1 D 0, log e D 1 ,
e
log x
D exp log x D x;
x > 0:
Wegen Satz 9.11 konvergiert daher T0 auf .
1; 1/ gegen , und es gilt
Satz Die Logarithmusfunktion logW .0; 1/ ! R ist streng monoton steigend und
stetig differenzierbar, und es gilt
log.1 C x/ D .x/ D x (i) log0 x D 1=x ,
(ii) log.xy/ D log x C log y
///// (i) Da die Ableitung der exp-Funktion nirgends verschwindet, ist nach
Satz 9.4 auch die log-Funktion überall differenzierbar, und es gilt
1
1
1
D
D :
exp0 .log x/
exp.log x/
x
Daher ist folgende Definition sinnvoll.
exp.log xy/ D xy
Definition Für a > 0 und x 2 R ist
ax WD exp.x log a/:
exp.log x C log y/ D exp.log x/ exp.log y/ D xy:
(i) .ax /0 D ax log a,
(ii) axCy D ax ay ,
Zusatz Die Logarithmusfunktion ist reell analytisch auf .0; 1/ und besitzt die
Potenzreihendarstellung
.
1/n1
nD1
/////
xn
x2
x3
Dx
C
:::;
n
2
3
jxj < 1:
Für die Funktion W .
1; 1/ ! R mit .x/ D log.1 C x/ gilt
.n/ .x/ D .
1/n1
.n 1/!
;
.1 C x/n1
1 .n/
.
1/n1
.0/ D
;
n!
n
n 1;
(iii) .ab/x D ax b x ,
(iv) axy D .ax /y ,
für alle a; b > 0 und x; y 2 R . ///// Alle Eigenschaften folgen unmittelbar aus der Definition von ax . Zum
Beispiel
axCy D exp..x C y/ log a/
D exp.x log a C y log a/
wie man unschwer mit Induktion zeigt. Da außerdem .0/ D 0, ist
T0 .x/ D
1
X
.
1/n1
nD1
xn
x2
x3
Dx
C
::: :
n
2
3
Satz Für jedes a > 0 ist die Funktion x 7! ax streng monoton steigend und stetig
differenzierbar auf R , und es gilt:
Da 1=x auf .0; 1/ unendlich oft differenzierbar ist, ist es auch der Logarithmus.
Tatsächlich ist er sogar reell analytisch.
1
X
/////
Es folgen die wichtigsten Eigenschaften der allgemeinen Potenzfunktion.
Da exp umkehrbar ist, muss (ii) gelten. /////
log.1 C x/ D
jxj < 1:
Potenzen einer positiven reellen Zahl a haben wir bisher für rationale Exponenten
n=m erklärt. Doch genau wie im Beweis von Satz 10.3 zeigt man, dass mit a D
exp.log a/ auch
n
an=m D exp
log a ;
n 2 Z; m 2 N:
m
Es ist sowohl
als auch
(j)
x3
x2
C
:::;
2
3
Allgemeine Potenzen
für alle x; y > 0. (ii)
172
Nun folgt auf jedem Intervall Œ
; .
1; 1/ aus (j) die Abschätzung
1
1 ˇˇ .n/ ˇˇ
;
n 1:
ˇ .x/ˇ n!
.1 /n
sowie limx!1 log x D 1 und limx!0 log x D 1.
log0 x D
Der Logarithmus und allgemeine Potenzen
D exp.x log a/ exp.y log a/ D ax ay ;
und
173
Sinus und Cosinus
10-C
10-C
.ax /0 D exp.x log a/0
Sinus und Cosinus
oft differenzierbar, mit
D exp.x log a/ log a D ax log a:
u.2n/ D .
1/n u;
(j)
Entsprechend alles andere. /////
r
Mit a haben wir zugleich auch die allgemeine Potenz x von x > 0 für beliebige reelle r definiert. Dazu ebenfalls die wichtigsten Eigenschaften.
u.2n/ .0/ D 0;
T0 u D
(i) .x r /0 D r x r 1 ,
Es ist log x r D log.exp.r log x// D r log x und
r
rx
D r x r 1 :
.x r /0 D exp.r log x/0 D exp.r log x/ D
x
x
I
/////
x 2nC1
:
.2n C 1/!
I
I
n 0;
mit einer von I abhängenden Konstanten M . Wegen Satz 9.12 konvergiert
daher T0 u auf R gegen u, und wir erhalten u D T0 u D s . /////
Definition Die durch (2) und (3) eindeutig definierten Funktionen heißen Sinus
und Cosinus und werden mit ›sin‹ und ›cos‹ bezeichnet, gelegentlich auch mit ›s ‹
und › c ‹. Sinus und Cosinus
Es gibt genau eine zweimal differenzierbare Funktion s W R ! R mit
s 00 C s D 0;
s.0/ D 0;
10.4
s 0 .0/ D 1;
c 00 C c D 0;
c.0/ D 1;
(ii) sin.
x/ D sin x und cos.
x/ D cos x ,
(iii) sin2 x C cos2 x D 1,
c 0 .0/ D 0:
Beide Funktionen sind reell analytisch und besitzen die auf ganz R konvergierenden
Potenzreihendarstellungen
s.x/ D
1
X
x 2nC1
.
1/n
;
.2n C 1/!
nD0
c.x/ D
Satz Für die Sinus- und Cosinusfunktion gilt:
(i) sin0 x D cos x und cos0 x D sin x ,
und genau eine zweimal differenzierbare Funktion c W R ! R mit
(4)
.
1/n
sup ju.n/ j sup juj C sup ju0 j M;
r
(3)
1
X
nD0
(ii) log x D r log x . (2)
u.2nC1/ D .
1/n ;
Aus (j) folgt ferner, dass auf jedem kompakten Intervall I alle Ableitungen
von u gleichmäßig beschränkt sind:
r
Satz
n 0:
die Taylorreihe von u daher
Satz Für jedes r 2 R ist die Funktion x 7! x r auf .0; 1/ stetig differenzierbar,
und es gilt
10-C
u.2nC1/ D .
1/n u0 ;
Insbesondere ist dann
x
/////
174
1
X
nD0
x 2n
.
1/n
:
.2n/!
///// Wie im Beweis von Satz 10.1 definieren wir s und c durch die Reihen
in (4). Diese haben Konvergenzradius 1, sie können daher für alle x 2 R
gliedweise beliebig oft differenziert werden. Die Gleichungen (2) und (3) sind
dann leicht zu verifizieren. Damit ist die Existenz von Lösungen gezeigt.
Um deren Eindeutigkeit zu zeigen, sei u irgendeine zweimal differenzierbare
Lösung zum Beispiel der Gleichung (2). Wegen u00 D u ist dann u beliebig
(iv) sin.x C y/ D sin x cos y C cos x sin y ,
(v) cos.x C y/ D cos x cos y sin x sin y ,
für alle x; y 2 R . ///// (i) und (ii) Dies ergibt sich aus der Potenzreihendarstellung. Alternativ kann man beispielsweise auch zeigen, dass s 0 wie auch c ebenfalls
Lösungen von (3) sind, also gleich c sein müssen.
(iii) Wegen
.s 2 C c 2 /0 D 2ss 0 C 2cc 0 D 2sc 2cs D 0
ist s 2 C c 2 konstant, also gleich s 2 .0/ C c 2 .0/ D 1.
(iv) und (v) Fixiere ein y 2 R , und betrachte die Funktionen u und v , die
175
Sinus und Cosinus
durch
u.x/
v.x/
D
c.x/ s.x/
s.x/ c.x/
s.x C y/
c.x C y/
10-C
0
u .x/ D s.x/s.xCy/Cc.x/c.xCy/
c.x/c.xCy/Cs.x/s.xCy/ D 0;
und ebenso v 0 .x/ D 0. Also gilt
oder
s.y/
c.y/
D
s.x C y/
c.x C y/
Das ist gerade die Behauptung. /////
/////
und
sin x > 0;
x 2 .0; /:
Aus Stetigkeitsgründen gibt es wegen c.0/ D 1 ein ı > 0 , so dass
c.x/ > 0;
x 2 Œ0; ı:
Wegen s 0 D c ist dann s strikt wachsend auf Œ0; ı, wegen s.0/ D 0 also
auch
(j)
s.x/ > 0;
x 2 .0; ı:
Wir nehmen nun an, dass s.x/ > 0 für alle x > 0 , und führen dies zu einem
Widerspruch.
Wegen c 0 D s ist dann c strikt fallend auf Œ0; 1/. Wäre c an irgendeiner
Stelle 0, so gäbe es auch ein x0 mit c.x0 / < 0 , und es folgte
s 0 .x/ D c.x/ c.x0 / < 0;
x x0 :
Dann aber kann s nicht mehr für alle x > 0 positiv sein. Also ist c strikt
fallend und überall positiv. Wegen s 0 D c ist dann s strikt wachsend, und aus
c 0 .x/ D s.x/ s.x0 / < 0;
definieren. Wegen (j) gilt > 0, und per definitionem gilt weiter s.x/ > 0
für 0 < x < . /////
/////
D 0;
2
sin
D 1:
2
Auf Grund des letzten Satzes ist
c 0 .x/ D s 0 .x/ < 0;
x 2 .0; /:
Nach Satz 9.6 ist also c strikt fallend auf Œ0; . Wegen c.0/ D 1, s./ D 0
und
c 2 ./ C s 2 ./ D c 2 ./ D 1
Satz Es gibt eine eindeutig bestimmte reelle Zahl > 0, so dass
sin D 0
WD inf f 2 .0; 1/ W s./ D 0g
cos
:
Wegen s 2 .x/ C c 2 .x/ D 1 ist dieses Gleichungssystem äquivalent zu
s.x C y/
c.x/ s.x/
s.y/
D
:
c.x C y/
s.x/ c.x/
c.y/
10.5
176
10.6 Satz Die Cosinusfunktion bildet das Intervall Œ0; streng monoton fallend
auf Œ
1; 1 ab. Außerdem gilt
v.x/ D v.0/ D c.y/;
c.x/ s.x/
s.x/ c.x/
Sinus und Cosinus
folgt, dass auch c nicht für alle x > 0 positiv sein kann. Somit erhalten wir
einen Widerspruch.
Somit besitzt s mindestens eine Nullstelle in .0; 1/ , und wir können
definiert werden. Aus den bereits bewiesenen Ableitungsregeln folgt
u.x/ D u.0/ D s.y/;
10-C
x x0 ;
muss dann c./ D 1 sein. Schließlich folgt aus Satz 10.4 und 10.5
2s.=2/c.=2/ D s./ D 0;
also c.=2/ D 0, und damit auch s.=2/ D 1. /////
Nun können wir endlich feststellen, dass sin und cos periodische Funktionen
sind. Tatsächlich gelten eine ganze Reihe »periodischer Beziehungen«.
10.7 Satz Die Funktionen sin und cos sind antiperiodisch mit der Periode und periodisch mit der Periode 2 . Das heißt, es gilt
sin.x C / D sin x;
sin.x C 2/ D sin x;
cos.x C / D cos x;
cos.x C 2/ D cos x:
Außerdem gilt
sin.x C =2/ D cos x;
cos.x C =2/ D sin x:
///// Dies folgt aus den Additionstheoremen von Satz 10.4 für die Funktionen s und c und deren speziellen Werten bei =2 und . Zum Beispiel:
s.x C / D s.x/c./ C c.x/s./ D s.x/c./ D s.x/:
177
Sinus und Cosinus
10-C
und damit auch s.x C 2/ D s.x C / D s.x/. /////
Für den Graphen der Sinusfunktion bedeutet dies zum Beispiel:
Verschiebung um 2 führt ihn in sich selbst über,
Verschiebung um und Spiegelung an der x-Achse ebenso,
10-D
10.8
178
und die Absolutgeschwindigkeit ist gleichförmig kP .t /k D 1. Die Länge der Bahn
vom Zeitpunkt 0 bis zum Zeitpunkt t ist demnach t – dies ist intuitiv klar, wird aber
noch durch die Integralrechnung bestätigt werden. Nimmt man diese Länge als Maß
des zwischen den Punkten .0/, .0; 0/ und .t/ eingeschlossenen Winkel, so erhält
man die Schuldefinition des Sinus und Cosinus:
Verschiebung um =2 ergibt den Graphen der Cosinusfunktion.
Bis jetzt ist noch nicht klar, was dieser Sinus mit dem »Schul-Sinus« zu tun hat.
Dies wird mit dem folgenden Satz und seiner Erläuterung klarer werden.
Weitere trigonometrische Funktionen
sin t D
Gegenkathete
;
Hypotenuse
cos t D
Ankathete
;
Hypotenuse
wobei die Länge der Hypotenuse im Einheitskreis 1 ist.
Satz Die Abbildung
W R ! R2 ;
t 7! .cos t; sin t /
bildet das Intervall Œ0; bijektiv auf den oberen Einheitskreissektor
˚
S C D .x; y/ W x 2 C y 2 D 1; y 0 ;
10-D
Weitere trigonometrische Funktionen
Tangens und Cotangens
und das Intervall Œ; 2 bijektiv auf den unteren Einheitskreissektor
˚
S D .x; y/ W x 2 C y 2 D 1; y 0
Mit Sinus und Cosinus verbunden sind einige weitere trigonometrische Funktionen.
Wichtig für uns sind noch der Tangens und der Cotangens.
ab. Definition Die Tangens- und Cotangensfunktion sind definiert durch
/////
Wegen s 2 .t/ C c 2 .t/ D 1 und s.t/ 0 auf Œ0; ist klar, dass
W Œ0; ! S C :
Da c nach Satz 10.6 auf Œ0; strikt fällt, ist diese Abbildung injektiv. Und
sie ist surjektiv, denn zu jedem x 2 Œ
1; 1 existiert ein t 2 Œ0; mit
c.t/ D x;
und dann ist wegen s.t/ 0 auf Œ0; auch
q
p
s.t/ D 1 c 2 .t/ D 1 x 2 D y:
Die Behauptung zu W Œ; 2 ! S folgt analog. /////
Aus den beiden letzten Sätzen folgt, dass
.t/ D .cos t; sin t/
eine 2 -periodische Bewegung auf dem Einheitskreis beschreibt. Ihr Geschwindigkeitsvektor ist
P .t / D .
sin t; cos t/;
tanW R fx W cos x D 0g ! R;
x 7!
sin x
cos x
cotW R fx W sin x D 0g ! R;
x 7!
cos x
:
sin x
und
Andere Bezeichnungen sind tg und ctg. Es gilt also
tan x D tg x D
1
1
D
:
ctg x
tan x
Satz Die Funktionen tan und cot sind ungerade, periodisch mit der Periode ,
und auf ihren Definitionsbereichen stetig differenzierbar mit Ableitungen
tan0 x D
1
;
cos2 x
cot0 x D 1
sin2 x
:
///// Wir betrachten tan D sin = cos. Der Quotient einer geraden und einer
ungeraden Funktion ist immer ungerade. Außerdem gilt mit Satz 10.7
tan.x C / D
sin.x C /
sin x
sin x
D
D
D tan x:
cos.x C /
cos x
cos x
Die stetige Differenzierbarkeit folgt aus der Quotientenregel,
179
Weitere trigonometrische Funktionen
10-D
sin0 x cos x sin x cos0 x
cos2 x C sin2 x
1
D
D
;
2
cos x
cos2 x
cos2 x
da cos auf dem Definitionsbereich von tan nirgends verschwindet. /////
tan0 x D
Offenbar sind tan und cot unendlich oft differenzierbar. Sie sind sogar reell analytisch, und es gilt – Übungsaufgabe –
tan x D
1
X
.
1/n
nD0
x 2nC1
;
2n C 1
Die Umkehrfunktion der exp-Funktion ist die log-Funktion. Was sind die Umkehrfunktionen von sin , cos und tan ?
Um umkehrbar zu sein, muss eine Funktion injektiv sein. Eine periodische Funktion ist aber geradezu die Antithese einer injektiven Funktion – sie wiederholt sich
ja ständig. Um die betreffenden Funktionen ›umkehrbar zu machen‹, müssen wir
sie zunächst auf geeignete Intervalle einschränken. Hierfür gibt es unendlich viele
Möglichkeiten, doch die folgenden Einschränkungen sind wohl die naheliegendsten:
sinW Œ
=2; =2 ! Œ
1; 1;
tanW .
=2; =2/ ! R:
Diese Funktionen sind umkehrbar, die zugehörigen Umkehrfunktionen werden Arcus
Sinus, Arcus Cosinus und Arcus Tangens genannt, und mit
arctan
bezeichnet.
Die Funktionen
arcsinW Œ
1; 1 ! Œ
=2; =2;
arccosW Œ
1; 1 ! Œ0; ;
arctanW
R ! .
=2; =2/;
sind sämtlich stetig und im Innern ihrer Definitionsbereiche stetig differenzierbar,
und es gilt
arcsin0 x D p
1
1
x2
;
sowie
arctan0 x D
/////
1
;
1 C x2
x 2 R:
Wir betrachten arcsin als Beispiel. Die Funktion
besitzt im Innern des Definitonsbereiches eine strikt positive Ableitung, zudem werden die Endpunkte des Definitionsbereiches auf die Endpunkte des
Wertebereiches abgebildet. Nach Satz 9.10 ist sie daher umkehrbar, und die
Umkehrfunktion arcsin ist auf Œ
1; 1 stetig und im Innern differenzierbar.
Für die Ableitung gilt weiter
arcsin0 x D
1
1
D
;
cos y
sin0 y
y D arcsin x;
und da cos y positiv ist, gilt
p
p
cos y D 1 sin2 y D 1 x 2 :
h Bilderi
und
Satz
180
Analog werden die übrigen Behauptungen bewiesen. /////
cosW Œ0; ! Œ
1; 1;
arccos;
Weitere trigonometrische Funktionen
sinW Œ
=2; =2 ! Œ
1; 1
jxj < 1:
Arcusfunktionen
arcsin;
10-E
arccos0 x D p
1
1 x2
;
x 2 .
1; 1/;
Bemerkung. Die hier definierten Arcusfunktionen werden auch als die Hauptzweige der jeweiligen Arcusfunktion bezeichnet. Schränkt man sin, cos, tan auf
andere geeignete Intervalle ein, so erhält man entsprechende Nebenzweige dieser
Funktionen. 181
Exp, Sin und Cos im Komplexen
10-E
10-E
10-E
Exp, Sin und Cos im Komplexen
Exp, Sin und Cos im Komplexen
/////
Einsetzen und Ausrechnen ergibt
1
1
1
.iz/2 C .iz/3 C .iz/4 C : : :
2!
3!
4!
1
i
1
D 1 C iz z 2 z 3 C z 4 C : : :
2!
3!
4!
1
1
1
1
D 1 z2 C z4 C : : : C i z z3 C z5 C : : :
2!
4!
3!
5!
eiz D 1 C .iz/ C
Die Funktionen sin , cos und exp können eigentlich unterschiedlicher kaum sein:
sin und cos sind periodisch und beschränkt, mit unendlich vielen Nullstellen, exp
ist streng monoton und unbeschränkt, ohne jede Nullstelle.
Tatsächlich handelt es sich um ein und dieselbe Funktion. Der Zusammenhang
wird deutlich, wenn wie diese auch für komplexe Argumente betrachten. Mit Hilfe
der Potenzreihendarstellungen ist dies straightforward.
D cos z C i sin z:
Definition Für z 2 C ist
Da die Reihen absolut konvergieren, dürfen wir sie umordnen. /////
1
X
zn
exp z D
n!
Für reelle Argumente gilt erst recht
nD0
eit D cos t C i sin t;
sowie
2
sin z D
1
X
.
1/n
nD0
2nC1
z
;
.2n C 1/!
cos z D
1
X
.
1/n
nD0
2n
z
:
.2n/!
sin0 D cos;
10.9
Außerdem gilt die Funktionalgleichung
z; w 2 C:
///// Es genügt, die definierenden Potenzreihen gliedweise zu differenzieren. Die Funktionalgleichung wurde bereits mit Hilfe des Cauchyproduktes
bewiesen, siehe Satz 6.6. /////
Wie im Reellen folgt aus der Funktionalgleichung exp.
z/ exp z D 1, insbesondere also
für alle komplexen z . Die Exponentialfunktion verschwindet somit auch im Komplexen nirgends.
Wir schreiben nun wieder kürzer ez WD exp z .
Eulersche Formel Für alle z 2 C gilt
e D cos z C i sin z:
Satz Die Funktion
cisW R ! C;
t 7! eit
ab. ›cis‹ ist ein Akronym für ›cos C i sin‹. Diese Abbildung wickelt also die reelle
Gerade gleichmäßig mit der Periode 2 so um den Einheitskreis, dass
ei.sCt / D eis eit ;
oder
cis.s C t / D cis.s/ cis.t /:
exp z ¤ 0
iz
it
ist periodisch mit der Periode 2 und bildet das Intervall Œ0; 2/ bijektiv auf den
Einheitskreis
˚
S D z 2 C W jzj D 1
cos0 D sin :
exp.z C w/ D exp.z/ exp.w/;
t 2 R:
Identifizieren wir C mit R , und e in C mit .cos t; sin t/ im R2 , so erhalten wir
mit Satz 10.8 folgendes Ergebnis.
Satz Die Funktionen exp, sin und cos sind auf C beliebig oft differenzierbar,
sogar reell analytisch, und es gilt
exp0 D exp;
182
Es handelt sich also um einen Endomorphismus von .R; C/ nach .S; / . Insbesondere wird abgebildet auf 1, es gilt also die berühmte Eulersche Gleichung
ei C 1 D 0:
Sie verbindet die fünf wichtigsten Zahlen der Mathematik,
0;
1;
;
e;
i;
183
Exp, Sin und Cos im Komplexen
10-E
auf eine geradezu mystische Weise.
Die Funktionalgleichung für eix führt auch sofort zu den Additionstheoremen
der sin- und cos -Funktion. Es ist
ei.xCy/ D cos.x C y/ C i sin.x C y/
D eix eiy
D .cos x C i sin x/.cos y C i sin y/
D .cos x cos y sin x sin y/ C i .sin x cos x C cos x sin y/
Für reelle x; y sind alle sin - und cos -Terme reell. Ein Vergleich der Real- und Imaginärteile ergibt somit die Additionstheoreme von Satz 10.4.
Ebenso leicht erhält man die Formeln von Moivre:
.cos x C i sin x/n D einx D cos nx C i sin nx:
Schließlich gilt natürlich auch für reelle x
eix C eix
;
2
ix
ix
e e
sin x D Im eix D
:
2i
Beginnt man das Studium der Speziellen Funktionen mit der exp-Funktion im Komplexen, und insbesondere der cis-Funktion, so kann man cos und sin auch mit Hilfe
dieser Formeln definieren.
cos x D Re eix D
10-E
Exp, Sin und Cos im Komplexen
Auf Grund von Satz 10.9 existiert zu w genau ein 2 Œ0; 2/ mit
w D ei :
Somit existiert eine solche Darstellung z D r ei . Diese ist auch eindeutig,
denn notwendigerweise ist jzj D r jei j D r , und es gibt nur ein 0 < 2
mit ei D z=jzj. /////
Das Argument von z ¤ 0 ist also diejenige eindeutige reelle Zahl mit
ei D z=jzj;
0 < 2:
Dabei ist eindeutig nur wegen der Beschränkung auf Œ0; 2/ . Wegen der Periodizität der cis-Funktion gilt auch
z D r ei D r ei.C2n/ ;
Bisher kennen wir die kartesische Darstellung komplexer Zahlen als
und im Reellen ist damit alles gesagt. Im Komplexen gilt aber mehr.
Satz Es gibt es genau n verschiedene komplexe n-te Wurzeln der Zahl 1, die sogenannten n-ten Einheitswurzeln nk mit 0 k n 1, wobei
///// Offenbar ist z D 0 keine Wurzel aus 1. Somit können wir z D r ei
ansetzen, und es gilt
z n D r n ein D 1
z D a C ib:
Die cis-Funktion ermöglicht nun die ebenso nützliche Polardarstellung.
Satz und Definition Zu jedem z 2 C existieren genau ein r > 0 und genau ein
2 Œ0; 2/ mit
z D re :
i
Diese reelle Zahl heißt das Argument der komplexen Zahl z ¤ 0 . Jedes z 2 C kann geschrieben werden als
z
2 S:
z D r w;
mit
r D jzj > 0; w D
jzj
/////
n 2 Z:
Für z D 0 dagegen ist das Argument nicht wohldefiniert.
Mit Hilfe der Polardarstellung lassen sich leicht alle Wurzeln einer komplexen
Zahl bestimmen. Zuerst betrachten wir alle n-ten Wurzeln aus 1. Natürlich ist
p
n
1 D 1;
n D e2i=n :
Die Polardarstellung komplexer Zahlen
184
genau dann, wenn r D 1 und
n D 2k , D k 2=n
für ein k 2 Z. Also ist z D nk für ein k 2 Z mit n D e2i=n . Nach
Satz 10.9 sind dies genau n verschiedene Punkte, zum Beispiel für k D
0; : : : ; n. /////
Satz Zu jeder komplexen Zahl w D r ei
Wurzeln, nämlich
zk D nk z0 ;
0 k < n;
¤ 0 gibt es genau n verschiedene n-te
z0 D
p
n
r ei
=n
:
185
Exp, Sin und Cos im Komplexen
10-E
///// z0 ist sicher eine n-te Wurzel aus w . Ist z irgendeine weitere n-te
Wurzel, so ist z =z0 eine n-te Einheitswurzel, also nk für ein 0 k < n.
Das ergibt die Behauptung. /////
10-E
Exp, Sin und Cos im Komplexen
186
11-B
Die Regel von l’Hopital
(
.x/ D
11
x 0:
0;
bauen, mit denen man beispielsweise sogenannte Zerlegungen der Eins konstruiert.
Zur Abrundung des Themas » C 1 versus C ! « sei noch die folgende, vielleicht
überraschende Beobachtung von Borel erwähnt.
Das Gegenbeispiel von Cauchy
Satz (Borel) Zu jeder Folge .an /n0 reeller Zahlen existiert eine Funktion f 2
C 1 .R/ mit
Cauchys Gegenbeispiel Die Funktion W R ! R mit
(
2
e1=x ; x ¤ 0;
.x/ D
0;
x D 0;
1 .n/
f .0/ D an ;
n!
ist unendlich oft differenzierbar, und alle ihre Ableitungen bei 0 verschwinden:
.n/ .0/ D 0;
2
e1=x ; x > 0;
Aus dieser kann man weiter Funktionen der Art
(
1; jxj 1;
R ! Œ0; 1;
.x/ D
0; jxj 2
Ergänzungen
11-A
188
n 0:
n 0:
Das heißt, formal ist die Taylorreihe von f
T0 f .x/ D
1
X
an x n :
nD0
Die Taylorreihe dieser Funktion bei 0 verschwindet also identisch,
T0 D
X .n/ .0/
x n 0;
n!
Wächst jedoch .an / rasch genug an, so ist ihr Konvergenzradius 0, und die Taylorreihe hat nur formalen Charakter.
n0
sie hat insbesondere unendlichen Konvergenzradius. Aber natürlich ist die Funktion
selbst nicht die Nullfunktion, wird also nicht von ihrer Taylorreihe dargestellt.
Somit ist auch nicht reell analytisch.
/////
Auf R ist sicherlich beliebig oft differenzierbar. Genauer gilt
2
.r / .x/ D pr .1=x/ e1=x ;
x!0
Sehr häufig sind Grenzwerte wie
x!0
sin x
;
x
Daraus folgt wiederum leicht, dass alle .r / auch in 0 differenzierbar sind,
und dort alle Ableitungen verschwinden. /////
W R ! R mit
lim
x!0
1 cos2 x
x2
zu bestimmen – also Grenzwerte von der Form
lim
x!x0
r 0:
Eine nützliche Variante dieses Beispiels ist die Funktion
Die Regel von l’Hopital
lim
x ¤ 0;
für alle r 0 mit einem Polynom pr vom Grad 3r , wie man leicht durch
Induktion zeigt. Wegen lim t !1 t m et D 0 für alle m 0 folgt hieraus
lim .r / .x/ D 0;
11-B
f .x/
;
g.x/
f .x0 / D 0;
g.x0 / D 0:
Man spricht von ›unbestimmten Ausdrücken der Form
unbestimmter Ausdrücke gibt es eine nützliche Regel.
0
0
‹. Für diese und weitere
Regel von l’Hopital Seien f; g 2 C r .I / mit r 1, und in einem Punkt x0 2 I
gelte
189
Die Regel von l’Hopital
f ./ .x0 / D 0;
g ./ .x0 / D 0;
11-B
Dann existiert der Grenzwert limx!x0 f .x/=g.x/, und es gilt
x!x0
/////
f .x/
f .x/ f .x0 /
f .x/ f .x0 / g.x/ g.x0 /
W
:
D
D
g.x/
g.x/ g.x0 /
x x0
x x0
Die Grenzwerte der beiden Quotienten rechts existieren, und der zweite ist
nicht Null. Das Ergebnis folgt dann aus den Grenzwertsätzen.
Im allgemeinen Fall r 1 greifen wir auf die Taylorformel mit dem Restglied von Lagrange zurück. Da nach Annahme alle Ableitungen von f und
g bis zur Ordnung r 1 in x0 verschwinden, ist mit h D x x0 ¤ 0
1 .r /
f .x0 C h/hr ;
r!
g.x/ D
1 .r /
f .x0 C #h/hr
r!
mit gewissen ; # 2 .0; 1/. Also ist
Der Grenzwert auf der rechten Seite existiert für h ! 0, da g .r / .x0 / ¤ 0.
Das Ergebnis folgt damit wieder aus den Grenzwertsätzen. /////
(0)
lim f .x/ D lim g.x/ D 0;
x!x0
x!x0
oder
(1)
lim f .x/ D lim g.x/ D 1;
x!x0
x!x0
sowie
(1)
g 0 .x/ ¤ 0;
x 2 I:
Existiert dann limx!x0 f 0 .x/=g 0 .x/ als eigentlicher oder uneigentlicher Grenzwert, so existiert auch limx!x0 f .x/=g.x/ , und es gilt
(2)
lim
x!x0
f .x/
f 0 .x/
D lim 0
:
x!x
g.x/
0 g .x/
IW
.a; b/
x0 W a oder b
.a; 1/
1
.
1; b/
1
.a; c/ [ .c; b/
:
c
Man beachte, dass f und g in x0 nicht erklärt sein müssen, auch wenn x0 endlich
ist. Mit der Regel von l’Hopital ist
sin x
cos x
D lim
D 1;
x!0
x
1
2
1 cos x
sin x cos x
cos2 x sin2 x
D
lim
D
lim
D 1;
lim
x!0
x!0
x!0
x
1
x2
lim
x!0
und natürlich
f .x/ f .x0 /
f 0 .x/
D lim
D f 0 .x0 /:
lim
x!x0
x!x0
x x0
1
G
Bemerkung. Die Voraussetzungen an das Intervall I und den Punkt x0 sind
zum Beispiel in den folgenden Fällen erfüllt:
f .x/
f .r / .x0 C h/
D .r /
g.x/
g .x0 C #h/
1F
0 D lim
11.1 Verallgemeinerte Regel von l’Hopital Seien f; g 2 C 1 .I / und x0 ein eigentlicher oder uneigentlicher Randpunkt des (punktierten) Intervalls I . Ferner sei
Wir betrachten zuerst den Fall r D 1 . Dann ist für x ¤ x0
f .x/ D
190
Nun treten auch Grenzwerte für x ! 1 auf – f 0 und g 0 müssen also nicht unbedingt in x0 definiert sein. Auch interessiert man sich für unbestimmte Ausdrücke
der Form › 1
‹.
1
g .r / .x0 / ¤ 0:
f .x/
f .r / .x0 /
:
D .r /
g.x/
g .x0 /
Die Regel von l’Hopital
2x
x2
¤ lim D 2:
x!0 cos x
x!0 sin x
D 0; : : : ; r 1;
sowie
lim
11-B
G
2 F Man darf allerdings nicht vergessen zu überprüfen, ob tatsächlich alle Voraussetzungen der Regel erfüllt sind. So ist zum Beispiel
///// Beweis, Teil 1 Wir betrachten zuerst den Fall (0), und unterscheiden
hier weiter drei Fälle.
(i) x0 2 R . Wir können f und g in x0 durch den Wert 0 stetig fortsetzen. Dann gilt mit dem Mittelwertsatz und h D x x0
f .x/
f .x/ f .x0 /
f 0 .x0 C h/
D
D 0
g.x/
g.x/ g.x0 /
g .x0 C #h/
mit gewissen ; # 2 .0; 1/, da nach Voraussetzung g 0 auf I nicht verschwindet. Auf der rechten Seite können wir zum Grenzwert h ! 0 übergehen und
erhalten die Behauptung.
191
Die Regel von l’Hopital
11-B
11-B
(ii) x0 D 1 . Wir schreiben x D 1=t und betrachten den Grenzwert
t 0. Die für ii benötigten Voraussetzungen sind erfüllt, und es folgt
a<x<c<b
existiert dann nach dem verallgemeinerten Mittelwertsatz ein 2 .x; c/ mit
f .x/ f .c/
f .x/.1 f .c/=f .x//
f 0 ./
D
D
;
g 0 ./
g.x/ g.c/
g.x/.1 g.c/=g.x//
D lim
Genauer gesagt: Da der letzte Grenzwert existiert, existiert auch der erste, und
beide sind gleich.
(iii) x0 D 1. Genauso. /////
Um auch den Fall .1/ behandeln zu können, benötigen wir folgendes Resultat.
oder
f 0 ./
f .x/
D m.x/ 0 ;
g.x/
g ./
(j)
x!a
Zu zeigen ist:
f 0 .x/
f .x/
D A ) lim
D A:
x!a g 0 .x/
x!a g.x/
lim
Auch hier unterscheiden wir im Wesentlichen zwei Fälle.
(i) A D 1. Für c hinreichend nahe bei a übertrifft f 0 .x/=g 0 .x/ für
x 2 .a; c/ jede vorgegebene Schranke. Wählen wir jetzt noch x hinreichend
nahe bei a , wird m.x/ 1=2 wegen (k). Somit übertrifft wegen (j) auch
f .x/=g.x/ jede vorgegebene Schranke.
(ii) A 2 R . Dann gilt
ˇ ˇ
ˇ
ˇ
ˇ ˇ
ˇ
ˇ f .x/
f 0 ./
ˇ ˇ
ˇ
ˇ
ˇ g.x/ Aˇ D ˇm.x/ g 0 ./ Aˇ
ˇ 0 ˇ ˇ 0
ˇ
ˇ f ./ ˇ ˇ f ./
ˇ
jm.x/ 1jˇˇ 0 ˇˇ C ˇˇ 0
Aˇˇ:
g ./
g ./
///// Die Ableitung g 0 hat festes Vorzeichen auf I , da sie stetig ist und nirgends verschwindet. Somit ist g streng monoton, g.b/ g.a/ ¤ 0 , und die
Hilfsfunktion W Œa; b ! R mit
f .b/ f .a/
.g.x/ g.a//
g.b/ g.a/
wohldefiniert. Außerdem ist auf .a; b/ differenzierbar, und
.a/ D 0;
.b/ D 0:
Nach Voraussetzung wird der zweite Summand kleiner als jedes vorgegebene
" für c hinreichend nahe bei a. Wählen wir jetzt noch x hinreichend nahe
bei a, wird wegen (k) auch jm.x/ 1j und damit auch der erste Summand
hinreichend klein. Somit konvergiert auch f .x/=g.x/ gegen A.
(iii) Analog alle übrigen Fälle. /////
Also existiert nach dem Satz 9.5 von Rolle ein 2 .a; b/ mit
0 D 0 ./ D f 0 ./ f .b/ f .a/ 0
g ./:
g.b/ g.a/
Das ist aber gerade die Behauptung. /////
///// Beweis von Satz 11.1, Teil 2 Wir betrachten nun den Fall .1/, und
nehmen außerdem
I D .a; b/;
x0 D a 2 R
1 g.c/=g.x/
:
1 f .c/=f .x/
lim m.x/ D 1:
(k)
Mit g D id ist dies der »übliche« Mittelwertsatz.
.x/ D f .x/ f .a/ m.x/ D
Für jedes c 2 I gilt dann wegen .1/
Verallgemeinerter Mittelwertsatz Sind f; gW Œa; b ! R stetig, in .a; b/ differenzierbar, und hat g 0 keine Nullstelle in .a; b/, so gibt es ein 2 .a; b/ mit
f .b/ f .a/
f 0 ./
D 0 :
g.b/ g.a/
g ./
192
an. Zu je zwei weiteren Punkten x und c mit
f .x/
f .1=t/
lim
D lim
x!1 g.x/
t0 g.1=t /
f 0 .1=t / .
1=t 2 /
t0 g 0 .1=t/ .
1=t 2 /
f 0 .1=t /
f 0 .x/
D lim 0
D lim 0
:
x!1 g .x/
t0 g .1=t/
Die Regel von l’Hopital
Nun noch einige Beispiele.
3F
4F
t2
2t
2
D lim t D lim t D 0. G
t !1 et
t !1 e
t!1 e
lim t 2 et D lim
t!1
lim
t!1
log t
1=t
D lim
D 0. G
t!1 1
t
193
Konvexität
11-C
Andere unbestimmte Ausdrücke wie ›0 1‹ und › 1 1‹ lassen sich oft in eine
Form bringen, auf die die Regel von l’Hopital angewendet werden kann.
log x
1=x
5F
lim x log x D lim
D lim x D 0. G
D lim
x!0
x!0 1=x
x!0 1=x 2
x!0
6F
lim x log.1 C 1=x/ D lim
x!1
t!0
11-C
Konvexität
194
Umgekehrt folgt aus D.a; x/ < D.x; b/ für beliebige a < x < b in I , dass f
strikt konvex ist. Mit x D .1 t /a C t b folgt aus (1)
x
a
f .x/ f .a/ < t .f .b/ f .a//;
tD
:
b
a
/////
log.1 C t /
1=.1 C t/
D lim
D 1. G
t !0
t
1
)
Wegen x a > 0 ergibt dies
Und so weiter . . .
f .b/ f .a/
f .x/ .a/
<
;
x
a
b
a
11-C
also die Behauptung D.a; x/ < D.a; b/. Die beiden anderen Ungleichungen
folgen analog.
( Die Annahme D.a; x/ < D.x; b/ ist gleichbedeutend mit
Konvexität
Im Folgenden sei I immer ein offenes Intervall. Damit vermeiden wir umständliche
Formulierungen, die die Intervallenden betreffen.
f .x/ .a/
f .b/ f .x/
<
:
x
a
b
x
Definition Sei I ein offenes Intervall. Eine Funktion f W I ! R heißt strikt konvex, wenn für alle a ¤ b in I gilt:
(1)
f ..1 t/a C tb/ < .1 t /f .a/ C tf .b/;
Und x D .1 t/a C t b ist gleichbedeutend mit
x a D t.b a/;
0 < t < 1:
Einsetzen und Umformen ergibt (1), also die strikte Konvexität von f . /////
Die Funktion f heißt strikt konkav, wenn f strikt konvex ist. Eine Funktion f heißt nur konvex, wenn (1) mit ›‹ statt › <‹ gilt. Entsprechend
ist konkav definiert. Wir werden hier aber nur strikt konvexe und strikt konkave Funktionen betrachten.
Dies sind punktweise Definitionen. Es wird keinerlei Regularität der Funktion
vorausgesetzt, wie zum Beispiel Stetigkeit. Wir werden gleich klären, ob es konvexe,
unstetige Funktionen gibt.
Punktweise Konvexität
Notation Für u ¤ v setzen wir
f .u/ f .v/
;
u
v
die Sehnensteigung von f über dem Intervall zwischen u und v . Man beachte, dass
D.u; v/ D D.v; u/ gilt. D.u; v/ WD
11.2
Lemma Ist f W I ! R strikt konvex, so gilt für beliebige a < x < b in I
D.a; x/ < D.a; b/ < D.x; b/:
b x D .1 t/.b a/:
11.3
Lemma Ist f W I ! R strikt konvex, so ist für jedes x0 2 I die Funktion
x 7! D.x; x0 /
strikt wachsend auf I fx0 g. /////
Wende Lemma 11.2 an auf u < v in I mit
b D x0 ; falls u < v < x0 ;
a D x0 ; falls x0 < u < v;
x D x0 ; falls u < x0 < v:
In jedem Fall folgt D.u; x0 / < D.v; x0 /. /////
Wir können nun einen wichtigen Satz über strikt konvexe Funktionen beweisen,
der keine Annahmen über die Regularität der Funktion macht.
11.4 Satz Ist f W I ! R strikt konvex, so existieren in jedem Punkt x0 2 I die
links- und rechtsseitigen Ableitungen
f0 .x0 / D lim D.x; x0 /;
xx0
fC0 .x0 / D lim D.x; x0 /;
xx0
195
Konvexität
11-C
11-C
Konvexität
und für diese gilt f0 .x0 / fC0 .x0 /. Insbesondere ist f stetig. Außerdem gilt
f .x/ > f .x0 / C m.x x0 /;
x ¤ x0 ;
.x0 / D ..1 t /a C t b/ D .1 t /.a/ C t .b/:
Also ergibt sich
f ..1 t/a C t b/ D f .x0 /
für jedes m mit f0 .x0 / m fC0 .x0 /. D .x0 /
Die affine Funktion mit
D .1 t/.a/ C t .b/
.x/ D f .x0 / C m.x x0 /
< .1 t /f .a/ C tf .b/;
heißt eine Stützfunktion von f in x0 . Der Graph einer Stützfunktion liegt also strikt
unterhalb des Graphen der gestützten Funktion, ausgenommen den einzigen Punkt,
wo sie sich berühren.
///// Sei x0 2 I . Gemäß Lemma 11.3 wächst x 7! D.x; x0 / für x < x0
streng monoton und ist nach oben beschränkt. Also existiert nach Satz 5.12
von der monotonen Konvergenz
lim D.x; x0 / D f0 .x0 /:
xx0
Analog argumentiert man für fC0 .x0 / . Weiterhin folgt mit demselben Lemma
D.x0 h; x0 / < D.x0 ; x0 C h/;
h > 0:
Durch Grenzübergang h ! 0 folgt f0 .x0 fC0 .x0 /. Alle diese Differenzenquotienen sind für hinreichend kleine h > 0 insbesondere beschränkt,
woraus sich auch die Stetigkeit von f in x0 wie im Beweis von Satz 9.1
ergibt.
Schließlich folgt für x < x0 aus
f .x/ f .x0 /
D D.x; x0 / < f0 .x0 / m
x x0
durch Umformen wegen x x0 < 0 noch
f .x/ > f .x0 / C m.x x0 /;
x < x0 :
Analog für x > x0 . Damit ist alles gezeigt. /////
Bemerkung. Man kann die Existenz einer affinen Stützfunktion in jedem Punkt
auch als Definition der Konvexität wählen.
Angenommen, zu jedem Punkt x0 2 I existiert eine affine Funktion mit
f .x0 / D .x0 /;
196
f .x/ > .x/;
x ¤ x0 :
Sind dann a < b in I und x0 D .1 t/a C tb mit 0 < t < 1, so gilt für eine affine
Funktion
denn a ¤ x0 und b ¤ x0 . Die »Stützfunktionen-Definition« impliziert also die
»Sehnendefinition«, und Satz 11.4 zeigt, dass auch die umgekehrte Implikation gilt.
Beide Charakterisierungen sind also äquivalent. Konvexität und Differenzierbarkeit
Wir nehmen jetzt an, dass f ein- oder zweimal differenzierbar ist.
Satz Sei f W I ! R differenzierbar. Dann ist f strikt konvex genau dann, wenn
f 0 strikt wachsend ist. ///// ) Für x < y in I und alle hinreichend kleinen h > 0 gilt nach
Lemma 11.2
D.x; x C h/ < D.x; y/ < D.y h; y/:
Also auch
f 0 .x/ D lim D.x; x C h/ < lim D.y h; y/ D f 0 .y/:
h0
(
h0
Für a < x < b gilt nach dem Mittelwertsatz
D.a; x/ D f 0 ./
für ein 2 .a; x/;
D.x; b/ D f 0 ./
für ein 2 .x; b/:
Ist f 0 strikt wachsend, so ist also D.a; x/ < D.x; b/ für a < x < b in I .
Nach Lemma 11.2 ist dann f strikt konvex. /////
Der folgende Satz ist der für Anwendungen wichtigste und bequemste.
Satz Ist f W I ! R zweimal differenzierbar und f 00 auf I positiv, so ist f strikt
konvex. ///// Ist f 00 > 0 auf I , so ist mit Satz 9.7 f 0 strikt wachsend auf I , also
mit dem vorangehenden Satz f strikt konvex. /////
197
Ungleichungen
11-D
Wir formulieren den letzten Satz noch für konkave Funktionen, da wir ihn mehrmals benötigen.
Satz Ist f W I ! R zweimal differenzierbar und f 00 auf I negativ, so ist f strikt
konkav. Für a ¤ b in I gilt somit
f ..1 t /a C tb/ > .1 t/f .a/ C tf .b/;
0 < t < 1:
Nun noch einige Beispiele.
7F
exp ist strikt konvex auf R , log ist strikt konkav auf RC , denn
exp00 x D exp x > 0;
log00 x D 1
<0
x2
für x 2 R bzw x 2 RC . G
8F
11-D
r .x/ D x r ;
Für eine strikt konvexe Funktion f W I ! R gilt also
f ..1 t /a C t b/ < .1 t /f .a/ C tf .b/;
Somit ist r strikt konvex für r > 1 oder r < 0, und strikt konkav für 0 < r < 1.
In den beiden verbleibenden Fällen r D 0 oder r D 1 ist r linear, also weder strikt
konvex noch strikt konkav. G
9F
Für die Funktion f W x 7! x 3 gilt
(
> 0; x > 0;
f 00 .x/ D 6x
< 0; x < 0:
f ist also strikt konvex auf RC , strikt konkav auf R , und wechselt ihr Verhalten
bei x D 0 . Man sagt, f besitzt bei 0 einen Wendepunkt. G
11-D
Ungleichungen
0 < t < 1;
wenn a ¤ b zwei beliebige Punkte in I sind. Wir wollen nun eine entsprechende
Ungleichung für mehr als zwei Punkte formulieren.
Unter einer Konvexkombination oder verallgemeinerten arithmetischen Mittel von
reellen Zahlen x1 ; : : : ; xn versteht man eine Linearkombination
1 x1 C C n xn
mit nichtnegativen Gewichten 1 ; : : : ; n mit Gesamtsumme 1:
1 C C n D 1 mit i 0;
1 i n:
Dies impliziert
min xi mit r 2 R hat die zweite Ableitung
r00 .x/ D r .r 1/x r 2 :
198
Jensensche Ungleichung
Die allgemeine Potenzfunktion
r W R C ! R C ;
Ungleichungen
1in
n
X
i xi max xi ;
1in
iD1
denn jeden Faktor xi kann man nach unten durch min1in xi bzw oben durch
max1in xi abschätzen. Liegen also alle xi in einem Intervall, so auch jede ihrer
Konvexkombinationen.
Das typische Beispiel ist das arithmetische Mittel:
n
X
x1 C C xn
i xi ;
D
n
i D
iD1
1
:
n
Ein anderes Beispiel ist .1 t /a C t b mit 0 < t < 1.
11.5
Jensensche Ungleichung Ist f W I ! R strikt konvex, so gilt
f .1 x1 C C n xn / 1 f .x1 / C C n f .xn /
für jede Konvexkombination von Punkten in I . Gleichheit besteht dabei genau dann,
wenn alle xi gleich sind. /////
Sei xN D 1 x1 C C n xn , und
.x/ D f .x/
N C m.x x/
N
eine Stützfunktion von f in xN , welche nach Satz 11.4 ja existiert. Dann gilt:
199
Ungleichungen
11-D
f .x/
N D .x/
N D f .x/
N C m.1 x1 C C n xn x/
N
D
n
X
i f .x/
N Cm
iD1
D
D
n
X
iD1
n
X
n
X
i .xi x/
N
iD1
11-D
Ungleichungen
Young-, Hölder- & Minkowskische Ungleichung
Ein anderer, wichtiger Spezialfall ist der Fall n D 2. Hier schreibt man das erste
Gewicht in der Form
1
;
p
N C m.xi x//
i .f .x/
N
i .xi / iD1
n
X
1
p
1
D1
, qD
:
q
p
p
1
iD1
Dann ist auch 1 < q < 1, und man nennt q den zu p konjugierten Exponenten.
Man betrachtet also p; q mit
1
1
C D 1;
p
q
Eine wichtige Anwendung betrifft das arithmetisch-geometrische Mittel, kurz
AGM genannt.
Verallgemeinerte Ungleichung des AGM Seien 1 ; : : : n positive Gewichte mit
1 C C n D 1. Dann gilt für beliebige nichtnegative reelle Zahlen x1 ; : : : ; xn
die Ungleichung
xnn
Gleichheit gilt genau dann, wenn alle xi gleich sind. Der wichtigste Spezialfall ist die klassische Ungleichung zwischen dem arithmetischen und dem geometrischen Mittel,
.x1 xn /1=n .x1 C : : : C xn /=n;
die mit i D 1=n folgt.
///// Die Ungleichung ist sicher richtig, wenn mindestens ein xi verschwindet. Seien also alle xi und damit auch die beiden Mittel positiv. Die strikte
Konkavität des Logarithmus und die Jensensche Ungleichung ergeben dann
log.1 x1 C : : : C n xn / 1 log x1 C C n log xn
D
D
C C
log xnn
xnn :
Die Monotonie des Logarithmus liefern dann die Ungleichung. Gleichheit gilt
nach Satz 11.5 genau dann, wenn alle xi gleich sind. /////
1 < p; q < 1:
Die einzigen sogenannten selbstadjungierten Exponenten sind p D q D 2.
Youngsche Ungleichung Ist 1=p C 1=q D 1 mit 1 < p; q < 1, so gilt
ab 1 x1 C : : : C n xn :
log x1 1
log x1 1
1 < p < 1;
und das zweite Gewicht als
i f .xi /;
denn .x/ f .x/ für alle x 2 I . Außerdem gilt ›<‹ statt › ‹, wenn
xi ¤ xN für wenigstens ein i . Das ist genau dann der Fall, wenn nicht alle xi
gleich sind. /////
x1 1
200
ap
bq
C ;
p
q
a; b 2 RC :
Gleichheit gilt genau dann, wenn ap D b q . /////
Mit x D ap und y D b q ist dies gerade die AGM-Ungleichung:
x 1=p y 1=q x
y
C :
p
q
Oder man greift direkt auf die Konkavität des Logarithmus zurück:
1
1
y
x
C
:
log x 1=p y 1=q D log x C log y log
p
q
p
q
Gleichheit gilt genau dann, wenn x D y , also ap D b q . /////
Die Youngsche Ungleichung wirkt sehr unscheinbar, ist aber die Grundlage einiger fundamentaler und unentbehrlicher Ungleichungen. Deshalb soll hier noch ein
weiterer Beweis beschrieben werden.
///// Geometrischer Beweis der Youngschen Ungleichung Aus der Schulmathematik ist vielleicht bekannt, dass
Z a
Z b
bq
ap
t p1 dp;
s q1 dq:
D
D
p
q
0
0
201
Ungleichungen
11-D
11-D
Das heißt, ap =p ist die Fläche unter dem Graphen von t p1 zwischen 0
und a, und b q =q die Fläche unter dem Graphen von s q1 zwischen 0 und b .
Nun ist aber
kxkp ¤ 0;
Gleichheit gilt genau dann, wenn b D ap1 , ap D b q . /////
Auf dem Rn kennen wir bisher die euklidische oder natürliche Norm kk, sowie
die Summen- und die Maximumnorm, bezeichnet mit kk1 und kk1 . Zur Erinnerung:
X
jxi j;
kxk1 D max jxi j:
kxk1 D
1in
1in
Wir ergänzen diese nun zu einer ganzen Familie weiterer Normen.
Definition Für x D .x1 ; : : : ; xn / 2 Rn und p 2 Œ1; 1/ heißt
1=p
X
n
jxi jp
kxkp WD
iD1
die p-Norm von x . Wir müssen allerdings erst noch zeigen, dass es sich tatsächlich um Normen handelt. Für den ersten Schritt dorthin erinnern wir an das Standard-Skalarprodukt:
hx;yi D
n
X
xi yi ;
n
x; y 2 R :
x; y 2 Rn :
Für die selbstkonjugierten Exponenten p D q D 2 ist dies gerade die Ungleichung von Cauchy-Schwarz-Bunjakowski.
/////
n
X
1
1
1
jxi yi j C D 1;
p
q
kxkp kykq
iD1
P
da ja zum Beispiel niD1 jxi j D kxkpp . Dies ist die Behauptung. /////
Vereinbaren wir q D 1 als den zu p D 1 konjugierten Exponenten, so gilt die
Höldersche Ungleichung auch in diesem Fall:
Es genügt, x ¤ 0 und y ¤ 0 zu betrachten. Dann ist auch
x; y 2 Rn :
jhx;yij kxk1 kyk1 ;
Denn
jhx;yij n
X
jxi yi j iD1
n
X
jxi j max jyi j D kxk1 kyk1 :
iD1
1in
Nun der zweite Schritt.
Minkowskische Ungleichung Für 1 p 1 gilt
kx C ykp kxkp C kykp ;
x; y 2 Rn :
///// Für p D 1 und p D 1 ist dies die übliche Dreiecksungleichung. Für
1 < p < 1 schreiben wir
kx C ykpp D
n
X
jxi C yi jp1 jxi C yi j
iD1
n
X
iD1
Höldersche Ungleichung Mit 1 < p; q < 1 und 1=p C 1=q D 1 gilt
1 i n:
Summieren über 1 i n ergibt
iD1
jhx;yij kxkp kykq ;
kykq ¤ 0:
1 jxi jp
1 jyi jq
jyi j
jxi j
;
p C
p kxkp
q kykqq
kxkp kykq
Somit ist s q1 die Umkehrfunktion von t p1 . Daher fügen sich diese beiden
Flächenstücke, wie in Bild zzz skizziert, immer zu einer Figur zusammengefügt, die ein Rechteck mit den Kantenlängen a und b enthält. Also gilt
ap
bq
C :
p
q
202
Die Youngsche Ungleichung ergibt dann
1
1
1
C D1 , p
1D
:
p
q
q
1
ab Ungleichungen
jxi C yi jp1 jxi j C
n
X
jxi C yi jp1 jyi j DW ˙x C ˙y :
iD1
Mit dem zu p konjugierten Exponenten q und .p 1/q D p folgt mit der
Hölderschen Ungleichung
1=q X
1=p
X
n
n
D kx C ykpp=q kxkp :
˙x jxi C yi j.p1/q
jxi jp
iD1
iD1
Die analoge Ungleichung für ˙y ergibt zusammen
kx C ykpp kx C ykpp=q kxkp C kykp :
203
Ungleichungen
11-D
Mit p p=q D 1 folgt die Behauptung. /////
Korollar Für 1 p 1 ist kkp eine Norm auf Rn . ///// Für p 2 f1; 2; 1g ist dies bereits bekannt. Für alle übrigen p 2 .1; 1/
liefert die Minkowskische Ungleichung die Dreiecksungleichung. Die anderen Eigenschaften einer Norm sind leicht verifiziert. /////
Zum Abschluss erwähnen wir noch einen einfachen Zusammenhang zwischen
den verschiedenen p-Normen – wenn sie geeignet normalisiert sind.
Satz Für jedes x 2 Rn ist die normalisierte p-Norm,
X
1=p
n
1
1
xp WD 1=p kxkp D
;
jxi jp
n
n
iD1
eine monoton wachsende Funktion in p 2 Œ1; 1/ mit
lim xp D kxk1 :
p!1
///// Sei r 1 und p > 1 . Mit dem zu p konjugierten Exponenten q gilt
gemäß Hölder
n
1X
1 jxi jr
n
iD1
n
1=p
n
1 X q 1=q X
1
jxi jrp
n
xrr D
iD1
iD1
1
D 1=p kxkrrp D xrrp :
n
n
Ziehen der r -ten Wurzel liefert die erste Behauptung. Die zweite Behauptung
folgt mit
D
1
kxkrrp
11=q
xp D kxk1 x
Q p;
xQ D kxk1
1 x
und limp!1 p D 1 für jeden Vektor mit kk1 D 1. /////
11-D
.
Ungleichungen
204