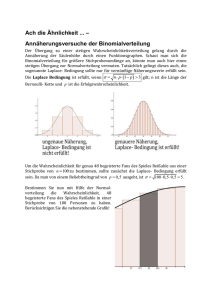
Skript - Humboldt-Universität zu Berlin

Humboldt-Universität zu Berlin
Institut für Theoretische Biologie
Skript zur Vorlesung
Biostatistik
Edgar Steiger
Verantwortlich für die Lehrveranstaltung:
Prof. Dr. Hanspeter Herzel
Lehrstuhl für Molekulare and Zelluläre Evolution
Institut für Theoretische Biologie, Charité und Humboldt-Universität zu Berlin
Invalidenstraße 43, 10115 Berlin, Tel.: 030-2093-9101, E-Mail: [email protected]
Inhaltsverzeichnis
1 Beschreibende Statistik
1.1 Zufall (Motivation) . . . . . .
1.1.1 Merkmale . . . . . . .
1.1.2 Skalentypen . . . . . .
1.2 Darstellung von Zufallsgrößen
1.2.1 Listen . . . . . . . . .
1.2.2 Grafische Darstellung
1.3 Maßzahlen . . . . . . . . . . .
1.3.1 Mittelwert . . . . . . .
1.3.2 Varianz . . . . . . . .
1.3.3 Median . . . . . . . .
1.3.4 Weitere Maßzahlen . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4
4
5
5
6
6
8
12
13
14
15
17
2 Wahrscheinlichkeiten
2.1 Ereignisse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Definition der Wahrscheinlichkeit . . . . . . . . . . . . . . . . . .
2.2.1 Rechnen mit Wahrscheinlichkeiten . . . . . . . . . . . . .
2.2.2 Bedingte Wahrscheinlichkeit und unabhängige Ereignisse
2.2.3 Totale Wahrscheinlichkeit . . . . . . . . . . . . . . . . . .
2.3 Satz von Bayes . . . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
23
23
24
26
27
28
29
3 Wahrscheinlichkeitsverteilungen
3.1 Zufallsvariablen . . . . . . . . . . . . . . . .
3.1.1 Erwartungswert und Varianz . . . .
3.2 Diskrete Verteilungen . . . . . . . . . . . .
3.2.1 Binomialverteilung: X ∼ Bin(n,p) .
3.2.2 Poisson-Verteilung: X ∼ P oiss(λ) .
3.3 Stetige Verteilungen . . . . . . . . . . . . .
3.3.1 Normalverteilung: X ∼ N (µ,σ 2 ) . .
3.3.2 Exponentialverteilung: X ∼ Exp(λ)
3.3.3 Gleichverteilung: X ∼ U (a,b) . . . .
3.3.4 Chi-Quadrat-Verteilung: Y ∼ χ2 (f )
3.3.5 t-Verteilung . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
30
30
31
33
33
35
36
36
41
44
46
48
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4 Schätzungen
50
4.1 Punktschätzungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
2
Inhaltsverzeichnis
4.2
Bereichsschätzungen und Konfidenzintervalle
4.2.1 Normalverteilung, Varianz bekannt . .
4.2.2 Normalverteilung, Varianz unbekannt
4.2.3 Andere Verteilungen . . . . . . . . . .
5 Testtheorie
5.1 Hypothesentests . . . . . . . . . . . .
5.1.1 Fehlertypen . . . . . . . . . . .
5.1.2 Einseitige und zweiseitige Tests
5.2 Spezielle Tests . . . . . . . . . . . . .
5.2.1 Gauß-Test . . . . . . . . . . . .
5.2.2 t-Test . . . . . . . . . . . . . .
5.2.3 Chi-Quadrat-Test . . . . . . . .
5.2.4 Zweistichproben-Tests . . . . .
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
51
51
52
53
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
55
55
57
58
58
58
61
62
65
1 Beschreibende Statistik
1.1 Zufall (Motivation)
In der Natur gibt es viele Prozesse, die sich nicht eindeutig (deterministisch) beschreiben lassen, weil sie ein zufälliges Element haben. Der radioaktive Zerfall ist ein Beispiel
für solch einen stochastischen“ Prozess, da die Zeit zwischen den Zerfallszeitpunkten
”
zweier Atomkerne nicht konstant, sondern immer zufällig ist.
Auch ist die Komplexität biomedizinischer Systeme ein Grund, diese mit wahrscheinlichkeitstheoretischen und statistischen Methoden zu beschreiben. Das menschliche
Genom besteht aus etwa 3 · 109 Basenpaare, wobei es bei etwa 3 · 106 Basenpaaren
zu Variationen (SNPs) kommen kann, die positive oder negative Auswirkungen auf
das Individuum haben können - diese Zusammenhänge müssen statistisch ausgewertet
werden. Weitere Beispiele sind das unkontrollierte Wachstum von Krebszellen (das
schon mit einer einzigen defekten Zelle beginnen kann), das Wachstum und Sterben
von Populationen sowie die komplizierten Prozesse in der Meteorologie.
Fast immer können bei Datenerhebungen nur endliche Stichproben aus einer Grundgesamtheit betrachtet werden (so ist es bei der Prognose von Wahlergebnissen nicht
möglich, alle Menschen eines Landes zu befragen, es muss eine kleinere, aber repräsentative Auswahl getroffen werden). Die Statistik versucht dann, aus diesen Daten auf
die Gesamtheit zu schließen.
Auch kann es wichtig sein, in den Daten Zusammenhänge zu erkennen oder diese
auszuschließen und eventuell Prognosen für die Zukunft zu machen. Dies ist die Aufgabe der Datenanalyse. Wichtig ist, dass eventuell entdeckte Assoziationen bzw. Korrelationen in den Daten nicht bedeuten, dass es auch einen kausalen Zusammenhang
gibt, weil wichtige Faktoren in den Daten nicht erfasst worden sind.
Ein weiteres zufälliges Moment ist die Messungenauigkeit bei Experimenten. So gab es
bei historischen Versuchen zur Messung der Lichtgeschwindigkeit bei jedem Durchgang
des Experiments einen anderen Wert für die eigentlich konstante Lichtgeschwindigkeit
(299 792 458 m
s ). Die Statistik hilft, die Messfehler zu kontrollieren und Rückschlüsse
auf die wahren Daten zu ermöglichen.
Weitere wichtige Aspekte der Statistik sind die Versuchsplanung, bevor ein Experiment durchgeführt wird, und das Testen von Hypothesen, bei dem Aussagen über die
Plausibilität von Beobachtungen getroffen werden.
4
1 Beschreibende Statistik
1.1.1 Merkmale
Ein Merkmal beschreibt eine bestimmte Eigenschaft eines Versuchsobjektes oder Individuums. Es wird grundsätzlich zwischen diskreten und stetigen Merkmalen unterschieden:
• diskretes Merkmal: Es gibt nur endlich viele Werte/Ausprägungen der Eigenschaft.
– Familienstand (ledig, in Partnerschaft, verheiratet, geschieden, ...)
– Klausurnote (an der Uni: 1,0; 1,3; 1,7; ...; 4,0; n.b.)
– DNA (für ein einzelnes Basenpaar sind nur die Kombinationen AT , T A,
CG und GC möglich, auf einem kompletten DNA-Strang mit etwa 3 · 109
Basenpaaren sind damit zwar sehr viele, aber eben nur endlich viele Kom9
binationen möglich (43·10 ))
– Blutgruppen (A, B, AB, 0)
• stetiges Merkmal: Alle Werte innerhalb eines Intervalls auf den reellen Zahlen
kommen in Frage.
– Zeit zwischen zwei Ereignissen (z.B. beim radioaktiven Zerfall)
– Wuchshöhe von Pflanzen
– Konzentration einer Lösung
– Temperatur
1.1.2 Skalentypen
Bei den Ausprägungen eines Merkmals wird zwischen verschiedenen Typen unterschieden, die sich hinsichtlich der Vergleichbarkeit von Merkmalen unterscheiden:
• Nominalskala: Es handelt sich um ein diskretes Merkmal, dessen Ausprägungen
sich in keine sinnvolle Rangfolge bringen lassen.
– Blutgruppen (A, B, AB, 0 - und es ist nicht sinnvoll zu sagen, dass A
”
größer als B“ sei.)
– Geburtsort
• Ordinalskala: Auch hier handelt es sich um ein diskretes Merkmal, aber eine
sinnvolle Rangfolge ist möglich (man spricht von einer Ordnungsrelation).
Allerdings ist keine Interpretation der Abstände vorhanden.
– Klausurnoten (Eine 1,3 ist besser als eine 2,3, und diese ist besser als eine
3,3. Aber es ist nicht sinnvoll zu sagen, dass 1,3 genauso so viel besser als
”
2,3 ist, wie 2,3 besser als 3,3 ist“.)
• Intervallskala: Für ein diskretes oder stetiges Merkmal gilt eine Intervallskala,
wenn die Ausprägungen in eine sinnvolle Rangfolge gebracht werden können und
5
1 Beschreibende Statistik
Tabelle 1.1: Urliste pH-Wert vs Wassertemperatur“
”
Nr.
pH-Wert
◦
C
1
6,9
14,5
2
6,5
14,5
3
6,8
14,8
4
7,3
15,1
5
7,2
14,8
die Abstände zwischen den Werten messbar sind. Allerdings gibt es keinen
Bezugspunkt bzw. Nullpunkt der Skala, so dass quantitative Aussagen der Art
doppelt so groß wie“ nicht möglich sind.
”
– Temperatur in Grad Celsius (Der Bezugspunkt 0 ◦ C ist nur durch den
Gefrierpunkt des Wassers festgelegt, eine Aussage wie 20 ◦ C sind doppelt
”
so warm wie 10 ◦ C“ ergibt keinen Sinn.)
– IQ (Der Bezugspunkt 100 ist nur als Durchschnitt der Bevölkerung festgelegt, eine Aussage wie Jemand mit IQ 110 ist 10% intelligenter als der
”
Durchschnitt der Bevölkerung“ ist nicht erlaubt.)
• Verhältnisskala: Die Verhältnisskala hat dieselben Eigenschaften wie die Intervallskala, aber zusätzlich die Eigenschaft, einen Nullpunkt zu besitzen, der
quantitative Vergleiche erlaubt.
– Temperatur in Kelvin (Im Unterschied zur Celsiusskala besitzt die Kelvinskala den absoluten Nullpunkt 0 K = −273,15 ◦ C, der eine Aussage wie
300 K sind doppelt so warm wie 150 K“ sinnvoll macht.)
”
– Größe in Zentimeter
– Zeit in Sekunden
1.2 Darstellung von Zufallsgrößen
1.2.1 Listen
Der erste Schritt nach einer Datenerhebung besteht darin, die erhobenen Daten in
einer Liste oder Tabelle zusammenzufassen. Die Anzahl der Datensätze wird meist
mit n, manchmal auch mit N bezeichnet.
Urliste
In einer Urliste werden die n Datensätze in der Reihenfolge ihrer Messung festgehalten.
Beispiel In Tabelle 1.1 ist ein Beispiel für eine Urliste zu sehen. Es wurden gleichzeitig
der pH-Wert und die Wassertemperatur eines Sees gemessen, insgesamt gibt es n = 5
Datenpaare. Die Daten werden paarweise bzw. gegeneinander ( versus“, vs“) gelistet,
”
”
um die zeitgleiche Messung deutlich zu machen.
6
1 Beschreibende Statistik
Tabelle 1.2: geordnete Liste pH-Wert vs Wassertemperatur“
”
Nr.
pH-Wert
◦
C
1
6,5
14,5
2
6,8
14,8
3
6,9
14,5
4
7,2
14,8
5
7,3
15,1
Tabelle 1.3: Blattlauszählung
Nr.
Anzahl
Nr.
Anzahl
1
5
11
13
2
17
12
19
3
20
13
3
4
0
5
33
6
21
7
42
8
7
14
27
15
25
16
4
17
17
18
2
9
0
19
34
10
44
20
21
Geordnete Listen
In der geordneten Liste werden die Daten nun nach der Größe eines Merkmals geordnet.
Die geordnete Liste verschafft einen besseren Überblick, allerdings könnten Informationen, die in der Reihenfolge der Messung enthalten waren, verloren gehen, wenn sie
nicht explizit festgehalten wurden.
Werden die ursprünglichen Daten in ihrer Reihenfolge mit x1 , x2 , . . . , xn bezeichnet,
so werden die Daten der geordneten Liste meist mit x(1) , x(2) , . . . , x(n) gekennzeichnet,
wobei x(i) für den i-ten Wert in der geordneten Liste steht. D.h. x(1) ist der kleinste
Wert der Messreihe und x(n) der größte.
Beispiel In Tabelle 1.2 wurde die Urliste aus Tabelle 1.1 nach den pH-Werten geordnet. Hier wäre zum Beispiel eine Information verloren, wenn die Messungen nacheinander im Laufe eines Tages gemacht wurden, da die Wassertemperatur von der Tageszeit
und der pH-Wert von der Temperatur abhängt.
Klassen
Wenn es sehr viele verschiedene Messwerte gibt, kann es sinnvoll sein, die Daten in
Klassen einzuteilen.
Beispiel Bei einer Untersuchung wurde die Anzahl der Blattläuse pro Pflanze in
einem Beet (n = 20 Pflanzen) bestimmt. Die Ergebnisse sind in Tabelle 1.3 zu sehen.
Nun wird die Zahl der Blattläuse in m = 4 Klassen eingeteilt:
• Klasse 1, keiner bis geringer Befall: {0, . . . ,10},
7
1 Beschreibende Statistik
Tabelle 1.4: Klasseneinteilung nach der Blattlauszählung
Klasse
Anzahl
1
7
2
9
3
2
4
2
• Klasse 2, mäßiger Befall: {11, . . . ,30},
• Klasse 3, starker Befall: {31, . . . ,40} sowie
• Klasse 4, sehr starker Befall: {41, . . . ,50}.
Diese Klasseneinteilung ergibt dann die (kleine) Tabelle 1.4. Zu beachten ist, dass in der
Zeile Anzahl“ der Tabelle jetzt nicht mehr die Anzahl der Blattläuse steht, sondern
”
die Anzahl der Pflanzen, deren Blattlausbefall der Klasse entspricht! Dementsprechend
ist die Summe der Einträge dieser Zeile 7 + 9 + 2 + 2 = 20 gerade gleich n.
Im Prinzip wurde mit der Klasseneinteilung ein neues diskretes Merkmal geschaffen,
mit dem die Daten weiter betrachtet werden können.
Die Breite der Klassen muss nicht immer gleich sein, oft ist dies jedoch sinnvoll.
Absolute und relative Häufigkeiten
Die absolute Häufigkeit hi gibt an, wie oft eine bestimmte Ausprägung i eines Merkmals im vorliegenden Datensatz auftaucht. Im Unterschied dazu gibt die relative
Häufigkeit Hi = hni an, wie groß der Anteil der Ausprägung i eines Merkmals am
gesamten Datensatz vom Umfang n ist.
Beispiel Im Blattlausbeispiel aus Tabelle 1.3 und 1.4 ist die absolute Häufigkeit des
Merkmals mäßiger Befall“ gerade h2 = 9. Die relative Häufigkeit berechnet sich zu
”9
= 0,45, d.h. 45 Prozent der untersuchten Pflanzen weisen einen mäßigen
H2 = hn2 = 20
Befall auf.
1.2.2 Grafische Darstellung
Die in den Listen erfassten Häufigkeiten liefern die Grundlage für grafische Darstellungen der Daten, die einen besseren Überblick über charakteristische Eigenschaften der
Verteilung der Daten bieten können. Je nach Art des Merkmals sind unterschiedliche
Diagramme sinnvoll, nachfolgend sollen die wichtigsten vorgestellt werden.
Auf der y-Achse (Ordinate) wird bei den meisten Diagrammen die Häufigkeit abgetragen. Es ist zu beachten, ob es sich um die relative oder absolute Häufigkeit handelt!
8
1 Beschreibende Statistik
Abbildung 1.1: Blattlauszählung: Balkendiagramm und Kreisdiagramm
Blattlausbefall − Kreisdiagramm
8
Blattlausbefall − Balkendiagramm
6
4
Klasse 4
Klasse 2
2
absolute Häufigkeit
Klasse 1
0
Klasse 3
Klasse 1
Klasse 2
Klasse 3
Klasse 4
Balkendiagramm
Im Balkendiagramm (auch Säulendiagramm oder Stabdiagramm) wird die Häufigkeit
hi der Merkmale dargestellt. Es können auch die relativen Häufigkeiten Hi dargestellt
werden, dazu muss lediglich die Achseneinteilung auf der y-Achse normiert werden, indem durch n geteilt wird - die relative Höhe der Balken zueinander ändert sich dadurch
nicht. Sind die Balken besonders schmal bzw. nur einfache vertikale Linien, spricht
man von einem Stabdiagramm, welches sich gut eignet, wenn viele Ausprägungen
darzustellen sind.
Beispiel Für das Blattlausbeispiel (Tabellen 1.3, 1.4) wird die absolute Häufigkeit
der einzelnen Klassen in einem Balkendiagramm in Abbildung 1.1 dargestellt.
Kreisdiagramm
Kreisdiagramme (oder Tortendiagramme) bieten sich besonders an, wenn die Häufigkeit von nominalskalierten Merkmalen dargestellt werden soll, da die Ausprägungen
nahezu gleichberechtigt um das Zentrum herum verteilt sind. Die relative Häufigkeit
entspricht dabei der Größe des Winkels des entsprechenden Kreissegmentes (αi =
Hi · 360◦ ). Zu beachten ist allerdings, dass das menschliche Auge Längenunterschiede
besser wahrnimmt als Flächenunterschiede, deshalb sind Balkendiagramme den Kreisdiagrammen vorzuziehen.
Beispiel Die Daten des Blattlausbeispiels sind in einem Kreisdiagramm in Abbildung
1.1 veranschaulicht. Es handelt sich um dieselben Informationen wie im Balkendia-
9
1 Beschreibende Statistik
Abbildung 1.2: Blattlauszählung: Histogramm und normiertes Histogramm
Blattlausbefall
− Histogramm
Blattlausbefall
- norm.
Histogramm
0,3
0,2
0
0,1
relative Häufigkeit
6
4
2
0
absolute Häufigkeit
8
0,4
Blattlausbefall − Histogramm
0
10
20
30
40
0
50
10
20
30
40
50
Anzahl der Blattläuse
Anzahl der Blattläuse
gramm daneben!
Histogramm
Das Histogramm ist ein Balkendiagramm, in dem die Werte gegen ihre (absoluten
oder relativen) Häufigkeiten abgetragen werden, wobei sich die Säulen des Diagramms
berühren. Liegen nicht zu viele diskrete Werte vor, kann direkt das Histogramm erstellt
werden. Handelt es sich um ein stetiges Merkmal oder liegen zu viele verschiedene
diskrete Ausprägungen vor, sollten die Daten geeignet in Klassen zusammengefasst
werden. Zu beachten ist, dass die Breite der Säulen sinnvollerweise die Breite der
Klassen repräsentiert.
Werden auf der Ordinate (y-Achse) statt der absoluten Häufigkeiten hi die relativen
Häufigkeiten Hi abgetragen, spricht man von einem normierten Histogramm.
Beispiel In Abbildung 1.2 sind das Histogramm mit absoluten Häufigkeiten und das
normierte Histogramm für die vier Klassen im Blattlausbeispiel (Tabellen 1.3, 1.4)
abgebildet.
Empirische kumulative Verteilungsfunktion (Summenhistogramm)
Diese Grafik baut direkt auf dem normierten Histogramm auf. Sie zeigt eine Funktion, die uns eine Antwort auf die Frage Wie viele Messwerte sind kleiner als oder
”
gleich einem gegebenen Messwert?“ liefert. Anschaulich entsteht die Abbildung der empirischen kumulativen Verteilungsfunktion, in dem zu jeder Säule im normierten Histogramm die Höhe aller Säulen links von ihr addiert werden. Mathematisch entspricht
10
1 Beschreibende Statistik
Abbildung 1.3: Blattlausbeispiel: Summenhistogramme für Klasseneinteilung und alle
Messwerte
0.8
0.6
0.4
relative Häufigkeit
0.0
0.2
0.8
0.6
0.4
0.2
0.0
relative Häufigkeit
1.0
Blattlausbefall − Summenhistogramm
1.0
Blattlaus − Klassensummenhistogramm
0
10
20
30
40
50
0
Anzahl der Blattläuse
10
20
30
40
Anzahl der Blattläuse
dies folgender Funktionsvorschrift:
F (k) =
k
X
Hi
i=1
Dies bedeutet, dass der Funktionswert für die Klasse k gerade der Summe aller relativen Häufigkeiten bis zur Klasse k (einschließlich k) entspricht. Dies ist natürlich nur
sinnvoll, wenn es eine Ordnungsbeziehung zwischen den Klassen gibt!
Das Summenhistogramm lässt sich verfeinern, indem folgende Funktionsvorschrift benutzt wird:
X 1
F (t) =
n
i: xi ≤t
Die Summe wird dabei über alle i, für die xi ≤ t gilt, gebildet. Der Summand n1 hängt
nicht von i ab! Anschaulich bedeutet die Formel, dass bei n verschiedenen Messwerten
jeder einzelne Messwert die relative Häufigkeit n1 besitzt, wenn also jeder Messwert
seine eigene Klasse bildet, ergibt sich gerade obige Formel.
Beispiel Die linke Grafik in Abbildung 1.3 zeigt das Summenhistogramm für die vier
Klassen des Blattlausbeispiels, in der rechten Grafik ist das Summenhistogramm für
alle einzelnen Werte eingezeichnet.
11
1 Beschreibende Statistik
Abbildung 1.4: Scatterplot pH-Wert vs Wassertemperatur“
”
15.5
15.0
14.0
14.5
Wassertemperatur °C
15.5
15.0
14.5
14.0
Wassertemperatur °C
16.0
pH vs °C mit Regressionsgerade
16.0
pH vs °C
6.0
6.5
7.0
7.5
8.0
6.0
pH−Wert
6.5
7.0
7.5
8.0
pH−Wert
Scatterplot
Ein Scatterplot oder Streudiagramm wird angelegt, wenn in der Messreihe paarweise
Merkmale gemessen werden. Dabei wird das eine Merkmale auf der Abszisse, das
andere auf der Ordinate abgetragen. Ziel ist zunächst, visuell einen Zusammenhang
(Korrelation) zwischen den Merkmalen zu erkennen. Die Regressionsanalyse (1.3.4)
versucht dann, einen funktionellen Zusammenhang (rechte Abbildung) zu finden.
Beispiel Wir betrachten das Beispiel mit dem pH-Wert und der Wassertemperatur
eines Sees (Tabelle 1.1). Aus der Urliste ergibt sich der in Abbildung 1.4 gezeigte
Scatterplot.
1.3 Maßzahlen
Maßzahlen bzw. statistische Kennwerte erlauben den Vergleich verschiedener Datensätze und ihrer unterschiedlichen Häufigkeitsverteilungen. Es wird zwischen Lagemaßen und Streuungsmaßen unterschieden. Erstere beschreiben einen Schwerpunkt der
Messwerte in der Verteilung, während letztere die Abweichungen von solchen Schwerpunkten beschreiben.
Die wichtigsten Beispiele für Lagemaße sind der Mittelwert und der Median, das
wichtigste Streuungsmaß ist die Varianz.
12
1 Beschreibende Statistik
Tabelle 1.5: Jungtiere bei Hauskatzen
Katze i
Jungtiere
1
3
2
6
3
4
4
6
5
2
6
7
7
3
8
3
1.3.1 Mittelwert
Das wichtigste und offensichtlichste Maß zur Beschreibung eines Datensatzes ist der
Mittelwert oder Durchschnitt. Es werden alle Werte eines Merkmals addiert und
dann durch die Anzahl der Werte geteilt, die erhaltene Zahl liegt zwischen den ursprünglichen Werten und gibt einen guten ersten Eindruck von der Größe der Messwerte.
Der Mittelwert ist auch eine gute Schätzung für die erwartete Größe eines Merkmals in einer Gesamtpopulation. Wird zum Beispiel bei 100 erwachsenen Frauen die
Körperlänge gemessen und daraus der Mittelwert x̄ = 1,66 m ermittelt, so würde man
bei einer zufällig ausgewählten Probandin aus der Gesamtbevölkerung genau diese
Körpergröße erwarten. Es ist klar, dass der Mittelwert eine bessere Näherung gewesen
wäre, hätte man statt 100 sogar eine Stichprobe von 1000 Frauen vermessen. Auch muss
die Stichprobe aus der gesamten Bevölkerung entnommen werden, da zum Beispiel die
durchschnittliche Körperlänge von 1000 unter-30-jährigen Berlinerinnen sich von der
erwarteten Körperlänge einer Deutschen unterscheiden könnte.
n
Mittelwert: x̄ =
1X
x1 + x2 + . . . + xn
=
xi
n
n i=1
Beispiel Es wurde bei 8 Hauskatzen die Anzahl der Jungtiere beim letzten Wurf
gezählt, es ergaben sich die in Tabelle 1.5 dokumentierten Werte.
Der Mittelwert für das Merkmal Anzahl der Jungtiere berechnet sich wie folgt:
3+6+4+6+2+7+3+3
34
=
= 4,25
8
8
D.h. die mittlere Anzahl von Jungtieren ist 4,25.
x̄ =
Der oben beschriebene Mittelwert wird manchmal auch arithmetischer Mittelwert
genannt, um ihn vom geometrischen Mittelwert zu unterscheiden:
Geometrisches Mittel: x̄geom =
√
n
x1 · x2 · . . . · xn =
n
Y
! n1
xi
i=1
Beispiel Das geometrische Mittel für das Hauskatzenbeispiel berechnet sich wie folgt:
√
√
8
8
x̄geom = 3 · 6 · 4 · 6 · 2 · 7 · 3 · 3 = 54 432 ≈ 3,91
13
1 Beschreibende Statistik
Beispiel In vier Proben wurden die Viruskonzentrationen 2 · 10−9 , 1 · 10−7 , 4 · 10−5
und 2 · 10−7 gemessen. Für den Mittelwert und das geometrische Mittel ergeben sich
folgende Werte:
0,000040302
1
(2 · 10−9 + 1 · 10−7 + 4 · 10−5 + 2 · 10−7 ) =
= 0,0000100755
4
4
= 1,00755 · 10−5
√
9+7+5+7
1
4
= (2 · 10−9 · 1 · 10−7 · 4 · 10−5 · 2 · 10−7 ) 4 = 16 · 10− 4
x̄ =
x̄geom
= 4 · 10−7
Hier wird deutlich, dass der Mittelwert in diesem Beispiel erheblich durch den größten
Wert 10−5 beeinflusst wird und die anderen Werte kaum Einfluss auf ihn haben. Das
geometrische Mittel ist hier stabiler und aussagekräftiger.
Manchmal wird auch der Logarithmus des geometrischen Mittels betrachtet:
n
log x̄geom =
1X
log xi
n i=1
D.h., der Mittelwert der logarithmierten Werte ist gerade der Logarithmus des geometrischen Mittels (für numerische Berechnungen am Computer ist es sinnvoller, die
Summe der Logarithmen zu bilden und durch n zu teilen, als die n-te Wurzel eines
Produktes von n Werten zu bestimmen).
1.3.2 Varianz
Die korrigierte Stichprobenvarianz ist der wichtigste Wert, um die Streuung der Messwerte um den Mittelwert herum zu beschreiben. Sie ist die gemittelte quadratische
Abweichung der Messwerte vom Mittelwert:
n
Varianz: s2 =
1 X
(xi − x̄)2
n − 1 i=1
Es wäre zu erwarten, dass die Summe statt durch n−1 durch n geteilt wird. Allerdings
weist die korrigierte“Varianz mit dem Nenner n − 1 bessere statistische Eigenschaften
”
auf und wird deshalb häufiger verwendet.
Standardabweichung
Direkt aus der Varianz ergibt sich die Standardabweichung s, die eine bessere Interpretation der Streuung um den Mittelwert ermöglicht, siehe dazu z.B. den Abschnitt
über die Normalverteilung 3.3.1.
14
1 Beschreibende Statistik
√
Standardabweichung: s =
v
u
u
s2 = t
n
1 X
(xi − x̄)2
n − 1 i=1
Beispiel Im Beispiel mit den Hauskatzen ergeben sich folgende Varianz und Standardabweichung (Mittelwert x̄ = 4,25):
s2 =
≈
1
8−1
⇒s =
3,36
√
s2
≈
1,83
(
(3 − 4,25)2 + (6 − 4,25)2 + (4 − 4,25)2 + (6 − 4,25)2
+
(2 − 4,25)2 + (7 − 4,25)2 + (3 − 4,25)2 + (3 − 4,25)2 )
1.3.3 Median
Der Median oder auch mittlerer Wert ist neben dem Mittelwert das zweite wichtige
Lagemaß. Liegen die Daten als geordnete Liste vor und gibt es eine ungerade Anzahl
von Messwerten, ist der Median x̃ gerade der Messwert in der Mitte, bei dem die
eine Hälfte der restlichen Messwerte kleiner und die andere größer als er ist. Ist die
Anzahl der Messwerte gerade, ist der Median das arithmetische Mittel aus den beiden
mittleren Werten.

 x(d n2 e) ,
Median: x̃ = x( n ) + x( n +1 )
2
 2
,
2
n ungerade
n gerade
Die sogenannte Aufrundungsfunktion dae bedeutet, dass a aufgerundet wird, sollte a
keine ganze Zahl sein. D.h. d7,5e = 8, aber auch d7,1e = 8, jedoch d7,0e = 7.
Der Median ist stabiler gegenüber Ausreißern in den Daten als der Mittelwert. Auch
ist er das sinnvollere Lagemaß, wenn die Daten nur ordinal-, aber nicht intervall- bzw.
verhältnisskaliert sind.
Beispiel Im Hauskatzenbeispiel 1.5 liegt eine gerade Anzahl (8) von Datensätzen vor,
d.h. für den Median ergibt sich:
x̃ =
x(4) + x(5)
3+4
=
= 3,5
2
2
15
1 Beschreibende Statistik
Quartile und Quantile
Eng verwandt mit dem Median sind die Quartile. Während der Median so definiert
ist, dass 50 Prozent der Messwerte kleiner als er sind, gilt für das erste Quartil Q1 ,
dass 25 Prozent der Messwerte kleiner sind, und für das dritte Quartil Q3 , dass 75
Prozent der Messwerte kleiner sind. Dem zweiten Quartil Q2 entspricht dann gerade
der Median, d.h. Q2 = x̃.
Der Median und die Quartile sind Spezialfälle der Quantile. Sei p eine Zahl zwischen
Null und Eins, dann bezeichnet man als das p-Quantil x̃p gerade denjenigen Messwert,
so dass p·100 Prozent der Messwerte kleiner sind. Es gilt also x̃ = Q2 = x̃0,5 , Q1 = x̃0,25
und Q3 = x̃0,75 .
Berechnet wird ein p-Quantil wie folgt (zur Aufrundungsfunktion siehe 1.3.3):

 x(n·p) + x(n·p+1) ,
2
p-Quantil: x̃p =

x(dn·pe) ,
wenn n · p ganzzahlig
sonst
Beispiel Für die Hauskatzen aus 1.5 sollen das erste und dritte Quartil sowie das
0,6-Quantil berechnet werden. 8 · 0,25 = 2 und 8 · 0,75 = 6 sind ganzzahlig, während
8·0,6 = 4,8 nicht ganzzahlig ist, dementsprechend werden die Quantile wie nachstehend
bestimmt:
x(2) + x(3)
3+3
=
=3
2
2
x(6) + x(7)
6+6
=
=
=6
2
2
= x(d4,8e) = x(5) = 4
x̃0,25 =
x̃0,75
x̃0,6
Boxplots
In einem Boxplot oder Box-Whiskers-Plot werden der Median, das erste und dritte
Quartil sowie die Range (s. 1.3.4) dargestellt. Ein solcher Plot eignet sich besonders, wenn dasselbe Merkmal in zwei verschiedenen Gruppen gemessen wurde und
anschließend verglichen werden soll.
Die Box“ stellt den Bereich zwischen dem ersten und dritten Quartil dar, der Me”
dian ist eine zusätzliche Linie in der Box. Die Whisker“ (englisch Schnurrhaare“)
”
”
verlängern die Box um die gesamte Variationsbreite. Manchmal werden die Whisker
nur als der anderthalbfache Interquartilsabstandes Q3 − Q1 eingezeichnet, und alle
Messwerte, die sich außerhalb dieses Bereichs befinden, werden durch einzelne Punkte
gekennzeichnet (und sind wahrscheinlich Ausreißer“).
”
16
1 Beschreibende Statistik
Tabelle 1.6: Jungtiere bei Haushunden
Hündin i
Jungtiere
1
7
2
4
3
5
4
5
5
8
6
3
7
10
8
4
Abbildung 1.5: Boxplot - Jungtiere von Haustieren
Boxplot Katze vs Hund
8
6
4
Anzahl der Jungtiere
2
6
5
4
3
2
Anzahl der Jungtiere
7
10
Boxplot Hauskatzen
Katze
Hund
Beispiel In Abbildung 1.5 ist links der Boxplot für die Anzahl der Jungtiere von
Hauskatzen (Tabelle 1.5) mit den oben (1.3.3) berechneten Werten zu sehen.
Beispiel Betrachten wir nun neben den Jungtieren der Hauskatzen noch einen weiteren Datensatz: Acht Hündinnen haben ebenfalls geworfen und wieder wurde die Anzahl der Jungtiere gezählt. Es haben sich die in Tabelle 1.6 dargestellten Werte ergeben.
In Abbildung 1.5 ist rechts ein vergleichender Boxplot für die Anzahl der Jungtiere
von Hauskatzen gegen Haushunde zu sehen.
1.3.4 Weitere Maßzahlen
Variationsbreite
Die Variationsbreite bzw. Spannweite (oder auch englisch Range) gibt einen sehr
groben Überblick darüber, in welchem Bereich sich die Messwerte befinden. Sie berechnet sich ganz einfach als Differenz aus dem größten und kleinsten Messwert.
17
1 Beschreibende Statistik
Variationsbreite: V ≡ R = xmax − xmin = x(n) − x(1)
Variationskoeffizient
Der Variationskoeffizient, oder auch relative Schwankung, normiert die vom Mittelwert abhängige Varianz, so dass sich die Streuungen mehrerer Stichproben mit unterschiedlichen Mittelwerten besser vergleichen lassen.
Variationskoeffizient: cv =
s
|x̄|
Standardfehler des Mittelwertes
Der Standardfehler des Mittelwertes ( SEM“) ist eine Kennzahl dafür, wie gut der
”
Mittelwert die Daten beschreibt.
s
SEM: sx̄ = √
n
Modalwert
Der Modalwert M o ist ein Lagemaß, dass sich auch für nominalskalierte Größen verwenden lässt. Der Modalwert einer Messreihe ist der am häufigsten vorkommende
Wert. Falls mehrere Werte gleich häufig vorkommen, gibt es mehrere Modalwerte.
Beispiel Für das Hauskatzenbeispiel 1.5 ergeben sich folgende Werte für die Variationsbreite, den Variationskoeffizienten und den Standardfehler des Mittelwertes:
R = x(8) − x(1) = 7 − 2 = 5
1,83
s
cv =
=
≈ 0,43
|x̄|
4,25
s
1,83
sx̄ = √ ≈
≈ 0,65
2,83
8
Als Modalwert ergibt sich M o = 3, denn der Wert 3 kommt dreimal in der Messreihe
vor und ist damit am häufigsten.
18
1 Beschreibende Statistik
Potenzmomente: Schiefe und Exzess
Die Schiefe gibt an, ob die Mehrheit der Messwerte sich eher rechts oder links vom
Mittelwert befindet - dementsprechend wird die Verteilung der Daten rechts- bzw.
linksschief genannt. Ist die Schiefe größer als Null, ist die Verteilung rechtsschief, ist
die Schiefe kleiner als Null, ist die Verteilung linksschief. Ist die Schiefe annähernd
gleich Null, ist die Verteilung etwa symmetrisch.
Die Wölbung ist ein Maß für die Steilheit der Verteilung der Messwerte. Sie erklärt
die Varianz genauer - je kleiner die Wölbung ist, desto mehr wird die Varianz durch
Messwerte in der Nähe des Mittelwertes erklärt. Ist die Wölbung größer, wird die Varianz durch einige besonders weit vom Mittelwert entfernte Messwerte erklärt. Meist
wird aber nur der Exzess betrachtet, der die Wölbung mit der Wölbung einer Normalverteilung (3.3.1) vergleicht. Ist der Exzess größer als Null, wird die Verteilung steil
genannt, ist der Exzess kleiner als Null, wird sie flach genannt.
Um Schiefe und Exzess bestimmen zu können, benötigen wir zunächst die Potenzmo”
mente“. Diese sind wie folgt definiert:
n
k-tes Potenzmoment: mk =
1X
(xi − x̄)k
n i=1
Offensichtlich ist s2 ≈ mP
2 , für sehr große n kann man den Unterschied vernachlässigen.
n
Außerdem gilt m2 = n1 i=1 x2i − x̄2 (Satz von Steiner, Verschiebungssatz).
Nun können wir Schiefe und Exzess definieren:
m3
Schiefe: S = √ 3
m2
m4
Wölbung: W = 2
m2
Exzess: E = W − 3
Beispiel Im Beispiel mit den Hauskatzen (Tabelle 1.5) ergeben sich S ≈ 0,29 und
E = −1,79. Der Exzess ist kleiner als Null, also ist die Verteilung eher abgeflacht. Die
meisten Katzen haben also eine Anzahl von Jungtieren nahe beim Mittelwert x̄ = 4,25.
Die Schiefe ist größer als Null, also ist die Verteilung eher rechtsschief. Das heißt, der
Großteil der Katzen hat etwas weniger Jungtiere als den Mittelwert x̄ = 4,25, aber
einige Ausreißer“ mit vielen Jungtieren ziehen den Mittelwert nach oben.
”
Stichprobenkovarianz und Korrelationskoeffizient
Abschließend werden noch zwei Maße vorgestellt, mit denen zwei Merkmale (xi und
yi ) einer Stichprobe in einen Zusammenhang gebracht werden können. Zunächst die
Stichprobenkovarianz:
19
1 Beschreibende Statistik
n
Kovarianz: sxy =
1 X
(xi − x̄) · (yi − ȳ)
n − 1 i=1
Ist die Kovarianz positiv, so besteht ein proportionaler Zusammenhang zwischen den
beiden Merkmalen - je größer die Werte von X, desto größer sind auch die Werte von
Y . Ist die Kovarianz negativ, so besteht ein antiproportionaler Zusammenhang, d.h.
große Werte xi gehen mit kleinen Werten yi einher und umgekehrt. Ist die Kovarianz
annähernd Null, besteht kein linearer Zusammenhang zwischen den Merkmalen (es
könnte aber durchaus nichtlineare Zusammenhänge geben!).
Die Kovarianz kann zwar die Tendenz einer Beziehung zwischen den Merkmalen zeigen,
allerdings hängt sie sehr von den Messwerten xi bzw. yi ab. Um deshalb die Stärke
der Beziehung zwischen den Merkmalen quantifizieren zu können, wird die Kovarianz
normiert, dies führt auf den (Pearsonschen) Korrelationskoeffizienten:
Korrelationskoeffizient: rxy =
sxy
sx · sy
sx und sy sind hier jeweils die Stichproben-Standardabweichung der xi respektive
yi . Für den Korrelationskoeffizienten gilt immer rxy ∈ [−1,1]. Ist rxy sehr nahe bei
+1, sind die Merkmale fast perfekt positiv korreliert und es besteht ein fast linearer proportionaler Zusammenhang zwischen ihnen. Ist umgekehrt rxy sehr nahe bei
−1, sind die Merkmale fast perfekt negativ korreliert und es besteht ein fast linearer
antiproportionaler Zusammenhang. Je näher der Korrelationskoeffizient bei Null liegt,
desto weniger kann von einem guten linearen Zusammenhang zwischen den Merkmalen
gesprochen werden. Ist der Korrelationskoeffizient schließlich gleich Null, gibt es gar
keinen linearen Zusammenhang (es könnte aber andere Zusammenhänge geben!).
Abbildung (1.6) veranschaulicht die Interpretation des Korrelationskoeffizienten. Das
vierte Bild macht besonders deutlich, dass es durchaus einen Zusammenhang zwischen
x und y geben kann, der aber vom Korrelationskoeffizienten nicht erkannt wird, da
dieser nur lineare Zusammenhänge zeigt.
Wird ein linearer Zusammenhang zwischen den Merkmalen vorausgesetzt, lassen sich
die yi linear durch die xi erklären, d.h. yi ≈ a + b · xi , wobei a und b nicht von i
abhängen und für alle Messwertpaare gleich sein sollen. Mit den in diesem Kapitel
vorgestellten Größen Mittelwert, Standardabweichung und Kovarianz lassen sich nun
Schätzwerte â und b̂ für die wahren“ Werte a und b berechnen:
”
b̂ =
sxy
s2x
â = ȳ − b̂ · x̄
Dies bezeichnet man auch als lineare Regression.
20
1 Beschreibende Statistik
Abbildung 1.6: Scatterplots und Korrelationskoeffizient.
rxy = − 0.8
6
●
●
8
−2
1.0
−1.0
−0.5
0.0
●
●
●
0.0
●
●●
0.5
1.0
●●
● ●
●
●
●
●●
●
●
●●
●
●
● ●● ●
●
●
●
●
●
●
●
●
●●● ●
●
● ●● ●
●
●
●
●●
●●●
● ●●● ●
● ●
●●
●
●●● ●
●
● ● ●●
●
●● ●
●
●
●●● ●
●
●●
●● ●
● ●● ● ●
● ●●
●
●
●
●
●
●
● ●
●
●●
●●
●
●
●
●● ●
●
● ● ●
●●
● ●●
●
●● ●
●
●
●
●
●
●
●
● ●
●●
● ●
●● ●
●●● ●●
●
● ●● ●
●● ●
● ●● ●
● ● ●
●
● ●●●
●
● ● ● ●● ●
●
●
● ●●
●
● ● ●●●●
●● ●●
●
● ●
● ●
● ●
●
●●●
● ●
●● ●
● ●● ●
●● ●●●
●
●
●
●● ● ●
●
●
●●●
●
●
●
●●●
●●
●
●
●●●●●● ●
●
●
●
● ●●
●
●
● ● ●
● ●●●●
●
●
●
●
● ●●
●● ●●● ●●
●●
●●
●
● ● ●●●●
●
● ●
●
●
●
●
●
● ●
●● ●
●●
●●
●
● ●●
●
●
●●●
●●●
● ● ●●
● ●
●● ●
●
● ● ●●● ●
●
● ●
●
●
●
●
●
●
●
●●
●
● ●● ●
●● ●●
●● ● ●●● ●●●●●● ● ● ●
●●
●● ● ● ●
● ● ●●
●
●●
● ●●
●
● ●
● ●● ●
●
● ●●
●● ● ●
● ●● ● ●
●
● ●
●
● ●●
● ●● ● ●
● ●● ● ●
●
●
●
●●●●● ●●
●● ● ●
● ●● ●
● ●
●●
●●
● ● ●●
● ●●●
●
●●
●●
●
●
●
●
●● ●
●
● ●
●
●
●
●●
●
●
●● ●
● ●
● ●●
●
●
●
●
●
−2
x
−1
0
x
21
1.0
●
●
●
●
●
●
● ●
0.5
5
●
●
4
●
−0.5
rxy = 0
3
●
●
●●
● ●
●
●●
●
● ●
●
●
●
●●
●
● ●
●
●
●
●
●●
●
●
● ●
●
●
●
●
●
● ●●
●
●● ●
●
●
●
●
●● ● ● ●●
●
● ●
● ●
●
●
●●●
●
●●
●
● ● ●●
●
●
●●● ●● ● ● ●
●
●●
● ●●●
●
●
●
● ● ●
●
●
●●
●●
●●
●● ● ● ●
●
●
● ●
● ●●● ●
●
●
●
●
●
●
●
●
●
●●
●
●● ●
● ●●
● ●
● ● ● ●●● ●
●● ●
●●
● ● ● ●●
●●●●● ●●● ●
●
●
●
● ● ●● ●
●●●
●
●
●●●● ● ● ●
●
●
●●
● ●● ●
●
●
● ●●● ●● ●●
●
●●
●● ● ●
● ●
●
●
● ●●
●
●
● ●
●
●●●●
●
●
●●●
● ●
●
●
●●●
●
●
●●
●●
●
● ●
●
●● ● ●
●
●●● ● ●
●
●
●
●
●
●
●
●
●●
●
●
●
●
● ●
●
● ● ● ●
●
●● ●
●● ●
●
●● ● ●●● ● ●
● ●●
●
●
●●
●● ●●● ● ● ●●
● ●
●●
●●●
●● ●
●●●●●
●
● ●● ● ●
●
●●● ●
●
●
●
●
●
●
●
●
●
●
●
●●
●
● ● ●●
● ●
●● ● ●
● ●
●● ●
●●●●●● ●● ●●
●
●
● ●●
●● ● ●● ● ●
●
● ●●●
●●●
●
●● ●●
●
● ●
●●
●
●●
●● ●●
●
● ●●
●
●●
●● ● ● ●
●
●●
●●●
●
●
● ● ● ●● ● ●
● ●●
●●●
●
●
●● ● ●● ●●●
●●
●
●
●●●
●
●●
● ●
●
●
●
●●
rxy = 0
2
●
●
x
y
● ●● ●
●
●
●
−1.0
1
●
0.5
●
x
0
●
0.0
●
● ●
●
●
●
●●
●
●
●
●
●
●
● ●
● ●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●● ● ●
● ●
●
●
●●
●
●
● ●
●
●●
●
● ●
● ●● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
● ●
●
● ●
●
● ●
●
●
●
● ●
● ●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●●
●
●
●
●
●●
● ●
●●●
●
●
●
●
●
● ●
●
●
●
●
● ●
●
●
●
●●
●
●
● ● ●
●
● ●
●●
●●
●●●
●
●
●
●
●
●●
● ●
●
●●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
● ●
●
●
●
● ●
●
●
●
●●
●
●●
●●●
●
● ●
● ●
●●
●
●
●
● ● ●
● ●
●
●●
●
●●
● ●
●●
●
●
●● ● ●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
● ●
●
●
● ●●
●
●
●
●
●
● ● ●
●●
●
●●
●
●
●● ●●
●
●
● ●●
●
●
●
●
● ●
●
●
●
●
●
●
● ●●
●
●
●
●●
●
●
●
●
●
●
●●
● ●
●
●
● ●
● ● ●
●
●● ●●
● ●
●
●
●●
●
●
●●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
● ●
●
●● ● ●
●
●
●●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
● ● ●
● ●
●
●●
●●
● ●
●
●
● ●
● ●
● ●
●
● ●
●
●
●
●● ●
●
●
●
●
●
●
●
●
● ●
●
● ●
4
2
y
6
●
−1
●
−0.5
●
●
●
●
−2
5
4
y
3
2
1
0
1.0
0.5
y
0.0
●
●
●
●
●
−0.5
●
●
●
●
●
●●
●
●●
●
●●
● ●
●● ●
●
●●●● ●
●●
●
●
●
● ●●
●●● ●●
● ● ●●●●
● ●●
●
● ●
● ● ●●
●● ● ●
●
●
●
●
●
●
●
●● ● ●●●
●●● ●●●
●
●● ● ● ● ● ●●
●
●
● ●
●
● ●●●●
● ●
●●
●●
●
●●
●●
●
● ●●●
●
●
●●
●
●●
●●
● ● ●●
●●●
●
●●
● ●●●●●●●
●
●
●
●
●●●●● ● ●●●
●
●
●
●
●●● ●●●●●
●● ●●
●
● ● ●
● ● ● ●●
●
● ●● ●
●●
●
●●
●
● ●
●
●
● ●●
●● ● ●
●
●
● ● ● ● ● ●● ●
●
●● ●● ● ●● ●
●
●
●
●
● ●
●
● ● ●●●● ●
● ●● ●
●
●
●●●
● ●● ●●
●●
●●
●
●
●
●
● ●
●● ●
● ●● ●● ●
●●
● ●●
●●●
●
●
●
● ●●●● ●
●●
●●●
● ●
●
●
●●
●
● ●● ●● ●
●●
● ●
●
●
●
●
●
●
●
● ● ● ●● ●
●
●
●
●
●●
● ●
●●
●
●
●● ● ● ●
●
●
●
●●
●
●
●
● ●
●
●●
●
● ●●
● ● ●● ●
●
● ●●
● ●
● ● ●●
●● ● ●
●●
●● ● ●●
● ●
● ●
●
●
●
●
● ●●●●●
●
●● ● ●
●●
●
● ● ●
●
●
●●
●
● ●●
●
●
●
● ●●● ●
●
●
●●
●
●● ●●● ● ● ● ●
●
●● ● ●
●
● ●
●
●
●● ●●
●
●●
●
●●●●●
●
●
●● ●
●
● ● ● ●●●
●
●
●
●
● ●
●● ● ●
●
●
●●
−1.0
●
●
0
●
●
−1.0
10
rxy = 0.9
1
2
1 Beschreibende Statistik
Beispiel Für unseren Datensatz mit den Hauskatzen und -hunden ist die Berechnung
der Kovarianz (trotz gleicher Anzahl von Messwerten) nicht sinnvoll, da die Werte
nicht in einem paarweisen Zusammenhang stehen. Betrachten wir deshalb wieder das
Beispiel aus 1.1 mit den pH-Werten (xi ) und der Wassertemperatur (yi ). Es ergeben
sich sxy = 0,063 und rxy = 0,78 für Kovarianz und Korrelationskoeffizient. Der Wert
0,063 der Kovarianz ist positiv und deutet damit auf einen linearen proportionalen
Zusammenhang hin, liegt allerdings nahe bei Null, so dass man vermuten könnte, dass
der Zusammenhang kaum ausgeprägt sei. Betrachten wir allerdings den Korrelationskoeffizienten, so wird deutlich, dass 0,78 nahe genug bei +1 ist, um einen linearen proportionalen Zusammenhang zwischen pH-Wert und Wassertemperatur anzunehmen.
Also sind pH-Wert und Wassertemperatur hier miteinander korreliert, d.h. aber nicht
zwangsläufig, dass es auch einen kausalen Zusammenhang gibt! Tatsächlich hängt aber
allgemein der pH-Wert wirklich von der Temperatur ab.
Wenden wir nun das lineare Regressionsmodell von oben (1.3.4) an, ergeben sich als
Schätzer für a und b die Werte b̂ = 0,61 und â = 10,5. In Abbildung 1.4 wurde im
rechten Bild die Regressionsgerade y = â + b̂ · x in den Scatterplot eingezeichnet.
22
2 Wahrscheinlichkeiten
Häufig möchte man, bevor ein Zufallsexperiment durchgeführt wird, Aussagen über die
Wahrscheinlichkeit bestimmter Ausgänge des Experiments treffen. Im Abschnitt 2.1
werden die dazu notwendigen Grundbegriffe definiert und anschließend im Abschnitt
2.2 der alltägliche Begriff Wahrscheinlichkeit“ auf ein mathematisches Fundament
”
gestellt. Schließlich wird noch die wichtige Bayes-Formel (2.3) betrachtet.
2.1 Ereignisse
Ein Zufallsexperiment ist ein Vorgang, vor dessen Durchführung nicht bekannt ist,
welchen Ausgang er nehmen wird. Allerdings sind die möglichen Ergebnisse bekannt.
Diese werden im Ereignisraum Ω zusammengefasst. Eine Teilmenge A von Ω wird
Ereignis genannt, ein Ereignis A umfasst also mehrere Ergebnisse.
Beispiel Wir betrachten das Zufallsexperiment Würfeln mit einem Würfel“. Bevor
”
wir den Würfel werfen, wissen wir nicht, welche Zahl wir werfen werden. Als mögliche
Ergebnisse kommen nur die Zahlen 1 bis 6 in Frage, der Ereignisraum Ω ist also die
Menge
Ω = {1,2,3,4,5,6}.
Die einzelnen Elemente (Ergebnisse) von Ω werden mit ω1 , ω2 usw. bezeichnet. Hier
ist also ω1 = 1, ω2 = 2, ..., ω6 = 6. Die Wahrscheinlichkeit eines einzelnen Ergebnisses
bezeichnen wir mit P (ωi ) ≡ pi .
Ist der Würfel fair (also p1 = p2 = . . . = p6 = 61 ), handelt es sich bei dem Zufallsexperiment sogar um ein Laplace-Experiment. Allgemein heißt ein Zufallsexperiment
Laplace-Experiment, wenn jedes Ergebnis des Ereignisraumes dieselbe Wahrscheinlichkeit besitzt: Für Ω = {ω1 , . . . ,ωk } gilt P (ωi ) = pi = k1 , i = 1, . . . ,k. Offensichtlich
ist dies nur sinnvoll, wenn der Ereignisraum endlich ist, später werden wir auch Zufallsexperimente kennenlernen, bei denen für den Ereignisraum z.B. Ω = N oder Ω = R
gilt.
Betrachten wir die Ereignisse A = {2,4,6} ( Es wird eine gerade Zahl gewürfelt“)
”
und B = {1,2,3} ( Es wird eine kleine Zahl gewürfelt“). Die Wahrscheinlichkeit P (A)
”
für das Ereignis A ist gerade die Summe der Elementarwahrscheinlichkeiten der in A
enthaltenen ωi , also:
1
1
=
6
2
1
1
Laplace
P (B) = P ({1,2,3}) = p1 + p2 + p3 = 3 · =
6
2
P (A) = P ({2,4,6}) = p2 + p4 + p6
23
Laplace
=
3·
2 Wahrscheinlichkeiten
Damit wird auch folgende Eigenschaft des sicheren Ereignisses deutlich: Betrachten
wir dasjenige Ereignis, welches alle Elemente aus Ω enthält, dann gilt:
P (Ω) = P ({1, . . . ,6}) =
6
X
pi
Laplace
=
i=1
6·
1
= 1,
6
d.h. P (Ω) = 1. Weiterhin wird noch eine Teilmenge von Ω definiert, die gar keine
Elemente aus Ω enthält, die leere Menge ∅. Hier gilt
P (∅) = 0.
Da Ereignisse Mengen sind, können wir die folgenden drei Mengenoperationen betrachten:
• Vereinigung A ∪ B: Alle Elemente aus A und alle Elemente aus B werden
zusammengefasst, wobei die Elemente, die sowohl in A als auch in B enthalten
sind, nur einmal aufgeführt werden.
A ∪ B = {2,4,6} ∪ {1,2,3} = {1,2,3,4,6}
• Durchschnitt A ∩ B: Das sind alle Elemente, die sowohl in A als auch in B
vorhanden sind. Haben A und B keine Elemente gemeinsam, ist A ∩ B = ∅, man
sagt, A und B sind disjunkt.
A ∩ B = {2,4,6} ∩ {1,2,3} = {2}
• Mengendifferenz A\B: Hiermit sind alle Elemente gemeint, die zwar in A, aber
nicht in B sind. Dann gelten offensichtlich folgende zwei Eigenschaften: A\A = ∅
und falls A und B disjunkt sind, gilt A\B = A.
A\B = {2,4,6}\{1,2,3} = {4,6}
Zuletzt definieren wir noch das Gegenereignis oder Komplementärereignis Ā = Ω\A,
das sind also alle Elemente des gesamten Raums Ω, die nicht in A enthalten sind. Es
gilt immer A ∪ Ā = Ω.
Ā = Ω\A = {1,2,3,4,5,6}\{2,4,6} = {1,3,5}
In Abbildung (2.1) sind diese vier Operationen grafisch in sogenannten Venn-Diagrammen dargestellt.
2.2 Definition der Wahrscheinlichkeit
Betrachten wir wieder ein Laplace-Experiment (2.1) mit Ω = {ω1 , . . . ,ωk } und P (ωi ) =
pi = k1 , i = 1, . . . ,k. Für ein beliebiges Ereignis A ⊆ Ω definieren wir dann die
24
2 Wahrscheinlichkeiten
Abbildung 2.1: Venn-Diagramme: Zu sehen sind die Vereinigung, die Schnittmenge,
die Mengendifferenz und das Komplement.
A
B
A
A∪ B
A
B
A∩ B
B
A
A\B
B
A
25
2 Wahrscheinlichkeiten
Wahrscheinlichkeit P (A) von A wie folgt:
Zahl interessierender Fälle
Zahl aller Fälle
Zahl der Elemente von A
=
Zahl der Elemente von Ω
Die Motivation dafür ist folgende: Wir führen ein Zufallsexperiment n-mal durch und
zählen die Versuchsausgänge, die dem Ereignis A entsprechen, dies seien hA Stück.
Dann ist die relative Häufigkeit HA = hA /n. Führen wir das Experiment noch öfter
durch, d.h. n wird immer größer, nähert sich der Wert der (immer wieder neu berechneten) relativen Häufigkeit HA einem Grenzwert an, dieser ist gerade P (A):
P (A) =
lim HA = P (A).
n→∞
Dieser Zusammenhang heißt Gesetz der großen Zahlen.
Falls Ω unendlich viele Elemente besitzt oder kein Laplace-Experiment vorliegt, funktioniert diese intuitive Definition der Wahrscheinlichkeit nicht. Eine allgemeinere Definition von Wahrscheinlichkeit liefern die Kolmogorovschen Axiome:
Eine Funktion P heißt Wahrscheinlichkeit, wenn für alle Teilmengen
A,B ⊆ Ω folgende Eigenschaften erfüllt sind:
1. 0 ≤ P (A) ≤ 1
2. P (Ω) = 1
3. A und B disjunkt ⇒ P (A ∪ B) = P (A) + P (B).
2.2.1 Rechnen mit Wahrscheinlichkeiten
Die Kolmogorovschen Axiome sind die Grundlage für folgende wichtige Rechenregeln
beim Rechnen mit Wahrscheinlichkeiten:
P (Ā) = 1 − P (A)
P (A ∪ B) = P (A) + P (B) − P (A ∩ B)
P (∅) = 0
Beispiel Beim Würfelwurf mit den Ereignissen A und B wie oben ergeben sich folgende Wahrscheinlichkeiten:
1
P (Ā) = 1 − P (A) = 1 −
2
1
= ,
2
1 1 1
P (A ∪ B) = P (A) + P (B) − P (A ∩ B) = + −
2 2 6
5
= .
6
26
2 Wahrscheinlichkeiten
2.2.2 Bedingte Wahrscheinlichkeit und unabhängige Ereignisse
Unabhängigkeit
Zwei Ereignisse A und B heißen (stochastisch) unabhängig, wenn gilt:
P (A ∩ B) = P (A) · P (B).
Manchmal schreibt man statt P (A ∩ B) auch P (A,B).
Beispiel Nehmen wir an, wir werfen eine faire Münze und einen fairen Würfel gleichzeitig. Offensichtlich beeinflusst das Ereignis K = Die Münze zeigt Kopf“ nicht das
”
Ereignis G = Der Würfel zeigt eine 6“. Also berechnet sich die Wahrscheinlichkeit
”
des Ereignisses K ∩ G wie folgt:
P (K ∩ G) ≡ P (K,G) = P (K) · P (G) =
1 1
1
· =
.
2 6
12
Beispiel Die Blutgruppe (A, B, AB oder 0) eines Menschen ist unabhängig von
seinem Rhesusfaktor (Rh+ oder Rh-). Die Wahrscheinlichkeiten für die einzelnen Merkmale sind wie folgt: P (0) = 0,38, P (A) = 0,42, P (B) = 0,13, P (AB) = 0,07 sowie
P (Rh+) = 0,85 und P (Rh−) = 0,15 (Verteilung in Deutschland). Daraus folgt:
P (AB,Rh−) = P (AB) · P (Rh−) = 0,07 · 0,15 = 0,0105
Bedingte Wahrscheinlichkeit
Oft sind zwei Ereignisse nicht unabhängig voneinander - so besteht zum Beispiel sicherlich ein Zusammenhang zwischen den Ereignissen H = Heute regnet es“ und M =
”
Morgen regnet es“. Jetzt ist es sinnvoll, die Wahrscheinlichkeit dafür anzugeben, dass
”
es morgen regnet, wenn ich weiß, dass es heute definitiv regnet. Dies wird bedingte
Wahrscheinlichkeit genannt und mit PH (M ) oder P (M |H) bezeichnet. Allgemein
bedeutet P (A|B), dass die Wahrscheinlichkeit für das Ereignis A gesucht ist, wenn
Ereignis B als bereits eingetreten vorausgesetzt wird. Mathematisch wird die bedingte
Wahrscheinlichkeit wie folgt definiert:
PB (A) ≡ P (A|B) =
P (A ∩ B)
P (B)
Äquivalent dazu ist P (A ∩ B) = P (B) · P (A|B), d.h. die Verbundwahrscheinlichkeit
P (A ∩ B) ist die Wahrscheinlichkeit für B (P (B)) mal die Wahrscheinlichkeit für A,
wobei B bereits eingetreten ist (P (A|B)).
Beispiel Eine Freundin wirft verdeckt zwei Würfel und teilt lediglich mit, dass die
Augensumme gleich 10 sei. Wie groß ist die Wahrscheinlichkeit, dass ein Pasch geworfen
27
2 Wahrscheinlichkeiten
wurde? Gesucht ist also die bedingte Wahrscheinlichkeit P (Pasch|Augensumme 10).
Die Verbundwahrscheinlichkeit ist
P (Pasch ∩ Augensumme 10) ≡ P (Pasch und Augensumme 10) ≡ P ({(5,5)}) =
1
36
und für die Wahrscheinlichkeit eine 10 zu werfen gilt
P (Augensumme 10) = P ({(6,4),(5,5),(4,6)}) =
3
1
=
.
36
12
Damit ergibt sich:
P (Pasch|Augensumme 10) =
P (Pasch ∩ Augensumme 10)
=
P (Augensumme 10)
1
36
1
12
=
1
.
3
2.2.3 Totale Wahrscheinlichkeit
Wir schreiben Ω als Vereinigung von disjunkten Mengen B1 ,B2 , . . . ,Bn , d.h.
˙ 2 ∪˙ . . . ∪B
˙ n.
Ω = B1 ∪B
(Man schreibt für die Vereinigung von zwei disjunkten Mengen B1 und B2 das Vereinigungszeichen mit einem Punkt darüber, um zu betonen, dass die Mengen keine
˙ 2 .)
Elemente gemeinsam haben: B1 ∪B
Dann gilt für ein beliebiges Ereignis A ⊆ Ω die Formel der totalen Wahrscheinlichkeit:
P (A) = P (B1 ) · P (A|B1 ) + . . . + P (Bn ) · P (A|Bn ).
Beispiel Eine Anglerin möchte gerne Forellen fangen und hat erfahren, dass es in den
drei Seen in ihrer Nachbarschaft unterschiedlich viele Forellen unter den Fischen gäbe.
See 1 hat fünfzig Prozent Forellen, See 2 noch zwanzig Prozent und See 3 schließlich
nur fünf Prozent Forellen. Sie kennt die Seen noch nicht und sucht sich nun zufällig
einen aus - wie groß ist die Wahrscheinlichkeit eine Forelle zu fangen (Ereignis F )? Wir
bezeichnen mit P (F |B1 ) = 0,5, P (F |B2 ) = 0,2 und P (F |B3 ) = 0,05 die Wahrscheinlichkeiten, in den entsprechenden Seen eine Forelle zu fangen. Der See wird zufällig
ausgewählt, also ist die Wahrscheinlichkeit P (Bi ) = 31 , i = 1,2,3. Damit ergibt sich:
P (F ) = P (F |B1 ) · P (B1 ) + P (F |B2 ) · P (B2 ) + P (F |B3 ) · P (B3 )
1
1
1
0,75
= 0,5 · + 0,2 · + 0,05 · =
= 0,25.
3
3
3
3
Die Anglerin wird also mit 25-prozentiger Wahrscheinlichkeit eine Forelle fangen.
28
2 Wahrscheinlichkeiten
2.3 Satz von Bayes
Betrachten wir noch einmal die Verbundwahrscheinlichkeit P (A∩B) = P (B)·P (A|B).
Umgekehrt gilt natürlich auch P (A ∩ B) = P (B ∩ A) = P (A) · P (B|A) und damit
P (A) · P (B|A) = P (B) · P (A|B) bzw. die Bayes-Formel
P (A|B) =
P (B|A) · P (A)
.
P (B)
Die Bayes-Formel verknüpft die bedingten Wahrscheinlichkeiten P (A|B) und P (B|A)
und ist nützlich, um Vorwissen ( a priori“) in die Berechnung der Wahrscheinlichkeit
”
zu integrieren. Häufig wird bei der Berechnung der Wahrscheinlichkeit P (B) im Nenner
die Formel für die totale Wahrscheinlichkeit benötigt.
Beispiel Es liegt ein Test für eine Erkrankung vor, die selten ist - etwa 0,1 Prozent
der Bevölkerung sind erkrankt. Der Test erkennt die Krankheit bei einer tatsächlich
kranken Person mit 100-prozentiger Wahrscheinlichkeit, bezeichnet aber auch fälschlicherweise 1 Prozent der Gesunden als krank. K und G sind die Ereignisse, dass eine
Person tatsächlich krank beziehungsweise gesund ist, und TK und TG bezeichnen das
entsprechende Testresultat. Die Wahrscheinlichkeiten sind dann wie folgt:
P (K) = 0,001 ⇒ P (G) = 0,999
P (TK |K) = 1
P (TK |G) = 0,01
Wie wahrscheinlich ist es, dass eine positiv getestete Person tatsächlich krank ist?
Das ist die bedingte Wahrscheinlichkeit P (K|TK ) und mit der Bayes-Formel sowie der
totalen Wahrscheinlichkeit P (TK ) = P (TK |G) · P (G) + P (TK |K) · P (K) ergibt sich:
P (TK |K) · P (K)
P (TK )
P (TK |K) · P (K)
=
P (TK |K) · P (K) + P (TK |G) · P (G)
1 · 0,001
1
=
≈
≈ 9%,
1 · 0,001 + 0,01 · 0,999
11
P (K|TK ) =
d.h. etwa 10 falschpositiv Getestete pro einer tatsächlich erkrankten Person!
29
3 Wahrscheinlichkeitsverteilungen
3.1 Zufallsvariablen
Oft werden, bevor ein Experiment durchgeführt wird, Eigenschaften der zufälligen
Messwerte vorausgesetzt, zum Beispiel hinsichtlich ihres zu erwartenden Mittelwerts,
der erwarteten Streuung um diesen und allgemein einer gewissen zu erwartenden Form
der Histogramme. Um diese Annahmen mathematisch exakt formulieren zu können,
benötigen wir den Begriff der Zufallsvariable: Dies ist eine Größe, deren exakten
Wert (die Realisierung x) wir erst kennen, nachdem wir das Experiment durchgeführt
haben. Vorher ist sie ein Platzhalter, allerdings mit bestimmten Eigenschaften, die
wir kennen: So wissen wir zum Beispiel vorher, ob X diskret oder stetig ist, je nachdem, ob X zum Beispiel die Anzahl von Jungtieren einer Hauskatze (X = 5) oder
die Wassertemperatur eines Sees (X = 20,361◦ C) beschreibt. Oder wir setzen bereits Eigenschaften der wahrscheinlichkeitstheoretischen Verteilung von X voraus, zum
Beispiel P (X = Kopf) = 0,5 beim Münzwurf oder P (85 ≤ X ≤ 115) = 0,68 beim
Messen des Intelligenzquotienten.
Für eine diskrete Zufallsvariable X wissen wir, dass sie nur abzählbar viele Realisierungen xi (i = 1,2,3, . . .) besitzt. Die Wahrscheinlichkeit für eine bestimmte Realisierung bezeichnen wir mit P (X = xi ) = pi . Wir haben in (1.2) und (1.3) bereits
das Histogramm und das Summenhistogramm kennengelernt. Nach dem Gesetz der
großen Zahlen (2.2) stabilisieren sich die Werte im Histogramm für große Stichprobenumfänge n gerade bei den Werten pi , und auch das abgeleitete Summenhistogramm
bekommt dann eine charakteristische Gestalt, diese wird durch die Verteilungsfunktion beschrieben:
X
FX (t) = P (X ≤ t) =
pi
i: xi ≤t
Diese Verteilungsfunktion hat wichtige Eigenschaften:
• 0 ≤ FX (t) ≤ 1
• limt→−∞ FX (t) = 0
• limt→+∞ FX (t) = 1
• FX ist monoton wachsend in t
Für eine stetige (kontinuierliche) Zufallsvariable X können wir keine Wahrscheinlichkeiten pi für einzelne Messwerte angeben, weil die Wahrscheinlichkeit, dass die
Zufallsvariable genau einen exakten Wert auf der reellen Achse trifft, gerade gleich 0
30
3 Wahrscheinlichkeitsverteilungen
ist. An die Stelle der pi tritt nun die Wahrscheinlichkeitsdichte f (x), eine Funktion
mit folgenden Eigenschaften:
• f (x) ≥ 0
R∞
• −∞ f (x) dx = 1.
Achtung: Die Wahrscheinlichkeitsdichte gibt keine Wahrscheinlichkeiten an! Vielmehr
ist die Wahrscheinlichkeit in der Fläche unter dem Graphen von f versteckt, und diese
wird gerade durch die Verteilungsfunktion bestimmt:
Die Verteilungsfunktion einer stetigen Zufallsvariablen wird über die Wahrscheinlichkeitsdichte wie folgt definiert:
Z t
FX (t) = P (X ≤ t) =
f (x) dx
−∞
Die Eigenschaften der Verteilungsfunktion sind dieselben wie im diskreten Fall. In
beiden Fällen gibt die Verteilungsfunktion die Wahrscheinlichkeit dafür an, dass die
Zufallsvariable X einen Wert kleiner oder gleich t annehmen wird. Außerdem gilt im
stetigen Fall:
Z b
P (a ≤ X ≤ b) =
f (x) dx = FX (b) − FX (a)
a
Wenn die genaue Gestalt der Verteilungsfunktion einer Zufallsvariablen bekannt ist,
zum Beispiel bei der Binomialverteilung oder Normalverteilung, schreiben wir X ∼
Bin(n,p) oder X ∼ N (µ,σ 2 ). Die Verteilungen werden dabei durch ihre Parameter charakterisiert (hier n und p bzw. µ und σ 2 ), mehr dazu in den entsprechenden
Abschnitten weiter unten.
3.1.1 Erwartungswert und Varianz
In (1.3.1) und (1.3.2) haben wir bereits die Begriffe Mittelwert und korrigierte Stichprobenvarianz für eine Stichprobe kennengelernt. Die Äquivalente für Zufallsvariablen
sind der Erwartungswert und die Varianz.
Erwartungswert
Zunächst die mathematische Definition:
Für eine diskrete Zufallsvariable X ist der Erwartungswert definiert durch
X
E(X) =
xi · pi
i
und für eine stetige Zufallsvariable X durch
Z∞
E(X) =
x · f (x) dx.
−∞
Man findet auch die Schreibweisen E [X] ≡ hXi ≡ E(X).
31
3 Wahrscheinlichkeitsverteilungen
Die Motivation für den Erwartungswert ist folgende: Angenommen, wir werfen 600-mal
einen fairen Würfel und erhalten 99-mal die 1, 101-mal die 2, 95-mal die 3, 100-mal
die 4, 103-mal die 5 und 102-mal die 6. Damit ergeben sich als relative Häufigkeiten
99
Hi = hni die Werte H1 = 600
= 0,165, H2 = 0,1683̄, . . ., H6 = 0,17. Der Mittelwert
ergibt sich zu
99 · 1 + 101 · 2 + 95 · 3 + 100 · 4 + 103 · 5 + 102 · 6
600
= H1 · 1 + H2 · 2 + . . . + H6 · 6
2113
=
= 3,5216̄.
600
x̄ =
Nach dem Gesetz der großen Zahlen (2.2) gilt lim Hi = pi =
n→∞
ergibt sich als erwarteter Wert“ des Würfelwurfs
”
1
6
= 0,16̄ und damit
E(X) = p1 · 1 + p2 · 2 + . . . + p6 · 6
1+2+3+4+5+6
=
= 3,5.
6
Varianz
Die Varianz ist für Zufallsvariablen das Analogon zur Stichprobenvarianz für Stichproben und wie folgt definiert:
X
X diskret: D2 (X) =
(xi − E(X))2 · pi
i
X stetig: D2 (X) =
Z∞
(x − E(X))2 · f (x) dx
−∞
Sie beschreibt jeweils die mittlere quadratische Abweichung der Zufallsvariablen von
ihrem Erwartungswert und beschreibt damit die Streuung der Verteilung um den Erwartungswert. Man findet auch die Schreibweisen V ar(X) ≡ V(X) ≡ D2 (X).
Für die Varianz gilt die Identität
D2 (X) = E([X − E(X)]2 ).
Manchmal kann es sinnvoller sein, die Varianz mit Hilfe des Verschiebungssatzes
D2 (X) = E(X 2 ) − (E(X))2 =
Z∞

x2 · f (x) dx − 
−∞
zu berechnen.
32
Z∞
−∞
2
x · f (x) dx
3 Wahrscheinlichkeitsverteilungen
Allgemein gilt sogar für jede Transformation g(X) einer Zufallsvariablen X die Eigenschaft
Z∞
E(g(X)) =
g(x)f (x) dx.
−∞
In den zwei folgenden Abschnitten (3.2) und (3.3) werden jetzt einige wichtige diskrete
und stetige Zufallsvariablen mit ihren besonderen Eigenschaften und Anwendungsbereichen vorgestellt.
3.2 Diskrete Verteilungen
3.2.1 Binomialverteilung: X ∼ Bin(n,p)
Die Binomialverteilung wird auch Mutter aller Verteilungen“ genannt, vor allem we”
gen ihrer engen Beziehung zur Normalverteilung (3.3.1). Wir betrachten zunächst das
Bernoulli-Schema: Es werden n unabhängige Versuche gemacht, jeder Versuch hat
dieselbe Treffer- oder Erfolgswahrscheinlichkeit p. Beispiele für dieses Setting sind der
wiederholte Münzwurf (Erfolg: Kopf, p = 21 ), der wiederholte Würfelwurf (Erfolg: 6,
p = 16 ) oder die Suche nach einer seltenen Krankheit in einer Bevölkerung ( Erfolg“:
”
Individuum ist krank, mit z.B. p = 0,001). Es interessiert nun die Wahrscheinlichkeit,
bei n Versuchen genau k Treffer zu erzielen:
n k
P (X = k) ≡ pk =
p (1 − p)n−k .
k
n!
Hierbei ist nk = k!(n−k)!
(sprich: n über k) und heißt Binomialkoeffizient. Dieser
ist die mögliche Anzahl von Kombinationen, k Erfolge auf n Versuche zu verteilen
(siehe Beispiel weiter unten). pk (1−p)n−k ist die Wahrscheinlichkeit, k-mal Erfolg und
demzufolge (n − k)-mal Misserfolg zu haben. Oft wird q = 1 − p ersetzt. Abbildung
(3.1) zeigt exemplarisch die Wahrscheinlichkeiten P (X = k) unter Binomialverteilung
mit n = 20 fix und verschiedenen Werten des Parameters p.
Weiterhin gilt:
FX (t) = P (X ≤ t) =
t X
n
k=0
k
pk (1 − p)n−k
E(X) = n · p
D2 (X) = n · p · (1 − p)
Ist n sehr groß, nähern sich die Werte der Binomialverteilung der einer Normalverteilung (3.3.1) mit µ = n · p und σ 2 = n · p · q an.
33
3 Wahrscheinlichkeitsverteilungen
Abbildung 3.1: Binomialverteilung für n = 20 und p ∈ {0,1; 0,3; 0,5; 0,7}
Binomialverteilung
0.25
●
0.20
●
●
●
●
0.15
●
●
●
●
●
●
0.10
P(X=k)
Bin(20; 0,1)
Bin(20; 0,3)
Bin(20; 0,5)
Bin(20; 0,7)
●
0.05
●
●
●
●
●
0.00
0
●
●
●
●
● ● ● ● ●
●
●
5
●
● ● ● ● ●
● ● ● ● ●
10
15
20
Erfolge k
Tabelle 3.1: Mögliche Versuchsausgänge im Bernoullischema mit n = 4 und k = 2
Durchgang
Erfolg/Misserfolg
34
1
+
+
+
-
2
+
+
+
-
3
+
+
+
4
+
+
+
3 Wahrscheinlichkeitsverteilungen
Beispiel Betrachten wir eine Versuchsreihe mit n = 4 Durchgängen und Erfolgswahrscheinlichkeit p = 0,25. Nehmen wir an, uns interessiert die Wahrscheinlichkeit,
genau zweimal Erfolg zu haben (k = 2). Wie könnten die Versuchsreihen aussehen? Tabelle (3.1) zeigt alle möglichen Varianten. Die einzelnen Durchgänge sind
stochastisch unabhängig, also berechnet sich die Wahrscheinlichkeit für den Versuchsausgang + + - -“ zu p · p · q · q, für den Versuchsausgang + - + - “ zu p · q · p · q usw., in
”
”
4!
= 42
jedem Fall ergibt sich gerade p2 · q 2 ≡ p2 (1 − p)2 . Insgesamt gibt es 6 = 2!(4−2)!)
verschiedene Versuchsausgänge, d.h.
4
P (X = 2) =
· p2 · q 2 = 6 · 0,252 · 0,752
2
27
=
≈ 21,1%.
128
3.2.2 Poisson-Verteilung: X ∼ P oiss(λ)
Wenn im Bernoulli-Schema die Erfolgswahrscheinlichkeit p sehr klein und die Anzahl
der Durchgänge n sehr groß ist, ist es günstiger, statt der Binomialverteilung die Poissonverteilung anzusetzen. Sie beschreibt sehr gut die Verteilung von seltenen Ereignissen und besitzt den Parameter λ, der die Erfolgshäufigkeit in einem festen Zeitintervall
beschreibt. Ausgehend von der Binomialverteilung mit Parametern n und p wird dann
die Poissonverteilung mit Parameter λ = n · p angesetzt. Die Wahrscheinlichkeit, im
Zeitintervall genau k Erfolge zu erzielen, ist bei der Poissonverteilung gegeben durch
P (X = k) ≡ pk ≡ Pλ (k) =
λk −λ
e .
k!
Abbildung (3.2) zeigt die Wahrscheinlichkeiten P (X = k) für X ∼ P oiss(λ) unter
verschiedenen Parameterwerten von λ.
Weiterhin gilt für die Poissonverteilung:
FX (t) = P (X ≤ t) =
t
X
λk
k=0
k!
e−λ
E(X) = λ
D2 (X) = λ
Typische Anwendungsbeispiele der Poissonverteilung sind der radioaktive Zerfall und
das Auftreten von Mutationen.
Ist λ sehr groß, nähern sich die Werte der Poissonverteilung der einer Normalverteilung
(3.3.1) mit Parametern µ = λ und σ 2 = λ an.
35
3 Wahrscheinlichkeitsverteilungen
Abbildung 3.2: Poissonverteilung für λ ∈ {0,5; 1; 5; 10}
0.6
Poissonverteilung
●
●
0.3
●
0.2
P(X=k)
0.4
0.5
●
Poiss(0,5)
Poiss(1)
Poiss(5)
Poiss(10)
●
●
●
●
0.1
●
●
●
●
●
0.0
●
●
0
●
●
●
●
●
●
5
●
●
●
●
●
●
●
●
10
●
●
●
●
15
Erfolge k
Beispiel Das radioaktive Isotop Iod-131 hat eine Zerfallsrate λ = 0,086/Tag (gerundet), dies entspricht einer Halbwertszeit von 8 Tagen (d.h. nach einer Zeit von 8 Tagen
sind in einer beliebigen Menge von Iod-131-Atomen nur noch die Hälfte der Atome von
der Art Iod-131, die andere Hälfte ist in andere Elemente zerfallen). Wie groß ist zum
Beispiel die Wahrscheinlichkeit, dass es in einer Probe vom Isotop Iod-131 an einem
Tag zu mindestens einem Zerfall kommt (P (X ≥ 1))? Mit Hilfe der Gegenwahrscheinlichkeit ergibt sich folgende Rechnung:
P (X ≥ 1) = 1 − P (X = 0) = 1 − P0,086 (0) = 1 −
0,0860 −0,086
e
= 1 − e−0,086
0!
≈ 0,082.
Also kommt es mit einer Wahrscheinlichkeit von etwa 8,2 Prozent zu mindestens einem
Zerfall am Tag.
3.3 Stetige Verteilungen
3.3.1 Normalverteilung: X ∼ N (µ,σ 2 )
Die Wahrscheinlichkeitsdichte einer normalverteilten Zufallsvariablen X lautet
1
1
exp − 2 (x − µ)2 .
f (x) = √
(3.1)
2σ
2πσ 2
Sie hat die charakteristische Glockenform, die in Abbildung (3.3) links zu sehen ist,
diese Kurve wird auch Gaußsche Glockenkurve genannt. Der Maximalpunkt der Dichte
36
3 Wahrscheinlichkeitsverteilungen
Abbildung 3.3: Normalverteilung (mit Parametern µ = 4 und σ 2 = 1). Links die
Dichtefunktion, rechts die Verteilungsfunktion.
Verteilungsfunktion N(4,1)
F(t)
0.0
0.0
0.2
0.1
0.4
0.2
f(x)
0.6
0.3
0.8
1.0
0.4
Normalverteilung N(4,1)
1
2
3
4
5
6
7
1
x
2
3
4
5
6
7
t
ist bei ihrem Parameter µ ∈ (−∞,+∞), der zweite Parameter σ 2 mit σ > 0 gibt an, wie
breit oder steil die Kurve ist. Insbesondere befinden sich die Wendepunkte des Graphen
der Funktion an den Stellen xW1 = µ − σ und xW2 = µ + σ. Die Verteilungsfunktion
der Normalverteilung lässt sich nicht explizit angeben, da das entsprechende Integral
über f (x) nicht analytisch zu bestimmen ist. Sie hat die Gestalt, die in Abbildung
(3.3) rechts zu sehen ist.
Für Erwartungswert, Varianz, Schiefe, Wölbung und Exzess einer normalverteilten
Zufallsvariablen gilt:
E(X) = µ
D2 (X) = σ 2
S=0
W =3⇒E=0
Standardnormalverteilung
Ein Spezialfall der Normalverteilung liegt für die Parameter µ = 0 und σ 2 = 1 vor und
wird Standardnormalverteilung genannt. Die Dichte der Standardnormalverteilung
wird manchmal dann mit φ(z) bezeichnet:
2
1
φ(z) = √ e−z /2
2π
37
3 Wahrscheinlichkeitsverteilungen
Für die Verteilungsfunktion der Standardnormalverteilung gilt dann:
Zt
φ(z) dz.
Φ(t) =
−∞
Auch dieses Integral lässt sich nur näherungsweise bestimmen, die Werte von Φ(z)
liegen aber in Tabellenform vor.
Wegen der Symmetrie der Normalverteilung gilt die wichtige Identität
Φ(−z) = 1 − Φ(z).
Wird der Wert FX (t) mit einem bestimmten t für eine normalverteilte Zufallsvariable
mit Parametern µ und σ 2 gesucht, muss zunächst die Substitution
z=
t−µ
σ
durchgeführt werden (Zentrierung und Standardisierung) und anschließend kann
der Wert Φ(z) = Φ( t−µ
σ ) in der Tabelle für die Standardnormalverteilung nachgeschlagen werden.
Die σ-Regel ist eine Faustregel, die angibt, wie viele Messwerte sich voraussichtlich
in einem bestimmten (von σ abhängigen) Bereich um den Erwartungswert µ befinden:
P (µ − 1σ ≤ X ≤ µ + 1σ) ≈ 68,3%
P (µ − 2σ ≤ X ≤ µ + 2σ) ≈ 95,5%
P (µ − 3σ ≤ X ≤ µ + 3σ) ≈ 99,7%
50% ≈ P (µ − 0,68σ ≤ X ≤ µ + 0,68σ)
90% ≈ P (µ − 1,65σ ≤ X ≤ µ + 1,65σ)
95% ≈ P (µ − 1,96σ ≤ X ≤ µ + 1,96σ)
99% ≈ P (µ − 2,58σ ≤ X ≤ µ + 2,58σ)
Abbildung (3.4) illustriert die Sigma-Regel.
Einen anderen Weg, sich der Standardnormalverteilung zu nähern, bieten die Quantile: Welchen Wert muss ich in die Verteilungsfunktion Φ einsetzen, um eine bestimmte
Wahrscheinlichkeit zu erhalten? So gibt zum Beispiel z(0,95) diejenige reelle Zahl an,
für die Φ(z(0,95) ) = 0,95 gilt. D.h. z(q) = Φ−1 (q).
38
3 Wahrscheinlichkeitsverteilungen
Abbildung 3.4: Sigma-Regel: Die Fläche unter der Dichtefunktion gibt gerade die
Wahrscheinlichkeit an.
Sigma−Regel
Sigma−Regel
95 %
f(x)
f(x)
68,3 %
µ − 1.96σ
µ − 2σ
−2
µ−σ
−1
µ
0
µ+σ
1
µ + 2σ
µ − 2σ
2
−2
x
µ + 1.96σ
µ−σ
−1
µ
0
µ+σ
1
µ + 2σ
2
x
Zentraler Grenzwertsatz
Die Bedeutung der Normalverteilung liegt einerseits darin, dass viele zufällige Vorgänge
sich in der Praxis gut mit einer Normalverteilung beschreiben lassen, z.B. Messfehler
bei technischen Geräten und die Brownsche Bewegung. Andererseits erscheint sie vor
allem im Zentralen Grenzwertsatz:
Die zentrierte standardisierte Summe von unabhängigen identisch verteilten Zufallsvariablen strebt gegen eine Standardnormalverteilung N (0,1).
Genauer: Wir betrachten Zufallsvariablen X1 ,X2 ,X3 ,. . ., die alle dieselbe Verteilung
(z.B. Binomialverteilung, Exponentialverteilung,...) besitzen und stochastisch unabhängig voneinander sind. Weiterhin haben sie jeweils den Erwartungswert µ und die
Varianz σ 2 (im Fall der Binomialverteilung also z.B. µ = n · p und σ 2 = n · p · (1 − p)).
Bilden wir nun die standardisierte zentrierte Summe
1
X1 − µ
Xn − µ
Zn = √ ·
+ ... +
,
σ
σ
n
dann gilt, dass Zn für n → ∞ gegen eine Zufallsvariable Z mit Z ∼ N (0,1) strebt. Oft
wird die Folgerung benutzt, dass sich für großes n die gemittelte Summe
n
X̄ =
1X
Xi
n i=1
39
3 Wahrscheinlichkeitsverteilungen
gut durch eine Normalverteilung N (µ, n1 σ 2 ) annähern lässt, oder äquivalent lässt sich
die Summe
n
X
Sn =
Xi
i=1
2
durch eine Normalverteilung N (nµ,nσ ) approximieren.
Beispiel Der Intelligenzquotient (IQ) wird mit einem Test bestimmt und ist so definiert, dass das durchschnittliche Testergebnis gerade einem IQ von 100 entspricht
und etwa 68,3 Prozent der Bevölkerung einen IQ zwischen 85 und 115 besitzen.
Darüberhinaus wird der IQ als normalverteilt angenommen. Demzufolge betrachten wir also eine Zufallsvariable IQ ∼ N (100,225), d.h. mit Mittelwert µ = 100
und Standardabweichung σ = 15 ⇒ σ 2 = 225. Wie viel Prozent der Bevölkerung
haben dann einen IQ zwischen 90 und 110? Dies entspricht der Wahrscheinlichkeit
P (90 ≤ IQ ≤ 110):
P (90 ≤ IQ ≤ 110) = FIQ (110) − FIQ (90)
90 − 100
110 − 100
−Φ
=Φ
15
15
≈ Φ(0,67) − Φ(−0,67)
= Φ(0,67) − (1 − Φ(0,67))
= 2 · Φ(0,67) − 1
≈ 2 · 0,74857 − 1
= 0,49714
Also haben etwa 49,7 Prozent der Bevölkerung einen IQ zwischen 90 und 110.
Beispiel In einem großen See werden regelmäßig Hechte gefangen. Die Hechte sind
durchschnittlich 90 cm lang und man geht davon aus, dass die Körperlänge der Hechte
einer Normalverteilung unterliegt. Etwa 10 Prozent der gefangenen Hechte sind länger
als 120 cm. Wie groß ist die Standardabweichung σ der normalverteilten Zufallsvariable
L der Körperlänge? Man rechnet wie folgt:
10% =
ˆ 0,1 = P (L ≥ 120) = 1 − P (L ≤ 120)
120 − 90
= 1 − FL (120) = 1 − Φ
σ
30
⇔Φ
= 0,9
σ
30
⇔
= Φ−1 (0,9)
σ
30
30
30
⇔ σ = −1
=
≈
Φ (0,9)
z(0,9)
1,28
= 23,4375.
40
3 Wahrscheinlichkeitsverteilungen
Abbildung 3.5: Exponentialverteilung (mit Parameter λ = 1/2). Links die Dichtefunktion, rechts die Verteilungsfunktion.
Verteilungsfunktion Exp(1/2)
0.6
F(t)
0.4
0.2
0.0
0.0
0.2
0.1
f(x)
0.3
0.8
0.4
1.0
Exponentialverteilung Exp(1/2) − Dichte
0
2
4
6
8
10
0
2
x
4
6
8
10
t
Die Standardabweichung der Körperlänge der Hechte beträgt rund 23,44 cm.
Beispiel Das radioaktive Iod-131 aus dem Beispiel für die Poissonverteilung (siehe
(3.2.2), λ = 0,086) wird in der Behandlung von Schilddrüsenerkrankungen eingesetzt.
Eine Spezialklinik besitzt deshalb viele Proben (n = 200) des radioaktiven Materials.
Wie wahrscheinlich ist es, dass es in allen Proben gemeinsam zu weniger als 50 Zerfällen
am Tag kommt? Dies entspricht der Wahrscheinlichkeit P (Sn ≤ 50) mit Sn wie oben im
Zentralen Grenzwertsatz (3.3.1) definiert. Der Zentrale Grenzwertsatz ergibt zunächst
(es gilt µ = σ 2 = λ bei der Poissonverteilung):
Sn
∼
approx
N (n · µ,n · σ 2 ) = N (n · λ,n · λ)
= N (200 · 0,086; 200 · 0,086) = N (17,2; 17,2)
Damit ergibt sich für die Wahrscheinlichkeit P (Sn ≤ 50):
50 − 17,2
P (Sn ≤ 50) = FSn (50) ≈ Φ
17,2
≈ Φ(1,91) ≈ 0,97193.
3.3.2 Exponentialverteilung: X ∼ Exp(λ)
Die Exponentialverteilung wird meist benutzt, wenn eine zufällige Zeitdauer modelliert werden soll. Man kann sie als Ergänzung zur Poisson-Verteilung (siehe (3.2.2))
41
3 Wahrscheinlichkeitsverteilungen
sehen: Die Poisson-Verteilung mit Parameter λ beschreibt die zufällige Anzahl von
seltenen Ereignissen in einem bestimmten Zeitintervall, die Exponentialverteilung mit
demselben Parameter λ beschreibt dann den zufälligen Zeitraum zwischen zwei dieser
seltenen Ereignisse. Sie besitzt folgende Dichte und Verteilungsfunktion:
(
λ · e−λx x ≥ 0
f (x) =
0
x<0
(
1 − e−λx x ≥ 0
.
FX (t) =
0
x<0
Die beiden Funktionen sind in Abbildung (3.5) zu sehen.
Weiterhin sind der Erwartungswert und die Varianz gegeben durch:
1
λ
1
D2 (X) = 2 .
λ
E(X) =
Die Exponentialverteilung wird zum Beispiel benutzt, um die Zeit zwischen zwei radioaktiven Zerfällen in einer Probe zu modellieren, für die Lebensdauer von Organismen, oder auch für die Zeit, bis ein technisches Gerät (z.B. eine Glühlampe) kaputt
geht. Manchmal interessiert dann nicht die Wahrscheinlichkeit, dass z.B. ein Organismus bis zu einem Zeitpunkt t lebt (FX (t) ≡ P (X ≤ t)), sondern dass er einen bestimmten Zeitpunkt t überlebt, dies ist dann durch die Überlebenswahrscheinlichkeit gegeben:
P (X ≥ t) = 1 − P (X ≤ t) = 1 − FX (t) = e−λx .
Abbildung (3.6) zeigt die Funktion der Überlebenswahrscheinlichkeit.
Eine interessante Eigenschaft der Exponentialverteilung ist ihre Gedächtnislosigkeit:
Es werden keine Ermüdungserscheinungen modelliert, d.h. zum Beispiel für die Lebensdauer einer Glühlampe, dass die Wahrscheinlichkeit, dass die Lampe noch 100 Tage
brennt, nicht davon abhängt, wie lange sie bis heute schon gebrannt hat. In manchen
Szenarien ist diese Eigenschaft der Exponentialverteilung unsinnig (Lebensdauern von
Lebewesen), manchmal ist sie aber tatsächlich gegeben (radioaktiver Zerfall). Eventuell
müssen dann kompliziertere Verteilungen benutzt werden, die eine Ermüdung berücksichtigen. Mathematisch ergibt sich die Gedächtnislosigkeit mit der bedingten Wahr-
42
3 Wahrscheinlichkeitsverteilungen
Abbildung 3.6: Überlebenswahrscheinlichkeit bei Exponentialverteilung (mit Parameter λ = 1/2).
0.6
0.4
0.0
0.2
1−F(t)
0.8
1.0
Überlebensdauer Exp(1/2)
0
2
4
6
8
10
t
scheinlichkeit (siehe (2.2.2)) wie folgt:
P ({X ≥ t0 + t} ∩ {X ≥ t0 })
P (X ≥ t0 )
P (X ≥ t0 + t)
=
P (X ≥ t0 )
P (X ≥ t0 + t|X ≥ t0 ) =
e−λ·(t0 +t)
e−λt0 · e−λt
=
−λ·t
0
e
e−λt0
−λt
=e
=
= P (X ≥ t).
Beispiel Das Darmbakterium Escherichia coli (E. coli) hat im Labor unter guten
Bedingungen eine Generationszeit von etwa 30 Minuten, d.h. ein einzelnes Bakterium
teilt sich nach etwa einer halben Stunde. Nehmen wir an, die Dauer zwischen zwei
Zellteilungen sei exponentialverteilt. Wie groß ist der Parameter λ? Wie wahrscheinlich
ist es, dass sich ein einzelnes Bakterium schon innerhalb der ersten 15 Minuten teilt?
Und wie wahrscheinlich ist es, dass sich ein einzelnes Bakterium, dass sich nach 30
Minuten noch nicht geteilt hat, innerhalb der nächsten 10 Minuten teilt?
Zunächst der Parameter λ: Der Erwartungswert der Exponentialverteilung ist 1/λ,
43
3 Wahrscheinlichkeitsverteilungen
also:
1 !
= 30 [min]
λ
1
⇔λ=
.
30
Für die Wahrscheinlichkeit, dass sich das Bakterium schon in der ersten Viertelstunde
geteilt hat, ergibt sich damit:
E(X) =
1
P (X ≤ 15) = FX (15) = 1 − e− 30 ·15
= 1 − e−1/2
≈ 0,39347.
Also teilt es sich mit etwa 39,3-prozentiger Wahrscheinlichkeit schon in den ersten 15
Minuten.
Wie steht es um das Bakterium, das sich in 30 Minuten noch nicht geteilt hat? Dass
die Zellteilung in den nächsten 10 Minuten geschieht, lässt sich durch die bedingte
Wahrscheinlichkeit P (X ≤ 30 + 10|X ≥ 30) beschreiben. Wegen der Gedächtnislosigkeit ergibt sich:
P (X ≤ 30 + 10|X ≥ 30) = P (X ≤ 10) = FX (10)
1
= 1 − e− 30 ·10 = 1 − e−1/3
≈ 0,28347.
Es kommt also mit etwa 28,3 Prozent Wahrscheinlichkeit in den nächsten 10 Minuten
zur Zellteilung, wobei die halbe Stunde Wartezeit mathematisch durch die angenommene Exponentialverteilung nicht modelliert und damit nicht berücksichtigt wurde.
3.3.3 Gleichverteilung: X ∼ U (a,b)
Wenn man annimmt, dass eine Zufallsgröße nur Werte auf einem begrenzten Intervall
[a,b] annimmt und es dabei keine bevorzugten Werte gibt, heißt die Zufallsvariable
gleichverteilt auf [a,b]. Die Wahrscheinlichkeitsdichte der Gleichverteilung lautet
(
1
, a≤x≤b
f (x) = b−a
0,
sonst.
Für Verteilungsfunktion, Erwartungswert und


0,
t−a
FX (t) = b−a
,


1,
Varianz ergeben sich:
t<a
a≤t≤b
b<t
a+b
2
1
2
D (X) =
(b − a)2 .
12
E(X) =
44
3 Wahrscheinlichkeitsverteilungen
Abbildung 3.7: Gleichverteilung (mit Parametern a = −1 und b = 5).
Verteilungsfunktion UNI(−1,5)
F(t)
0.0
0.00
0.2
0.05
0.4
0.10
f(x)
0.6
0.15
0.8
1.0
0.20
Gleichverteilung UNI(−1,5) − Dichte
−2
0
2
4
6
−2
0
x
2
4
6
t
Abbildung (3.7) zeigt Dichte und Verteilungsfunktion einer Gleichverteilung mit a =
−1 und b = 5.
Beispiel Bei Hausmeerschweinchen gibt es viele verschiedene Rassen mit unterschiedlicher Felllänge. Nehmen wir an, die Felllänge L genüge einer Gleichverteilung mit
Parametern a = 1 cm (Kurzhaarmeerschwein) und b unbekannt (z.B. Angorameerschwein). Aus Messungen ist bekannt, dass die Meerschweine im Mittel eine Felllänge
von 5 cm besitzen. Wie groß ist b? Wie viele Meerschweine besitzen eine Felllänge
zwischen 2 cm und 4 cm (z.B. Glatthaarmeerschwein)?
Der Erwartungswert einer Gleichverteilung ist E(L) = a+b
2 , mit einer erwarteten Felllänge von 5 cm ergibt sich also für den Parameter b:
5 = E(L) =
a+b
1+b
=
2
2
⇔ b = 9 [cm].
Und es gibt etwa 25 Prozent Meerschweine mit einer Felllänge zwischen 2 cm und 4 cm,
denn:
P (2 ≤ L ≤ 4) = FL (4) − FL (2)
3 1
2
1
4−1 2−1
−
= − = = .
=
9−1 9−1
8 8
8
4
45
3 Wahrscheinlichkeitsverteilungen
Abbildung 3.8: χ2 -Verteilung mit (von links nach rechts) 2, 3, 4 bzw. 5 Freiheitsgraden.
Chi²−Verteilung: Verteilungsfunktion
0.6
F(t)
0.4
0.2
0.0
0.0
0.2
0.1
f(x)
0.3
0.8
0.4
1.0
Chi²−Verteilung: Dichte
0
2
4
6
8
10
0
2
x
4
6
8
10
t
3.3.4 Chi-Quadrat-Verteilung: Y ∼ χ2 (f )
Wenn X1 , X2 , ... , Xf standardnormalverteilte unabhängige Zufallsvariablen sind,
dann ist die Summe ihrer Quadrate Y = X12 + X22 + . . . + Xf2 gerade χ2 -verteilt mit
Parameter f . Der Parameter f wird Anzahl der Freiheitsgrade genannt. Für die
Dichte der χ2 -Verteilung gilt
f
y
f (y) = cf · y 2 −1 · e− 2
mit Normierungskonstante cf
cf = √
1
2f
· Γ(f /2)
,
wobei
Z∞
Γ(x) =
tx−1 e−t dt
0
die Gamma-Funktion ist. Es gilt Γ(n) = (n − 1)! für n ∈ N.
Abbildung (3.8) zeigt Dichte und Verteilungsfunktion der χ2 -Verteilung für verschiedene Freiheitsgrade.
46
3 Wahrscheinlichkeitsverteilungen
Auch für die χ2 -Verteilung liegen die Werte ihrer Verteilungsfunktion FY (t) in Tabellenform vor. Für Erwartungswert und Varianz gilt
E(Y ) = f,
D2 (Y ) = 2f.
Die χ2 -Verteilung wird vor allem beim Chi-Quadrat-Test (siehe (5.2.3)) eingesetzt,
sowie wenn bei einer Stichprobe ein Konfidenzintervall für die Varianz σ 2 geschätzt
werden muss.
Beispiel Auf einem Erdbeerfeld wurde bei fünf verschiedenen Parzellen der Größe
1 m2 jeweils der zufällige Ertrag ρ der Sorte Fraise Rousse“ gemessen. Diese Sorte
”
hat einen durchschnittlichen Ertrag von 2 kg/m2 und einer Standardabweichung von
0,4 kg/m2 . Wir nehmen an, dass der Ertrag ρ einer Normalverteilung N (2 ; 0,16)
unterliegt. Auf den fünf Parzellen ergaben sich die Erträge ρ1 = 2,3 kg, ρ2 = 1,9 kg,
ρ3 = 2,6 kg, ρ4 = 2,1 kg und ρ5 = 1,8 kg. Wie groß ist die korrigierte Stichprobenvarianz? Wie ist diese (als Zufallsvariable S 2 ) verteilt? Und wie wahrscheinlich wäre
es gewesen, ein noch extremeres Ergebnis zu erzielen?
5
s2 =
1 X
(ρi − ρ̄)2
n − 1 i=1
1
(2,3 − 2,14)2 + (1,9 − 2,14)2 + (2,6 − 2,14)2 + (2,1 − 2,14)2 + (1,8 − 2,14)2
4
= 0,103 ⇔ s ≈ 0,321.
=
Wir wissen, dass X = ρ−2
eine standardnormalverteilte Zufallsvariable ist. Also ist
P50,4
2
2
Y = X1 + . . . + X5 = i=1 (ρi − 2)2 /0,16 eine χ2 -verteilte Zufallsgröße mit f = n = 5
P5
Freiheitsgraden. Wie unterscheidet sich Y von S 2 = 14 i=1 (ρi −ρ̄)2 ? Zunächst müssten
4
wir S 2 mit n−1
σ 2 = 0,16 multiplizieren, um dieselben Vorfaktoren zu erhalten. Man kann
2
2
dann annehmen, dass n−1
σ 2 S einer χ -Verteilung unterliegt. Aber: Wir haben ja nicht
mit µ = 2 normiert, sondern mit ρ̄ = 2,14! Dies führt dazu, dass wir einen Freiheitsgrad
2
2
verlieren, und es ist dann n−1
σ 2 S ∼ χ (n − 1).
Wie wahrscheinlich wäre ein noch extremeres Ergebnis gewesen? Dies entspricht der
Wahrscheinlichkeit P (S 2 > 0,103):
P (S 2 > 0,103) = 1 − P (S 2 ≤ 0,103)
n−1
n−1
4 2
4
= 1 − P ( 2 S2 ≤
0,103) = 1 − P (
S ≤
0,103)
σ
σ2
0,16
0,16
4 2
= 1 − P (χ2 ≤ 2,575) mit χ2 :=
S ∼ χ2 (4)
0,16
≈ 1 − 0,6313 (Werte der χ2 -Verteilung liegen tabelliert vor)
= 0,3687.
Es hätte also mit etwa 36,9-prozentiger Wahrscheinlichkeit ein noch extremeres Ergebnis der korrigierten Stichprobenvarianz geben können.
47
3 Wahrscheinlichkeitsverteilungen
Abbildung 3.9: t-Verteilung mit 1 (blau), 2 (rosa) bzw. 5 (rot) Freiheitsgraden im
Vergleich zur Standardnormalverteilung (schwarz gestrichelt).
t−Verteilung: Verteilungsfunktion
1.0
0.4
t−Verteilung: Dichte
t(1)
t(2)
t(5)
N(0,1)
F(t)
0.0
0.0
0.2
0.1
0.4
0.2
f(x)
0.6
0.3
0.8
t(1)
t(2)
t(5)
N(0,1)
−4
−2
0
2
4
−4
x
−2
0
2
4
t
3.3.5 t-Verteilung: T ∼ t(f )
Eine weitere in der Praxis wichtige Verteilung ist die t-Verteilung. Sie ist der Standardnormalverteilung N (0,1) sehr ähnlich und ergibt sich aus folgendem Zusammenhang:
Sind X1 , . . ., Xn unabhängige Zufallsvariablen mit Xi ∼ N (µ,σ 2 ) und weiterhin X̄ ihr
Mittelwert sowie S 2 die korrigierte Stichprobenvarianz, so gilt, dass
T =
X̄ − µ
√
S/ n
einer t-Verteilung mit f = n−1 Freiheitsgraden unterliegt, also T ∼ t(n−1). Allgemein
gilt auch für
X
T =q
Y
f
mit X ∼ N (0,1) und Y ∼ χ2 (f ), dass T ∼ t(f ).
Abbildung (3.9) zeigt die Dichte und Verteilungsfunktion der t-Verteilung für verschiedene Freiheitsgrade im Vergleich zur Standardnormalverteilung. Für große Werte
der Freiheitsgrade nähert sich die t-Verteilung stark der Standardnormalverteilung an.
Der Vollständigkeit halber sei hier die Dichte der t-Verteilung angegeben:
− f +1
Γ f +1
2
2
x2
f (x) = √
.
1+
f
f πΓ f2
48
3 Wahrscheinlichkeitsverteilungen
Γ(x) ist dabei genau so definiert wie oben bei der χ2 -Verteilung (3.3.4). Die Verteilungsfunktion lässt sich geschlossen angeben, ist aber sehr unhandlich und darauf soll hier
verzichtet werden. Auch für die t-Verteilung liegen Werte für verschiedene Freiheitsgrade tabelliert vor.
Erwartungswert und Varianz der t-Verteilung sind:
E(T ) = 0
D2 (T ) =
f
(falls f > 2).
f −2
Die t-Verteilung kommt vor allem bei der Berechnung von Konfidenzintervallen und
bei Hypothesentests zum Einsatz, siehe dazu auch die Abschnitte (4.2.2) und (5.2.2).
49
4 Schätzungen
Oft sind die Parameter einer Verteilung nicht bekannt (z.B. µ und σ 2 bei der Normalverteilung oder λ bei der Poissonverteilung), sollen aber anhand einer Stichprobe
bestimmt werden. Eine exakte Bestimmung der Parameter ist meist nicht möglich,
es können aber ungefähre Werte aus der Stichprobe abgeleitet werden, diese werden
als Schätzer oder Punktschätzung (4.1) bezeichnet und meist mit einem ˆ über dem
entsprechenden Buchstaben bezeichnet (also z.B. µ̂, σ̂ 2 , λ̂). Es können auch Bereiche
angegeben werden, in denen sich der wahre Parameter der Verteilung mit einer großen
Wahrscheinlichkeit befindet, dies heißt Bereichsschätzung und führt auf Konfidenzintervalle (4.2).
4.1 Punktschätzungen
Für eine Grundgesamtheit oder Population wird eine bestimmte Verteilung mit zugehörigen Parametern, der entsprechenden Verteilungsfunktion und im Falle einer stetigen Verteilung mit passender Wahrscheinlichkeitsdichte vorausgesetzt. Falls eine Normalverteilung angenommen wird, wären das z.B. die unbekannten Parameter µ und
σ 2 und die Wahrscheinlichkeitsdichte wie in Formel (3.1).
Aus einer Stichprobe von n unabhängigen Messungen aus der Grundgesamtheit können
wir nun lediglich die aus (1.3.1) und (1.3.2) bekannten Maßzahlen Mittelwert x̄ und korrigierte Stichprobenvarianz s2 bestimmen. Diese sind eine Annäherung für die wahren
Werte µ und σ 2 und werden demzufolge (Punkt-)Schätzer genannt. Weiterhin haben
wir in (1.2) das Histogramm kennengelernt, welches eine grafische Annäherung für die
Gestalt der Wahrscheinlichkeitsdichte ist.
Die Gestalt der Schätzer µ̂ und σ̂ 2 haben wir hier direkt angegeben mit
n
µ̂ = x̄ =
1X
xi
n i=1
n
σ̂ 2 = s2 =
1 X
(xi − x̄)2 .
n − 1 i=1
Die Herleitung dieser Schätzer und auch anderer für andere Verteilungen kann mit verschiedenen Techniken wie z.B. der Kleinste-Quadrate-Methode oder Maximum-Likelihood-Schätzung erfolgen. Weiterhin lassen sich viele Eigenschaften von Schätzern wie
z.B. Erwartungstreue und Konsistenz definieren (die z.B. die Division durch n − 1
statt n bei der korrigierten Stichprobenvarianz erklären). Solche Methoden und Eigenschaften sollen aber nicht Teil dieser Grundlagen-Vorlesung sein.
50
4 Schätzungen
4.2 Bereichsschätzungen und Konfidenzintervalle
Manchmal ist es sinnvoll, statt einer Punktschätzung für einen Parameter (meist der
Erwartungswert, im Falle der Normalverteilung also µ) lieber ein Intervall anzugeben,
in dem sich der wahre Parameter mit großer Wahrscheinlichkeit befindet. Konkret für
α = 0,05 sind also Intervallgrenzen a und b gesucht, so dass
P (µ ∈ [a,b]) = 1 − α = 0,95
gilt. (Eigentlich müsste man besser P ([a,b] 3 µ) schreiben, da nicht die Wahrscheinlichkeit gemeint ist, dass µ in dem Intervall liegt, sondern die Wahrscheinlichkeit, dass
das Intervall µ überdeckt.) Im Folgenden schauen wir uns die Konfidenzintervalle für
drei unterschiedliche Szenarien an.
4.2.1 Normalverteilung, Varianz bekannt
Nehmen wir an, wir haben eine Stichprobe x1 , . . ., xn aus einer normalverteilten
Grundgesamtheit genommen (X1 , . . ., Xn sind unabhängig identisch verteilt mit Xi ∼
N (µ,σ 2 )), wobei wir die Varianz σ 2 kennen und ein Konfidenzintervall für den unbekannten Erwartungswert µ zum Niveau α = 0,05 angeben wollen. Wir können ausnutzen, dass die Summe von normalverteilten Zufallsvariablen wieder normalverteilt
mit entsprechenden Parametern ist (hier ohne Beweis). Konkret gilt für den Mittelwert
n
1X
Xi ∼ N
X̄ =
n i=1
σ2
µ,
n
.
2
Es fällt auf, dass mit σn gerade das Quadrat des Standardfehlers des Mittelwertes
σx̄ = √σn (bei bekannter Standardabweichung, siehe auch (1.3.4)) in die Berechnung
eingeht. Die normalverteilte Zufallsvariable X̄ wird durch die Transformation
X̄ − µ
Z=p
σ 2 /n
zentralisiert und standardisiert, für die nun standardnormalverteilte Zufallsvariable
Z ∼ N (0,1) lässt sich das Konfidenzintervall zum Niveau α leicht angeben:
1 − α = P −z(1− α2 ) ≤ Z ≤ +z(1− α2 )
!
X̄ − µ
= P −z(1− α2 ) ≤ p
≤ +z(1− α2 ) ,
σ 2 /n
wobei z(1− α2 ) das entsprechende (1 − α2 )-Quantil der Standardnormalverteilung ist:
Φ(z(1− α2 ) ) = 1 −
51
α
.
2
4 Schätzungen
Betrachten wir nun die linke Ungleichung aus dem Inneren der Wahrscheinlichkeit und
lösen nach µ auf:
X̄ − µ
−z(1− α2 ) ≤ p
σ 2 /n
σ
⇔ X̄ − z(1− α2 ) · √ ≤ µ,
n
analog für die rechte Ungleichung, und es ergibt sich
1−α=P
−z(1− α2 )
=P
X̄ − µ
≤p
≤ +z(1− α2 )
σ 2 /n
!
σ
σ
X̄ − z(1− α2 ) · √ ≤ µ ≤ X̄ + z(1− α2 ) · √
n
n
.
Wenn wir also nun die realisierte Stichprobe X1 = x1 , . . ., Xn = xn betrachten, haben
wir das Konfidenzintervall zum Niveau α = 0,05:
σ
σ
√
√
; x̄ + z(0,975) ·
95% = P µ ∈ x̄ − z(0,975) ·
n
n
σ
σ
≈ P µ ∈ x̄ − 1,96 · √ ; x̄ + 1,96 · √
.
n
n
4.2.2 Normalverteilung, Varianz unbekannt
Nehmen wir an, wir haben wieder eine Stichprobe x1 , . . ., xn aus einer normalverteilten Grundgesamtheit genommen (X1 , . . ., Xn sind unabhängig identisch verteilt
mit Xi ∼ N (µ,σ 2 )), wobei wir diesmal die Varianz σ 2 nicht kennen, aber wieder
ein Konfidenzintervall für den unbekannten Erwartungswert µ zum Niveau α = 0,05
angeben wollen. Die Herleitung des Konfidenzintervalls ist analog wie eben, nur dass
die Varianz auch mit der korrigierten Stichprobenvarianz s2 geschätzt werden muss,
wodurch die Quantile t(1− α2 ;n−1) der t-Verteilung (siehe (3.3.5)) ins Spiel kommen und
sich folgendes Konfidenzintervall ergibt:
s
s
µ ∈ x̄ − t(1− α2 ;n−1) · √ ; x̄ + t(1− α2 ;n−1) · √ .
n
n
Auch für den Schätzer s2 der Varianz σ 2 lässt sich übrigens ein Konfidenzintervall
angeben, mit der χ2 -Verteilung ergibt sich nämlich:
#
"
n−1
n−1
2
2
2
·s ; 2
·s .
σ ∈
χ2(1− α ;n−1)
χ( α ;n−1)
2
2
52
4 Schätzungen
4.2.3 Andere Verteilungen
Sei nun schließlich noch eine Stichprobe x1 , . . ., xn aus einer Grundgesamtheit entnommen, die nicht normalverteilt ist (oder sogar eine unbekannte Verteilung besitzt),
und wir kennen weder Erwartungswert noch Varianz. Dann muss der Stichprobenumfang n so groß sein, dass die Anwendung des zentralen Grenzwertsatzes (siehe (3.3.1))
sinnvoll ist. In diesem Fall haben wir ein Konfidenzintervall durch
s
s
µ ∈ x̄ − z(1− α2 ) · √ ; x̄ + z(1− α2 ) · √ .
n
n
Beispiel Betrachten wir wieder die Erträge des Erdbeerfeldes (siehe (3.3.4) aus dem
Beispiel zur χ2 -Verteilung. Wir haben also die Erträge ρ1 = 2,3 kg, ρ2 = 1,9 kg,
ρ3 = 2,6 kg, ρ4 = 2,1 kg und ρ5 = 1,8 kg erhalten und wollen nun herausfinden,
wie groß der Ertrag der Sorte Fraise Rousse“ ist (wir nehmen an, wir kennen den
”
Ertrag noch nicht). Die Standardabweichung σ = 0,4 sei aber bekannt, darüberhinaus
nehmen wir an, dass die Erträge einer Normalverteilung unterliegen. Wie groß ist das
95-Prozent-Konfidenzintervall? Wie groß sind das 95-Prozent- und das 99-ProzentKonfidenzintervall, wenn wir die Standardabweichung σ nicht kennen?
Im Fall der bekannten Standardabweichung σ = 0,4 ergibt sich:
σ
σ
µ ∈ ρ̄ − z(0,975) · √ ; ρ̄ + z(0,975) · √
n
n
0,4
0,4
≈ 2,14 − 1,96 · √ ; 2,14 + 1,96 · √
5
5
≈ [1,789 ; 2,491] .
Ist die Standardabweichung unbekannt, vergrößert sich das Konfidenzintervall:
s
s
µ ∈ ρ̄ − t(0,975;n−1) · √ ; ρ̄ + t(0,975;n−1) · √
n
n
0,321
0,321
≈ 2,14 − t(0,975;4) · √ ; 2,14 + t(0,975;4) · √
5
5
0,321
0,321
≈ 2,14 − 2,776 · √ ; 2,14 + 2,776 · √
5
5
≈ [1,741 ; 2,539] .
Und das Konfidenzintervall wird nochmal größer, wenn wir mehr Sicherheit haben
53
4 Schätzungen
Abbildung 4.1: Konfidenzintervalle am Beispiel der Erdbeerernte.
1.5
2.0
2.5
3.0
Konfidenzintervalle
95% mit sigma
95% ohne sigma
99% ohne sigma
wollen und auf 99 Prozent gehen:
s
s
µ ∈ ρ̄ − t(0,995;n−1) · √ ; ρ̄ + t(0,995;n−1) · √
n
n
0,321
0,321
≈ 2,14 − t(0,995;4) · √ ; 2,14 + t(0,995;4) · √
5
5
0,321
0,321
≈ 2,14 − 4,604 · √ ; 2,14 + 4,604 · √
5
5
≈ [1,479 ; 2,801]
Und tatsächlich liegt auch der wahre Wert µ = 2 innerhalb beider 95-Prozent-Konfidenzintervalle (und erst recht innerhalb des 99-Prozent-Konfidenzintervalls). Abbildung (4.1) zeigt die Resultate.
54
5 Testtheorie
Die Testtheorie ist wahrscheinlich die wichtigste Anwendung der Statistik in der Biologie. Mit einem statistischen Test wird untersucht, ob die erhobenen Daten einer
vorher formulierten Aussage widersprechen oder sie bekräftigen. Da immer nur ein
Ausschnitt der Grundgesamtheit (die Stichprobe) beobachtet wird, kann es dabei zu
Fehlern kommen, wobei versucht wird, diese zu kontrollieren.
5.1 Hypothesentests
Jeder statistische Test folgt folgendem Schema:
1. Formulierung der Nullhypothese H0 :
Es wird immer eine Nullhypothese H0 gegen ihre Alternative H1
getestet. Alle möglichen Ausgänge des Experiments fallen entweder in
die Nullhypothese oder in die Alternative. Typische Nullhypothesen
(und ihre zugehörigen Alternativen) sind:
• H0 : µ = µ0 vs. H1 : µ 6= µ0 (Ist der Mittelwert einer Stichprobe
gleich einem vorgegebenen Wert µ0 ?)
• H0 : FX (t) = FY (t) vs. H1 : FX (t) 6= FY (t) (Entspricht die
Verteilung einer Stichprobe Y der einer bekannten Verteilung von
X?)
• H0 : µX = µY vs. H1 : µX 6= µY (Es wurden zwei Stichproben aus unterschiedlichen Grundgesamtheiten genommen. Stimmen ihre Mittelwerte annähernd überein oder sind die Gruppen
zu verschieden?)
2. Wahl des Signifikanzniveaus α:
Wir möchten die Gefahr begrenzen, dass wir uns am Ende gegen die
Nullhypothese entscheiden, obwohl sie doch wahr gewesen wäre. Diesen
Fehler bezeichen wir mit α, siehe (5.1.1).
3. Wahl des geeigneten Tests
Je nach der Art unserer Nullhypothese und den bereits bekannten
Eigenschaften unserer Stichprobe gibt es eine Vielzahl an Tests, die
die Daten der Stichprobe auswerten. Wichtig sind die (eventuell unbekannte) Verteilung der Stichprobe, ihre bekannten und unbekannten
55
5 Testtheorie
Parameter, wurden ein oder zwei Stichproben genommen, wird einoder zweiseitig getestet (siehe (5.1.2),...
Beispiele für Tests sind der Gaußtest, der t-Test, der Chi-QuadratTest, der Kolmogorov-Smirnov-Test und der Rangsummentest, es gibt
noch viele mehr.
4. Berechnung der Teststatistik:
Die meisten Tests berechnen letztendlich eine einzelne Zahl aus der
Stichprobe, die Teststatistik oder Prüfgröße genannt wird. Diese
wird dann mit einem Wert verglichen, der sich aus der Art des Tests,
dem Umfang der Stichprobe und dem Signifikanzniveau ergibt (meist
sind diese Werte in Tabellen zu den entsprechenden Tests bereits vorhanden). Statistiksoftware gibt meistens einen p-Wert aus, der dann
mit dem Signifikanzniveau α verglichen werden muss.
5. Ablehnung oder Beibehaltung von H0
Der Vergleich der Teststatistik mit dem Tabellenwert ist die Grundlage unserer Entscheidung: Passen die Daten der Stichprobe zur Nullhypothese? Wenn nicht, dann verwerfen wir die Nullhypothese und
entscheiden uns für die Alternative (Ablehnen der Nullhypothese).
Wenn die Daten die Nullhypothese doch plausibel erscheinen lassen,
können wir sie nicht verwerfen, bzw. es kommt zur Beibehaltung der
Nullhypothese. Achtung: Wir können die Nullhypothese nicht beweisen
und deshalb nicht sagen, dass sie wahr sei (sie bleibt eine Hypothese,
die aber eventuell durch die Daten bekräftigt wird).
Grundsätzlich wird bei statistischen Tests zwischen parametrischen und nichtparametrischen Tests unterschieden. Bei einem parametrischen Test setzen wir eine
bestimmte Art von Verteilung voraus (und Verteilungen werden über ihre Parameter
charakterisiert). Die Nullhypothese und die Alternative lassen sich dann über diese Parameter definieren (z.B. H0 : µ ≤ µ0 vs. H1 : µ > µ0 ). Bei einem nichtparametrischen
Test setzen wir keine bestimmte Verteilung voraus und müssen andere Wege finden,
die Nullhypothese zu formulieren und eine Entscheidung zu treffen (Beispiele sind der
Rangsummentest und der Kolmogorov-Smirnov-Test).
Es gibt auch Testmethoden, die nicht direkt auf der Berechnung einer Teststatistik
beruhen, wie die Monte-Carlo-Simulationen oder Bootstrapping-Tests. Diese werden
in dieser Grundlagenvorlesung aber nicht betrachtet.
Wenn statistische Tests mit Statistiksoftware durchgeführt werden, wird meistens nicht
die Teststatistik ausgegeben, sondern ein Wert p ∈ [0; 1]. Dieser p-Wert gibt an,
wie wahrscheinlich die ausgewertete Stichprobe ist, wenn die Nullhypothese stimmen
würde. Das Signifikanzniveau α muss vor der Berechnung des p-Wertes gewählt worden
56
5 Testtheorie
Tabelle 5.1: Fehler bei Signifikanztests
H0 beibehalten
H0 abgelehnt
H0 wahr
korrekt (1 − α)
Fehler 1. Art (α)
H0 falsch
Fehler 2. Art (β)
korrekt (1 − β)
sein, im letzten Schritt der Testroutine wird die Entscheidung dann wie folgt gewählt:
p ≤ α ⇒ Ablehnung der Nullhypothese
p > α ⇒ Beibehaltung der Nullhypothese.
Ein wichtiger Aspekt der (wenig intuitiven) Logik von Beibehaltung“ und Ableh”
”
nung“ der Nullhypothese ist, dass wir das, was wir eigentlich zeigen wollen, besser in
der Alternative formulieren: Passen die Daten dann nicht zur (ohnehin unerwünschten)
Nullhypothese, können wir uns ruhigen Gewissens (bzw. mit einem maximalen Fehler
von α, siehe (5.1.1)) für die Alternative entscheiden.
5.1.1 Fehlertypen
Das Signifikanzniveau α eines Tests ist eine vor der Durchführung des Tests gewählte
Größe, um den Fehler 1. Art des Tests zu begrenzen: Wir entscheiden uns anhand der Stichprobe fälschlicherweise dazu, die Nullhypothese abzulehnen; sie trifft
tatsächlich für die Grundgesamtheit zu (und unsere Stichprobe war leider nur eine
schlechte Repräsentation der Grundgesamtheit).
Analog gibt es auch einen Fehler 2. Art: Wir entscheiden uns anhand der Stichprobe
irrtümlich dafür, die Nullhypothese beizubehalten, obwohl in Wahrheit die Alternative
für die Grundgesamtheit gilt (aber unsere Stichprobe zufälligerweise eher der Nullhypothese entspricht). Der Fehler 2. Art wird häufig mit β bezeichnet.
Tabelle (5.1) zeigt nochmal die möglichen Konsequenzen bei der Entscheidung bei
einem Hypothesentest.
Beispiel Zum Nachweis des Miniermottenbefalls einer Kastanie wird eine Stichprobe
von n Kastanienblättern des Baumes genommen und die Anzahl k der befallenen
Blätter gezählt (die Larven der Miniermotte fressen sich durch die Blattsubstanz).
Ist k größer als ein bestimmter Wert k0 , gilt der Baum als gefährdet. Wir wählen
Nullhypothese und Alternative wie folgt:
H0 : k ≤ k0 Baum ist nicht gefährdet
H1 : k > k0 Baum ist gefährdet.
Nun kann es sein, dass wir aufgrund des auffälligen Aussehens der betroffenen Blätter
einen zu großen Anteil betroffener Blätter in der Stichprobe haben und die Stichprobe keine gute Repräsentation der Grundgesamtheit (alle Blätter der Kastanie) ist.
57
5 Testtheorie
Lehnen wir dann fälschlich die Nullhypothese ab, obwohl der Baum gar nicht gefährdet
ist, haben wir eine falsch-positive Entscheidung getroffen und den Fehler 1. Art
begangen. Im umgekehrten Fall (der Baum ist tatsächlich gefährdet, aber in unserer Stichprobe waren zu wenige befallene Blätter) hätten wir eine falsch-negative
Entscheidung getroffen (H0 beibehalten, obwohl H1 stimmt) und den Fehler 2. Art
gemacht.
5.1.2 Einseitige und zweiseitige Tests
Bei einem parametrischen Test sprechen wir je nach Art der Nullhypothese von einem
einseitigen oder zweiseitigen Test. Im Prinzip bedeutet zweiseitiges Testen, dass
die Alternative aus zwei getrennten Bereichen besteht (und beim einseitigen Testen
dementsprechend nur aus einem Bereich). Betrachten wir einen Test für den Parameter µ einer Verteilung, der dem Erwartungswert entspricht, so haben wir folgende
Möglichkeiten für die Nullhypothese:
• H0 : µ ≤ µ0 ⇒ die Alternative umfasst den Bereich µ ∈ (µ0 ,∞) und es handelt
sich um einen einseitigen Test
• H0 : µ ≥ µ0 ⇒ die Alternative ist hier µ ∈ (−∞,µ0 ) und der Test ist einseitig
• H0 : µ = µ0 ⇒ die Alternative besteht aus den zwei getrennten Bereichen
µ ∈ (−∞,µ0 ) und µ ∈ (µ0 ,∞) und es ist ein zweiseitiger Test
• H0 : µa ≤ µ ≤ µb ⇒ auch hier ist der Test zweiseitig, denn die Alternative ist
zweiteilig: µ ∈ (−∞,µa ) und µ ∈ (µb ,∞) (H0 umfasst hier die Menge µ ∈ [µa ,µb ])
Bei vielen Tests hat die Wahl eines ein- oder zweiseitigen Tests Auswirkungen auf die
Bestimmung des Tabellenwerts zum Vergleich mit der Teststatistik, darauf wird im
Abschnitt über den Gaußtest nochmal eingegangen (5.2.1).
5.2 Spezielle Tests
5.2.1 Gauß-Test
Das einfachste Beispiel für einen Hypothesentest ist der Gauß-Test für eine einzelne
Stichprobe (machmal auch u-Test oder z-score genannt). Es wird davon ausgegangen,
dass die Grundgesamtheit normalverteilt ist mit unbekanntem Erwartungswert µ und
bekannter Varianz σ 2 (d.h. X ∼ N (µ,σ 2 )) und es soll nun auf den Erwartungswert µ
getestet werden gegen den vorgegebenen Wert µ0 .
Betrachten wir zunächst den Fall, dass die Nullhypothese H0 : µ ≤ µ0 lautet und
das Signifikanzniveau α gewählt wurde. Die Stichprobe X1 , . . ., Xn sei unabhängig
identisch verteilt zu X (also Xi ∼ X). Dann gilt für den Mittelwert X̄, dass X̄ ∼
2
N (µ, σn ) (hier ohne Beweis). Damit ist unter der Nullhypothese
Z=
X̄ − µ0
√ ∼ N (0,1) (zentralisiert und standardisiert).
σ/ n
58
5 Testtheorie
Abbildung 5.1: Entscheidungen beim Gauß-Test, H0 : µ ≤ µ0 .
f(z)
H0 : µ ≤ µ0
f(x)
H0 : µ ≤ µ0
z(1−α)
1−α
krit. Wert
1−α
α
−2
−1
µ0
0
x
1
α
2
−2
Messwerte
−1
0
0
z
1
2
Werte der Teststatistik
Dieser Wert Z ist unsere
Teststatistik: Für eine Realisierung X1 = x1 , . . ., Xn = xn
√
0
berechnen wir z = n · x̄−µ
σ . Manchmal wird statt z auch u benutzt.
Als Vergleichswert für unsere Teststatistik nehmen wir das (1 − α)-Quantil z(1−α) aus
der Tabelle der Standardnormalverteilung und entscheiden uns wie folgt:
(
z > z(1−α) ⇒ H0 verwerfen
H0 : µ ≤ µ0 ⇒
z ≤ z(1−α) ⇒ H0 beibehalten
Denn: Ein zu hoher Wert von z (der z-score) bedeutet, dass sich der Mittelwert der
Stichprobe grafisch bereits am rechten Ende der Gaußkurve befindet und es sehr unwahrscheinlich ist, dass er annähernd mit dem Wert µ0 übereinstimmt oder kleiner als µ0 ist. Der z-score befindet sich dann im Ablehnbereich (z(1−α) ,∞), dessen
Flächeninhalt unter der Gaußkurve gerade α ist.
Die Abbildung (5.1) zeigt diesen Sachverhalt: Links ist das ursprüngliche Problem
(liegt der Mittelwert zu weit vom Wert µ0 entfernt?) zu sehen. Rechts daneben dasselbe
Problem nach der Transformation in die Teststatistik z. Die Nullhypothese würde hier
nicht verworfen werden, da z im (1 − α)-Bereich liegt.
Analog wird im Fall H0 : µ ≥ µ0 verfahren, mit folgender Entscheidungsregel:
(
z < z(1−α) ⇒ H0 verwerfen
H0 : µ ≥ µ0 ⇒
z ≥ z(1−α) ⇒ H0 beibehalten
59
5 Testtheorie
Abbildung 5.2: Entscheidungen beim Gauß-Test, H0 : µ ≥ µ0 und H0 : µ = µ0 .
H0 : µ ≥ µ0
H0 : µ = µ0
1−α
− z(1−α2)
f(z)
f(z)
− z(1−α)
1−α
+ z(1−α2)
α
α
2
2
α
z
−2
−1
0
0
1
2
−2
Werte der Teststatistik
z
−1
0
0
1
2
Werte der Teststatistik
Der Ablehnbereich für diese Nullhypothese ist in Abbildung (5.2) links zu sehen. Die
Nullhypothese würde hier verworfen werden, da z im roten Ablehnbereich liegt.
Wie sieht es nun im Falle eines zweiseitigen Tests mit der Nullhypothese H0 : µ = µ0
aus? Die Teststatistik Z bleibt dieselbe.
Hier wollen wir nun jedoch keine zu großen Abweichungen des Mittelwerts nach rechts
und nach links zulassen. Der Flächeninhalt unter der Gaußkurve über dem Ablehn˙ r ,∞) muss aber wieder α betragen, d.h. es muss gelten zr = z(1− α )
bereich (−∞,zl )∪(z
2
und wegen der Symmetrie zl = −zr = −z(1− α2 ) . Damit ergibt sich folgende Entscheidungsregel:


z < −z(1− α2 ) ⇒ H0 verwerfen
H0 : µ = µ0 ⇒ −z(1− α2 ) ≤ z ≤ z(1− α2 ) ⇒ H0 beibehalten


z > z(1− α2 ) ⇒ H0 verwerfen
In Abbildung (5.2) ist rechts der zweiseitige Ablehnbereich für die Nullhypothese H0 :
mu = µ0 zu sehen. Die Nullhypothese würde hier beibehalten werden, da z nicht im
roten Ablehnbereich liegt.
Häufig kann nicht davon ausgegangen werden, dass die Grundgesamtheit normalverteilt
ist, so dass ein Gauß-Test nicht angebracht scheint. Allerdings lässt sich für einen
genügend großen Stichprobenumfang n (meist n > 30) der zentrale Grenzwertsatz
(siehe (3.3.1)) anwenden und es kann doch der einfache Gauß-Test angewendet werden.
60
5 Testtheorie
Beispiel Im Beispiel zum Abschnitt (5.2.2) über den t-Test wird dieser mit dem
Gauß-Test verglichen.
5.2.2 t-Test
Auch beim t-Test (oder Student’s t-Test) wird wie beim Gauß-Test eine normalverteilte Grundgesamtheit auf den Erwartungswert µ gegen einen vorgegebenen Wert µ0
getestet, der einzige Unterschied zum Gauß-Test besteht darin, dass die Varianz σ 2
nicht bekannt ist und durch die korrigierte Stichprobenvarianz s2 geschätzt werden
muss. Dementsprechend wird als Teststatistik die Größe
t=
x̄ − µ0
√
s/ n
berechnet. Diese ist aber nicht mehr standardnormalverteilt, sondern entspricht einer
t-Verteilung (siehe (3.3.5)) mit n−1 Freiheitsgraden, statt der z-scores wie beim GaußTest werden also die Quantile der t-Verteilung als Vergleichsgröße für die Teststatistik
herangezogen.
Analog wie beim Gauß-Test werden dann folgende Entscheidungsregeln für die entsprechenden ein- bzw. zweiseitigen Tests formuliert:
(
t > t(1−α;n−1) ⇒ H0 verwerfen
H0 : µ ≤ µ0 ⇒
t ≤ t(1−α;n−1) ⇒ H0 beibehalten
(
t < t(1−α;n−1) ⇒ H0 verwerfen
H0 : µ ≥ µ0 ⇒
t ≥ t(1−α;n−1) ⇒ H0 beibehalten


t < −t(1− α2 ;n−1) ⇒ H0 verwerfen
H0 : µ = µ0 ⇒ −t(1− α2 ;n−1) ≤ t ≤ t(1− α2 ;n−1) ⇒ H0 beibehalten


t > t(1− α2 ;n−1) ⇒ H0 verwerfen
Beispiel In der Tremorforschung werden bei Ratten Refraktärzeiten gemessen. Man
nimmt an, dass diese normalverteilt sind mit Erwartungswert µ0 = 1,3 ms. Es wurden
vier Refraktärzeiten gemessen: x1 = 1,6 ms, x2 = 1,7 ms, x3 = 1,9 ms und x4 =
1,8 ms. Nun soll zum Signifikanzniveau α = 0,1 = 10% untersucht werden, ob die
Testreihe den vermuteten Erwartungswert µ0 unterstützt oder ihm eher widerspricht.
Die Nullhypothese lautet also:
H0 : µ = µ0 .
61
5 Testtheorie
Es ergeben sich folgende Werte aus der Stichprobe:
x̄ = 1,75 ms
s = 0,129 ms
s
√ = 0,065 ms
n
x̄ − µ0
1,75 − 1,3
√ =
= 6,97
⇒t=
0,065
s/ n
t(n−1;1− α2 ) = t(3;0,95) = 2,353 (zweiseitiger Test!)
Da nun t > t(3;0,95) , muss die Nullhypothese also zum Signifikanzniveau 10% verworfen
werden.
Wie sähe die Entscheidung aus, wenn die Varianz σ 2 = 0,32 der Refraktärzeit als
bekannt vorausgesetzt wird? Dann muss der Gauß-Test eingesetzt werden und es wird
folgende Teststatistik berechnet:
√ x̄ − µ0
n
σ
1,75 − 1,3
=2· √
0,32
≈ 1,591
z=
Jetzt ist −z(0,95) < z < z(0,95) = 1,65, und demzufolge kann die Nullhypothese zum
Niveau α = 0,1 nicht verworfen werden.
5.2.3 Chi-Quadrat-Test
Chi-Quadrat-Varianz-Test
Auch der χ2 -Varianztest geht von einer normalverteilten Grundgesamtheit aus, mit
unbekannten Parametern µ und σ 2 , welche wieder durch ihre Punktschätzungen Mittelwert x̄ und korrigierte Stichprobenvarianz s2 angenähert werden. Allerdings testet
der χ2 -Test nicht den Erwartungswert µ, sondern die unbekannte Varianz σ 2 auf einen
vorgegebenen Wert σ02 . Folgende Teststatistik kommt dabei zum Einsatz:
n
χ2 =
s2 · (n − 1) X
=
σ02
i=1
xi − x̄
σ0
2
.
Diese ist χ2 -verteilt mit f = n − 1 Freiheitsgraden, dementsprechend kommen bei
der Entscheidungsfindung die Quantile der χ2 -Verteilung (siehe (3.3.4)) zum Einsatz.
Die χ2 -Verteilung ist nicht symmetrisch, also sind das linke und rechte Quantil nicht
62
5 Testtheorie
identisch.
(
2
H0 : σ ≤
σ02
⇒
χ2 ≤ χ2(1−α;n−1) ⇒ H0 beibehalten
(
2
H0 : σ ≥
σ02
⇒
χ2 > χ2(1−α;n−1) ⇒ H0 verwerfen
χ2 < χ2(α;n−1) ⇒ H0 verwerfen
χ2 ≥ χ2(α;n−1) ⇒ H0 beibehalten

2
2


χ < χ( α ;n−1) ⇒ H0 verwerfen
2
H0 : σ 2 = σ02 ⇒
χ2( α ;n−1) ≤ χ2 ≤ χ2(1− α ;n−1) ⇒ H0 beibehalten
2
2


χ2 > χ2 α
(1− ;n−1) ⇒ H0 verwerfen
2
Beispiel Betrachten wir das Beispiel mit den Refraktärzeiten bei Ratten von oben
(5.2.2). Kann zum Signifikanzniveau α = 0,1 anhand der Stichprobe die Hypothese
verworfen werden, dass die Varianz den Wert σ02 = 0,32 übertrifft (H0 : σ 2 ≥ 0,32)?
s = 0,129 wurde oben schon berechnet, damit ergibt sich folgender Wert der Teststatistik χ2 :
χ2 =
0,1292 · 3
s2 · (n − 1)
=
2
σ0
0,32
≈ 0,156.
χ2(0,9;3)
Es ist
= 6,251 und damit χ2 < χ2(0,9;3) , also kann die Nullhypothese σ 2 ≥ 0,32
verworfen werden.
Chi-Quadrat-Anpassungstest
Eine wichtige Methode ist der χ2 -Anpassungstest, der untersucht, ob eine Stichprobe
X1 = x1 , . . ., Xn = xn einer bestimmten Verteilung unterliegt (d.h. Xi ∼ X und
X hat die vorgegebene Verteilungsfunktion FX (t)) oder signifikant davon abweicht.
Man kann also zum Beispiel untersuchen, ob die Stichprobe aus einer Gleichverteilung
(X ∼ U N I(a,b)), Binomialverteilung (X ∼ Bin(n∗ ,p)) oder Normalverteilung (X ∼
N (µ,σ 2 )) kommt, aber auch jede andere Verteilung ist denkbar.
Dazu wird die Stichprobe in m Klassen eingeteilt. Bei diskreten Verteilungen wie
der Binomialverteilung Bin(n∗ ,p) bietet es sich z.B. an, für jeden möglichen Wert
k = 0, . . . ,n∗ eine eigene Klasse anzulegen, d.h. m = n∗ . Bei stetigen Verteilungen wie
z.B. der Normalverteilung N (µ,σ 2 ) sollten die Klassen als Intervalle gewählt werden,
in die die Stichprobenergebnisse fallen können.
Nun wird für jede der i = 1, . . . ,m Klassen die erwartete (bzw. theoretische) absolute
Häufigkeit htheor
berechnet. Im Fall einer diskreten Verteilung wäre dann gerade
i
htheor
= n · pi ,
i
∗
∗
für die Binomialverteilung also z.B. htheor
= n · ni pi (1 − p)n −i . Bei einer stetigen
i
Verteilung gilt für die erwartete Häufigkeit des Intervalls [ai ,bi ] dann
htheor
= n · P (ai ≤ X ≤ bi ) = n · (FX (bi ) − FX (ai )) ,
i
63
5 Testtheorie
Abbildung 5.3: Empirische Verteilung im Histogramm gegen die theoretische Dichte.
Der χ2 -Test wertet für jede Klasse i den Unterschied in der Fläche
des Balkens (hSP
i , blau) gegen die Fläche unter dem Funktionsgraphen
(htheor
,
rot)
aus.
i
Chi−Quadrat−Anpassungstest
0.3
0.2
0.0
0.1
rel. Häufigkeit
0.4
0.5
hSP
i
htheor
i
1
2
3
4
5
x
bi −µ
ai −µ
für die Normalverteilung also z.B. htheor
=
n
·
Φ(
)
−
Φ(
)
.
i
σ
σ
In beiden Fällen gibt htheor
die Anzahl von Versuchsergebnissen an, die voraussichtlich
i
in der Klasse i landen, wenn unsere Nullhypothese stimmt:
theor
H0 : hSP
, i = 1, . . . ,m.
i = hi
Alternativ können wir auch formulieren
H0 : Die Stichprobe hat eine Verteilung mit der Verteilungsfunktion FX (t).
Der Test untersucht also, ob die durch das Experiment gewonnene empirische kumulative Verteilungsfunktion FSP (t) (siehe auch (1.2.2)) annähernd der Verteilungsfunktion
FX (t) entspricht. Veranschaulicht wird das in Abbildung (5.3) mit dem normierten Histogramm und der Dichte (Erinnerung: Die Verteilungsfunktion ist gerade das Integral
der Dichtefunktion).
Als Teststatistik berechnen wir dazu:
m
theor 2
X
(hSP
)
i − hi
.
χ2 =
theor
h
i
i=1
theor
Stimmt die Nullhypothese und sind die Unterschiede der hSP
rein zufällig,
i zu den hi
2
2
so ist χ eine χ -verteilte Zufallsgröße mit f = n − 1 − r Freiheitsgraden und Erwartungswert f , ist also χ2 f sollte die Nullhypothese verworfen werden. Dies führt
64
5 Testtheorie
zu folgender Entscheidungsregel (zum Signifikanzniveau α):
(
χ2 > χ2(1−α;f ) ⇒ H0 verwerfen
H0 : Verteilung mit FX (t) ⇒
χ2 ≤ χ2(1−α;f ) ⇒ H0 beibehalten
Wie wird die Anzahl der Freiheitsgrade f = n − 1 − r bestimmt? Hier ist r die Anzahl
der Parameter der vorgegebenen Verteilung FX (t), die nicht bekannt sind und aus der
Stichprobe geschätzt werden müssen. Testen wir z.B. auf Gleichverteilung auf dem
Intervall [0,5], so ist r = 0, da keine unbekannten Parameter geschätzt werden müssen.
Testen wir auf eine Binomialverteilung mit n∗ = 12 und unbekanntem p, so müssen wir
x̄
schätzen und demzufolge ist r = 1. Wird auf eine Normalverteilung
p durch p̂ = 12
mit unbekannten Parametern µ und σ 2 getestet, so werden diese durch µ̂ = x̄ und
σ̂ 2 = s2 geschätzt und demnach ist r = 2.
Beispiel Es wurde eine DNA-Sequenz untersucht, die 64 Nukleotide enthält. Diese
sind jeweils durch ihre Nukleobasen charakterisiert (A,T,C,G). Man könnte vermuten,
dass jede der vier Möglichkeiten mit derselben Häufigkeit anzutreffen ist, d.h. pi =
1
theor
= 14 · 64 = 16, und die Nullhypothese lautet
4 = pA = pT = pG = pC . Damit ist hi
H0 : hSP
i = 16, i ∈ {A,T,C,G}.
Nun ergab sich aber aus der Stichprobe folgendes Bild: 8-mal A, 8-mal T, 24-mal C
und 24-mal G. Zum Signifikanzniveau α = 0,05 wird nun untersucht, ob dies signifikant
von der in der Nullhypothese formulierten Gleichverteilung abweicht:
(8 − 16)2 + (8 − 16)2 + (24 − 16)2 + (24 − 16)2
4 · 82
=
= 16
16
16
= 7,815
χ2 =
χ2(3;0,05)
Also sollte H0 abgelehnt werden, denn die Sequenz weicht signifikant von einer Gleichverteilung ab (χ2 > χ2(3;0,05) ).
5.2.4 Zweistichproben-Tests
Es gibt viele Situationen, in denen nicht nur eine Stichprobe auf eine bestimmte
Eigenschaft getestet werden muss, sondern Daten aus zwei Stichproben vorliegen und
gegeneinander getestet werden müssen. So gibt es zum Beispiel bei einer medizinischen
Studie Daten aus einer PatientInnen-Gruppe, die mit einem neuen Medikament behandelt wurden, welche dann mit den Daten einer Kontrollgruppe verglichen werden,
die nur ein Placebo erhalten hat.
Zweistichproben-t-Test
Der Zweistichproben-t-Test kommt zum Einsatz, wenn die Erwartungswerte zweier
Stichproben A und B gegeneinander getestet werden. Es wird dabei davon ausgegangen, dass beide Stichproben normalverteilt sind mit derselben (unbekannten) Varianz
65
5 Testtheorie
σ 2 und unterschiedlichen Erwartungswerten µA und µB . Das heißt die Hypothesen
lauten
H0 : µA = µB vs. H1 : µA 6= µB .
Dabei können zwei verschiedene Szenarien auftreten:
1. verbundene Stichproben: Beide Stichproben haben denselben Stichprobenumfang
n und die Messwerte der Stichproben lassen sich paarweise verbinden. Dies wäre
zum Beispiel der Fall, wenn bei n PatientInnen vor der Behandlung Blutwerte
gemessen werden, und nach einem Jahr und erfolgter Behandlung bei denselben
n PatientInnen wieder Blutwerte gemessen werden. Es stellt sich die Frage, ob
sich die Blutwerte durch die Behandlung verbessert haben.
2. unabhängige Stichproben: Die beiden Stichproben sind unabhängig voneinander,
d.h. es gibt keine Verbindung zwischen ihnen. Sie können auch unterschiedlichen
Umfang nA und nB besitzen. Dies wäre der Fall bei dem oben geschilderten
Kontrollgruppen-Szenario. Allerdings wäre die Unabhängigkeit z.B. nicht gegeben, wenn es sich um eine Zwillingsstudie handeln würde.
Im ersten Fall kann einfach der Einstichproben-t-Test angewendet werden: Liegen die
Werte x1 , . . ., xn aus Gruppe A und y1 , . . ., yn aus Gruppe B vor, die paarweise
zusammengehören, so bilden wir die Differenzen d1 = x1 − y1 , . . ., dn = xn − yn und
testen dann die Differenzen di der Messwerte auf den Erwartungswert µ0 = 0 wie im
Einstichproben-Fall (gibt es keinen Unterschied zwischen den Stichproben, sollte die
erwartete Differenz gleich Null sein).
Der zweite Fall mit unabhängigen Stichproben ist aufwändiger. Zunächst muss die
Standardabweichung sp der gepoolten“ Stichproben berechnet werden:
”
s
(na − 1) · s2A + (nB − 1) · s2B
.
sp =
nA − 1 + nB − 1
Daraus wird dann die Prüfgröße t berechnet:
t=
x̄ − ȳ
q
sp · n1A +
≡
1
nB
x̄ − ȳ
·
sp
r
nA · nB
.
nA + nB
Diese ist t-verteilt mit f = nA + nB − 2 Freiheitsgraden, als Entscheidungsregel zum
Signifikanzniveau α ergibt sich also:


t < −t(1− α2 ;nA +nB −2) ⇒ H0 verwerfen
H0 : µA = µB ⇒ −t(1− α2 ;nA +nB −2) ≤ t ≤ t(1− α2 ;nA +nB −2) ⇒ H0 beibehalten


t > t(1− α2 ;nA +nB −2) ⇒ H0 verwerfen.
66
5 Testtheorie
Beispiel Im Treibhaus wurde ein neues Pestizid getestet. Von 27 Getreidepflanzen
wurden 14 zufällig ausgewählt und mit dem Pestizid behandelt, die übrigen 13 blieben
unbehandelt. Nach einigen Tagen wurde die Anzahl der Getreidekäferlarven gezählt
und es soll nun getestet werden, ob zum Signifikanzniveau α = 0,01 eine Veränderung
zu messen ist. Folgende Daten wurden aus den Messwerten berechnet:
nA = 13 ; x̄ = 3,47 ; sA = 0,85
nB = 14 ; ȳ = 1,36 ; sB = 0,77.
Es ergibt sich für die gepoolte Stichprobenvarianz und daraus folgend für die Teststatistik t:
r
12 · s2A + 13 · s2B
sp =
25
= 0,81
r
3,47 − 1,36
13 · 14
⇒t=
·
0,81
27
= 6,76.
Es ist t(1−0,01/2;25) = 2,79, da also t > t(1−0,01/2;25) gilt, kann die Nullhypothese
verworfen werden. Zum Signifikanzniveau α = 0,01 gab es also eine Veränderung durch
das neue Pestizid.
Zweistichproben-Varianz-Test
Kurz vorgestellt werden soll hier die Möglichkeit des F-Testes, auf die Varianz zweier
unabhängiger normalverteilter Stichproben zu testen. Für die Nullhypothese
2
2
2
2
H0 : σA
= σB
vs. H1 : σA
6= σB
wird die Prüfgröße
F =
s2A
s2B
berechnet. Diese ist F-verteilt mit fA = nA − 1 Zählerfreiheitsgraden und fB = nB − 1
Nennerfreiheitsgraden (F ∼ F (fA ,fB )). Die F-Verteilung wurde in diesem Skript nicht
vorgestellt, ihre Werte liegen aber auch tabelliert vor und können für die folgende
Entscheidungsregel benutzt werden:


F < F( α2 ;fA ;fB ) ⇒ H0 verwerfen
2
2
H0 : σA = σB ⇒ F( α2 ;fA ;fB ) ≤ F ≤ F(1− α2 ;fA ;fB ) ⇒ H0 beibehalten


F > F(1− α2 ;fA ;fB ) ⇒ H0 verwerfen.
Der F-Test sollte insbesondere vor jedem Zweistichproben-t-Test für unabhängige
Stichproben eingesetzt werden, da dieser voraussetzt, dass die Stichproben in etwa
2
2
dieselbe Varianz haben. Verwirft der F-Test die Nullhypothese H0 : σA
= σB
zum
Signifikanzniveau αF , so sind die Ergebnisse des folgenden t-Tests kritisch zu hinterfragen.
67
5 Testtheorie
Beispiel Im Getreidekäfer-Beispiel (5.2.4) ergibt sich folgender Wert der Teststatistik
für den F-Test:
F =
s2A
0,852
= 1,22
=
s2B
0,772
Als Quantile der F-Verteilung zum Signifikanzniveau αF = 0,02 erhält man aus der
Tabelle:
F(0,01;12;13) = 0,24
F(0,99;12;13) = 3,96
Da also 0,24 ≤ F ≤ 3,96 gilt, sollte die Nullhypothese nicht abgelehnt werden und die
Durchführung des t-Tests war sinnvoll.
Rangsummentest
Alle bisher vorgestellten Tests bis auf den χ2 -Anpassungstest setzen voraus, dass
die Stichproben einer Normalverteilung unterliegen oder dass zumindest die Stichprobenumfänge so groß sind, dass der Zentrale Grenzwertsatz (3.3.1) die Verwendung dieser Tests sinnvoll werden lässt. Mit dem Rangsummentest soll hier nun ein
Zweistichproben-Test vorgestellt werden, der keine Annahme über die Art der Verteilung der Stichproben A und B trifft. Solche Tests werden verteilungsunabhängig
oder nichtparametrisch (da Verteilungen über ihre Parameter charakterisiert werden)
genannt.
Beim Rangsummentest (oder auch Wilcoxon-Rangsummentest bzw. äquivalent MannWhitney-U-Test) wird die Frage untersucht, ob die Verteilungen FA (t) und FB (t) sich
um einen Wert θ unterscheiden, d.h. ob FA (t) = FB (t − θ) gilt. Es wird also davon
ausgegangen, dass die beiden Stichproben prinzipiell dieselbe, nicht näher spezifizierte,
Verteilung besitzen, deren Verteilungsfunktionen um den Wert θ verschoben sind. Aus
Stichprobe A liegen die Messwerte x1 , . . ., xnA vor und aus Stichprobe B die Werte y1 ,
. . ., ynB , insgesamt also n = nA + nB Daten. Nun werden beide Gruppen gemeinsam
sortiert: Der kleinste Wert aus beiden Gruppen bekommt den Rang 1, der zweitkleinste
Wert den Rang 2 und so weiter bis schließlich der größte Wert aus beiden Gruppen
den Rang n = nA + nB erhält. Stimmen zwei Messwerte überein, so erhalten beide
den mittleren Rang als Rangzahl. Die Rangzahl zu jedem Messwert bezeichnen wir
mit R(xi ) bzw. R(yj ). Für die Prüfgröße berechnen wir nun die Rangsummen RA und
RB :
RA =
RB =
nA
X
i=1
nB
X
R(xi )
R(yj ) =
j=1
68
n(n + 1)
− RA
2
5 Testtheorie
Als Nullhypothese wird H0 : θ = 0 gegen H1 : θ 6= 0 getestet. Die entsprechende
Prüfgröße U bestimmen wir wie folgt:
nA (nA + 1)
2
nB (nB + 1)
U B = RB −
= nA · nB − UA
2
U = min(UA ,UB )
UA = RA −
Die Entscheidung wird nach folgender Regel getroffen:
(
U < U(α;nA ;nB ) ⇒ H0 verwerfen
H0 : θ = 0 ⇒
U ≥ U(α;nA ;nB ) ⇒ H0 beibehalten.
Die kritischen Werte U(α;nA ;nB ) liegen für kleine Werte von nA und nB tabelliert vor.
Manchmal findet man auch tabellierte Werte für die Prüfgröße RA , dann braucht die
Größe U nicht bestimmt zu werden.
Gilt nA > 20 und nB > 20, so kann statt des Rangsummentests auch ein Gauß-Test
eingesetzt werden mit der Teststatistik
z=
RA − µA
wobei
σA
nA (n + 1)
2
r
p
nA · nB · (n + 1)
σA = V ar(RA ) =
.
12
µA = E(RA ) =
Beispiel Die Ergebnisse einer Biostatistik-Nachklausur werden ausgewertet. Es haben
16 Studentinnen und Studenten geschrieben. Von diesen haben die 11 StudentInnen aus
Gruppe A regelmäßig die Hausaufgaben während des Semesters bearbeitet, während
die 5 StudentInnen aus Gruppe B nur unregelmäßig die Hausaufgaben bearbeiteten.
Die erreichten Punktzahlen sind in Tabelle (5.2) aufgelistet, ebenso die sich daraus
ergebenden Rangzahlen.
Für die Rangsummen RA und RB ergeben sich also die Werte:
RA = 15 + 9,5 + 12 + 11 + 9,5 + 13 + 16 + 6 + 4 + 5 + 14 = 115
16 · 17
RB = 7 + 2 + 3 + 1 + 8 = 21 =
− 115
2
Und damit als Teststatistik U :
11 · 12
= 49
2
5·6
UB = 21 −
= 6 (= 11 · 5 − 49)
2
⇒ U = min(UA ,UB ) = UB = 6
UA = 115 −
69
5 Testtheorie
Tabelle 5.2: Klausurergebnisse Biostatistik, Ränge.
StudentIn
Gruppe A oder B
Punktzahl
Rang
StudentIn
Gruppe A oder B
Punktzahl
Rang
1
A
34,5
15
2
B
22
7
3
A
25
9,5
4
A
29
12
5
B
17,5
2
9
A
37
16
10
A
21
6
11
B
19
3
12
B
9
1
13
A
20
4
6
A
26,5
11
14
A
20,5
5
7
A
25
9,5
15
B
24
8
8
A
30
13
16
A
31
14
Zum Signifikanzniveau α = 0,05 und den Parametern nA = 11 und nB = 5 finden wir
in der Tabelle den kritischen Wert U(0,05;11;5) = 9. Damit gilt U < U(0,05;11;5) , also
kann die Nullhypothese verworfen werden. Das heißt, zum Signifikanzniveau α = 0,05
ist ein Zusammenhang zwischen Bearbeitung der Hausaufgaben und Punktzahl in der
Klausur anzunehmen.
70