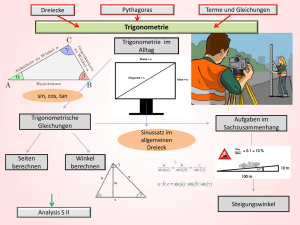
Quadratzahlen, Quadratwurzeln und Potenzen

Patrick Pirklbauer
Matrikelnummer: 1011616
Quadratzahlen, Quadratwurzeln und
Potenzen
Mathematisches Seminar für LAK
621.416
Kursleiterin: Univ.-Prof. Dr.phil. Karin Baur
Institut für Mathematik und wissenschaftliches Rechnen der
Karl-Franzens-Universität Graz
Inhaltsverzeichnis
1 Einleitung
2
2 Quadratzahlen
2.1 Wichtige Zahlenmengen . . . . . . . . . . . . . . . . . . .
2.2 Bündelungen von Zahlen . . . . . . . . . . . . . . . . . . .
2.3 „Rechteck- und Quadratzahlen“ - geometrische Deutung . .
2.4 Schreibweise und Eigenschaften von Quadratzahlen . . . .
2.4.1 Schreibweise . . . . . . . . . . . . . . . . . . . . . .
2.4.2 Einige Eigenschaften von Quadratzahlen . . . . . .
2.4.3 „Trick“ zur Berechnung von Fünfer-Quadratzahlen .
2.5 Dreieckszahlen . . . . . . . . . . . . . . . . . . . . . . . . .
2.6 Erweiterung auf R . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
. 3
. 3
. 3
. 5
. 5
. 5
. 7
. 8
. 10
3 Quadratwurzeln
11
3.1 Definition einer Quadratwurzel . . . . . . . . . . . . . . . . . . . . . 11
3.2 Rechenregeln und Eigenschaften von Quadratwurzeln . . . . . . . . . 12
4 Potenzen
4.1 Potenzen mit natürlichen Exponenten . . . . . . . . . . . . . . .
4.1.1 Definition von Potenzen mit natürlichen Exponenten . .
4.1.2 Rechenregeln für Potenzen mit natürlichen Exponenten .
4.2 Potenzen mit ganzzahligen Exponenten . . . . . . . . . . . . . .
4.2.1 Definition von Potenzen mit ganzzahligen Exponenten .
4.2.2 Rechenregeln für Potenzen mit ganzzahligen Exponenten
4.3 Potenzen mit rationalen Exponenten . . . . . . . . . . . . . . .
4.3.1 Definition von Potenzen mit rationalen Exponenten . . .
4.3.2 Rechenregeln für Potenzen mit rationalen Exponenten .
4.3.3 Existieren Wurzeln aus positiven reellen Zahlen? . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
14
14
14
15
15
15
16
17
17
17
17
5 Literaturverzeichnis
21
5.1 Elektronische Quellen . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
6 Abbildungs- und Tabellenverzeichnis
21
6.1 Abbildungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
6.2 Tabellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
1
1
Einleitung
Vor langer Zeit war es für die Menschen sehr wichtig mit Zahlen umgehen zu können,
denn die Fähigkeit mit Zahlen hantieren zu können, war für sie mehr oder weniger
das Tor zu einem reichen und sorgenfreien Leben.
Im Laufe der Jahre wurden immer neue mathematische Objekte, Formeln, etc. definiert und die Mathematik wurde stets weiterentwickelt.
In dieser Arbeit werden speziell die Themen:
• Quadratzahlen,
• Quadratwurzeln und
• Potenzen
behandelt und näher beschrieben.
Es werden vom jeweiligen Thema stets die Eigenschaften erklärt und die Definition
angeführt. Zur Veranschaulichung sind hin und wieder auch einige Beispiele hinzugefügt worden. Es wurde vor allem bei Definitionen stets versucht, im Vorhinein
alles das, was eventuell unklar bzw. unbekannt sein könnte zu definieren bzw. zu
erklären, damit die Arbeit möglichst leicht verständlich ist.
2
2
Quadratzahlen
Zum Beginn dieses Kapitels werden kurz zwei wichtige Zahlenmengen - insofern noch
nicht bekannt - erklärt.
2.1
Wichtige Zahlenmengen
Bei der ersten Zahlenmenge handelt es sich um die sogenannten natürlichen Zahlen,
die mit dem Symbol N dargestellt werden und definiert sind als N := {1, 2, 3, 4, 5, 6, ...}.
Erweitert man die natürlichen Zahlen noch durch die Zahl 0, dann erhält man die
Zahlenmenge N0 := {0, 1, 2, 3, 4, 5, 6, ...}, wobei auch diese Zahlenmenge von einigen
Autoren als Menge der natürlichen Zahlen definiert wird. In dieser Arbeit werden wir
aber zwischen N und N0 unterscheiden. Erweitert man wiederum die Menge N0 durch
bestimmte, sogenannte „negative ganze Zahlen“, also {..., −6, −5, −4, −3, −2, −1},
so erhält man eine weitere Zahlenmenge Z := {..., −3, −2, −1, 0, 1, 2, 3, ...}, die als
ganze Zahlen bezeichnet werden.
2.2
Bündelungen von Zahlen
Die ganzen Zahlen kann man wiederum in gerade ganze Zahlen {..., 2, 4, 6, 8, ...} und
ungerade ganze Zahlen {..., 1, 3, 5, 7, ...} aufteilen. Schon vor langer Zeit kannte man
diese Bündelung in Paaren, wobei vermutet wird, dass man andere Bündelungen
noch nicht kannte. Wie wir leicht nachprüfen können, sind die geraden Zahlen durch
zwei teilbar, wohingegen wir für Zahlen, die durch drei teilbar sind, keine Bezeichnung haben. Während wir Zahlen, die bei der Division durch zwei den Rest eins
haben, als ungerade Zahlen bezeichnen, haben wir wiederum keine Bezeichnung für
Zahlen, die bei der Division durch drei den Rest eins oder zwei besitzen. Die meisten Kinder haben keine Probleme damit, die Folge der geraden Zahlen aufzuzählen,
wobei es für sie immer schwieriger wird, wenn man zum Beispiel die Folge der durch
drei, vier oder noch größeren Ziffern teilbaren Zahlen verlangt. Zum Einüben, muss
aber das „kleine Einmaleins“, also die „Dreierfolge“ 3, 6, 9, 12, ..., die „Viererfolge“
4, 8, 12, ... und alle weiteren Folgen inklusive der „Neunerfolge“ 9, 18, 27, ... auswendig gelernt werden. Einzig die „Zehnerfolge“ 10, 20, 30, ... ist natürlich wieder ganz
leicht zu berechnen (vgl. Taschner, 2013, S. 85-86).
2.3
„Rechteck- und Quadratzahlen“ - geometrische Deutung
Früher war für die Menschen das Bündeln der Zahlen vor allem deshalb wichtig,
weil es sie lehrte zu multiplizieren und auch gleichzeitig zu verstehen, was die Multiplikation geometrisch bedeutete. Zeichnet man beispielsweise ein „Sechserbündel“
als sechs dicke Punkte in einer Zeile an eine Tafel oder ein Stück Papier und macht
das sieben mal untereinander, so hat man die Zahl 42 als „Rechteckzahl“ dargestellt. Natürlich könnte man auch jeden Punkt einzeln abzählen und würde auch
auf das gleiche Ergebnis kommen, bräuchte dafür aber wesentlich mehr Zeit. Dieses
Zählen ist also unnötig, denn die Rechnung 6 ∗ 7 liefert sofort die richtige Lösung.
Will Platon zum Beispiel, dass in seinem Staat genau 5040 Bürger leben dürfen,
so muss er diese nicht alle einzeln abzuzählen, denn es genügt, wenn er sie in der
3
Form eines Rechtecks antreten lässt. Er könnte zum Beispiel alle Bürger in einer
Zweierreihe aufstellen lassen, dann müsste es 2520 solcher Zweierreihen geben, denn
2 ∗ 2520 = 5040. Da aber 2520 eine sehr große Zahl ist, müsste Planton wieder sehr
weit zählen und bräuchte dafür sehr viel Zeit. Aus diesem Grund wäre es natürlich
viel geschickter und zeitsparender, wenn Platon zum Beispiel Reihen zu je 84 Bürger
erstellen würde. Wir wissen, es müsste dann 60 solcher Reihen zu je 84 Bürger geben, denn durch Nachrechnen erhalten wir 84 ∗ 60 = 5040. Man kann also erkennen,
dass je näher man das Rechteck einem Quadrat annähert, das Multiplizieren umso
effektiver wird und das simple Abzählen immer besser ersetzt.
Abbildung 1: Darstellung quadratischer Muster von Punkten
Hat man nun - so wie in Abbildung 1 dargestellt - genau so viele „Punkte“, dass
man das Rechteck-Muster zu einem quadratischen Muster umformen kann, so heißt
die durch die Punkte dargestellte Zahl eine Quadratzahl. Die ersten Quadratzahlen
wären:
0∗0=0
1∗1=1
2∗2=4
3∗3=9
4 ∗ 4 = 16
..
.
(vgl. Taschner, 2013, S. 86-87)
Hinweis:In dieser Arbeit wird die Zahl 0 als erste Quadratzahl angenommen, was
auch für die nächsten Kapitel wichtig ist.
4
2.4
2.4.1
Schreibweise und Eigenschaften von Quadratzahlen
Schreibweise
Für Quadratzahlen gibt es auch eine eigene kürzere Schreibweise:
Statt immer 0 ∗ 0 = 0, 1 ∗ 1 = 1 bzw. 2 ∗ 2 = 4 usw. zu schreiben, kann man
auch kurz 02 = 0, 12 = 1 bzw. 22 = 4 usw. schreiben.
Dauraus folgt:
0 ∗ 0 = 02
1 ∗ 1 = 12
2 ∗ 2 = 22
..
.
2.4.2
Einige Eigenschaften von Quadratzahlen
Die Folge 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, ... der Quadratzahlen wächst
relativ schnell an und trotzdem hat diese Folge eine faszinierende „Eigenschaft“:
Die Folge der Differenzen jeder Quadratzahl zu ihrer vorhergehenden ergibt genau
die Folge der ungeraden natürlichen Zahlen, also:
1−0=1
4−1=3
9−4=5
16 − 9 = 7
25 − 16 = 9
36 − 25 = 11
..
.
(vgl. Taschner, 2013, S. 87)
Anders formuliert: Jede ungerade Zahl ist Differenz zweier aufeinanderfolgender
Quadratzahlen.
Allgemein:
2k + 1 = (k + 1)2 − k 2 , ∀k ∈ N0 .
5
Das bedeutet natürlich, dass man die (n + 1) − te Quadratzahl ermitteln kann indem
man (bei der 0 beginnend) jeweils die n-te Quadratzahl mit dem n-ten Glied der
Folge der ungeraden natürlichen Zahlen addiert (mit n ∈ N). Also:
0+1=1
1+3=4
4+5=9
9 + 7 = 16
16 + 9 = 25
25 + 11 = 36
..
.
Daraus kann man folgern, dass die Summe der ersten n (n ∈ N) ungeraden Zahlen
eine Quadratzahl ist und zwar genau die Zahl n2 .
Es gilt zum Beispiel für n = 8:
1| + 3 + 5 + 7 +{z
9 + 11 + 13 + 15} = 64 = 82
die ersten 8 ungerade Zahlen
Für n ∈ N kann man allgemeiner auch schreiben:
n2 = 1 + 3 + 5 + 7 + · · · + (2n − 1)
Hierzu wieder ein Beispiel (für n = 7):
72 = 1 + 3 + 5 + 7 + 9 + 11 + |{z}
13
|{z}
=49
=2∗7−1
|
{z
}
=49
(vgl. Scheid & Schwarz, 2008, S. 61)
Da bisher nur Quadratzahlen aus dem Produkt von zwei gleichen positiven ganzen Zahlen bzw. von zwei gleichen Zahlen aus N0 gebildet und diskutiert worden
sind, könnte man sich die Frage stellen, ob man auch aus dem Produkt von zwei
gleichen negativen ganzen Zahlen eine Quadratzahl erhält?
Wir wissen es gilt:

(−1) ∗ (−1) = 1 



(−2) ∗ (−2) = 4 

(−3) ∗ (−3) = 9
=Folge der Quadratzahlen

(−4) ∗ (−4) = 16 



..

.
Wir sehen also, dass auch das Produkt zweier gleicher negativer ganzer Zahlen eine
Quadratzahl ergibt. Wir können auch erkennen, dass die Folge der Quadratzahlen,
die aus dem Produkt von zwei gleichen negativen ganzen Zahlen gebildet worden ist
und die Folge der Quadratzahlen, die aus dem Produkt von zwei gleichen positiven
ganzen Zahlen gebildet worden ist, identisch sind.
6
Hinweis: Natürlich ist die Zahl 0, da sie weder positiv noch negativ ist, als Spezialfall zu betrachten, wurde aber in dieser Arbeit beim Produkt zweier gleicher
positiver ganzer Zahlen mitbehandelt, obwohl sie streng genommen nicht zu den
positiven ganzen Zahlen gehören würde.
Wir können auch erkennen, dass folgendes gilt:
(−1) ∗ (−1) = 1 ∗ 1
(−2) ∗ (−2) = 2 ∗ 2
(−3) ∗ (−3) = 3 ∗ 3
(−4) ∗ (−4) = 4 ∗ 4
..
.
Durch die obigen Überlegungen können wir nun eine weitere sehr wichtige Eigenschaft von Quadratzahlen feststellen:
Eine Quadratzahl ist immer nichtnegativ!
Es gilt also:
a ∗ a = a2 ≥ 0, ∀a ∈ Z.
2.4.3
„Trick“ zur Berechnung von Fünfer-Quadratzahlen
Für Zahlen die mit einer 5 enden (zB.: 15, 25, 35, 45, ...), kann man ihre Quadratzahl
ganz leicht ausrechnen, sogar so leicht, dass es mit Kopfrechnen möglich ist.
Aber Vorsicht: Dieser „Trick“ funktioniert nur bei Zahlen die eine 5 am Ende haben!
Der TRICK: Zum Beispiel für die Zahl 65:
Multipliziere die Zahl ohne die Einerziffer 5 - in diesem Fall die 6 - mit ihrem
Nachfolger (6 + 1 = 7) und hänge an das Produkt (6 ∗ 7 = 42) die Zahl 25 an
⇒ Ergebnis = 4225
Weitere Beispiele:
152 = 225
252 = 625
352 = 1225
452 = [4 ∗ (4 + 1)]25 = 2025
[a]52 = [a ∗ (a + 1)]25, ∀a ∈ N0
Beweis: Alle Fünferzahlen lassen sich in der Form darstellen: 10 ∗ n + 5, ∀n ∈ N0 .
Also gilt für ihr Quadrat: (10 ∗ n + 5)2 = 100n2 + 100n + 25 = 100 ∗ n(n + 1) + 25.
(vgl. http://de.wikipedia.org/wiki/Quadratzahl)
7
2.5
Dreieckszahlen
Weiter oben haben wir als geometrische Deutung für die Multiplikation, die Rechteckbzw. Quadratzahlen kennen gelernt. In diesem Unterkapitel beschäftigen wir uns mit
den sogenannten Dreieckszahlen.
Abbildung 2: Einige Dreickszahlen
Wie man in Abbildung 2 erkennen kann, haben Dreieckszahlen eine gewisse Ähnlichkeit mit Steinhaufen. Will man eine Dreieckszahl berechnen, nimmt man die vorige
Dreieckszahl und addiert die Anzahl der „Punkte“ in der untersten Reihe des neuen
Dreiecks hinzu.
Zum Beispiel berechnet man die nächste Dreieckszahl nach der 10 wie folgt:
Die unterste Reihe hat 5 Punkte, also erhält man für die nächste Dreieckszahl mit
unserer „Regel“: 10 + 5 = 15
Wir können also alle weiteren Dreieckszahlen berechnen und erhalten so die Folge
der Dreieckszahlen:
Folge der Dreieckszahlen: 1, 3, 6, 10, 15, 21, 28, 36, . . .
Wenn wir uns die obige Folge genau ansieht, können wir erkennen, dass die Zahl 36
sowohl als Quadratzahl als auch als Dreieckszahl vorkommt.
Tabelle 1: Summen aus zwei aufeinanderfolgenden Dreieckszahlen
Addition zweier Dreieckszahlen
1+3
3+6
6 + 10
10 + 15
15 + 21
21 + 28
28 + 36
...
8
Ergebnis
4
9
16
25
36
49
64
...
Aus der Tabelle 1 können wir erkennen, dass nicht nur die Zahl 36 sowohl bei der
Quadratzahlen-Folge als auch bei der Dreieckszahlen-Folge vorkommt, sondern die
beiden Folgen auch einen weiteren „Zusammenhang“ besitzen. Man kann erkennen,
dass man stets eine Quadratzahl erhält, wenn man zwei aufeinanderfolgende Dreieckszahlen addiert. Der Grund dafür ist vor allem mit Hilfe des folgenden Diagramms
leicht zu erkennen:
Abbildung 3: Erklärung für „Zusammenhang“ von Dreickszahlen und Quadratzahlen
Man betrachtet - wie in Abbildung 3 dargestellt - ein Quadrat mit vier Reihen, wobei
jede Reihe jeweils vier Punkte besitzt und ziehen eine diagonale Linie etwas oberhalb
der diagonalen Punkte im Quadrat. Man erkennt, dass sowohl die Punkte oberhalb
der Linie, als auch die Punkte unterhalb der Linie ein Dreieck bilden. Bei genauerer
Betrachtung erkennt man, dass das untere Dreieck genau das nächstgrößere Dreieck
bildet. Diese Eigenschaft bzw. diese Beziehung zwischen den entsprechenden Dreiecken gilt nicht nur für dieses Quadrat, sondern für jedes beliebige Quadrat mit n
Reihen, bei dem jede Reihe aus jeweils n Punkten besteht (n ∈ N).
Von diesen „gepunkteten“ Diagrammen kommt man leicht zur Flächenberechnung
von Quadraten. Wir wissen, dass man die Fläche eines Quadrats mit Seitenlänge 4
berechnet mit:
A = 4 ∗ 4 = 42 = 16 Quadrat- bzw. Flächeneinheiten
Oder allgemein für ein Quadrat mit Seitenlänge a:
A = a ∗ a = a2 FE
Beschäftigt man sich vermehrt mit Quadratzahlen bzw. Flächenberechnungen von
Quadraten, so kommt man evtl. zur sogenannten Quadratfunktion f (x) = x2 , welche
die Grundlage für die Parabel bildet. Die Parabel wiederum findet man in vielen
Lebensbereichen, sei es bei Satellitenschüsseln, Autoscheinwerfern, im Sport bei der
Berechnung von Würfen und vielen weiteren Bereichen, wieder (vgl. Crilly, 2009, S.
16-17).
9
2.6
Erweiterung auf R
Wir haben bisher die Zahlenmengen N, N0 und Z kennen gelernt. Wollen wir aber
zwei Zahlen aus den ganzen Zahlen nicht multiplizieren, sondern dividieren, stoßen
wir auf ein Problem. Es ist nämlich nicht möglich jede Division in der Menge der
ganzen Zahlen durchzuführen. Zum Beispiel besitzt 46 keine Lösung innerhalb der
Menge der ganzen Zahlen. Wir ergänzen also Z durch alle Brüche mit ganzzahligem
Zähler und ganzzahligem - aber von 0 verschiedenen - Nenner. Das Ergebnis dieser
Erweiterung ist eine Menge, bei der jede Division - mit Ausnahme durch die Zahl
0 - durchführbar ist. Jede ganze Zahl kann man auch in der Bruchform - mit der
Zahl 1 im Nenner - aufschreiben, also können wir diese erweiterte Zahlenmenge aufschreiben als:
Q := { m
| m ∈ Z ∧ n ∈ N}, wobei
n
a
b
∼
c
d
:⇔ ad = bc, mit a, c ∈ Z ∧ b, d ∈ N
Diese Zahlenmenge heißt Menge der rationalen Zahlen und hat als Symbol Q. Die
heißen Brüche, wobei m als Zähler und n als Nenner bezeichTerme von der Art m
n
net werden (vgl. Hoffmann, 2013, S. 54).
Durch diese spezielle Definition der rationalen Zahlen, soll klar werden, dass zum
Beispiel die beiden Brüche 31 und 26 äquivalent sind, also den gleichen Wert haben.
Die rationalen Zahlen können natürlich auf der Zahlengerade dargestellt werden,
es stellt sich allerdings bei genauerer Betrachtung die Frage, ob auch jede Zahl
des Zahlenstrahles einer bestimmten rationalen Zahl entspricht? Anders formuliert:
Deckt Q alle Zahlen auf dem Zahlenstrahl ab, oder bestehen Lücken zwischen zwei
rationalen Zahlen? Da der Zahlenstrahl wirklich alle Zahlen enthält, enthält er auch
zum Beispiel die Zahl, die die Bedingung x2 = 2 erfüllt. Wären jetzt keine Lücken
zwischen zwei rationalen Zahlen, so müsste diese Zahl auch in der Menge der rationalen Zahlen zu finden sein. Es gibt aber keine rationale Zahl, die die Bedingung
x2 = 2 erfüllt (Der Beweis hierzu wird in einem späteren Kapitel dieser Arbeit nachgebracht). Auf ähnliche Weise lässt sich auch zeigen, dass es ausser dieser Lücke,
noch unendlich viele weitere Lücken gibt. Diese Lücken in der Menge der rationalen
Zahlen werden irrationale Zahlen genannt und motivieren dazu noch eine „größere“
Zahlenmenge einzuführen und zwar die sogenannten reellen Zahlen. Eine Zahl die
rational oder irrational ist, heißt reelle Zahl und wird mit dem Symbol R bezeichnet.
Reelle Zahlen können addiert, subtrahiert, multipliziert oder dividiert werden und
das Ergebnis ist wiederum eine reelle Zahl (vgl. Hoffmann, 2013, S. 123-128).
Wir halten hier fest, dass folgendes gilt:
N$Z$Q$R
In dieser Arbeit haben wir bislang nur ganze Zahlen quadriert und wollen hierzu
erwähnen, dass der Begriff des „Quadrierens“ natürlich auch auf die Menge der
reellen Zahlen ausgeweitet werden kann. Es gilt auch weiterhin:
a ∗ a = a2 > 0, ∀a ∈ R
10
3
Quadratwurzeln
In diesem Kapitel beschäftigen wir uns mit dem sogenannten Wurzelziehen aus Zahlen. Für das Wurzelziehen bzw. für eine Quadratwurzel gibt es ein eigenes Zeichen
√
und zwar . Lassen wir nur Zahlen aus R+
0 zu, dann definiert das Wurzelziehen die
Umkehrung zum Quadrieren. In den folgenden Unterkapiteln wird erklärt, wie eine
(Quadrat-)Wurzel definiert ist und welche Eigenschaften eine solche besitzt.
3.1
Definition einer Quadratwurzel
+
Sei a ∈ R+
0 . Eine Quadratwurzel der Zahl a ist diejenige Zahl b ∈ R0 , deren Quadrat
die Zahl a ergibt. Symbolisch geschrieben:
√
a = b ⇔ a = b2
√
Hierzu ein Beispiel: 9 = 3, da 9 = 32
(vgl. Hoffmann, 2013, S. 129)
Hinweis: Die Zahl bzw. der Term unter der Wurzel wird als Radikand bezeichnet,
also im obigen Fall würde man sagen:
3 ist die Quadratwurzel des Radikanden 9.
ACHTUNG: Die Gleichung x2 = y, für y > 0 besitzt allgemein zwei Lösungen,
die Quadratwurzel aus einer Zahl ist jedoch immer nur die nichtnegative Lösung der
√
beiden Ergebnisse. Es gilt also immer y > 0!
Dadurch wird erreicht, dass die Quadratwurzel eindeutig definiert ist. Es gibt also
√
√
im obigen Fall zwei Lösungen x1 = y und x2 = − y, die beide die Gleichung
erfüllen.
11
3.2
Rechenregeln und Eigenschaften von Quadratwurzeln
Da wir die Quadratwurzel nun eindeutig definiert haben, lassen sich einige Rechenregeln ableiten:
√
•
a>0
∀a ∈ R+
0
•
√
x2 =| x |
∀x ∈ R
•
√
( a)2 = a
∀a ∈ R+
0
•
√
√ √
a ∗ b = a ∗ b ∀a, b ∈ R+
0
•
r
√
a
a
√ =
b
b
+
∀a ∈ R+
0 und ∀b ∈ R
Achtung: Beim Addieren und Subtrahieren können nur gleichartige Quadratwurzeln addiert bzw. subtrahiert werden.
√
√
√
√
√
Beispiel: m a − n a + 3m a + 4n a = (4m + 3n) a
(vgl. Hoffmann, 2013, S. 130)
Zweite Schreibweise für die Quadratwurzel einer Zahl: Wir kennen bislang
√
die übliche Schreibweise für eine Wurzel durch das Symbol . Es existiert allerdings
noch eine weitere interessante Schreibweise: Da x2 das Quadrat einer Zahl angibt,
1
können wir x 2 für eine Quadratwurzel einer Zahl schreiben.
Nachtrag:
√
2 ist eine irrationale Zahl.
Beweis: (indirekt)
√
Annahme:
2 ist eine rationale
√
√ Zahl.
Es gilt 2 ∈ Q ⇒ ∃r, s ∈ N : 2 = rs , wobei rs ein gekürzter Bruch ist, also r und s
teilerfremd sind.
Wir quadrieren nun beide Seiten der Gleichung und erhalten
r2
2 = 2 ⇔ 2s2 = r2
s
2
⇒ r muss eine gerade natürliche Zahl sein, da 2s2 gerade ist.
⇒ r = 2n mit n ∈ N beliebig ⇒ r ist auch gerade.
⇒ 2s2 = 4n2 ⇒ s2 = 2n2 ⇒ s ist gerade.
Also sind r und s gerade und könnten somit gekürzt werden, was aber ein Widerspruch zu unserer √
Annahme wäre, dass r und s teilerfremd sind.
Also muss gelten: 2 ∈
/Q
(vgl. Skript Prof. Lettl zu Analysis 1, S. 8)
12
Ausblick: Nach der obigen Definition der Quadratwurzel einer nichtnegativen reellen Zahl, können wir die reelle Quadratwurzel als Funktion folgendermaßen definieren:
Sei
f : [0 ; ∞ [ → [0 ; ∞ [
x 7→ y = x2
die bijektive Einschränkung der Quadratfunktion auf R+
0 . Dann heißt die Umkehrfunktion dieser Funktion f Quadratwurzelfunktion und es gilt:
√
y 7→ x = y.
(vgl. http://de.wikipedia.org/wiki/Quadratwurzel)
Abbildung 4: Der Graph der Quadratwurzelfunktion y =
13
√
x
4
Potenzen
Bislang haben wir uns in dieser Arbeit nur mit Potenzen beschäftigt, die entweder
die Zahl 2 (beim Quadrieren), oder die Zahl 21 (beim Wurzelziehen) als Exponenten
hatten. In diesem Kapitel werden wir den Begriff der Hochzahl bzw. des Exponent
auf gewisse Zahlenmengen erweitern.
4.1
Potenzen mit natürlichen Exponenten
Wir wissen bereits, dass eine Zahl a mit sich selbst multipliziert als Ergebnis a2 hat,
was man das Quadrat von a oder die zweite Potenz von a nennt. In diesem Fall
würde man a als Basis der Potenz oder als Grundzahl bezeichnen und die Zahl 2 als
Exponent oder Hochzahl der Potenz. Angelehnt an diese Definition definiert man
a ∗ a ∗ a = a3 , a ∗ a ∗ a ∗ a = a4 usw.
4.1.1
Definition von Potenzen mit natürlichen Exponenten
Sei a ∈ R ∧ n ∈ N, dann definiert man:
n
a
| ∗ a ∗ a{z∗ . . . ∗ a} = a
n−mal
Hier heißt a ∈ R die Basis und n ∈ N der Exponent der Potenz an .
Hierzu wieder ein paar Beispiele:
• 61 = 6
• −16 = −1, aber (−1)6 = 1
• 104 = 10 ∗ 10 ∗ 10 ∗ 10 = 10000
1
1
1
1
1
1 4
• 10
= 10
∗ 10
∗ 10
∗ 10
= 10000
= 0,0001
• 0,15 = 0,1 ∗ 0,1 ∗ 0,1 ∗ 0,1 ∗ 0,1 = 0,00001
• 07 = 0 bzw. allgemein: 0n = 0, ∀n ∈ N
(vgl. Hoffmann, 2013, S. 132-133)
14
4.1.2
Rechenregeln für Potenzen mit natürlichen Exponenten
Für das Rechnen mit Potenzen mit natürlichen Exponenten gelten folgende Rechengesetze:
•
am ∗ an = am+n
∀a ∈ R ∧ ∀m, n ∈ N
•
(a ∗ b)n = an ∗ bn
∀a, b ∈ R ∧ ∀n ∈ N
am
= am−n
an
a n an
= n
b
b
•
•
(am )n = amn
•
∀a ∈ R \ {0} ∧ ∀m > n ∈ N
∀a ∈ R, ∀b ∈ R \ {0} ∧ ∀n ∈ N
∀a ∈ R ∧ ∀m, n ∈ N
Achtung: Nur gleichartige Potenzen können addiert und subtrahiert werden!
Beispiel: 23 + 24 − 25 = 23 ∗ (1 + 2 − 4) = −23 = −8
(vgl. Hoffmann, 2013, S. 133)
4.2
Potenzen mit ganzzahligen Exponenten
Wenn wir auf die Rechenregeln für Potenzen mit natürlichen Exponenten zurückblicken, erkennen wir, dass die dritte Rechenregel nur für Zahlen m > n ∈ N gilt.
Damit diese Regel auch auf für Zahlen m ≤ n gültig wird, müssen Potenzen mit
ganzzahligen Exponenten definiert werden.
4.2.1
Definition von Potenzen mit ganzzahligen Exponenten
Sei a ∈ R \ {0} ∧ n ∈ N, dann definiert man:
a−n =
1
an
Spezialfall: Betrachtet man den Spezialfall n = 0, dann definiert man:
a0 = 1, ∀a ∈ R \ {0} (genauer sogar ∀a ∈ C \ {0})
(vgl. Hoffmann, 2013, S. 136-137)
ACHTUNG: Wenn man den Spezialfall genau betrachtet, erkennt man, dass die
Zahl 0 ausgenommen ist. Das liegt daran, dass die Potenz 00 in den meisten Analysislehrbüchern undefiniert gelassen wird. Allerdings werden der Potenz 00 in manchen
Fällen aus Gründen der Zweckmäßigkeit zwei verschiedene Werte zugeordnet:
• 00 = 0, da 0b = 0 ∀b ∈ R+
• 00 = 1, da a0 = 1 ∀a ∈ R \ {0}
15
4.2.2
Rechenregeln für Potenzen mit ganzzahligen Exponenten
Die weiter oben definierten Rechenregeln für Potenzen mit natürlichen Exponenten
gelten auch für Potenzen mit ganzzahligen Exponenten. Der einzige Unterschied besteht darin, dass gewisse Bedingungen auf größere Zahlenmengen ausgedehnt werden
können. Es gilt:
•
am ∗ an = am+n
∀a ∈ R \ {0} ∧ ∀m, n ∈ Z
•
(a ∗ b)n = an ∗ bn
∀a, b ∈ R \ {0} ∧ ∀n ∈ Z
•
•
•
am
= am−n
an
a n an
= n
b
b
(am )n = amn
∀a ∈ R \ {0} ∧ ∀m, n ∈ Z
∀a, b ∈ R \ {0} ∧ ∀n ∈ Z
∀a ∈ R \ {0} ∧ ∀m, n ∈ Z
ACHTUNG: Die obigen Regeln sind stets nur für alle a ∈ R \ {0} bzw. für alle
a, b ∈ R \ {0} definiert, da die Potenz 0n für negative n ∈ Z nicht definiert ist. Es
würde nämlich nach Definition gelten:
(für n ∈ N)
0−n =
1
1
=
n
0
0
Da aber eine Division durch 0 nicht zulässig ist, muss man die Zahl 0 stets für a
bzw. a, b ausschließen, um die allgemeine Richtigkeit der Rechenregeln zu bewahren.
Natürlich sind die Rechenregeln aber für entsprechende Hochzahlen auch für Potenzen der Form 0n gültig (vergleiche dies auch mit den Rechenregeln für Potenzen mit
natürlichen Exponenten).
Beispiele:
• 0,4 ∗ 10−3 + 10−3 + 1,6 ∗ 10−3 = 3 ∗ 10−3
• x−2 ∗ x−3 ∗ x4 = x−2−3+4 = x−1 =
2
• (a2 b−3 ) = a4 b−6 =
1
x
a4
b6
(vgl. Hoffmann, 2013, S. 136-137)
16
4.3
Potenzen mit rationalen Exponenten
Als letztes werden wir den Potenzbegriff noch auf Potenzen mit rationalen Exponenten ausdehnen.
4.3.1
Definition von Potenzen mit rationalen Exponenten
Sei a ∈ R+ , m ∈ Z ∧ n ∈ N, dann definiert man:
m
an =
√
n
am
Hat man als Basis die Zahl 0, so definiert man:
m
0n =
√
n
0m = 0
(vgl. Hoffmann, 2013, S. 138)
4.3.2
Rechenregeln für Potenzen mit rationalen Exponenten
Die bereits bekannten Rechenregeln für Potenzen mit natürlichen bzw. ganzzahligen
Exponenten, gelten auch für Potenzen mit rationalen Exponenten.
Beispiele:
√
√
3
2
• 9 2 = 93 = 729 = 27
√ 2
√ 2
• 3 2 = 32 ∗
2 = 9 ∗ 2 = 18
√
3
3
1
4
• a 2 ∗ a = a 2 ∗ a 2 = a 2 = a2
(vgl. Hoffmann, 2013, S. 138)
4.3.3
Existieren Wurzeln aus positiven reellen Zahlen?
Satz: Existenz von Wurzeln aus positiven reellen Zahlen
Für jedes x ∈ R+ und jedes k ∈ N existiert genau ein y ∈ R+ mit y k = x (Schreib√
1
weise: y = k x = x k ).
Beweis:
zz. : ∃!y ∈ R+ mit y k = x
1. Existenz:
√
1. Fall: x = 1 ⇒ y = 1 ist die Lösung
2. Fall: x 6= 1 (dh.: 0 < 1 < x ∨ x > 1)
Behauptung 1: ∀n ∈ N gibt es Intervalle In = [an , bn ] mit folgenden Eigenschaften:
(i) akn ≤ x ≤ bkn
(ii) | In |=
1 n−1
2
| I1 |
17
Rekursive Definition der Intervalle In :
n = 1:
falls x > 1: Setze a1 := 1, b1 := x, dh.: I1 = [1, x]
k
k
also gilt:
√ 1 = 1 ≤ x ≤ x (da 1 ≤ x; k ≥ 1)
⇒(i) √
⇒(ii)
falls 0 < x < 1: Setze a1 := x, b1 := 1, dh.: I1 = [x, 1]
k
k
also gilt:
√ x ≤x<1=1
⇒(i) √
⇒(ii)
Es sei In = [an , bn ] mit den gewünschten Eigenschaften bereits konstruiert.
Konstruktion von In+1 :
an + b n
Setze m :=
... Mittelpunkt des Intervalls und
2

an+1 bn+1


z}|{ z}|{



 [an , m] , falls x ≤ mk
√
In+1 :=
⇒ In+1 erfüllt (i)


[m , bn ] , falls x > mk



 |{z} |{z}
an+1
bn+1
für (ii): | In+1 |=

an + bn − 2an



 m − an =
2





=



2b − an − bn 


 bn − m = n

2
IV 1
= 2
∗
1 n−1
2
∗ | I1 |=
1 n
2
∗ | I1 |
b n − an
IV
= 12 ∗ | In | =
2
√
Behauptung 2: Die oben konstruierten Intervalle (In )n∈N bilden eine Intervallschachtelung.
zz. : (IS1) und (IS2) gelten
√
(IS1) In+1 ⊂ In gilt laut Konstruktion
n
1
ε
(IS2) Es sei 0 < ε ∈ R : ∃n ∈ N mit
<
2
2 | I1 |
mit diesem n gilt dann: | In |=
1 n−1
2
18
∗ | I1 |< ε
√
Behauptung 3: Die Intervalle Jn = akn , bkn bilden eine Intervallschachtelung
(Jn )n∈N .
(IS1) Aus In+1 ⊂ In , dh.: 0 ≤ an ≤ an+1 ≤ bn+1 ≤ bn folgt:
√
0 ≤ akn ≤ akn+1 ≤ bkn+1 ≤ bkn also Jn+1 ⊂ Jn
(IS2) Abschätzung der Länge von Jn : Es sei ε > 0 gegeben:
| Jn |= bkn − akn
bin. F ormel
=
k−2
k−2
k−1
(bn − an ) ∗ bk−1
+
b
a
+
.
.
.
+
b
a
+
a
≤
n
n
n
n
n
n
≤ (bn − an ) ∗ bk−1
+ . . . + bk−1
= (bn − an ) ∗ k ∗ bk−1
1
1
1
0
Es sei nun ε > 0 gegeben. Setze ε :=
ε
k ∗ bk−1
1
0
(IS2) gilt für (In )n∈N : ∃n ∈ N mit | In |< ε
0
Für dieses n gilt: | Jn | ≤ | In | ∗k ∗ b1k−1 < ε ∗ k ∗ bk−1
=ε
1
⇒ (IS2) gilt für (Jn )n∈N ⇒ Behauptung 3
√
Es sei nun y ∈ R mit y ∈ In ∀n ∈ N (Vollständigkeitsaxiom)
Behauptung 4: Es gilt: y k = x und y > 0
Wir zeigen: ∀n ∈ N gilt: x ∈ Jn und y k ∈ Jn (damit erhalten wir: x = y k )
Durch Konstruktion von (In )n∈N und (i) gilt: x ∈ Jn
und es gilt: ∀n ∈ N : y ∈ In ⇒ y k ∈ Jn
19
√
√
2. Eindeutigkeit: (der Lösung y)
0
0
Sei y ∈ R+ und y 6= y, dann gilt:

=x
z}|{

0
0 k 


0 < y < y ⇒ yk < y

√
⇒ Eindeutigkeit

0
0 k

0 < y < y ⇒ y < yk 

|{z} 
=x
(vgl. Skript Prof. Lettl zu Analysis 1, S. 9)
20
5
Literaturverzeichnis
Crilly, T. (2009). 50 Schlüsselideen Mathematik. Heidelberg: Springer Spektrum.
Hoffmann, M. (2013). Mathematik. Formeln, Regeln und Merksätze(3. Auflage).
München: Compact Verlag.
Lettl, G. (2013). Skriptum zur Analysis 1. Universität Graz. Institut für Mathematik und wissenschaftliches Rechnen.
Scheid, H. & Schwarz, W. (2008). Elemente der Arithmetik und Algebra(5. Auflage). Heidelberg: Springer Spektrum.
Taschner, R. (2013). Die Zahl die aus der Kälte kam. Wenn Mathematik zum Abenteuer wird. München: Carl Hanser Verlag.
5.1
Elektronische Quellen
„Quadratwurzel“(2014). Wikipedia. [Online]. http://de.wikipedia.org/wiki/Quadratwurzel
[Zugriff am: 26.12.2014].
„Quadratzahl“(2014). Wikipedia. [Online]. http://de.wikipedia.org/wiki/Quadratzahl
[Zugriff am: 23.12.2014].
6
6.1
Abbildungs- und Tabellenverzeichnis
Abbildungen
Abbildung 1: aus Crilly, T. (2009). 50 Schlüsselideen Mathematik. S. 16. Heidelberg:
Springer Spektrum.
Abbildung 2: aus Crilly, T. (2009). 50 Schlüsselideen Mathematik. S. 16. Heidelberg: Springer Spektrum.
Abbildung 3: aus Crilly, T. (2009). 50 Schlüsselideen Mathematik. S. 17. Heidelberg: Springer Spektrum.
Abbildung 4: aus http://de.wikipedia.org/wiki/Quadratwurzel [Zugriff am: 26.12.2014].
6.2
Tabellen
Tabelle 1: aus aus Crilly, T. (2009). 50 Schlüsselideen Mathematik. S. 17. Heidelberg:
Springer Spektrum.
21