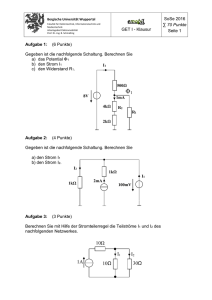
Übungsaufgaben Halbleiterschaltungstechnik

Übungsaufgaben HLST
SS 2010
Übungsaufgaben Halbleiterschaltungstechnik
Aufgabenkatalog:
www.ime.jku.at => Downloads => Downloads Halbleiterschaltungstechnik
Übungsmodus:
• Anwesenheitspflicht
• Gemeinsames Lösen ausgewählter Übungsaufgaben
• 2 Übungstests:
o Ende November/Anfang Dezember und Ende Jänner
o 3 gleichwertige Aufgaben je Test
o 100 Punkte je Test
o Minimum: 100 Punkte gesamt
• Vorlesungsklausur:
o Februar
o Theorieteil und Rechenteil (analog zu Übungstests)
o Mündliche Abschlussprüfung nach bestandener schriftlicher Klausur
_________
Institut für Mikroelektronik
1
Johannes Kepler Universität Linz
Ersatzspannungsquelle, Ersatzstromquelle
(siehe auch Praktikum GLE, Kapitel 3.1)
Jedes lineare Netzwerk kann bezüglich seiner elektrischen Eigenschaften (Zusammenhang Spannung U Strom I) in einem Zweig bzw. zwischen 2 Klemmen durch eine Ersatzschaltung ersetzt werden, die aus
• einer idealen Spannungsquelle + Serienwiderstand
• oder: einer idealen Stromquelle + Parallelleitwert besteht.
Ein lineares Netzwerk besteht aus den Elementen R, L, C sowie idealen Konstantstrom- und/oder
Spannungsquellen.
I
Ri
U0
U
I
Ersatzspannungquelle mit Ri
lineares
Netzwerk
U
I
I0
Äquivalentes
elektrisches
Klemmenverhalten
Gi
U
Ersatzstromquelle mit Gi
Bestimmung der Ersatzquellen-Parameter:
• U0 ist gleich der Leerlaufspannung ULL zwischen jenen Klemmen, bzgl. denen die Ersatzquelle bestimmt
werden soll, zu setzen bzw. I0 gleich dem Kurzschlußstrom IKS:
unbekanntes
Netzwerk
unbekanntes
Netzwerk
ULL
IKS
Achtung: Die direkte Bestimmung des Kurzschlußstroms sollte in der Praxis vermieden werden, da ein
Kurzschließen der Klemmen meist zur Überlastung des Netzwerks führt!
1
• Der Innenwiderstand Ri =
wird gleich dem Widerstand (Impedanz) zwischen den Klemmen gesetzt.
Gi
Dazu werden bei bekannter Innenschaltung des Netzwerks alle Spannungsquellen durch Kurzschlüsse
(Uj = 0) und alle Stromquellen durch Leerläufe (Ij = 0) ersetzt.
Achtung: Ri bezeichnet eine reine Rechengröße für das Ersatzmodell und keinen physikalisch
vorhandenen Widerstand!
Beispiel: Der strichliert eingerahmte Schaltungsteil soll durch eine Ersatzquelle ersetzt werden
Bestimmung einer Ersatzspannungsquelle:
R2
R1 + R2
RR
• Ri: Spannungsquelle durch KS ersetzen ⇒ Ri = 1 2
R1 + R2
• Leerlaufspannung: ohne ZL (Ia=0) ⇒ U LL = U B
R1
Ia
UB
R2
Ua
ZL
p
Bestimmung einer Ersatzstromquelle:
Ia
• Kurzschlußstrom: Klemmen kurzgeschlossen, Ua=0 ⇒ I KS =
• Gi =
1
Ri
UB
R1
U0 =ULL
Ri
Ua
ZL
Ia
Ersatzspannungquelle
I0 =IKS
Gi
Ersatzstromquelle
Ua
ZL
Beide Ersatzquellen bewirken in ZL den
gleichen Laststrom wie im „Originalnetzwerk“!
Superpositionsgesetz für lineare Netzwerke (Helmholtz)
Enthält ein lineares Netzwerk (⇒ NWteil ohne z.B. Dioden!) mehrere Quellen, so kann der Strom bzw. die
Spannung in einem Zweig durch Superponieren der Wirkungen der einzelnen Quellen bestimmt werden.
D.h.: Es wird jeweils nur eine Quelle betrachtet, alle anderen werden entfernt (⇒ Spannungsquelle: U=0
(KS), Stromquelle: I=0 (Leerlauf) ). Nun wird der Strom oder die Spannung im Zweig bestimmt. Dies wird
für alle Quellen durchgeführt und abschließend werden die Einzelwirkungen überlagert.
Beispiel 1) Gegeben:
Ia
500Ω
U0=10V
1kΩ
1kΩ
Gesucht: Ua
Ua
I0=10mA
a) Bestimmung von Ua1, dem Anteil aufgrund der Spannungsquelle U0:
Ia
500Ω
U0
1kΩ
1kΩ
⇒ U a1 = U 0
Ua1
1kΩ 1kΩ
500Ω + 1kΩ 1kΩ
=
U0
= 5V
2
b) Bestimmung von Ua2, dem Anteil aufgrund der Stromquelle I0:
Ia
500Ω
1kΩ
1kΩ
⇒ U a 2 = I 0 (500Ω 1kΩ 1kΩ ) = I 0 250Ω = 2.5 V
Ua2
I0=10mA
c) Superponieren der Einzelwirkungen:
U a = U a1 + U a 2 = 7.5 V
Achtung: Beim Betrachten der Einzelwirkungen können Leerläufe und Kurzschlüsse auftreten.
Ia
I0
Ia
Ua
U0
U0
Ia
I0
U0
Ua
Die Spgs.-quelle liefert keinen Beitrag zu Ua
! (Die ideale Stromquelle hält I0 aufrecht)
Ua
Die Stromquelle liefert keinen Beitrag zu Ua !
(Die ideale Spannungsquelle hält U0 aufrecht)
Ia
Ua
I0
Beispiel 2)
Gegeben: U1 = 10V, U2 = 2V
I1 = 0.5mA
R1 = 2kΩ, R2 = 100Ω
R3 = 10kΩ, RL = 2kΩ
I1
I2
U1
R3
R2
U2
R1
Ua
RL
Gesucht:
Ua , I2
Lösungswege:
a) Bestimmung von Ua und I2 mittels Superposition der Wirkungen der 3 Einzelquellen (U1, U2, I1).
Lsg: Ua = 0.09V + 1.802V + 0V = 1.892V, I2 = -0.9mA + 1.982mA - 0.5mA = 0.582mA
b)
Bestimmung einer Ersatzspannungsquelle für den Schaltungsteil linksseitig der gegebenen Klemmenanschlüsse, indem ULL (für das Netzwerk ohne RL) und Ri (für U1=U2=0 (KS),I1=0 (LL)) bestimmt wird.
Lsg: U0 = 0.0943V + 1.887V + 0V = 1.9813V (mittels Superposition bestimmt), Ri = R1||R2||R3 = 94.34Ω
Mit dieser Ersatzquelle lässt sich Ua einfach berechnen:
Ua = U0
RL
= 1.892 V
RL + Ri
c) Bestimmung einer Ersatzstromquelle Lsg: I0 = 1mA + 20mA+0mA = 21mA (mittels Superposition bestimmt).
Übungsaufgaben HLST
SS 2010
Aufgabe 3: Grafische Netzwerkanalyse von nichtlinearen Strom- und Spannungsteilern
Gegeben seien die folgenden 4 Schaltungen. Überlegen Sie sich, wie mit Hilfe der StromSpannungs-Kennlinien der Bauteile die Teilspannungen (in a) bzw. Teilströme (in b)
bestimmt werden können.
R1
R
Ug
Ug
R2
a)
Ig
R1
R2
Ig
R
b)
_________
Institut für Mikroelektronik
4
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
Aufgabe 6: Spannungsstabilisierung mit Zenerdioden
Zener-Dioden sind Dioden mit definiertem Durchbruchverhalten in Sperrrichtung
vergleichsweise niederohmig. Sie können aufgrund des steilen Kennlinienverlaufes im
Durchbruch zur Spannungsstabilisierung verwendet werden. Die folgende Schaltung zeigt
eine dafür geeignete Schaltung bestehend aus einer Zenerdiode, einem Vorwiderstand und
einer variablen Last.
Die Schaltung soll für die folgenden Spezifikationen ausgelegt werden:
• Eingangsspannung schwankt zwischen den Werten
U min = 10 V und
U max = 15 V
• Z-Diode:
Zenerspannung U Z , Nenn = 8,2 V ,
maximale Verlustleistung PV ,max = 0,2 W
minimaler Strom durch die Zener-Diode I Z ,min = 1 mA
• Last:
minimale Belastung I L ,min = 0 (Leerlauf)
maximale Belastung I L ,max = 4 mA
Für a) und b) wird im Folgenden angenommen, dass Uz ≈ Uz.Nenn (warum ist diese Annahme
gerechtfertigt?)
a)
Berechnen Sie anhand der vorgegebene Daten der Zener-Diode den maximal erlaubten
Strom I Z ,max . Warum sollte auch der minimale Strom I Z ,min nicht unterschritten
werden?
b)
Da der Strom durch die Zener-Diode in dem Bereich zwischen I Z ,min und
I Z ,max liegen sollte, ergibt sich auch ein minimaler und ein maximaler Vorwiderstand.
Berechnen Sie diesen Widerstandsbereich und wählen Sie einen geeigneten
Vorwiderstand R aus der E24-Normreihe aus.
1.0 / 1.1 / 1.2 / 1.3 / 1.5 / 1.6 / 1.8 / 2.0 / 2.2 / 2.4 / 2.7 / 3.0 / 3.3 / 3.6 / 3.9 / 4.3 / 4.7 /
5.1 / 5.6 / 6.2 / 6.8 / 7.5 / 8.2 / 9.1
Die Zener-Diode kann etwas genauer durch ein Ersatzschaltbild modelliert werden (gilt
solange die Spannung an der Z-Diode > Uz,Nenn ist! Gilt nicht für Dioden in
Vorwärtsrichtung!)
_________
Institut für Mikroelektronik
7
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
Ersatzschaltung
c)
Ein Maß für die Güte der Stabilisierungsschaltung ist der Stabilisierungsfaktor S ,
welcher das Verhältnis der relativen Spannungsänderung am Eingang der Schaltung zur
relativen Spannungsänderung am Ausgang der Schaltung angibt. Berechnen Sie mit
Hilfe der Kleinsignalersatzschaltung der Zener-Diode die Aussgangsspannungsschwankung ∆Ua sowie den Stabilisierungsfaktor für Leerlauf und Volllast (berechnen
Sie dazu RL unter der Annahme Ua ≈ Uz,Nenn).
d)
Berechnen Sie mit Hilfe der Großsignalersatzschaltung eine Beziehung, die die
Ausgangsspannung in Abhängigkeit der Eingangsspannung angibt. Verwenden Sie dazu
den Überlagerungssatz.
_________
Institut für Mikroelektronik
8
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
Aufgabe 7: Kleinsignal-Abschwächer
Die gegebene Schaltung kann dazu verwendet werden um kleine Wechselspannungen zu
dämpfen, wobei der Dämpfungsgrad mit dem Potentiometer RV variiert werden kann.
a) Zeichnen Sie das Gleichstromersatzschaltbild und zeigen Sie die Funktion des
Abschwächers grafisch. Zeichnen Sie 2 Potistellungen ein und kennzeichnen Sie die stärkere
Abschwächung. Geben Sie den Diodenstrom unter der Annahme, dass UD in der GleichstromAnalyse konstant mit 0.6V angenommen werden kann, an.
b) Geben Sie den differenziellen Widerstand der Diode D in Abhängigkeit vom
Diodenstrom ID an.
c) Zeichnen Sie das (linearisierte) Kleinsignalersatzschaltbild des Abschwächers.
Die Kondensatoren können für die Wechselstrombetrachtung durch Kurzschlüsse ersetzt
werden, da die Werte für C sehr groß seien.
d) Das Verhältnis von u a / ue = k ist mit dem Potentiometer RV einstellbar. Geben Sie aus
dem Kleinsignalersatzschaltbild eine Beziehung für den dazu nötigen differenziellen
Diodenwiderstand rD sowie für den zugehörigen Diodenstrom ID an.
e) Berechnen Sie (aus a) und d)) die Widerstandswerte RV,max und RV,min um eine
Abschwächung im Bereich k = 1/3..1/100 zu erreichen.
f) Berechnen Sie ID,min und ID,max.
Hinweise:
zu a) Alle transienten Vorgänge sind angeklungen!
zu c) Benutzen Sie als Diodengleichung I D ≅ I S ⋅ e
UD
m⋅U T
mit m = 2 und UT=25mV.
_________
Institut für Mikroelektronik
9
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
Aufgabe 8: Bipolartransistor
a)
Skizzieren Sie den Aufbau eines npn sowie pnp-Bipolartransistors.
b)
Erläutern Sie anhand der Skizzen dessen Funktionsweise. Warum kommt es zur
Stromverstärkung?
c)
Skizzieren Sie eine Eingangskennlinie, Übertragungskennlinie und ein
Ausgangskennlinienfeld und geben Sie gegebenenfalls Gleichungen an, die diese
Verläufe beschreiben.
d)
Zeichnen Sie das 4-Quadrantenkennlinienfeld eines Transistors. Beschreiben Sie die
Methode mit der Sie das Kennlinienfeld aufnehmen würden.
e)
Geben Sie das Kleinsignal-Ersatzschaltbild des Transistors an, und bestimmen Sie den
Ersatzwiderstand der Basis-Emitterstrecke.
Aufgabe 9: Arbeitspunkteinstellung eines Bipolartransistors mittels Basisspannungsquelle
a)
Was versteht man unter einer Arbeitspunkteinstellung eines Transistors und warum ist
diese überhaupt nötig?
b)
Der Kollektorstrom im Arbeitspunkt kann durch einprägen eines Basisstroms bzw.
durch anlegen einer Basis-Emitterspannung vorgegeben werden. Beschreiben Sie die
Vor- und Nachteile der beiden Methoden hinsichtlich Temperaturstabilität und
Bauteilstreuungen.
_________
Institut für Mikroelektronik
10
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
Aufgabe 10: Arbeitspunkteinstellung eines Bipolartransistors mittels Basisstromeinstellung
Gegeben ist untenstehende Schaltung mit einer Versorgungsspannung U B = 15 V . Es soll mit
Hilfe des Widerstandes R1 ein Basisstrom I B = 10 μA eingestellt werden.
UB
UB
R1
RC
C >>
C >>
ua
ue
U BE
a)
Welcher Art der Arbeitspunkteinstellungen aus Aufgabe 9) entspricht diese Schaltung
am ehesten?
b)
Dimensionieren Sie den Widerstandswert R1 . Nehmen Sie dazu
U BE ≈ 0,7 V an.
c)
Angenommen U BE betrage 0,6 V . Berechnen Sie die relative Spannungsänderung von
UBE sowie die relative Stromänderung von IC. Interpretieren Sie das Resultat!
Aufgabe 11: Arbeitspunkteinstellung eines Bipolartransistors mittels Basisspannungsteiler
UB
UB
RC
R1
C >>
C >>
ue
IB
ua
I2
U
R2 BE
_________
Institut für Mikroelektronik
11
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
a)
Durch Einfügen eines Widerstandes R2 wird verhindert, dass sich der Arbeitspunkt
des Transistors bei schwankendem I B ändert. Dazu wird I 2 = 10 ⋅ I B gewählt.
Berechnen Sie unter Annahme von U BE = 0,7 V und U B = 15 V die Widerstände R1
und R2 , damit ein Basisstrom von I B = 10 μA fließt.
b)
Welche Nachteile bleiben dennoch bestehen?
Aufgabe 12: Arbeitspunkteinstellung eines Bipolartransistors mittels Stromgegenkopplung
UB
UB
RC
R1
C >>
ue
C >>
IC
IB
I2
U BE
R2
RE
ua
U RE
a)
Erläutern anhand der obigen Schaltung die Wirkungsweise der Stromgegenkopplung.
b)
Welchen Einfluss hat die Stromgegenkopplung auf die Spannungsverstärkung?
Was kann man dagegen tun?
c)
Stellen Sie mit Hilfe der Widerstände den folgenden Arbeitspunkt ein:
I C = 10 mA , B = 100 , U BE ≈ 0,7 V . Weiterhin soll gelten: U RE = 1 V , U B = 15 V .
d)
Berechnen Sie die exakten Werte für U BE und I B durch Iteration.
⎡ ⎛U
Hinweis: Für den Transistor gilt die folgende Beziehung: I C = I 0 ⎢exp⎜⎜ BE
⎣ ⎝ UT
−14
I 0 = 10 A und der Temperaturspannung U T = 25 mV .
⎞ ⎤
⎟⎟ − 1⎥ mit
⎠ ⎦
_________
Institut für Mikroelektronik
12
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
Aufgabe 13: Kleinsignalersatzschaltbild
Berechnen Sie unter Verwendung des Kleinsignalersatzschaltbildes eines npnBipolartransistors
B
C
B
S
=ˆ
B
B⋅iB
S ⋅u BE
u BE
C
B
iB
=ˆ
iB
C
1 B
S B +1
u BE
E
E
B⋅iB
S ⋅u BE
E
a)
die Temperaturabhängigkeit von IC; Berücksichtigen Sie dazu Schwankung von UBE
zufolge Temperaturänderungen mit ΔU BE ,T = u BE ,T ≈ −2mV / K ⋅ ΔT
b)
Eingangswiderstand re =
c)
d)
Ausgangswiderstand ra =
ue
ie
ia = 0
ua
ia
ue = 0
Leerlaufspannungsverstärkung A =
ua
ue
ia = 0
der folgenden beiden Schaltungen:
UB
UB
UB
R1
RC
UB
R1
RC
ia
ia
ue
ie
u BE
ua
ue
ie
u BE
R2
ua
RE
_________
Institut für Mikroelektronik
13
Johannes Kepler Universität Linz
Übungsbeispiele 1. Test
R5
I
1.) Gegeben ist eine Brückenschaltung mit Dioden
als nichtlinearen Elementen.
A
R1
D1
D2
Id
R4
I
R2
R1 = R2 = R3 = R4 = R5 = 2 Ω
U = 0,6 V
I = 0,8 A
D1 = D2 = D3 mit
Is = 50 nA, Ut = 25 mV, m = 2
Ud
B
R3
Diodenkennlinie
⎛ Ud
⎞
I d = I S ⋅ ⎜ e m ⋅U t − 1⎟
⎜
⎟
⎝
⎠
D3
U
Gesucht:
Diodenkennlinie
a) Vereinfachen Sie die Schaltung
mit Hilfe der Theorie der
Ersatzspannungs- oder -stromquelle bezüglich der Klemmen A
und B (ohne Diode D1)
b) Bestimmen Sie die Diodenspannung Ud und den Diodenstrom Id der Diode D1 graphisch
unter Verwendung der Diodenkennlinie.
c) Berechnen Sie Ud und Id der
Diode D1 durch Iteration (3
Iterationschritte). Geben Sie in
jedem Schritt Ud und Id an und
rechnen Sie immer mit den
exakten Werten im
Taschenrechner weiter.
d) Berechnen Sie den
Ausgangswiderstand ra der
Schaltung zwischen den beiden
Klemmen A und B (inklusive
Dioden).
Hinweis:
1.6
1.5
1.4
1.3
1.2
1.1
1.0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2
Diodenspannung V
Beachten Sie die Eigenschaften von Strom- und Spannungsquellen,
und welche Elemente Einfluß auf die Rechnung haben.
Lösung:
a) Ersatzspannungsquelle: U 0 = 2,2V Ri = 2 Ω I k = 1,1A
b) Konstruktion der Lastgerade mit Hilfspunkten (z.B: I (Ud =1V ) = 0.6A )
c) AP mit Iteration: Ud = 0,82194 V, Id = 0,68903 A
d) Mittels Näherungsformel: rd = 72,57 mΩ , somit ra = Ri || rd = 70,02mΩ
2.) Gegeben ist folgende Emitterschaltung mit Stromgegenkopplung
+Ub
R2
Ri
RC
C
C
UCE
≈
Ue
ug
ua
R1
RL
RE
Gegeben:
R1=1,8 kΩ
R2= 5,1 kΩ
RE= 120 Ω
RC= 270 Ω
Ri= 470 Ω
RL = 2,2 kΩ
CÆ∞
uG= 1 V
UCE ≥ 1 V
Ub= 12 V
UBE,0=0,7 V (für Arbeitspunktbestimmung)
B = β = 100, UT=25mV
Gesucht:
a) Bestimmen Sie den Arbeitspunkt (IC,0, UCE,0, UC,0, Ua,0) der Schaltung, wobei der
Basisstrom in der Rechnung zu berücksichtigen ist.
b) Bestimmen Sie für RL=∞ die Aussteuergrenzen am Ausgang und berechnen Sie
daraus die maximal mögliche Wechselamplitude ûa für symmetrische Aussteuerung
um den Arbeitspunkt (Beachten Sie dabei den Emitterwiderstand).
c) Zeichnen Sie das vollständige Kleinsignalersatzschaltbild der gesamten Schaltung
(inklusive Earlyleitwert gce).
d) Bestimmen Sie mit Hilfe der Schaltung in Punkt c) den Eingangswiderstand re und
den Ausgangswiderstand ra des Transistorverstärkers (ohne Generator, ohne Last und
ohne Earlyleitwert).
e) Bestimmen Sie die Betriebsverstärkung AB=ua/ug und daraus Û a .
Lösung:
a) Mithilfe der Netzwerkgleichungen (R1, R2, UBE,0, RE) ergibt sich: I B , 0 = 180,7 µ A ;
I C ,0 = 18,07mA ; U C , 0 = 7,12V ; U CE ,0 = 4,93V ; U a ,0 = 0V (über C entkoppelt)
b) U a , symmetrisch = min{4,88V ; 2,712V } = 2,712V
c) KS-ESB
d) re = R1 R2
B
S red
= 1,2 kΩ ; ra = 270 Ω
e) A = − S red RC = −2,203 ; AB = −1,41 ; Uˆ a = AB u G = 1,41V
Bsp 1: Diode
33Ω
Für die Dioden gelte
UD
⎛ mU
⎞
I D = I S ⎜ e T − 1⎟
mit IS = 0.01pA, m = 1.2, UT = 25mV.
⎜
⎟
⎝
⎠
Bestimmen Sie die Spannungen U1 und U2 für die Fälle
a) I0 = +100 mA
Hinweis: Zwecks einfacher Rechnung
b) I0 = -100 mA.
sollen die Ströme von in Sperrrichtung
U1
I0
U2 Lösung:
a) U1 = 3.3V, U2 = 0.877V
b) U1 = -3.3V, U2 = -1.796V.
gepolten Dioden vernachlässigt werden.
Bsp 2: Diode
Bestimmen Sie den differentiellen Widerstand bezüglich der eingezeichneten
Klemmen für die Fälle
a) U0>0
b) U0<0.
R
D1
U0
D2
Lösung:
a) rdiff=rD1
b) rdiff=R+rD2.
Begründung:
Für eine in Sperrichtung gepolte Diode gilt rdiff → ∞ .
Bsp 3: Zenerdiode
D1:
IZ
S1
10mA
0.8V
3V
20Ω
Ua
200Ω
D1
IZ
UR
Bestimmen Sie Ua und IZ für die
Fälle
a) S1=offen,
b) S1=geschlossen.
Lösung:
a) Ua = 3.2V, IZ = 10mA
b) Ua = 2V, IZ = 0mA
Hinweis: Diese Zenerdiodenkennlinie
gilt auch für das folgende Beispiel!
Bsp 4: Zenerdiode
12Ω
Bestimmen Sie UL sowie PD1 und PD2 für die Fälle
a) U0=+5V
b) U0=-4V.
100Ω
D1
U0
D2
UL
Lösung:
a) UL = +3.8V, PD1= 49.6mW, PD2= 186mW
b) UL = -3.57V, PD1= 0mW, PD2= 0mW
Emitterschaltung mit Stromgegenkopplung und endlichem CE:
U0
U0
UBE = 0,6 V; U0 = 12 V; β = 500;
UT = 25 mV
Vernachlässigungen:
1. B +1 ≈ B
2. I quer >> I B
27K
Ue
Ua
3K3
470
CE
Gesucht: AP, |A(ω)|, |re(ω)|
Arbeitspunkt:
3300
3300
U e0 =
U0 =
⋅ 12 = 1,307 V
3300 + 27000
30300
U − U BE 1,307 − 0,6
=
= 1,504 mA
I C 0 ≈ I E 0 = e0
470
470
I B0 =
I C0
β
=
1,504 ⋅ 10 −3
= 3,008 µA
500
Querstrom im Spannungsteiler:
U0
12
=
= 396 µA → die 3 µA Basisstrom sind vernachlässigbar
Iq =
27000 + 3300 30300
I
1,504 ⋅ 10 −3
U a0 = U 0 − 2700 I C0 = 12 − 2700 ⋅ 1,504 ⋅ 10 −3 = 7,939 V
S = C0 =
= 60,164 mS
25 ⋅ 10 −3
UT
Kleinsignalersatzschaltbild:
ie
iB
iC
Ersatzschaltbild für re:
ia
B
S
ue
R1
R2
RE
Z E = RE
B
S
iE
RC
27K
ua
3K3
B RE
CE
RE
1
jω C E
RE
=
=
1
jωC E R +
1 + jωRE C E
E
j ωC E
⇒
B ZC,E
⎛B
⎞
re = 27 K 3K 3 ⎜ + B Z E ⎟
⎝S
⎠
Verstärkung:
u
− RC S
− RC S ⋅ (1 + jωRE C E )
− RC S
A(ω ) = a = − RC S red =
=
=
=
S
RE
ue
1
SR
j
ω
R
C
+
+
E
E
E
1+ SZ E +
ZE
1+ S
B23
1 + jωRE C E
1
<< S Z E →
vernachlässigt
1
1
1 + jωRE C E
. Da (= 16,62 Ω ) << RE (= 470 Ω ) gilt vereinfacht RE + ≈ RE
1
R
S
S
+ jωC E E + RE
S
S
678
RC 1 + jω R E C E
1 + jωR E C E
und somit: A(ω ) ≈ − RC
=−
⋅
C
RE
RE
+ RE
1 + jω E
jω C E
S
S
{
= − RC
Kleinsignalparameter der Kollektorschaltung
Ubat
Die Kollektorschaltung heißt auch
Emitterfolger, da die Ausgangsspannung um UBE verschoben der
Eingangsspannung folgt.
iB
→
Im Folgenden gilt B +1 ≈ B
für den Fall, dass B >> 1 .
≈
RE
UG
B
S
RG
RG
iC = B iB
RE
uG
Kleinsignalersatzschaltbild
Differentieller Eingangswiderstand re:
Der Spannungsabfall an RE ist RE i E = RE (B + 1)i B ≈ BRE i B ,
d.h. lässt man iC weg und rinnt daher nur iB durch RE, so muss der
Widerstand um die Stromverstärkung erhöht werden, um den gleichen
Spannungsabfall zu erhalten ⇒ nebenstehendes Ersatzschaltbild ohne iC
NUR für die Berechnung von re:
iB
B
S
re
( B + 1) R E
Durch Transformation der ausgangsseitigen Impedanzen mit B + 1 ≈ B
B
B
lässt sich re so leicht berechnen: re = + (B + 1) RE ≈ + BRE
S
S
≈ BR E
ACHTUNG: Diese Transformation ist nicht erlaubt, wenn der Earlyleitwert gCE = 1/rCE
berücksichtigt werden muss!
Differentieller Ausgangswiderstand ra mit Berücksichtigung der Eingangsbeschaltung (RG):
Definition: ra =
ua
ia
Maschen an Ein- und Ausgang:
B⎞
⎛
(1) i B ⎜ RG + ⎟ + u a = 0 ⇒
S⎠
⎝
uG =0
iB
iC = B iB
(2)
RG
B
S
ra =
ia
ue
≈
RE
uG
ua
u a = (i B + iC + ia ) RE
ua
ua
RE
+ ( B + 1)
ua
RG + BS
=
1
RE
⇒
iB = −
ia =
nebenstehendes Ersatzschaltbild ohne iB und ohne iC NUR
für die Berechnung von ra:
+ ( B + 1) iB RE
ua = ( B + 1) iB RE
HLST_Emitterfolger.doc, 31.03.2005, Di
⎫⎪
⎬ ⇒
⎪⎭
A=
ua
− ( B + 1)i B
RE
1
+ B +1B
RG + S
B
S
RG
R
≈ G
B +1 B
B +1
ua
=
ue
≈
RE
Kleinsignal-Leerlaufspannungsverstärkung:
Bi
S B
B
S
B ⎞
⎛ RG
1⎞
⎛R
⎜
ra = RE ||
+ S ⎟ ≈ RE || ⎜ G + ⎟
⎜ B + 1 B + 1⎟
⎝ B S⎠
⎠
⎝
d.h. durch Transformation der eingangsseitigen
Impedanzen mit B1+1 ≈ B1 lässt sich ra leicht berechnen ⇒
ue =
ua
RG +
( B + 1) RE
1
1
=
≈
B + ( B + 1) R
1 + ( B +1B) SR
1 + SR1
E
S
E
E
1
S
ra
Übungsaufgaben HLST
SS 2010
Aufgabe 20: Basisschaltung
Zeichnen Sie das Kleinsignalersatzschaltbild und bestimmen Sie
• die Spannungsverstärkung.
• den Eingangswiderstand.
• den Ausgangswiderstand.
Aufgabe 21: Arbeitspunkteinstellung eines zweistufigen Verstärkers
Gegeben ist folgende Verstärkerstufe mit den Arbeitspunkten U B = 20 V , U B1 = 15 V ,
U C 2 = 12 V , I C1 = 10 mA , U BE1 = U BE 2 = 0,6 V . Für die Stromverstärkung beider
Transistoren gelte B1 = B2 = 200 . Der Widerstand R4 habe einen Wert von 400 Ω . Die
Zenerspannung der Zenerdiode beträgt U Z = 6,4 V .
UB
UB
R1
UB
R4
IC1
T1
Ue
UB1
T2
R2
UC2
Ua
R3
a)
Berechnen Sie den Kollektorstrom des zweiten Transistors.
b)
Berechnen Sie zur Einstellung der gegebenen Werte die 3 Widerstände R1 bis R3 .
c)
Ermitteln Sie die Kollektor-Emitter-Spannungen beider Transistoren.
_________
Institut für Mikroelektronik
20
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
Aufgabe 22: Zweistufiger Transistorverstärker
Gegeben sei die oben abgebildete Verstärkerschaltung mit den folgenden Bauteilwerten.
U 0 = 12 V
R1 = 1 MΩ , R2 = 700 Ω , R3 = 2,7 kΩ , R4 = 1,2 kΩ
U BE1 = U BE 2 = 0,6 V , B1 = 200 , B2 = 100
B +1 ≈ B
a)
In welchen Grundschaltungen werden die Transistoren T1 und T2 betrieben?
b)
Bestimmen die Kollektorströme I C1 und I C 2 .
c)
Ermitteln Sie anhand des Kleinsignalersatzschaltbildes des Verstärkers
• den Eingangswiderstand
• den Ausgangswiderstand
• die Leerlaufspannungsverstärkung.
Aufgabe 23: Temperaturkompensierte Spannungsquelle
Gegeben ist die untenstehende Spannungsquelle. Der Arbeitspunkt des Transistors ist durch
die Dioden temperaturkompensiert.
a)
Erläutern Sie kurz die Wirkungsweise dieser Temperaturkompensation.
b)
Berechnen Sie unter Vernachlässigung des Basisstromes und unter der Annahme
R2
U F = U BE das Verhältnis X =
, so dass der Arbeitspunkt des Transistors
R1 + R2
möglichst gut temperaturstabilisiert ist.
c)
d)
Berechnen Sie allgemein die Ausgangsspannung U a .
Wie kann die Schaltung verändert werden, um eine optimale Temperaturkompensation
_________
Institut für Mikroelektronik
21
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
zu erreichen?
Aufgabe 24: Stromspiegel
Gegeben ist die temperaturkompensierte Stromquelle, die mit U CC = 10 V versorgt wird.
a)
Warum werden Stromspiegel oft nur als integrierte Schaltung hergestellt?
b)
Zeigen Sie, dass I L ≈ I 1 gilt.
c)
Bestimmen Sie den Widerstand R1 , so dass die Stromquelle 1 mA liefert ( U BE ≈ 0,7 V )
d)
Wie groß darf der Lastwiderstand maximal gewählt werden, damit der von der
Stromquelle gelieferte Strom nicht zusammenbricht?
Es sei gegeben U CE ≥ U CE , sat = 0,1 V
e)
Wie sieht der Stromspiegel mit pnp-Transistoren aus?
_________
Institut für Mikroelektronik
22
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
Aufgabe 26: Differenzverstärker mit realer Stromquelle
a) Erläutern Sie (unter Vernachlässigung von Ri) das Prinzip des abgebildeten
Differenzverstärkers.
Jede beliebige Kombination von u1 und u2 kann als Überlagerung einer Gleichtakt- und einer
Gegentaktaussteuerung betrachtet werden.
b)
Ermitteln Sie für Gegentaktaussteuerung (u1=-u2) aus dem Kleinsignalersatzschaltbild
• die Leerlaufdifferenzverstärkung Aed=ua1/(u1-u2)
• den Differenzeingangswiderstand red=(u1-u2)/iB1
ra=ua1/ia1
• den Ausgangswiderstand
sowohl für ideale wie für reale Stromquelle.
c)
Ermitteln Sie für Gleichtaktaussteuerung (u1=u2) aus dem Kleinsignalersatzschaltbild
• die Leerlaufgleichtaktverstärkung Agl=2 ua1 /(u1+u2)
• den Gleichtakteingangswiderstand rgl=(u1+u2)/(2 iB1)
sowohl für ideale wie für reale Stromquelle.
d) Bestimmen Sie die Gleichtaktunterdrückung (CMRR = Agl/Aed). Interpretieren Sie!
e) Die Stromquelle kann unter Umständen durch einen Widerstand ersetzt werden. Welche
Auswirkungen hat das auf die Funktion?
_________
Institut für Mikroelektronik
24
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
Aufgabe 28: Differenzverstärker mit Transkonduktanz-Eingangsstufe
+UB
UB = 15 V
UT ≈ 25mV
B = 300 (B+1 ≈ B)
I3 = 10 mA
RE = 50Ω
RC = 1kΩ
T3
RE
T4
≈I2
I2
≈(I1-I2)
T5
I1
≈(I1-I2)·B
T2
T1
Ue1
≈I1
≈I2
Ue2
Ua
RC
I3
-UB
Die Abbildung zeigt eine verbesserte Version des Differenzverstärkers aus Aufgabe 26. Die
Kollektor-widerstände wurden hierzu durch einen Stromspiegel ersetzt, welcher dazu beiträgt
die Leerlaufverstärkung drastisch zu erhöhen. Durch die Verwendung des Sromspiegels
besitzt die erste Stufe praktisch einen Stromausgang. Der Stromspiegel ist als ideal
anzunehmen. Die Stromquelle I3 sei ideal angenommen, weshalb Gleichtakt-auslenkungen
nicht berücksichtigt werden müssen.
a)
Bestimmen Sie die Ausgangsspannung Ua in Abhängigkeit der Ströme I1 und I2
unter der Annahme I1 > I2.
b)
Berechnen Sie die Ausgangsspannung Ua in Abhängigkeit der Differenzeingangsspannung Ued=Ue1-Ue2. Verwenden Sie hierzu die Übertragungskennlinie von T1
und T2. Bestimmen Sie weiters die Aussteuergrenzen von Ua (UCE > 0.1 V).
Bedenken Sie, dass der Transistor T5 für I2 > I1 sperrt.
c)
Berechnen Sie die Eingangsoffsetspannung Uoffs und zeichnen Sie die Spannungstransferkennlinie. Hinweis: Uoffs ist die nötige Differenzeingangsspannung damit
Ua=0V ist. Anmerkung: In der Realität tragen Produktionstoleranzen und die
Earlyleitwerte der einzelnen Transistoren wesentlich zur Offsetspannung bei.
d)
Berechnen Sie aus Punkt c) die Leerlaufdifferenzverstärkung Aed = ∂U a / ∂U ed für
Kleinsignale.
e)
Welche Verstärkung Ua/Ue1 stellt praktisch sich ein, wenn der Ausgang mit der
Basis von T2 verbunden wird? Verallgemeinern Sie hierzu den Verstärker durch
eine Ersatzschaltung. Für welchen Eingangsspannungsbereich kann der Verstärker
verwendet werden?
_________
Institut für Mikroelektronik
26
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
Aufgabe 29: Dreistufiger Transistorverstärker
Gegeben ist die untenstehende dreistufige Transistorschaltung bestehend aus einem
Differenzverstärker sowie einem Transistoren in Emitter- bzw. in Kollektorschaltung.
Zur Vereinfachung der Rechnung sollen die Transistoren als symmetrisch angenommen
werden, d. h. die npn-Transistoren haben die gleichen Kennwerte wie die pnp-Transistoren.
• Stromverstärkung B = 50
• Basis-Emitter-Spannung U BE ≈ 0,7 V
• Kollektor-Emitter-Spannung in Sättigung U CE , sat = 0,3 V
R1
R1
R2=1kΩ
IB3
IC1
IC2
+10 V
T3
IC4
IC3
T1
T2
IB4
T4
UE
UA
R3
R4
R5
–5 V
a)
Dimensionieren Sie Widerstände R1 , R3 , R4 , R5 so, damit für U E = 0 und U A = 0
durch jeden Transistor ein Kollektorstrom I C = 1 mA fließt.
Vernachlässigen Sie nicht die Basisströme.
b)
Welche Phasendifferenz ϕ besteht zwischen dem harmonischen Signalen am Eingang
und am Ausgang? (Die parasitären Kapazitäten der Transistoren sind nicht zu
berücksichtigen)
c)
Wie groß ist die Gleichtaktunterdrückung (CMRR)?
_________
Institut für Mikroelektronik
27
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
Aufgabe 30: Colpitts-Oszillator
a)
Zeichnen Sie das Kleinsignalersatzschaltbild des Oszillators und bestimmen Sie daraus
die komplexe Schwingbedingung.
b)
Bestimmen Sie die Resonanzfrequenz und berechnen Sie einen Wert für R aus
der komplexen Schwingbedingung.
c)
Berechnen Sie die den Arbeitspunkt und daraus die Steilheit des Transistors.
d)
Wie kann für eine gegebene Betriebsspannung die Schwingbedingung erfüllt werden?
_________
Institut für Mikroelektronik
28
Johannes Kepler Universität Linz
2. Beispiel: Schwingbedingung eines Oszillators
Gegeben:
Colpitts-Oszillator in Emitterschaltung
C1 = C2 Æ ∞
R3
C2
Ca
Gesucht:
L
a) Zeichnen Sie das vereinfachte
Kleinsignalersatzschaltbild.
Cb
b) Ermitteln Sie die beiden reellen
Schwingbedingungen.
Hinweise:
1.) Verwenden Sie iC=S⋅uBE und nicht iC=B⋅iB
2.) Die beiden reellen Gleichungen brauchen nicht
mehr weiter vereinfacht werden.
T1
R2
R1
C1
Lösung:
a) Kleinsignalersatzschaltbild
ia–Y⋅ uBE
Y⋅ uBE
ia
L
S⋅ uBE
Ca
ia–uBE ⋅ (Y+S)
Cb
B
S
R2
Y =
1
R2
+
S
B
+ j ωC b
b) Schwingbedingungen
(1)
(2)
1
⋅ i a + j ωL ⋅ Y ⋅ u BE + u BE = 0
j ωC a
1
⋅ i a + R 3 ⋅ [i a − u BE ⋅ (Y + S )] = 0
j ωC a
uBE
R3
(
(1)
1
⋅ i a + (1 + j ωL ⋅ Y ) ⋅ u BE = 0
j ωC a
⋅
(2)
⎞
⎛ 1
⎜⎜
+ R 3 ⎟⎟ ⋅ i a − R 3 ⋅ (Y + S ) ⋅ u BE = 0
⎠
⎝ j ωC a
⋅ −
(
⎡
⎛ 1
⎞
1
+ R 3 ⎟⎟ + R 3 ⋅ (Y + S ) ⋅
⎢(1 + j ωLY ) ⋅ ⎜⎜
j ωC a
⎝ j ωC a
⎠
⎣
u BE ≠ 0
[1 + jωL ⋅ (
2
1
R2
(
+
S
B
1
R2
+
1
j ωC a
)
)
⎤
⎥ ⋅ u BE = 0
⎦
S
B
bzw. − ω 2 +
)]
(
) + (1 − ω
(
1
R2
+
S
B
R3 C b
Realteil:
1 − ω 2 LC b − ωL ⋅
+ S)= 0
+ j ωC b ⋅ (1 + j ωC a R 3 ) + R 3 ⋅
LC b + j ωL ⋅
Imaginärteil:
ωL ⋅
+ R3
⇒
(1 + jωLY ) ⋅ (1 + jωC a R 3 ) + R 3 ⋅ (Y
[1 − ω
1
j ωC a
(
1
R2
2
)+
1
R2
+
S
B
)]⋅ (1 + jωC
a
(
1
R2
R3 ) + R3 ⋅
(
+
1
R2
S
B
+
)
+ j ωC b + S = 0
S
B
)
LC b ⋅ ωC a R 3 + ωC b R 3 = 0
1
1
+
=0
LC a LC b
+
S
B
) ⋅ ωC
a
R3 + R3 ⋅
(
1
R2
+
S
B
)
+S =0
)
+ S + j ωC b = 0
Übungsaufgaben HLST
SS 2010
Aufgabe 33: Gegentaktoszillator
Gegeben sei die untenstehende Oszillatorschaltung mit den identischen Transistoren T1 und
T2.
a)
Zeichnen Sie das Kleinsignalersatzschaltbild ohne gekreuzte Leitungen auf.
b)
Ermitteln Sie die Schwingbedingung und bestimmen Sie daraus die Resonanzfrequenz
und die Dimensionierungsvorschrift für R .
Aufgabe 34: MOSFET
a)
Kreuzen Sie an, um welchen Transistortyp es sich bei den folgenden Schaltsymbolen
handelt.
n-Kanal, selbstsperrend
n-Kanal, selbstleitend
p-Kanal, selbstsperrend
p-Kanal, selbstleitend
b)
Skizzieren Sie den Aufbau eines n-Kanal sowie p-Kanal-MOSFET.
c)
Worin besteht der Unterschied zwischen dem selbstleitenden und selbstsperrenden Typ?
d)
Erläutern Sie anhand der Skizzen dessen Funktionsweise. Wie kommt es für U GS > U th
_________
Institut für Mikroelektronik
31
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
zum Stromfluss zwischen Drain und Source?
e)
Skizzieren Sie eine Kennlinie des Ausgangskennlinienfeldes und geben Sie für jeden
Bereich der Kennlinie (Sperrbereich, ohmscher Bereich, Abschnürbereich) die
zugehörige Formel zur Berechnung des Drainstromes an.
f)
Welchen Vorteil bieten MOSFETs im Gegensatz zu Bipolartransistoren?
_________
Institut für Mikroelektronik
32
Johannes Kepler Universität Linz
1. Beispiel:
Kaskadierung von Stromquellen
Gegeben:
Kaskadierte Stromquelle bestehend aus einem Bipolartransistor
und und einem Feldeffekttransistor.
Transistor T1, gegeben durch S1, rCE
Ub
Ub
RL
R1
Transistor T2, gegeben durch S2, rDS
Widerstände R1, R2, RE
Ia
T2
Gesucht:
a) Zeichen Sie das vollständige Kleinsignalersatzschaltbild der
nebenstehenden Schaltung mit oben beschriebenen
Transistoren.
T1
b) Berechnen Sie den Ausgangswiderstand ra bezüglich der
beiden eingezeichneten Klemmen, wobei Sie:
1) CGS = 0 (T2)
2) iB = 0 (T1)
berücksichtigen
(Zeichnen Sie wenn nötig ein vereinfachtes KleinsignalESB)
R2
RE
0V
c) Berechnen Sie Ia und ra für:
R1 = 4,7 kΩ
R2 = 1 kΩ
Ub = 15 V
UBE = 0,7 V
S1 = 75 mS
rCE = 500 kΩ
S2 = 10 mS
rDS = 100 kΩ
RE = 1 kΩ
Übungsaufgaben HLST
SS 2010
Aufgabe 36: MOS-Stromspiegel
Gegeben ist der folgende Stromspiegel, der einen Strom I D = 3 mA durch den
Lastwiderstand R L treiben soll.
a)
Bestimmen Sie aus der Eingangskennlinie der (identischen) n-Kanal-MOSFETs die
Parameter U th und I S .
b)
Geben Sie
b1) rechnerisch unter Verwendung der Kennliniengleichung
b2) grafisch durch Einzeichnen der Arbeitsgerade
den Widerstand R an, damit sich der geforderte Strom I D einstellt
c)
Bestimmen Sie die Steilheit S der Transistoren
c1) rechnerisch
c2) grafisch.
_________
Institut für Mikroelektronik
34
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
Aufgabe 37: MOS-Differenzverstärker
Gegeben ist folgender Differenzverstärker mit 2 identischen MOSFETs vom Anreicherungstyp (normally-off), der von einer bipolaren Stromquelle gespeist wird.
U CC = 12 V
R
I D1
I D2
U
GS
1
U
U e1
R
Ua
R1
G
S2
Ue2
I0
R2
RE
− U CC = −12 V
a)
Berechnen Sie für R1 = 2 kΩ , R2 = 8 kΩ , R E = 400 Ω , B = 60 und U BE = 0,8 V den
Konstantstrom I 0 . Vernachlässigen Sie dabei nicht den Basisstrom.
2
⎛U
⎞
Die MOSFETs haben die Kennlinie I D = I S ⎜⎜ GS − 1⎟⎟ für U GS > U th , sonst I D = 0
⎝ U th
⎠
mit I S = 30 mA und U th = 1,9 V .
U
b) Zeigen Sie, dass die folgende Beziehung gilt: I D1 − I D 2 = I S diff ,
U th
wobei U diff die Differenzspannung am Eingang U diff = U e1 − U e 2 ist.
c)
Berechnen Sie die Drainströme I D1 und I D 2 für U diff = 0,2 V durch Umstellen der
Knotengleichung am Punkt C nach einem der beiden Ströme und anschließendem
Einsetzen in die Beziehung von Aufgabe b.
d)
Berechnen Sie mit den Werten aus Aufgabe c) die Ausgangsspannung Ua für R = 500 Ω
Berechnen Sie mit Hilfe der Spannungsverstärkung aus dem Kleinsignalersatzschaltbild
die Amplitude der Ausgangsspannung û a , wenn am Eingang eine Wechselspannung
der Amplitude uˆ diff = 0,2 V anliegt und vergleichen Sie die beiden Werte.
_________
Institut für Mikroelektronik
35
Johannes Kepler Universität Linz
Übungsaufgaben HLST
SS 2010
Aufgabe 38: Analyse eines Logikgatters
Gegeben ist das folgende Logikgatter.
a)
Zu welcher Schaltungsfamilie gehört dieses Gatter?
b)
Welche Logikfunktion Out = f (I1,I2,I3) wird realisiert?
c)
Überprüfen Sie die in b) aufgestellte Logikfunktion, indem Sie für jede Pinbelegung am
Eingang der Schaltung den logischen Wert am Ausgang in folgende Tabelle eintragen.
I1
I2
I3
Out
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
Aufgabe 39: Entwurf eines Logikgatters
Entwerfen Sie die Schaltung eines CMOS-OR-Gatters.
_________
Institut für Mikroelektronik
36
Johannes Kepler Universität Linz