20 Charakteristische Funktionen

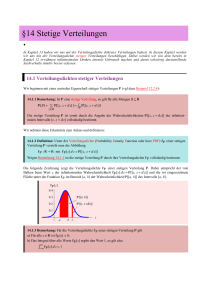
§20 Charakteristische Funktionen
Viele Probleme im Umgang mit Verteilungen lassen sich einfacher behandeln, wenn man sie in einen geeigneten
Raum abbildet. Die Verwendung von derartigen Transformationen ist manchmal dann von Vorteil, wenn sich ein
Problem direkt nur schwer behandeln lässt. In diesem Fall versucht man, das ursprüngliche Problem zu
transformieren, das transformierte Problem zu lösen und die Lösung des transformierten Problems wieder zurück
zu transformieren um auf diese Weise das ursprüngliche Problem zu lösen.
Wir befassen uns in diesem Abschnitt mit drei derartigen Transformationen. Die erste dieser Transformationen
wird bei diskreten Verteilungen, deren Träger eine Teilmenge von 0 ist, angewendet. Die zweite Transformation
verwendet man bei stetigen Verteilungen, deren Träger eine Teilmenge von @0, ¶@ ist. Die dritte
Transformationen eignet sich für beliebige stetige Verteilungen. In allen drei Fällen handelt es sich in gewisser
Weise um Spezialfälle jener Transformation, welche einer beliebigen Verteilung ihre charakteristische Funktion
zuordnet.
20.1 Die erzeugende Funktion
Achtung! Unter einer diskreten Verteilung bzw unter einer diskreten Zufallsvariablen verstehen wir in diesem
Abschnitt stets eine Verteilung bzw eine Zufallsvariable, deren Träger eine Teilmenge von 0 ist.
20.1.1 Definition: Ist eine diskrete Verteilung mit der Verteilungsdichte , so heißt die durch
k
@sD = ڦ
k=0 @kD s
im Konvergenzbereich dieser Reihe definierte Funktion , die erzeugende Funktion (im Englischen generating function) der Verteilung . Unter der erzeugenden Funktion Z einer diskreten Zufallsvariablen Z versteht
man die erzeugende Funktion ihrer Verteilung Z .
20.1.2 Bemerkung: Bei der erzeugenden Funktion einer diskreten Verteilung handelt es sich offenbar
um ein Polynom bzw um eine Potenzreihe, deren Konvergenzradius r ¥ 1 ist. Es gilt nämlich stets
@1D = ڦ
k=0 @kD = 1
Damit können wir die erzeugende Funktion einer diskreten Verteilung im Intervall D - r, r@ beliebig oft
gliedweise differenzieren und integrieren.
Die Berechnung der erzeugenden Funktion einer diskreten Verteilung läuft auf die Berechnung des
Erwartungswerts @sZ D von sZ hinaus, wobei die Zufallsvariable Z die Verteilung besitzt. Die erzeugende
Funktion einer diskreten Verteilung lässt sich daher mit Mathematica mühelos ermitteln (um "schöne"
Formeln zu erhalten, vereinfache man gegebenenfalls die Ergebnisse mit Hilfe von Simplify bzw FullSimplify und
verwende dabei die Bedingungen über die Parameter der jeweiligen Verteilung). Handelt es sich bei der diskreten
Verteilung um eine in Mathematica implementierte Verteilung, so lässt sich die erzeugende Funktion von aber auch unter Verwendung des Befehls CharacteristicFunction ermitteln:
à CharacteristicFunction@distribution, - Â Log@sDD
liefert die erzeugende Funktion @sD der diskreten, in Mathematica implementierten Verteilung distribution.
Warum wir als Argument den Ausdruck -Â Log@sD verwenden wird klar werden, wenn wir uns mit der charakteristischen Funktion einer beliebigen Verteilung befassen (man vergleiche dazu Bemerkung 20.4.2).
20_Charakteristische_Funktionen.nb
Wir wollen nun die erzeugenden Funktionen von einigen wichtigen, in Mathematica implementierten diskreten
Verteilungen ermitteln:
20.1.3 Beispiel: Man ermittle die erzeugende Funktion der diskreten Gleichverteilung @8m, n<D.
ô
Lösung: Wegen
CharacteristicFunction@DiscreteUniformDistribution@8m, n<D, -‰ Log@sDD
−sm + s1+n
H1 − m + nL H−1 + sL
besitzt die diskrete Gleichverteilung @8m, n<D die erzeugende Funktion
@8m,n<D @sD =
sn+1 - sm M
1
Ism + sm+1 + … + sn M =
n+m-1
Hn - m + 1L Hs - 1L
20.1.4 Beispiel: Man ermittle die erzeugende Funktion der Binomialverteilung @n, kD.
ô
Lösung: Wegen
CharacteristicFunction@BinomialDistribution@n, pD, -‰ Log@sDD
H1 − p + p sLn
besitzt die Binomialverteilung @n, pD die erzeugende Funktion
n
@n, pD @sD = ⁄nk=0 K k O pk H1 - pLn-k sk = H1 - p + p sLn
20.1.5 Beispiel: Man ermittle die erzeugende Funktion der negativen Binomialverteilung @n, pD.
ô
Lösung: Wegen
CharacteristicFunction@NegativeBinomialDistribution@n, pD, -‰ Log@sDD
p
n
1 − H1 − pL s
besitzt die negative Binomialverteilung @n, pD die erzeugende Funktion
@n, pD @sD = ڦ
K
k=0
pn
n+k-1 n
O p H1 - pLk sk =
n-1
H1 - s + p sLn
Diese Potenzreihe konvergiert offenbar für alle s œD - r, r@ mit r = 1 êH1 - pL.
20.1.6 Beispiel: Man ermittle die erzeugende Funktion der Poissonverteilung @lD.
99
20_Charakteristische_Funktionen.nb
100
ô
Lösung: Wegen
CharacteristicFunction@PoissonDistribution@lD, -‰ Log@sDD
H−1+sL λ
besitzt die Poissonverteilung @lD die erzeugende Funktion
k
-l l sk = ‰l Hs-1L
@lD @sD = ڦ
k=0 ‰
k!
Diese Potenzreihe konvergiert offenbar für alle s œ .
Die erzeugenden Funktionen besitzen eine Reihe von interessanten Eigenschaften:
20.1.7 Satz: Ist eine diskrete Verteilung, so gilt für alle n œ 0
1 HnL
@nD =
@0D
n! Eine diskrete Verteilung ist somit durch ihre erzeugende Funktion vollständig bestimmt - oder anders
ausgedrückt - die erzeugenden Funktionen zweier diskreter Verteilungen stimmen genau dann überein, wenn
die beiden Verteilungen überein stimmen.
ô
Beweis: Die erzeugende Funktion ist jedenfalls im Intervall D - 1, 1@ beliebig oft differenzierbar. Damit gilt für
alle n œ 0 und alle s œD - 1, 1@
HnL
@sD =
„n ¶
@kD sk = ڦ
k Hk - 1L … Hk - n + 1L @kD sk-n
⁄
k=n
„ sn k=0 was offenbar
HnL
@0D = n ! @nD
zur Folge hat.
20.1.8 Satz: Ist Z eine diskrete Zufallsvariable, so gilt für alle n œ mit der Eigenschaft, dass die n-te Potenz
von Z integrierbar ist
HnL
@Z HZ - 1L HZ - 2L … HZ - n + 1LD = Z @1D
Man nennt diesen Erwartungswert das n-te faktorielle Moment von Z. Ist Z integrierbar bzw quadratisch
integrierbar, so gilt speziell
@ZD = Z' @1D
bzw
@ZD = Z'' @1D + Z' @1D - HZ' @1DL2
ô
Beweis: Die erzeugende Funktion Z ist bekanntlich im Intervall D - 1, 1@ beliebig oft differenzierbar. Damit gilt
für alle n œ und alle s œD - 1, 1@
HnL
Z @sD =
„n ¶
@kD sk = ڦ
k Hk - 1L … Hk - n + 1L Z @kD sk-n
⁄
k=n
„ sn k=0 Z
20_Charakteristische_Funktionen.nb
101
Bei einer Reihe mit lauter positiven Gliedern darf man die Limesbildung und die Summation vertauschen. Außerdem ist eine Potenzreihe, welche an der Stelle 1 konvergiert, an dieser Stelle linksseitig stetig. Also gilt
HnL
HnL
k-n =
Z @1D = limsÆ1 Z @sD = limsÆ1 ⁄¶
k=n k Hk - 1L … Hk - n + 1L Z @kD s
= ڦ
k=n k Hk - 1L … Hk - n + 1L Z @kD = @Z HZ - 1L HZ - 2L … HZ - n + 1LD
Ist speziell Z integrierbar bzw quadratisch integrierbar, so folgt daraus
'
@ZD = ڦ
k=1 k Z @kD = Z @1D
bzw
''
@Z HZ - 1LD = ڦ
k=2 k Hk - 1L Z @kD = Z @1D
und damit
@ZD = AZ 2 E - @ZD2 = @Z HZ - 1LD + @ZD - @ZD2 = Z'' @1D + Z' @1D - HZ' @1DL2
20.1.9 Satz: Sind die beiden diskreten Zufallsvariablen X und Y unabhängig, so gilt für alle s aus dem Konvergenzbereich der erzeugenden Funktion X +Y der Summe X + Y dieser beiden Zufallsvariablen
X +Y @sD = X @sD Y @sD
Für zwei beliebige diskrete Verteilungen und gilt damit
* @sD = @sD @sD
ô
Beweis: Für alle s aus dem Konvergenzbereich der erzeugenden Funktion X +Y gilt wegen Satz 19.1.3
X +Y @sD = @s X +Y D = @s X sY D = @s X D @sY D = X @sD Y @sD
Es folgen wieder einige Beispiele:
20_Charakteristische_Funktionen.nb
102
20.1.10 Beispiel: Von der diskreten Zufallsvariablen Z ist bekannt, dass für alle k œ 0 die
Wahrscheinlichkeit Z @zD = @8Z = k<D proportional zu gk ist (wobei 0 < g < 1 vorausgesetzt wird). Man
berechne den Erwartungswert @ZD von Z.
ô
Lösung: Natürlich kann diese Frage mit den üblichen Methoden gelöst werden. Wir zeigen nun aber, wie sich diese
Fragestellung unter Verwendung der erzeugenden Funktion behandeln lässt:
Aus der Angabe entnimmt man, dass für alle k œ 0 offenbar Z @zD = @8Z = k<D = a gk gilt, wobei der Proportionalitätsfaktor a noch unbekannt ist. Damit gilt für die erzeugende Funktion Z @sD von Z
@kD sk = ڦ
a gk sk =
Z @sD = ڦ
k=0 k=0
a
1-gs
Nun ist aber bekanntlich Z @1D = 1, was a = 1 - g zur Folge hat. Wegen Satz 20.1.8 gilt daher
@ZD = Z' @1D =
ag
H1 - gL2
20.1.11 Beispiel: Von der diskreten Zufallsvariablen Z ist bekannt, dass für alle k œ 0 die
Wahrscheinlichkeiten Z @kD = @8Z = k<D der Rekursionsbeziehung
Z @k + 2D = a Z @k + 1D + b Z @kD
genügen, wobei a + b + Z @0D H1 - aL < 1 ist. Man berechne die Wahrscheinlichkeit Z @2D = @8Z = 2<D sowie
den Erwartungswert @ZD von Z.
ô
Lösung: Für die erzeugende Funktion Z @sD von Z gilt
Z @sD = Z @0D + Z @1D s + ڦ
@kD sk = Z @0D + Z @1D s + ڦ
Ha Z @k - 1D + b Z @k - 2DL sk =
k=2 Z
k=2
= Z @0D + Z @1D s + a s ڦ
@kD sk + b s2 ڦ
@kD sk =
k=1 Z
k=0 Z
= Z @0D + Z @1D s - Z @0D a s + a s Z @sD + b s2 Z @sD
und damit
Z @sD =
Z @0D + Z @1D s - Z @0D a s
1 - a s - b s2
wobei zwischen den vier Parametern Z @0D, Z @1D, a und b wegen Z @1D = 1 die Beziehung
Z @1D = 1 - a - b - Z @0D H1 - aL
gelten muss. Wegen Satz 20.1.7 bzw Satz 20.1.8 ergibt sich daher für die Wahrscheinlichkeit @8Z = 2<D bzw den
Erwartungswert @ZD von Z
@8Z = 2<D = Z'' @0D ê2 = a H1 - b - Z @0DL - a2 H1 - Z @0DL + b Z @0D
@ZD = Z' @1D =
1 + b - Z @0D
1-a- b
Zur Herleitung dieser beiden Formeln haben wir dabei Mathematica verwendet:
20_Charakteristische_Funktionen.nb
103
GenFun@s_D := Hf0 + f1 s - f0 a sL ê H1 - a s - b s2 L
Simplify@D@GenFun@sD, 8s, 2<D ê. 8s Æ 0, f1 Æ 1 - a - b - f0 H1 - aL<D ê 2
Simplify@D@GenFun@sD, sD ê. 8s Æ 1, f1 Æ 1 - a - b - f0 H1 - aL<D
Clear@GenFunD
H−1 + f0L α2 + f0 β − α H−1 + f0 + βL
−1 + f0 − β
−1 + α + β
20.1.12 Beispiel: Man bestimme die Wahrscheinlichkeit dafür, dass man eine Eintrittskarte erhält, bei der die
Summe der ersten und letzten drei Ziffern der Registriernummer gleich sind, wenn diese Registriernummer
sechsstellig ist und einen beliebigen Wert zwischen 111 111 und 999 999 annehmen kann.
ô
Lösung: Die Zufallsvariable Xi , welche die i-te Stelle einer zufällig ausgewählten Registriernummer bezeichnet, ist
offenbar auf der Menge 81, 2, …, 9< gleichverteilt. Außerdem sind die Zufallsvariablen X1 , X2 , …, X6 vollständig
unabhängig. Wegen Satz 20.1.9 besitzen die Zufallsvariablen Y = X1 + X2 + X3 und Z = X4 + X5 + X6 die erzeugenden Funktionen
Y @sD = X @sD X @sD X @sD
1
2
3
bzw
Z @sD = X @sD X @sD X @sD
4
5
6
Für die Wahrscheinlichkeit dafür, dass die Summe X der ersten drei Ziffern und die Summe Y der letzten drei
Ziffern einer zufällig ausgewählten Registriernummer übereinstimmen, gilt auf Grund von Symmetrieüberlegungen
27
@8X = Y <D = ⁄27
k=3 @8X = k<D @8Y = k<D = ⁄k=3 @8X = k<D @8Y = 27 - k<D = @8X + Y = 27<D
Bei der von uns gesuchten Wahrscheinlichkeit @8X = Y <D handelt es sich offenbar um den Koeffizient von s27 der
erzeugenden Funktion
X +Y @sD = X @sD Y @sD = X @sD X @sD … X @sD
1
2
6
Dieser Koeffizient lässt sich mit den Befehlen CharacteristicFunction, Apart (damit wird die erzeugende Funktion
der Gleichverteilung auf der Menge 81, 2, …, 9< in ein Polynom umgeformt) und Coefficient (damit lassen sich die
Koeffizienten eines Polynoms ermitteln) mühelos berechnen:
CoefficientBApart@CharacteristicFunction@DiscreteUniformDistribution@81, 9<D, -‰ Log@sDDD6 , s, 27F êê
N
0.0554944
20.1.13 Beispiel: Die diskreten Zufallsvariablen N, X1 , X2 , … seien vollständig unabhängig, die
Zufallsvariablen X1 , X2 , … seien identisch verteilt mit der (gleichen) erzeugenden Funktion X . Man
ermittle die erzeugende Funktion Z der Zufallsvariablen Z = X1 + X2 + … + X N .
ô
Lösung: Für alle s aus dem Konvergenzbereich von Z folgt aus dem Satz von der totalen Wahrscheinlichkeit
zusammen mit Satz 19.1.3 und Satz 20.1.9
X1 +X2 +…+X N 8N = n<D @8N = n<D =
Z @sD = @sZ D = @s X1 +X2 +…+X N D = ⁄¶
n=0 @s
X1 +X2 +…+Xn D @8N = n<D = ⁄¶ @s X1 D @s X2 D … @s Xn D @8N = n<D =
= ڦ
n=0 @s
n=0
20_Charakteristische_Funktionen.nb
104
n
= ڦ
n=0 X @sD @8N = n<D = N @ X @sDD
20.1.14 Beispiel: Wie groß ist die Wahrscheinlichkeit dafür, beim Würfeln mit n = 8 Würfeln die
Augensumme m = 30 zu erzielen?
ô
Lösung: Wir bezeichnen mit Xi die mit dem i-ten Würfel gewürfelte Augenzahl und mit Z = X1 + X2 + … + Xn
die dabei erzielte Augensumme. Da die Zufallsvariablen X1 , X2 , …, Xn vollständig unabhängig sind, gilt wegen
Satz 20.1.9 für die erzeugende Funktion von Z offenbar
Z @sD = X @sD X @sD … Xn @sD
1
2
Die von uns gesuchte Wahrscheinlichkeit @8Z = m<D entspricht dem Koeffizienten von sm der erzeugenden Funktion Z @sD und lässt sich (man vergleiche Beispiel 20.1.12) mit Hilfe von Mathematica mühelos berechnen:
n = 8; m = 30;
CoefficientAApart@CharacteristicFunction@DiscreteUniformDistribution@81, 6<D, -‰ Log@sDDDn , s, mE êê N
Clear@n, mD
0.0747719
Der Begriff der erzeugenden Funktion lässt sich folgendermaßen verallgemeinern:
20.1.15 Definition: Ist = 8 f0 , f1 , f2 , …< eine Folge von reellen Zahlen, so nennt man die durch
k
@sD = ڦ
k=0 fk s
im Konvergenzbereich dieser Reihe definierte Funktion die erzeugende Funktion der Folge . Damit
entspricht die erzeugende Funktion Z einer diskreten Zufallsvariablen Z offenbar der erzeugenden Funktion
der Folge = 8Z @0D, Z @1D, Z @2D, …<. Analog zu Satz 20.1.7 gilt für alle n œ 0 wieder
fn =
1 HnL
@0D
n! 20.1.16 Beispiel: Sei Z eine diskrete Zufallsvariable und sei = 8@8Z > 0<D, @8Z > 1<D, @8Z > 2<D, …<. Man
zeige, dass zwischen der erzeugenden Funktion Z der Zufallsvariablen Z und der erzeugenden Funktion der Folge für alle s aus dem Intervall D - 1, 1@ die folgende Beziehung besteht
1 - Z @sD
@sD =
1-s
ô
Lösung: Da alle Koeffizienten der erzeugenden Funktion durch 1 beschränkt sind, konvergiert diese Potenzreihe jedenfalls für alle s aus dem Intervall D - 1, 1@. Für diese s gilt aber
H1 - sL @sD = ڦ
@8Z > k<D sk - ڦ
@8Z > k<D sk+1 =
k=0
k=0
= @8Z > 0<D - ڦ
H@8Z > k - 1<D - @8Z > k<DL sk =
k=1
k
= 1 - @8Z = 0<D - ڦ
k=1 @8Z = k<D s = 1 - Z @sD
20_Charakteristische_Funktionen.nb
105
20.1.17 Beispiel: A1 , A2 , …, An seien vollständig unabhängige
Wahrscheinlichkeit dafür, dass höchstens m dieser Ereignisse eintreten.
Ereignisse.
Gesucht
ist
die
ô
Lösung: Die Zufallsvariable Z gebe an, wieviele der Ereignisse A1 , A2 , …, An eintreten. Mit den Abkürzungen
pi = @Ai D und qi = 1 - @Ai D ergibt sich für die erzeugende Funktion Z @sD von Z
Z @sD = ⁄nk=0 @8Z = k<D sk = ⁄nk=0 @:
genau k der Ereignisse
>D sk = ¤ni=1 Hqi + pi sL
A1 , A2 , …, An treten ein
Für die erzeugende Funktion der Folge = 8@8Z § 0<D, @8Z § 1<D, …, @8Z § n<D< der von uns gesuchten
Wahrscheinlichkeiten gilt daher mit den in Beispiel 20.1.16 verwendeten Bezeichnungen für alle s œD - 1, 1@
@sD = ⁄nk=0 @8Z § k<D sk = ⁄nk=0 H1 - @8Z > k<DL sk = ⁄nk=0 sk - ⁄nk=0 H@8Z > k<DL sk =
= 1 + s + s2 + … + sn - @sD =
1 - Z @sD ¤ni=1 Hqi + pi sL - sn+1
1 - sn+1
=
1-s
1-s
1-s
Für beliebige Wahrscheinlichkeiten p1 , p2, …, pn und ein beliebiges m § n lässt sich die gesuchte Wahrscheinlichkeit @8Z § m<D (man vergleiche Beispiel 20.1.12) mühelos mit Hilfe von Mathematica ermitteln. Beispielsweise gilt:
p = 80.2, 0.4, 0.1, 0.6, 0.4, 0.2, 0.6, 0.4, 0.2, 0.5<;
n = Length@pD; m = 4;
GenFun@s_D := HApply@Times, H1 - p + s pLD - sn+1 L ê H1 - sL;
Coefficient@Apart@GenFun@sDD, s, mD
Clear@p, n, m, GenFunD
0.741823
20.2 Die Laplace-Transformation
Achtung! Wir befassen uns in diesem Abschnitt nur mit stetigen Verteilungen bzw stetigen Zufallsvariablen, deren
Träger eine Teilmenge von @0, ¶@ ist.
20.2.1 Definition: Ist eine stetige Verteilung mit der Verteilungsdichte , so heißt die durch
@sD = Ÿ 0 ‰-s z @zD „ z
¶
auf @0, ¶@ definierte Funktion , die Laplace-Transformierte der Verteilung . Unter der Laplace-Transformierten Z einer stetigen Zufallsvariablen Z versteht man die Laplace-Transformierte ihrer Verteilung Z .
20.2.2 Bemerkung: Für die Laplace-Transformierte einer stetigen Verteilung gilt stets
@sD = Ÿ 0¶ ‰-s z @zD „ z § Ÿ 0¶ @zD „ z = 1 = @0D
Aus dem Satz von der beschränkten Konvergenz (auf den wir hier nicht näher eingehen wollen) folgt daraus,
dass die Laplace-Transformierte einer stetigen Verteilung im Intervall D 0, ¶@ beliebig oft differenzierbar
ist und dabei die Operationen Differenziation und Integration vertauscht werden dürfen.
Im Prinzip lässt sich die Laplace-Transformierte einer stetigen Verteilung mit der Verteilungsdichte mit
Hilfe von Mathematica ermitteln, indem man einfach das in der Definition auftretende Integral auswertet. Einfacher
geht es, wenn man dazu den in Mathematica implementierten Befehl LaplaceTransform verwendet. Handelt es sich
bei der stetigen Verteilung um eine in Mathematica implementierte Verteilung, so lässt sich die Laplace-Trans-
20_Charakteristische_Funktionen.nb
106
bei der stetigen Verteilung um eine in Mathematica implementierte Verteilung, so lässt sich die Laplace-Transformierte von auch unter Verwendung des Befehls CharacteristicFunction bestimmen:
à LaplaceTransform@ @zD, z, sD
liefert die Laplace-Transformierte @sD der stetigen Verteilung mit der Verteilungsdichte @zD.
à CharacteristicFunction@distribution, Â sD
liefert die Laplace-Transformierte @sD der stetigen, in Mathematica implementierten Verteilung distribution.
Warum wir als Argument den Ausdruck  s verwenden, wird klar werden, wenn wir uns mit der charakteristischen Funktion einer beliebigen Verteilung befassen (man vergleiche dazu Bemerkung 20.4.2).
Wir wollen nun die Laplace-Transformierte von einigen wichtigen, in Mathematica implementierten stetigen
Verteilungen ermitteln:
20.2.3 Beispiel: Man ermittle die Laplace-Transformierte der Gleichverteilung @8a, b<D (mit 0 § a < b).
ô
Lösung: Wegen
CharacteristicFunction@UniformDistribution@8a, b<D, ‰ sD
−−a s + −b s
−
H−a + bL s
besitzt die Gleichverteilung @8a, b<D die Laplace-Transformierte
b
@8a,b<D @sD = Ÿ a ‰- s z
-a s - ‰-b s
1
„z = ‰
b-a
s Hb - aL
20.2.4 Beispiel: Man ermittle die Laplace-Transformierte der Dreiecksverteilung @8a, b<D (mit 0 § a < b).
ô
Lösung: Wegen
CharacteristicFunction@TriangularDistribution@8a, b<D, ‰ sD
as
bs 2
−
−
4 2 − 2
Ha − bL2 s2
besitzt die Dreiecksverteilung @8a, b<D die Laplace-Transformierte
-a sê2 - ‰-b sê2 L2
a+bLê2 - s z 4 Hz - aL
b
- s z 4 Hb - zL „ z = 4 H‰
‰
„
z
+
‰
ŸHa+bLê2
a
Hb - aL2
Hb - aL2
s2 Hb - aL2
@8a,b<D @sD = Ÿ H
20_Charakteristische_Funktionen.nb
20.2.5 Beispiel: Man ermittle die Laplace-Transformierte der Exponentialverteilung @lD.
ô
Lösung: Wegen
CharacteristicFunction@ExponentialDistribution@lD, ‰ sD
λ
s+λ
besitzt die Exponentialverteilung @lD die Laplace-Transformierte
@lD @sD = Ÿ
l
¶ -s z
‰
l ‰-l z „ z =
0
l+s
20.2.6 Beispiel: Man ermittle die Laplace-Transformierte der Gammaverteilung amma@a, lD.
ô
Lösung: Wegen
CharacteristicFunction@GammaDistribution@a, lD, ‰ sD
H1 + s λL−α
besitzt die Gammaverteilung amma@a, lD die Laplace-Transformierte
amma@a,lD @sD =
1
¶ -s z -a a-1 -zêl
l z
‰
„ z = H1 + l sL-a
Ÿ ‰
G@aD 0
20.2.7 Beispiel: Man ermittle die Laplace-Transformierte der Chi-Quadrat Verteilung hi@nD.
ô
Lösung: Wegen
CharacteristicFunction@ChiSquareDistribution@nD, ‰ sD
H1 + 2 sL−nê2
besitzt die Chi-Quadrat Verteilung hi@nD die Laplace-Transformierte
hi@nD @sD =
1
¶ -s z -nê2 -zê2 nê2-1
‰
2
‰
z
„ z = H1 + 2 sL-nê2
G@n ê2D Ÿ 0
20.2.8 Beispiel: Man ermittle die Laplace-Transformierte der Extremwertverteilung xtrem@m, bD.
ô
Lösung: Wegen
CharacteristicFunction@ExtremeValueDistribution@m, bD, ‰ sD
−s µ Gamma@1 + s βD
107
20_Charakteristische_Funktionen.nb
108
besitzt die Extremwertverteilung xtrem@m, bD die Laplace-Transformierte
xtrem@m,bD @sD =
1 ¶ -s z Hm-zLêb - ‰Hm-zLêb
‰
‰
„ z = ‰-m s G@1 + b sD
b Ÿ0
Die Laplace-Transformation besitzt eine Reihe von interessanten Eigenschaften. Ohne auf den Beweis näher
eingehen zu können (man benötigt dazu ein tiefliegendes Wissen über komplexe Analysis), beginnen wir mit der
sogenannten Umkehrformel:
20.2.9 Satz (Umkehrformel): Ist eine stetige Verteilung mit Verteilungsdichte , so gilt für alle z > 0
1
g+Â ¶ Â s z
@zD =
@sD „ s
Ÿ
‰
2 p  g- ¶
wobei g eine beliebige Konstante ist, welche so gewählt werden muss, dass die Realteile aller singulären
Stellen von kleiner als g sind. Eine stetige Verteilung ist somit durch ihre Laplace-Transformierte vollständig bestimmt - oder anders ausgedrückt - die Laplace-Transformierten zweier stetiger Verteilungen
stimmen genau dann überein, wenn die beiden Verteilungen überein stimmen.
Im Prinzip lässt sich die Verteilungsdichte einer stetigen Verteilung aus der Laplace-Transformierten mit
Hilfe von Mathematica ermitteln, indem man einfach dieses komplexe Integral auswertet. Einfacher geht es, wenn
man dazu den in Mathematica implementierten Befehl InverseLaplaceTransform verwendet:
à InverseLaplaceTransform@ @sD, s, zD
berechnet die Verteilungsdichte jener stetigen Verteilung , welche die Laplace-Transformierte besitzt.
Wir zeigen die Verwendung der Befehle LaplaceTransform und InverseLaplaceTransform an einem Beispiel (man
beachte allerdings, dass diese beiden Befehle leider oft nicht zum Ziel führen, da Mathematica die dabei auftretenden Integrale nur in seltenen Fällen tatsächlich berechnen kann):
20.2.10 Beispiel: Für die Gammaverteilung berechne man die Laplace-Transformierte mit Hilfe des Befehls
LaplaceTransform. Anschließend ermittle man aus dieser Laplace-Transformierten wieder die
Verteilungsdichte der Gammaverteilung unter Verwendung des Befehls InverseLaplaceTransform.
ô
Lösung: Die Gammaverteilung amma@a, lD besitzt die Verteilungsdichte
f@z_D := PDF@GammaDistribution@a, lD, zD; f@zD
z
−
λ z−1+α λ−α
Gamma@αD
a) Wendet man auf diese Verteilungsdichte den Befehl LaplaceTransform an, so erhält man die Laplace-Transformierte der Gammaverteilung:
lt@s_D := LaplaceTransform@f@zD, z, sD; lt@sD
1 −α
s+
λ−α
λ
b) Wendet man auf diese Laplace-Transformierte den Befehl InverseLaplaceTransform an, so erhält man wieder
die Verteilungsdichte der Gammaverteilung:
20_Charakteristische_Funktionen.nb
109
InverseLaplaceTransform@lt@sD, s, zD
z
−
λ z−1+α λ−α
Gamma@αD
Clear@f, ltD
20.2.11 Satz: Ist Z eine stetige Zufallsvariable, so gilt für alle n œ mit der Eigenschaft, dass die n-te Potenz
von Z integrierbar ist
HnL
@Z n D = H-1Ln Z @0D
Ist Z integrierbar bzw quadratisch integrierbar, so gilt speziell
@ZD = -Z' @0D
bzw
@ZD = Z'' @0D - HZ' @0DL2
ô
Beweis: Die Laplace-Transformierte Z einer stetigen Zufallsvariablen Z ist im Intervall D 0, ¶@ bekanntlich
beliebig oft differenzierbar, wobei die beiden Operationen Differenziation und Integration vertauscht werden
dürfen. Damit gilt für alle n œ und alle s œD 0, ¶@
HnL
Z @sD =
„ n ¶ -s z
¶ „n
¶
Z @zD „ z = Ÿ
H‰-s z Z @zDL „ z = H-1Ln Ÿ zn ‰-s z Z @zD „ z
Ÿ0 ‰
n
0 „ sn
0
„s
Falls Z n integrierbar ist, so ist die n-te Ableitung der Laplace-Transformierten Z @sD an der Stelle s = 0 rechtsseitig
stetig und die beiden Operationen Limesbildung und Integration dürfen vertauscht werden (diese Tatsache folgt
ebenfalls aus dem Satz von der beschränkten Konvergenz). Damit gilt
HnL
HnL
Z @0D = lims∞0 Z @sD = H-1Ln lims∞0 Ÿ
= H-1Ln Ÿ
¶ n -s z
¶
z ‰
Z @zD „ z = H-1Ln Ÿ lims∞0 Hzn ‰-s z Z @zDL „ z =
0
0
¶ n
z Z @zD „ z = H-1Ln @Z n D
0
Ist speziell Z integrierbar bzw quadratisch integrierbar, so folgt daraus
@ZD = -Z' @0D
bzw
@Z 2 D = Z'' @0D
und damit
@ZD = @Z 2 D - @ZD2 = Z'' @0D - HZ' @0DL2
20_Charakteristische_Funktionen.nb
110
Vollständig analog zu Satz 20.1.9 zeigt man
20.2.12 Satz: Sind die beiden stetigen Zufallsvariablen X und Y unabhängig, so gilt für alle s > 0
X +Y @sD = X @sD Y @sD
Für zwei beliebige stetige Verteilungen und gilt damit
* @sD = @sD @sD
Es folgen wieder einige Beispiele:
20.2.13 Beispiel: Von der stetigen Zufallsvariable Z ist bekannt, dass für alle z ¥ 0 die Verteilungsdichte
Z @zD proportional zu g z ist (wobei 0 < g < 1 vorausgesetzt wird). Man berechne den Erwartungswert @ZD
von Z.
ô
Lösung: Natürlich kann diese Frage mit den üblichen Methoden gelöst werden. Wir zeigen aber wieder, wie sich
diese Fragestellung unter Verwendung der Laplace-Transformation behandeln lässt:
Aus der Angabe entnimmt man, dass für alle s ¥ 0 offenbar Z @zD = a g z gilt, wobei der Proportionalitätsfaktor a
noch unbekannt ist. Damit gilt für die Laplace-Transformierte Z @sD von Z
Z @sD = Ÿ
a
¶ -s z
‰
a gz „ z =
s - Log@gD
0
Nun ist aber bekanntlich Z @0D = 1, was a = -Log@gD zur Folge hat. Wegen Satz 20.2.11 gilt damit
@ZD = -Z' @0D = -
a
HLog@gDL2
20.2.14 Beispiel: Unter Verwendung der Laplace-Transformation zeige man die beiden Faltungsformeln
amma@a, lD * amma@ b, lD = amma@a + b, lD
hi@mD * hi@nD = hi@m + nD
ô
Lösung: Wegen Satz 20.2.12 und Satz 20.2.9 müssen wir nur zeigen, dass das Produkt der Laplace-Transformierten der beiden Verteilungen auf der linken Seite mit der Laplace-Transformierten der Verteilung auf der
rechten Seite übereinstimmt:
CharacteristicFunction@GammaDistribution@a, lD, ‰ sD CharacteristicFunction@GammaDistribution@ b, lD, ‰ sD ==
CharacteristicFunction@GammaDistribution@a + b, lD, ‰ sD êê FullSimplify
True
CharacteristicFunction@ChiSquareDistribution@mD, ‰ sD CharacteristicFunction@ChiSquareDistribution@nD, ‰ sD ä
CharacteristicFunction@ChiSquareDistribution@m + nD, ‰ sD êê FullSimplify
True
20.2.15 Beispiel: Die Zufallvariablen X1 , X2 , X3 seien vollständig unabhängig und exponentialverteilt mit
den Parametern l1 = 1 bzw l2 = 2 bzw l3 = 3. Gesucht ist die Verteilungsdichte von Z = X1 + X2 + X3 .
ô
20_Charakteristische_Funktionen.nb
111
Lösung: Für alle s > 0 gilt wegen Satz 20.2.12 zusammen mit Beispiel 20.2.5
1
2
3
6
=
Z @sD = X +X +X @sD = X @sD X @sD X @sD =
1 2 3
1
1
1
1 + s 2 + s 3 + s H1 + sL H2 + sL H3 + sL
Wendet man nun auf Z die Umkehrformel an
InverseLaplaceTransform@6 ê HH1 + sL H2 + sL H3 + sLL, s, zD
3 −3 z I−1 + z M2
so erhält man direkt die gesuchte Verteilungsdichte Z
Z @zD = :
3 H-1 + ‰z L2 ‰-3 z für z ¥ 0
0
sonst
Der Begriff der Laplace-Transformierten lässt sich folgendermaßen verallgemeinern:
20.2.16 Definition: Ist eine stetige und beschränkte Abbildung von @0, ¶@ in , so nennt man die durch
@sD = Ÿ
¶ -s z
‰
@zD „ z
0
auf D 0, ¶@ definierte Funktion die Laplace-Transformierte der Funktion . Damit entspricht die LaplaceTransformierte Z einer stetigen Zufallsvariablen Z der Laplace-Transformierten ihrer Verteilungsdichte.
Z
20.2.17 Beispiel: Sei Z eine stetige Zufallsvariable. Man zeige, dass zwischen der Laplace-Transformierten
der Verteilungsfunktion Z und der LaplaceTransformierten der Verteilungsdichte Z von Z für alle
s > 0 die folgende Beziehung gilt
1
@sD = s @sD
ô
Lösung: Partielle Integration liefert für alle s > 0
@sD = Ÿ
z=¶ 1 ¶
1
1
¶ -s z
‰
@zD „ z = - ‰-s z @zD ¶z=0 + Ÿ ‰-s z @zD „ z = @sD
s
s 0
s
0
20_Charakteristische_Funktionen.nb
112
20.3 Die Fourier-Transformation
Achtung! Wir befassen uns in diesem Abschnitt nur mit stetigen Verteilungen bzw stetigen Zufallsvariablen.
20.3.1 Definition: Ist eine stetige Verteilung mit der Verteilungsdichte , so heißt die durch
¶ ‰Â s z @zD „ z = ¶ Cos@s zD @zD „ z +  ¶ Sin@s zD @zD „ z
@sD = Ÿ-¶
Ÿ-¶
Ÿ-¶
auf definierte komplexwertige Funktion , die Fourier-Transformierte der Verteilung . Unter der FourierTransformierten Z einer stetigen Zufallsvariablen Z versteht man die Fourier-Transformierte ihrer Verteilung
Z .
ô
Zwischen der Laplace-Transformierten @sD einer stetigen Verteilung , deren Träger eine Teilmenge von @0, ¶@
ist, und der Fourier-Transformierten @sD dieser Verteilung besteht für alle s ¥ 0 offenbar die Beziehung
@sD = @Â sD
20.3.2 Bemerkung: Für die Fourier-Transformierte einer stetigen Verteilung gilt stets
¶ ‰Â s z @zD „ z § ¶ @zD „ z = 1 = @0D
@sD = Ÿ-¶
Ÿ-¶ Aus dem Satz von der beschränkten Konvergenz folgt daraus, dass die Fourier-Transformierte einer
stetigen Verteilung in ganz beliebig oft differenzierbar ist und dabei die Operationen Differenziation und
Integration vertauscht werden dürfen.
Im Prinzip lässt sich die Fourier-Transformierte einer stetigen Verteilung mit der Verteilungsdichte mit
Hilfe von Mathematica ermitteln, indem man einfach das in der Definition auftretende Integral auswertet. Einfacher
geht es, wenn man dazu den in Mathematica implementierten Befehl FourierTransform verwendet. Handelt es sich
bei der stetigen Verteilung um eine in Mathematica implementierte Verteilung, so lässt sich die Fourier-Transformierte von auch unter Verwendung von CharacteristicFunction bestimmen:
à FourierTransform@ @zD, z, sD
2p
liefert die Fourier-Transformierte @sD der stetigen Verteilung mit Verteilungsdichte @zD. Man beachte,
dass der von Mathematica mit dem Befehl FourierTransform ermittelte Ausdruck noch mit 2 p multipliziert
werden muss, um die im Rahmen der Stochastik verwendete Version der Fourier-Transformierten zu erhalten.
à CharacteristicFunction@distribution, sD
liefert die Fourier-Transformierte @sD der stetigen, in Mathematica implementierten Verteilung distribution.
Wir wollen nun die Fourier-Transformierte von einigen wichtigen, in Mathematica implementierten stetigen
Verteilungen ermitteln (man beachte, dass sich die Fourier-Transformierte vieler Verteilungen nicht mit Hilfe
elementarer Funktionen ausdrücken lässt):
20.3.3 Beispiel: Man ermittle die Fourier-Transformierte der Gleichverteilung @8a, b<D.
ô
Lösung: Wegen
20_Charakteristische_Funktionen.nb
113
CharacteristicFunction@UniformDistribution@8a, b<D, sD
−
J− a s + b s N
H−a + bL s
besitzt die Gleichverteilung @8a, b<D die Fourier-Transformierte
@8a,b<D @sD = Ÿ a ‰ Â s z
b
 a s - ‰  b sL
1
„ z = Â H‰
b-a
s Hb - aL
20.3.4 Beispiel: Man ermittle die Fourier-Transformierte der Dreiecksverteilung @8a, b<D.
ô
Lösung: Wegen
CharacteristicFunction@TriangularDistribution@8a, b<D, sD
4 −
as
bs 2
2 − 2
Ha − bL2 s2
besitzt die Dreiecksverteilung @8a, b<D die Fourier-Transformierte
@8a,b<D @sD = Ÿ Ha+bLê2 ‰ Â s z
a
4 Hz - aL
4 Hb - zL
4 H‰ Â a sê2 - ‰ Â b sê2 L2
b
„z +Ÿ
‰Âsz
„z = 2
2
Ha+bLê2
Hb - aL
Hb - aL
s2 Hb - aL2
20.3.5 Beispiel: Man ermittle die Fourier-Transformierte der Laplaceverteilung @a, lD.
ô
Lösung: Wegen
CharacteristicFunction@LaplaceDistribution@a, lD, sD
s α
1 + s2 λ2
besitzt die Laplaceverteilung @a, lD die Fourier-Transformierte
¶
@a,lD @sD = Ÿ-¶ ‰ Â s z
1 - z-a êl
‰Âas
‰
„z =
2l
1 + l2 s2
20_Charakteristische_Funktionen.nb
114
20.3.6 Beispiel: Man ermittle die Fourier-Transformierte der Normalverteilung @m, sD.
ô
Lösung: Wegen
CharacteristicFunction@NormalDistribution@m, sD, sD
s µ−
s2 σ2
2
besitzt die Normalverteilung @m, sD die Fourier-Transformierte
¶
@m,sD @sD = Ÿ-¶ ‰ Â s z
1
2p s
2
2
2 2
‰-Hz-mL êH2 s L „ z = ‰ Â m s ‰- s s ê2
20.3.7 Beispiel: Man ermittle die Fourier-Transformierte der Extremwertverteilung xtrem@m, bD.
ô
Lösung: Wegen
CharacteristicFunction@ExtremeValueDistribution@m, bD, sD
s µ Gamma@1 − s βD
besitzt die Extremwertverteilung xtrem@m, bD die Fourier-Transformierte
¶
xtrem@m,bD @sD = Ÿ-¶ ‰ Â s z
1 Hm-zLêb - ‰ Hm-zLêb
‰
„ z = ‰ Â m s G@1 - Â b sD
b
Die Fourier-Transformation besitzt eine Reihe von interessanten Eigenschaften. Ohne auf den Beweis näher
eingehen zu können, beginnen wir wieder mit der sogenannten
20.3.8 Satz (Umkehrformel): Ist eine stetige Verteilung mit Verteilungsdichte , so gilt für alle z œ 1 +¶ - s z
@zD =
@sD „ s
Ÿ
2 p -¶ ‰
Eine stetige Verteilung ist somit durch ihre Fourier-Transformierte vollständig bestimmt - oder anders
ausgedrückt - die Fourier-Transformierten zweier stetiger Verteilungen stimmen genau dann überein, wenn die
beiden Verteilungen überein stimmen.
Im Prinzip lässt sich die Verteilungsdichte einer stetigen Verteilung aus der Fourier-Transformierten mit
Hilfe von Mathematica ermitteln, indem man einfach dieses Integral auswertet. Einfacher geht es, wenn man dazu
den in Mathematica implementierten Befehl InverseFourierTransform verwendet:
à InverseFourierTransform@ @sD, s, zD ê 2 p
berechnet die Verteilungsdichte jener stetigen Verteilung , welche die Fourier-Transformierte besitzt.
Man beachte, dass der von Mathematica mit dem Befehl InverseFourierTransform ermittelte Ausdruck noch
durch 2 p dividiert werden muss, um die gesuchte Verteilungsdichte zu erhalten.
Wir zeigen die Verwendung der Befehle FourierTransform und InverseFourierTransform an einem Beispiel (man
beachte wieder, dass diese beiden Befehle leider oft nicht zum Ziel führen, da Mathematica die dabei auftretenden
Integrale nur in seltenen Fällen berechnen kann):
20_Charakteristische_Funktionen.nb
115
20.3.9 Beispiel: Für die Normalverteilung berechne man die Fourier-Transformierte mit Hilfe des Befehls
FourierTransform. Anschließend ermittle man aus dieser Fourier-Transformierten wieder die
Verteilungsdichte der Normalverteilung unter Verwendung des Befehls InverseFourierTransform.
ô
Lösung: Die Normalverteilung @m, sD besitzt die Verteilungsdichte
f@z_D := PDF@NormalDistribution@m, sD, zD; f @zD
Hz−µL2
−
2 σ2
2π σ
a) Wendet man auf diese Verteilungsdichte den Befehl FourierTransform an und multipliziert man das Ergebnis mit
2 p , so erhält man die Fourier-Transformierte der Normalverteilung:
ft@s_D := FourierTransform@f@zD, z, s, Assumptions -> 8s > 0<D Sqrt@2 pD; ft@sD
s µ−
s2 σ2
2
b) Wendet man auf diese Fourier-Transformierte den Befehl InverseFourierTransform an und dividiert man das
Ergebnis durch 2 p , so erhält man wieder die Verteilungsdichte der Normalverteilung:
InverseFourierTransform@ft@sD, s, z, Assumptions Æ 8s > 0<D ê Sqrt@2 pD
Hz−µL2
−
2 σ2
1
σ2
2π
Clear@f, ftD
Analog zu Satz 20.2.11 und Satz 20.2.12 zeigt man
20.3.10 Satz: Ist Z eine stetige Zufallsvariable, so gilt für alle n œ , welche die Eigenschaft besitzen, dass die
n-te Potenz von Z integrierbar ist
HnL
@Z n D = H-ÂLn Z @0D
Ist Z integrierbar bzw quadratisch integrierbar, so gilt speziell
@ZD = -Â Z' @0D
bzw
@ZD = -Z'' @0D + HZ' @0DL2
20_Charakteristische_Funktionen.nb
116
20.3.11 Satz: Sind die beiden stetigen Zufallsvariablen X und Y unabhängig, so gilt für alle s œ X +Y @sD = X @sD Y @sD
Für zwei beliebige stetige Verteilungen und gilt damit
* @sD = @sD @sD
Es folgen wieder einige Beispiele:
20.3.12 Beispiel: Man zeige: Eine stetige Zufallsvariable Z besitzt genau dann eine symmetrische
Verteilungsdichte, wenn ihre Fourier-Transformierte reell ist.
ô
Lösung: a) Besitzt Z eine symmetrische Verteilungsdichte Z , so gilt für alle s œ ¶
Z @sD = Ÿ-¶ ‰ Â s z Z @zD „ z = Ÿ-¶ ‰ Â s z Z @zD „ z + Ÿ
=Ÿ
0
¶ Âsz
‰
Z @zD „ z =
0
¶ -Â s z
¶
H‰
+ ‰  s z L Z @zD „ z = 2 Ÿ Cos@s zD Z @zD „ z œ 0
0
b) Ist die Fourier-Transformierte von Z reell, so gilt für alle s œ Z @sD = Ÿ-¶ Cos@s zD Z @zD „ z
¶
und
Ÿ-¶ Sin@s zD Z @zD „ z = 0
¶
und damit
-Z @sD = Ÿ-¶ ‰ Â s z -Z @zD „ z = Ÿ-¶ Cos@s zD -Z @zD „ z + Ÿ-¶ Sin@s zD -Z @zD „ z =
¶
¶
¶
= Ÿ-¶ Cos@-s zD Z @-zD „ z - Ÿ-¶ Sin@-s zD Z @-zD „ z = Ÿ-¶ Cos@s zD Z @zD „ z = Z @sD
¶
¶
¶
Die Fourier-Transformierten von Z und -Z stimmen überein, also besitzen Z und -Z die gleiche Verteilung, womit
gezeigt ist, dass die Verteilungsdichte Z von Z symmetrisch ist.
20.3.13 Beispiel: Für die Fourier-Transformierten der beiden Zufallsvariablen X bzw Y gilt
1+Âs
1-Âs
X @sD =
bzw y @sD =
2
1+s
1 + s2
Gesucht sind ihre Verteilungsdichten X bzw Y .
ô
Lösung: Der Befehl InverseFourierTransform liefert (nach langer Rechnung)
InverseFourierTransform@H1 + ‰ sL ê H1 + s2 L, s, z, Assumptions Æ 8z ≥ 0<D ê Sqrt@2 pD
InverseFourierTransform@H1 + ‰ sL ê H1 + s2 L, s, z, Assumptions Æ 8z < 0<D ê Sqrt@2 pD
−z
0
und
20_Charakteristische_Funktionen.nb
117
InverseFourierTransform@H1 - ‰ sL ê H1 + s2 L, s, z, Assumptions Æ 8z ≥ 0<D ê Sqrt@2 pD
InverseFourierTransform@H1 - ‰ sL ê H1 + s2 L, s, z, Assumptions Æ 8z < 0<D ê Sqrt@2 pD
0
z
also gilt
X @zD = :
‰-z
0
für z > 0
sonst
bzw
0
Y @zD = : z
‰
für z > 0
sonst
20.3.14 Beispiel: Die Zufallsvariablen X1 , X2 , …, Xn seien vollständig unabhängig und identisch verteilt mit
der (für alle i œ 81, 2, …, n< gleichen) Verteilungsdichte
1
X @xD =
p I1 + x2 M
Gesucht ist die Verteilungsdichte Z ihrer Summe Z = X1 + X2 + … + Xn
ô
Lösung: a) Wir überprüfen zuerst, ob es sich bei der positiven Funktion X tatsächlich um eine Verteilungsdichte
handelt:
Integrate@1 ê Hp H1 + x2 LL, 8x, -•, •<D
1
b) Für die Fourier-Transformierte Z @sD von Z gilt wegen Satz 20.3.11
Z @sD = X @sD X @sD … X @sD
1
2
1
Unter Verwendung der Befehle FourierTransform und InverseFourierTransform lässt sich die gesuchte Verteilungsdichte Z von Z damit leicht ermitteln:
ft@s_D := FourierTransform@1 ê Hp H1 + x2 LL, x, sD Sqrt@2 pD
InverseFourierTransform@Hft@sDLn , s, zD ê Sqrt@2 pD
Clear@ftD
n
π In2 + z2 M
20.4 Die charakteristische Funktion
Wir beginnen wieder mit einer Definition:
20_Charakteristische_Funktionen.nb
118
20.4.1 Definition: Ist eine diskrete bzw stetige Verteilung mit der Verteilungsdichte , so heißt die durch
@sD = ⁄zœ ‰  s z @zD
bzw
¶
@sD = Ÿ-¶ ‰ Â s z @zD „ z
auf definierte komplexwertige Funktion , die charakteristische Funktion der Verteilung . Unter der
charakteristischen Funktion Z einer diskreten bzw stetigen Zufallsvariablen Z versteht man die charakteristische Funktion ihrer Verteilung Z .
ô
Ist eine beliebige Verteilung mit der Verteilungsfunktion , so definiert man ganz allgemein
¶
@sD = Ÿ-¶ ‰ Â s z Z @„ zD
wobei das dabei auftretende Integral als Lebesque-Stieltjes-Integral zu verstehen ist.
Im Prinzip lässt sich die charakteristische Funktion einer diskreten bzw stetigen Verteilung mit der
Verteilungsdichte mit Hilfe von Mathematica ermitteln, indem man einfach die in der Definition auftretende
Summe bzw das dort auftretende Integral auswertet. Handelt es sich bei der diskreten bzw stetigen Verteilung um
eine in Mathematica implementierte Verteilung, so lässt sich die charakteristische Funktion von in vielen
Fällen auch unter Verwendung des Befehls CharacteristicFunction bestimmen:
20_Charakteristische_Funktionen.nb
119
à CharacteristicFunction@distribution, sD
liefert die charakteristische Funktion @sD der diskreten bzw stetigen, in Mathematica implementierten
Verteilung distribution.
20.4.2 Bemerkung: Zwischen der erzeugenden Funktion einer diskreten Verteilung , deren Träger eine
Teilmenge von 0 ist bzw der Laplace-Transformierten einer stetigen Verteilung , deren Träger eine
Teilmenge von [0,¶[ ist bzw der Fourier-Transformierten einer stetigen Verteilung sowie der charakteristischen Funktion von gelten die folgenden Beziehungen:
@sD = @-Â Log@sDD bzw @sD = @Â sD bzw @sD = @sD
Aus der Definition der charakteristischen Funktion folgt unmittelbar:
20.4.3 Bemerkung: Besteht zwischen den beiden Zufallsvariablen X und Y die Beziehung Y = a + b X , so gilt
Y @sD = @‰ Â Y s D = @‰ Â Ha+b X L s D = ‰ Â a s X @b sD
Die charakteristische Funktion besitzt eine Reihe von tiefliegenden Eigenschaften, welche in erster Linie für
theoretische Untersuchungen von Bedeutung sind. Wir erwähnen diese Eigenschaften ohne Beweise:
20.4.4 Satz: Eine Verteilung ist durch ihre charakteristische Funktion vollständig bestimmt - oder anders
ausgedrückt - die charakteristischen Funktionen zweier Verteilungen stimmen genau dann überein, wenn die
beiden Verteilungen überein stimmen.
Die charakteristische Funktion wird vor allem im Zusammenhang mit einer - auch für die Praxis sehr wichtigen Konvergenzart verwendet:
20.4.5 Definition:
a) Die Folge Hn Lnœ von Verteilungen konvergiert schwach gegen die Verteilung , wenn für alle z œ , in
denen stetig ist, die Folge Hn @zDLnœ gegen @zD konvergiert.
b) Die Folge HZn Lnœ von Zufallsvariablen konvergiert in Verteilung gegen die Zufallsvariable Z, wenn die
Folge HZn Lnœ ihrer Verteilungen schwach gegen die Verteilung Z von Z konvergiert.
Der direkte Nachweis der schwachen Konvergenz einer Folge von Verteilungen ist oft recht mühsam. In diesem
Zusammenhang ist der folgende Satz von großer Bedeutung:
20.4.6 Satz: Die Folge Hn Lnœ von Verteilungen konvergiert genau dann schwach gegen die Verteilung ,
wenn die Folge Hn Lnœ ihrer charakteristischen Funktionen punktweise gegen die charakteristische Funktion von konvergiert.
An zwei Beispielen wollen wir die Anwendung dieses Satzes sowie die Bedeutung der schwachen Konvergenz
insgesamt demonstrieren:
20_Charakteristische_Funktionen.nb
120
20.4.7 Beispiel: Sei H pn Lnœ eine Folge von Zahlen aus dem Intervall D 0, 1@ mit der Eigenschaft, dass die
Folge Hn pn Lnœ gegen eine Zahl l > 0 konvergiert. Man zeige, dass dann die Folge H@n, pn DLnœ der
Binomialverteilungen schwach gegen die Poissonverteilung @lD konvergiert. Damit ist gezeigt, dass sich für
große n und kleine p die Binomialverteilung @n, pD durch die Poissonverteilung @n pD approximieren lässt.
ô
Lösung: Für die charakteristische Funktion der Binomialverteilung @n, pn D bzw der Poissonverteilung @lD gilt
CharacteristicFunction@BinomialDistribution@n, pn D, sD
CharacteristicFunction@PoissonDistribution@lD, sD
n
J1 − pn + s pn N
J−1+ s N λ
Nun gilt aber offenbar für alle s œ limnض H1 - pn + ‰  s pn Ln = limnض H1 +
Âs
n pn H‰ Â s - 1L n
L = ‰ l H‰ -1L
n
womit unsere Behauptung wegen Satz 20.4.6 gezeigt ist.
Wir wollen die Behauptung, dass sich für große n und kleine p die Binomialverteilung @n, pD durch die Poissonverteilung @n pD approximieren lässt, auch graphisch veranschaulichen:
Manipulate@Plot@8CDF@BinomialDistribution@n, pD, zD, CDF@PoissonDistribution@n pD, zD<, 8z, -1, 3 n p<,
PlotStyle Æ [email protected], Red<, [email protected], Blue<<, PlotPoints Æ 100,
AspectRatio Æ 0.5, AxesOrigin Æ 8-1, 0<, PlotRange Æ All, AxesLabel Æ 8z, @zD<,
ImageSize Æ 8200, 120<D,
8n, 2, 50, 1, Appearance Æ "Labeled"<, 88p, 0.5<, 0.03, 0.5, Appearance Æ "Labeled"<D
n
2
p
0.429
HzL
1.0
0.8
0.6
0.4
0.2
-0.5
0.0
0.5
1.0
1.5
2.0
20.4.8 Beispiel: Für jedes n œ sei Zn = HYn - n pL ê
2.5
z
n p H1 - pL , wobei Yn eine mit den Parametern n und
p binomialverteilte Zufallsvariable bezeichnet. Man zeige, dass die Folge HZn Lnœ in Verteilung gegen eine
20_Charakteristische_Funktionen.nb
121
@0, 1D-verteilte Zufallsvariable Z konvergiert. Damit ist gezeigt, dass sich für große n die Binomialverteilung
@n, pD durch die Normalverteilung @n p,
n p H1 - pL D approximieren lässt.
ô
Lösung: Für die charakteristische Funktion der Binomialverteilung @n, pn D bzw der Normalverteilung @0, 1D gilt
CharacteristicFunction@BinomialDistribution@n, pD, sD
CharacteristicFunction@NormalDistribution@0, 1D, sD
n
J1 − p + s pN
s2
−
2
Wegen Bemerkung 20.4.3 gilt damit für die charakteristische Funktion der Zufallsvariablen Zn (wir verwenden die
Abkürzung q = 1 - p und entwickeln die auftretenden Exponentialfunktionen in eine Reihe)
Zn @sD = Exp@-Â n p sê
= Hq Exp@-Â p sê
n p q D H1 - p + p Exp@Â sê
n p q D + p Exp@Â q sê
n p q DLn =
n p q DLn =
= H1 - p s2 êH2 nL - q s2 êH2 nL + o@1 ênDLn = H1 -
s2
+ o@1 ênDLn
2n
Mit o@1 ênD bezeichnen wir dabei einen Ausdruck, welcher die Eigenschaft limnض Hn o@1 ê nDL = 0 besitzt. Damit
gilt für alle s œ 2
s2
limnض Zn @sD = limnض H1 + o@1 ê nDLn = ‰-s ê2 = Z @sD
2n
womit unsere Behauptung wegen Satz 20.4.6 gezeigt ist.
Wir wollen die Behauptung, dass sich für große n die Binomialverteilung @n, pD durch die Normalverteilung
@n p,
n p H1 - pL D approximieren lässt, auch graphisch veranschaulichen und dabei die maximale Differenz
zwischen den beiden Verteilungsfunktionen ermitteln (bei der Berechnung der maximalen Differenz achte man
darauf, dass die Verteilungsfunktion der Binomialverteilung eine linksseitig stetige Stufenfunktion ist):
20_Charakteristische_Funktionen.nb
122
Manipulate@Show@With@8s = Sqrt@n p H1 - pLD<,
8Plot@8CDF@BinomialDistribution@n, pD, zD, CDF@NormalDistribution@n p, sD, zD<, 8z, n p - 2 s, n p + 2 s<,
PlotStyle Æ [email protected], Red<, [email protected], Blue<<, PlotPoints Æ 100,
AspectRatio Æ 0.5, AxesOrigin Æ 8n p, 0<, PlotRange Æ All, AxesLabel Æ 8z, @zD<,
ImageSize Æ 8230, 130<D,
Graphics@88Red, Text@"Differenz:", [email protected], 0.3<DD,
Text@Max@Join@
Table@Abs@CDF@BinomialDistribution@n, pD, zD - CDF@NormalDistribution@n p, sD, zDD,
8z, 0, n<D,
Table@Abs@CDF@BinomialDistribution@n, pD, z - 1D - CDF@NormalDistribution@n p, sD, zDD,
8z, 0, n<DDD,
[email protected], 0.3<DD<<D<DD,
8n, 1, 1000, 1, Appearance Æ "Labeled"<, 8p, 0.1, 0.9, Appearance Æ "Labeled"<D
n
326
p
0.252
HzL
1.0
0.8
0.6
0.4
0.2
Differenz: 0.0296346
z
70
75
80
85
90
95