Weitere Beispiele zur Anwendung komplexer Zahlen

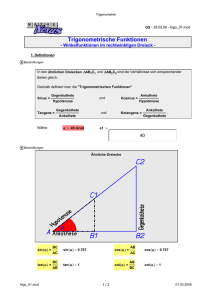
Weitere Beispiele zur Anwendung
komplexer Zahlen
Harmonische Schwingungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
27
Anwendung: Zeigerdiagramm bei der Wechselstromrechnung
. . . . . . . . . . . . .
28
Additionstheoreme für Sinus und Kosinus . . . . . . . . . . . . . . . . . . . . . . . .
34
Formel von Machin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
Harmonische Schwingungen
Es soll die Überlagerung zweier gleichfrequenter harmonischer Schwingungen, z.B. zweier
Wechselspannungen
u1 (t) = u1 sin(ω t + ϕ1 ),
u2 (t) = u2 sin(ω t + ϕ2 ),
bestimmt werden. Man löst diese Aufgabe durch Komplexifizierung der Schwingungen, d.h.
man betrachtet:
u1 (t) = u1 ei(ωt+ϕ1 ) = u1 ei ωt ei ϕ1 ,
u2 (t) = u2 ei(ωt+ϕ2 ) = u2 ei ωt ei ϕ2 ,
und addiert die komplexen Größen:
u(t) = u1 (t) + u2 (t) = u1 ei ωt ei ϕ1 + u2 ei ωt ei ϕ2 = ei ωt u1 ei ϕ1 + u2 ei ϕ2
= ei ωt Aei ϕ = Aei(ωt+ϕ) .
27
Weitere Beispiele zur Anwendung komplexer Zahlen
Nun ist die Summe u(t) der Sinusschwingungen gerade der Imaginärteil von u(t) :
u(t) = Im (Aei(ωt+ϕ) ) = A sin(ω t + ϕ).
Die Hauptaufgabe besteht darin, die komplexe Zahl u1 ei ϕ1 + u2 ei ϕ2 in trigonometrischer bzw.
exponentieller Form als Ai ϕ darzustellen.
Bemerkung 0.1
• Anstelle von Sinusschwingungen hätte man auch Kosinusschwingungen betrachten
können.
• Die Betrachtung ist aber nur für gleichfrequente Schwinungen möglich.
Anwendung: Zeigerdiagramm bei der Wechselstromrechnung
Quelle: Wikipedia http://de.wikipedia.org/wiki/Komplexe Wechselstromrechnung
Sehr verwirrend ist zunächst, dass in der Elektrotechnikgemäß DIN 1302 die imaginäre Einheit
mit j und nicht mit i bezeichnet wird, da i für die Stromstärke reseviert ist.
Charakterisierende Werte
Eine sinusförmige Wechselspannung mit dem Maximalwert û und dem Nullphasenwinkel
ϕu :
u(t) = û sin(ω t + ϕu ).
Momentanwerte, die sich zeitlich ändern werden mit Kleinbuchstaben bezeichnet.
1 = Scheitelwert Û, 2 = Spitze-Spitze-Wert, 3 = Effektivwert Ueff =
Periodendauer T ,
28
q R
1 T
T
0
u(t)u(t) dt, 4 =
Anwendung: Zeigerdiagramm bei der Wechselstromrechnung
Der Effektivwert eines Wechselstroms entspricht dem Wert eines Gleichstroms, der in einem ohmschen
Widerstand dieselbe Wärme erzeugt . Aus dem Effektivwert und dem Form√
faktor 2 eines sinusförmigen Wechselstroms kann dessen Amplitude ı̂ berechnet werden
√
ı̂ = 2 · Ieff
Bei nicht sinusförmigem Wechselstrom ergibt sich in Abhängigkeit der Kurvenform ein anderer
Zusammenhang zwischen Scheitelwert und Effektivwert.
Weltweit wird die elektrische Energieversorgung am häufigsten mit sinusförmigem Wechselstrom vorgenommen.
Physikalische Grundlagen
Als passive lineare Elemente des Wechselstromkreises treten Ohmsche Widerstände, Spulen
(Induktivitäten) oder Kondensatoren (Kapazitäten) auf. Für diese Elemente gilt:
• Ohmscher Widerstand R: die Stromstärke ist der Spannung proportional:
i=
u
.
R
• Spule L: die Stromstärkeänderung ist zur Spannung proportional:
Z
di
u
=
⇐⇒ L · i = u(t) dt.
dt
L
• Kondensator C: die Spannungsänderung ist zur Stromstärke proportional:
Z
du
i
=
⇐⇒ C · u = i(t) dt.
dt
C
Komplexe Größen
Formelzeichen komplexer Größen werden gemäß DIN 1304-1 und DIN 5483-3 durch einen
Unterstrich gekennzeichnet. So wäre die komplexe Spannung zur sinusförmigen Spannung
gerade
u(t) = û(cos(ω t + ϕu ) + j sin(ω t + ϕu )) = ûej(ωt+ϕu )
und die Spannung u(t) = Re u(t) dem Realteil der komplexen Spannung.
Häufig werden die Amplituden und die Nullphasenwinkel zu den komplexen Effektivwerten
û
U = √ ej ϕu = Uej ϕu .
2
29
Weitere Beispiele zur Anwendung komplexer Zahlen
Zeiger
Eine sinusförmige Spannung u(t) = û sin(ω t) mit der Phasenverschiebung Null wird eine
komplexe Spannung U(t) = ûej ωt und ein Zeiger u = û zugeordnet.
Komplexe Spannung:
u(t) = û ejωt = û (cos(ωt) + j sin(ωt))
Wechselspannung:
Zeiger: u = û
Rotierender
Zeiger:
u(t) = Re U (t)
û ejωt
û
u(t) = û sin(ωt)
Das Ohmsche Gesetz für komplexe Größen
Der komplexe Widerstand (auch Impedanz genannt) ist
Z = R + jX ,
dabei ist R der Wirkwiderstand (Resistanz) und X der Blindwiderstand (Reaktanz). Weiterhin
wird
√
Z = |Z | = R 2 + X 2
als Scheinwiderstand bezeichnet.
Der allgemeine Ansatz lautet
Z =
u ûej(ωt+ϕu ) û j(ϕu −ϕi )
=
= e
.
i
ı̂ej(ωt+ϕi )
ı̂
Ohmscher Widerstand
Da der Ohmsche Widerstand R eine reelle Größe ist erhält man mit
u
= R,
i
dass ej(ϕu −ϕi ) = 1 sein muss bzw. ϕu − ϕi = 0. D.h. u und i sind gleichphasig. Der komplexe
Widerstand (Impedanz) ist dann
u û
ZR = R = = .
i
ı̂
30
Anwendung: Zeigerdiagramm bei der Wechselstromrechnung
Induktiver Widerstand
An einer Spule mit der Induktivität L gilt
u di
d
u
=
= (ı̂ej(ωt+ϕi ) ) = ı̂ej(ωt+ϕi ) j ω ⇐⇒ i =
(−j).
L dt
dt
Lω
Mit Hilfe der Eulerschen Formel erhält man
ej
−π
2
= cos
−π
2
und damit
i = ı̂ej(ωt+ϕi ) =
+ j sin
−π
2
= −j
û j(ωt+ϕu − π )
2 .
e
Lω
Für die Nullphasen gilt hier
π
ϕi = ϕu −
2
⇐⇒ ϕu − ϕi =
π
2
.
Im Falle der idealen Spule ist u gegenüber i um π2 phasenverschoben. Man sagt in diesem Fall
auch, dass die Spannung der Stromstärke vorauseilt. Mit ϕu = 0 ergibt sich damit die folgende
Situation:
Rotierende Zeiger:
û e
jωt
Wechselstromgrößen:
û
u(t) = û sin(ωt)
i(t) = ı̂ sin(ωt + ϕi )
ϕi = − π2
ı̂
ı̂ ej(ωt+ϕi )
u = û
Zeigerdiagramm:
i = ı̂ ejφi
In diesem Fall gilt für die Impedanz
Z L = jXL =
u
= j ω L.
i
Kapazitiver Widerstand
Am Kondensator mit der Kapazität C gilt nun
i
du
d
=
= (ûej(ωt+ϕu ) ) = ûej(ωt+ϕu ) j ω .
C
dt
dt
31
Weitere Beispiele zur Anwendung komplexer Zahlen
Mit Hilfe der Eulerschen Formel erhält man
π
ej 2 = cos
und damit
π
2
+ j sin
π
2
=j
π
π
i = ı̂ej(ωt+ϕi ) = Cu ω ej 2 = C ω ûej(ωt+ϕu + 2 ) .
Für die Nullphasen gilt in diesem Fall
ϕi = ϕu +
π
2
π
⇐⇒ ϕu − ϕi = − .
2
Im Falle des idealen Konsators ist u gegenüber i um − π2 phasenverschoben. Man sagt hier,
dass die Spannung der Stromstärke hinherhinkt.
Die Impedanz ist dann
u
1
Z C = jXC = = −j
.
i
Cω
RCL-Reihenschaltung
Wir berechnen die komplexe Spannung u(t) und den Phasenwinkel ϕu für die Reihenschaltung
mit dem Zeigerdiagramm für die Teilspannungen u R (t), u C (t) und u L (t).
In Reihenschaltung liegt überall die Stromstärke i(t) vor und die Spannung ergibt sich
als Überlagerung (Summe) der Teilspannungen. Bei der Reihenschaltung dient der Zeiger der Stromstärke i als Aufganspunkt. Wir nehmen an, dass i in Richtung der x-Achse
liegt.
a) Die am Ohmschen Widerstand liegende Teilspannung u R (t) = Ri(t) ist mit der Stromstärke
in Phase. Ihr Zeiger u R = iR liegt damit in Richtung des Zeiger i.
b) Am induktiven Widerstand Z L = jXL = j ω L liegt folglich die Teilspannung u L (t) = j ω Li(t) mit
π
dem Zeiger u L = i ω L ej 2 = j i ω L und eilt dem Zeiger i um π2 voraus.
i(t)
c) Am kapazitiven Widerstand Z C = jXC = −j ω1C liegt folglich die Teilspannung u C (t) = −j ω C
mit dem Zeiger u C =
32
i
ωCe
j −π
2
= −j
i
ωC
und hinkt dem Zeiger i um
π
2
nach.
Anwendung: Zeigerdiagramm bei der Wechselstromrechnung
RCL-Reihenschaltung:
Zeigerdiagramm
uC
uL − uC
u
uL
uL − uC
ϕu
uC
uR
Die Addition der drei Spannungszeiger den Zeiger u = u R + u C + u L als Vektoraddition bzw.
Addition der zugehörigen komplexen Zahlen. Die Phasenverschiebung ϕu ergibt sich nun als
Argument der komplexen Zahl u. Die Spannung u(t) ist somit
u(t) = Re u(t) = Re u ej ωt = Re ûej ϕu ej ωt = Re û ej(ωt+ϕu ) = û sin(ω t + ϕu ).
Leistung und Scheinleistung
Der Momentanwert der Leistung p ist das Produkt der reellen Momentanwerte von Spannung
und Strom. Die zeitunabhängige komplexe Größe
S = U I = Sej(ϕu −ϕi ) = P + jQ
wird in DIN 5483-3 und DIN 40110-1 als komplexe Leistung oder komplexe Scheinleistung
bezeichnet. Darin sind die in der Wechselstromtechnik üblichen Kenngrößen der Leistung
enthalten:
• die Scheinleistung S
• die Wirkleistung P
• die Blindleistung Q
S = |S | = UI,
P = Re S = UI cos(ϕu − ϕi ),
Q = Im S = UI sin(ϕu − ϕi ),
sowie der Leistungsfaktor cos(ϕu − ϕi ) =
P
.
S
Bemerkung 0.2
Einschränkungen
Es ist zu beachten, dass die komplexe Wechselstromrechnung nur für Netzwerke im eingeschwungenen Zustand anwendbar ist. Dies folgt auch aus der Forderung nach einem
sinusförmigen Verlauf aller Spannungen und Ströme in der zu untersuchenden Schaltung.
33
Weitere Beispiele zur Anwendung komplexer Zahlen
Somit kann mit dieser Methode der komplexen Wechselstromrechnung nicht die Berechnung
von Schaltvorgängen, wie das An- und Ausschalten, Pulse oder Pulsfolgen erfolgen. Diese
Vorgänge können jedoch mit Hilfe von Differenzialgleichungen beschrieben werden.
Weiterhin müssen auch alle Bauelemente einer Wechselstromschaltung wie Widerstände,
Kondensatoren und Spulen lineare Eigenschaften im betrachteten Frequenzbereich zeigen.
Dies trifft beispielsweise bei Spulen mit magnetischer Sättigung oder Kondensatoren, deren
Dielektrizitätszahl von der elektrischen Feldstärke abhängt, nicht zu. Ferner sind in der Regel
die Kennlinien von Halbleiterbauelementen nicht linear. In all diesen Fällen würde bei einer
sinusförmigen Spannung ein nicht sinusförmiger Strom entstehen (oder umgekehrt), und die
komplexe Wechselstromrechnung kann dann nicht angewendet werden.
Additionstheoreme für Sinus und Kosinus
Die Additionstheoreme für Sinus und Kosinus lassen sich elementar geomatrisch herleiten. Das ist nicht ganz einfach und merken kann man sich die Additionstheoreme auch
nur schwer. Mit Hilfe komplexer Zahlen und der Eulerschen Formel geht es aber ganz einfach.
Satz 0.3 (Additionstheoreme)
Für beliebige Winkel α, β ∈ R gilt:
sin(α + β ) = sin α cos β + cos α sin β ,
sin(α − β ) = sin α cos β − cos α sin β ,
cos(α + β ) = cos α cos β − sin α sin β ,
cos(α − β ) = cos α cos β + sin α sin β .
Beweis: Die Eulersche für α bzw. β lautet:
ei α = cos α + i sin α
bzw. ei β = cos β + i sin β .
Analog erhält man
ei(α+β ) = cos(α + β ) + i sin(α + β ) = ei α ei β ,
da die Potenzgesetze auch für komplexe Zahlen gelten. Wir berechnen das Produkt
ei α ei β = (cos α + i sin α) (cos β + i sin β )
= cos α cos β − sin α sin β + i (cos α sin β + sin α cos β )
34
Formel von Machin
Zwei komplexe Zahlen sind genau dann gleich, wenn ihre Real- und Imaginärteile gleich sind,
folgich gilt:
cos(α + β ) = cos α cos β − sin α sin β ,
sin(α + β ) = cos α sin β + sin α cos β .
Analog erhält man die anderen beiden Formeln aus
ei(α−β ) = ei α e−i β
und der Anwendung der Eulerschen Formel.
Alternativ kann man auch verwenden, dass ei(α−β ) = ei(α+(−β )) ist und der Kosinus eine gerade
Funktion, d.h. cos(−x) = cos x, bzw. der Sinus eine ungerade Funktion, d.h. sin(−x) = − sin x,
ist (siehe reelle Funktionen). Damit ist der Satz vollständig bewiesen.
Formel von Machin
John Machin (1680–1751) war ein englischer Astronom und Mathematiker. Seine Formel zur
Berechnung von π4 und damit π lautet:
Lemma 0.1 (Formel von Machin)
π
4
= 4 arctan
1
1
− arctan
.
5
239
Wir wollen als erstes die Richtigkeit der Formel nachweisen. Mit Hilfe komplexer Zahlen
errechnet man sofort
(5 + i)4 (239 − i) = (25 − 1 + 10i)2 (239 − i) = (576 + 480i − 100)(239 − i) = (476 + 480i)(239 − i)
= 113764 + 480 + (114720 − 476)i = 114244 + 114244i
Das Argument der komplexen Zahl z0 = 114244 + 114244i ist tan ϕ0 = 114244
= 1 und
114244
damit
π
ϕ0 = arctan 1 = .
4
Andererseits kann man das Argument auch aus dem Argument der Zahlen z1 = 5 + i
und z2 = 239 − i bestimmen. Es gilt tan ϕ1 = 15 ist das Argument von z1 und das Argu1
ment von z14 ist gerade 4 mal das Argument von z1 , also 4 arctan
von z2
5 . Das Argument
1
1
1
ergibt sich aus tan ϕ2 = − 239 und damit ϕ2 = arctan − 239 = − arctan 239
. Das Argument des Produkts zweier komplexer Zahlen ist gerade die Summe der Argumente, deshalb
35
Weitere Beispiele zur Anwendung komplexer Zahlen
gilt
ϕ0 =
π
4
Damit ist die Formel bewiesen.
= 4ϕ1 + ϕ2 = 4 arctan
1
1
− arctan
.
5
239
Wie kommt man aber auf so eine Formel??
Zunächst muß man wissen, dass Machin mit Zettel und Bleistift rechnete und auch keine
Ahnung von komplexen Zahlen hatte. Zu seiner Zeit waren aber bereits Formeln von Euler
verfügbar, so hatte Euler gezeigt, dass gilt
π
4
= arctan
1
1
+ arctan .
2
3
Wie man mit komplexen Zahlen leicht überprüft ist
(2 + i)(3 + i) = 6 − 1 + 5i = 5 + 5i.
Euler hat seine Formel aber rein geometrisch bewiesen und Machin dürfte schon das Additionstheorem für den Tangens gekannt haben.
Lemma 0.2
Für beliebige Winkel α, β ∈ R gilt:
tan(α + β ) =
tan α + tan β
.
1 − tan α tan β
Wir beweisen diese Formel mit Hilfe der Additionstheoreme für Sinus und Kosinus:
tan(α + β ) =
sin(α + β )
sin α cos β + cos α sin β
cos α cos β (tan α + tan β )
tan α + tan β
=
=
=
cos(α + β ) cos α cos β − sin α sin β cos α cos β (1 − tan α tan β ) 1 − tan α tan β
Gute Zahlen zum Rechnen sind immer 1, 2, 5, 10. Da die Sache mit
versuchen wir es einmal mit 15 . Wir beginnen also mit
tan α =
1
2
und
1
3
so gut funktioniert,
1
.
5
Aus dem Additiontheorem für den Tangens ergibt sich nun
tan(2α) =
2 · 15
2 tan α
2 · 25
10
5
=
=
=
=
.
2
1
5(25 − 1) 24 12
1 − tan α 1 − 52
Nochmalige Anwendung führt auf
tan(4α) =
36
5
2 · 12
2 tan(2α)
10 · 122
120
120
=
=
=
=
= 1, 0084... ≈ 1.
2
2
2
2
5
12(12 − 5 ) 144 − 25 119
1 − tan (2α) 1 − 2
12
Formel von Machin
Damit ergibt sich der Term 4α = 4 arctan 15 . Den zweiten Term erhalten wir indem wir
β = 4α −
π
4
setzen. Dann ist
tan β =
tan(4α) + tan − π4
1 − tan(4α) tan − pi4
=
120
119
1+
−1
120
119
=
(120 − 119)119
1
=
.
119(120 + 119)
239
D.h. wir haben die folgende Formel erhalten:
π
4
= 4α − β = 4 arctan
1
1
− arctan
.
5
239
Bemerkung 0.4
Mit Hilfe seiner Formel gelang es Machin, die Zahl π auf 100 Stellen genau zu berechnen
(Weltrekord seiner Zeit).
Bei Funktionenreihen werden wir sehen, warum die Formel von Machin der Formel von Leibniz
π
= arctan 1 für die näherungsweise Berechnung von π überlegen ist.
4
37