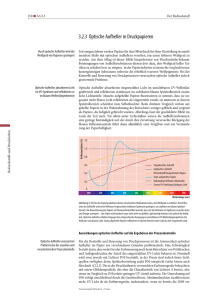
Zustände in klassischer Mechanik und Quantenmechanik

Klassische Mechanik
Quantenmechanik
Reiner Zustand
Punkt im Phasenraum P: (q, p) ∈ P
Strahl im Hilbertraum H oder Projektionsoperator P̂ψ = |ψihψ|
Reelle Funktionen auf P
A:P→R
Observable
Selbstadjungierte Operatoren
 : H → H, † = Â
Wert einer Observablen in einem reinen Zustand
Erwartungswert von  im Zustand |ψi
hÂiψ = hψ|Â|ψi = tr(P̂ψ Â)
Meßwert festgelegt
Wahrscheinlichkeitsverteilung für die
möglichen Meßwerte von Â
A(q, p)
Zeitentwicklung eines
Hamiltonsche Bewegungsgleichungen
∂H
∂H
, ṗi = −
q̇i =
∂pi
∂qi
Phasenraumvolumen zeitlich konstant
(Satz von Liouville)
reinen Zustandes
Schrödingergleichung
d
i~ |ψ(t)i = Ĥ|ψ(t)i
dt
Zeitentwicklungsoperator Û = e−iĤt/~
unitär
(Erhaltung der Wahrscheinlichkeit)
Zeitentwicklung des Wertes einer Observablen
d
1
d
A(q(t), p(t)) = {A, H}
hÂiψ = h[Â, Ĥ]iψ
dt
dt
i~
Gemischter
Wahrscheinlichkeitsverteilung ρ(q, p)
auf P:
ρ(q, p) ∈ R, ρ(q, p) ≥ 0,
Z
d3N q d3N p ρ(q, p) = 1
reiner Zustand:
ρ(q, p) = δ(q − q 0 )δ(p − p0 )
Zustand
Dichtematrix ρ̂:
ρ̂† = ρ̂,
hψ|ρ̂|ψi ≥ 0 ∀ |ψi ∈ H,
trρ̂ = 1
reiner Zustand:
ρ̂ = P̂ψ = |ψihψ|
Erwartungswert in einem gemischten Zustand
Z
hAiρ =
d3N q d3N p ρ(q, p)A(q, p)
hÂiρ̂ = tr(ρ̂Â)
Zeitentwicklung eines gemischten Zustandes
∂ρ
dρ̂
1
= −{ρ, H}
= − [ρ̂, Ĥ]
∂t
dt
i~
(Liouville-Gleichung)
(von-Neumann-Gleichung)
Vorzeichen!
nach Römer und Filk