Arbeitsblatt 1 Test 3 S7M3 2017

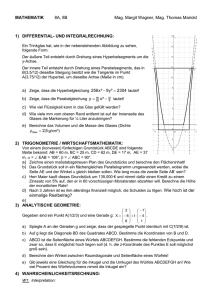
Klasse S7M3
(Krone)
1)
Arbeitsblatt 1 3. Test
Wahrscheinlichkeitsverteilungen
07.03.2017
Eine faire Münze wird 80 mal geworfen. Wie groß ist die Wahrscheinlichkeit,
a. höchstens 45 mal bzw.
b. zwischen 36 und 42 mal
bzw.
c. genau 41 mal "Kopf" zu werfen?
Berechne auch die Näherungen mit der Normalverteilung.
2) In einer Stadt ist der IQ eine normalverteilte Zufallsvariable mit μ = 100 und σ = 15.
a. Welchen IQ muss man haben, um zu den intelligentesten 2% der Einwohner zu
gehören?
b. Die Stadt hat 9800 Einwohner. Bei wie vielen kann man einen IQ über 120 erwarten?
c. Wie viele Einwohner haben einen IQ zwischen 80 und 120?
In einer anderen Stadt haben 20 % der Einwohner einen IQ von über 120 und 10 %
unter 90.
d. Bestimme den durchschnittlichen IQ und die Standardabweichung.
3) Nach dem Messen der Länge von 100 Birnen
ergibt sich die nebenstehend abgebildete
Verteilung.
a. Berechne P(X≤10).
b. In welchem Bereich -k ≤ X ≤ +k liegen 80 % aller Äpfel?
c: In welchem Bereich 7 ≤ X ≤ +k liegen 90 % aller Äpfel?
4) Ein Händler bietet Gurkensamen an, die erfahrungsgemäß zu 95 % keimfähig sind.
a. Welche Wahrscheinlichkeitsverteilung liegt vor? Begründe.
Berechne die Wahrscheinlichkeit , dass von 500 ausgesäten Körnern
(1) höchstens 470 keimen.
(2) zwischen 470 und 490 keimen.
Rechne jeweils mit der Binomialverteilung und der Annäherung durch die
Normalverteilung.
b. Mindestens wie viele Samenkörner werden mit 90 % iger Wahrscheinlichkeit keimen?
Klasse S7M3
(Krone)
Arbeitsblatt 1 3. Test
Wahrscheinlichkeitsverteilungen
07.03.2017
5) Die erwartete Leuchtdauer von Glühlampen beträgt 500 Stunden bei einer
Standardabweichung von 20 Stunden.
a. Berechne die Wahrscheinlichkeit, dass eine Glühlampe mindestens 520 h hält.
b. Berechne die Wahrscheinlichkeit, dass eine Glühlampe zwischen 480 h und 520 h hält.
c. Berechne die Grenzen einer zum Erwartungswert symmetrischen Umgebung, in der
99 % der Leuchtdauern aller Glühlampen liegen.
Für eine neue, technisch verbesserte Glühlampe gilt:
20 % der Glühlampen halten maximal 500 Stunden, 15 % mindestens 600 h.
d. Berechne den Erwartungswert und die Standardabweichung.
6) In einer Urne sind 5000 Kugeln, von denen 1000 rot sind. Es werden 100 Kugeln ohne
Zurücklegen gezogen.
Gesucht ist die Wahrscheinlichkeit P(19X21) für 19 bis 21 rote Kugeln.
a. Berechne P(19X21) näherungsweise mit der Binomialverteilung.
b. Berechne P(19X21) durch Annäherung mit der Normalverteilung.
c. Berechne P(19X21) exakt.
Angenommen, man würde 100 aus 5000 Kugeln mit Zurücklegen ziehen und wüsste nicht
die Anzahl der roten Kugeln, aber die Wahrscheinlichkeit für das Ziehen von höchstens 20
und von mindestens 26 roten Kugeln wäre P(X20)  40 % bzw. P(X26)  10 % .
d. Berechne die Anzahl der roten Kugeln in der Urne.