Erziehung nach Auschwitz

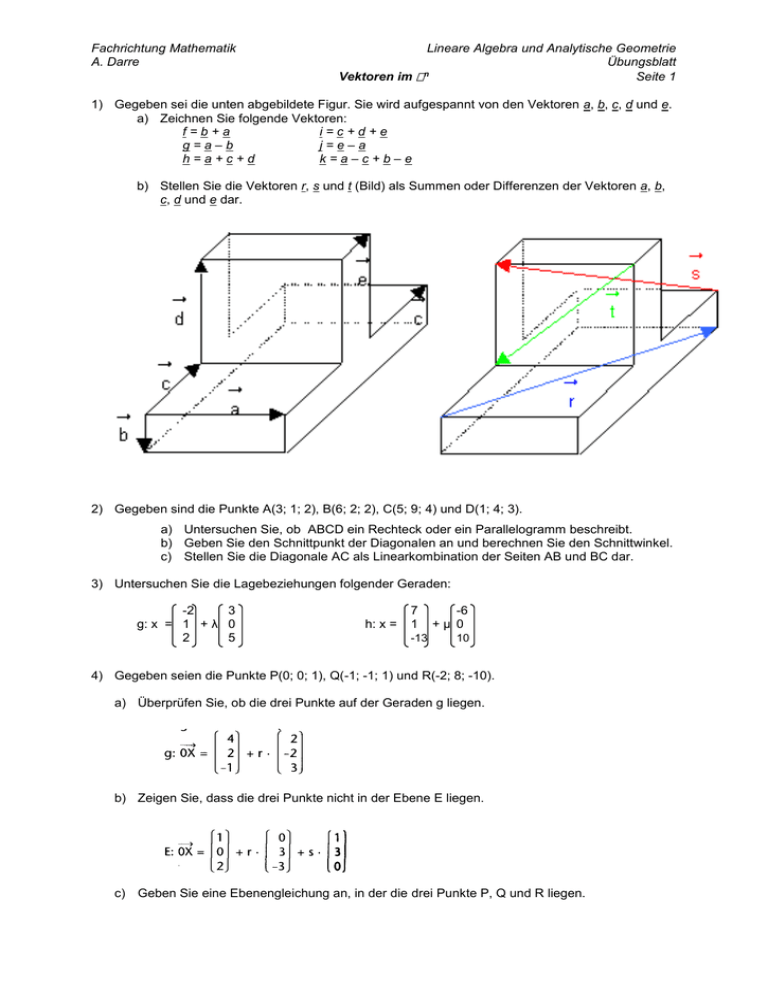
Fachrichtung Mathematik
A. Darre
Lineare Algebra und Analytische Geometrie
Übungsblatt
Vektoren im n
Seite 1
1) Gegeben sei die unten abgebildete Figur. Sie wird aufgespannt von den Vektoren a, b, c, d und e.
a) Zeichnen Sie folgende Vektoren:
f=b+a
i=c+d+e
g=a–b
j=e–a
h=a+c+d
k=a–c+b–e
b) Stellen Sie die Vektoren r, s und t (Bild) als Summen oder Differenzen der Vektoren a, b,
c, d und e dar.
2) Gegeben sind die Punkte A(3; 1; 2), B(6; 2; 2), C(5; 9; 4) und D(1; 4; 3).
a) Untersuchen Sie, ob ABCD ein Rechteck oder ein Parallelogramm beschreibt.
b) Geben Sie den Schnittpunkt der Diagonalen an und berechnen Sie den Schnittwinkel.
c) Stellen Sie die Diagonale AC als Linearkombination der Seiten AB und BC dar.
3) Untersuchen Sie die Lagebeziehungen folgender Geraden:
-2
3
g: x = 1 + λ 0
2
5
h: x =
7
1
-13
-6
+µ 0
10
4) Gegeben seien die Punkte P(0; 0; 1), Q(-1; -1; 1) und R(-2; 8; -10).
a) Überprüfen Sie, ob die drei Punkte auf der Geraden g liegen.
b) Zeigen Sie, dass die drei Punkte nicht in der Ebene E liegen.
c) Geben Sie eine Ebenengleichung an, in der die drei Punkte P, Q und R liegen.
Fachrichtung Mathematik
A. Darre
Lineare Algebra und Analytische Geometrie
Übungsblatt
Vektoren im n
Seite 2
4)
5)
6)
Gegeben seien die Punkte A, B, C sowie die Gerade g durch
A(6; -2; 0), B(-2; 6; 4), C(2; 14; -4),
2
-4
g: x = 14 + λ -20
-4
14
a) Zeigen Sie, dass die Ortsvektoren der Punkte A, B und C linear unabhängig sind.
b) Es sei eine Ebene ‫ ﻉ‬durch die Punkte A, B und C gegeben.
Geben Sie die Parametergleichung der Ebene an.
Stellen Sie die Gleichung der Ebene ‫ ﻉ‬in Koordinatenform dar.
c) Zeigen Sie, dass die drei Punkte A, B und C ein gleichschenkliges Dreieck bilden.
d) Durch die Punkte A und B verläuft eine Gerade h.
Geben Sie die Parametergleichung dieser Geraden an.
Die Gerade g schneidet diese Gerade in einem Punkt S.
Bestimmen Sie die Koordinaten dieses Punktes.
Begründen Sie, warum S gleichzeitig der Spurpunkt der Ebene ‫ ﻉ‬ist.
e) Berechnen Sie den Schnittwinkel φ unter welchem die Gerade h die Ebene ‫ ﻉ‬schneidet.
Erläutern Sie Ihr Vorgehen.
f)
Es gibt einen Kreis , auf welchem die Punkte A, B und C liegen.
Bestimmen Sie die Kreisgleichung von .
Hinweis: Gesucht ist also der Umkreis des Dreiecks ABC.
3
2
3
.
.
7) Gegeben ist die Ebene E: x = 0 + r 1 + s 2 .
2
7
5
a) Liegen die Punkte A(8; 3; 14), B(1; 1; 0), C(4; 0; 11) in der Ebene E?
b) Ermitteln Sie den Parameter, sodass der Punkt P (bzw. Q) in E liegt.
P(4; 1; p), Q(q; 0; 7)
8) Die Punkte P0(0 ; 0 ; 4), A(5 ; 0 ; 0) und B(0; 4; 0) legen eine Ebene E fest.
a) Tragen Sie die Punkte in ein kartesisches Koordinatensystem ein und
kennzeichnen Sie einen Ausschnitt der Ebene E.
b) Ermitteln Sie die Parametergleichung von E.
Hinweis: Vektor OP0 sei Stützvektor
Fachrichtung Mathematik
A. Darre
Lineare Algebra und Analytische Geometrie
Übungsblatt
Vektoren im n
Seite 3
1
2
.
9) Gegeben ist die Gerade g: x = 2 + r -3
-1
0,5
.
Ermitteln Sie die Koordinaten der aller Durchstoßpunkte durch die
Koordinatenebenen: Dxy, Dyz, Dxz.
10) Geben Sie die Formel zur Winkelberechnung zwischen zwei Vektoren an und interpretieren Sie
diese.
11) Gegeben seien die drei Punkte A(2; 1; -2), B(3; 0; 1) und C(0; 3; 4).
a) Die Punkte A, B und C bilden ein Dreieck. Berechnen Sie den Umfang, die Innenwinkel sowie
den Flächeninhalt des Dreiecks.
b) Das Dreieck ABC bildet mit dem Ursprung O(0; 0; 0) eine dreiseitige Pyramide. Wie groß ist
das Volumen dieses Körpers?
c) Die Punkte A, B und C spannen eine Ebene E1 auf. Geben Sie die Ebenengleichung in
Parameterdarstellung und parameterfreier Form an.
d) Gegeben sei eine Gerade g durch die Punkte G(0; 4; 1) und H(3; -2; -1). Geben Sie die
Gleichung von g in Parameterform an und bestimmen Sie rechnerisch die Koordinaten der
Durchstoßpunkte durch die Koordinatenebenen.
e) Zeigen Sie, dass die Gerade g und die Ebene E1 genau einen Durchstoßpunkt besitzen.
Ermitteln Sie die Koordinaten dieses Punktes. In welchem Winkel schneidet g die Ebene E 1?
f) Es sei ein Punkt P(-1; -3; 4) gegeben, mit welchem das Dreieck ABC gemeinsam eine
dreiseitige Pyramide bildet. Berechnen Sie das Volumen dieser Pyramide ABCP und geben
Sie das Verhältnis der Volumina von den Pyramiden ABCP und ABCO an.
g) Die Punkte B, C und P bilden eine Ebene E2. Ermitteln Sie die Parametergleichung von E2
und bestimmen Sie den Normalenvektor. Geben Sie mit Hilfe des Normalenvektors die
parameterfreie Gleichung der Ebene an.
h) Zeigen Sie, dass die Ebenen E1 und E2 einander schneiden und berechnen Sie den
Schnittwinkel.
12) In einem kartesischen Koordinatensystem ist ein Quader ABCDEFGH mit den Punkten A(10; 0;
0), D(0; 0; 0) und F(10; 6; 8) gegeben. Die Fläche ABCD liegt in der x-y-Ebene.
a) Geben Sie die Koordinaten der restlichen Punkte des Quaders an, und zeichnen Sie
den Quader in ein kartesisches Koordinatensystem.
b) Berechnen Sie die Länge der Raumdiagonale AG.
c) Der Diagonalenschnittpunkt S des Vierecks DCGH und der Punkt F bestimmen eine
Gerade. Ermitteln Sie die Koordinaten des Durchstoßpunktes T dieser Geraden durch
die x-y-Ebene.
13) In einem kartesischen Koordinatensystem ist ein schiefes Prisma ABCDEFGH mit der
Grundfläche ABCD durch die Eckpunkte A(4; -2; -3), B(8; 2; -1), C(6; 3; 1), D(2; -1; -1) und
H(1; 0; 5) gegeben. Die Punkte D und H gehören zu ein und denselben Körperkante.
a) Ermitteln Sie die Koordinaten der restlichen Eckpunkte des Prismas. Zeichnen Sie
dieses Prisma in ein Koordinatensystem.
b) Weisen Sie nach, das die Grundfläche ABCD ein Rechteck ist.
c) Berechnen Sie das Volumen des Prisma ABCDEFGH.
14) Gegeben ist von einem Würfel die Seitenlänge a = 6 LE und der Punkt A(3; 4; 1), welcher
parallel zur x-y-Ebene liegt.
a) Bestimmen Sie die Koordinaten aller Punkte.
b) Ermitteln Sie rechnerisch die Koordinaten des Schnittpunktes der Raumdiagonalen.
c) Auf den Würfel wird eine Pyramide gesetzt, deren Grundfläche der Deckfläche des
Würfels entspricht. Die Höhe der Pyramide sei hP = 3 LE. Ermitteln Sie die
Koordinaten des Fußpunktes der Pyramide MP und der Spitze S.
d) Stellen Sie den Sachverhalt graphisch dar.