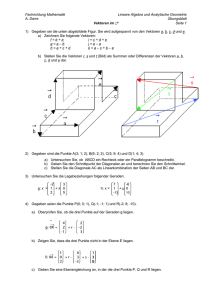
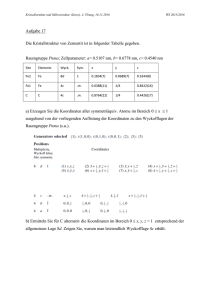
+ + xy ( z ) - - AB DC CB - - AB DC CB = + + AB CD BC + + = AB BC

Man subtrahiert jeweils die Koordinaten von A von
 b1  a1 


den Koordinaten von B. AB = b2  a 2


b  a 
3
 3
Wie berechnet man zu zwei
Punkten A und B den Vektor AB ?
Man addiert die Quadrate der Komponenten und
zieht aus dem Ergebnis die Wurzel. Bezeichnet man
Wie berechnet man die Länge eines
die Komponenten mit x, y (,z), so gilt
Vektors?
a  x 2  y 2 (  z2 )
Man stellt zum Ortsvektor OA
Eine Vektorkette auf.
Beispiel Parallelogramm ABCD:
Wie ermittelt man in der
Vektorrechnung i. A. die
Koordinaten eines Punktes A?
OD = OA + AB = OA + BC
Vereinfache die Vektorkette
AB  DC  CB
AB  DC  CB = AB  CD  BC
= AB  BC  CD  AD
Wo liegt im StandardKoordinatensystem vom Ursprung
aus gesehen die Zahl 1 der xAchse?
1 Kästchen-Diagonale nach links unten
Wie ermittelt man die Koordinaten
des Mittelpunkts MEF einer Strecke
EF?
Wie ermittelt man die Koordinaten
des Schwerpunkts S eines
Dreiecks?
Man berechnet jeweils den Durchschnitt der beiden
Koordinaten.
 x1  x 2 y1  y 2 z1  z2 
|
|
2
2 
 2
MEF( 
Man berechnet jeweils den Durchschnitt der drei
Koordinaten.
 x1  x 2  x 3 y1  y 2  y3 z1  z2  z3 
|
|

3
3
3


S( 
®
b
®
-b
®
a
®
®
a+b
®
b
®
-b
Geometrische Addition und Subtraktion zweier Vektoren
Wie zeigt man, dass zwei Strecken
AB und CD parallel sind?
Wie weist man nach, dass ein
Dreieck ABC bei B einen rechten
Winkel hat.
Wie zeigt man, dass ein Viereck
EFGH ein Parallelogramm ist?
Welche (minimale) Zusatz–
bedingung macht ein Parallelo–
gramm zu einem Rechteck?
Wie überprüft man, ob ein Viereck
ein Quadrat ist?
Wie addiert man geometrisch zwei
Vektoren, von denen jeweils ein
Pfeil gegeben ist.
Wie subtrahiert man geometrisch
zwei Vektoren?
Wie multipliziert man geometrisch
einen Vektor mit einer Zahl k?
Wie zeigt, man dass 6 Punkte
ABCDEF ein Prisma bilden mit
ABC und DEF als parallele
Seitenflächen?
Wie berechnet man den Abstand
eines Punktes einer Funktion f zum
Ursprung?
Wie berechnet man bei einer
Wurzelfunktion f(x) = ....
günstig die Extremstellen?
Man weist nach, dass der eine (Strecken-)Vektor ein
Vielfaches des anderen ist (die Vektoren sind
kollinear sind): AB  k  CD für ein k 0
Mit der Umkehrung des Satzes von Pythagoras.
2
2
BA  BC  AC
2
(Nur) zwei gegenüberliegende Seitenvektoren
müssen gleich sein. EF  HG oder EH  FG
a) 1 rechter Winkel
b) gleich lange Diagonalen
Man zeigt, dass das Viereck ein Rechteck mit 2
gleich langen benachbarten Seiten ist oder dass das
Viereck eine Raute mit einem rechten Winkel ist.
Man legt den einen Pfeil durch Parallelverschiebung
mit dem Fußpunkt an die Spitze des anderen. Der
Summenvektor zeigt vom Fußpunkt des ersten zu
Spitze des zweiten Vektors. (s. u.)
Man addiert den Gegenvektor des Subtrahenden.
(s. u.)
Man zeichnet den Vektor k-mal so lang und hält die
Richtung bei. Fall k<0 ist, ändert man die
Orientierung.
Die Verschiebungsvektoren AD, BE und CF
müssen alle gleich sein.
d(O, f(x)) =
x 2  f ( x )2
Man berechnet die Extremstellen des Terms unter
der Wurzel. (Die y-Werte mit der Wurzelfunktion
berechnen!)