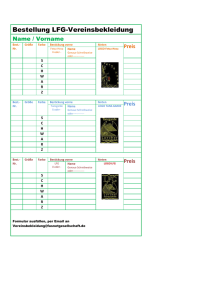
Mathematische Symbole - MTA

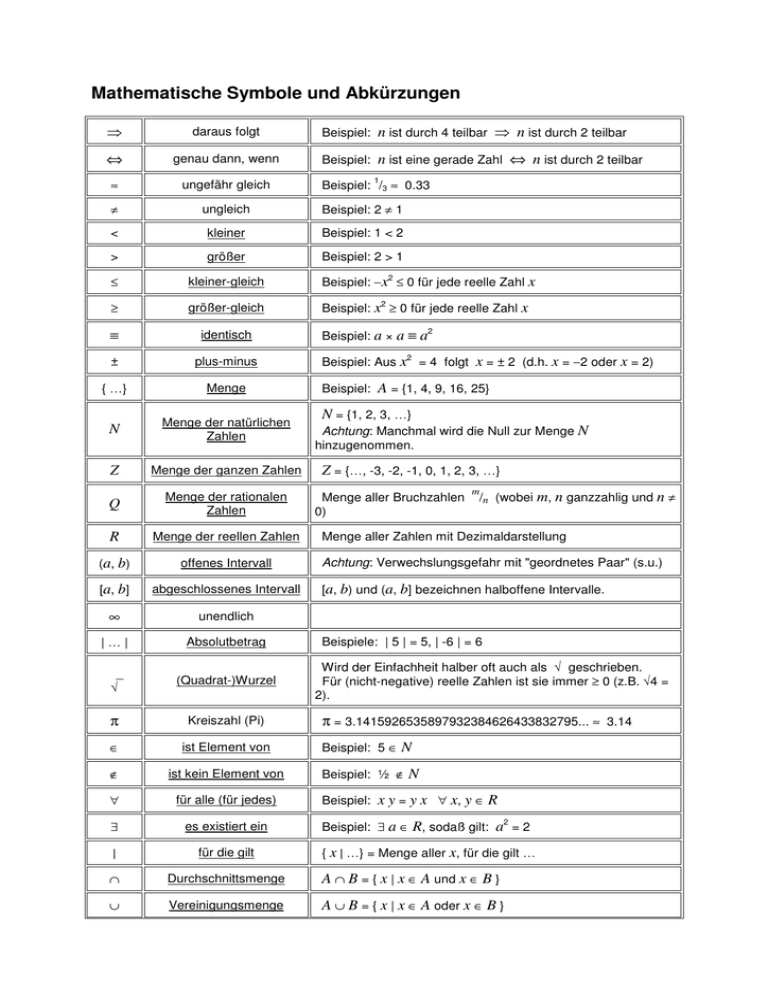
Mathematische Symbole und Abkürzungen
⇒
daraus folgt
Beispiel:
n ist durch 4 teilbar ⇒ n ist durch 2 teilbar
⇔
genau dann, wenn
Beispiel:
n ist eine gerade Zahl ⇔ n ist durch 2 teilbar
≈
ungefähr gleich
≠
ungleich
Beispiel: 2 ≠ 1
<
kleiner
Beispiel: 1 < 2
>
größer
Beispiel: 2 > 1
≤
kleiner-gleich
Beispiel: −x ≤ 0 für jede reelle Zahl x
≥
größer-gleich
Beispiel: x ≥ 0 für jede reelle Zahl x
≡
identisch
±
plus-minus
{ …}
Menge
N
Menge der natürlichen
Zahlen
Z
Menge der ganzen Zahlen
Q
Menge der rationalen
Zahlen
R
Menge der reellen Zahlen
( a, b)
offenes Intervall
[a, b]
abgeschlossenes Intervall
∞
unendlich
|…|
Absolutbetrag
_
√
(Quadrat-)Wurzel
π
Kreiszahl (Pi)
∈
ist Element von
Beispiel: 5 ∈ N
∉
ist kein Element von
Beispiel: ½ ∉ N
∀
für alle (für jedes)
∃
es existiert ein
|
für die gilt
∩
Durchschnittsmenge
A ∩ B = { x | x ∈ A und x ∈ B }
∪
Vereinigungsmenge
A ∪ B = { x | x ∈ A oder x ∈ B }
1
Beispiel: /3 ≈ 0.33
2
2
Beispiel: a × a ≡ a
2
2
Beispiel: Aus x = 4 folgt
Beispiel:
x = ± 2 (d.h. x = −2 oder x = 2)
A = {1, 4, 9, 16, 25}
N = {1, 2, 3, …}
Achtung: Manchmal wird die Null zur Menge N
hinzugenommen.
Z = {…, -3, -2, -1, 0, 1, 2, 3, …}
Menge aller Bruchzahlen
0)
m
/n (wobei m, n ganzzahlig und n ≠
Menge aller Zahlen mit Dezimaldarstellung
Achtung: Verwechslungsgefahr mit "geordnetes Paar" (s.u.)
[a, b) und (a, b] bezeichnen halboffene Intervalle.
Beispiele: | 5 | = 5, | -6 | = 6
Wird der Einfachheit halber oft auch als √ geschrieben.
Für (nicht-negative) reelle Zahlen ist sie immer ≥ 0 (z.B. √4 =
2).
π = 3.1415926535897932384626433832795... ≈ 3.14
Beispiel:
x y = y x ∀ x, y ∈ R
Beispiel: ∃ a ∈ R, sodaß gilt:
a2 = 2
{ x | …} = Menge aller x, für die gilt …
⊆
ist Teilmenge von
Beispiel:
N⊆Z
⊇
ist Obermenge von
Beispiel:
Z⊇N
\
Komplementärmenge
^
hochstellen (Potenz)
∧
logisches und
∨
logisches oder
¬
logisches nicht
{}
leere Menge
≅
isomorph
Kann im konkreten Fall verschiedene Bedeutungen haben,
z.B., daß zwei Mengen "gleichmächtig" sind.
( a, b)
geordnetes Paar
Achtung: Verwechslungsgefahr mit "offenes Intervall" (s.o.)
×
kartesisches Produkt
zweier Mengen
R2
zweidimensionaler Raum
R3
dreidimensionaler Raum
A\B={x∈A|x∉B}
Dafür sind auch die Schreibweisen
gebräuchlich.
A ~ B und A – B
2
Beispiel: Schreibweise x^2 anstelle von x
Dafür ist auch das Symbol φ gebräuchlich.
A × B = { (a, b) | a ∈ A, b ∈ B }. Ausgesprochen: "A kreuz
B ".
Manchmal auch für die Multiplikation zweier Zahlen
verwendet.
Mathematische Formalisierung der Zeichenebene als R × R .
Ausgesprochen: "R zwei".
Formalisierung des dreidimensionalen Raumes als R × R
×R.
n
Verallgemeinerung: R
(n = 4, 5, …).
Vektoren werden fett daregstellt.
Beispiel: a = (3, 4).
a
Vektor
|…|
Betrag eines Vektors
||
parallel
Schreibweise: a
|| b
⊥
normal (orthogonal)
Schreibweise: a
⊥b
∆
Dreieck
Beispiel: | (3, 4) | = 5.
Schreibweise für das Dreieck mit Eckpunkten A, B und C:
∆ABC
Achtung: Verwechslungsgefahr mit "Änderung" (s.u.)
Winkel
f(x)
Zuordnungsvorschrift für
Funktionen
o
Verkettung von Funktionen
→
Zuordnungsvorschrift für
Funktionen
→
asymptotisches Verhalten:
"gegen"
Schreibweise:
CAB (für den Winkel mit Scheitel A).
3
Beispiel: Durch f(x) = x ist eine Funktion
definiert.
(f o g) (x) =
f (g(x))
Beispiel: Durch
definiert.
2
f:R→R
f : x → x2 ist eine Funktion f : R → R
Beispiel: x wächst für x → ∞ ("x gegen Unendlich") über jede
Schranke.
e
Eulersche Zahl
|
bedingte
Wahrscheinlichkeit
< ...>
Erwartungswert
µ
Erwartungswert
σ2
Varianz
σ
Standardabweichung
'
Ableitung
Beispiel: (x
''
Zweite Ableitung
Beispiel: (x
∆
Differenz, Änderung
d
Differential
d/dx
Differenzieren
e = 2.7182818284590452353602874713526... ≈ 2.718
Schreibweise: p(A|B)
Beispiel: < a > für den Erwartungswert der Zufallsvariable a.
Eine andere Schreibweise dafür ist E(a).
Übliche Bezeichnung für den Erwartungswert einer
Zufallsvariable.
Übliche Bezeichnung für die Varianz einer Zufallsvariable.
Übliche Bezeichnung für die Standardabweichung einer
Zufallsvariable.
2 '
) = 2x
3 ''
) = 6x
Differenzenquotient: ∆f/∆x
Achtung: Verwechslungsgefahr mit "Dreieck" (s.o.)
Ableitung ("Differentialquotient"): df/dx.
Dies wird ausgesprochen als "df nach dx".
2
2
2
Beispiel: d(x )/dx = 2x.
Ausgesprochen: "d nach dx von ...".
2
d /dx
Zweimal differenzieren
|
an der Stelle
∫ ... dx
unbestimmtes Integral
∫ab ... dx
bestimmtes Integral
|
Differenz an den Stellen
2
Beispiel: d (sin x)/dx = − sin x.
Ausgesprochen: "d zwei nach dx-Quadrat von ...".
2 '
Beispiel: (x
) |x=5 = 10
2
Beispiel: ∫ x dx
Beispiel: ∫0
3
= x3/3
x2 dx = 9
Wird für das bestimmte Integral verwendet.
2
2
3 2
3
3
Beispiel: ∫1 3x dx = x |1 = 2 − 1 =
7