34011 - Mathe-CD

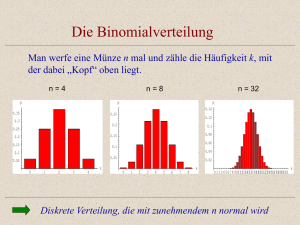
STOCHASTIK
Binomialverteilung
at
he
-c
d
Kaum Theorie, aber viel Training
.d
e
Einführung:
Mehr Theorie in 34012
Zusätzliche Aufgabensammlung in 34021
Ausführliche Erklärung des Einsatzes dreier Rechner:
.m
CASIO fx 9860
CASIO ClassPad II
TI Nspire CAS
fü
rw
w
w
Grafikrechner:
CAS-Rechner:
D
EM
O
Datei Nr. 34 011
Umgeschrieben:
Stand: 20. Oktober 2013
Text deutlich geändert!
Friedrich W. Buckel
INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
www.mathe-cd.de
34011
Binomialverteilung 1
2
Inhalt
§2
3
1.1
Das Experiment „Ziehen ohne/mit Zurücklegen“ – Zufallsvariable
3
Berechnung der Wahrscheinlichkeiten aus dem Baumdiagramm
4
1.2
Das Glücksrad – ganz ausführliche Berechnung mittels Kombinatorik
6
1.3
Andere Beispiele – kurze Berechnung mit TR
9
(a)
Würfeln
9
(b)
Defekte Schrauben finden
(c)
Münze werfen
(d)
Spielkarten ziehen
.d
e
Binomialverteilung - Einführung
10
11
at
he
-c
d
§1
Binomialverteilung – Theorie und Formeln
12
13
Berechnung einer kompletten Wertetafel für BinomialPDf
(1) mit TI Nspire CAS
(2) mit CASIO ClassPad
16
19
Binomialverteilung – Musterbeispiele
20
§4
Verteilungsfunktion für die Binomialverteilung
24
4.1
Berechnung von Intervall-Wahrscheinlichkeiten
24
4.2
Hintergrund einer Verteilungsfunktion
26
27
Weiteres Training Binomialverteilung
28
5.1
fü
rw
w
§3
w
.m
(3) mit dem GTR CASIO FX-9860 (o.ä.)
15
Berechnung von Intervall-Wahrscheinlichkeiten
28
(1)
Weniger als / Höchstens
28
(2)
Mindestens / Mehr als
30
(3)
Von … bis / Zwischen
32
Histogramm
D
EM
O
§5
5.2
§6
§7
Umfangreichere Anwendungsaufgaben
Der Erwartungswert einer Zufallsvariablen
35
40
5.1
Wiederholung (Vom Mittelwert zum Erwartungswert)
42
5.2
Erwartungswert bei der Binomialverteilung
43
Arbeiten mit Tabellen zur Binomialverteilung
44
Anhang:
Hinweis: Die Dreimal-Mindestens-Aufgabe wird im Text 31110 besprochen
Friedrich Buckel
www.mathe-cd.de
34011
Binomialverteilung 1
24
§ 4 Die Verteilungsfunktion für die Binomialverteilung
4.1 Berechnung von Intervall-Wahrscheinlichkeiten
Einführungs-Beispiel (6b)
Eine Maschine stellt Schrauben her und produziert dabei mit 10 % relativer Häufigkeit fehlerhafte
Schrauben. Wie groß ist die Wahrscheinlichkeit, dass man unter fünfzig überprüften Schrauben
höchstens 2
B:
C:
mehr als 5 aber höchstens 8
D:
mehr als 3
E:
weniger als 5
Klarstellung: Ein Ereignis ist die Menge
der dazu gehörenden Ergebnisse. Also
eine „Ergebnismenge“. Gebräuchlich ist
aber auch der Begriff „Ereignismenge“,
nicht als Menge von Ereignissen,
sondern als die zu einem Ereignis
gehörende Menge von Ergebnissen.
.d
e
A:
mindestens 7
at
he
-c
d
defekte findet?
Lösung:
Zuerst MUSS man eine Zufallsvariable definieren und dazu diesen Pflichttext schreiben:
Es sei X die Anzahl der defekten Schrauben unter 50 ausgewählten.
X ist binomial verteilt mit pdef = 0,1 (10% sind defekt).
Definitionsbereich für X: D = 0 ; 1; ... ; 49 ; 50 .
„binomial verteilt“ heißt, dass man die Wahrscheinlichkeiten für X mittels der
Binomialverteilung berechnet.
.m
Wissen:
w
Jedes der drei genannten Ereignisse lässt sich durch eine Ungleichung beschreiben.
w
Ereignis A: Man findet höchstens 2 defekte Schrauben:
fü
rw
Zugehörige Ereignismenge:
Wahrscheinlichkeit:
X  2:
A  0 ; 1; 2
P  A   P  X  2   P  X  0   P  X  1  P  X  2 
Für solche Summen enthalten die modernen Rechner die binomiale Verteilungsfunktion.
Diese heißt binomialCDf (bei CASIO) oder binomCDf (bei TI Nspire).
CASIO:
D
EM
O
Menü: Interaktiv – Verteilungen – (diskret) – binomialCDf50
TI Nspire:
Menü: Wahrscheinlichkeit – Verteilungen – BinomialCdf:
Ergebnis:
Merke:
Friedrich Buckel
P  A   P  X  2   0,1117
Die Funktion BinomialCDf berechnet die Summe der Wahrscheinlichkeiten
von a (unterer Wert) bis b (oberer Wert).
www.mathe-cd.de
34011
Binomialverteilung 1
Ereignis B:
25
Man findet weniger als 5 defekte Schrauben:
X  5:
Ereignismenge:
B  0 ; 1; 2; 3; 4
B kann man auch so beschreiben:
X  4.
Man findet höchstens 4 defekte Schrauben:
CASIO ClassPad:
TI Nspire:
Ergebnis:
P  X  5   P  X  4   0,4312
Hinweis:
Man beachte, dass jeder Hersteller die Reihenfolge der Parameter selbst
.d
e
Berechnung:
at
he
-c
d
festlegen kann:
CASIO: (von , bis , n, p)
TI: (n, p, von , bis)
Die Anzahl der angezeigten Dezimalstellen kann man selbst im Rechner einstellen.
Man findet mehr als 5 aber höchstens 8 defekte Schrauben:
Jetzt verwendet man eine Doppelungleichung:
5  X  8:
Oder besser so:
6X8
.m
Ereignis C:
Ergebnismenge:
CASIO ClassPad:
Ergebnis:
P  5  X  8   P  6  X  8   0,3260
TI Nspire:
fü
rw
w
w
Berechnung:
C  6 ; 7 ; 8
Ereignis D:
X3
Ergebnismenge:
D  4 ; 5 ; ... ; 50
Man findet mindestens 7 defekte Schrauben:
X7
Ergebnismenge:
E  7 ; 8 ; ... ; 50
D
EM
O
Ereignis E:
Man findet mehr als 3 defekte Schrauben:
Berechnungen:
CASIO ClassPad:
TI Nspire:
HINWEIS:
Einfachere oder ältere Rechner haben möglicherweise nicht die Möglichkeit, für die
Verteilungsfunktion eine untere Schranke einzugeben, sie verwenden stets dafür die Zahl 0.
Dann muss man im Beispiel C so vorgehen:
P C  P 6  X  8  P  X  8  P  X  5
Von der Wahrscheinlichkeit für die Werte 0 ; 1; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ;8 subtrahiert man die
Wahrscheinlichkeit für die Zahlen, die nicht zu C gehören, also von 0 ; 1; 2 ; 3 ; 4 ; 5 .
Friedrich Buckel
www.mathe-cd.de
34011
Binomialverteilung 1
26
4.2 Hintergrund einer Verteilungsfunktion
Die Binomialverteilung dient der Berechnung einzelner Werte: P  X  x 
Beispiel:
Beim Würfeln tritt jede Augenzahl mit der Wahrscheinlichkeit
Beim Experiment 5-mal Würfeln erhält man also mit p1 
1
6
1
6
auf.
eine Eins, und mit p2 
5
6
keine Eins.
Die Wahrscheinlichkeit für die Anzahl X der geworfenen
Einsen kann man mit der Binomialverteilung berechnen:
.d
e
P  X  0    56   0,4019
5
at
he
-c
d
4
5
P  X  1     61   65   0,4019
1
 
2
3
5
P  X  2       61    56   0,1608
2
 
3
2
5
P  X  3       61    56   0,0322
3
4
1
5 
P  X  4       61    56   0,0032
4
 
P  X  5    61   0,0001
.m
5
w
Rechner verwenden die Bezeichnung PDf.
w
Die Verteilungsfunktion der Binomialverteilung berechnet üblicherweise die Summe der
Wahrscheinlichkeiten von 0 bis x: P  X  x   P  0  X  x 
fü
rw
Man kann also aus obiger Tabelle berechnen:
P  X  0   P  X  0   0,4019
P  X  1  P  X  0   P  X  1  0,4019  0,4019  0,8038
…..
D
EM
…..
O
P  X  2   P  X  0   P  X  1  P  X  2   0,8038  0,1608  0,9646
P  X  5   P  X  0   ...  P  X  5   1
!!!
(Abweichungen ergeben sich durch Addition gerundeter Werte.)
Neue Rechner verwenden die Verteilungsfunktion, für die man die Abkürzung CDf verwendet,
auch schon für untere Grenzen, die größer als 0 sind.
Friedrich Buckel
www.mathe-cd.de
34011
Binomialverteilung 1
27
Das Diagramm für die Binomialverteilung nennt man
in dieser Form ein Stabdiagramm.
Es besteht aus 6 Stäben, von denen der letzte so
Schaubilder für Verteilungsfunktionen stellt man
oft als Treppenkurven dar.
P  X  1  0,8038 ist dann eine horizontale Strecke
von x = 1 bis vor x = 2.
at
he
-c
d
.d
e
kurz ist, dass man ihn nur noch als Punkt darstellen kann.
usw.
w
Diese Werte wachsen durch die fortgesetzte
.m
Bei x = 2 springt die Treppe zum nächsten Wert 0,9645,
w
Aufsummierung an bis sie den Wert 1 erreichen.
fü
rw
Bei großem n sind die letzten Einzelwerte der
Binomialverteilung in der Regel sehr klein,
so dass der kumulierte Wert schon viel früher
D
EM
O
als 1 angezeigt wird.
Friedrich Buckel
www.mathe-cd.de
34011
Binomialverteilung 1
28
§ 5 Training Binomialverteilung
Siehe auch Text 34021 – Aufgabensammlung zur Binomialverteilung
5.1 Training zur Berechnung von Intervall-Wahrscheinlichkeiten
(1)
Weniger als / Höchstens - Aufgaben
Beispiel 7a
(Zugehöriges 7b folgt später)
.d
e
Mit einem idealen Würfel wird 100-mal gewürfelt.
Mit welcher Wahrscheinlichkeit erzielt man höchstens 5 Einsen bzw. höchstens 20 Einsen?
at
he
-c
d
Lösung:
X sei die Zahl der Einsen. X ist binomial verteilt mit p  61 .
P  X  5   FB  5,100, 61   0,0004
P  X  20   FB  20,100, 61   0,848
Beispiel 8a
.m
Bei einem Test gibt es pro Frage 3 mögliche Antworten. Ein Prüfling kreuzt nur durch Raten an.
Mit welcher Wahrscheinlichkeit hat er von 24 Fragen weniger als ein Viertel richtig?
w
Lösung:
w
X sei die Zahl der richtig angekreuzten Fragen. X ist binomial verteilt mit p  31 .
fü
rw
P  X  6   P  X  5   FB  5,24, 31   0,138
Ergebnis: Mit 13,8% Wahrscheinlichkeit hat er nur 0 bis 5 Richtige angekreuzt.
Beispiel 9a
O
Beim Verpacken von Eiern gehen immer wieder einige zu Bruch. Die Erfahrung zeigt, dass in einer
Zwölfer-Packung durchschnittlich ein Ei beschädigt ist.
D
EM
Mit welcher Wahrscheinlichkeit enthält eine Schachtel mit 12 Eiern
a)
kein beschädigtes Ei?
b)
weniger als 2 beschädigte Eier?
c)
weniger als 4 beschädigte Eier?
Lösung:
Die Wahrscheinlichkeit, dass ein Ei beschädigt ist, ist
1
12
. Es sei X die Zahl der beschädigten Eier in
einer 12er-Packung. X ist binomial verteilt.
a)
11
P  X  0    12

b)
P  X  2   P  X  1  FB 1,12, 121   0,736
c)
P  X  4   P  X  3   FB  3,12, 121   0,986
12
Friedrich Buckel
 fB  0,12, 121   0,352
www.mathe-cd.de
34011
Binomialverteilung 1
29
Aufgabe 10
30 % der Personen in Schieldorf sind Linkshänder.
Mit welcher Wahrscheinlichkeit findet man dort unter 10 Testpersonen
a)
genau 3 Linkshänder?
b)
höchstens 5 Linkshänder?
c)
weniger als 4 Linkshänder?
X sei die Anzahl der Linkshänder. X ist binomial verteilt mit p = 0,3.
P  X  3   fB  3;10;0,3   0,267
b)
P  X  5   FB  5;10;0,3   0,953
c)
P  X  4   P  X  3   FB  3;10;0,3   0,650
at
he
-c
d
a)
.d
e
Lösung:
d. h. etwa 27%.
d. h. etwa 95%.
D
EM
O
fü
rw
w
w
.m
d. h. etwa 65%.
Friedrich Buckel
www.mathe-cd.de
34011
(2)
Binomialverteilung 1
30
Mindestens – Aufgaben / Mehr als - Aufgaben
Mit der zuvor besprochenen Verteilungsfunktion kann man auch diese Aufgaben erledigen.
Dazu muss man auf das Gegenereignis umschalten und die Höchstens-Aufgabe verwenden.
Merke:
X  5 (mindestens 5)
Also gilt:
Beispiel 6c
P  X  4  1 P  X  4
.d
e
Also gilt:
X  4 (höchstens 4)
ist das Gegenteil von
X  4 (höchstens 4)
ist das Gegenteil von
P  X  5  1 P  X  4
at
he
-c
d
X  4 (mehr als 4)
(6a Seite 38 und 6b Seite 39 gehören dazu)
Eine Maschine stellt Schrauben her und produziert dabei mit 5 % relativer Häufigkeit fehlerhafte
Schrauben. Wie groß ist die Wahrscheinlichkeit dafür,
dass unter zehn überprüften Schrauben mehr als 2 defekt sind?
b)
dass unter zwanzig überprüften Schrauben mindestens 2 defekt sind.
D
EM
O
fü
rw
w
w
.m
a)
Friedrich Buckel
www.mathe-cd.de