QUZPAEBJ eyx HC st MLWVG q - Heldermann

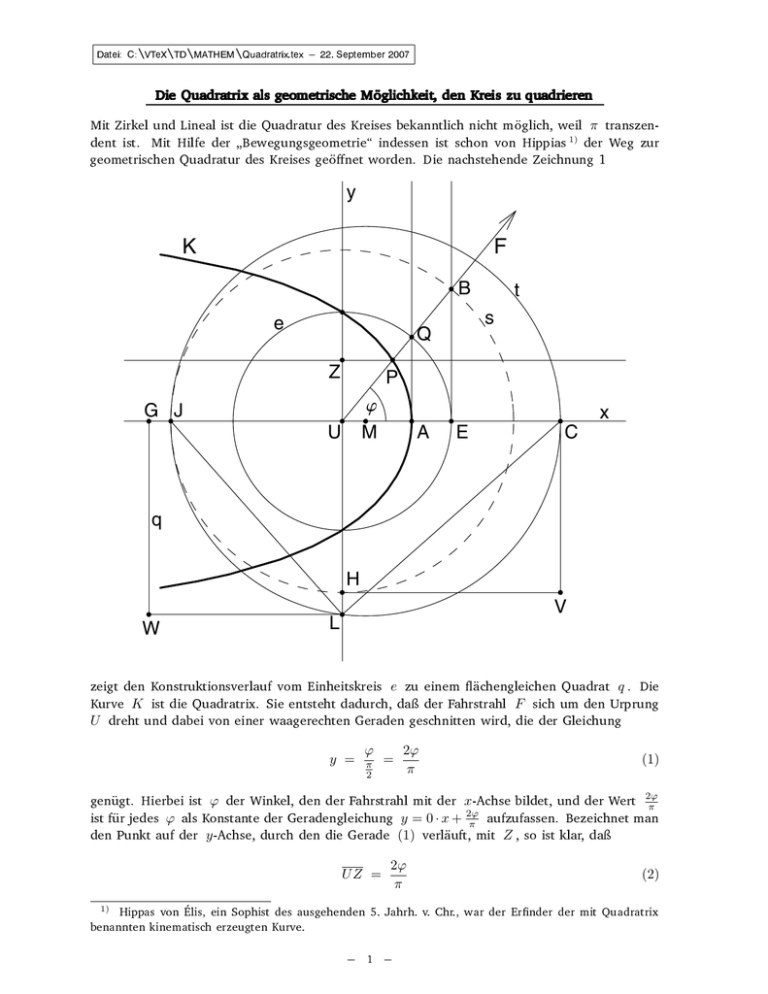
Datei: C:\VTeX\TD\MATHEM\Quadratrix.tex 22. September 2007
Die Quadratrix als geometrische M
Moglichkeit,
oglichkeit, den Kreis zu quadrieren
Mit Zirkel und Lineal ist die Quadratur des Kreises bekanntlich nicht moglich, weil π transzendent ist. Mit Hilfe der ‰Bewegungsgeometrie indessen ist schon von Hippias 1) der Weg zur
geometrischen Quadratur des Kreises geonet worden. Die nachstehende Zeichnung 1
y
K
F
B
e
s
Q
Z
t
P
j
M
G J
U
x
A
E
C
q
H
W
V
L
zeigt den Konstruktionsverlauf vom Einheitskreis e zu einem achengleichen Quadrat q . Die
Kurve K ist die Quadratrix. Sie entsteht dadurch, da der Fahrstrahl F sich um den Urprung
U dreht und dabei von einer waagerechten Geraden geschnitten wird, die der Gleichung
y =
ϕ
π
2
=
2ϕ
π
(1)
genugt. Hierbei ist ϕ der Winkel, den der Fahrstrahl mit der x -Achse bildet, und der Wert 2ϕ
π
ist fur jedes ϕ als Konstante der Geradengleichung y = 0 · x + 2ϕ
π aufzufassen. Bezeichnet man
den Punkt auf der y -Achse, durch den die Gerade (1) verlauft, mit Z , so ist klar, da
UZ =
2ϕ
π
(2)
Hippas von E lis, ein Sophist des ausgehenden 5. Jahrh. v. Chr., war der Ernder der mit Quadratrix
benannten kinematisch erzeugten Kurve.
1)
1 Datei: C:\VTeX\TD\MATHEM\Quadratrix.tex 22. September 2007
gilt. Die Gesamtheit der Punkte P , die als Schnittpunkte des Fahrstrahls F = F (ϕ) mit der
zum jeweiligen ϕ gehorigen Geraden y = 2ϕ
π entstehen, bilden die Quadratrix. Die folgende
iπ
, i = 0, 1, 2, . . . , 26 , die zugehorigen
Zeichnung 2 zeigt den Fahrstrahl fur die Werte ϕ = 32
2ϕ
waagerechten Geraden y = π und die jeweiligen Schnittpunkte:
Um die Parameterdarstellung der Quadratrix zu gewinnen, mu r = U P = U P (ϕ) bestimmt
werden. Weil die Winkel 4AU P = ϕ und 4U P Z als Wechselwinkel an Parallelen ubereinstimmen, liegen in den rechtwinkligen Dreiecken M U ZP und M U AQ ahnliche Dreiecke vor.
Also hat man die Verhaltnisbeziehung
UP
QU
=
.
UZ
QA
(3)
Nun ist QU als Radius des Einheitskreises gleich 1 und uberdies, sofern man den Punkt A
schon als durch die Quadratrix erlangt ansieht, QA = sin ϕ . Mithin erhalt man, wenn man
noch (2) berucksichtigt, in
r = UP =
UZ
2ϕ
=
sin ϕ
π sin ϕ
(4)
die gesuchte Parameterdarstellung der Quadratrix.
Bewegt man den Fahrstrahl F um den Ursprung U , so wandert der Punkt P auf der Kurve K .
Lat man ϕ gegen Null gehen, so erhalt man den Punkt A , der zu ϕ = 0 gehort. Wenn ϕ
gegen Null geht, strebt cos ϕ gegen 1 . Das bedeutet, da man nicht einfach auf U A = cos ϕ
schlieen darf, wie die Zeichnung bei oberachlicher Betrachtung nahelegt. Vielmehr mu man
U A = lim r(ϕ) = lim
ϕ→0
ϕ→0
2ϕ
π sin ϕ
(5)
berechnen. Das lat sich ohne Umstande mit der l'Hospitalschen Regel erledigen:
2ϕ
2
2
= lim
=
.
ϕ→0 π sin ϕ
ϕ→0 π cos ϕ
π
lim
(6)
Oder man berechnet den Schnittpunkt des Fahrstrahls F , der als Gerade betrachtet die Gleichung
y = (tan ϕ)x hat, mit der Geraden (1) . Das ergibt 2ϕ
π = (tan ϕ)x , also
x =
1
2ϕ
2 cos ϕ
ϕ
=
.
·
·
π tan ϕ
π
sin ϕ
2 (7)
Datei: C:\VTeX\TD\MATHEM\Quadratrix.tex 22. September 2007
Hier erhalt man wegen des bekannten Grenzwertes limϕ→0 sinϕϕ = 1 dasselbe Ergebnis:
lim
ϕ→0
2 cos ϕ
ϕ
2
·
=
.
π
sin ϕ
π
(8)
Betrachtet man fur die Quadratrix, wie es die Zeichnung zeigt, den speziellen Wert ϕ = arccos π2 ,
gilt tatsachlich U A = cos ϕ , so da der Punkt Q als Schnittpunkt des Fahrstrahls mit dem
Einheitskreis senkrecht uber A zu liegen kommt.
Wir erzeugen nun, ausgehend von ϕ = arccos π2 , den Kehrwert π2 geometrisch nach dem
ersten Strahlensatz, demzufolge in den beiden ahnlichen rechtwinkligen Dreiecken 4QU A und
M BU E die Verhaltnisbeziehung
UB
UE
=
UQ
UA
(9)
gilt. Berucksichtigt man die wegen der gezielten Wahl von ϕ = arccos π2 geltende Gleichung
U A = cos ϕ = π2 und die Tatsache, da sowohl U E als auch U Q Radien im Einheitskreis sind,
erhalt man aus (9)
UB =
UB
UB
UE
π
1
=
.
=
= 2 =
1
2
UQ
UA
π
(10)
Schlagt man nun einen Kreis s (in der Zeichnung gestrichelt) um den Nullpunkt U mit dem
Radius U B = π2 , so schneidet dieser Kreis die x -Achse im Punkt J und die y -Achse im Punkt
H mit dem Ergebnis
π
JU = HU =
.
(11)
2
Der nachste Schritt besteht darin, den Punkt C rechter Hand auf der x -Achse mit der Distanz 2
vom Ursprung U festzulegen und anschlieend den Punkt M zu konstruieren. M soll der
Mittelpunkt der Strecke
JC = JU + U C =
sein. Es gilt also
U M = JM − JU =
π
2
+2=
4+π
2
4−π
1 4+π π
=
.
·
−
2
2
2
4
(12)
(13)
Ein dritter Kreis t wird nun um den Punkt M mit dem Radius 4+π
geschlagen. Dabei entsteht
4
der Schnittpunkt L mit der y -Achse. Auf diese Weise gelangt man zu dem rechtwinkligen Dreieck
ber dem ‰Thales-Halbkreis JC . Das Rechteck U HV C hat die Seitenlangen 2 und
4JLC u
π/2 , also den Inhalt π . Seine Seitenlangen sind gleich den Hypotenusenabschnitten U C bzw.
JU des Dreiecks 4JLC . Nun folgt abschlieend aus dem H
ohensatz die Flachengleicheit
des Quadrates GW LU mit dem Rechteck U HV C , womit der Einheitskreis in der Tat rein
geometrisch quadriert ist.
Allerdings stutzt sich die ganze Konstruktion auf die Kenntnis der Lage von A , und diese Lage
lat sich nicht allein mit Zirkel und Lineal gewinnen, sondern erfordert die Hilfe der kinematisch
erzeugten Quadratrix.
√
Die Lange π der Strecke U L lat sich im ubrigen leicht analytisch bestatigen. Nach (13)
ange des Radius 4+π
des
gilt U M = 4−π
4 , und die Strecke M L hat nach Konstruktion die L
4
Kreises t . Weil 4U M L rechtwinklig ist mit der Hypotenuse M L , erhalt man fur die Lange
der Strecke U L
s
4+π
4
2
−
4−π
4
2
=
√
1√
8π + 8π = π ,
4
was, wie nicht anders zu erwarten, mit dem geometrischen Ergebnis ubereinstimmt.
3 (14)
Datei: C:\VTeX\TD\MATHEM\Quadratrix.tex 22. September 2007
√
Zusammenfassung: Akzeptiert man, da zur geometrischen Konstruktion von π der Punkt A
mittels der kinematisch erzeugten
Quadratrix zur Verfugung gestellt wird (also ohne Zirkel und
√
Lineal !), kann der Weg bis zu π in wenigen und ganz einfachen Konstruktionsschritten mit
Zirkel und Lineal zuruckgelegt werden.
1. Errichtung des Lotes in Punkt A , das den Einheitskreis im Punkte Q schneidet,
2. Errichtung des Lotes in Punkt E ,
3. Fahrstrahl F durch U und Q ziehen, um den Schnittpunkt B des Fahrstrahls mit dem im
Punkt E errichteten Lot zu erlangen,
4. Kreis s mit dem durch U B bestimmten Radius schlagen, um den Schnittpunkt J auf der
x -Achse zu erhalten,
5. Punkt C zwei Einheiten rechts von U auf der x -Achse festlegen,
6. Mittelpunkt der Strecke JC konstruieren,
7. Kreis t mit dem durch M C bestimmten Radius schlagen, um den Schnittpunkt L auf der
y -Achse zu erhalten.
√
Fertig, denn die Strecke U L hat die gesuchte Lange π .
4