4 Pythagoras, Sinus, Kreis und Co.

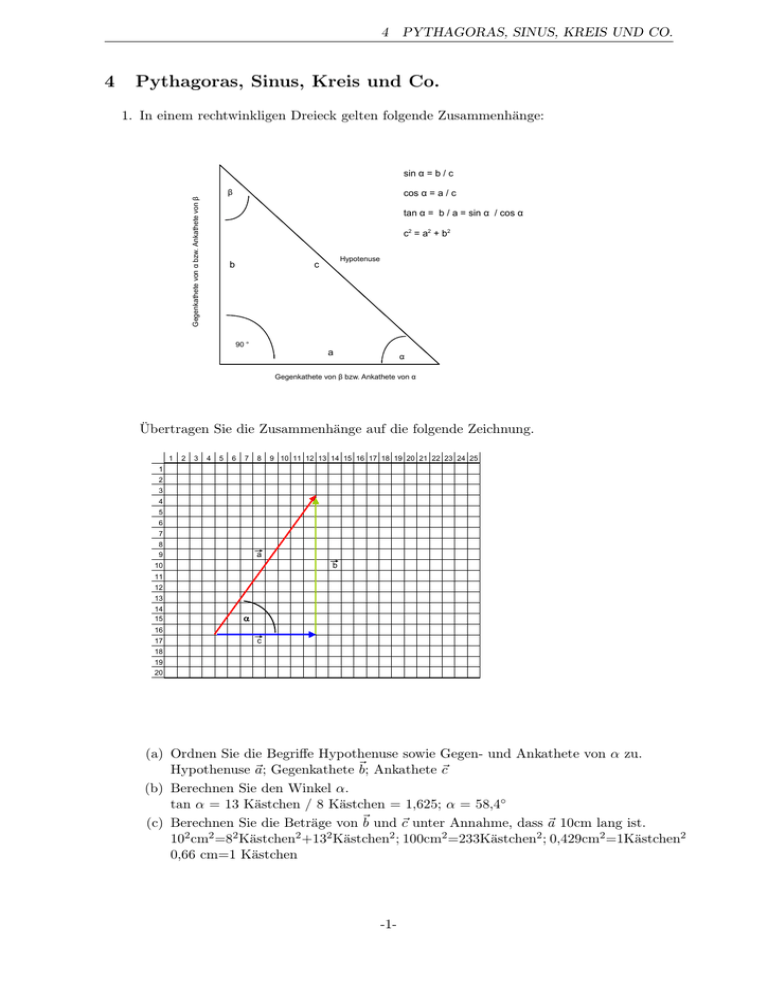
4
Pythagoras, Sinus, Kreis und Co.
1. In einem rechtwinkligen Dreieck gelten folgende Zusammenhänge:
sin α = b / c
β
Gegenkathete von α bzw. Ankathete von β
4
PYTHAGORAS, SINUS, KREIS UND CO.
cos α = a / c
tan α = b / a = sin α / cos α
c2 = a2 + b2
b
Hypotenuse
c
90 °
a
α
Gegenkathete von β bzw. Ankathete von α
Übertragen Sie die Zusammenhänge auf die folgende Zeichnung.
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
1
2
3
4
5
6
7
8
9
a
b
10
11
12
13
14
15
16
17
α
c
18
19
20
(a) Ordnen Sie die Begriffe Hypothenuse sowie Gegen- und Ankathete von α zu.
Hypothenuse ~a; Gegenkathete ~b; Ankathete ~c
(b) Berechnen Sie den Winkel α.
tan α = 13 Kästchen / 8 Kästchen = 1,625; α = 58,4◦
(c) Berechnen Sie die Beträge von ~b und ~c unter Annahme, dass ~a 10cm lang ist.
102 cm2 =82 Kästchen2 +132 Kästchen2 ; 100cm2 =233Kästchen2 ; 0,429cm2 =1Kästchen2
0,66 cm=1 Kästchen
-1-
4
PYTHAGORAS, SINUS, KREIS UND CO.
Vektoraddition am Beispiel der Kraftwirkung mehrerer Kräfte auf einen Körper.
F1
F2
F3
F4
y
Fres = F1 + F2 + F3 + F4
=500N
=300N
=250N
=200N
Fres
F1
F2
Reihenfolge beliebig
30°
45°
20°
F4
F3
F1x = F1 cos30° = 433N
F2x = F2 cos45° = - 212N
F3x = F3 cos20° = - 235N
F4x = F4 cos15° = 193N
Summen
x
15°
F1y = F1 sin30° = 250N
F2y = F2 sin45° = 212N
F3y = F3 sin20° = - 85N
F4y = F4 sin15° = - 52N
179N
325N
Fresx = Fres cos α = 179N
Fresy = Fres sin α = 325N
tan α = 325N/179N = 1,82
α = arctan (tan α)
= 61,2°
Der Betrag der resultierenden Kraft Fres kann mittels Pythagoras ermittelt werden.
q
p
Fres = Fresx 2 + Fresy 2 = (179N )2 + (325N )2 = 371N
2. Sie tragen eine Henkeltasche mit 10 kg Kartoffeln. Jemand kommt Ihnen zu Hilfe und
m
jeder nimmt einen Henkel. Es gilt: F=m·g, mit g=9,81 sec
2.
(a) Wie groß ist die Kraft F pro Henkel, wenn Sie alleine tragen?
F=
98, 1N
=49,05N
2
-2-
4
PYTHAGORAS, SINUS, KREIS UND CO.
(b) Wie groß ist die Kraft F pro Henkel, wenn Sie zusammen tragen und die Henkel
einen Winkel von 60◦ bilden? Gehen Sie von einer symmetrischen Anordnung aus.
cos30◦ =
Fg
2
F
F=49,05N·
1
1
=49,05N·
=56,6N
cos30◦
0,86
a)
b)
F
F
F
F
Fg = F + F
Fg
Fg
Fg/2
α
F
Vektorzerlegung:
cos α = (Fg/2) / F
Achtung - Werte betrachten. Die Kraft im Henkel nimmt zu. D.h. die Henkel
könnten reissen.
-3-
4
PYTHAGORAS, SINUS, KREIS UND CO.
sinus α
3. In einem Kreis gelten folgende Beziehungen:
90 °
π/2
r2 = [ r . (sin α) ] 2 + [ r . (cos α) ] 2
r
r2 = r 2 [ (sin α)2 + (cos α)2 ]
r . (sin α)
1 = (sin α)2 + (cos α)2
α
2π
π
180 °
r . (cos α)
360 °
cosinus α
270 °
3π/2
(a) Angenommen der Winkel α vergrößert sich mit einer zeitlich konstanten Zuwachsrate von ω ·t. Berechnen Sie r· sin α. Erstellen Sie eine Wertetabelle mit markanten
1
Punkten. Setzen Sie ω = 1 · sec
vorraus.
t in sec
0
0,785
1,05
1,57
3,14
4,71
6,28
r·sin ω·t
0◦
0,5 r
0,707 r
r
0
-r
0
entspricht
0
30◦
45◦
90◦
180◦
270◦
360◦
bzw.
0
π/6
π/4
π/2
π
3π/2
2π
-4-
4
PYTHAGORAS, SINUS, KREIS UND CO.
(b) Stellen Sie Ihr Ergebnis grafisch dar.
sinus( ω t )
1
0,8
0,6
0,4
0,2
0
0
1,57
3,14
4,71
6,28
-0,2
-0,4
-0,6
-0,8
-1
t in sec
-5-
4
PYTHAGORAS, SINUS, KREIS UND CO.
1
4. Kenngrößen einer Schwingung sind Amplitude â, Frequenz f und Periodendauer T= .
f
sinus ω t
1,5
1
Periodendauer T
Amplitude â
0,5
0
0
1,57
3,14
4,71
6,28
7,85
9,42
10,99
12,56
-0,5
-1
π
2π
3π
4π
360 °
570 °
720 °
-1,5
180 °
α
Frequenz f = 1/T
(a) Berechnen Sie die Periodendauer einer 1GHz-Schwingung.
1
f = 1GHz = 109 Hz =109
sec
1
T = = 10−9 sec = 1 nsec
f
(b) Mit welcher Frequenz rotiert die Erde?
sec
T = 24h = 24h ·60 min
h · 60 min = 86400sec
1
1
f=
=
= 11,6µHz
T
86400sec
(c) Die Amplitude â eines sinusförmigen Signals beträgt 10V. Die Frequenz f beträgt
2π
1
30 Hz. Wie groß ist der Momentanwert des Signals a(t) = â · sin T · t nach 2 Minuten, wenn das Signal mit positiver Flanke im Nulldurchgang startet (s.o.)?
T = 1/f = 30sec, d.h. s(t = 2 min) = 0 V, denn 2 Minuten sind ein ganzzahliges Vielfaches von 30 Sekunden.
-6-
4
PYTHAGORAS, SINUS, KREIS UND CO.
(d) Welchen Signalpegel erwarten Sie nach tB = 2,2 Minuten?
a(t) = â · sin
2π
2π
· t = 10V · sin
· 132 sec = 10V · 0,5877 = 5,88 V.
T
30 sec
(e) Zu welcher Zeit tritt dieser Signalpegel mit identischem Gradienten zum ersten
Mal auf?
2, 2min · 60sec
tB
min
=
= 4, 4
T
30sec
0,4· T = 12 sec
Kontrolle:
a(t) = â · sin
2π
2π
· t = 10V · sin
· 12 sec = 10V · 0,5877 = 5,88 V
T
30 sec
-7-
4
PYTHAGORAS, SINUS, KREIS UND CO.
5. Auf einer CD-ROM befindet sich eine spiralförmige Spur mit Daten. Das Laufwerk
gewährleistet eine konstante Datenrate Dr von 150kByte
. Mit welcher Drehzahl N muss
sec
das Laufwerk sich drehen, damit eine Spur bei R = 5 cm gelesen werden kann. Nehmen
Sie an, dass pro 1µm ein bit gelesen wird.
Datendichte
Dα
h
Byte
m
i
Datenrate
Dr
h
Byte
sec
i
Drehzahl
N
1
min
Umlaufdauer
T
[ sec ]
Radius
R
[m]
1 Byte
= 8 Bit
N
=
Dd
1
T
= 125 ·
103 Byte
m
1
m
8·10−6 Byte
pro Umdrehung:
Anzahl Byte
= Dd · 2πR
= Dr · T = Dr ·
⇒
Dd · 2πR
⇒
N
= Dr ·
=
=
1
N
1
N
Dr
Dd ·2πR
150·103 Byte
sec
125·103 Byte
·2π·5·10−2 m
m
1
1
= 3, 82 sec
= 3, 82 sec
·
60sec
min
1
= 229 min
-8-