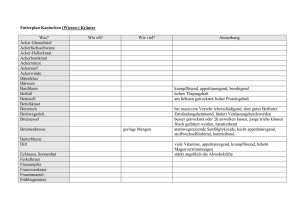
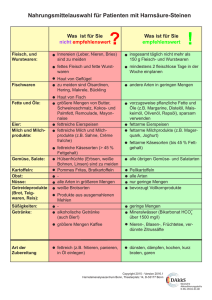
1. Logik, Mengen, Relationen

1. Logik, Mengen, Relationen
1.1.
Aussagen
Aussagen, Aussagensätze. Eine Aussage drückt einen Tatbestand oder Fakt aus. Deshalb sind
Frage- Aufforderungs-, Befehls-, Wunsch-, Zweifelssätze keine Aussagesätze. Sie sind nicht
Gegenstand der Aussagenlogik, sondern werden in anderen Gebieten der Logik behandelt.
Aussagen sind
„2 * 2 = 4“
„10 ist eine Primzahl“
„Wien ist die Hauptstadt von Österreich“
Aussagen werden mit p, q usw. bezeichnet.
Aussagen werden nach ihrem Wahrheitsgehalt in wahre und falsche unterschieden
Def.: p heißt eine Aussage, wenn p einen Tatbestand ausdrückt.
Die Aussage p heißt zweiwertige Aussage, wenn p entweder wahr oder falsch ist.
Wir betrachten nur die zweiwertigen Aussagen, für die das tertium non datur (ein Drittes ist
nicht gegeben) gilt, sie sind entweder wahr oder falsch.
Der Wahrheitswert „wahr“ wird mit t
Der Wahrheitswert „falsch“ wird mit f bezeichnet.
Jeder Aussage p ist eindeutig ein Wahrheitswert aus der Menge {t, f} zugeordnet. Diese
Wahrheitswertfunktion wird mit w(p) bezeichnet, w(p)∈{t,f}.
Der Wahrheitswert einer konkreten Aussage wird durch das entsprechende Fachgebiet
ermittelt, die Logik sagt etwas über den Wahrheitswert der Verknüpfung von Aussagen aus.
1.2.
Aussagenvariablen und Aussagenformen (Propositionen)
Die Sätze „x ist eine Primzahl“, „y ist der Bruder von Thomas Mann“ sind keine Aussagen,
aber x und y können bestimmte konkrete Werte aus bestimmten Klassen X oder Y annehmen,
für die p(x) oder q(y) Aussagen darstellen.
X - Klasse der natürlichen Zahlen
Y - Klasse der mit Th.Mann verwandten Personen 1. Grades
Def.: Eine Formulierung p(x) mit der Variablen x∈X heißt Aussageform, wenn sie durch die
Substitution konkreter Wert x=x1 ∈X in eine zweiwertige Aussage übergehen. Die Klasse der
so entstehenden Aussagen heißt Bereich der Aussagenformen.
Aussageformen selbst haben keinen Wahrheitswert.
1.3.
Ausagenverknüpfungen
Die Negation (Verneinung)
Die Negation einer Aussage p ist genau die Aussage, die den Wahrheitswert f hat, wenn p den
Wahrheitswert t hat. Die Negation von p wird mit ¬p bezeichnet.
Die Wahrheitsfunktion der Negation läßt sich mittels Wertetabelle darstellen
p
t
f
¬p
f
t
Für die doppelte Negation ¬¬p gilt dann
p
t
f
¬p
f
t
¬¬p
t
f
deswegen gilt w(p)=w(¬¬p), oder anders gesprochen, die doppelte Negation einer Aussage ist
die Aussage selbst.
Die Konjunktion (UND-Verbindung)
Die Konjunktion zweier Aussagen p und q p∧q ist genau dann wahr, wenn gleichzeitig p und
q den Wahrheitswert wahr haben. Ansonsten ist die Konjunktion falsch
p
t
t
f
f
q
t
f
t
f
p∧q
t
f
f
f
Der Wahrheitswert der Konjunktion zweier Aussagen ist unabhängig von der Reihenfolge der
Aussagen und auch von jeglicher zeitlicher Abhängigkeit, die in konkreten Aussagen implizit
enthalten sein könnte.
„Stefan wurde reich und zog nach Salzburg“
Die Konjunktion ist prinzipiell dann und nur dann wahr, wenn alle Teilaussagen wahr sind.
Die Disjunktion (ausschließendes ODER)
Die Disjunktion von zwei Aussagen p und q p∨p ist genau dann wahr, wenn wenigstens eines
der beiden Disjunktionsglieder wahr ist.
p
t
t
f
f
q
t
f
t
f
p∨p
t
t
t
f
Die Disjunktion mehrerer Aussagen ist genau dann wahr, wenn wenigstens eines der
Disjunktionsglieder wahr ist.
„Die Zahl π ist gerade oder ungerade, oder π ist keine natürliche Zahl“
Alle aussagenlogischen Verknüpfungen können allein durch die bisher beschriebenen
Verknüpfungen dargestellt werden, diese Gruppe von Wahrheitsfunktionen ist vollständig.
Trotzdem nutzt man noch andere Verknüpfungen wie Implikation, Äquivalenz, Schefferstrich
usw.
Implikation
Die Implikation dient der logischen Fassung sprachlicher wenn..., dann ... Aussagen. Sie ist
genau nur dann falsch wenn in „p impliziert q“ p wahr und q falsch ist.
p
t
t
f
f
q
t
f
t
f
p→q
t
f
t
t
¬p∨q
t
f
t
t
¬(p∧¬q)
t
f
t
t
Wenn 2*2=5, dann ist der Mond ein Planet - ist eine wahre Aussagenverknüpfung
Wenn 2*2=4, dann befindet sich Spittal in Niederösterreich- ist eine falsche
Aussagenverknüpfung. Ein inhaltlicher Zusammenhang zwischen p und q ist nicht
erforderlich.
Aus der Wahrheit darf nur die Wahrheit folgen, aus der Falschheit kann beliebiges folgen.
Wie man sieht, ist p→q auch durch eine Verknüpfung von Negation und Disjunktion bzw.
Negation und Konjunktion darstellbar.
Die Implikation beschreibt eine hinreichende Bedingung: p hinreichend für q: q, falls p bzw.
eine notwendige Bedingung: q ist notwendig für p.
Die Äquivalenz
Die Äquivalenz von p und q p↔q ist genau dann wahr, wenn beide Teilaussagen denselben
Wahrheitswert haben.
p
t
t
f
f
q
t
f
t
f
p↔q
t
f
f
t
Sprachlich drückt die Äquivalenz eine notwendige und hinreichende Bedingung aus.
Die Äquivalenz p↔q entspricht der komplexen Aussage (p→q)∧(q→p).
Tautologie
Eine Tautologie nennt man eine Aussagenverknüpfung, deren Wahrheitswertfunktion
identisch wahr ist, den entsprechenden aussagenlogischen Ausdruck ein aussagenlogisches
Gesetz.
p∨¬p
Eine aussagenlogische Verknüpfung, die identisch falsch ist, nennt man eine Kontradiktion,
die entsprechenden Ausdrücke kontradiktorische Ausdrücke.
p∧¬p
1.4.
Die Folgebeziehung und der Beweis
Man sagt, daß eine Aussage q aus den Aussagen p1,. p2 , p3 ,..., pn folgt, oder daß zwischen den
Prämissen p1,. p2 , p3 ,..., pn und der Konklusion q eine Folgebeziehung besteht, wenn die
Wahrheit der Prämissen (aus rein formalen Gründen) die Wahrheit der Konklusion garantiert.
Bsp.: p, pq folgt q
Das Dreieck ABC ist rechtwinklig
Wenn das Dreieck ABC rechtwinklig ist, so gilt die Beziehung a²+b²=c² folgt
Im Dreieck ABC gilt die Beziehung a²+b²=c²
Kriterium
Aus p1,. p2 , p3 ,..., pn Þ q genau dann, wenn der Ausdruck
( p ∧ p ∧...∧ p ) → q
1
2
n
ein aussagenlogisches Gesetz ist.
Wichtige Schlußregeln
modus ponens (Abtrennungsregel)
p, p → q
q
modus tollens
p → q , ¬q
¬p
Kettenschlußregel
p → q, q → r
p→r
Weiter wichtige Folgebeziehungen bzw. Schlußregeln sind
( p → q) → r , p → q Þ r
( p ∨ r ), ( p → q ), ( r → q ) Þ q
[q ∧ ( ¬p → ¬q )] Þ p
( p → q ), ( q → p ) Þ p ↔ q
( p → q ) Þ ( ¬q → ¬p)
( ¬q → ¬p) Þ ( p → q )
Fallunterscheidung
Indirekter Beweis
Schluß auf Äquivalenz
Kontraposition
Kontraposition
Diese Folgebeziehungen werden zum Beweisen genutzt.
Der Beweis ist eine regelgeleitete Ableitung der Wahrheit einer Behauptung aus der Wahrheit
der Voraussetzungen.
Man unterscheidet:
Direkter Beweis
Aus Annahmen des Beweises (Prämissen), die als wahr bekannt (schon bewiesen) sind
(Theoreme) oder als wahr angenommen werden (Axiome), wird mit Hilfe der Schlußregeln in
Teilschritten die Behauptung bewiesen.
Die Schlußregeln, die von Teilschritt zu Teilschritt führen, können verschieden sein.
Der direkte Beweis ist relativ geradlinig und oft auch konstruktiv, in dem er eine theoretische
Konstruktion des zu beweisenden mathematischen Objektes liefert.
Manchmal nutzt man, um pq zu zeigen , erst einen Nachweis qp, um einen Beweisansatz
zu finden.
Bsp. pp sei „Wenn a≠b, dann gilt (a+b)/2 > √ab, a>0, b>0, reelle Zahlen
Man beachte aber, daß (qp)(pq) keine Tautologie ist und somit dies kein gültiger
Schluß (Bsp.: Wenn 1=1, dann ist -1=+1)
Aber: wenn pq wahr ist, dann ist p eine hinreichende Bedingung für q und q eine
notwendige Bedingung für p.
Bsp.: Die Teilbarkeit einer natürlichen Zahl n durch 2 ist notwendig aber nicht hinreichend für
die Teilbarkeit von n durch 4.
Für drei natürliche Zahlen a,b,c ist die Teilbarkeit von a durch c und b durch c hinreichend,
aber nicht notwendig für die Teilbarkeit von a+b durch c.
Indirekter Beweis
Um eine Behauptung (Konklusion) A zu beweisen, wird ihre Negation ¬A (negierte
Konklusion) zu den anderen Prämissen hinzugefügt. Aus diesen Prämissen wird nun ein
logischer Widerspruch hergeleitet. Man zeigt, daß es unmöglich ist, daß die Beweisannahmen
und die negierte Beweisbehauptung gleichzeitig wahr sein können. Unter der Voraussetzung,
daß die Beweisannahmen wahr sind, muß nun auch die Konklusion wahr sein.
Schluß auf eine Äquivalenz
(notwendige und hinreichende Bedingung)
Man schließt aus (pq)∧(qp) auf pq und sagt p ist eine notwendige und hinreichende
Bedingung für q
Bsp.: Es sei a eine ganze Zahl. Dann gilt: a ist genau dann eine gerade Zahl, wenn a² eine
gerade Zahl ist.
Vollständige Induktion
Diese Beweisverfahren nutzt die Schlußregeln der Logik und die Eigenschaften der
natürlichen zahlen.
Es sei A(n) eine Eigenschaft A für die natürliche zahl n.
Man zeigt nun:
Es gilt A(1) bzw. A(0)
Wenn A(n) wahr, dann ist A(n+1) wahr
Dann gilt A(n) für alle natürlichen Zahlen
- Induktionsbasis
- Induktionsschritt
- Induktionsschluß
Dabei nutzt man die Eigenschaft, daß der unmittelbare Nachfolger der natürlichen Zahl n die
Zahl n+1 ist. Im Prinzip kann die Induktionsbasis auch ab der Zahl m>1 gewählt werden, dann
gilt halt A(n) für alle natürlichen Zahlen von n≥m. Man spricht auch von der Vererbung der
Eigenschaft A von n auf n+1.
Bsp.:
a) Man weise nach, daß in einem konvexen ebenen n-Eck (n≥3) die Summe aller Innenwinkel
stets gleich (n-2)*180° ist. (vollständige Induktion!)
b) Jede natürliche Zahl n ist ihrem Nachfolger gleich.
Aussageformen und Quantoren
Anstelle Aussagen werden Aussageformen gebildet, die eine oder mehrere Variablen
enthalten
„x ist durch zwei teilbar“
„z ist ein ebenes Vieleck“
„u ist größer als v“
Der Wahrheitswert solcher Aussageformen ergibt sich durch das Einsetzen konkreter Objekte
anstelle der Variablen..
Aber auch die Quantifikation von Aussageformen macht aus ihnen konkrete Aussagen. Sie
nimmt auf keine konkreten Individuen Bezug, sondern sagt etwas über die Existenz eines
Individuums mit einer konkreten Eigenschaft oder aber darüber das alle Individuen eines
gegebenen Bereichs die entsprechende Eigenschaft haben.
Es gibt natürliche Zahlen, die durch 7 teilbar sind.
Alle reellen Zahlen haben ein nicht negatives Quadrat.
Man schreibt q=∀xP(x) und liest „für alle x ist P(x)“. Dies ist eine zweiwertige Aussage, die
genau dann den Wert t besitzt, wenn für jedes konkrete x1 aus eine Klasse X P(x1) eine wahre
Aussage ist, ansonsten hat ∀xP(x) den Wahrheitswert f. Das Symbol ∀ heißt der Allquantor.
Man schreibt r=∃xP(x) und liest „Es existiert ein x, so daß P(x)“. r ist eine zweiwertige
Aussage, die genau dann wahr ist, wenn ein konkretes x1 aus der Klasse X existiert, für das
P(x1) wahr ist. Das Symbol ∃ heißt Existenzquantor.
Dann heißen die Beispiele jetzt ∃xH(x) und ∀xK(x)
Es gilt folgende Beziehung zwischen den ∃- und ∀-Aussagen.
¬(∀xH(x)) ∃x¬H(x)
¬(∃xH(x)) ∀x¬H(x)
Axiomatik
Die moderne Mathematik ist axiomatisch aufgebaut. D.H., die Grundlage einer bestimmten
Theorie bilden bestimmt Behauptungen (Axiome), die als wahr vorausgesetzt werden. Alle
anderen Aussagen dieser mathematischen Theorie folgen entsprechenden den logischen
Schlußregeln aus diesen Axiomen. Für derartige Axiomensysteme sind dann die
Widerspruchsfreiheit, die Vollständigkeit, und die Unabhängigkeit der Axiome.
Axiomatik in der Geometrie Euklid
Axiomatik in der Arithmetik Peano u.a.
Peano’sche Axiomatik der Theorie der natürlichen Zahlen:
1. 0 ist eine natürliche Zahl
2. Zu jeder natürlichen Zahl n gibt es genau einen Nachfolger n’.
3. Es gibt keine natürliche Zahlen, deren Nachfolger 0 ist.
4. Die Nachfolger zweier verschiedener natürlichen Zahlen sind voneinander verschieden.
5. Enthält eine Menge natürlicher zahlen die Zahl 0 und mit jeder natürlichen Zahl n auch
ihren Nachfolger n’, so enthält sie alle natürlichen Zahlen.
Jede formalisierte widerspruchsfreie Theorie S, die die formale Arithmetik enthält, ist
prinzipiell unvollständig. D.H. S enthält inhaltlich wahre Aussagen, die nicht entscheidbar
sind, d.h. weder A noch nicht-A sind herleitbar. Auch jede endliche Erweiterung des
Axiomensystems von S ist unvollständig.
Die Widerspruchsfreiheit von S ist zwar mit den Mitteln von S (soweit hinreichend reich)
ausdrückbar, aber nicht in diesem System beweisbar.
2. Grundbegriffe der Mengenlehre
2.1 Definition
Unter einer Menge versteht man eine Zusammenfassung einzelner, wohlunterschiedener
Objekte unserer Anschauung oder unseres Denkens zu einer Gesamtheit, wobei von jedem
Objekt eindeutig feststeht, ob es zur Menge gehört oder nicht. (G.Cantor)
Man schreibt für eine Menge M und ein Element
x∈M , wenn x Element von M ist und
x∉M, wenn x nicht Element von M ist
Mengen können (1) durch die Auflistung aller ihrer Elemente und (2) durch die Angabe einer
charakteristischen Eigenschaft P Angegeben werden.
X = {1;2;3}
X = {x | x = k³ ∧ k∈Ν
Ν}
Die Angabe (1) bringt im Falle unendlich vieler Element Schwierigkeiten mit sich.
Leere Menge: Eine Menge X, die kein Element enthält, nennt man die leere Menge und
schreibt X=∅.
Die Menge aller ellipsoiden Quadrate ist leer, die Menge aller 200-jährigen Spittaler ist
ebenfalls leer.
Die Menge, die alle Elemente enthält, gehört nicht zur Mathematik, sondern zur Theologie.
Mengen werden durch Venn-Diagramme veranschaulicht.
1. Mengenrelationen
Mengen könne folgende Relationen zueinander haben.
1. Sie sind elementefremd, d.h. disjunkt. s. Bild oben, M und N sind disjunkt.
2. M und N enthalten mindestens ein gemeinsames Element.
Def.: Wenn alle Elemente von M auch Element von N sind, so nennt man M eine Teilmenge
von N.
∀x(x∈M gilt x∈N
Man schreibt M⊆N und nennt diese Relation die Inklusion von M in N.
Man sagt außerdem, daß N die Obermenge von M sei und schreibt deshalb manchmal N⊇M.
Offensichtlich gilt M ⊆ M.
Def.:
M ist eine echte Teilmenge von N, wenn n mindestens ein Element enthält, für das x∉M gilt.
∃x (x∈N ∧ x∉M). Man schreibt M ⊂ N.
Die Menge aller Rhomben ist eine echte Teilmenge der Menge aller Vielecke.
Mengengleichheit
Zwei Mengen M und N heißen genau dann gleich (M = N), wenn sie dieselben Elemente
enthalten.
Es sei U die Menge aller durch 7 teilbaren natürlichen Zahlen, V die Menge aller Vielfachen
von 7.
Es gilt U⊆V und V⊆U und letztlich U=V.
N=M M ⊆ N ∧ N ⊆ M
Bsp.:
R={x | x+x = x}, S={x | x∈N ∧ 35,7x+4,58=0}
R={0}, S=∅
R≠S
Die Menge mit dem Element 0 ist ungleich der leeren Menge !!
2. Mengenoperationen
Gegeben seien zwei Mengen M1 und M2.
Vereinigung von Mengen
Die Vereinigung zweier Mengen M1 und M2 ist eine Menge M, zu der genau die Elemente
gehören, die wenigstens zu einer der beiden Mengen M1 und M2 gehören.
Man schreibt M = M1 ∪ M2
x∈M x∈M1 ∨ x∈M2
Anschaulich wird dies in einem Venn-Diagramm dargestellt.
Die Vereinigung von M1,,M2,M3,...Mn ist die Menge M aller derjenigen Elemente die in
mindestens einer der Mengen M1, M2, M3, ... Mn enthalten ist. Man schreibt
M∪∅=M
M=
M
1≤ n ≤ n
n
i
M
oder M =
i =1
i
Durchschnitt von Mengen
Der Durchschnitt M zweier Mengen M1 und M2 ist die Menge aller derjenigen Elemente, die
sowohl zu M1 und zu M2 gehören.
Symbolisch: x∈M1∩M2 x∈M1 ∧ x∈M2
Der Durchschnitt M der Mengen M1, M2, M3, ..., Mn ist die menge aller derjenigen Elemente,
die in jeder der mengen M1, M2, M3, ... ,Mn enthalten sind, symbolisch
n
M=
Mi oder M = M i .
1≤ i ≤ n
1
Auch diese Mengen lassen sich graphisch als Venn-Diagramm darstellen.
Zwei Mengen, die keine gemeinsamen Elemente haben, haben eine leere Durchschnittsmenge.
M1∩M2 = ∅.
Bsp.: G1 und G2 seien die Punktmengen zweier sich schneidender Geraden in einer Ebene.
G1∩G2 ist dann der Schnittpunkt der beiden Geraden.
Für diese Operationen gelten folgenden Gesetzmäßigkeiten
(A∪B)∩A = A
(A∩B)∪A = A
A∪B = B∪A
A∩B = B∩A
Differenz zweier Mengen
Die Differenzmenge M=M1\M2 der beiden Mengen M1 und M2 enthält genau diejenigen
Elemente, die in M1 und nicht in M2 enthalten sind.
x∈M1\M2x∈M1∧∉M2
Für diese Operation gilt kein Kommutativgesetz
M1\M2 ≠ M2\M1
Komplementmenge
Es sei U ein Grundbereich aller Element, die im gegebenen Fall Element von Mengen seien
könne.
Dann gilt:
Die Komplementmenge M einer Menge enthält genau die Elemente (aus dem Grundbereich
U), die nicht Element von M sind.
Der Zusammenhang von Differenz mit der Universalmenge U (seinem Komplement) lautet
M1\M2 = M1∩ M 2
Für die Komplementmenge gelten u.a. folgende Zusammenhänge:
M =U\M
M∩ M =∅
M∪ M =U
Beispiele:
1. Es sei U die Menge der natürlichen Zahlen und M die Menge der geraden Zahlen. Dann ist
M die Menge der ungeraden Zahlen.
2. Es sei U die Menge der rationalen Zahlen, M wie gehabt, dann ist M die Vereinigung der
Menge der ungeraden Zahlen mit der Menge der nichtganzen rationalen Zahlen.
3. Es sei U die Menge der Punkte auf einer Ebene und K die Menge der Punkte außerhalb und
auf einer Kreislinie k. Dann ist K die Menge aller Punkte innerhalb des Kreises, aber ohne
die Kreislinie selbst. (Offene Menge)
3. Rechenregeln
Es seien A, B, C ... Teilmengen der Universalmenge M
1. A∩B = B∩ , A∪B=B∪A
2. (A∩B)∩C = A∩(B∩C)
(A∪B)∪C = A∪(B∪C)
3. A∩(A∪C) = A
B∪(B∩C) = B
4. A∩(B∪C) = (A∩B) ∪ (A∩C)
A∪(B∩C) = (A∪B)∩(A∪C)
5. A∪∅ = A, A∩∅ = ∅
A∩M = A, A∪M = M
6. A ist genau dann Komplement von A, wenn gilt:
(A∪ A = M) ∧ (A∩ A = ∅)
Kommutativgesetz
Assoziativgesetze
Verschmelzungsgesetze
Distributivgesetze
∅ - Nullelement
M - Einselement
Komplementeigenschaften
Beim Vergleich der Operationen ∪ und ∩für mengen mit den Operationen + und * für Zahlen
zeigt sich, daß für Mengen neben bekannten algbraischen Eigenschaften (Rechenregeln) neue
Eigenschaften auftauchen, denn z.B. die Verschmelzungsgesetze
a*(a+c) = a, a + (a*c)=a und das umgekehrte Distributivgesetz a + (b*c)= (a+b)*(a+c) gelten
für Zahlen im allgemeinen nicht , ebenso eine Gleichung derart a + 1 = 1 (wenn man das
Einselement mit der 1 gleichsetzt)
Die Menge aller Teilmengen {X | X ⊆ M }einer gegebenen Menge M heißt Potenzmenge und
wird mit P(M) bezeichnet.
Nun bilden die Mengen hinsichtlich der Operationen Potenzmenge, Durchschnitt,
Vereinigung eine Mengenalgebra, ein konkretes Modell einer Boolschen Algebra.
4. Mächtigkeit von Mengen
Eine Menge M, M≠∅, die endlich viele Elemente enthält, heißt endliche Menge, eine Menge
M, die aus unendlich vielen Elementen besteht, heißt unendliche Menge.
Es sei nun µ(M) - die Anzahl der Elemente einer endlichen Menge M
Gleichmächtige Menge
Zwei Mengen A, B besitzen die gleiche Mächtigkeit, wenn man jedem Element a , a∈A
eineindeutig ein Element b, b∈B zuordnen kann.
Wenn nun a1 und a2, beide ∈A einem Element b∈B zugeordnet sind, dann gilt a1=a2.
Man schreibt A glm B und sagt A und B seien gleichmächtig, bzw. besitzen den gleichen
Mächtigkeitstyp (Kardinalzahlen). Alle gleichmächtigen Mengen bilden eine Menge, die
durch diesen Typ charakterisiert ist.
Für die Relation glm gilt nun
(i) A glm A
(ii) A glm B B glm A
(iii) A glm B ∧B glm C A glm C
(Reflexivität)
(Symmetrie)
(Transitivität)
Gegeben seien drei Mengen:
M1 = {Peter, Paul, Franz}
M2 = {a², b², 9²}
M3 = {∅, {∅}, {∅, {∅}}
Zwischen diesen Mengen kann man eine eineindeutige Zuordnung der Elemente vornehmen,
µ(M1) = µ(M2) = µ(M3) = 3. Somit gehören diese Mengen zur Menge der dreielementigen
Mengen.
Abzählbare Mengen
Eine Menge A heißt abzählbar (unendlich), wenn gilt A glm N mit N 0 {0,1,2,3,4,...}
Eigenschaften (Theorem):
1. Eine beliebige unendliche Teilmenge einer abzählbaren Menge M ist wieder eine
abzählbare Menge
n
2. Es seien A1, A2, A3, ...An abzählbare Mengen. Dann gilt M =
A
k =1
k
ist eine abzählbare
Menge. Auch wenn gewisse Ak endliche Mengen sind, bleibt die Abzählbarkeit erhalten.
3. Die Vereinigung abzählbar vieler abzählbarer Mengen ist eine abzählbare Menge.
4. Aus jeder unendlichen Menge kann eine abzählbare Menge als Teilmenge herausgesondert
werden.
5. Wenn eine Menge M unendlich ist und A eine abzählbare Teilmenge von M und die
Menge M/A = B auch unendlich ist, so gilt M glm B
Bsp.:
Die Menge Z der ganzen Zahlen ist abzählbar.
Z = N ∪ {-1, -2, -3, -4,...}
N ist abzählbar, {-1, -2, -3, -4,...}ist abzählbar.
Man ordne jedem Element -n in {-1, -2, -3, -4,...} die Zahl n-1∈N zu.
Dann gilt -1 0, -2 1, , -k k-1,
Somit gibt es eine eineindeutige Zuordnung von N zu {-1, -2, -3, -4,...}.
Dann seien A1 die Menge N und A2 die Menge {-1, -2, -3, -4,...}, nach dem oben angeführten
Theorem gilt nun auch, daß M abzählbar ist.
Die Menge Q der rationalen Zahlen ist eine abzählbare Menge
Für Q gibt es folgende Darstellung Q = {
Dann bilde man Ak = {
m
| m∈Z ∧ k∈N\{0} ∧ m und k sind teilerfremd}
k
m
| m∈Z ∧ k∈N\{0} ∧ m und k sind teilerfremd} mit fixiertem k
k
z.B. ist A1 = Z
A2 = {..., −
5
3
1 1 3 5
,−2 ,− ,−1,− ,0, ,1, ,2 , , ...} usw.
2
2 2 2 2
2
∞
Alle Ak sind abzählbar, also auch die Vereinigung
A
k =1
k
= P.
Die Menge R aller reellen Zahlen ist aber überabzählbar. Alle Mengen, die mit R
gleichmächtig sind, nennt man Kontinuum.
Z.B. ist die Menge C = {x | x∈R ∧ 0 < x ≤ 1} hat die Mächtigkeit des Kontinuums.
Allgemein kann man sagen, daß die Menge C gleichmächtig ist der Menge aller Teilmengen
der Menge der natürlichen Zahlen, d.h. das Kontinuum ist der Menge aller Teilmengen der
Menge der natürlichen Zahlen gleichmächtig und überabzählbar.
C glm {A | A ⊆ N }
Die Menge aller Teilmengen {X | X ⊆ M }einer gegebenen Menge M heißt bekanntlich
Potenzmenge und wird mit P(M) bezeichnet.
C glm P(N)
5. Der Begriff der Abbildung
Beispiel : Veränderung der Länge eines Stabes durch Temperaturveränderung.
A - Menge der Temperaturen, t∈A = {t |t im Bereich von t1 und t2}
B - Menge der Längen L∈B = {L | L im Bereich von L1 und L2}
Jeder Temperatur t aus A entspricht nun genau eine Länge L aus B, d.h.
∀t∈A∃!L∈B so daß t L
Allgemein:
Eine Zuordnung zweier Mengen heißt Abbildung (Funktion) f von A auf B, falls jedem
Element x∈A eindeutig ein Element y∈B zugeordnet ist, symbolisch
f: A B mit x y = f(x).
Das Element y = f(x) ∈ B wir d Bild von x genannt (Funktionswert), x ist der Ursprung.
Wichtig: Jedem x muß ein y zugeordnet, aber nicht jedem y. Außerdem können einem y
mehrere x zugeordnet sein, aber nicht umgekehrt.
Für den Fall, daß in der Zuordnung f jedem y=f(x)∈B nur ein Wert x∈A entspricht, sagt man,
daß die Abbildung eineindeutig sei.
6. Kartesisches Produkt
Ein Paar von zwei Objekten heißt ein geordnetes Paar (a,), wenn es auf die Reihenfolge der
Objekte ankommt, d.h. (a,b)≠(b,a), falls a≠b. Zwei geordnete Paare (a,b) und (c,d) sind genau
dann gleich, wenn a=c ∧ b=d gilt.
(a,b) ≠ {a,b}, denn {a, b} = {b, a}, das hieße aber (a,b)=(b,a) bei a≠b,
deshalb wird (a,b) als {a, {a,b}}definiert.
Geordnete Paare trifft man in Stadtplänen, bei der Beschreibung der Schachzüge, die
Koordinaten-Darstellung von Punkten im Kartesischen Koordinatensystem
In der Verallgemeinerung führt man das n-Tupel (a1,a2,a3,...an) ein, dessen Elemente das (n-1)Tupel (a1,a2,a3,...an-1) und das Element an sind.
(a1,a2,a3,...an) = {{(a1,a2,a3,...an-1)},{ (a1,a2,a3,...an-1), an}}
Z.B. lassen sich die Punkte im 3-dimensionalen Raum eindeutig durch ein3-Tupel (Tripel)
beschreiben, im n-dimensionalen Raum durch ein n-Tupel.
Def.:
A und B seien Mengen. Dann heißt die Menge AxB = {(a,b) | a∈A ∧ b∈B} die Produktmenge
der Mengen A und B oder auch das Kartesische Produkt. (Auch Kreuzmenge9.
Bsp.
{1,2,3x{1,2,3,4} als 3x4 Matrize geordneter Paare.
NxN ergibt ein Zahlengitter im 1. Quadranten.
Eigenschaften:
Für beliebige Mengen A, B, C gilt
(i) A ≠ B A x B ≠ B x A
(ii) A x (B∪C) = (A x B) ∪ (A x C)
(iii) A x (B∩C) = (A x B) ∩ (A x C)
nicht kommutativ
Distributivgesetz
Distributivgesetz
Der Begriff des Kartesischen Produktes läßt sich auf n-fache Produkte von Mengen
A1,,A2, ,An ausdehnen.
A1 x A2 x ... x An = {(a1,a2,a3,...an) | ∀i (ai∈Ai}
So ist auch der 3-dimensionale reelle Raum R³ erklärt, ebenso Rn
6. Relation
Es sei S, A1, A2, A3 ein Informationssystem
A3
A1
S
A2
Man bezeichne nun mit E = {S, A1, A2, A3} die Menge der Elemente und mit B die Menge der
geordneten Paare, zwischen denen Beziehungen (Relationen) bestehen.
L = {(S,A1), (S, A2), (S, A3), (A1,S), (A2,S), (A3,,S), (A1, A2), (A2,,A1)} ⊂ E x E
L legt die Struktur im System fest und ist eine Teilmenge von ExE.
Allgemein:
Jede Teilmenge R eines Kartesischen Produktes AxB der Mengen A und B heißt eine
zweistellige Relation zwischen A und B, geschrieben R⊂AxB.
Jede Teilmenge R⊂A1 x A2 x ... x An heißt n-stellige Relation.
Besonders wichtig sind binäre Relationen. Solche sind z.B. die Äquivalenzrelation und die
Ordnungsrelation.