Höhere Mathematik I für Bau, Geo, Umwelt — Blatt 3

T ECHNISCHE U NIVERSITÄT M ÜNCHEN
Z ENTRUM M ATHEMATIK
PD Dr. Andreas Johann
Höhere Mathematik I für Bau, Geo, Umwelt — Blatt 3
Wintersemester 2016/2017
Zentralübung
Z3.1. Zeigen Sie, dass der Raum Abb(R, R) aller Abbildungen der reellen Zahlengerade auf sich selbst die
Vektorraumaxiome erfüllt. Für f , g ∈ Abb(R, R) und α ∈ R definieren wir eine Addition ⊕ und eine
Skalarmultiplikation punktweise, d.h. nach folgenden Regeln:
(a) h = f ⊕ g ist die Funktion in Abb(R, R), für die gilt:
h(x) = f (x) + g(x).
(b) k = α f ist die Funktion in Abb(R, R), für die gilt:
k(x) = α · f (x).
2
Z3.2. (a) Zeigen Sie, dass folgende Ausdrücke Normen im R sind, wobei v =
v1
v2
. Zeichnen Sie jeweils
die Mengen {v ∈ R2 | kvk = 1}.
(i) kvk∞ = max{|v1 |, |v2 |} (Maximumsnorm)
(ii) kvk1 = |v1 | + |v2 |
q
(iii) kvk2 = v12 + v22 (Euklidische Norm)
2
(b) Zeigen Sie, dass folgende Ausdrücke keine Normen im R definieren, wobei v =
v1
v2
.
(i) kvk = v1 + v2
(ii) kvk = |v1 |
(iii) kvk = v12 + v22
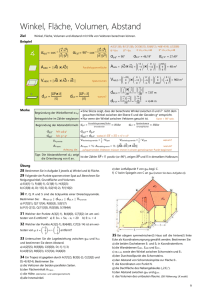
Z3.3. Zeigen Sie mit Hilfe des Skalarproduktes: Es schneide in einem Dreieck mit Eckpunkten A, B und C
die Winkelhalbierende im Punkt C die gegenüberliegende Seite c im rechten Winkel. Dann haben die an
C angrenzenden Seiten a und b gleiche Länge.
Tutorübungen
T3.1. Wir betrachten die Vektoren aus R4

1
 1
x=
 1
1



,


0
 −1 

y=
 1 ,
1


2
 −6 

z=
 4 
2
(a) Berechnen Sie x + y, 2x, − 12 z, 2x − 12 z.
(b) Überprüfen Sie am Beispiel der obigen Vektoren die Gültigkeit der Dreiecksungleichung bzgl. der
euklidischen Norm
kx + yk2 ≤ kxk2 + kyk2
sowie bzgl. der Maximumsnorm
kx + yk∞ ≤ kxk∞ + kyk∞ .
T3.2. Gegeben sei ein Dreieck im Anschauungsraum, bei welchem zwei Seiten durch die Vektoren
 


2
−2
a =  1 ,
b= 2 
2
1
bezüglich eines kartesischen Koordinatensystems gegeben sind.
Bestimmen Sie einen Vektor c für die dritte Seite, sowie sämtliche Seitenlängen und Winkel des Dreiecks.
T3.3. Der Kurs eines Segelbootes soll im Winkel α zur
Windrichtung verlaufen. Auf das Segel wirkt nur
die zu seiner Fläche orthogonale Komponente der
Windkraft FW . Diese wollen wir mit FS bezeichnen. Auf das Boot wirkt wiederum nur die in
Fahrtrichtung liegende Komponente der Segelkraft
FS , da das „Schwert“ eine Abdrift des Bootes verhindert. Die Kraftkomponente in Fahrtrichtung bewirkt den Vortrieb und sei mit FB bezeichnet. Welchen Winkel muss das Segel zum Wind haben, um
einen maximalen Vortrieb zu liefern?
Wind
FB
Segel
FW
FS
Durch „Kreuzen“ kann ein Segelboot auch direkt
gegen den Wind fahren. Wie funktioniert das?
T3.4. Wir definieren für ein n ∈ N den Raum der reellen Polynome mit Grad kleiner oder gleich n auf dem
Intervall [0, 1] als
)
(
n
X
ak x k mit ak ∈ R für k = 0, 1, . . . , n .
Pn ([0, 1]) := p : [0, 1] → R : p(x) =
k=0
Betrachten Sie nun P2 ([0, 1]) zusammen mit dem Skalarprodukt
Z 1
h p1 , p2 i :=
p1 (x) · p2 (x)dx
für p1 , p2 ∈ P2 ([0, 1]) .
0
Überprüfen Sie nun ob dieses Skalarprodukt die Skalarprodukt-Axiome aus der Vorlesung erfüllt.
Die Tutoraufgaben werden am 4.11.2016 besprochen.