Arbeitsblatt - Additionstheoreme 1

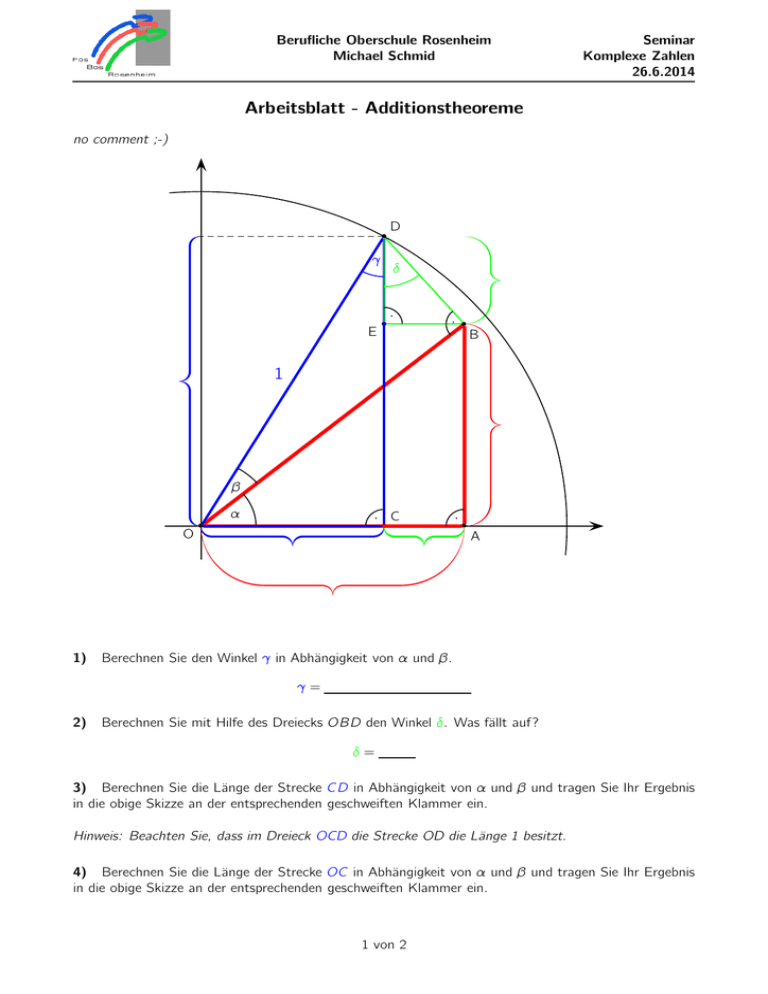
Berufliche Oberschule Rosenheim
Michael Schmid
Seminar
Komplexe Zahlen
26.6.2014
Arbeitsblatt - Additionstheoreme
no comment ;-)
D
b
γ
δ
·
b
E
b
·
B
1
β
α
· C
b
b
O
1)
·
b
A
Berechnen Sie den Winkel γ in Abhängigkeit von α und β.
γ=
2)
Berechnen Sie mit Hilfe des Dreiecks OBD den Winkel δ. Was fällt auf?
δ=
3) Berechnen Sie die Länge der Strecke CD in Abhängigkeit von α und β und tragen Sie Ihr Ergebnis
in die obige Skizze an der entsprechenden geschweiften Klammer ein.
Hinweis: Beachten Sie, dass im Dreieck OCD die Strecke OD die Länge 1 besitzt.
4) Berechnen Sie die Länge der Strecke OC in Abhängigkeit von α und β und tragen Sie Ihr Ergebnis
in die obige Skizze an der entsprechenden geschweiften Klammer ein.
1 von 2
Berufliche Oberschule Rosenheim
Michael Schmid
Seminar
Komplexe Zahlen
26.6.2014
5) Berechnen Sie die Länge der Strecke BD in Abhängigkeit von β und beschriften Sie mit Ihrem
Ergebnis die entsprechende Kante in der obigen Skizze.
BD =
Hinweis: Nutzen Sie das rechtwinklige Dreieck OBD.
6) Berechnen Sie die Länge der Strecke OB in Abhängigkeit von β und beschriften Sie mit Ihrem
Ergebnis die entsprechende Kante in der obigen Skizze.
OB =
7)
Weisen Sie rechnerisch nach, dass
OA = cos(α) · cos(β)
gilt. Beschriften Sie anschließend die entsprechende geschweifte Klammer in der obigen Skizze.
8) Berechnen Sie die Länge der Strecke AB in Abhängigkeit von α und β und tragen Sie Ihr Ergebnis
in die obige Skizze an der entsprechenden geschweiften Klammer ein.
AB =
9)
Weisen Sie rechnerisch nach, dass
CA = sin(α) · sin(β)
gilt. Beschriften Sie anschließend die entsprechende geschweifte Klammer in der obigen Skizze.
10) Berechnen Sie die Länge der Strecke ED in Abhängigkeit von α und β und tragen Sie Ihr Ergebnis
in die obige Skizze an der entsprechenden geschweiften Klammer ein.
ED =
11 - geschafft!)
Bestimmen Sie mit Hilfe aller geschweiften Klammern, Formeln für
sin(α + β) =
und
cos(α + β) =
Hinweis: Werfen Sie anschließend einen Blick in Ihre/eine Formelsammlung (Stichwort: Additionstheoreme)!
2 von 2