Optik_des_Auges

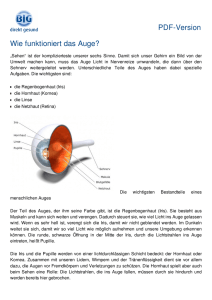
1
Optik des Auges
Basisinformation für den Medizinerversuch
Im Versuch untersuchen Sie die Grundfunktion des menschlichen Auges bei der Abbildung von
unterschiedlich weit entfernten Gegenständen auf die Netzhaut. Sie bestimmen dazu die Brechkräfte
sowohl von gekrümmten Flächen und in Wasser eingebetteten Linsen. Sie lernen die Möglichkeiten
der Brechkraftkorrektur mittels Vorsatzlinsen (Brillen) kennen.
1. Vorbemerkungen
Bevor mit der Betrachtung des Auges als optischem Instrument begonnen wird, soll
zunächst seine Bedeutung für den Wahrnehmungsprozess erläutert werden. Um das
Sehen zu verstehen, reicht die Kenntnis der physikalischen Zusammenhänge
natürlich nicht aus. Vielmehr muss das Auge als ein Glied in einer physiologischen
Kette verstanden werden. Erst das Zusammenspiel aller beteiligten Prozesse lässt
das Auge zu einem einzigartigen Sinnesorgan werden.
Man kann die optische Wahrnehmung vereinfachend in folgende Abschnitte
unterteilen:
A) Im Auge als optischem Instrument wird der Gegenstand auf der Netzhaut
abgebildet.
B) Zellen auf der Netzhaut (Rezeptoren) wandeln das Licht in elektrische Reize um.
Diese Signale werden schon innerhalb des Auges über ein Netzwerk aus Zellen
(Neuronen) miteinander verknüpft und weitergeleitet. Dadurch erfolgt beispielsweise eine Kontrastverstärkung
C) Auf Grund unserer Erfahrung werden die optischen Bilder zu interpretierbaren
Objekten.
100
Lichtintensität
20
Ort
I*m±1 = Im±1 - Im /10
I1 =100
- 10
-10
I*1 =80
I2 =100
-10
-2
I*2 =88
I3 =20
-10 -2
I*3 =8
I4 =20
-2
-2
I*4 =18
100
Lichtreiz
20
Ort
Im Praktikumsversuch wird ausschließlich nur der Schritt A) untersucht. Die weiteren Schritte B) - D)
stehen hier außerhalb unserer Betrachtung. Sie zu kennen ist aber
wichtig, um zu verstehen, warum man
was sieht. So wird in Abb. 1 zur
Demonstration des Schrittes C) die
Verknüpfung
der
Reize
von
benachbarten Rezeptoren vereinfachend dargestellt:
Abb. 1: Erläuterung des Simultankontrasts:
In der Wahrnehmung ist die Rate der
elektrischen Impulse der Neuronen von
Bedeutung. Je höher die Rate, desto
intensiver der Eindruck (hohe Intensität
verursacht 100 Impulse, niedrige 20). Ein
erregtes Neuron hemmt die Rate seiner
Nachbarn im Verhältnis zu seiner eigenen
Erregung (hier: jeweils 1/10). An Grenzen
zwischen zwei unterschiedlich hellen Flächen
kommt es daher zur Verstärkung des hellen
Teils und zur Schwächung des dunkleren. Im
Quadrat der Abb.2. werden die Kreuzungen
von weniger schwarzer Fläche umrandet als
die Zwischenstücke, daher werden sie nicht
so stark aufgehellt.
2
Optik des Auges
Abb. 2: Beispiel für Simultankontrast:
Fixiert man im rechten Beispiel den Punkt in der Mitte,
scheinen die Kreuzungen dunkler als die weißen
Gebiete dazwischen.
Ein gereizter Rezeptor unterdrückt den Reiz des Nachbarrezeptors um einen Wert,
der proportional zu seiner eigenen Reizung ist (im dargestellten Beispiel jeweils um
1/10 seines Reizes). Damit erfolgt eine Kontrastverstärkung der Sehreize beim
Übergang von Hell-Dunkel (sog. Simultankontrast).
Beispiele für die Verarbeitungsleistung unseres visuellen Apparates sind in Abb. 3
zu sehen. Ohne Erfahrung könnte das Auge allein den Würfel, die Schrift oder die
Wellenlinie nicht identifizieren.
Abb. 3: Gesehenes wird aus der Erfahrung interpretiert: Würfel, Wort, Wellenlinie
2. Anatomie des Auges
Abb. 4-oben zeigt einen Längsschnitt durch das menschliche Auge entlang der
optischen Achse. Das Licht passiert, vom Beobachtungsgegenstand kommend,
zuerst eine fast sphärisch gekrümmte Fläche, die Hornhaut. Sie ist stärker gekrümmt
als der übrige Teil des Augapfels und steht daher vor.
Dahinter befindet sich die vordere Augenkammer, die mit Wasser gefüllt ist. Sie wird
durch die Regenbogenhaut (lat. Iris) von der hinteren Augenkammer getrennt. Die
Iris bildet eine zentrale kreisrunde Blende, die Pupille. Durch eingelagerte Muskel-
OptikdesAuges
3
zellen ist der Durchmesser variabel und regelt damit die ins Auge einfallende
Lichtintensität und die Schärfentiefe.
Der Iris folgt die Augenlinse. Sie besteht aus ca. 20000 zwiebelartigen Schichten, die
von der Linsenkapsel eingeschlossen werden. Die Eigenspannung der Linse würde
sie zu einer Kugel zusammenziehen. Diesem Bestreben wirken die Zonulafasern
entgegen. Durch sie wird die Linse flach gezogen. Sie sind die Aufhängung der Linse
im Auge und enden am Ciliarmuskel. Er umgibt die Zonulafasern und die Linse
ringförmig und ermöglicht durch seine Kontraktion, daß die Linse in ihre ursprüngliche Gestalt zurückfallen kann. Das Resultat ist eine in ihrem Krümmungsradius,
und damit in ihren Abbildungseigenschaften, variable Linse. Man nennt diesen
Vorgang Akkommodation. Da dies eine außergewöhnliche Eigenschaft des Auges
darstellt, die wesentlich das Verständnis des Abbildungsvorgangs mitbestimmt, wird
dieser Eigenschaft der Linse im Praktikumsversuch besondere Aufmerksamkeit
geschenkt.
Werden die Fasern vollständig entspannt, ist der kleinste Linsenradius erreicht.
Dieser Zustand legt zugleich den kleinsten möglichen Abstand fest, den das Auge
scharf abbilden kann (Nahpunkt). Mit zunehmendem Alter verschlechtern sich die
elastischen Eigenschaften der Linse. Das heißt, der Nahpunkt rückt weiter vom Auge
weg. Die Variation der Brechkraft der Augenlinse, die sogenannte Akkommodationsbreite, ist in Abhängigkeit des Lebensalters in Tab. 1 dargestellt.
Alter in Jahren
Nahpunkt in cm
Akkommodationsbreite in dpt
10
-7
14,3
20
-9
11,1
30
-12
8,3
40
-21
4,8
50
-60
1,7
60
-120
0,8
70
-120
0,8
80
-120
0,8
Tab.1: Verringerung der Akkommodationsfähigkeit mit dem Alter
Hinter der Linse befindet sich der Glaskörper. Er hat einen Flüssigkeitsanteil von
98% und gibt dem Auge seine Form.
Den Weg des Lichtes beendet schließlich die Netzhaut (lat. Retina). Sie umschließt
den Glaskörper. In ihr wird das Licht zu 99,9% absorbiert und in elektrische Impulse
umgewandelt. Für die Absorption besitzt die Retina verschiedene Rezeptoren. Sie
werden zunächst grob nach ihrem Aussehen in Zapfen und Stäbchen unterteilt. Die
Zapfen sind für das Farbensehen verantwortlich und die Stäbchen unterscheiden hell
und dunkel. Von den Rezeptoren leiten Nervenfasern die elektrischen Impulse in das
Gehirn weiter.
3. Auge als optisches Instrument
Für das Verständnis der uns interessierenden optischen Abbildung im Auge kann
dieses durch ein Ersatzmodell beschrieben werden, das in Abb.3 unten dargestellt
ist. In seiner optischen Funktion kann das Auge modelliert werden durch einen mit
einer sphärischen Eintrittsfläche versehenen „Glaskörper", in den die variable
Augenlinse eingehängt ist. Für das Verständnis der Optik des Auges ist es wesentlich, daß der Großteil der Augenbrechkraft durch die Hornhautkrümmung bewirkt
wird, währenddessen die Augenlinse eine Anpassung der Abbildung an variable
Gegenstandsweiten ermöglicht.
4
Optik des Auges
n3
n2
Abb. 3: Anatomie des Auges (oben) und optisches Ersatzmodell (unten)
Optische Kenngrößen des Auges
Brechzahl des Kammerwassers und des Glaskörpers
Brechzahl der Linse
Radius der Hornhaut
1,3365
1,358
7,829 mm
Radius der hinteren Linsenfläche
Ferne
17,055mm
22,785mm
10mm
-6mm
Nähe
14,169mm
18,930mm
5,33mm
-5,33mm
Ort des hinteren Brennpunktes
Ort des vorderen Hauptpunktes
Ort des hinteren Hauptpunktes
-15,707mm
24,387mm
1,348mm
1,602mm
-12,377mm
21,016mm
1,722mm
2,086mm
Vordere Brennweite des Auges
Hintere Brennweite des Auges
OptikdesAuges
5
4. Berechnung des Strahlenverlaufs im Auge
4.1 Brechungsgesetz
Fundamental für alle weiteren Berechnungen ist das Brechungsgesetz, das die
Ausbreitung des Lichtstrahls beim Übergang zwischen zwei lichtdurchlässigen
Stoffen mit den Brechzahlen n1 und n2 beschreibt .
n 1 ⋅ sin α = n 2 ⋅ sin β
( 4.1.)
Aus diesem Gesetz folgern alle weiteren Formeln.
4.2. Abbildung durch eine Kugelfläche
Im weiteren wird die Brechung eines Lichtstrahls an einer Kugelfläche betrachtet. Um
mit praktikablen Messgrößen zu arbeiten, ist es zweckmäßig, Längen entlang der
optischen Achse von einem festen Bezugspunkt aus zu wählen. Dabei ist der
Scheitelpunkt S am geeignetsten. Im weiteren Verlauf werden, wie üblich, die
Entfernungen vom Scheitel zum Gegenstand mit g bzw. zum Bild mit b und der
Krümmungsradius mit r bezeichnet. Zu berechnen ist die Bildweite in Abhängigkeit
von der Gegenstandsweite.
Abb.4.: Abbildung durch eine Kugelfläche
Man erhält aus geometrischen Überlegungen
n1 n2 n2 − n1
+
=
g
b
r
Die Bildweite für unendlich ferne Gegenstände nennt man Brennweite f. Daraus folgt
für Abb.4, wenn das Bild im Gebiet mit n2 liegt:
f =
n2
r
n 2 − n1
6
Optik des Auges
Vertauscht man Gegenstand und Bild, so daß dieses im Gebiet mit n1 liegt, erhält
man:
n1
f '=
r
n 2 − n1
Da die Brennweite von der Ausbreitungsrichtung des Lichtes abhängt, wird die von
der Richtung unabhängige Brechkraft D definiert. Die Brechkraft ist der Quotient aus
Brechzahl und zugehöriger Brennweite (Einheit: 1 1/m= 1 dpt).
D=
n 2 n1
=
f
f'
4.3. Abbildung durch eine dünne Linse
Eine dünne Linse besteht aus zwei Kugelflächen, zwischen denen sich ein
homogenes Material befindet, und deren Scheitelpunktabstand vernachlässigbar
klein gegenüber Bild- und Gegenstandsweite ist. Daher wird nach Durchgang der
ersten Fläche die Bildweite b1 zur Gegenstandsweite g2 der zweiten Fläche.
Abb.5: Bildentstehung bei einer dünnen Linse
Mit der Formel 4.3 und Abbildung 4.2 erhält man folgende Gleichungen:
n 1 n 2 n 2 − n1
+
=
g b1
r1
−
n 2 n3 n3 − n 2
+
=
b1 b
r2
Die Addition beider Gleichungen unter Berücksichtigung der Definition von
Brennweite und Brechkraft ergibt:
OptikdesAuges
7
n1 n3 n 2 − n1 n3 − n2
+
=
+
g
b
r1
r2
D=
n 2(n L − n)
=
, für n 3 = n 1 = n, n 2 = n L und r1 = − r2 = r
f
r
4.4 Die Kombination von 2 dünnen Linsen
Da das Auge aber ein System aus mehreren optischen Elementen (Hornhaut, Linse;
eventuell unterstützt von Brille oder Kontaktlinse) ist, ist die Frage zu beantworten,
wie sich die Brennweite des Systems aus den Brennweiten der Einzelelemente
ergibt. Dazu betrachten wir als erstes den Fall von zwei hintereinander stehenden
dünnen Linsen. Beide Linsen sollen sich im gleichen Medium mit der Brechzahl n
befinden. Konstruiert wird die Abbildung nach folgendem Verfahren (Abb. 4.5):
L2
L1
f1
f2
f1
f2
f1
d
L2
L1
f1
d
Abb.6 Das System aus zwei dünnen Linsen
8
Optik des Auges
Zuerst berücksichtigt man nur die optische Wirkung von L1. Aus Brennpunktstrahl
und Parallelstrahl wird der Ort des Bildes von L1 bestimmt. Dann sucht man
denjenigen Strahl, der als Mittelpunktstrahl durch L2 laufen würde. Berücksichtigt
man nun die Linse L2, so wird dieser Strahl nicht beelnflußt, da er ja Mittelpunktstrahl
von L2 ist. Der Parallelstrahl nach L1 knickt allerdings zum Brennpunkt von L2 ab. Aus
dem Schnittpunkt beider Strahlen findet man das Bild der Linsenkombination.
Nach einiger Rechnung findet man:
1 1 1
d
= + −
f G f1 f 2 f1f 2
bzw.:
D G = D1 + D 2 −
d
D1D 2
n
(4.10.)
Für die Näherung d → 0 erhält man
DG = D1 + D2
(4.11)
In diesem Fall kann man dann die gesamte Brechkraft als Summe der
Teilbrechkräfte berechnen. Diese Gleichung gilt auch, wenn eine Kugelfläche
beteiligt ist und Bild- und Gegenstandsseite verschiedene Brechzahlen besitzen.
4.5 Die Kombination Kugelfläche- Linse
In diesem Abschnitt sollen die physikalischen Grundlagen für die Behandlung von
Auge und Augenmodell abgeschlossen werden. Zu Grunde liegt beiden ein System
aus einer Kugelfläche (Hornhaut) und einer Linse (Abb.4.6.). Beide haben den
Abstand e voneinander. Die Gegenstandsweite wird vom Scheitelpunkt der
Kugelfläche gemessen. Auf der Gegenstandsseite soll Luft sein (n=1). Weiterhin hat
die Linse (Brechzahl nL) beidseitig den gleichen Radius (im Modell, nicht in der
Realität!). Die Umgebung der Linse habe die Brechzahl n. Bild- und Brennweite
werden vom Scheitelpunkt der Austrittsfläche der Linse gemessen.
g
n
rH
rL
e
b
d
nL
n
Abb.7 Größenbezeichnung bei der Kombination Kugelfläche- Linse
Ziel soll es sein, eine Gleichung für die Lage des Bildes zu finden, in der nur
messbare Größen enthalten sind.
OptikdesAuges
9
Die gesuchte Formel erhält man, indem zunächst mit Hilfe von Formel (4.3.) die
Bildweite der Kugelfläche (b=bhorn) bestimmt wird. Das Ergebnis wird dann in
Gleichung (4.8.) unter Beachtung des Abstandes e eingesetzt:
n δn
nL
=
−
b rL d − n L rL a
δna − nrL
wobei a = e − b Horn und δn = n L − n
(4.12.)
Aus dieser Gleichung folgen beim Übergang g → ∞ die Brennweite und die
Brechkraft:
⎛⎛
⎞
nr ⎞
n L ⎜ ⎜ e − H ⎟ δn − nrL ⎟
n −1 ⎠
n δn
⎝⎝
⎠
D= =
−
nrH ⎞
f rL ⎛
⎜e −
⎟ ( δnd − n L rL ) − enrL
n −1 ⎠
⎝
Die Näherung für eine dünne Linse (d → 0) ergibt:
D=
n
=
f
2δn −
rL n(n − 1)
n
n
e(n − 1) − nrH
= +
rL
f L f Horn − e
und für e << fHorn folgt näherungsweise:
D ≈ DLinse + DHorn
5. Versuchsaufbau
Das Augenmodell (Abb.5) besteht aus einem wassergefüllten Glaskasten, der an
einer Seite eine sphärisch gekrümmte Oberfläche („Hornhaut“) besitzt. Dazu wurde
ein Nullstärken-Brillenglas verwendet. In den Kasten ist eine Mattscheibe als
Bildschirm eingehängt. Seine Position längs der optischen Achse kann über eine
Skala abgelesen werden. Das durchscheinende Bild wird von der Rückseite des
Glaskastens aus aus betrachtet. Herzstück des Augenmodells ist eine in ihrer
Brechkraft variable Linse. Sie besteht aus einem flexiblen Kunststoffbalg, der sich
über einen Kolben mit Silikonöl der Brechzahl 1,5 auffüllen läßt. Am Kolben ist eine
Skala zum Ablesen der Kolbenverstellung und damit der Volumenänderung in der
Linse angebracht.
Zum Versuchsaufbau gehören weiterhin Blenden verschiedenen Durchmessers
sowie Vorsatzlinsen (Brillengläser) mit Brechkräften zwischen +2dpt und –0,75dpt.
10
Optik des Auges
Kolben
Wasser
Gegenstand
optische Bank
Vorsatzlinse
“
Hornhaut
Schirm
Blende
variable Linse
Abb. 8: Augenmodell
6. Aufgaben:
6.1: Bestimmen Sie die Brechkraft der sphärischen Eintrittsfläch „Hornhaut“) !
Zu diesem Zweck wird die variable Linse aus dem Glaskasten entfernt. Eine
Vorsatzlinse (2dptr) wird verwendet, um Bilder innerhalb des wassergefüllten
Glaskastens zu erhalten. Für mehrere Gegenstandsweiten g sind die Bildweiten b (in
Wasser mit n=1.33) zu messen. Die Meßgrößen g und b werden entsprechend der
Abbildungsgleichung
1 n
n
+ =
= DHorn + DVorsatzlinse
g b fW
in der Form n/b über 1/g aufgetragen. Die Brechkraft des Systems "Vorsatzlinse+
Eintrittsfläche" ist gleich dem Schnittpunkt der Geraden mit der Y-Achse.
6.2: Messen die Sie Brechkraft des Augenmodells bei eingehängter variabler
Linse!
Hierzu wird die Vorsatzlinse entfernt und die variable Linse in den Glaskasten
eingehängt. Schieben Sie die variable Linse möglichst dicht an die gekrümmte
Eintrittsfläche. Führen Sie für 2 unterschiedliche Füllvolumina der variablen Linse
(z.B. Kolbenstand 30 und 80) die Messungen analog zu 6.1 durch. Es sind
mindestens 3 verschiedene, geeignet gewählte Gegenstandsweiten einzustellen. Die
Auswertung erfolgt analog zu 6.1, wobei Sie hier die Gesamtbrechkraft D = DHorn +
DLinse erhalten. Geben Sie DLinse für die beiden Füllvolumina an.
6.3: Untersuchen Sie die Akkomodationsfähigkeit der "aufpumpbaren" Linse!
Hierzu arbeiten Sie wie in 6.2 ohne Vorsatzlinse, halten aber die Position der
Mattscheibe und damit die Bildweite (b=bconst) fest. Bestimmen Sie für einen
möglichst großen Bereich der Gegenstandsweite g das jeweilige Füllvolumen in der
variablen Linse (d.h. den Kolbenstand), um eine gute Abbildung auf der
festgehaltenen Mattscheibe zu erhalten. Bestimmen Sie die zu den jeweiligen
OptikdesAuges
11
Gegenstandsweiten passenden Brechkräfte der aufgepumpten Linse. Tragen Sie die
Brechkräfte der variablen Linse über dem Kolbenstand auf und vergleichen Sie das
Ergebnis mit dem von 6.2. Wie groß ist im Augenmodell die Akkomodationsbreite der
"Augenlinse"?
6.4: Untersuchungen an luftgefüllten Linsenkörpern in Wasser
Setzen Sie anstelle der "Augenlinse" eine luftgefüllte Konvex- bzw. Konkavlinse in
das Wasserbecken und beobachten Sie den Strahlverlauf. Können Sie das Ergebnis
erklären?
6.5: Korrektur von Fehlsichtigkeit
Entfernen Sie die "Augenlinse" aus dem Wasserbecken. Das entspricht der Situation
nach einer Operation des grauen Stars. Um eine deutliche Abbildung zu erreichen,
ist eine Vergrößerung der Augenbrechkraft erforderlich. das kann beispielsweise
durch Vorsetzen einer geeignet starken Sammellinse erfolgen.
Zur Demonstration der Korrektur der Kurzsichtigkeit mit einer Zerstreuungslinse
stellen Sie bei eingesetzter „Augenlinse“ (Kolbenstand xx) die Mattscheibe auf
yymm. Für die Abbildung entfernter Gegenstände ist dieser Abstand eigentlich zu
lang. Eine deutliche Abbildung erreicht man durch Vorsetzen einer Zerstreuungslinse
mit negativer Brechkraft. Wählen Sie eine geeignete Vorsatzlinse aus, um den
Gegenstand in 5m Entfernung deutlich abzubilden. Ist es möglich, mit trotz der
Vorsatzlinse näher liegende Gegenstände abzubilden?
Als Anlage:
Auswertung der Aufgaben 6.1, 6.3 und 6.5
12
Optik des Auges
6.3 variable Linse in Wasser
Kolbenstellung x=30
g luft
b wasser
2.63
1/g
1.33/b
0.33
0.38022814
4.03030303
4.15
0.32
0.24096386
4.15625
6.25
0.317
0.16
4.1955836
Kolbenstellung x = 55
6.25
0.241
0.16
5.5186722
4.15
0.245
0.24096386
5.42857143
2.63
0.253
0.38022814
5.256917
1.04
0.294
0.96153846
4.52380952
0.73
0.324
1.36986301
4.10493827
0.73
0.251
1.36986301
5.29880478
1
0.243
1
5.47325103
2.28
0.219
0.43859649
6.07305936
3.8
0.211
0.26315789
6.30331754
Kolbenstellung x= 80
Linsenbrechkräfte
x (mm)
D (dptr)
30
1.4
55
2.8
80
3.6
6.5 Korrektur von Fehlsichtigkeit
Korrektur der Weitsichtigkeit
Kammerlänge = 24 cm, Linse variiert zwischen 35 mm (Ferne) und ,ax. 55mm (Nähe).
Korrekturlinse 1dptr
Korrektur der Kurzsichtigkeit
Kammerlänge = 28,5 cm, Linse variiert zwischen 55 mm (korr, Ferne) und
max. 85mm (korr, Nähe) bzw. 60 (ohne Brille, Nähe).
Korrekturlinse -0.75dptr
Variable Linse in Wasser
7
6
y = -0.9257x + 6.4979
5
1.33/b (1/m)
y = -1.1872x + 5.7056
4
y = -0.7673x + 4.3272
3
Kolbenstellung x=30
Kolbenstellung x=55
Kolbenstellung x=80
2
1
0
0
0.2
0.4
0.6
0.8
1/g (1/m)
1
1.2
1.4
1.6
OptikdesAuges
13
6.1 Bestimmung der Brennweite der „Hornhaut“
Bild in Wasser
g luft (m)
x luft
b wasser (m)
1/g
1.33/b
4.05
0.05
0.48887218 0.24691358 2.72054752
2.38
0.08
0.51142857 0.42016807 2.60055866
0.96
0.24
0.63172932 1.04166667 2.10533206
0.4512782
Bild in Luft
b luft
x luft
g wasser
1.33/g
1/b
0.425
2.59
2.39864662 0.55447934 2.35294118
0.455
1.56
1.62421053 0.81885936
2.1978022
0.76
0.35
0.71443609 1.86160808 1.31578947
0.96
0.23
0.62421053 2.1306914
1.04166667
Brechkraft: D=2.9
Brenweite in Luft: fL = 35 cm
Brennweite in Wasser F w = 46cm
Hornhaut, Bild in Wasser und in Luft
3
1.33/b wasser (1/m)
2.5
Bild in Wasser
y = -0.7801x + 2.9198
2
Bild in Luft
1.5
y = -0.8362x + 2.8488
1
0.5
0
0
0.5
1
1.5
1/g (1/m)
2
2.5