3. Strukturbestimmung

Vorlesung
“Charakterisierung
von Halbleitermaterialien I”
3. Strukturbestimmung
Materials for Electronics and Energy Technology
Einführung
3. Strukturbestimmung
Charakt Hableiter-Mat
Matthias Bickermann
Strukturbestimmung
Realstruktur:
Kristalldefekte
Kristallstruktur:
Kristallographie
– Röntgenmethoden
– Grundlagen der Röntgenographie
– Laueaufnahmen
– Elektronenbeugung: EBSD und Polfiguren
– Diffraktometrie
– Grazing Incidence
– Hochausflösende Röntgenbeugung
– Röntgentopographie
Halbleiter kristallisieren meist in
einfachen, dicht gepackten
Strukturen (Teil 1 der Vorlesung)
Þ keine Strukturaufklärung nötig
Punktdefekte:
Þ Elektrische und optische Eigensch.
Liniendefekte: Versetzungen
Gitterkonstante: Verspannungen,
Fehlpassungen (Heteroepitaxie)
Kristallorientierung: Fehlorientierungen, Substratorientierung
– Defektätzen
Flächendefekte: Stapelfehler,
Korngrenzen
Volumendefekte: Fehlorientierungen,
Fremdkristalle, (Agglomerate)
(c) 2011 PD Dr. M. Bickermann, I-MEET, Uni Erlangen
3. Strukturbestimmung
3. Strukturbestimmung
Röntgenographie
Charakt Hableiter-Mat
Matthias Bickermann
Bragg-Bedingung
Röntgenographie
Charakt Hableiter-Mat
Matthias Bickermann
Röntgenstrahlen
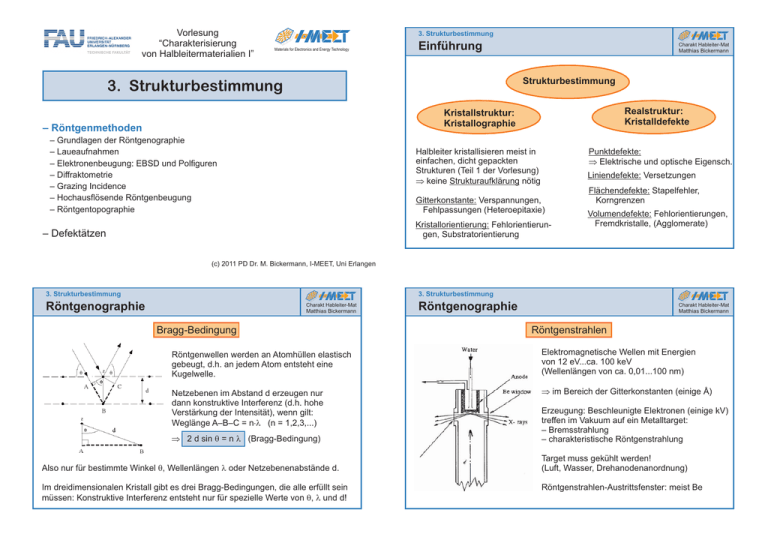
Röntgenwellen werden an Atomhüllen elastisch
gebeugt, d.h. an jedem Atom entsteht eine
Kugelwelle.
Elektromagnetische Wellen mit Energien
von 12 eV...ca. 100 keV
(Wellenlängen von ca. 0,01...100 nm)
Netzebenen im Abstand d erzeugen nur
dann konstruktive Interferenz (d.h. hohe
Verstärkung der Intensität), wenn gilt:
Weglänge A–B–C = n×l (n = 1,2,3,...)
Þ im Bereich der Gitterkonstanten (einige Å)
Þ 2 d sin q = n l (Bragg-Bedingung)
Also nur für bestimmte Winkel q, Wellenlängen l oder Netzebenenabstände d.
Im dreidimensionalen Kristall gibt es drei Bragg-Bedingungen, die alle erfüllt sein
müssen: Konstruktive Interferenz entsteht nur für spezielle Werte von q, l und d!
Erzeugung: Beschleunigte Elektronen (einige kV)
treffen im Vakuum auf ein Metalltarget:
– Bremsstrahlung
– charakteristische Röntgenstrahlung
Target muss gekühlt werden!
(Luft, Wasser, Drehanodenanordnung)
Röntgenstrahlen-Austrittsfenster: meist Be
3. Strukturbestimmung
3. Strukturbestimmung
Röntgenographie
Charakt Hableiter-Mat
Matthias Bickermann
Röntgenographie
charakteristische Röntgenstrahlung
Charakt Hableiter-Mat
Matthias Bickermann
Laue-Aufnahme
Elektronen schlagen ein Elektron aus der
inneren Atomhülle (K, L, M usw.) heraus.
Ein Elektron der äußeren Schale rutscht
unter Energiegewinn (Lichtaussendung)
nach.
Þ Übergang nur aus besetzten Schalen
Þ Röntgenenergie einer Schale nimmt
mit der Ordnungszahl stark zu.
Laue-Aufnahme in Transmission
vgl. 2 d sin q = n l (Bragg-Bedingung)
Þ hohe Intensität der Röntgenstrahlung!
Feinstruktur der Atomhülle: Übergänge
spalten weiter auf (Ka ® Ka1, Ka2 usw.)
mit festem Intensitätsverhältnis.
Þ keine monochromatische Strahlung!
3. Strukturbestimmung
Ein fest montierter Kristall wird mit “weißem”
Röntgenlicht bestrahlt. q und d sind durch
die Kristallorientierung vorgegeben, man
erhält eine stereographische Projektion der
(reziproken) Netzebenen bei Winkeln 2q als
Punkte mit gleichem nl/d.
Die Aufnahme erfolgt in Transmission/Vorwärtsstreuung (kleine Kristalle) oder
Reflektion/Rückstreuung auf Röntgenfilm oder Speicherleuchtstoff-Folie.
Da die Kristallstruktur (d) meist bekannt ist, wird die Laue-Aufnahme vorwiegend
zur Bestimmung der Orientierung (q) von Einkristallen (z.B. Substraten) verwendet.
3. Strukturbestimmung
Laue-Bilder
Charakt Hableiter-Mat
Matthias Bickermann
Laue-Bilder
hcp/Wurzit m (10-10)
hcp/Wurzit (0001)
Charakt Hableiter-Mat
Matthias Bickermann
hcp/Wurzit a (11-20)
hcp/Wurzit off-orientiert
c [0001]
a [10-10]
m [11-20]
c [0001]
14° off-orientiert bzgl. c-Achse
in Richtung der a-Achse
(und Kristall um 45° verdreht)
Berechnung der off-Orientierung x zu einer Fläche:
Typischerweise werden Winkelausschnitte –30° < q < 30° um
den einfallenden Strahl gemessen
a [10-10]
m [11-20]
x = ½ arctan (L/D) mit L = Abstand auf dem Film
D = Abstand Film-Kristall
3. Strukturbestimmung
3. Strukturbestimmung
Laue-Bilder
fcc/Zinkblende (100)
Charakt Hableiter-Mat
Matthias Bickermann
fcc/Zinkblende (110)
fcc/Zinkblende (111)
Elektronenbeugung
Charakt Hableiter-Mat
Matthias Bickermann
Prinzipiell lassen sich Beugungsbilder des Atomgitters auch mit Elektronen- oder
Neutronenstrahlen erzeugen (gleiches Prinzip).
Electron Back-Scatter Diffraction (EBSD)
Kikuchi-Linien: “Laue-Aufnahmen mit dem REM”
Probe wird zum Elektronenstrahl verkippt:
Rückgestreute Elektronen werden auf einem
Phosphoreszenzschirm detektiert.
– Beugungsbild mit Laue-Symmetrie
– Linienbreite umgekehrt proportional zum
Netzebeneabstand
[111]
Raumgruppe 43m
Kikuchi-Linien können auch im TEM erzeugt
werden (Dunkelfeld, versetzte Blende).
{100} {111} {110}
[110]
[100]
3. Strukturbestimmung
Elektronenbeugung
Electron Back-Scatter Diffraction (EBSD):
Bestimmung der lokalen Kornorientierung
3. Strukturbestimmung
Charakt Hableiter-Mat
Matthias Bickermann
Elektronenbeugung
Charakt Hableiter-Mat
Matthias Bickermann
Electron Back-Scatter Diffraction (EBSD):
Pole Map: Mapping der lokalen Kornorientierung z.B. polykristalliner Schichten
– Polfigur: Stereographische Projektion
eines Reflexes, z.B. (0001)
(j-w-Auftragung)
– Inverse Polfigur: Abbildung der
Oberflächennormalen auf das
“Kugelachtel” des reziproken Raums
zwischen [001], [101] und [111]
(damit werden auch alle möglichen
Orientierungen abgedeckt)
Computergestützte
Bestimmung der
Kristallorientierung
Bilder oben:
verteilte Kornorientierung (untexturiert)
Bilder unten:
(111)-Texturierte Probe.
3. Strukturbestimmung
3. Strukturbestimmung
Elektronenbeugung
Charakt Hableiter-Mat
Matthias Bickermann
Diffraktometrie
Charakt Hableiter-Mat
Matthias Bickermann
Ziel: Messung der Intensität der gebeugten Röntgenstrahlung
in Abhängigkeit vom Beugungswinkel q.
Electron Back-Scatter Diffraction (EBSD):
Mapping der lokalen Kornorientierung
Warum? Die Wellen werden am periodischen Gitter (genauer: an den
Elektronen der Atomhüllen) gestreut. Die Bragg-Bedingung erzeugt aber
keine unendlich scharfe Reflexlinie sondern eine “Intensitäts-Verteilung” um q.
Die Halbwertsbreite B(hkl, q, l) der Intensitätsverteilung ist proportional zum
–2pi(hu+kv+lw)
Strukturfaktor F(hkl, q, l) = ån fn (q, l) × e
,
der die Atomstreufaktoren f aller Atomabstände r = (u v w) unter
Berücksichtigung der Phasenverschiebung zum Wellenvektor k = (h k l)
der einfallenden Röntgenwelle aufsummiert.
Beispiel AlN: Bild der Oberfläche, Inverse Polfigur mit EBSD, Kornfigur (w-Figur) mit EBSD
3. Strukturbestimmung
Die Halbwertsbreite B idealer Kristalle ist im Bereich weniger Bogensekunden;
so lassen sich Gitterabstands-Änderungen Dd/d von 10 –6 detektieren!
Keine andere Methode ist so empfindlich gegenüber solchen Änderungen!
Þ Spannungsfelder um Schichtübergänge, Versetzungen, Defektcluster,
Verkippungen/Verdrehungen durch Subkorngrenzen, “Gitterdurchbiegung”, ...
3. Strukturbestimmung
Diffraktometrie
Charakt Hableiter-Mat
Matthias Bickermann
Diffraktometrie
Si(220)
Ziel: Messung der Intensität der gebeugten Röntgenstrahlung
in Abhängigkeit vom Beugungswinkel q.
Þ 2 d sin q = n l (Bragg-Bedingung)
Unterschiedliche Wellenlängen
werden unter unterschiedlichem
Bragg-Winkel gebeugt.
– monochromatische Wellenlänge notwendig
– planparallele Röntgenstrahlung notwendig
Problem: Die reale Röntgenröhre emittiert
Weißlicht als Punktlichtquelle!
Þ Kollimatoren / Aperturblenden
Þ “Monochromator-Kristalle”
Aperturen oder Filter separieren eine
charakteristische Röntgenlinie
1
(z.B. Cu Ka1, 0.06°-Apertur oder 23μm Ni-Folie)
Charakt Hableiter-Mat
Matthias Bickermann
3. Strukturbestimmung
3. Strukturbestimmung
Diffraktometrie
Charakt Hableiter-Mat
Matthias Bickermann
Pulverdiffraktometrie
Charakt Hableiter-Mat
Matthias Bickermann
Im Pulver sind alle Kristallorientierungen gleichverteilt (idealerweise).
Si(220)
– Vergleich mit Standardmessungen (”PDF-Files”)
indexing after
JCPDS 25-1133
Unterschiedliche Wellenlängen
werden unter unterschiedlichem
Bragg-Winkel gebeugt.
Aperturen oder Filter separieren eine
charakteristische Röntgenlinie
(z.B. Cu Ka1, 0.06°-Apertur oder 23μm Ni-Folie)
Beim Filtern gehen allerdings
auch 60% der Ka1-Linie
verloren (aber billig!)
3. Strukturbestimmung
– Identifikation von Fremdphasen
(Beugung in anderen Winkeln q als der Hauptkristall)
3. Strukturbestimmung
Pulverdiffraktometrie
Charakt Hableiter-Mat
Matthias Bickermann
– Bei nicht-unendlicher Gitterausdehnung wird die konstruktive
Interferenz auch im Umfeld der “scharfen” Bragg-Bedingung erfüllt.
Intensitätsmaximum bei
2 t sin qB = m l
(Bragg-Bedingung)
Pulverdiffraktometrie
Charakt Hableiter-Mat
Matthias Bickermann
– Bestimmung der Partikelgröße t mit der Scherrer-Formel
t = 0,9 l / (B×cos q)
Beispiel: Y2O3:Eu nach Temperbehandlung
B = 0,19° Þ t = 253 nm
Halbwertsbreite durch
2 t sin q1 = (m–1) l
2 t sin q2 = (m+1) l
Þ B = q1 – q2
genaue Betrachtung:
Scherrer-Formel
t = 0,9 l / (B×cos q)
B = 0,23° Þ t = 114 nm
B = 0,25° Þ t = 80 nm
B = 0,38° Þ t = 35,4 nm
B = 0,76° Þ t = 14,1 nm
3. Strukturbestimmung
Diffraktometrie an dünnen Schichten
3. Strukturbestimmung
Charakt Hableiter-Mat
Matthias Bickermann
Charakt Hableiter-Mat
Matthias Bickermann
– Messung dünner Schichten mit streifendem Einfall (Grazing Incidence XRD)
Þ Die Röntgenstrahlen treffen nur Netzebenen in der Oberflächenschicht
counts per second [a.u.]
– Messung dünner Schichten mit streifendem Einfall (Grazing Incidence XRD)
Þ Die Röntgenstrahlen treffen nur Netzebenen in der Oberflächenschicht
Diffraktometrie an dünnen Schichten
Einfallswinkel typischerweise < 4°, aber größer als Totalreflektionswinkel
– Röntgenstrahl wird in der Oberflächenschicht absorbiert
Einfallswinkel kleiner als Totalreflektionswinkel: Glancing Incidence XRD
– Beugung der evaneszenten Welle (nur einige Oberflächenlagen)
3. Strukturbestimmung
Hochauflösende Röntgenbeugung
Beispiel: In2O3 auf Si(111)-Substrat
3. Strukturbestimmung
Charakt Hableiter-Mat
Matthias Bickermann
Abschätzung der maximalen “Auflösung” eines Diffraktometers:
n λ = 2d sin θ
Differenzierung nach θ:
0 = 2(Δd/Δθ) sin θ + 2d cos θ
Δd/d = – cos θ/ sin θ × Δθ = – cot θ/ Δθ
Bei Δθ = 0,02° und θ = 75°: Δd/d = 0,01 %
Man beachte: Die min. Divergenz einer
Röntgenröhre mit Kollimator und Monochromator beträgt ebenfalls ca. 0,02°.
Das reicht meistens für Heteroepitaxieschichten, aber nicht für Spannungen
aufgrund Versetzungen o.ä.
Rockingkurven-Halbwertsbreite
Rockingkurve eines idealen Si(440)-Reflexes
idealer Kristalle: 0.6” bis 12”
Wie erhält man eine bessere Winkelund Wellenlängeneinstellung? Þ Hochauflösende Diffraktometrie!
Hochauflösende Röntgenbeugung
Charakt Hableiter-Mat
Matthias Bickermann
Prinzipieller Aufbau:
– Beam conditioner
Doppel- bzw. Vierfachkristall
(Winkelgenauigkeit maximieren)
Aperturblende/Monochromator
(um z.B. CuKa2 auszublenden)
– Probe (drehbar um bis zu 5 Achsen)
– Zwei-Achsen-Aufbau:
offener Detektor (alle Wellenlängen)
für schnelle Messungen
oder
Drei-Achsen-Aufbau:
Analysator (Monochromator oder Spalt)
für orientierungssensitive Messungen
(Trennung von Dd und Dq)
– Detektor (wird typischerweise auf dem
Bragg-Winkel q des gewünschten
Reflexes gehalten)
3. Strukturbestimmung
3. Strukturbestimmung
Hochauflösende Röntgenbeugung
Charakt Hableiter-Mat
Matthias Bickermann
“Doppelkristallmessungen”
Hochauflösende Röntgenbeugung
Charakt Hableiter-Mat
Matthias Bickermann
Die Rockingkurve
Si(220)
Idealfall “ebene Welle” technisch
nicht realisierbar. Lösung:
Man misst die Autokorrelationsfunktion
der beiden Beugungs-Reflektivitäten.
Þ Rocking-Kurve
Wird ein Referenz-Kristall vorgeschaltet
und der passende Winkel eingestellt
(2q, falls gleiche Kristalle verwendet
werden), so werden nur Strahlen
durchgelassen, die von beiden gebeugt
werden: Exzellente Monochromatisierung!
– Die Halbwertsbreite ist nur ca. 40%
höher als im Idealfall
– Die gebeugte Intensität ist ca. 80%
der idealen Intensität
– Man erreicht Dd/d-Werte von 5×10 –5
specimen
2q
reference
crystal
3. Strukturbestimmung
Hochauflösende Röntgenbeugung
3. Strukturbestimmung
Charakt Hableiter-Mat
Matthias Bickermann
Achtung: Auf einer
Oberfläche können
Rockingkurven nur
von ausgewählten
Reflexen aufgenommen
werden!
Beobachtbare erlaubte Reflexe einer Si(001)-Oberfläche,
eingehender Strahl in der (100)-Ebene
(kleines Bild: eingehender Strahl in der (110)-Ebene)
Mit “channel cut”-Kristallen kann man Mehrfachbeugung an einem Kristall
erzielen: Gleiche Halbewertsbreite, aber steilerer Abfall (weniger Hintergrund).
Hochauflösende Röntgenbeugung
Charakt Hableiter-Mat
Matthias Bickermann
3. Strukturbestimmung
3. Strukturbestimmung
Hochauflösende Röntgenbeugung
Charakt Hableiter-Mat
Matthias Bickermann
Hochauflösende Röntgenbeugung
Charakt Hableiter-Mat
Matthias Bickermann
600
Double Crystal Rocking Curve: Beispiele
without growth
optimization
intensity [cps]
500
GaAs
Al0,6Ga0,4 As
Beispiel: Mapping der RockingkurvenHalbwertsbreite eines SiC-Kristalls
zur Bestimmung der “Gitterdurchbiegung”
in verschiedenen Kristallbereichen
400
300
FWHM=0.57°
200
100
0
Crystal B
intensity [cps]
500
400
FWHM=0.09°
300
200
100
Al0,3Ga0,7 As
Al0,6Ga0,4 As
Al0,3Ga0,7 As
GaAs
Interferenzerscheinungen
im “Sandwich Layer”
(Þ Bragg-Reflektor)
0
0
1
2
3
4
5
diffraction angle [°] (arb. origin)
AlN-Einkristall mit Mosaizität
(Subkorngrenzen)
3. Strukturbestimmung
Reciprocal Space Maps
B. M. Epelbaum et al., Investigation of lattice plane bending in large (0001)SiC crystals using
high-energy X-ray technique, phys. stat. sol. (c) 2 (2005) 1288.
3. Strukturbestimmung
Charakt Hableiter-Mat
Matthias Bickermann
Reciprocal Space Maps
Charakt Hableiter-Mat
Matthias Bickermann
Die Doppelkristall-Rockingkurve entsteht
als Schnitte durch den Beugungsreflex
im reziproken Raum entlang der Ewaldkugel (nur Probenrotation, y-Achse).
Im Drei-Achsen-Aufbau wird für versch.
y-Stellungen jeweils ein 2y-f-Scan
durchgeführt (Analysator bewegt sich
doppelt so schnell wie Probe).
Man erhält so ein “Abbild” des
Reflexes im reziproken Raum über
q y (Þ Dd, Verspannungen) und
q z (Þ Dq, Verkippungen/Verdrehungen)
Vor allem wichtig bei komplexen
Schichtabfolgen!
Verspannungen/
Gitterfehlpassungen und
Verkippungen können in
der Rockingkurve nicht
unterschieden werden,
aber sehr wohl in
reciprocal space maps!
3. Strukturbestimmung
Reciprocal Space Maps
3. Strukturbestimmung
Charakt Hableiter-Mat
Matthias Bickermann
Röntgentopographie
Charakt Hableiter-Mat
Matthias Bickermann
Beispiel GaN on Sapphire:
– Schicht und Substrat sind
jeweils von Mosaizität
(verkippten Bereichen) geprägt.
– Die Gitterfehlpassung wird auch
durch die horizontale Verschiebung zwischen Schicht und
Substrat sichtbar
– Dagegen sind Verspannungen
in beiden Materialien gering.
Synchrotron-WeißlichtRöntgentopographie (SWBXT)
Laue-Aufnahme mit großflächigem, parallelem, weißen Röntgenstrahl
Aus Laue-Punkten werden Flächen so groß wie der Strahlquerschnitt
Trotz mit homogener Strahlintensität (z.B. bei Synchrotronstrahlung):
Man sieht Strukturen (Intensitätsverteilung) in den einzelnen Laue-Bildern!
Þ lokale Abbildung von Defekten!
3. Strukturbestimmung
Röntgentopographie
3. Strukturbestimmung
Charakt Hableiter-Mat
Matthias Bickermann
Im Labor (ohne Synchrotron) haben sich zwei weitere Verfahren durchgesetzt.
Duch Verwendung einer Röntgenröhre wird nur eine Wellenlänge (z.B. Cu-Ka)
verwendet:
Berg-Barrett-Topographie
– Aufnahme in realer Größe
Probleme mit Strahldivergenz
– kleiner Abstand Kristall-Film,
sonst Doppelbild durch Cu-Ka1/2
Lang-Topographie:
– enge Streifenblende (Kollimator)
– saubere Trennung von Cu-Ka 1/2
– Kristall und Film werden synchron
im Strahl verschoben
– ohne Verschiebung ist auch eine
Ansicht eines Streifens durch den
Kristall möglich
(”section topography”)
Röntgentopographie
Charakt Hableiter-Mat
Matthias Bickermann
Orientierungskontrast
Verkippte Bereiche treffen nicht die
Beugungsbedingung: Abbildung als
Bereiche ohne Intensität (gilt auch
z.B. für Kleinwinkelkorngrenzen)
Lang-Topographien von AlN mit Domänenstruktur
(Bild unten mit 1,3° Verkippung des Kristalls)
3. Strukturbestimmung
3. Strukturbestimmung
Röntgentopographie
Charakt Hableiter-Mat
Matthias Bickermann
Röntgentopographie
Versetzungen, Stapelfehler und
Korngrenzen
– geben ein direktes Bild aufgrund ihrer
Versetzung
Verspannungen um den Defekt
(Orientierungskontrast)
Þ Erhöhung der Streuintensität bei Di
– es gilt das g×b-Kriterium, d.h. Versetzungen
mit dem Burgersvektor b in der Ebene
des Wellenvektors g (d.h. g×b = 0) sind
unsichtbar
– es gibt noch ein “dynamisches Bild” aufgrund einer Umverteilung der Energie im
sich ausbildenden Borrmann-Fächer DC´E
Þ verringerte Intensität im Bereich In
(je nach Kristalldicke mehr oder minder
unscharf)
Die Bestimmung der Versetzungsdichte ist limitiert
auf < 106 cm –2 (sonst Überlagerung der Abbildungen)
3. Strukturbestimmung
Röntgentopographie
Charakt Hableiter-Mat
Matthias Bickermann
links:
Versetzungen in
Silizium (dunkel:
direktes Bild; hell:
dynamisches Bild)
rechts:
Versetzungen in
GaAs (aufgrund der
hohen Absorption der
Röntgenstrahlung
nur dynamisches
Bild mit Informationen
nahe der Oberfläche)
3. Strukturbestimmung
Charakt Hableiter-Mat
Matthias Bickermann
Röntgentopographie
Defektbildung bei der Prozessierung eines Siliziumwafers:
(im Ausgangszustand waren keine Kontraste sichtbar!)
(a) Sauerstoffpräzipitation nach Hochtemperaturdiffusion
(b) plastische Verformung nach Hochtemperatur-Epitaxie
(c) fertiger Wafer mit Bauelementen
Bestimmung der Richtungen von Versetzungen
und Abgleitungen in AlN mit dem g×b-Kriterium
Charakt Hableiter-Mat
Matthias Bickermann
3. Strukturbestimmung
Literatur
3. Strukturbestimmung
Charakt Hableiter-Mat
Matthias Bickermann
Literatur
Charakt Hableiter-Mat
Matthias Bickermann
Literatur zum Thema Röntgenmethoden
Literatur zum Thema Rockingkurven und Röntgentopographie
– W. Kleber, H.-J. Bautsch, J. Bohm, Einführung in die Kristallographie, Verlag
Technik, Berlin 1998 bzw. Oldenbourg Wissenschaftsverlag, München 2002.
– W. Borchardt-Ott, Kristallographie: Eine Einführung für Naturwissenschaftler,
Springer-Verlag, Berlin und Heidelberg 1997.
– L.H. Schwartz, J.B. Cohen, Diffraction from Materials, Springer-Verlag,
New York 1987.
– L. Spieß, G. Teichert, R. Schwarzer, H. Behnken, C. Genzel,
Moderne Röntgenbeugung: Röntgendiffraktometrie für Materialwissenschaftler,
Physiker und Chemiker , Vieweg+Teubner, Wiesbaden 2009.
– P.F. Fewster, X-ray Scattering from Semiconductors, Imperial College Press,
London 2003 (Vertrieb durch World Scientific Press, Singapore).
– J. W. Jeffrey, Methods in X-Ray Crystallography, Academic Press, London 1971.
– D.K. Bowen, B.K. Tanner, High Resolution X-Ray Diffractometry and Topography,
Taylor & Francis, Boca Raton (FL), USA 1998.
– B.K. Tanner, X-ray Diffraction Topography, Pergamon, Oxford 1976.
– B.K. Tanner, D.K. Bowen, Advanced X-ray scattering techniques for the
characterization of semiconducting materials, J. Crystal Growth 126 (1993) 1.
– M. Dudley, in: D. Bloor, R. Brook, M. Flemings, S. Mahajan, R. Cahn (Eds.),
Encyclopedia of Advanced Materials, Vol. 4, Pergamon Press, New York 1994.
– R. Köhler, High-Resolution X-Ray Topography, Appl. Phys. A 58 (1994) 149.
– D.R. Black, G.G Long, X-Ray Topography, NIST Special Publication No. 960-10
(2004).
– B. Raghothamachar, M. Dudley, J.C. Rojo, K. Morgan, L.J. Schowalter,
J. Crystal Growth 250 (2003) 244.
Weiterführende Information zum Thema EBSD
– http://www.ebsd.com/ebsd-explained/ebsdexplained.htm
– http://www.bede.com