10. Das Wasserstoffatom quantenmechanisch 10. Das
Werbung

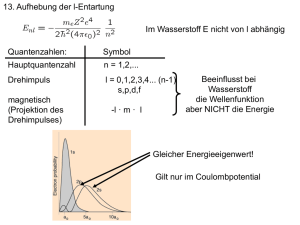
10. Das Wasserstoffatom quantenmechanisch 9.1. Operatoren, Messwerte 9.2. Zeitabhängige und stationäre Schrödingergleichung 9.3. Beispiel 1: Ebene Wellen als Lösung der Potentialfreien Schrödingergleichung 9.4. Beispiel 2: Der unendliche Potentialtopf 9.5. Beispiel 3: Die Potentialstufe 9.6. Der Tunneleffekt 9.6.1. Tunneleffekt Beispiel 1: Alphazerfall von Kernen 9.6.2. Tunneleffekt Beispiel 2: Rastertunnelmikroskop 9.7 Der (quantenmechanische) harmonische Oszillator 1dim 10. Das Wasserstoffatom quantenmechanisch 3dim 10.1. Bewegung im Zentralfeld Was gibt Neues?? 10.2. Der Drehimpuls in der Quantenmechanik Drehimpuls!! 10.3. Radialteil 10.4. Vergleich Bohrmodel-Quantenmechanisches H 10. Das Wasserstoffatom quantenmechanisch Stationäre Schrödingergleichung in 3 Dimensionen (x,y,z) ! ( R,θ,φ ) ∆ „Breitengrade“ Laplace Operator in Kugelkoordinaten: Betrachte die Schrödingergleichung in 3 Dimensionen, da das Potential im Wasserstoff ein Zentralpotential ist geht man zu Kugelkoordinaten über. 10. Das Wasserstoffatom quantenmechanisch Sphärische Polarkoordinaten Kugelkoordinaten: x=r sinθ cosφ y= r sinθ sinφ Z=r cosθ Laplace Operator in Kugelkoordinaten: „Breitengrade“ Stationäre Schrödingergleichung für Zentralpotential in Kugelkoordianten Produktansatz: Ψ(r,θ,φ)= R(r) T(θ) P(φ) Hängt nur von φ ab Hängt nur von r,θ ab ) Beide Seiten müssen konstant sein C1 Lösung: Da die Funktion eindeutig sein muß, soll gelten: P(φ)=P(φ + 2nπ) Teilen durch Ganzzahlig (m) m2Z Stationäre Schrödingergleichung für Zentralpotential in Kugelkoordianten Produktansatz: Ψ(r,θ,φ)= R(r) T(θ) P(φ) C1 = ml2 umsortieren, nach r und θ Hängt nur von r,θ ab Hängt nur von φ ab ) Beide Seiten müssen konstant sein C1 hängt nur von r ab hängt nur von θ ab Lösung: ) Beide Seiten müssen konstant sein C 2 Da die Funktion eindeutig sein muß, soll gelten: P(φ)=P(φ Legendresche + nπ) substituiere ξ=cosθ ! Differentialgleichung Allgemeine Lösung: Zugeordnete Kugelfunktionen Plm Teilen durch C2 = l(l+1), l 2 N Ganzzahlig (m) T=Plm (cos(θ)) T(θ) P(φ) = Plm (cos(θ)) eimφ = Ylmm(θ,φ) εZ Kugelflächenfunktionen 10. Das Wasserstoffatom quantenmechanisch 10.2. Der Drehimpuls in der Quantenmechanik Physikalische Größe Operator 10. Das Wasserstoffatom quantenmechanisch 10.2. Der Drehimpuls in der Quantenmechanik Physikalische Größe Operator 10. Das Wasserstoffatom quantenmechanisch l = 0,1,2,3 .... -l≤ ml ≤ l Drehimpulsquantenzahl Magnetische Quantenzahl Unschärferelation im Drehimpuls: ∆ lz ∆ lx > ~ ∆ lz ∆ ly > ~ ∆ lx ∆ ly > ~ z m~ Beispiel l=2 x,y Komponente unbestimmt m=-2,-1,0,1,2 2 dimensionale Welt? 10. Das Wasserstoffatom quantenmechanisch 1. Länge des Drehimpulsvektors ist quantisiert! 2. kann nicht beliebig im Raum stehen: Richtung ist quantisiert! Was ist die z (Quantisierungsachse)? hier weiter Stationäre Schrödingergleichung für Zentralpotential in Kugelkoordianten Produktansatz: Ψ(r,θ,φ)= R(r) T(θ) P(φ) C1 = ml2 umsortieren, nach r und θ Hängt nur von r,θ ab C2 = l (l+1) Hängt nur von φ ab ) Beide Seiten müssen konstant sein C1 hängt nur von r ab hängt nur von θ ab Lösung: ) Beide Seiten müssen konstant sein C 2 Da die Funktion eindeutig sein muß, soll gelten: P(φ)=P(φ Legendresche + nπ) substituiere ξ=cosθ ! Differentialgleichung Allgemeine Lösung: Zugeordnete Kugelfunktionen Plm Teilen durch C2 = l(l+1), l 2 N Ganzzahlig (m) T=Plm (cos(θ)) T(θ) P(φ) = Plm (cos(θ)) eimφ = Ylmm(θ,φ) εZ Kugelflächenfunktionen auflösen negativ Für r! 1 vernachlässige 1/r und 1/r2 Vollständige Lösung (Laguerre Polynome): hängen von n&l ab Wie Bohrmodel! Beschränkung für l l<0,1,2,... n hängt NICHT von l ab 10. Das Wasserstoffatom quantenmechanisch Ψnlm(r,θ,φ)= Rnl(r) T(θ)lm Pm(φ) = Rnl(r) Ylm(θ φ) Quantenzahlen: Symbol Hauptquantenzahl n = 1,2,... Drehimpuls l = 0,1,2,3,4... (n-1) s,p,d,f magnetisch (Projektion des Drehimpulses) Grundzustand n=1 l=0 m=0 n=2 l=0 m=0 l=1 m=-1 m=0 m=1 n2 Möglichkeiten -l · m · l keine Bohrsche Kreisbahn! KEIN Drehimpuls. “Entartet” (gleiche Energie) 10. Das Wasserstoffatom quantenmechanisch Ψnlm(r,θ,φ)= Rnl(r) T(θ)lm Pm(φ) = Rnl(r) Ylm(θ φ) |Rnl(r)|2 Wahrscheinlichkeit ein Elektron in einem Volumenelement am Abstand r zu finden r|Rnl(r)|2 Wahrscheinlichkeit ein Elektron in einer Kugelschale bei r zu finden Höchste Dichte am Kern! Maximum beim Bohrschen Radius 10. Das Wasserstoffatom quantenmechanisch Ψnlm(r,θ,φ)= Rnl(r) T(θ)lm Pm(φ) = Rnl(r) Ylm(θ φ) |Rnl(r)|2 Wahrscheinlichkeit ein Elektron in einem Volumenelement am Abstand r zu finden r|Rnl(r)|2 Wahrscheinlichkeit ein Elektron in einer Kugelschale bei r zu finden 1 Knoten! 10. Das Wasserstoffatom quantenmechanisch Ψnlm(r,θ,φ)= Rnl(r) T(θ)lm Pm(φ) = Rnl(r) Ylm(θ φ) Y00 = C1 Y10= C2 cosθ Y11= C3 sinθ eiφ Y20=C4(2cos2θ –sin2θ) Y21=C5(cosθ –sinθ eiφ Y22=C6 sin2θ e2iφ Polardarstellung: Abstand von (0,0) ist Funktionswert Z-Achse (Quantizierungsachse) 10. Das Wasserstoffatom quantenmechanisch Ψnlm(r,θ,φ)= Rnl(r) T(θ)lm Pm(φ) = Rnl(r) Ylm(θ φ) Y00 = C1 Y10= C2 cosθ Y11= C3 sinθ eiφ Y20=C4(2cos2θ –sin2θ) Y21=C5(cosθ –sinθ eiφ Y22=C6 sin2θ e2iφ Polardarstellung: Abstand von (0,0) ist Funktionswert Z-Achse (Quantizierungsachse) 10. Das Wasserstoffatom quantenmechanisch Verbreitete Darstellung: Form nur „Stilisiert“ Sind nicht gleichzeitig messbar 10. Das Wasserstoffatom quantenmechanisch Vergleich Bohrsches Atommodell - Quantenmechanik Quantenmechanik r-Abhängigkeit Radius verschmiert Bohr Planetenbahnen rn rn=a0/Z n2 Dichte Drehimpuls kann bei r=0 maximal sein 0 bei r=0 L=n~ 10. Das Wasserstoffatom quantenmechanisch 10. Das Wasserstoffatom quantenmechanisch en g n n o r u t k k le wir l E e e s r h e nd wec a b h c m r o Coul rmung du relektroneneffekte hi Meh c s b A h! Fehlt noc 11. Aufhebung der L-Entartung 12. Der Spin – Feinstruktur cher s i t e n g d ma n u r g f u a Atom n e m i r ” u t e k ström Korre s i e r K “ er Kräfte d 13. Atome in äusseren Magnetfeldern ern d l e F ren e s s u der Zeemaneffekt nä ome i At 11. Aufhebung der L-Entartung Im Wasserstoff E nicht von l abhängig Quantenzahlen: Symbol Hauptquantenzahl n = 1,2,... Drehimpuls l = 0,1,2,3,4... (n-1) s,p,d,f magnetisch (Projektion des Drehimpulses) -l · m · l Beeinflusst bei Wasserstoff die Wellenfunktion aber NICHT die Energie Erstaunlicherweise gleicher Energieeigenwert! Gilt nur im Coulombpotential 11. Aufhebung der L-Entartung Lithium n=1 Z=3 Äussere Elektron sieht Z=1? En=13,6/n2 für n>2 ?? l-Entartung aufgehoben! 2s fester gebunden als 2p 11. Aufhebung der L-Entartung 2s Dichte innerhalb der 1s Hülle Abgeschirmetes Potential Z=3 Z=1 l-Entartung aufgehoben! 2s fester gebunden als 2p 11. Aufhebung der L-Entartung Gelbe Natrium Linien: Gelbes Licht 589 nm Na: 2 Elektronen n=1 8 n=2 1 n=3 10. Das Wasserstoffatom quantenmechanisch 10. Das Wasserstoffatom quantenmechanisch 11. Aufhebung der L-Entartung 12. Der Spin – Feinstruktur 12.1. Elektronespin 12.2. Spin Bahn Kopplung, die Feinstruktur 12.3. Lambshift 12.4. Hyperfeinstruktur 13. Atome in äusseren Magnetfeldern der Zeemaneffekt 12. Bahn-, Spinmagnetismus, Feinstuktur 12.1. Der Elektronenspin Nach unserem heutigen Wissen ist das Elektron punktförmig, denoch hat es einen internen Drehimpuls Bahndrehimpuls Interner Drehimpuls Interner Drehimpuls SPIN bei Elektronen Punktteilchen!! Es gibt kein anschauliches Bild 12. Bahn-, Spinmagnetismus, Feinstuktur Experimenteller Hinweis: Aufspaltung der Wasserstoff Balmer α Sommerfeld hatte klassische Erklärung 12. Bahn-, Spinmagnetismus, Feinstuktur 1925 G.E. Uhlenbeck S. Goudsmit „Spinning Electrons and the Structure of Spectra“ 12. Bahn-, Spinmagnetismus, Feinstuktur What the historians forget - and also the physicists - is that in the discoveries in physics chance, luck plays a very, very great role. Of course, we do not always recognize this. If someone is rich then he says "Yes, I have been clever, that is why I am rich"! And the same is being said of some one who does something in physics "yes, a really clever guy.....". Leiden – Ehrenfest –Paschen Helium Spektrum One of the things which stuck to me is that in Paschen's experiments on the helium line, its fine stucture and the relativistic explanation, there was a forbidden component which was obviously present. And when I talked to the theoreticians about that forbidden component ......... but you know how theoreticians are ...... they then say: "Poor experiments". I found a formula for the doublets in the spectra, claiming that it was exactly the same formula as used by Sommerfeld for the X-ray doublets. And I told this to Ehrenfest. At that stage it was all wrong but Ehrenfest never discouraged anyone and said: "That's nice, we'll publish it". And there was a short little piece in "Naturwissenschaften Uhlenbeck came to the Hague - where I lived and he lived there too. I had promised to write a short article for "Physica", then in Dutch, and I did it together with him, which was really great. Because he knew nothing, but was so good; he asked all those questions I had never asked, and from that collaboration to make things clear emerged a few, as we now know, important results. One of the first results that came out was a new interpretation of the spectrum of hydrogen Well the note was submitted and published [6]. Directly, the next day, I received a letter from Heisenberg and he refers to our "mutige Note" (courageous note). I did not even know we needed courage to publish that. I wasn't courageous at all. I think I still have Heisenberg's letter. In it he writes a formula ......... I did not understand a bit of it. And then he says somewhere: "What have you done with the factor 2?" Which factor? Not the slightest notion, and the formula given without derivation. http://www.lorentz.leidenuniv.nl/history/spin/goudsmit.html 12. Bahn-, Spinmagnetismus, Feinstuktur 1925 G.E. Uhlenbeck S. Goudsmit „Spinning Electrons and the Structure of Spectra“ Elektronen haben einen “Inneren Drehimpuls” z Quantisierungsachse ½~ 0 ms=§½ħ -½ ~ zusätzliche Quantenzahl: ms n,l,ml,ms 12. Bahn-, Spinmagnetismus, Feinstuktur 1) Kreisstrom erzeugt magnetisches Diploment Leiterschleife: 2) Magnetischer Dipol in Magnetfeld hat potentielle Energie B Strom I Fläche A Magnetisches Dipolmoment µ= IA senkrecht auf A 3) Kreisendes Teilchen erzeugt Magnetfeld S N Drehimpuls l 12. Bahn-, Spinmagnetismus, Feinstuktur Drehimpuls l 1) Kreisstrom erzeugt magnetisches Diploment r Umlaufzeit T Leiterschleife: Strom I Fläche A Magnetisches Dipolmoment µ= IA senkrecht auf A π r2 Bohrsche Magneton magnetisches Moment eines Elektrons von l=1~ 12. Bahn-, Spinmagnetismus, Feinstuktur Analog: Magnetisches Moment des Elektrons für einen Kreisstrom wäre g=1 g: g-Faktor des Elektrons gs=2,0023 Dirac Theorie (relativistische QM) g=2 QED: Wechselwirkung mit Strahlungsfeld Der g Faktor ist eine Proportionalitätskonstante zwischen Drehimpuls und magnetischem Moment. Für Elektronen auf einer Kreisbahn ist er 1. Es gibt keine klassiche Erklärung für Werte ungleich 1. Halbklassisches Modell der Feinstruktur: Im System des Elektrons: e- B Feld durch Kreisbewegung des Kerns msz = § ~ QM nur Mittelwert Gesamtdrehimpuls j s j mit Kosinussatz l 12. Bahn-, Spinmagnetismus, Feinstuktur Größenordnung ∆ Els 10-4 eV vgl. (3.4eV n=2) 12. Bahn-, Spinmagnetismus, Feinstuktur Beispiel: s=1/2 l=1 s j=1+1/2 = 3/2 j l j=3/2 s j l j=1-1/2 =1/2 l=1 j=1/2 12. Bahn-, Spinmagnetismus, Feinstuktur Wie stark ist das Magnetfeld? e- B Feld durch Kreisbewegung des Kerns 10-4eV 10-23 Am2 B = 1 Tesla = 104 Gauss Durch Magnetfeld sind l und s gekoppelt z mj j=1+1/2 = 3/2 Magnetfeld bewirkt Drehmoment B-Feld l Kreisel weicht senkrecht aus -> Präzession um l s da l nicht fest l von Aussen l und s um ihre Summe j s 12. Bahn-, Spinmagnetismus, Feinstuktur l=1, j=3/2 n=2, l=0,1 l=0, j=s l=1, j=1/2 Was fehlt??? n=1 l=0 l=0 j=s ∆En=10eV ∆EFS=10-4eV Schrödinger gleichung ohne Spin Feinstruktur LS Bisher Nichtrelativistisch! 12. Bahn-, Spinmagnetismus, Feinstuktur Relativistische Effekte: l=1, j=3/2 n=2, l=0,1 l=0, j=s l=1, j=1/2 n=1 l=0 l=0 j=s 2p3/2 2p1/2,2s1/2 Dirac Gleichung Relativistische Schrödingergleichung Massenzunahme Geschwindigkeitsabhängig n,l abhängig 1s1/2 ∆En=10eV ∆EFS=10-4eV ∆Erel=10-4eV Schrödinger gleichung ohne Spin Feinstruktur LS Relativistische Effekte Notation: nlj n=2, l=1, j=3/2 2p3/2 n=1, l=0, j=s=1/2 1s1/2 12. Bahn-, Spinmagnetismus, Feinstuktur l=1, j=3/2 n=2, l=0,1 l=0, j=s l=1, j=1/2 n=1 l=0 l=0 j=s 2p3/2 2p1/2,2s1/2 1s1/2 ∆En=10eV ∆EFS=10-4eV ∆Erel=10-4eV Schrödinger gleichung ohne Spin Feinstruktur LS Relativistische Effekte Innerhalb Diractheorie En,j,l = En,j,l+-1 1947 W.Lamb, R. Retherford 2p1/2,2s1/2 sind 4 10-6 eV (!!!) verschieden hier weiter 2p3/2 2p1/2,2s1/2 2s1/2 2p1/2 10-6eV treibe 2p1/2 2s1/2 Übergang mit Hochfrequenz (109 Hz) 1s1/2 rege 2p1/2,2s1/2 mit e an Erzeuge atomaren Wasserstoff 2p1/2 strahlt Photon aus, 2s1/2 metastabil 12. Bahn-, Spinmagnetismus, Feinstuktur Lambshift Quantenelektrodynamik “Selbstwechselwirkung” mit dem Strahlungsfeld Anschauliches Bild: Innerhalb ∆E ∆t>~ Emission und Reabsorbtion von virtuellen Photonen Elektron ist “verschmiert” ca 10-16 m vgl. Kern 10-15m Bohrsche Bahn 10-10m Maximaler Effekt nahe am Kern: 2s ist etwas weniger gebunden als 2p g-Faktor des Elektrons: 2.00231 Photonenrückstoß führt zu “Zitterbewegung” 12. Bahn-, Spinmagnetismus, Feinstuktur l=1, j=3/2 n=2, l=0,1 l=0, j=s l=1, j=1/2 n=1 l=0 l=0 j=s 2p3/2 2p1/2,2s1/2 -8 2p3/2 +4.6 10 eV 2s1/2 +4.3 10-6eV 2p1/2 1s1/2 ∆En=10eV ∆EFS=10-4eV ∆Erel=10-4eV ∆ ELamb =4 10-6eV Schrödinger gleichung ohne Spin Feinstruktur LS Relativistische Effekte Lambshift QED -6 10-8eV 12. Bahn-, Spinmagnetismus, Feinstuktur, Lambshift 10. Das Wasserstoffatom quantenmechanisch 11. Aufhebung der L-Entartung 12. Der Spin – Feinstruktur 12.1. Elektronespin 12.2. Spin Bahn Kopplung, die Feinstruktur 12.3. Lambshift 12.4. Hyperfeinstruktur 13. Atome in äusseren Magnetfeldern der Zeemaneffekt 12. Bahn-, Spinmagnetismus, Feinstuktur, Lambshift 12.4. Hyperfeinstruktur Auch der Kern hat einen Spin (und Ausdehung!) Bohrsche Magneton: magnetische Moment eines Elektrons auf einer Kreisbahn mit l=1 Kernmagneton: I = 0,1,..... -I · mI· I Proton Spin I=1/2 magnetisches Kernmoment zu I: g Faktor des Kerns gproton = 5.585 694 675 gneutron = -3.826 085 45 12. Bahn-, Spinmagnetismus, Feinstuktur, Lambshift 12.4. Hyperfeinstruktur Atomhülle magnetisches Kernmoment zu I: wegen µI (Kernmasse) typisch 103 kleiner als FS Kern B Feld durch Atomhülle mit Drehimpuls J=l+s Gesamtdrehimpuls des Atoms F Hüllendrehimpuls J I Kernspin 12. Bahn-, Spinmagnetismus, Feinstuktur, Lambshift Übersicht Drehimpulskopplung Gesamtdrehimpuls des Atoms F Hüllendrehimpuls J I Kernspin Hyperfeinstruktur Bahndrehimpuls der Hülle L Hüllendrehimpuls J Elektronenspin s Feinstruktur 12. Bahn-, Spinmagnetismus, Feinstuktur, Lambshift l=1, j=3/2 n=2, l=0,1 l=0, j=s l=1, j=1/2 n=1 l=0 l=0 j=s 2p3/2 2p1/2,2s1/2 2p3/2 2s1/2 2p1/2 F=1 1s1/2 ∆En=10eV ∆EFS=10-4eV ∆Erel=10-4eV Schrödinger gleichung ohne Spin Feinstruktur LS Relativistische Effekte 5.8 10-6eV ∆ELamb =4 10-6eV Lambshift QED F=0 ∆EHFS=10-6eV Hyperfein struktur (Kern) 12. Bahn-, Spinmagnetismus, Feinstuktur, Lambshift Weitere Effekte des Kerns auf die Energieeigenwerte: Elektrisches Feld: • Endliche Kernausdehnung (Abweichung von 1/r bei kleinen Abständen) •Elektrisches Quadrupolmoment des Kerns 12. Bahn-, Spinmagnetismus, Feinstuktur, Lambshift Elektronen haben einen „internen“ Drehimpuls von +- ½ und ein damit verbundenes magnetisches Moment (das doppelt so gross ist wie in der klassischen Physik) 12. Der Spin – Feinstruktur 12.1. Elektronespin 12.2. Spin Bahn Kopplung, die Feinstruktur 12.3. Lambshift 12.4. Hyperfeinstruktur Je nach Richtung des magnetischen Momentes von Elektron und Bahn (Projektion des Elektronenspins auf den Bahndrehimpuls) ergibt sich eine Energie (aus der magnetischen WW) Aufgrund der Wechselwirkung des Elektrons mit dem virtuellen Photonenfeld des Vakuums (Quantenelektrodynamik) egibt sich eine weitere kleine Energieverschiebung Wie Feinstruktur, jedoch zwischen dem Gesamtdrehimpuls der Hülle und dem Gesamtdrehimpuls des Kerns (ist aufgrund der Kernmasse viel kleiner als die Spin-Bahn Kopplung)