Teil 10 - WueCampus2

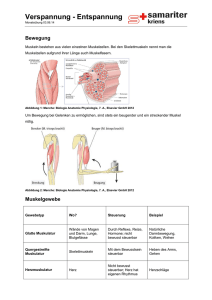
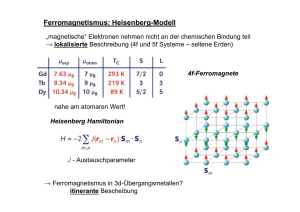
2.17 Verspannte Quantenfilme
Baut man Heterostrukturen aus Materialien mit unterschiedlicher Gitterkonstante auf, so kann
unterhalb einer kritischen Schichtdicke die Gitterfehlanpassung durch elastische Verspannung
aufgefangen werden (siehe Abb. 2.17.1). Diese Gitterverzerrung in uniaxialer Richtung führt
zu einer Änderung der Bandstruktur.
Abbildung 2.17.1: Links: Eine Schicht aus einem Material mit einer Gitterkonstanten a0
wird zwischen zwei Schichten mit Gitterkonstanten a1 eingebracht. Parallel zur Schicht passt
sich die Gitterkonstante der Zwischenschicht dem Substrat an, senkrecht dazu vergrößert sich
die Gitterkonstante.
Zur Beschreibung der Verspannung definiert man einen Verspannungskoeffizienten dies ist
der relative Unterschied der Gitterkonstanten von Substrat und aufgebrachtem Material,
bezogen auf die natürliche Gitterkonstante des Schichtmaterials:

a mat  a Sub
a mat
(2.17.1)
mit asub = a|| als Gitterkonstante des Substratmaterials. Bei Druckverspannung (compressive
strain) ist ε>0, bei Zugverspannung (tensile strain) ist ε<0. Den Einfluss der Verspannung auf
die Bandstruktur eines Materials kann weiter in einen isotropen Druckanteil (Volumen der
Einheitszelle ändert sich) und einen uniaxialen Verzerrungsanteil (kubische Einheitszelle
wird quaderförmig) zerlegt werden. Der Druckanteil bewirkt eine Änderung der Bandlücke
(Vergrößerung bei kompressiver Verspannung, Verkleinerung bei tensiler Verspannung), der
uniaxiale Anteil reduziert die Symmetrie und bewirkt eine Aufspaltung der entarteten
Valenzbänder am Γ-Punkt. Durch die sogenannte kp-Störungstheorie können die Änderungen
der Bandlückenenergien in der Nähe des Γ-Punktes berechnet werden. Daraus ergeben sich
Energieverschiebungen der Bandkanten und damit Änderungen in den optischen
Übergangsenergien zwischen Leitungsband und Schwer-, Leicht- bzw. Spin-Bahnabgespaltenem Band. Abb. 2.17.2 zeigt die Auswirkungen von Verspannung auf die
energetische Lage der Bänder.
- 78 -
Abbildung 2.17.1: Auswirkung von Verspannung auf die Bandstruktur eines Halbleiters.
Link: Zugverspannung, rechts: Druckverspannung. Die Energie des Leitungsbandes ändert
sich um H’, die des HH/LH Valenzbandes um H-H’. Relevant ist allerdings vor allem die
Änderung der Bandlücke, die sich um H ändert.
Der isotroper Druckanteil und der uniaxiale Verspannungsanteil hängen über die
Deformationspotentiale und Komponenten des Elastizitätstensors vom Verspannungskoeffizienten ab
C  C12
H  2a 11
Isotroper Druckanteil:

(2.17.2a)
C11
C  2C12

S  2b 11
Uniaxialer Verspannungsanteil:
(2.17.2b)
C11
Werte für Deformationspotentiale und Elastizitätsmodule von wichtigen Halbleitern sind in
der folgenden Tabelle aufgeführt:
- 79 -
Die Änderung der Bandlücken für Leitungsband-Schwerloch, Leitungsband-Leichtloch und
Leitungsband - split-off Band Übergänge sind wie folgt:
Ehh = H-S
Elh = H+S- 
ESO = H++


mit   2 S 2 /  

ist der energetische Abstand zwischen HH/LH Band und dem slip-off Band.
Neben der Verschiebung der Bänder ändern sich bei Verspannung die effektiven Massen der
Ladungsträger. Aufgrund des Symmetriebruchs muss man nun die effektiven Massen parallel
zur Schicht und senkrecht getrennt betrachten. In Abb. 2.17.2 ist die Auswirkung von
kompressiver Verspannung auf die Dispersion der Valenzbänder dargestellt. Durch die
Verspannung wird z.B. das schwere Loch parallel zur Schicht leichter und senkrecht dazu
schwerer.
Abbildung 2.17.1: Dispersion des HH/LH Valenzbänder ohne Verstpannung (links) und bei
kompressiver Verspannung (rechts)
Konsequenzen für Halbleiterlaser
Durch die Aufhebung der Entartung von Schwer- und Leichtlochband ist die Emission des
Lasers eindeutig polarisiert. Wir erinnern uns an Abschnitt 2.13 (Auswahlregeln für optische
Übergänge). Für Quantenfilme liefert der Leitungsband – Schwerlochübergang nur
Verstärkung für TE polarisiertes Licht, der Leitungsband – Leichtlochübergang vor allem
Verstärkung für TM polarisiertes Licht. Wegen der Aufspaltung der Valenzbänder ist in
verstpannten Quantenfilmen nur ein Valenzband für den Laserbetrieb relevant.
Kompressiv verspannte Quantenfilme => Leitungsband – Schwere Löcher => TE Polarisation
Zugverspannte Quantenfilme => Leitungsband – Leichte Löcher => TM Polarisation
Die Aufhebung der Entartung hat neben der eindeutigen Festlegung der Polarisation noch
einen weiteren Vorteil: Sie verringert die Zustandsdichte im Valenzband und damit den
Schwellenstrom des Lasers. Warum ist das so? Eine notwendige (allerdings nicht
- 80 -
hinreichende) Bedingung für das Anschwingen des Lasers ist der durch Gleichung 2.9.5.
festgelegte Mindestabstand der Quasi-Fermienergien. Dieser muss größer als die Energie des
optischen Übergangs sein. Betrachtet man einen ungepumpten Laser, so liegen beide QuasiFermienergien ungefähr in der Mitte der Bandlücke bei der gleichen Energie. Erhöht man nun
die Ladungsträgerdichte im Quantenfilm, so schieben die Quasi-Fermienergien in Richtung
der Bänder. Aufgrund der Ladungsneutralität (n=p) und der kleineren Zustandsdichte im
Leitungsband schiebt die Quasi-Fermienergie der Elektronen allerdings viel schneller als die
Quasi-Fermienergie der Löcher. Verringert man die Zustandsdichte der Löcher (z.B. durch
Verspannung), so erhält man für die gleiche Ladungsträgerdichte einen größeren Abstand der
Quasi-Fermienergien. Die Laserbedingung E F  E  EG wird daher bei einer kleineren
Ladungsträgerdichte (und damit bei einer kleineren Stromdichte) erreicht. Am besten wäre ein
Material mit gleichen Elektronen- und Lochmassen, sowie nur einem Valenzband. Durch die
Verspannung des Quantenfilms kann man diesem Idealfall ein Stück weit näher kommen, da
durch die Aufhebung der Entartung nur ein Valenzband am Laserbetrieb beteiligt ist.
Weiterhin werden schwere Löcher durch kompressive Verspannung in der Ebene des
Quantenfilms (die ist relevant für die Zustandsdichte) leichte (siehe Abb. 2.17.1):
2.18 Spontane Rekombination
Wir hatten in Abschnitt 2.10 einen Zusammenhang zwischen der Verstärkung und der
spontanen Emissionsrate in die Lasermode hergeleitet (Gleichung 2.10.4):
Rsp' 
v g gnsp
(2.18.1)
V
Spontane Emission in die Lasermode ist allerdings nur ein sehr kleiner Anteil der gesamten
spontanen Emission. Für die gesamte spontante Emissionsrate müssen wir über alle Moden, in
die spontan emittiert wird, summieren.
Für die gesamte spontante Emission in einem Frequenzinterval dv ergibt sich damit:
Rsp d (h ) 
R
'
sp
 nsp
Moden

Moden
vg g
VP
 nsp
vg g
VP
N Moden
(2.18.2)
mit gemittelten Werte für die Gruppengeschwindigkeit vg , die Verstärkung g und das
Modenvolumen VP . Bei der Mittelung der Verstärkung muss die Polarisationsabhängigkeit
der Verstärkung berücksichtigt werden:
g
1
2 gTE  gTM 
3
(2.18.3)
Diese Mittelung ist vor allem für Quantenfilme relevant, für Volumenmaterial ist
g  g TM  g TE .
Die Anzahl der Moden kann über die Zustandsdichte der Photonen bestimmt werden:
N Moden   Phot ( )VP d
(2.18.4)
- 81 -
Die Zustandsdichte der Photonen in einem Medium mit Brechungsindex n und Gruppenindex
ng ist:
8
 Phot ( )  3 n 2 ng 2 (2.18.5)
c
Diese Zustandsdichte der Photonen taucht auch im Planck’schen Strahlungsgesetz auf:
 ( ) 
1 8h 3
8 2
1

hv
 EPhoton ( )  Phot ( ) f Bose  Einstein ( ) (2.18.6)
h / kT
3 h / kT
3
1
c e
1
c e
Hier ist natürlich n=ng=1. Das Produkt aus den drei Faktoren: Energie pro Photon, Dichte der
Zustände und deren Besetzungswahrscheinlichkeit ergibt die Energiedichte in einem
Hohlraum. Für die gesamte spontane Emissionsrate ergibt sich damit:
Rsp 
1
 Phot ( )v g nsp g
h
(2.18.7)
Durch Einsetzen des Ausdrucks für g erhalten wir schließlich:
4ne 2
Rsp 
h M T  Phot ( ) f 2 (1  f1 )
 0 h 2 c 3 m02
(2.18.8)
M T ist das gemittelte Matrixelement für TE/TM polarisierte Übergänge.
2.19 Nichtstrahlende Rekombination
a) Rekombination an Defekten (Shockley-Read-Hall Rekombination)
Die Konzentration von Verunreinigungen und Fehlstellen kann durch moderen
Epitaxieverfahren auf einen sehr kleinen Wert reduziert werden. Rekombination kann
allerdings auch an Dotieratomen stattfinden, die natürlich in (elektrisch gepumpten)
Halbleiterlasern vorhanden sind.
In erster Näherung ist die Rekombinationsrate an Derekten proportional zur Ladungsträgerdichte: RDefekt = AN. Eine genauere Rechnung für Defekte in der Mitte der Bandlücke liefert:
R
pn  ni2
 n 0 ( p  ni )   p 0 ( n  ni )
(2.19.1)
Für n=p>> ni kann man schreiben:
pn  ni2
n2
n


R
 n 0 ( p  ni )   p 0 (n  ni ) n( n 0   p 0 )  n 0   p 0
(2.19.2)

n0 und p0 sind die Einfangzeiten für Elektronen und Löcher. Ist ein Defekt mit einem
Ladungsträger besetzt, so muss erst ein Ladungsträger der entgegengesetzen Polarität
eingefangen werden, damit der Defekt wieder für nichtstrahlende Rekombination zur
Verfügung steht. Die Rekombinationsrate ist damit wie in Gleichung 2.19.2 zu sehen durch
die größere der beiden Zeitkonstanten bestimmt.
- 82 -
b) Auger Rekombination
Bei der Augerrekombination rekombiniert ein Elektron aus dem Leitungsband mit einem
Loch aus dem Valenzband. Die freiwerdende Energie wird an ein weiteres Elektron
übertragen, das die Energie durch Emission von Phononen an das Gitter abgibt. Je nach Art
der beteiligten Ladungsträger unterscheidet man verschiedene Auger Prozesse, von denen drei
in Abb. 2.19.1 dargestellt sind.
Abbildung 2.19.1: Darstellung von drei verschiedenen Auger Prozessen im Banddiagramm.
Die vier zur Kennzeichnung verwendeten Buchstaben repräsentieren die vier am Prozess
beteiligten Teilchen, so sind z.B. beim CHHS Prozess ein Elektron (C), zwei Löcher aus dem
Schwerlochband (H) und ein Loch aus dem abgespaltenen Band (S) beteiligt.
Die Übergangswahrscheinlichkeit hängt von der Besetzung der Zustände ab. Für den CCCHProzess kann man ansetzen:
P13  f C1 f C 2 (1  fV 3 )(1  f C 4 )
(2.19.3)
In Boltzmann Näherung kann man für die Verteilungsfunktionen schreiben:
fC  e
 ( E  E F ,C ) / kT
1  fV  e

 ( E F ,V  E ) / kT
N  ( E  EC ) / kT
e
NC

P  ( ECV  E ) / kT
e
NV
(2.19.4a)
(2.19.4b)
Damit wird aus (2.19.3)
P13 
N 2 P  ( E1  E2  E3 ) / kT
e
N C2 NV
(2.19.5)
Die Es sind die energetischen Abstände der beteiligten Zustände zu den Bandkanten, so ist
z.B. E1 = E1 - EC . Zustand (4) liegt sehr weit oben im Leitungsband und ist damit mit sehr
großer Wahrscheinlichkeit nicht besetzt, man kann daher (1  f C 4 ) =1 setzten. Aus diesem
Grund taucht E4 nicht in Formel 2.19.5 auf.
- 83 -
Setzt man Ladungsneutralität an (N=P) und versteckt den Exponentialterm und NC, NV in
einer Konstanten C, so folgt aus Gleichung 2.19.5 die bekannte Formel für die
Augerrekombination:
R Auger  CN 3
(2.19.6)
Energie und Impuls bleiben bei Augerprozessen erhalten, d.h. wir haben für den CCCH
Prozess die Auswahlregeln:
k1 + k2 = k3 + k4
und
E1 + E2 = E4 - (Eg + E3)
(2.19.7)
Aufgrund der Auswahlreglen sind Augerübergänge erst ab einer bestimmten Mindestenergie
für E4 möglich, der sogenannten Schwellenenergie ET. So muss sicherlich gelten: E4 EG,
sonst ist die Energieerhaltung nicht zu erfüllen. Aufgrund der Impulserhaltung ergeben sich
zusätzliche Einschränkungen, so können z.B. die Zustände (1) und (3) nicht direkt
übereinander liegen. In diesem Fall müsste man auf das Teilchen im Zustand (2) Energie, aber
keinen Impuls übertragen, was nicht möglich ist.
Für den CCCH Prozess ergibt sich als Schwellenenergie:
ET  E 4 
2mC  mH
EG
mC  mH
(2.19.8)
Die Schwellenenergie ist proportional zur Bandlücke des Halbleiters, damit ist
Augerrekombination vor allem in Materialen mit kleiner Bandlücke relevant (für Laser mit
Wellenlänge  > 1.3 µm). Dieser Effekt ist in Abb. 2.19.2 dargestellt. Der Augerkoeffizient
steigt von 1 µm bis 6 µm Wellenlänge um mehr ca. drei Größenordnungen an. Die
Realisierung von langwelligen Laser mit  > 3 µm wird damit extrem schwierig. Einen
Ausweg bieten hier sogenannten Quantenkaskadenlaser, bei denen die Übergänge nicht
zwischen Leitungs- und Valenzband, sondern zwischen quantisierten Zuständen im
Leitungsband stattfinden.
Wellenlänge (µm)
Abbildung 2.19.2: Auger-Koeffizient als Funktion der Wellenlänge des optischen Übergangs
in verschiedenen Halbleitermaterialen
- 84 -