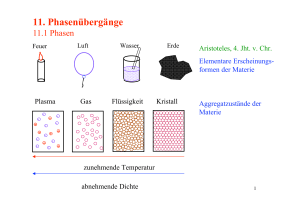
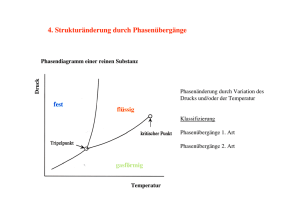
Physikalische Umwandlungen reiner Stoffe

Physikalische Umwandlungen
reiner Stoffe
Lernziele:
 Phasendiagramme, die Stabilität von Phasen
 Phasengrenzen, typische Phasendiagramme
 Phasenübergänge, die TD Gleichgewichtkriterien
 Die Abhängigkeit der Stabilität von den Bedingungen
 Die Lage der Phasengrenzlinien
 Die Klassifikation der Phasenübergänge nach Ehrenfest
 P. Atkins, J. de Paula, “Physikalische Chemie”, Wiley-VCH Verlag GmbH&
Co, 2013, 4.1, 4.2.
 G. Wedler, H-J. Freund, „Lehrbuch der Physikalischen Chemie“, Wiley-VCH
Verlag GmbH& Co, 2013.
Physikalische Umwandlungen reiner Stoffe
Beispiele:
• Verdampfen einer Flüssigkeit
• Schmelzen von Eis
• Umwandlung von Graphit
↓
Diamant
Phasenübergänge reiner Stoffe → verlaufen ohne Aenderung der chemischen
Zusammensetzung des Systems
Freiwillige Zustandsänderung bei T = ct und p = ct → immer in Richtung
kleiner G des Systems.
1. Phasendiagrame
Phase – Materie mit homogener, chemischer Zusammensetzung und
räumlich konstantem, physikalischem Zustand.
Stoff → verschiedene feste Phasen
Beispiel: Weisser & Schwarzer
Phosphor (Allotrop)
Phasenübergang – spontane Umwandlung einer Phase in eine andere Phase
(gegebenen p und charakteristischen T)
Beispiel:
p = 1 bar → T = 0○C – Eis: die stabilste Phase von Wasser
T > 0○C – Flüssigkeit: die stabilste Phase von Wasser
T > 0○C → G ↓ wenn Eis schmilzt.
T < 0○C → G ↓ : flüssiges Wasser gefriert.
1.a Die Stabilität von Phasen
Ttrans = Phasenübergangstemperatur wenn die
Gleichgewicht sich befinden (bei gegebenen Druck).
beide
Phasen
im
G erreicht ein Minimum.
Phasenübergänge:
 Phasenübergänge mit hohen Geschwindigkeiten (Beispiel: in Gasen
und Flüsigkeiten)
 Phasenübergänge mit geringen Geschwindigkeiten (Beispiel: GGraphit <
GDiamant bei normaler T und normalen p).
Metastabile Phasen
1.b Phasengrenzen
Phasendiagram = graphische Darstellung der p- und Temperaturbereiche,
in denen die einzelnen Phasen thermodynamisch stabil sind.
Phasengrenzlinien = Wertpaare (p, T), bei denen zwei Phasen miteinander
im Gleichgewicht sind.
p
Eine verallgemeinerte Darstellung
Flüssigkeit
Feststoff
 Dampfdruck
Sublimationsdruck
 Siedetemperatur
Tripelpunkt
Gas
 Kritischer Punkt
Beispiel: überkritisches CO2
Kritischer
Punkt
T
Phasengrenzen
Dampfdruck = der Druck der Gasphase, die sich mit der kondensierten
Phase in Gleichgewicht befindet.
 Die Phasengrenzlinien des Gleichgewichts Flüssigkeit/Gas
 Die Phasengrenzlinien des Gleichgewichts Feststoff/Gas
T
Dampfdruck
(immer mehr Moleküle besitzen
genügend Energie, um die zwischenmolekularen Anziehungskräfte zu ihren
Nachbarn zu überwinden).
Kritischer Punkt und Siedepunkt
A. Wenn die Flüssigkeit in einem offenen Gefäss erhitzt wird
Sieden = die Verdampfung des gesamten, flüssigen Körpers bei eine
Temperatur wo der Dampfdruck mit dem äusseren Druck übereinstimmt.
Siedetemperatur (Siedepunkt) = die T bei dem der Dampfdruck der
Flüssigkeit = pext
z. B. Wasser TS = 99.6○ C (Standardsiedepunkt)
B. Wenn die Flüssigkeit in einem geschlossenen Gefäss erhitzt wird,
findet der Siedevorgang nicht statt.
Der Dampfdruck und die Dichte des Dampfs nehmen mit T
kontinuierlich zu.
Kritischer Punkt und Siedepunkt
 Die Flüssigkeit dehnt sich aus, wodurch ihre
Dichte geringfügig abnimmt.
Tkrit : ist die Dichte des Dampfs gleich der Dichte
der flüssigen Phase
Die Phasengrenzfläche verschwindet
Dampfdruck).
T ≥ Tkrit
homogene Phase
T < Tkrit
Flüssigkeit/Gas Phasen
T > Tkrit
(kritischer
Grenzflächen existieren nicht
mehr.
z.B. Üeberkritisches Kohlendioxid
Schmelzpunkt und Tripelpunkt
Schmelztemperatur (Schmelz Punkt) = die T bei der sich flüssige und
feste Phase miteinander im Gleichgewicht befinden.
Schmelz- und Erstarrungsvorgang laufen bei derselben Temperatur ab :
TSm = TErst
Standardschmelztemperatur, TSm = Schmelztemperatur bei 1 bar.
Tripelpunkt = bei bestimmten Werten (p, T), können 3 Phasen eines
Stoffes existieren
Typische Phasendiagramme
CO2
Das experimentell bestimmte
Phasendiagramm von
Kohlendioxid.
 pTriple ist grösser
Atmosphärendruck
als
der
 Unter normalen Bedingungen
existiert kein flüssiges CO2.
 Zur Erzeugung der flüssigen
Phase muss ein Druck von
mindestens 0.52 MPa ausgeübt
werden .
Typische Phasendiagramme
He zeigt bei tiefen Temperaturen ein ungewöhnliches Verhalten:
 ein Gleichgewicht zwischen fester und Gasphase existiert nicht.
 He Atome schwingen durch ihre geringe
Masse mit sehr grosser Amplitude > ein
Festkörper wäre nicht stabil !
 Festes He : nur wenn man einen Druck
anlegt.
Man muss zwischen den Isotopen 3He und 4He unterscheiden:
- Reines 4He : zwei flüssige Phasen (Flüssigkeit, und Suprafluid)
- Phasenübergang zwischen zwei flüssigen Phasen
> λ-linie als
Grenzphase
- Reines 3He hat auch eine suprafluide Phase
Typische Phasendiagramme
Kohlenstoff kommt in mehreren
allotropen festen Phasen vor.
Feststoffe
auf
Kohlenstoff-Basis:
Diamant und Graphit
Bei p = 1 bar und Temperaturen
unterhalb 4000 K ist Graphit die
thermodynamisch stabile Phase des
Kohlenstoff.
Diamant bei Raumtemperatur ist stabil
und wandelt sich erst oberhalb 500 °C
merklich in Graphit um.
Typische Phasendiagramme
Wasser :
 Die Wassermoleküle haben im
hexagonalen Gitter einen grösseren
Abstand zueinander als im flüssigen,
ungeordneten Zustand
 Wasser hat mehr feste Phasen als
jeder andere Stoff: 16 kristalline, und
fünf amorphe Phase.
 Wasser hat als kritische Punkt: bei
647K !
 Wasser ermöglicht Unterkühlung:
Auch unter natürlichen Bedingungen
kann es bis −23 °C flüssig bleiben.
2. Phasenübergänge
2.1. Das TD Gleichgewichtskriterium
Das chemische Potenzial = die molare Freie Enthalpie Gm für reine Stoffe.
µ = ein Mass für die Möglichkeit einer Zustandsänderung der betreffenden
Substanz in einem System.
Eine Schlussfolgerung aus dem 2. Hauptsatz der
TD → Im Gleichgewicht ist das chemische
Potenzial eines Stoffs überall in der Probe gleich
gross, unabhängig davon, wie viele Phasen
koexistieren.
µ
Das TD Gleichgewichtskriterium
Beispiel: ein System bei dem:
- µ1 an einem Ort 1 + µ2 an einem anderen Ort 2 → µ1 ≠ µ2
- Eine Stoffmenge dn von 1 → 2 transportiert
Die Freie Enthalpie: µ1dn ↓ + µ2dn ↑
Die Gesamtänderung: dG = (µ2 - µ1)dn
Gleichgewicht ⇒ G = Konstant ⇒ µ1 = µ2
Die Phasenübergangstemperatur Ttrans = Tµ1 = µ2
2.2. Die Abhängigkeit der Stabilität von den
Bedingungen
T ↓ + p ↑ : die feste Phase eines Stoffs ⇒ µ ↓ (der niedrigste Wert)
↓
die stabile Phase
µ = f(T) ⇒ bei T ↑ → µ einer anderen Phase (festen / flüssigen) sinkt unter
den Wert für den Festkörper ab
Phasenübergang (sofern keine kinetische Hemmung vorliegt)
a. Die Temperaturabhängigkeit der Stabilität von
Phasen
Die Freie Enthalpie G = f(T,p)
µ reiner Stoff → G
∂µ
( ) p = −Sm
∂T
∂µ
( )p < 0
∂T
Sm > 0
Sm(g) > Sm(l)
Sm(l) > Sm(s)
b. Die Druckabhängigkeit des Schmelzpunkts
TSm ↑ wenn p ↑ bei den meisten Stoffen
∂G
( )T = V
∂p
µ reiner Stoff → Gm
Vm > 0
∂µ
( )T = Vm
∂p
(
∂µ
)T > 0
∂p
Vm(l) > Vm(s) ⇒ steigt µ(s) weniger als µ(l) ⇒ TE↑
Die Abhängigkeit der Stabilität von den
Bedingungen
Wasser: Vm(l) < Vm(s) ⇒
steigt µ(s) stärker als µ(l)
Beispiel: wie ändert sich µ von Wasser und
Eis (0○C): p1 = 0,1 MPa → p2 = 0,2 MPa
∆µ = Vm ∆p
Vm = M / ρ
∆µ =
MWasser= 18,02 g
ρWasser= 0,999 g
mol-1
cm-3
TE
M∆p
ρ
∆µEis= +1,97 J mol-1
∆µWasser= +1,80 J mol-1
ρEis= 0,917 g cm-3
Die beiden Phasen: Gleichgewicht (p1) → bei p2 ⇒ schmilzt das Eis !
c. Die Druckabhängigkeit des Dampfdrucks
Auf
die
kondensierte
Der Dampfdruck der Phase↑
Phase ausgeübter Druck
Die Molekule
entweichen
als Gas
Die Beziehung zwischen dem Dampfdruck p bei
Anlegen eines Drucks ∆p und dem Dampfdruck p’
p = p '⋅ exp(
Vm (l )∆p
)
RT
Die Zunahme des Dampfdrucks einer kondensierten Phase bei steigendem Druck
2.3. Die Lage der Phasengrenzlinien
Phasengrenzlinie – die Wertpaare von p und T bei denen zwei Phasen
koexistieren
Die Lage der Phasengrenzlinien → µ1(pT) = µ2(pT)
Lösung → eine Funktion p(T)
a. Die Steigungen der Phasengrenzlinien
T und p ändern sich in
infinitesimalen Schritten
µ1 = µ2
Bewegung: zu einem anderen Punkt der Phasengrenzlinie → die Bedingung ist
immer erfüllt
Die Steigungen der Phasengrenzlinien
dµ1 = dµ2
dG = Vdp – SdT
-S1,mdT + V1,mdp = -S2,mdT + V2,mdp
Si,m – molare Entropie
Vi,m – molare Volumen der jeweiliger Phase
(V2,m - V1,m)dp = (S2,m – S1,m)dT
dp ∆ tr S
=
dT ∆ trV
Die Clapeyron’sche Gleichung
∆trS = S2,m – S1,m : Phasenübergangsentropie
∆trV = V2,m – V1,m : Volumenänderung während des
Phasenübergangs
b. Die Phasengrenzlinie fest/flüssig
Der Schmeltzvorgang: T + Aenderung der molaren Enthalpie des Systems ∆H
Die Clapeyron’sche Gleichung
∆SmV
∆SmH >0 (einzige Ausnahme 3He)
∆SmV >0 (und relativ klein)
dp ∆ Sm H
=
dT T∆ SmV
dp
>0
dT
Integration von dp/dT unter der Annahme, dass ∆SmH
und ∆SmV ≠ f(T)
∆ Sm H dT
=
dp
∫p '
∆ SmV T∫' T
p
T
p = p '+
∆ Sm H  T 
ln 
∆ SmV  T ' 
Die Phasengrenzlinie fest/flüssig
Wenn T ≅ T’ :
 T −T'  T −T'
T 
ln  = ln1 +
≅
T' 
T'

T'
∆ Sm H
(T − T ')
p = p '+
∆ SmVT '
Die typische Phasengrenze
fest/flüssig steigt steil an
TSm↑ wenn p ↑
c. Die Phasengrenzlinie flüssig/gasförmig
∆V H
T
Verdampfungsentropie eines Stoffes bei T
dp ∆V H
=
dT T∆V V
Die Clapeyron’sche Gleichung
∆VH >0
∆VV >0 (grosser Wert)
dp
>0
dT
Aber kleiner als für Phasengrenze fest/flüssig
Vm(g) >> Vm(l) ⇒ ∆VV ≅ Vm(g)
Ein ideales Gas:
Vn ( g ) =
RT
p
∆V V
dp
=
dT
 RT 

T 

 p 
Die Phasengrenzlinie flüssig/gasförmig
Die Clausius Clapeyron’sche
Gleichung für die Abhängigkeit
des Dampfdrucks von T
d ln ( p ) ∆V H
=
dT
RT 2
Wie ändert sich : der Dampfdruck ↔ T
und Siedetemperatur ↔ p ?
∆V H
∫p ' d ln( p ) = R
p
∆V H
dT
∫T ' T 2 = − R
T
1 1
 − 
T T'
p’ – Dampfdruck bei Temperatur T’
Dampfdruckkurve
 p
∆V H
ln  = −
R
 p' 
1 1
 − 
T T'
p = p' e − χ
wo χ = −
∆V H
R
Die Dampfdruckkurve endet bei der kritischen Temperatur Tkrit
1 1
 − 
T T'
d. Die Phasengrenzlinie fest/gasförmig
Die Sublimationsenthalpie
∆ Sub H = ∆ Sm H + ∆V H
Die Steigung der Phasengrenzlinie
fest/gasförmig ist in der Nähe des
Tripelpunktes steiles als diejenige der
Phasengrenzlinie flüssig/gasförmig
Die Sublimationsenthalpie > die Verdampfungsenthalpie
TSub ≅ TV (die Clapeyron’sche Gleichung )
Pictet-Trouton’sche Regel
Pictet-Trouton’sche Regel = die Standardverdampfungsentropie für
viele verschiedene Flüssigkeiten liegt ungefähr bei 85 J/K mol.
∆V H θ
kJmol −1
θV
°C
∆V S θ
JK −1mol −1
Benzol
30.8
80.1
87.2
Tetrachlorkohlenstoff
30.0
76.7
85.8
Cyclohexan
30.1
80.7
81.8
Schweffelwasserstoff
18.1
-60.4
87.9
Metan
8.18
-161.5
73.2
Wasser
40.7
100.0
109.1
Actuelle Entdeckungen
"Borophen": Die Schichtstruktur und elektronischen Eigenschaften sind denen des Graphens
ganz ähnlich.
 2D Borophen-Schichten: ein Intermediat zwischen rein kovalent gebundenem Graphen und
substrat-stabilisiertem Silicen oder Germanen.
 Die Bandstruktur und damit das elektronische Verhalten von Borophen kann beispielsweise
leicht durch Substrat-Wechselwirkungen oder einer Funktionalisierung der Oberfläche
verändert werden.
2.4. Die Klassifikation der Phasenübergange nach
Ehrenfest
Unterschiedliche Phasenübergänge :
 häufig - Schmelzen, Verdampfen
 seltener – verschiedene Modifikationen von Festkörper (leitend und
superleitend), Flüssigkeiten (superfluide Phasen)
Klassifikation nach Ehrenfest : einorden anhand der TD
Ein Uebergang von einer Phase α zu einer Phase β :
 dµ β

 dp
 dµ β

 dT
  dµα 
 − 
 = Vβ ,m − Vα ,m = ∆ trV
T  dp T
  dµα 
∆ tr H
 − 
S
S
=
−
+
=

β ,m
α ,m
dT
Ttr
p
p 
Die Klassifikation der Phasenübergänge nach
Ehrenfest
Existieren Übergänge (Schmelzen, Verdampfung):
∆ tr H ≠ 0
∆ trV ≠ 0
Die Steigerungen des chemischen Potenzials = f(p)
↓
Die beiden Seiten des Übergangs müssen verschieden sein
 dµ 


 dp T
 dµ 


 dT  p
Ändern sich am Punkt des Phasesübergangs sprunghaft
Die Klassifikation der Phasenübergänge nach
Ehrenfest
Phasenübergang erster Ordnung:
 dµ 
 → ändert sich sprunghaft

 dT  p
Cp → die Steigerung der Enthalpie: f(T)
↓
Eine Singularität der H Funktion
H ändert sich bei infinitesimaler
Temperatur T
Temperaturänderung um einen
endlichen Betrag
Temperatur T
Die Klassifikation der Phasenübergänge nach
Ehrenfest
Phasenübergang erster Ordnung:
Beispiel: Wasser
siedendes Wasser → T = konstant, obwohl ständig Wärme zugeführt wird
↓
Die Wärmezufuhr ist die treibende Kraft für den Übergang und nicht die
Temperaturerhöhung
Temperatur T
Die Klassifikation der Phasenübergänge nach
Ehrenfest
Phasenübergang zweiter Ordnung:
 dµ 
 → stetig verläuft, aber nicht

 dT  p die zweite Ableitung
µ(T) → ein stetiger Verlauf: eine Kurve, die auf beiden
Seiten die gleiche Steigung besitzt
Volumen und Entropie
↓
Ändern sich nicht während des
Übergangs
Temperatur T
Cp → eine Unstetigkeit, wird aber
nicht singular
Temperatur T
Die Klassifikation der Phasenübergänge nach
Ehrenfest
Phasenübergang zweiter Ordnung:
Beispiel:
 Die Umwandlung der normalleitenden zur supraleitenden feste Phase von
Metallen bei tiefem T
 Die Umlagerung der Kristallstruktur eines Festkörpers, die unter Änderung
der Symmetrie der Struktur verläuft
Die Klassifikation der Phasenübergänge nach
Ehrenfest
λ Übergänge:
→ Nicht erster Ordnung sind,
Cp → unendlich
Cp → steigt in der Regel bereits lange vor dem
eigentlichen Phasenübergang
Beispiel:
 Ordnungs/Unordnungsübergabe → Legierungen:
Das Einsetzen ferromagnetischen Verhaltens
 Der Übergang vom flüssigen zum suprafluiden He
Phasenübergänge zweiter Ordnung und λ-Ordnung Mikroskopische Interpretation
Beispiel: Umlagerung der Kristallstruktur eines Festkörpers → Änderung der
Symmetrie der Struktur
T ↑ → der Kristall soll sich in derjenigen Raumrichtung mehr
ausdehnen wo die kürzeren Kanten der Elementarzelle liegen
Der Kristall → kubische Symmetrie. T ↑ ⇒ gleichmässige
Ausdehnung in alle 3 Raumrichtungen
Sowohl die Wechselwirkungsenergie der Atome als auch
das Volumen des Festkörper ändert sich köntinuerlich
↓
Die Phasenübergang kann nicht 1. Ordnung sein
(der ist 2. Ordnung)
Phasenübergänge zweiter Ordnung und λ-Ordnung Mikroskopische Interpretation
Beispiel: λ-Übergang → die Unordnung von CuZn
T = 0○C → alle Atome vollständig geordnet
T ↑ → der Übergang ist
kooperativ ⇒ Inseln
↓
Die Inseln wechseln mit
steigender T
T = 742○C ⇒ vorliegen nur einen Phase (die Inseln sind zufällig im ganzen
Festkörper verteilt)
Bei Annährung an 742○C → Cp ↑ → kann eine zunehmende
Wärmemenge zur Unordnung verbraucht werden (gespeichert als
termische Bewegung)
↓
Die Phasenübergang ist λ-Ubergang
Lernziele:
 Phasendiagramme, die Stabilität von Phasen
 Phasengrenzen, typische Phasendiagramme
 Phasenübergänge, die TD Gleichgewichtkriterien
 Die Abhängigkeit der Stabilität von den Bedingungen
 Die Lage der Phasengrenzlinien
 Die Klassifikation der Phasenübergänge nach Ehrenfest
 P. Atkins, J. de Paula, “Physikalische Chemie”, Wiley-VCH Verlag GmbH&
Co, 2013, 4.1, 4.2.
 G. Wedler, H-J. Freund, „Lehrbuch der Physikalischen Chemie“, Wiley-VCH
Verlag GmbH& Co, 2013.