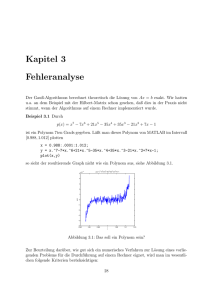
Theoretische Physik 3 Elektrodynamik

Theoretische Physik 3
Elektrodynamik
Urbaan M. Titulaer
1. Auflage
1
Vorwort
Dieses vorliegende Skript ist die Vorlesungsunterlage von Prof. Urbaan Maria
Titulaer in LATEX. Ich habe beim Lernen für die Klausur mit dem Aufsetzen
begonnen, weil es nicht nur eine Lernhilfe war, sondern vor allem weil erstens LATEX besser zu lesen ist und zweitens weil dieses Skript nun korrigierund erweiterbar ist. Obwohl mir meine Studienkollegen dieses getexte Skript
durchgesehen haben (herzlichen Dank dafür), bin ich mir sicher, dass sich
noch zahlreiche Fehler eingeschlichen haben. Ich wäre deshalb sehr dankbar,
wenn ihr mir die Fehler per email berichtet ([email protected]),
damit entweder eine Fehlersammlung ins Netz gestellt werden kann oder
später korrigierte Neuauflagen erscheinen können.
Einige Bilder habe ich aus dem alten maschinegeschriebenen Skript weggelassen, weil sie unter LATEX schwer zu verwirklichen gewesen wären (vorallem
im ersten Teil, da auch viele aus den Methoden bekannt sind).
Ich wünsche viel Spaß beim Lesen :-) und hoffe, dass dieses Skript eine kleine
Verbeserung beim Lernen für die doch ziemlich schwierige Elektrodynamik
darstellt.
Michael Bergmair
2
Contents
1 Die
1.1
1.2
1.3
Maxwellschen Gleichungen
4
Überblick der Elektrodynamik . . . . . . . . . . . . . . . . . . 4
Mathematische Beschreibung von Vektorfeldern . . . . . . . . 7
Die Maxwell Gleichungen . . . . . . . . . . . . . . . . . . . . . 17
2 Elektrostatik und Magnetostatik
2.1 Die Multipolentwicklung in der Elektrostatik
2.2 Elektrostatik in Anwesenheit von Leitern . .
2.3 Die elektrostatische Energie . . . . . . . . .
2.4 Dielektrika . . . . . . . . . . . . . . . . . . .
2.5 Magnetostatik . . . . . . . . . . . . . . . . .
2.6 Die magnetische Energie . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 Elektromagnetische Strahlung
3.1 Lösungen der freien Maxwellgleichung . . . . . . . . . . . . .
3.2 Wellen an Grenzflächen und in Hohlleitern . . . . . . . . . .
3.3 Skalares und Vektorpotential . . . . . . . . . . . . . . . . . .
3.4 Strahlung einer lokalisierten Verteilung von Ladungen und
Strömen . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5 Streuung elektromagnetischer Strahlung . . . . . . . . . . .
4 Die spezielle Relativitätstheorie
4.1 Das Verhalten der Maxwellgleichungen unter Galilei - Transformationen . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2 Die Postulate der speziellen Relativitätstheorie; die Lorentztransformation . . . . . . . . . . . . . . . . . . . . . . . . .
4.3 Vierervektoren und Tensoren; Relativistische Mechanik . . .
4.4 Relativistische Elektrodynamik . . . . . . . . . . . . . . . .
4.5 Die Lorentzgruppe . . . . . . . . . . . . . . . . . . . . . . .
3
.
.
.
.
.
.
21
21
28
36
43
51
56
65
. 65
. 74
. 79
. 85
. 93
102
. 102
.
.
.
.
109
118
127
131
1
1.1
Die Maxwellschen Gleichungen
Überblick der Elektrodynamik
Die Elektrodynamik beschäftigt sich mit den Kräften, die elektrisch geladene
Teilchen aufeinander ausüben. Nach dem Coulombschen Gesetz ist die Kraft,
wie die Gravitationskraft, zentral und umgekehrt proportional zum Quadrat
des Abstandes zwischen den Teilchen.
~ 1 = −K
~ 2 = e1 e2 r~1 − r~2
K
|~
r1 − r~2 |3
(1.1)
In diesem Ausdruck bezeichnen e1 und e2 die elektrischen Ladungen im
Gaußschen Einheitensystem. Diese Einheiten sind so gewählt, dass die Kraftkonstante im obigen Gesetzt gleich eins ist (im cgs-System). Anders als die Masse
kann die elektrische Ladung sowohl positives als auch negatives Vorzeichen
haben. Da weiter das Superpositionsprinzip gilt (Kräfte ausgeübt von verschiedenen geladenen Teilschen auf ein vorgegebenes Teilchen dürfen einfach
addiert werden) und es in der Welt genauso viele positive wie negative Ladungen gibt (makroskopische Ladungsneutralität), können elektrisch geladene
Kraftwirkungen einander weitgehend kompensieren: Positiv geladene Kerne
umgeben sich z.B. mit negativ geladenen Elektronen und bilden Atome und
Moleküle, die nach außen nur noch schwache elektrische Wirkungen zeigen.
Bei der näheren Untersuchung der elektrischen Kräfte ergab sich, dass das
Coulombsche Gesetz nur für ruhende Ladungen gilt. Das Gesetz, das die
Kräfte zwischen bewegenden Ladungen beschreibt (Liénard-Wiechert-Gesetz)
ist sehr viel komplizierter: Die Kraft hängt von den Geschwindigkeiten der
beiden Teilchen ab und ist weiter nicht- instantan: Die Kraft ausgeübt vom
Teilchen 1 auf Teilchen 2 zur Zeit t enthält nicht die Geschwindigkeit zur
Zeit t, sondern zur Zeit t0 = t − |~r(t0 )|/c, wobei ~r(t0 ) der Abstand der beiden
Teilchen zur Zeit t0 ist.
Wegen der Kompliziertheit des Kraftgesetzes wählt man eine mathematisch
äquivalente Beschreibung, die auf Faraday zurückgeht: Elektrische Ladungen
erzeugen nach Gesetzen, die wir noch näher angeben werden, elektrische und
~ r, t) und B(~
~ r, t). (Aus historischen Gründen wird die
magnetische Felder E(~
~ aber als magnetische Induktion bezeichnet). Ein Teilchen mit der
Größe B
Ladung e und Geschwindigkeit ~v , das sich am Ort ~r befindet, erfährt eine
Kraft gleich
~ r, t)].
~ r, t) = e[E(~
~ r, t) + ~v × B(~
(1.2)
K(~
c
Die Größe c ist die Lichtgeschwindigkeit im Vakuum; sie erscheint zuerst nur,
~ und B
~ dieselbe physikalische Dimension zu geben und die
um den Größen E
4
~ festzulegen. (Das obige Lorentzsche Gesetz ist zugleich eine
Größe von B
~ und B).
~
Messvorschrift für die Größen E
~ reduziert sich das Coulombsche Gesetzt auf die
Nach der Einführung von E
~ einer ruhenden, punktförmigen Ladung e’
Aussage: das elektrische Feld E
im Punkt ~r ist gegeben durch:
~0
~ r) = e0 ~r − r .
E(~
|~r − r~0 |3
(1.3)
Die magnetische Induktion verschwindet in diesem Falle.
~ r, t)
Es ist die Aufgabe der (mikroskopischen) Elektrodynamik, die Felder E(~
~ r, t) zu berechnen für vorgegebene Werte der Orte und Geschwindigkeiten
und B(~
aller in einem System anwesenden geladenen Teilchen. Dies geschieht durch
Lösunger der Maxwellgleichungen (im Vakuum). Es erweist sich dabei als
bequem, statt mit den Orten und Geschwindigkeiten der einzelnen Teilchen
mit den Ladungs- und Stromdichten, definiert durch
ρ(~r, t) =
N
X
ei δ(~r − r~i (t))
(1.4)
ei v~i (t)δ(~r − r~i (t))
(1.5)
i=1
und
~j(~r, t) =
N
X
i=1
wobei ei , r~i (t) und v~i (t) die Ladung, der Ort und die Geschwindigkeit des i-ten
Teilchens darstellen, zu arbeiten. Die explizite Form der Maxwellgleichungen
werden wir im dritten Abschnitt dieses Kapitels nach einer mathematischen
Einleitung im zweiten Abschnitt geben. Ein Großteil der weiteren Vorlesung
wird sich dann mit der Lösung der Maxwellgleichungen für vorgegebene ρ
und ~j beschäftigen.
In den meisten physikalischen Systemen sind ρ(~r, t) und ~j(~r, t) allerdings
keine vorgegebenen Größen; der zeitliche Verlauf der Teilchengeschwindigkeiten
~ r, t) und B(~
~ r, t) ab. Wir
~vi (t) hängt über die Lorentzkraft wieder von E(~
müssen also zwei Probleme parallel lösen.
~ und B
~ für vorgegebene
• Das elektrodynamische Problem: Bestimme E
ρ und ~j.
• Das mechanische Problem: Bestimme die zeitliche Änderung von ρ und
~ und B.
~
~j für vorgegebene E
Das mechanische Problem muss nicht nur für die im Raum frei beweglichen
Ladungen, sondern auch für die gebundenen Ladungen in den Atomen, Molekülen
5
und makroskopischen Körpern gelöst werden. Dabei erweist es sich als
günstig, die Ladungsdichte und Stromdichte, verursacht von den gebundenen
Ladungen in einer elektrischen Polarisationsdichte P~ (~r, t) und einer Mag~ (~r, t), auszudrücken.
netisierungsdichte M
~ B,
~ P~
Auf diese Weise erhält man Maxwellgleichungen, die die vier Felder E,
~ mit den Beiträgen der freien Ladungen zur Ladungs- und Stromdichte
und M
verknüpfen; dies sind die sogenannten makroskopischen Maxwellgleichungen.
Sie können etwas kompakter geschrieben werden, falls man zwei Hilfsfelder
~ r, t) = E(~
~ r, t) + 4π P~ (~r, t)
D(~
(1.6)
~ r, t) = B(~
~ r, t) − 4π M
~ (~r, t)
H(~
(1.7)
einführt. Weil die makroskopischen Maxwellgleichungen zwei zusätzliche,
zuerst unbekannte, Felder enthalten, reichen sie meistens nicht aus, um
~ B,
~ P~ und M
~ zu bestimmen (Das schwierige Problem der Bestimmung der
E,
Ladungs- und Stromdichten für gebundene Ladungen kann nicht durch das
Definieren neuer Größen gelöst werden!). Man hat aber, zuerst experimentell,
gefunden, dass für viele Materialien ein sehr einfacher Zusammenhang zwis~ und den Feldern E
~ und B
~ besteht. Z.B.
chen den Materialgrößen P~ und M
gilt für einfache Dielektrika
~ r, t)
P~ (~r, t) = χE(~
(1.8)
~ (~r, t) = χm B(~
~ r, t)
M
(1.9)
wobei χ, die elektrische Suszeptibilität, eine für das Material spezifische Konstante, ist. Beziehungen vom Typ 1.8 bzw. 1.9 heißen konstitutive Gleichungen. Die theoretische Herleitung solcher Beziehungen ist unerwartet
kompliziert, und zum Teil erst in den letzten Jahrzehnten gelungen. Weiter
sind sie immer nur in mehr oder weniger guter Näherung gültig. In dieser
Vorlesung werden wir uns aber um die Herleitung nicht kümmern und die
konstitutiven Gleichungen nur benützen, um die makroskopischen Maxwellgleichungen zu einem lösbaren System zu machen.
Der letzte Teil der Vorlesung beschäftigt sich mit der speziellen Relativitätstheorie.
Logisch gesehen ist sie kein Teil der Elektrodynamik, wurde aber entwickelt, um Schwierigkeiten, die bei der Beschreibung von elektrodynamischen
Phänomenen in relativ zueinander bewegten Koordinatensystemen aufgetreten waren, zu lösen (Einsteins Arbeit zur Relativitätstheorie hieß ”Zur
Elektrodynamik bewegter Körper.”).
6
1.2
Mathematische Beschreibung von Vektorfeldern
Ein Vektorfeld F~ (~r, t) besteht aus drei Komponenten, Fx (~r, t), Fy (~r, t) und
Fz (~r, t). Vektorfelder traten zuerst in der Hydrodynamik auf, und verschiedene
in der Theorie der Vektorfelder übliche Bezeichnungen lassen diesen Ursprung
erkennen. Die Flussdichten in der Hydrodynamik sind definert als
Fx (~r, t)dtd2 O
(1.10)
= Masse, die im Zeitintervall dt um t durch ein Flächenelement d2 O um ~r
senkrecht zur x- Achse strömt (in der positiven x- Richtung) und ähnlich für
Fy und Fz . Durch ein willkürliche orientiertes Flächenelement strömt dann
pro Sekunde eine Masse F~ (~r, t)n̂d2 O, wobei n̂ ein Einheitsvektor senkrecht
zum Flächenelement ist. Wir können dies noch etwas kompakter schreiben,
~ einführen mit der Größe d2 O und der Richtung n̂:
indem wir den Vektor d2 O
2
~
Fluss durch d O = F~ (~r, t)d2 O.
Als Nächstes betrachten wir eine geschlossene Fläche S. Durch diese Fläche
strömt pro Sekunde netto eine Masse
I I
~
Q=
F~ (~r, t)d2 O
(1.11)
S
~ so orientieren, dass
nach außen. Dabei soll man die Flächenelemente d2 O
n̂ überall nach außen zeigt. Diese Größe Q nennt man die Ergiebigkeit
sämtlicher im durch S umschlossenen Volumen V befindlichen Quellen der
Flüssikkeitsströmung. Der Kreis durch die Integralzeichen ist eine Erinnerung daran, dass es sich um ein Integral um eine geschlossene Fläche handelt. Quellen mit negativer Ergiebigkeit werden auch Senken genannt. Als
Nächstes wollen wir jetzt die Quellen innerhalb V lokalisieren. Dazu teilen
wir das Volumen V in Teilvolumina V1 und V2 ein. Die umschließenden
Flächen seien S1 und S2 . Die innere Trennfläche ist Teil beider Oberflächen;
sie ist aber in den beiden Fällen entgegengesetzt orientiert. Es gilt also
I I
~
Q = Q1 + Q2
mit Qi =
F~ (~r, t)d2 O
(1.12)
Si
weil sich die Integrale über die Trennfläche aufheben. Durch Wiederholung
dieses Prozesses kann man letztendlich Q als Integral über eine Ergiebigkeitsdichte oder Quellendichte q(~r, t) schreiben
I I
Z Z Z
2~
~
Q=
F (~r, t)d O =
q(~r, t)d3~r
(1.13)
S
V
7
wobei q(r, t) als das Oberflächenintegral für einen infinitesimalen Quader mit
Kantenlängen ds, dy und dz aufgefasst werden kann. Innerhalb des Quaders
entwickeln wir jetzt F~ (~r, t) in eine Taylorreihe um einen der Eckpunkte ~r0
∂ F~
F~ (~r, t) = F~ (~r0 , t) + (~r − ~r0 )
+ ...
∂~r
(1.14)
und vernachlässigen Terme höherer Ordunung. Für das Integral über die
Quaderfläche erhält man so
½·
¸
¾
∂Fx
3
q(~r0 , t)d ~r = dydz Fx (~r0 , t) + dx
− Fx (~r0 , t)
(1.15)
∂x
¸
¾
½·
∂Fy
− Fy (~r0 , t)
(1.16)
+dxdz Fy (~r0 , t) + dy
∂y
½·
¸
¾
∂Fz
+dxdy Fz (~r0 , t) + dz
− Fz (~r0 , t)
(1.17)
∂z
= d3~r
∂Fx ∂Fy ∂Fz
+
+
∂x
∂y
∂z
(1.18)
Wir haben also die Quellendichte q(~r, t) identifiziert mit der Größe
div F~ :=
∂Fx ∂Fy ∂Fz
+
+
,
∂x
∂y
∂z
(1.19)
die auch die Divergenz des Vektorfeldes F~ genannt wird. Die Definition
kann etwas kompakter geschrieben werden, indem wir den Nabla-Operator
∇ einführen:
µ
¶
∂ ∂ ∂
∇=
, ,
;
(1.20)
∂x ∂y ∂z
es gilt dann
div F~ = ∇F~ .
(1.21)
Der mathematische Satz, den wir oben auf etwas heuristische Weise bewiesen
haben
I I
Z Z Z
2~
~
Fd O =
∇F~ d3 r
(1.22)
S
V
heißt (mathematischer) Gaußscher Satz ; er ist inzwischen in der Vektoranalysis natürlich auch streng bewiesen worden, unter gewissen Voraussetzungen
über Regularität von F~ und S.
Ein hydrodynamisches Strömungsfeld F~ ist natürlich nicht durch seine Quellendichte allein festgelegt (Ein einziges Feld q(~r, t) kann keine drei Felder
8
F~ (~r, ) festlegen!). Bei vorgegebenem q(~r, t) gibt es immer unendlich viele
F~ (~r, t), deren Divergenz gleich q(~r, t) ist. Eine spezielle Klasse von Lösungen
bilden die Potentialströmungen, die aus einem Potential φ(~r, t) herleitbar
sind:
F~φ (~r, t) = −∇φ(~r, t)
(1.23)
´
³
Das Vektorfeld ∇φ = ∂φ
, ∂φ , ∂φ heißt der Gradient von φ. Das Vektorfeld
∂x ∂y ∂z
F~φ (~r, t) hat die Divergenz q(~r, t), falls φ der Potentialgleichung
µ
2
∇ φ := ∇∇φ =
∂2
∂2
∂2
+
+
∂x2 ∂y 2 ∂z 2
¶
φ = −q
(1.24)
genügt. Potentialströmungen haben die zusätzliche Eigenschaft, dass das
Linienintegral
Z
~
r2
F~φ d~s = φ(~r1 ) − φ(~r2 )
(1.25)
~
r1
nur von den Endpunkten des Integrationsweges, nicht aber vom gewählten
Weg abhängt. Insbesondere gilt für jeden geschlossenen Weg C
I
F~φ d~s = 0.
(1.26)
C
Diese Beziehung gilt aber nicht für ein willkürliches Strömungsfeld. Falls wir
z.B. C um eine Wirbellinie legen, so ist anschaulich klar, dass F~ immer in der
Richtung von d~s zeigt (falls C entsprechend orientiert ist) und das Integral
also einen nichtverschwindenden Wert hat. Die Größe
I
Z=
F~ d~s,
(1.27)
C
auch Zirkulation genannt, ist also ein Maß für die Stärke der von C umschlossenen Wirbel. Zur näheren Lokalisierung der Wirbelstärke können wir
wieder den Weg C aufgebaut denken aus zwei geschlossenen Wegen C1 und
C2 ; wie im Falle der Quellendichte gilt wieder
Z = Z1 + Z2 ,
und im Grenzfall immer feinere Unterteilungen
ZZ
~ r, t)d2 O
~
ζ(~
Z=
(1.28)
(1.29)
O
wobei O eine willkürliche durch C umrandete Fläche ist. Die Größe ζ~ heißt
Wirbeldichte: Es ist eine Vektorgröße, die entlang der Wirbellinie gerichtet
9
ist. Die Zirkulation für einen infinitesimalen Rechteckweg mit Kantenlängen
dy und dz (also senkrecht zur x- Achse) beträgt nach dieser Definition
dZ = ζx (~r, t)dydz.
(1.30)
Andererseits findet man durch Einsetzen der Taylorentwecklung und Auswertung des Integrals
¶
µ
∂Fz ∂Fy
dydz.
(1.31)
dZ =
−
∂y
∂z
Ähnliche Rechnungen für Flächenelemente senkrecht zur y- und z- Achse
liefern letzendlich
µ
¶
∂F
∂F
∂F
∂F
∂F
∂F
y
x
z
y
x
z
~ r, t) =
(1.32)
ζ(~
−
,
−
,
−
∂y
∂z ∂z
∂x ∂x
∂y
oder auch
~ r, t) = ∇ × F~ := rotF~ .
ζ(~
(1.33)
Die Größe rotF~ heißt die Rotation von F~ ; in der englischsprachigen Literatur
wird sie auch mit curl F~ bezeichnet. Unsere obigen Überlegungen können
zusammengefasst werden in dem Stokesschen Satz :
I
ZZ
~
~
F d~s =
rotF~ d2 O.
(1.34)
C
O
~ mit derjenigen von C übereinstimmen.
Dabei soll die Orientierung von d2 O
Auch dieser Satz kann in der Vektoranalysis streng hergeleitet werden. Aus
dem Stokesschen Satz folgt, dass das Flächenintegral nicht von der Wahl der
Fläche abhängen kann. Dies lässt sich auch direkt zeigen: Aus zwei durch C
berandete Flächen lässt sich eine geschlossenen Fläche S bilden, die, für den
einfachen Fall, dass die Flächen O1 und O2 sich nicht schneiden, ein Volumen
V umschließen. Falls die Flächen im selben Sinn orientiert sind, so gilt z.B.
im skizzierten Fall
I I
ZZ
ZZ
2~
2~
~
~
~
rotF d O =
rotF d O −
F~ d2 O.
(1.35)
O1
O2
Andererseits gilt auf Grund des Gaußschen Satzes
I I
ZZZ
2~
~
rotF d O =
div rotF~ d3~r.
(1.36)
V
Nun gilt aber
div rotF~ = ∇(∇ × F~ ) =
X
ijk
10
²ijk
∂ ∂
Fk = 0.
∂ri ∂rj
(1.37)
Damit ist das Verschwinden des Integrals über die geschlossene Fläche S, und
damit die Gleichheit der zwei Flächenintegrale über O1 und O2 bewiesen.
~ r, t) nur dann die RoAus Gl.1.37 folgt weiters noch, dass ein Vektorfeld ζ(~
tation eines anderen Vektorfeldes sein kann, falls es der Zusatzbedingung
~ r, t) = 0
div ζ(~
(1.38)
genügt. Diese Zusatzbedingung erlaubt es, eine der Komponenten von ζ~ zu
bestimmen (bis auf eine Konstante), falls die zwei anderen Komponenten
bekannt sind: Ein Feld, das der Bedingung Gl.1.38 genügt, hat effektiv nur
zwei unabhängige Komponenten. Es ist deshalb nicht von vornherein unsinnig anzunehmen, dass ein Vektorfeld F~ durch seine Quellen q(~r, t) = div F~
und seine Wirbel ζ~ = rotF~ ”bis auf einige Konstanten” festgelegt ist. Diese
genaue mathematische Formunlierung dieses ”Haupsatzes der Vektoranalysis” lautet:
~ r, t), das
Gegeben sind ein skalares Feld q(~r, t) und Vektorfeld ζ(~
die Zusatzbedingung div ζ~ = 0 erfüllt. Die Felder q und ζ~ sollen
weiters nur im Endlichen von Null verschieden sein. Es existiert
dann genau ein Vektorfeld F~ (~r, t), für das gilt:
rotf~ = ζ~
div F~ = q
(1.39)
und das weiters für r → ∞ mindestens wie r−2 nach Null strebt.
Der Beweis benützt einen der zwei Hilfssätze, die als Greensche Sätze bekannt
sind. Wir werden deshalb zuerst diese Sätze beweisen. Dazu wählen wir ein
Vektorfeld F~ der Gestalt
F~ (~r, t) = ψ(~r, t)∇φ(~r, t),
(1.40)
wobei ψ und φ skalare Felder sind. Es gilt dann
div F~ = ∇(ψ∇φ) = ∇ψ∇φ + ψ∇2 φ.
Einsetzen in den Gaußschen Satz
I I
ZZZ
2~
~
Fd O =
div F~ d3~r
S
liefert
I I
(1.41)
(1.42)
V
ZZZ
2~
(∇ψ∇φ + ψ∇2 φ)d3~r.
ψ(∇φd O) =
V
11
(1.43)
Durch Vertauschen von ψ und φ erhält man
ZZZ
ZZ
2~
(∇φ∇ψ + φ∇2 ψ)d3~r.
φ(∇ψd O) =
(1.44)
V
S
Subtraktion der beiden Ausdrücke liefert
ZZ
ZZZ
2~
(φ∇ψ − ψ∇φ)d O =
(φ∇2 ψ − ψ∇2 φ)d3~r
S
(1.45)
V
Die Formeln Gl.1.43 und Gl.1.45 sind als erster und zweiter Greenscher Satz
bekannt.
Als nächstes zeigen wir die Eindeutigkeit der Lösung des im Hauptsatz der
Vektoranalysis gestellten Problems. Dazu nehmen wir zuerst an, es gäbe
zwei Lösungen F~1 (~r) und F~2 (~r) mit
div F~i = q
∇ × F~i = ζ~
(1.46)
∇ × F~d = 0.
(1.47)
Für die Differenz F~d muss also gelten
div F~d = 0
Aus ∇ × F~d = 0 folgt insbesonders, dass das Linienintegral
Z~r2
F~d d~s
(1.48)
~
r1
nur von ~r1 und ~r2 abhängen kann; das Linienintegral kann also benützt werden, um ein Potential φ zu bestimmen, wofür gilt
F~d = −∇φ
(1.49)
(Vgl. die Konstruktion eines Potentials für ein konservatives
¡ 1 ¢Kraftfeld in der
~
Mechanik,
S.9 des Skriptums Mechanik). Wegen Fi = O r2 gilt auch F~d =
¡1¢
O r2 ; man kann dann durch geschickte Wahl der Integrationskonstante
erreichen, dass gilt
µ ¶
1
φ=O
(1.50)
r
Aus div F~d = 0 folgt ∇∇φ = ∇2 φ = 0. Wir wählen jetzt im ersten Greenschen
Satz φ = ψ mit der oben konstruierten Funktion φ und wählen für V eine
Kugel mit Radius R. Wir erhalten dann
µ ¶
ZZZ
ZZZ
1
2 3
2 3
~
I(R) :=
|∇φ| d ~r =
|Fd (~r)| d ~r = O
(1.51)
R
v
V
12
(Der Integrand im Oberflächenintegral ist von der Ordnung R12 R1 ; die Oberfläche
ist 4πR2 ). Das Integral ist einerseits wegen der Positivität des Integrandes
eine monoton nicht-abnehmende Funktion von R, andererseits soll es der
Ordnung R−1 sein; das geht nur, falls gilt F~d = 0, also F~1 (~r) = F~2 (~r). Damit
ist der Eindeutigkeitsbeweis gelierfert.
Nachdem wir jetzt die Eindeutigkeit bewiesen haben, zeigen wir als nächstes
die Existenz der gesuchten Lösung. Wir tun dies mittels einer expliziten
Konstruktion der Lösung. Dazu schreiben wir zunächst (um Konsistenz mit
später benötigten Formeln herzustellen)
~ r, t) = 4π~c(~r, t).
ζ(~
q(~r, t) = 4πρ(~r, t)
(1.52)
Weiters schreiben wir die gesuchte Lösung als
F~ = F~ρ + F~~c
(1.53)
∇F~ρ = 4πρ
(1.54)
∇F~~c = 0
(1.55)
∇ × F~ρ = 0
(1.56)
mit
4π
∇ × F~~c = 4π~c = ~j
(1.57)
c
und nehmen weiters noch an, dass die beiden Komponenten geschrieben werden können in der Form
F~ρ = −∇φ
~
F~~c = ∇ × A
~=0
mit∇A
(1.58)
Durch diese Wahl sind die Bedingungen ∇×F~ρ = 0 und ∇F~~c = 0 automatisch
erfüllt, wie man leicht nachweist: es gilt z.B.
~=
∇∇ × A
X
²ijk
ijk
∂ ∂
Ak = 0.
∂xi ∂xj
(1.59)
Damit auch die restlichen Bedingungen erfüllt sind muss gelten
und
−∇2 φ = −4πρ
(1.60)
~ = 4π~c.
∇×∇×A
(1.61)
Letztere Beziehung kann noch etwas umgeformt werden: es gilt
~
~ = ∇(∇A)
~ − ∇2 A
∇×∇×A
13
(1.62)
~ = grad div A
~ − ∇2 A
~ (Beweis:
oder rot rot A
~ i=
(∇ × ∇ × A)
X
²ijk ²klm
jklm
=
X
jklm
∂ ∂
Am
∂xj ∂xl
X
∂ ∂
∂ ∂
(δil δjm − δim δjl )
Am =
Am
∂xj ∂xl
∂x
j ∂xl
jlm
Ã
!
X ∂2
∂ X ∂
=
Am −
Ai =
2
∂xi m ∂xm
∂x
j
j
²kij ²klm
(1.63)
~ − ∇2 A)
~ i .)
(grad div A
~ = 0 erhalten wir letztendlich:
Wegen ∇A
~ = −4π~c.
∇2 A
(1.64)
~ eine
Wir erhalten also sowohl für φ als auch für jede Komponente von A
Gleichung vom Typ der Poissongleichung:
∇2 φ(~r) = −4πρ(~r).
(1.65)
Diese Gleichung lösen wir jetzt mittels der Methode der Greenschen Funktion,
d. h. wir suchen zuerst eine Lösung der Gleichung
∇2 Gφ (~r, ~r0 ) = −4πδ(~r − ~r0 ),
(1.66)
wobei die Vektor-δ-Funktion δ(~r) definiert ist als
δ(~r) = δ(x)δ(y)δ(z)
(1.67)
und schreiben die Lösung von Gl.1.65 als
ZZZ
φ(~r) =
d3~r0 Gφ (~r − ~r0 )ρ(~r0 ).
(1.68)
Die Greensche Funktion des Problems (1.65) ist
Gφ (~r − ~r0 ) =
1
|~r − ~r0 |
Beweis: Für ~r 6= ~r0 gilt (mit ~r0 = ~r − ~r0 ): Gφ (~r0 ) =
∇Gφ −
~r0
r03
;
∇2 Gφ = −
14
(1.69)
1
r0
3
~r0~r0
+3 5 =0
3
r0
r0
(1.70)
Die Funktion ∇2 Gφ erfüllt also die erste Eigenschaft der δ- Funktion: Sie
verschwindet für ~r 6= ~r0 . Zur Bestimmung
der δ- Funktion
RRR der Koeffizienten
0 3
müssen wir als Nächstes das Integral
Gφ (~r, ~r )d ~r bestimmen über ein
0
Gebiet V das den Punkt ~r = ~r entählt. Wir wählen dafür eine Kugel mit
Radius r0 . Nach dem Gaussschen Satz gilt dann
ZZZ
Zπ Z2π
I I
2
3
∇ Gφ d ~r =
2~
∇Gφ d O = −
V
0
also
0
~r0 ~r0 2
r sin θdθdφ
r03 r0 0
(1.71)
ZZZ
∇2 Gφ d3~r = −4π.
(1.72)
Damit ist der Beweis der Beziehung (1.66) mit der vorgegebenen Form von
G(~r, ~r0 ) geliefert.
Die Lösung des Hauptproblems der Vektoranalysis ist also:
~
F~ = −∇φ + ∇ × A
mit
ZZZ
φ(~r) =
(1.73)
ZZZ
ρ(~r0 )d3~r0
|~r − ~r0 |
~ r) =
A(~
Wir brauchen noch die Zusatzbedingung
µ ¶
1
~
F (~r) = O 2
r
~c(~r0 )d3~r0
|~r − ~r0 |
(1.74)
(1.75)
zu verifizieren für den Fall, dass ρ(~r) und ~c(~r) nur in einem endlichen Gebiet
von Null verschieden sind. Dazu reicht es aus, zu zeigen, dass gilt
µ ¶
µ ¶
1
~ r) = O 1 .
A(~
φ(~r) = O
(1.76)
r
r
Nehmen wir jetzt an, das Gebiet in dem ρ(~r) und ~c(~r) von Null verschieden
sind, liegt innerhalb der Kugeloberfläche r = R. Dann gilt für r > 2R :
|~r − ~r0 | > 21 r für |r0 | < R.
Also
¯Z Z Z
¯ Z
Z
¯
ρ(~r0 )d3~r0 ¯¯
|ρ(~r0 )|d3~r0
2
¯
≤
≤
|ρ(~r0 )|d3~r0
(1.77)
|φ(~r)| = ¯
|~r − ~r0 | ¯
|~r − ~r0 |
r
für r > 2R.
¡ ¢
Das ist aber genau mit φ(~r) = O 1r gemeint. Ähnliche Beziehungen lassen
15
~ auf völlig analoge Weise herleiten.
sich für die einzelnen Komponenten von A
Damit ist der Beweis des Hauptsatzes der Vektoranalysis zu Ende.
Durch Nachlesen des Beweises kann man noch zeigen, dass die auf Seite 10
zuerst bequemlichkeitshalber auferlegten Bedingungen in Wirklichkeit immer
gültig sein müssen:
1. Ein Vektorfeld F~ (~r) kann immer geschrieben werden als Summe eines
wirbelfreien oder longitudinalen Anteils F~ρ und eines quellenfreien oder
transversalen Anteil F~~c.
2. Ein wirbelfreies Feld kann immer geschrieben werden als (minus der)
Gradient einer Potentialfunktion φ
F~ρ = −∇φ
(1.78)
3. Ein quellenfreies Feld kann geschrieben werden als die Rotation eines
~ r)
sogenannten Vektorpotentials A(~
~
F~~c = ∇ × A
(1.79)
~ festDurch diese Beziehung wird nur der transversale Anteil von A
gelegt; das Vektorpotential
~0 = A
~ + ∇χ
A
(1.80)
führt zum selben Feld F~c . Diese Freiheit kann man dadurch ausnutzen
dass man die Zusatzbedingung
~=0
div A
(1.81)
stellt. Für gewisse Probleme erweist es sich aber als bequemer, einen
~ festzulegen. Eine Transformation vom Typ
anderen Wert für div A
Gl.(1.80) heißt Eichtransformation.
¡ ¢
4. Falls F~ (~r) der Bedingung F~ (~r) = O r12 genügt und wir für F~ρ und
F~~c die gleiche Bedingung verlangen, so ist die unter 1. diskutierte
Aufspaltung eindeutig. Sonst kann F~ (~r) Beiträge enthalten, die sowohl
wirbel- als auch quellenfrei sind. Solche Beiträge haben die Gestalt
F~0 (~r) = −∇φ0 (~r)
mit∇2 φ0 (~r) = 0.
(1.82)
Funktionen φ0 , die der Laplace - Gleichung ∇2 φ0 (~r) = 0 genügen,
heißen harmonische Funktionen. Sie werden später noch systematisch
diskutiert.
16
1.3
Die Maxwell Gleichungen
~ und B
~ dadurch, dass sie
Die Maxwell Gleichungen bestimmen die Felder E
von beiden die Divergenz und die Rotation festlegen. Wie im vorhergehenden
Abschnitt gezeigt wurde, reicht dies aus, um die beiden Felder zu bestimmen.
Als erstes betrachten wir die Divergenz des elektrischen Feldes. Das Coulombsche Gesetz für des Feld einer ruhenden Ladung lautet
also gilt
0
~ r) = e0 ~r − ~r = −e0 ∇ 1
E(~
|~r − ~r0 |
|~r − ~r0 |
(1.83)
~ r) = 4πe0 δ(~r − ~r0 ).
∇E(~
(1.84)
Für eine Verteilung ruhender Ladungen mit Ladungsdichte ρ(~r) gilt also nach
dem Superpositionsprinzip
~ r) = 4πρ(~r).
∇E(~
(1.85)
Weil es keine experimentellen Hinweise für Abweichungen von diesem Gesetz
für bewegte Ladungen gab (und seitdem auch nicht gegeben hat), schlug
Maxwell vor, dieses Gesetz auch für willkürlich bewegte Ladungen vorauszusetzen:
~ r, t) = 4πρ(~r, t)
∇E(~
(1.86)
Trotz wiederholter Versuche gibt es noch immer keine reproduzierbaren Experimente, in denen magnetische Ladungen (magnetische Monopole) nachgewiesen
werden konnten. Wir werden also, wie Maxwell, annehmen, dass es solche
~ - Feld ist also quellenfrei:
magnetischen Ladungen nicht gibt. Das B
~ r, t) = 0
∇B(~
(1.87)
~ betrachten wir das Induktionsgesetz: In einem
Zur Bestimmung von ∇ × E
Stromkreis, der sich in einem zeitlich veränderlichen Magnetfeld befindet,
wird ein elektrischer Strom erzeugt. Die antreibende Kraft beträgt nach
Faraday
I
ZZ
1d
~
~ r, t).d2 O
~
E(~r, t).d~s = −
B(~
(1.88)
c
dt
C
S
wobei C eine Kurve entlang des Stromkreises und S eine durch C berandete
Fläche ist (Umlaufsinn des Stromkreises und Orientierung der Fläche sollen
~ ist die Wahl der Fläche
miteinander konsistent gewählt werden.) Wegen div B
für das Ergebnis belanglos. Anwendung des Stokesschen Satzes liefert nun
Z Z
ZZ
1d
2~
~
~ d2 O
~
(∇ × E)d O = −
B
(1.89)
c
dt
S
17
Weil das Induktionsgesetz für jeden Stromkreis gelten muss, können wir
schließen
~ r, t) + 1 ∂ B(~
~ r, t) = 0
∇ × E(~
(1.90)
c ∂t
Das Auftreten der Konstante − 1c im Faradayschen Gesetz kann auch aus den
~ und B
~ verstanden werden. In
Transformationseigenschaften der Felder E
~ = m~a
der klassischen Mechanik ist die Beschleunigung, und damit wegen K
auch die Kraft, in allen Inertialsystemen gleich. Dies muss natürlich auch
für die Lorentzkraft gelten:
0
~ + ~v × B
~ =E
~ 0 + ~v × B
~0
E
c
c
(1.91)
wobei die ungestrichenen Größen sich auf ein System in Ruhe und die gestrichenen sich auf ein mit gleichförmiger Geschwindigkeit ~v − ~v 0 bewegtes System
beziehen.
Falls wir insbesondere das gestrichene System momentan mit dem Probeteilchen
mitbewegen lassen, so gilt
~0 = E
~ + ~v × B.
~
E
c
(1.92)
Betrachte jetzt einen Stromkreis, der aus einem ruhenden Drahtbügel C1
und einer mit der Geschwindigkeit v in der -y Richtung bewegten Schleife C2
besteht. Das ganze befindet sich ein einem konstanten Magnetfeld B in der -z
Richtung (in die Ebene der Zeichnung hinein) im Ruhesystem des Bügels C1 .
~ - Feld soll in diesem System verschwinden. Auf eine Einheitsladung,
Das E
~0 = vB
die den Stromkreis durchläuft, wirkt in C1 kein Feld, in C2 ein Feld E
c
in der x Richtung. Insgesamt gilt also
I
ZZ
v
1d
~
~ 2 O.
Eds = − Bl = −
Bd
(1.93)
c
c dt O
Für diese spezielle Konfiguration kann also das Faradaysche Gesetz aus den
~ und B
~ hergeleitet werden.
Transformationseigenschaften von E
Als Ausgangspunkt für die Formulierung der vierten Maxwellgleichung nehmen
wir das Oerstedsche Gesetz für das Magnetfeld eines unendlichen Drahtes mit
einem stationären Strom I. Das Magnetfeld läuft in Kreisen um den Stromdraht herum und hat die Größe B(r) = 2I/cr auf einem Kreis mit dem
Radius r. Es gilt also nach Integration über einen solchen Kreis
I
~ s = 2πrB(r) = 4π I .
(1.94)
Bd~
c
C
18
Man überzeugt sich leicht, dass dies auch für eine willkürliche, den Stromdraht in positiver Richtung umschließende Kurve gilt. Wir können dann auch
auf den Fall verallgemeinern, dass der Strom nicht in einem Draht konzentriert ist, sondern kontinuierlich verteilt. Das verallgemeinerte Oerstedsche
Gesetz lautet also
I
ZZ
4π
~ s=
~
~jd2 O.
Bd~
(1.95)
c
C
O
(mit willkürlichem C, ~j stationär)
Mit Hilfe des Stokesschen Satzes und der Willkürlichkeit von C erhält man
die differentielle Form
~ = 4π ~j
∇×B
(~j stationär)
(1.96)
c
Die Konstante 1/c ist als experimentelles Messergebnis zu betrachten und
hat einen anderen Stellenwert als die Konstante 1/c im Induktionsgesetz,
~
die letztendlich auf die Wahl der Einheiten der magnetischen Induktion B
zurückzuführen war.
~ kann nicht ohne weiteres auch für nichtstaDer obige Ausdruck für ∇ × B
tionäre Ströme gültig sein. Durch Bildung der Divergenz würde man wegen
~ =0 das Ergebnis
∇(∇ × B)
∇~j = 0
(1.97)
erhalten. Dies ist aber nicht mit dem Gesetz der Ladungserhaltung im Einklang. Letzteres sagt aus, dass die Gesamtladung, die in einem Volumen V
enthalten ist, sich nur mittels Ein- und Ausströmen durch die Oberfläche
ändern kann:
ZZZ
I I
d
3
~
~j(~r, t)d2 O
ρ(~r, t)d ~r = −
(1.98)
dt
V
(V ist beliebig)
oder in differentieller Form (über den Gaußschen Satz)
∂ρ(~r, t)
= −∇~j(~r, t).
(1.99)
∂t
Maxwell hat deshalb vorgeschlagen, das Gesetz Gl.1.96 durch Hinzufügen des
sogenannten Verschiebungsterms abzuändern :
~
4π
1 ∂E
= ~j.
(1.100)
c ∂t
c
Bildung der Divergenz und Benützung der ersten Maxwellgleichung liefern
jetzt die korrekte Beziehung:
"
#
~
4π ∂ρ
4π ~
1
∂
E
1∂ ~
~−
∇E = −
=
∇j
(1.101)
∇ ∇×B
=−
c ∂t
c ∂t
c ∂t
c
~−
∇×B
19
Wir schreiben jetzt die vier Maxwell Gleichungen noch mal zusammen:
~ = 4πρ
∇E
(1.102)
~ =0
∇B
(1.103)
~
~ + 1 ∂B = 0
∇×E
(1.104)
c ∂t
~
~ − 1 ∂ E = 4π ~j
(1.105)
∇×B
c ∂t
c
Zum Schluss dieses Abschnittes zeigen wir noch, dass diese Gleichungen auch
für ρ = 0 und ~j = 0 nichttriviale Lösungen haben. Bilden der Rotation der
dritten Maxwellgleichung liefert in diesem Fall
~ = ∇(∇E)
~ − ∇2 E
~ = − 1 ∂ (∇ × B)
~
∇ × (∇ × E)
c ∂t
(1.106)
Einsetzen der ersten und vierten Maxwellgleichung liefert
~ =
∇2 E
~
1 ∂ 2E
c2 ∂t2
(1.107)
Auf ähnliche Weise erhält man durch Bildung der Rotation der vierten Maxwellgleichung:
2~
~ = 1 ∂ B.
∇2 B
(1.108)
c2 ∂t2
~ und B
~ genügen also der Wellengleichung
Alle Komponenten von E
¸
·
1 ∂2
2
(1.109)
∇ − 2 2 f (~r, t) = 0
c ∂t
deren Lösungen sich mit der Geschwindigkeit c fortpflanzende Wellen sind
(Näheres über diese elektromagnetischen Wellen später in der Vorlesung).
Diese Wellen wurden von Maxwell mit den Lichtwellen identifiziert. Die
Übereinkunft zwischen der Ausbreitungsgeschwindigkeit c der Lichtwelle und
der Kraftkonstante 1/c im Oerstedschen Gesetz war wohl das überzeugendste
Argument für die Richtigkeit der Maxwellschen Theorie.
Ganz zum Schluss noch eine historische Bemerkung: Die oben angegebenen
Gleichungen gelten für Ladungen ρ(~r, t) und Ströme ~j(~r, t) im Vakuum (oder:
einschließlich der Ladungen und Ströme innerhalb von Atomen, Molekülen
und makroskopischen Körpern). Formal gesehen sind sie ein Spezialfall der
(später zu behandelnden) von Maxwell formulierten sogenannten Maxwellschen
Gleichungen. Die fundamentale Bedeutung der Vakuum- oder mikroskopischen Maxwellgleichungen wurde zuerst von Lorentz klar erkannt.
20
2
Elektrostatik und Magnetostatik
In diesem Kapitel beschäftigen wir uns mit den Feldern, verursacht von
zeitunabhängigen Ladungen und Strömen. Bis auf Lösungen der homogenen
Gleichungen (elektromagnetische Wellen), mit denen wir uns im nächsten
~ und B
~ zeitunKapitel beschäftigen werden, sind dann auch die Felder E
abhängig, und die Maxwellgleichungen lauten:
~ = 4πρ
∇E
(2.1)
~ =0
∇B
~ =0
∇×E
(2.2)
(2.3)
~ = 4π ~j
∇×B
(2.4)
c
~ - Feld also wirbelfrei und das B
~ - Feld quellenfrei.
In diesem Fall ist das E
Sie können mit den im vorigen Kapitel behandelten Methoden aus ρ bzw.
~ und B
~ nicht, wie im zeitabhängigen
~j bestimmt werden. Weil die Felder E
Fall, miteinander verknüpft sind, können wir die Elektrostatik (die Bestim~ für eine stationäre Ladungsdichte) und die Magnetostatik (die
mung von E
~ für eine stationäre Stromverteilung) getrennt behandeln.
Bestimmung von B
2.1
Die Multipolentwicklung in der Elektrostatik
Durch den Vergleich mit den im Abschnitt 1,2 hergeleiteten Ergebnissen sieht
man sofort, dass gelten muss
~ = −∇φ
E
Die Lösung der Gleichung lautet
φ(~r) =
mit∇2 φ = −4πρ
ZZZ
ρ(~r0 ) 3 0
d ~r .
|~r − ~r0 |
(2.5)
(2.6)
Wir nehmen jetz an, die Ladungsdichte ist nur innerhalb einer Kugel mit
~ - Feld außerhalb
dem Radius a von Null verschieden und betrachten das E
der Kugel. Es wird sich dabei herausstellen, dass das Feld in genügend großer
Entfernung kaum mehr von den genauen Details der Ladungsverteilung abhängt,
sondern nur noch von gewissen globalen Eigenschaften, den sogenannten Multipolmomenten der Ladungsverteilung. Um dies zu zeigen, entwickeln wir die
Funktion |~r − ~r0 |−1 in einer Taylorreihe in ~r0 um den Punkt ~r0 = 0
µ ¶
µ ¶
1
1
1 X 0∂ 0 1
1 X 0 0 ∂2
1
:=
= +
ri ri
+
ri rj 0 0
+..... = (2.7)
0
R
|~r − ~r |
r
∂
R ~r0 =0 2! i,j
∂ri rj R
21
∞
X
(−1)n X
n!
n=0
ri01 ...ri0n
i1 ,...,in
∂
∂ 1
...
∂ri1 ∂rin n
(2.8)
Einsetzen der obigen Entwicklung im Ausdruck für das Potential φ(~r) liefert
Z
φ(~r) =
0
ρ(~r )
∞
X
−1n
n=0
=
∞
X
(−1)n
n=0
n!
n
ri01 ...ri0n
∂
∂ 1 3
...
d ~r
∂ri1 ∂rin r
(2.9)
∞
(n)
Pi1 ,...,in
Die Größen
X
∂ 1
∂
...
:=
φn (~r).
∂ri1 ∂rin r
n=0
(2.10)
Z
(n)
Pi1 ,...,in
=
ri01 ...i0n ρ(~r)d3~r
(2.11)
heißen (elektrische) Multipolkomponenten n-ter Ordnung. Die 3n Multipolkomponenten n-ter Ordnung bilden zusammen einen Tensor n-ter Stufe:
das Multipolmoment n-ter Ordnung. Das vom Multipolmoment n-ter Ordnung erzeugte Potential φ(~r) fällt für große r wie r−(n+1) ab, wie wir gleich
noch im Detail zeigen werden. Weil die Multipolkomponenten selbst mit
Hilfe der Ungeleichung
Z
(n)
n
Pi1 ,...,in < a Qabs ; Qabs = |ρ(~r0 )|d3~r
(2.12)
abgeschätzt werden können, verlieren die Terme in der Multipolentwicklung
für r >> a mit zunehmenden n rasch an Bedeutung.
Mathematisch konvergiert die Reihe für alle ~r außerhalb der kleinsten Kugel,
die die Ladungsverteilung völlig umschließt; es gibt also eine möglichst günstige
Wahl für den Ursprung.
Als nächstes werden wir jetzt die niedrigsten Terme der Entwicklung einzeln
betrachten:
1. n = 0
Z
Q
(0)
mit Q := P = ρ(~r0 )d3~r0
(2.13)
φ0 (r) =
r
das heißt: in großen Abständen nähert sich das Potential dem Potential einer Punktladung im Ursprung an, die Stärke der Punktladung ist
gleich der totalen Ladung der Ladungsverteilung.
Zwischenbemerkung: Die Multipoltentwicklung kann natürlich genauso
für das Gravitationpotential einer Massenverteilung aufgeschrieben werden; sie liefert die Rechtfertigung dafür, dass man Gravitationspotential der Sonne oder der Erde in der Keplertheorie dur dasjenige einer
22
Punktmasse im Schwerpunkt ersetzen darf. Allerdings spürt ein Satellit auf einer erdnahen Bahn durchaus die höheren Multipolmomente
der Massenverteilung; das genaue Studium der Satellitenbahen bildet
inzwischen sogar die genauste Methode zur Bestimmung der Multipolmomente der Massenverteilung innerhalb der Erde (mit gewissen Einschränkungen, die im weiteren Teil dieses Abschnitts noch klar werden). Es gibt allerdings einen wichtigen Unterschied zwischen Elektrostatik und Gravitation: Weil Massen immer positiv sind, ist das
gravitationelle ”Monopolmoment” P (0) immer ungleich Null; das elektrostatische Monopolmoment dagegen kann verschwinden, wie z.B. für
Atome und Moleküle der Fall ist (Ladungsneutralität).
2. n = 1
∂ 1
~r
= p~ 3
∂ri r
r
(2.14)
~ 1 (~r) = −∇φ1 (~r) = T (~r)~p
E
(2.15)
(1)
φ1 (~r) = −P1
R
Der Vektor p~ = ~rρ(~r)d3~r heißt das elektrische Dipolmoment. Das
korrespondierende elektrische Feld ist
wobei
1
T (~r) = 3
r
µ
~r~r
−I + 3 2
r
¶
(2.16)
der sogenannte Dipoltensor ist. Das Feld fällt also ab wie r−3 und
hat eine Winkelverteilung, gegeben durch den Faktor −1 + 3~r~r/r2 . Für
einen Dipol in z-Richtung sind die Komponenten des elektrischen Feldes
µ
¶
3xz
3yz
3z 2 1
Ex = 5
Ey = 5
Ez = −1 + 2
(2.17)
r
r
r
r3
Das Musterbeispiel einer Ladungsverteilung mit nichtverschwindendem
Dipolmoment besteht aus zwei Punktladungen e1 und e2 in ~r1 und ~r2 :
ρ(~r) = e1 δ(~r − ~r1 ) + e2 δ(~r − ~r2 )
(2.18)
p~ = (e1 + e2 )~r1 + (~r2 − ~r1 )e2
(2.19)
mit
Für den wichtigen Sonderfall e1 = −e2 (keine Nettoladung) erhält man
p~ = e~s
23
(2.20)
wobei ~s der Vektor ist, der von der negativen zur positiven Ladung
+e u
¡
µ
¡
~s ¡
¡
¡
−e ¡
u
zeigt;
in diesem Fall ist p~ also unabhängig von
der Wahl des Ursprungs. Weiter sieht man, dass das Dipolmoment
invariant ist unter der Transformation
~s0 = εs
e0 = e/ε
(2.21)
In dem Limes ε → 0 entsteht ein ”idealer Dipol”, d. h. eine Ladungsverteilung,
deren höhere Multipolmomente alle verschwinden [wegen P (n) = O (²n−1 )]
und dessen Potential für alle r 6= 0 durch φ1 (~r) gegeben ist (weil r > |s0 |
im Grenzfall überall erfüllt ist). Ideale Dipole sind gelegentlich bequeme Gedankenkonstruktionen für theoretische Überlegungen, aber
deren Bedeutung soll nicht überbewertet werden.
3. n = 2
1 (2) ∂ 2 1
1 (2)
φ2 (~r) = Pij
= Pij Tij (~r)
2
∂ri rj r
2
Der Tensor
(2.22)
Z
Q=P
(2)
=
~r~rρ(~r)d3~r
oder in der Komponentenschreibweise
Z
Qij = ri rj ρ(~r)d3 r
(2.23)
(2.24)
heißt das Quadrupolmoment der Ladunsverteilung ρ(~r). Der Tensor
Q ist offensichtlich symmetrisch: Qij = Qji . Er kann weiters zerlegt
werden gemäß
1
(2.25)
Qij = tr(Q)δij + Q̃ij
3
mit
1
Q̃ij = Qij − tr(Q)δij
(2.26)
tr(Q) = Qii
3
Dabei heißt tr(Q) die Spur des Tensors Q und Q˜ij heißt das reduzierte
Dipolmoment. Einsetzen dieser Zerlegung im Ausdruck für φ2 (~r) ergibt,
24
dass nur Q̃ij zum Potential beiträgt: Die Spur des Tensors T verschwindet wegen ∇2 1r = 0.
Der reduzierte Quadrupoltensor hat fünf unabhängige Elemente. Jedes
Quadrupolfeld lässt sich darstellen als das Feld eines geschickt gewählten
Rhombus wie nebenan gezeichnet. Auch für die Spezifikation des Rhombus sind fünf Daten notwendig: Drei Eulerwinkel für die Orientierung
der Figur im Raum, das Achsenverhältnis s1 /s2 und die Stärke es21 .
Das Potential ist invariant unter der Transformation
si → εsi (i = 1, 2)
e → e/ε2
(2.27)
und der Limes ε → 0 ergibt den idealen Quadrupol.
+e
u
JJ

J

J

Ju −e
−e u
JJ


J
J 

Ju
+e
4. n > 2:
Die höheren Mulitpolmomente sind für die Praxis nicht sehr wichtig.
Wir bestimmen hier nur die Zahl der unabhängigen und für das Potential relevanten Parameter. Zuerst bemerken wir, dass die Multipoltensoren gegen paarweise Vertauschung der Indizes invariant sind.
Für den Wert einer Mulipolkomponente der Ordnung n ist nur wichtig,
wieviele Indizes die Werte x,y und z annehmen; nennen wir diese Zahlen
nx , ny und nz . Bei vorgegebenem nx kann ny die Werte 0 bis n − nx
annehmen; nz liegt dann fest. Insgesamt hat das Multipolmoment n-ter
Ordnung also
n
X
n − nx + 1 =
nx =0
1
(n + 1) (n + 2)
2
(2.28)
verschiedene Elemente. Diese sind aber nicht alle für das Potential
außerhalb der Ladungsverteilung relevant. Mittels der Zerlegung
(n)
(n)
Pi1 ...in = Si3 ...in δi1 i2 + P̃i1 ...in
25
(2.29)
mit
1 (n)
Si3 ...in = Pi,i,i3 ...in
(2.30)
3
zeigt man, dass die Teilspur Si3 ...in nicht beobachtbar ist; sie wird im
Ausdruck für das Potential multipliziert mit
1
∂ ∂ ∂
∂ 1
∂
∂ 1
∂
∂
∇2 = 0 (2.31)
...
= ∇2
...
=
...
∂ri ∂ri ∂ri3 ∂rin r
∂ri3 ∂rin r
∂ri3 ∂rin
r
Solche Teilspuren lassen sich für jedes Paar Indizes bilden; insgesamt
gibt es also 21 n(n − 1) unbeobachtbare Linearkombinationen der Multipolkomponenten n-ter Ordnung. Die Zahl der unabhängigen, im Fernfeld beobachtbaren Komponenten beträgt also
1
1
(n + 1) (n + 2) − n (n − 1) = 2n + 1.
2
2
(2.32)
Die Zahl 2n+1 ist also auch gleich der Zahl der unabhängigen Lösungen
der Laplace-Gleichung ∇2 φ = 0, die im Unendlichen wie r−n−1 abfallen.
Dieses Ergebnis erhält man auch auf natürliche Weise aus der Lösung
der Laplace-Gleichung in Kugelkoordinaten, die wir in der Vorlegung
Quantenmechanik durchgeführt haben. Dabei wird sich herausstellen,
dass die allgemeinste Lösung der Laplace-Gleichung geschrieben werden
kann als
φ(~r) =
l
∞ X
X
¡
¢
Alm rl + Blm r−(l+1) Ylm (θ, φ)
(2.33)
l=0 m=−l
wobei Ylm (θ, φ) die sogenannten Kugelfunktionen sind und Alm und
Blm willkürliche Konstanten. In unserem Fall suchen wir ein Potential,
das im Unendlichen mindestens wie r−1 verschwindet; deshalb müssen
sämtliche Alm verschwinden. Die Blm müssen, wie der Vergleich mit
der oben erhaltenen allgemeinen Lösung (Gl.2.11) zeigt, Linearkombi(l)
nationen der Pi1 ,...,il sein; aus der Struktur von Gl.2.33 geht hervor,
dass es genau (2l + 1)l relevante Linearkombinationen geben darf.
Bemerkung 1
Weil nicht alle Komponenten der Multipolmomente mit n > 2 für das Potential außerhalb der Verteilung relevant sind, lässt sich umgekehrt auch nicht
die komplette Ladungsverteilung aus dem äußeren Potetial rekonstruieren.
So hat z.B. jede kugelsymmetrische Ladungsverteilung nach außen nur ein
Monopolmoment:
26
~
Aus Symmetriegründen muss das E-Feld
rein radial gerichtet sein. Andererseits folgt aus dem Gaußschen Satz für eine Kugel mit Radius R > a:
ZZ
ZZZ
2
2 ~
~
Eêr d O = 4πR |E(R)| =
4πρd3~r = 4πQ
(2.34)
R
~ r) = ~r3 Q; genau das Monopolfeld. Der Satz (2.34) heißt elektroalso: E(~
r
statischer Gaußscher Satz.
Bemerkung 2
Die in Gl.2.33 erhaltenen Zusatzlösungen erhält man durch Betrachtung einer
Ladungsverteilung, die nur für |~r| > a von Null verschieden ist. Die Greensche Funktion |~r − ~r0 |−1 kann dann nach ~r entwickelt werden:
∞
X 1
1
∂
∂
=
ri1 . ..rin
...
0
|~r − ~r | n=0 n!
∂ri1 ∂rin
also
φ(~r) =
∞
X
(−1)n
n=0
n!
mit
µ ¶
∞
X
(−1)n
∂ 1
1
∂
=
...
ri1 ...rin
0
R ~r=0 n=0 n!
∂ri1 ∂ri0n r0
(2.35)
(n)
ri1 ...rin Pext i1 ...in
=
φext
r)
n (~
(2.36)
n=0
ZZZ
(n)
Pext i1 ...in
:=
∞
X
d3~rρ(~r)
∂
∂ 1
...
.
∂ri1 ∂rin r
(2.37)
(n)
Weil der Tensor Pext symmetrisch und für jedes Paar Indizes spurlos ist,
kann man wieder zeigen, dass es genau 2n + 1 unabhängige Lösungen der
Ordnung n gibt; weiters sind diese offensichtlich Polynome der Ordnung n in
den Komponenten von r:
(0)
(1)
φext
r) = Pext φext
r) = ~rP~ext
0 (~
1 (~
usw.
(2.38)
Die Form (2.33) erhält man durch Umdefinitionen, die wir nicht weiters
nachvollziehen werden.
27
2.2
Elektrostatik in Anwesenheit von Leitern
In Metallen und Halbleitern, im weiteren Leiter genannt, gibt es frei be~
wegliche Ladungsträger. Falls im Inneren dieser Materialien ein E-Feld
~
herrscht, so werden sich die positiven Ladungsträger in Richtung von E,
die negativen in entgegengesetzter Richtung bewegen. In der Elektrostatik,
~
wo das E-Feld
aus einem Potential herleitbar ist, wird also Ladung von den
Maxima von φ(~r) weg- und auf die Minima von φ(~r) zuströmen. Ein stationärer Zustand kann nur existieren, falls φ(~r) im Leiter (einschließlich des
Randes) überhaupt keine Maxima oder Minima mehr aufweist:
φ(~r) ist konstant innerhalb eines Leiters.
Wegen ∇2 φ = −4πρ verschwindet dann auch die Ladungsdichte im Inneren
des Leiters: In einem Leiter können nur auf der Oberfläche Ladungen existieren. Dies ist natürlich eine Idealisierung, die z.B. die Wärmebewegung
der Ladungsträger, sowie gewisse Quanteneffekte (Pauli - Verbot) vernachlässigt.
Diese bewirken, dass die Ladungen sich in Wirklichkeit in einer dünnen,
aber nicht unendlich dünnen, Schicht in der Nähe der Oberfläche aufhalten können. Solange die Dicke dieser Schicht gegenüber den Abmessungen des Körpers vernachlässigbar ist, kann man sie aber als unendlich dünn
behandeln. Eine weitere Einschränkung der Verwendbarkeit der in diesem
Abschnitt behandelten Theorie betrifft die Zeitskala: Wenn die Zahl der
Ladungsträger oder deren Beweglichkeit niedrig ist, so kann es sehr lange bis
sich der stationäre eingestellt hat, gegebenfalls sogar länger als die Dauer des
Experiments oder der Erscheinung, die man beschreiben will.
Das Potential einer auf die Oberfläche S beschränkten Ladungsverteilung
mit Flächendichte (= Ladung pro Oberflächenelement) ω(~r) beträgt
ZZ
ω(~r) 2 0
φ(~r) =
d ~r (r0 läuft über S)
(2.39)
0
r − ~r |
S |~
Wenn ~r sich der Oberfläche nähert, z.B. für ~r → ~r0 in der Skizze, bleibt
φ(~r) stetig. Um dies zu zeigen, spart man zuerst aus der Oberfläche eine
Kreisfläche mit dem Radius ∆r um den ”Schnittpunkt” ~r0 aus.
28
s~
r
|~r − ~r0 | ¶¶
¶
¶
¶
s¶
s
~r0
S
~r0
∆r
Das Integral über den Rest der Oberfläche ist stetig, weil der Integrand nirgendwo singulär ist. Das Integral über die Kreisfläche ist (für ein glattes
ω(~r))
ZZ
∆r
ω(~r0 ) 2 0
d ~r =
|~r − ~r0 |
Z∆rZ2π
0
¡ 3¢
ω(~r0 ) 0
0
|~
r
−
~
r
|
d|~
r
−
~
r
|dφ
+
O
∆r
0
0
|~r − ~r0 |
(2.40)
0
Für ~r → ~r0 ergibt dies:
¡
¢
2πω(~r0 )∆r + O ∆r3
(2.41)
(Die Fehlerabschätzung erfolgt durch Taylorentwicklung von ω(~r0 ) um den
Punkt ~r0 ). Der Beitrag der Kreisfläche ist also für alle ~r außerhalb der
Oberfläche stetig und bleibt beschränkt für ~r → ~r0 ; der Beitrag der Kreisfläche, und damit der ganze Ausdruck für φ(~r), ist also stetig für ~r → ~r0 ,
und der Grenzwert ist der gleiche auf beiden Seiten. Mittels einer ähnlichen
Abschätzung erhält man das gleiche Ergebnis für die Ableitungen von φ(~r)
~ r). Weil
parallel zur Oberfläche, also für die Tangentialkomponenten von E(~
~ innerhalb des Leiters verschwinden, sollen
die Tangentialkomponenten von E
sie auch außerhalb des Leiters nach Null gehen, wenn man sich der Oberfläche
~ = 0). Das E-Feld
~
nähert (Alternativer Beweis aus ∇ × E
steht also an der
Oberfläche senkrecht zur Oberfläche.
~ zeigt an der Oberfläche einen Sprung. Diesen
Die Normalkomponente von E
könnte man wie oben durch Integration über einer kleinen Kreisfläche bestimmen; einen direkteren Zugang bietet aber der elektrostatische Gaußsche
Satz, angewandt auf eine ”Pillendose” mit kreisförmigen Durchschnitt wie
nebenan skizziert, mit Radius ∆r und infinitesimaler Höhe dh. Im Integral
29
¾ ∆r -
dh
6
?
I I
S
ZZZ
2~
∇2 φ d3~r ' −4πω(~r0 )π(∆r)2
∇φd O =
S
(2.42)
V
liefert die Mantelfläche einen Beitrag der Ordnung ∆r(dh)2 , der für infinitesimales dh vernachlässigt werden kann. Der Boden gibt einen verschwindenden
~
Beitrag, weil im Inneren des Leiters das E-Feld
verschwindet. Der Beitrag
des Deckels beträgt
−π(∆r)2 En (~r0 + dh) ' −π(∆r)2 En (~r0 + εên )
(2.43)
für dh → 0. Wir erhalten also:
En (~r0 + εên ) = 4πω(~ro ),
(2.44)
~ bezeichnet. Diese hat also an der
wobei En die Normalkomponente von E
Oberfläche einen Sprung der Größe 4πω(~r0 ).
Beispiel 1:
Leitende Kugel mit Gesamtladung Q und Radius a. Das Feld außerhalb der
~ = Q~r/r3 . An der Oberfläche
Kugel ist radialsymmetrisch und beträgt E
~ auf Null; dies korrespondiert mit einer Oberflächenladungsdichte
springt E
ω=
Q
,
4πa2
(2.45)
wie auch aus der Symmetrie des Problems leicht zu erraten ist. Das Potential
beträgt φ = Q/r für r > a. Für r ≤ a hat φ(~r) den konstanten Wert
φa = Q/a. Das Verhältnis
Q
C=
(2.46)
φa
heißt die Kapazität eines Leiters; für eine Kugel gilt C = a.
φ
6
a
-
r
30
Beispiel 2:
b¯
¯
¯
¯
¯ a
Kugelkondensator: Zwei leitende konzentrische Kugeln mit Radien a und
b. Falls die Ladung auf der inneren Kugel Q beträgt, so wird auf der Innenoberfläche der äußeren Kugel insgesamt eine Ladung −Q induziert; es
gilt
Q
−Q
ω1 =
ω2 =
.
(2.47)
2
4πa
4πb2
Das Potential beträgt
Q
φ(~r) = + k,
(2.48)
r
wobei k eine Konstante ist. Der Potentialunterschied zwischen den beiden
Kugeln beträgt
µ
¶
1 1
b−a
V =Q
−
=Q
,
(2.49)
a b
ab
die Kapazität ist definiert als
C=
Q
ab
=
.
V
b−a
(2.50)
Im Grenzfall a → ∞, b → ∞ bei festem D = b − a nähert sich dies dem Wert
C=
O
,
4πd
(2.51)
wobei O = 4πa2 die Oberfläche der Kugel ist. Dieses Ergebnis gilt auch,
unter Vernachlässigung von Randeffekten, für einen ”aus den beiden Kugeln
herausgeschnittenen” ebenen Plattenkondensator.
Elektrostatische Probleme mit Leitern
Bis jetzt haben wir die Oberflächenladungsdichte als bekannt vorausgesetzt,
31
oder aus der Symmetrie des Problems einfach herleiten können. In praktischen Problemen ist dies typischerweise nicht der Fall. Dort kann man
entweder den Leiter isoliert halten und seine Gesamtladung vorgeben oder
ihn mit einem Leiter sehr großer Kapazität verbinden und damit sein Potential vorgeben (in der Praxis meistens durch Erden, wodurch er das Potential
φ = 0 erhält). Wie sich die Ladung genau über die Oberfläche verteilt ist
nicht vorgegeben; es soll ein Teil der Lösung des Problems ausmachen.
Die typische Aufgabe ist also: Bestimme eine Lösung der Poissongleichung
∇2 φ(~r) = −4πρ(~r) mit vorgegebenen ρ(~r) unter den Nebenbedingungen, dass
für jeden der vorhandenen Leiter gilt
entweder
1. φ(~r) = φi auf der Oberfläche des i-ten Leiters
2.
oder
HH
~ = 4πQi , wobei das Integral über die Oberfläche des
∇φ(~r)d2 O
i-ten Leiters läuft.
Si
Zur Lösung dieser Aufgabe gibt es keine allgemeine Methode, wie für das
Hauptproblem der Vektorechnung. Wohl aber können wir über den Greenschen Satz leicht die Eindeutigkeit beweisen. Die Differenz zweier Lösungen
des obigen Problems muss nämlich eine Lösung der Laplace-Gleichung
∇2 φd = 0 sein mit den Randbedingungen:
φd = 0 auf Leitern vom Typ 1
HH
~ = 0 auf Leitern vom Typ 2
∇φd d2 O
Anwendung des ersten Greenschen Satzes (1.43) mit Ψ = φ = φd und V das
Volumen außerhalb sämtlicher Leiter liefert
ZZZ
X I I
2 3
~
|∇φd (~r)| d ~r = −
φi
∇φd (~r)d2 O
(2.52)
V
i
Si
wobei die Summe über sämtliche Leiter im Problem läuft, und die Oberflächennormalen
immer vom Leiter nach außen gerichtet sind. Weil φd (~r) auf jeder Leiteroberfläche konstant ist, kann der Faktor φd (~r) = φi vor das Integral geschrieben
werden. In der Summe über i ist in jedem Term entweder der erste oder der
zweite Faktor gleich Null. Es muss also gelten:
∇φd (~r) = 0 −→ φd (~r) = cst,
(2.53)
wobei die Konstante gleich Null sein muss, falls es mindestens einen Leiter
vom Typ 1 gibt, oder falls V bis ins Unendliche reicht.
32
Der Nutzen dieses Eindeutigkeitssatzes ist, dass falls wir irgendeine Lösung
konstruiert oder erraten haben, wir sicher sein können, dass diese auch die
einzige Lösung ist. Ein praktisches numerisches Verfahren wird im nächsten
Abschnitt kurz diskutiert werden. Für einfache, hochsymmetrische Probleme
liefert die Methode der Bildladungen oft eine Lösung in geschlossener Form.
Beispiel 1:
´
´ r
´ ¡@
´
¡
´
@ R
R´
¡´´
@
¡´ ´
@
´
¡
r ´ ´
@r
−e ´´
+e
´
´
´
Punktladung gegenüber unendlicher, leitender, geerdeter Platte. Wir legen
die Platte in die y-z-Ebene und die Ladung in ~a = (a, 0, 0). Im Halbraum
x ≥ 0 erfüllt das Potential
φ(~r) =
e
e
−
|~r − ~a| |~r + ~a|
(2.54)
die Poissongleichung ∇2 φ = −4πeδ(~r − ~a) und die Randbedingung φ(~r) = 0
für x = 0. Es ist eine, also die Lösung des Problems. Unmittelbar rechts von
der Platte gilt
Ex (x = 0 + ε) = −
∂φ
ea
ea
2ea
=− 3 − 3 =− 3
∂x
R
R
R
(2.55)
mit R2 = a2 + y 2 + z 2 .
Die Oberflächenladungsdichte ist deshalb
ω=
1
1 ea
Ex (x = 0 + ε) = −
,
4π
2π R3
(2.56)
und die Gesamtladung auf der Platte ist
ZZ
ea
ω dydz = −
2π
Z∞ Z2π
0
0
¯∞
¯
ea
ρ dρdφ
¯
p
=
¯ = −e,
2
2
(ρ2 + a2 )3/2
ρ + a ¯0
33
(2.57)
also genau minus die Punktladung. Das induzierte Feld am Ort der Punktladung beträgt
¯
¯
x
+
a
~ ind (~a) = −e
¯ êx = − e êx .
E
(2.58)
|~r + ~a|3 ¯~r=~a
4a2
Die Ladung wird also durch die Platte angezogen mit der Kraft
µ
¶
2
e
~ = −
K
, 0, 0 .
4a2
(2.59)
Beispiel 2: Punktladung gegenüber einer geerdeten leitenden Kugel:
```
```
`
R ¡¯
¡¯
¡θ0 ¯ 0
s −e
```
s
```
``
+e
Wir versuchen wieder den Effekt der auf die Kugel influenzierten Ladungsverteilung
außerhalb der Kugel durch eine Bildladung −e0 innerhalb der Kugel darzustellen.
Aus Symmetriegründen plazieren wir die Bildladung auf der Achse durch
Punktladung und Kugelmittelpunkt in einem Abstand s0 vom Zentrum. Der
Abstand der Punktladung vom Zentrum sei s, der Radius der Kugel sei R.
Unser Ansatz ist also
φ(~r) =
e
e0
−
|~r − ~s| |~r − ~s0 |
(2.60)
mit ~s = sêz ; ~s0 = s0 êz .
Für einen Punkt auf der Kugel gilt
|~r − ~s|2 = R2 + s2 − 2Rs cos θ
(2.61)
|~r − ~s0 |2 = R2 + s02 − 2Rs0 cos θ
(2.62)
Damit das Potential auf der Kugel verschwindet, muss gelten
R2 + s2 − 2Rs cos θ
e2
=
e02
R2 + s02 − 2Rs0 cos θ
34
(2.63)
p
Dies ist für alle θ erfüllt, falls R2 = ss0 und e0 /e =
s0 /s; es gilt also
0
2
0
s = R /s und e = −eR/s. Die Bildladung, und damit auch die gesamte auf
der Kugel induzierte Ladung (Satz von Gauß) ist also immer kleiner als e.
e0
Das induzierte Feld am Ort ~s beträgt − |s−s
0 |2 êz . Die Kraft zwischen Punktladung und Kugel beträgt also
Kz = −
ee0
ee0 s
e2 Rs
e2 R
=
−
=
−
∼
−
|s − s0 |2
(s2 − R2 )2
(s2 − R2 )2
s3
(2.64)
für s >> R.
Für s − R = a << R erhält man e0 ' −e und
Kz ' −
e2 R2
e2
'
−
,
4R2 a2
4a2
also das vorher erhaltene Ergebnis für die ebene Platte.
35
(2.65)
2.3
Die elektrostatische Energie
Die potentielle Energie zweier Punktladungen e1 und e2 in ~r1 und ~r2 beträgt
nach Coulomb
e1 e2
V (~r1 , ~r2 ) =
= e1 φ2 (~r1 ) = e2 φ1 (~r2 ).
(2.66)
|~r1 − ~r2 |
Die potentielle Energie kann also wahlweise als die Energie der Ladung e1 im
Feld der Ladung e2 oder als die Energie der Ladung e2 im Feld der Ladung
e1 aufgefasst werden. Ganz analog gilt für die potentielle Energie von N
Punktladungen
V (~r1 , ..., ~rN ) =
N
−1
X
i=1
N
N
X
1 X ei ej
ei ej X ei ej
=
=
,
r
rij
2 i6=j rij
j=i+1 ij
i<j
(2.67)
wobei rij = |~ri − ~rj |; dieses Ergebnis lässt sich auch schreiben als
V (~r1 , ..., ~rN ) =
N
X
ei φ(i) (~ri |{~rj }),
(2.68)
i=1
wobei φ(i) (~ri |{~rj }) das Potential aller Ladungen j 6= i ist. Falls es zusätzlich
noch ein äußeres elektrostatisches Potential φ0 (~r) gibt, so hat man noch einen
zusätzlichen Term
N
X
V0 (~r1 , ..., ~rN ) =
ei φ0 (~r).
(2.69)
i=1
Man beachte das Fehlen des Faktors 12 . Dies hat damit zu tun, dass die
Positionen der Ladungen, die als Quellen des Feldes φ0 auftreten, nicht als
Variablen des Systems betrachtet werden; es ist daher nicht sinnvoll, die Energie V0 zwischen den Ladungen ei und den Quellen von φ0 (~r) ”aufzuteilen”.
Die obigen Ausdrücke werden für eine kontinuierliche Ladungsverteilung ρ(~r)
U = U0 + Uint
mit
(2.70)
Z
U0 = ρ(~r)φ0 (~r)d3~r
ZZ
1
ρ(~r)ρ(~r0 ) 3 3 0
d ~rd ~r .
Uint =
2
|~r − ~r0 |
Die Wechselwirkungsenergie kann auch geschrieben werden als
Z
1
Uint =
ρ(~r)φint (~r)d3~r
2
36
(2.71)
(2.72)
(2.73)
wobei φint(~r) die Lösung der Poisson-Gleichung ∇2 φint (~r) = −4πρ(~r) ist.
Unter Benützung dieser Gleichung erhält man
Z
Z
Z
1
1
1
2
3
2 3
~ int (~r)|2 d3~r.
Uint = −
∇ φint (~r)φint (~r)d ~r =
|∇φint | d ~r =
|E
8π
8π
8π
(2.74)
Man kann sich also auch die Wechselwirkungsenergie als über den Raum ver1 ~
schmiert, mit der Dichte u(~r) = 8π
|Eint (~r)|2 , vorstellen.
Die Selbstenergie
Wenn wir im gerade hergeleiteten Ausdruck für Uint für ρ(~r) eine Summe von
δ-Funktionen einsetzen, so erhalten wir zusätzlich zur Wechselwirkungsenergie auch noch Selbstenergieterme, die durch das Weglassen der Einschränkung
i 6= j in Gl.2.72 entstanden sind. Für Punktladungen sind diese sogar divergent: es kostet unendlich viel Energie, die Ladung eines Elektrons in einem
Punkt zu konzentrieren! Diese Energie ist aber nicht praktisch nützbar,
solange es nicht gelingt, z.B. ein Elektron zu spalten und in Komponenten
mit noch kleinerer Ladung zu zerlegen. Unendlichkeiten lassen sich vermeiden, wenn man sich Ladungen auf kleine Kügelchen verteilt denkt. Das
Hinzunehmen der Selbstenergieterme führt auch dazu, dass Uint , im Gegensatz zu V ({~ri }), eine positiv-definite Größe ist.
Konkret erhält man für zwei Punktladungen (und φ0 (~r) = 0)
~ r) = e1 ~r − ~r1 + e2 ~r − ~r2
E(~
|~r − ~r1 |3
|~r − ~r2 |3
(2.75)
und deshalb für die Energiedichte
1 ~
e21
e22
e1 e2 (~r − ~r1 )(~r − ~r2 )
2
u(~r) =
|E(~r)| =
+
+
.
4
4
8π
8π|~r − ~r1 |
8π|~r − ~r2 |
4π |~r − ~r1 |3 |~r − ~r2 |3
(2.76)
Die ersten beiden Terme sind Selbstenergieterme. Sie liefern bei Integration
über den Raum außerhalb einer Kugel mit Radius a
e2i
4π
8π
Z∞
e2i
1 2
ρ
dρ
=
.
ρ4
2a
(2.77)
a
Der Beitrag zur Selbstenergie des Gebiets r < a hängt vom spezifischen Modell für die ”Punktladung” ab. In der klassischen Theorie gibt es keinen Anhaltspunkt für die Wahl des Abschneideparameters a. In der Relativitätstheorie
trägt aber die elektrostatische Selbstenergie (wegen E = mc2 ) zur Masse z.B.
37
des Elektrons bei. Dieser Beitrag wird von der Ordnung der Ruhemasse m0
für
e2
e2
∼ mc2 −→ a0 =
' 2, 8.10−13 cm;
(2.78)
a0
mc2
a0 heißt der klassische Elektronenradius. Experimentell gibt es auch keinerlei
Hinweise für eine räumliche Struktur des Elektrons! Auch theoretisch gibt
es kein befriedigendes Modell für den ”Aufbau” des Elektrons, in dem die
Schwierigkeiten der unendlichen Selbstenergie umgangen werden kann. Man
hat aber formale Rechenvorschriften entwickelt, die es erlauben ”mit den
Unendlichkeiten zu leben”, d.h. trotz der in der Theorie vorkommenden Divergenzen für alle experimentell zugänglichen Größen endliche Ergebnisse zu
erhalten (Renormierungsverfahren in der Quantenelektrodynamik, entwickelt von Tomonaga, Schwinger und Feynman).
Betrachten wir jetzt den Wechselwirkungsterm in u(~r). Dieser liefert nach
Integration (in Polarkoordinaten um ~r1 )
~qr
½
>
½
½
½
ρ~½½
½
½
½
½
½
q½ θ
~r1
¾
~r21
-q
~r2
Z
e1 e2
~r − ~r1 ~r − ~r1 + ~r12 3
d (~r − ~r1 )
4π
|~r − ~r1 |3 |~r − ~r1 + ~r12 |3
Z
ρ − r12 cos θ
e1 e2
=
dρ sin θdθdφ
2
4π
(ρ2 + r12
− 2ρr12 cos θ)3/2
¯∞
Z
¯
e1 e2
−1
¯ sin θdθdφ
=
2
4π
(ρ2 + r12 − 2ρr12 cos θ)1/2 ¯0
e1 e2
,
=
r12
also das bekannte Ergebnis für die Wechselwirkungsenergie.
(2.79)
(2.80)
(2.81)
(2.82)
Multipolentwicklung für die elektrostatische Energie
Als nächstes betrachten wir die Energie einer Ladungsdichte ρ(~r) in einem
vorgegebenen äußeren Potential φ0 (~r):
Z
U0 = ρ(~r)φ0 (~r)d3~r.
(2.83)
38
Taylorentwicklung von φ0 (~r) um den Ursprung ergibt
¯
∞
¯
X
∂
1
∂
¯
φ0 (~r) =
ri1 ...rin
...
φ0 ¯
n!
∂ri1 ∂rin ¯
.
(2.84)
¯
Z
∞
¯
X
1
∂
∂
¯
φ0 ¯
U0 =
ri1 ...rin ρ(~r)d3~r
...
¯
n!
∂r
∂r
i1
in
n=0
(2.85)
n=0
r=0
Einsetzen in Gl.2.83 ergibt
¯
∞
¯
X
1 (n)
∂
∂
¯
=
φ0 ¯
Pi1 ,...,in
...
n!
∂ri1 ∂rin ¯
n=0
r=0
(2.86)
r=0
mit den vorher (Gl.2.11) definierten Multipolmomenten P (n) . Mehr explizit
erhält man
~ 0 (0) − 1 Qij ∂ Ej (0) + ...
U0 = Qφ0 (0) − p~E
(2.87)
2
∂ri
In relativ schwach variierenden Feldern spielen also nur die niedrigeren Multipolmomente eine Rolle. Ausdrücke wie Gl.2.85 oder Gl.2.87 sind nützlich,
wenn wir Kräfte und Drehmomente berechnen wollen, die auf einen Körper
mit im körperfesten System vorgegebenem ρ(~r) wirken. Diese erhält man
durch Differenzieren von U0 nach den Schwerpunktskoordinaten oder einem
Orientierungswinkel des Körpers. Wir werden nur einige einfache Beispiele
diskutieren.
1. Dipol in einem homogenen Feld: Die Feldenergie beträgt
~ = −pE0 cos θ
U0 = −~pE
(2.88)
~ sonst wirkt ein Drehmoment der
Die Energie ist minimal für p~||E;
Größe
~ | = −| ∂U0 | = | − pE sin θ|
|N
(2.89)
∂θ
~ 0 und wird mit
Die Richtung steht senkrecht zu p~ und E
~ = p~ × E
~0
N
richtig beschrieben.
39
(2.90)
2. Kraft auf eine starre Ladungsverteilung: Dazu bestimmen wir die
Abhängigkeit von U0 vom Ort, um den die Taylorentwicklung vorgenommen wird.
¯
Z
¯
∂
3
~ =−
K
ρ(~r + ~a)φ0 (~r)d ~r¯¯
(2.91)
∂~a
~a=0
=
∂
~ 0 (~a) − 1 Qij ∂ E0j (~a) + ...)~a=0
(Qφ0 (~a) − p~E
∂~a
2
∂ri
~ 0 (0) + pi ∇E0i (0) + 1 Qij ∇ ∂ E0j + ...
= QE
2
∂ri
(2.92)
(2.93)
In einem inhomogenen Feld hängt die Schwerpunktsbewegung also vom Dipolmoment und von den höheren Multipolmomenten ab. Insbesondere kann man
ein inhomogenes Feld dazu benützen, einen Strahl von Molekülen nach der
Richtung ihrer elektrischen Dipolmomente zu sortieren. Das magnetische
Analogon (Stern - Gerlach) war ein Schlüsselexperiment für die Quantenmechanik.
Der Satz von Thomson (später Lord Kelvin)
Im letzten Abschnitt haben wir gezeigt, dass die Ladungsträger auf Leitern sich so verteilen, dass das Potential innerhalb jedes Leiters konstant ist.
Wir werden jetzt zeigen, dass dies genau die Verteilung ist, für die die elektrostatische Energie minimal ist bei vorgegebenen Gasamtladungen auf den
einzelnen Leitern. Dies wurde zuerst von Thomson gezeigt.
Wir betrachten die elektrostatische Energie
ZZ
XZ
1X
ρi (~r)ρj (~r0 )
0
U=
φ0 (~r)ρi (~r)d3~r
(2.94)
d~rd~r +
2 i,j
|~r − ~r0 |
i
in Abhängigkeit von den Ladungsdichten ρi (~r) auf den einzelnen Leitern.
Dabei ist φ0 (~r) das Potential der fest vorgegebenen Ladungsverteilungen
außerhalb der Leiter (im unendlichen Raum). Damit U minimal ist unter
den Nebenbedingungen
Z
ρi (~r)d3~r = Qi
(2.95)
Vi
muss nach Lagrange gelten
!
Ã
Z
N
X
δ
ρi (~r)d3~r
U−
φi
δρi (~r)
V
i
i
i = 1, ..., N
(2.96)
wobei die Konstanten φi sogenannte Lagrange-Multiplikatoren sind.
In Worten: Nur Variationen von U , die gleichzeitig auch eine oder mehrere
40
der Nebenbedingungen verletzen, können zu einer Variation von U führen.
Dies ist sicherlich eine notwendige Bedingung für die Existenz eines Minimums.
Ausarbeiten von Gl.2.96 liefert
X Z ρj (~r0 )
φ0 (~r) +
d3~r0 = φi
für ~r ∈ Vi
(2.97)
0|
|~
r
−
~
r
j
(die Einschränkung erfolgt, weil ρi (~r) nur innerhalb Vi von Null verschieden
ist). Der Multiplikator φi hat also die Bedeutung des Potentials auf dem
Leiter i.
Ein Variationsprinzip kann fast immer für eine genäherte oder numerische
Lösung eines physikalischen Problems genützt werden. Im vorliegenden Fall
könnte man mit irgendeiner Verteilung der Ladungen auf den Oberflächen
~
anfangen und daraus E-Feld
und elektrostatische Energie bestimmen. (In
der Praxis mit einer diskretisierten Verteilung der Ladungen). Zunächst
bewegt man einige der Ladungen etwas auf den Oberflächen umher (am
~
besten in der Richtung des berechneten E-Feldes)
und prüft nach, ob dies
zu einer Verringerung der Energie führt; bei genügend kleinen Verschiebungen entlang Etg ist dies immer der Fall und das Energiefunktional entscheidet was genügend klein ist! Dies wiederholt man, bis keine nennenswerte
Verbesserungen der Energie mehr erreichbar sind (oder bis die verfügbare
Rechenzeit zu Ende ist).
Für φ0 = 0 lässt sich die Energie im stationären Punkt durch Einsetzen der
Stationaritätsbeziehungen (Gl.2.96), schreiben als
N
1X
U=
Qi φi
2 i=1
(2.98)
wobei die φi aus der Lösung des Problems folgen, also Funktionen der {Qj }
sind. Insbesondere gilt auf Grund des Superpositionsprinzips der Maxwellgleichungen
N
X
φ(~r) =
Qi φ(i) (~r)
(2.99)
i=1
(i)
wobei φ (~r) die Lösung ist mit Qi = 1, Qj = 0 für j 6= i. Falls wir insbesondere den Wert von φ(i) (~r) auf dem Leiter j mit Γji andeuten:
φ(i) (~r) = Γji
so gilt
φi =
für ~r ∈ Vj
X
j
41
Γij Qj
(2.100)
(2.101)
Die Inverse C der Matrix Γ heißt Kapazitätsmatrix.
Es gilt also auch
X
Qi =
Cij φj .
(2.102)
j
Für die elektrostatische Energie kann man schreiben
U=
X
1X
Qi Γij Qj =
φi Cij φj .
2 ij
ij
(2.103)
Die Kapazitätsmatrix wurde bestimmt aus dem Problem, in dem auf allen
Leitern die Ladung vorgegeben ist. Wenn wir C einmal haben, können wir
aber auch Probleme, in denen auf einigen der Leiter φi statt Qi gegeben ist,
auf Probleme mit nur vorgegebenem Qi zurückführen. Falls k der {Qi } und
für die restlichen Leiter die φj vorgegeben sind, so lassen sich aus Q = Cφ
(N lineare Gleichungen) die restlichen Q’s und φ’s bestimmen.
Zum Schluss zeigen wir noch, dass die Matrizen C und Γ symmetrisch sind.
Dazu betrachten wir zuerst zwei willkürliche Ladungsverteilungen ρ(~r) und
ρ0 (~r). Die korrespondierenden Potentiale seien φ(~r) und φ0 (~r). Jetzt gilt
ZZ
Z
Z
ρ(~r)ρ0 (~r) 3 3 0
0
3
d ~rd ~r = ρ(~r)φ (~r)d ~r = ρ0 (~r)φ(~r)d3~r
(2.104)
|~r − ~r0 |
(Greensches Reziprozitätstheorem).
Für zwei stationäre Verteilungen
auf einem vorgegebenen Satz von Leitern
P
P
reduziert sich dies zu i Qi φ0i = i Q0i φi oder
X
X
X
Qi Γij Q0j =
Q0i Γij Qj =
Qi Γji Q0j
(2.105)
ij
ij
ij
Dies kann nur dann für beliebige {Qi } und {Q0i } gelten, falls Γij = Γji , also
falls Γ, und damit auch C symmetrisch ist.
42
2.4
Dielektrika
In diesem Abschnitt beschäftigen wir uns mit der Behandlung von Ladungen,
die sich innerhalb von Atomen, Molekülen oder Isolatoren befinden. Wir
nehmen an, diese Gebilde besitzen keine Nettoladung, sondern nur Dipol- und
höhere Mulitpolmomente. In einer Koninuumsbeschreibung werden hieraus
Dipol- und höhere Multipoldichten p(n) (~r). Das elektrostatische Potential φp
einer solchen Verteilung findet man durch eine Umformung des Ausdruckes
2.9:
Z
∞
X
(−1)n
∂
∂
1
(n)
φp (~r) =
pi1 ,...,in (~r0 )
...
d3~r0
(2.106)
0|
n!
∂r
∂r
|~
r
−
~
r
i
i
n
1
n=1
Falls die Multipoldichten nur in einem endlichen Gebiet von Null verschieden
sind, kann man jetzt alle ∂r∂ j durch − ∂r∂ j ersetzen und partiell integrieren. Das
Ergebnis ist
Z
ρp (~r0 ) 3 0
d ~r
(2.107)
φ(~r) =
|~r − ~r0 |
mit
∞
X
(−1)n ∂
∂ (n)
ρ(~r) =
p
...
n! ∂ri1 ∂rin i1 ,...,in
n=1
(2.108)
die sogenannte Polarisationsladungsdichte. Eine alternative Schreibweise ist
ρp (~r) = −∇P~ (~r)
mit
(2.109)
∞
X
∂ (n)
−1n ∂
...
p
Pi (~r) =
n ∂ri2 ∂rin i2 ,...,in
n=1
(i)
= pi (~r) −
1 ∂ (2)
1 ∂ ∂ (3)
pij (~r) +
p (~r)...
2 ∂rj
6 ∂rj ∂rk ijk
(2.110)
In der Praxis sind die höheren Multipolmomente meist gegenüber der Dipoldichte
vernachlässigbar; dann kann P~ (~r) mit der Dipoldichte identifiziert werden.
Im zeitabhängigen Fall ist mit der Polarisationsladungsdichte ρ(~r, t) = −∇P~ (~r, t)
auch ein Polarisationsstrom verbunden. Aus dem Ladungserhaltungssatz
∂
ρ folgt
∇~j = − ∂t
∂
∇~jp (~r, t) = ∇P~ (~r, t).
(2.111)
∂t
Es liegt nahe, für den Polarisationsstrom
~
~jp (~r, t) = ∂ P~ (~r, t) + c∇ × M
∂t
43
(2.112)
anzusetzen. Dies heißt nicht, dass die von den gebundenen Ladungen verursachte Stromdichte immer gleich der Zeitableitung von P~ ist; die Differenz
wird aber durch die magnetische Multipoldichten gegeben (diese sind nicht
mit Ladungsdichten verknüpft!).
Falls wir in den Maxwellgleichungen Ladungs- und Stromdichte aufspalten
gemäß
ρ(~r, t) = ρf (~r, t) − ∇P~ (~r, t)
(2.113)
~)
~j(~r, t) = ~jf (~r, t) + ∂ P~ (~r, t) + (c∇ × M
∂t
(2.114)
wobei ρf und ~jf die Beiträge der freien Ladungsträger darstellen, so erhält
man für die zwei inhomogenen Maxwellgleichungen
~ = 4πρf − 4π∇P~
∇E
(2.115)
~
~ − 1 ∂ E = 4π ~jj + 4π ∂ P~ (~r, t).
(2.116)
∇×B
c ∂t
c
c ∂t
~ + 4π P~ auf; die Gleichungen lassen
Es tritt also immer die Kombination E
sich kompakter schreiben mit den Hilfsgrößen
So erhält man
~ r, t) = E(~
~ r, t) + 4π P~ (~r, t).
D(~
(2.117)
~ = 4πρf
∇D
(2.118)
~
~ − 1 ∂ D = 4π ~jf .
∇×B
(2.119)
c ∂t
c
Die letzte Gleichung wird in Anwesenheit von Magnetisierungsströmen noch
weiter modifiziert. Sie ist aber für die Elektrostatik sowieso noch nicht
notwendig.
Nach diesem Exkurs in die Elektrodynamik kehren wir jetzt wieder zur reinen
Elektrostatik zurück, also zur Diskussion der Gleichungen
~ = 4πρf
∇D
(2.120)
~ =0
∇×E
(2.121)
In praktischen Problemen ist die Polarisation P~ (~r) nicht eine vorgegebene
Größe, sondern eine der zu bestimmenden Größen. Für viele Materialien
folgt aus der Quantentheorie oder aus der statistischen Physik, dass P~ (~r) auf
~ und B
~ am gleichen Ort zusammenhängt.
einfache Weise mit den Feldern E
44
Im einfachsten Fall (und für genügend schwache Felder) besteht ein linearer
~
Zusammenhang zwischen P~ und E:
~ r)
P~ (~r) = χ(~r)E(~
(2.122)
dabei heißt χ(~r) der elektrische Suszeptibilitätstensor. Dieser Tensor soll
sämtliche Symmetrien des untersuchenden Materials bestitzen. So ist z.B.
ein kubischer Kristall invariant unter Drehungen um 90◦ um die z-Achse.
Dabei gilt
êx → êy êy = −êx êz → êz
(2.123)
also
χxx → χyy
χyy → χxx
χxy → −χyx
(2.124)
Für ein kubisches (und natürlich auch für ein isotropes) Medium gilt also
χxx = χyy
χxy = 0
(2.125)
und analog
χzz = χxx
χxz = 0
χyz = 0
(2.126)
Der Suszeptibilitätstensor ist also ein Vielfaches des Einheitstensors:
~
χ = χI; P~ = χE.
(2.127)
Die Kombination ε = I + 4πχ (Matrixgleichung), bzw. ε = 1 + 4πχ (skalare
~ und E
~ bewirkt, heißt dielekGleichung), welche die Verknüpfung zwischen D
trische Matrix, bzw. dielektrische Konstante.
Randwertaufgaben mit Dielektrika An einer Grenzfläche zwischen zwei
Dielektrika muss gelten
~ tg ist stetig (aus ∇ × E
~ = 0)
E
~ n ist stetig (aus ∇D
~ = 0)
D
Letztere Beziehung impliziert, dass En an der Oberfläche einen Sprung hat:
E1n + 4πP1n = E2n + 4πP2n
(2.128)
E1n − E2n = 4π(P2n − P1n ) := 4πωp
(2.129)
also
mit der Polarisationsoberflächenladungsdichte ωp (ein auf der Oberfläche
konzentrierter Term in der Ladungsdichte, ρp = −∇P~ ).
45
Beispiel 1: Homogen polarisierte Kugel
Wir betrachten eine spontan polarisierte Kugel (z.B. ein Ferroelektrikum)
mit Polarisation P~ und Radius a. Das Gesamtdipolmoment ist also
4
p~ = πa3 P~
3
(2.130)
Es liegt also nahe, für das Potential außerhalb der Kugel anzusetzen
p~~r
r3
φ(~r) =
(r > a)
(2.131)
Damit Etg stetig sein kann, muss auch φ(~r) stetig sein. Weiter gilt innerhalb
der Kugel
∇2 φ = −4πρp = 4π∇P~ = 0
(2.132)
also auch dort muss φ harmonisch sein. Wegen der Regularität für R = 0
und der Stetigkeit für r = a kommt dann nur
p~~r
a3
φ(~r) =
(r < a)
(2.133)
in Betracht. Für die Normalkomponenten von E gilt also:
p~ ~r
a3 r
(r < a)
(2.134)
p~ ~r
r3 r
(r > a)
(2.135)
p~ ~r
= −4πP1n
a3 r
(2.136)
E1n = −
E2n = 2
Für r = a gilt daher
E1n − E2n = −3
die oben hergeleitete Randbedingung ist also immer erfüllt.
Beispiel 2: Dielektrische Kugel in einem homogenen Feld
In Abwesenheit der Kugel gilt
~ 0~r.
φ(~r) = φ0 (~r) = −E
(2.137)
Wir versuchen jetzt eine Lösung, bei der die Kugel homogen polarisiert ist:
φ(~r) = φ0 (~r) +
p~~r
r3
(r > a)
(2.138)
φ(~r) = φ0 (~r) +
p~~r
a3
(r < a)
(2.139)
46
Das elektrische Feld im Inneren der Kugel beträgt also
~ r) = E
~ 0 (~r) − p~ = E
~ 0 (~r) − 4π P~ (~r).
E(~
3
a
3
(2.140)
Das Feld im Inneren der Kugel ist homogen, was mit dem Ansatz einer
homogenen Polarisation verträglich ist. Der Wert von P~ kann jetzt aus der
Materialgleichung bestimmt werden. Für ein isotropes Material muss gelten
~ = χ(E
~ 0 − 4π P~ )
P~ = χE
3
oder
P~ =
χ
3 ε−1~
~
E0 .
4π E0 =
4π ε + 2
1+ 3 χ
(2.141)
(2.142)
~ Feld im Inneren der Kugel beträgt
Das E~ 0.
~ =E
~ 0 − 4π P~ = 3 E
E
3
ε+2
(2.143)
~ < |E
~ 0 |. Der Zusatzterm − 4π P~ heißt Depolarisationsfeld.
Weil ε > 1 gilt |E|
3
Der Ansatz homogener Polarisation führt auch für ein homogenes dielektrisches Ellipsoid zum Ziel. Für andere Geometrien sind die Lösungen des
dielektrischen Randproblem sehr viel komplizierter.
Beispiel 3: Das Hohlraumfeld
Eien mathematische triviale Variante des vorherigen Beispiels erhält man
dadurch, dass man einen kugelförmigen Hohlraum (ε = 1) in einem ”unendlichen” Dielektrikum mit dielektrischer Konstante ε betrachtet. Weit
~ ∞ haben. Näher am Hohlraum
weg vom Hohlraum soll das Feld den Wert E
sollte man das Feld der ”fehlenden” Kugel spüren. Wir setzen also an
~ r − p~0~r
φ(~r) = −E~
r3
(r > a)
(2.144)
Im Inneren setzen wir ein homogenes Feld an
~ c~r
φ(~r) = −E
(r < a)
(2.145)
~c E
~ ∞)
Aus der Stetigkeit von φ folgt (für p~0 E
E∞ +
p0
= Ec
a3
(2.146)
2p0
) = Ec
a3
(2.147)
und aus der Stetigkeit von Dn
ε(E∞ −
47
Elimination von p0 aus den beiden Gleichungen liefert
Ec =
3ε
E∞ ,
2ε + 1
(2.148)
also immer größer als E∞ . Für das Dipolmoment der fehlenden Polarisation
erhält man
ε−1 3
p0 =
a E∞ .
(2.149)
2ε + 1
Das lokale Feld
In den obigen Beispielen haben wir innerhalb eines Dielektrikums konstante
oder wenigstens räumlich schwach variierende Felder gefunden. Dies kann
natürlich nur auf einer groben, makroskopischen Skala richtig sein, nicht
aber auf der atomaren Skala, wo man rasche Variationen des Feldes erwarten sollte. Diese Variationen sind nicht nur von akademischen Interesse;
sie spielen eine Rolle, wenn man versucht, die dielektrischen Eigenschaften
von dichten Medien (z.B. Flüssigkeiten oder Festkörpern) aus denjenigen von
atomaren oder molekularen Bausteinen herzuleiten. Als einfachstes Beispiel
betrachten wir nach Lorentz ein kubisches Gitter, auf dem sich Moleküle mit
molekularer Polarisierbarkeit α befinden:
~ loc
P~mol = αE
~ loc das Feld am Ort des Atoms darstellt.
wobei E
höherer Multipolmomente gilt also
(2.150)
Bei Vernachlässigung
~ loc
P~ = nαE
(2.151)
~ loc mit dem makroskopiswobei n die Dichte der Moleküle darstellt. Falls E
~ identifizierbar wäre, würde also gelten
chen Feld E
χ = nα
ε = 1 + 4πnα
(falsch)
(2.152)
Zur Berechnung des tatsächlichen Zusammenhangs bringen wir um den Mittelpunkt eines Moleküls eine Kugeloberfläche mit Radius groß gegenüber
der Gitterkonstante, aber klein gegenüber den Abstäden, innerhalb denen
~ variiert an. Das Feld E
~ loc setzt sich zusamdas makroskopische Feld E
men aus Beiträgen der Dipole außerhalb und innerhalb der Kugel (die eine
~ loc = E
~ f ern + E
~ nah . Den
reine mathematische Hilfskonstruktion darstellt): E
Beitrag der fernen Moleküle kann man makroskopisch berechnen. (Die Mulitpolentwicklung zeigt ja, dass in genügend großer Entfernung die Details der
48
Ladungsverteilung irrelevant werden). Das Feld eines unendlich homogenen
polarisierten Körpers mit ausgesparter Kugel beträgt
~ f ern = E
~ −E
~ Kugel .
E
(2.153)
Im Beispiel 1 haben wir gefunden, dass im Inneren der Kugel gelten muss
~ Kugel = − 4π P~
E
3
(2.154)
also
~ f ern = E
~ + 4π P~ = (1 + 4π χ)E
~ = ε + 2 E.
~
E
(2.155)
3
3
3
Dieses Feld ist nicht identisch mit dem in Beispiel 3 berechneten Hohlraumfeld! Dort war der ausgesparte Raum ein echtes physikalisches ”Loch”, das
~ f ern
die Homogenität im Außenraum zerstörte. Wir bemerken noch, dass in E
der Radius der ausgesparten Kugel nicht eingeht.
@
@
¡
¡
I
@
@
¡
@
I
@¡
I
@
@
¡
@
I
@¡
I
@
@
¡
@
I
@¡
I
@
@
¡
@
I
@¡
¡
¡
@
@
~ nah müssen wir die Beiträge der einzelnen Dipole inZur Berechnung von E
nerhalb der Kugel aufsummieren. Diese kommen wegen der Symmetrie des
Gitters immer in Gruppen von acht Stück auf den Eckpunkten eines Würfels
~ Felder
mit dem Mittelpunkt im Ursprung vor. Wir zeigen jetzt, dass die Eeiner solchen Gruppe sich genau zu Null addieren. Die x- Komponente des
Feldes eines Dipols am Ort ~r(x, y, z) beträgt (im Ursprung)
Ex =
3(x2 px + xypy + xzpz ) − r2 px
r5
(2.156)
Wenn die Beiträge von (±x, ±y, ±z) (8 Kombinationen) aufsummiert werden, kürzen sich die Beiträge proportional zu py und pz sofort, und die
Beiträge proportional zu px wegen x2 = 13 r2 (Gleichheit der Kanten des
49
Würfels). Dieselbe Rechnung lässt sich natürlich für Ey und Ez genauso
durchführen. Wir erhalten also auf Grund der Symmetrie des Problems
~ nah = 0
E
(2.157)
~ loc = E
~ f ern + E
~ nah = ε + 2 E
~
E
(2.158)
3
Das Ergebnis für ein kubisches Gitter wird im Mittel auch für eine Flüssigkeit
oder für einen isotropen amorphen Festkörper gelten. Für den Zusammenhang zwischen Polarisation und Feld erhalten wir also
¶
µ
Eloc
ε+2
χ = nα
= nα
(2.159)
E
3
oder auch
µ
¶
ε−1
ε+2
= nα
(2.160)
4π
3
ε−1
4π
=
nα (kubische Materialien)
(2.161)
ε+2
3
Dies ist die berühmte Clausius-Mossotti Beziehung. Für nicht-kubische Ma~ nah
terialien kann man ähnliche, aber nich identische Beziehungen herleiten (E
ist nicht mehr Null!). Physikalisch ist es nicht immer gerechtfertigt für α die
Suszeptibilität des Moleküls in der Gasphase einzusetzen; in Flüssigkeiten
oder Festkörpern können Moleküle etwas ”zerquetscht” werden, was auch
ihre Suszeptibilität ändern kann. Zum Schluss bemerken wir noch, dass die
Clausius-Mossotti Beziehung für 4π
nα > 1 keine Lösung mehr hat; wenn
3
diese Größe von unten nach Eins strebt, geht ε nach unendlich, d.h. auch ein
infinitesimal kleines Feld kann eine endliche Polarisation hervorrufen (spontane Polarisation; Ferroelektrizität). Allerdings bricht schon für niedrige
Werte das einfache physikalische Bild, das der Clausius-Mossotti Beziehung
zu Grunde liegt, zusammen; die starken elektrostatischen Kräfte können zur
Verzerrung des Gitters führen, die Linearität der Beziehung zwischen p~ und
~ loc ist nicht länger gesichert und Schwankungen in Größe und Richtung der
E
individuellen molekularen Dipole können nicht länger vernachlässigt werden.
Schlussbemerkung: Einheitensysteme
~ und D
~ im Vakuum physikalisch
Aus dem Vorhergehenden folgt, dass die Felder E
identisch sind. Im MKSA-Einheitensystem sind die beiden Größen mit verschiedenen Dimensionen behaftet und unterscheiden sich auch im Vakuum
durch die ”Naturkonstante” ε0 . Dies hat messtechnische Vorteile, kann aber
das Verständnis des physikalischen Sachverhalts etwas erschweren. Eine
schöne Parabel über diese Frage findet man in:
HBG Casimir, Helvetica Physica Acta 41 (1968) 741.
50
2.5
Magnetostatik
Das Grundproblem der Magnetostatik, das heißt die Lösung der Geleichungen
~ =0
~ = 4π ~j
∇B
∇×B
(2.162)
c
wurde schon beim Hauptproblem der Vektoranalysis mit dem Ansatz
~ =∇×A
~ gelöst. Unter der Nebenbedingung ∇A
~ = 0 ist die Lösung
B
Z
1 ~j(~r0 )d3~r0
~
A(~r, t) =
(2.163)
c
|~r − ~r0 |
Diese Lösung gilt nur, falls ∇~j = 0 (sonst ergibt sich ein Widerspruch mit
~ = 0). Dies ist aber in der Statik wegen ∇~j = − ∂ρ immer erfüllt. Die
∇×B
∂t
~ = 0:
obige Lösung erfüllt dann auch die Nebenbedingung ∇A
Z ~ 0 3 0 Z
3 0
j(~r )d ~r
~j(~r0 )∇ d ~r
∇
=
|~r − ~r0 |
|~r − ~r0 |
Z
Z h
i d3~r0
3 0
d
~
r
0
0
0~ 0
= − ~j(~r )∇
=
∇
j(~
r
)
=0
(2.164)
|~r − ~r0 |
|~r − ~r0 |
~ Feld findet man aus Gl.2.163:
Für das BZ
~j(~r0 ) 3 0 1 Z ~j(~r0 ) × (~r − ~r0 ) 3 0
1
~
~
B =∇×A=
∇×
d ~r =
d ~r
c
|~r − ~r0 |
c
|~r − ~r0 |
(2.165)
was eine Erweiterung des Biot-Savartschen Gesetzes auf kontinuierlich verteilte
Ströme darstellt.
Die magnetostatische Multipolentwicklung
Wir betrachten jetzt das Vektorpotential einer lokalisierten stationären Stromverteilung,
und entwickeln wie vorher den Faktor |~r − ~r0 |−1 um ~r0 = 0:
Z
Z
~r
1
0 3 0
ji (~r )d ~r + 3 ~r0 ji (~r0 )d3~r0 + ...
(2.166)
Ai (~r) =
cr
cr
die höheren Terme werden wir nicht explizit berücksichtigen. Zur Umformung dieser Integrale benützen wir eine Identität für ein quellenfreies, nur
im Endlichen von Null verschiedenes Vektorfeld ~j(~r) und zwei willkürliche
skalare Felder f (~r) und g(~r):
Z
f (~r)~j(~r)∇g(~r) + g(~r)~j(~r)∇f (~r)d3~r = 0
(2.167)
51
Der Beweis erfolgt durch partielle Integration:
Z
Z
Z
Z
3
3
3
~
~
~
f j∇gd ~r = − g∇(f j)d ~r = − gf ∇jd ~r − g~j∇gd3~r,
(2.168)
wobei der erste Term wegen ∇~j = 0 verschwindet. Einsetzen von f = 1 und
g = ri liefert
Z
Z
~j(~r)∇ri d3~r = ji (~r)d3 r = 0
(2.169)
und zeigt also das Verschwinden des ersten Terms in Gl.2.166. Einsetzen von
f = ri und g = rj liefert
Z
(ri jj + rj ji )d3~r = 0
(2.170)
also
Z
~r
Z
0
3
~r ji d ~r = rj
1
= − rj ²ijk
2
Z
rj0 ji (~r0 )d3~r0
1
= − rj
2
Z
1
(~r × ~j(~r0 ))k d3~r = − (~r ×
2
0
(ri0 jj − rj0 ji )d3~r0
(2.171)
Z
~r0 × ~j(~r0 )d3~r0 )i .
Mit der Definition des magnetischen Dipolmoments m
~
Z
1
m
~ =
~r × ~j(~r)d3~r
2c
(2.172)
(2.173)
reduziert sich Gl.2.166 damit zu
~ × ~r
~ r) = m
A(~
r3
~ Feld ist
Das zugehörige Bµ
¶
∂
m
~ × ~r
∂
∂ 1
Bi = ²ijk
= −²ijk
²klm ml
=
3
∂rj
r
∂rj
∂rm r
k
µ
¶
µ
¶
∂ ∂
1
∂ ∂ 1
2
−mi ∇ +
mj
=
mj
für ~r 6= 0
∂ri ∂rj
r
∂ri ∂rj r
Wir erkennen hier den Dipoltensor Tij =
~ = Tm
B
~
(2.175)
∂ ∂ 1
:
∂ri ∂rj r
~ = T p~
analog zu E
52
(2.174)
(2.176)
Diese Analogie hat zur Bezeichnung magnetisches Dipolmoment geührt. Das
kanonische Beispiel einer Verteilun, die ein magnetisches Dipolmoment besitzt, ist ein Kreisstrom mit dem Radius a und der Stärke j0 ; m
~ steht offensichtlich senkrecht zur Stormebene und hat den Wert
1
m=
2c
Z2π
aj0 a dφ =
πa2
j0 .
c
(2.177)
0
Dipoldichte (Magnetisierung)
~ (~r).
Als nächstes betrachten wir eine kontinuierliche Verteilung von Dipolen M
Deren Vektorpotential ist offensichtlich
Z
~ r) =
A(~
1
~ (~r ) × ∇
M
d3~r0 =
|~r − ~r0 |
0
0
Z
~ (~r0 )
∇0 × M
d3~r0
|~r − ~r0 |
(2.178)
Es ist zu beachten, dass beim ”Herüberbringen” des ∇× mittels partieller
Integration kein Minuszeichen entsteht:
¸
µ
¶
·Z
¶
Z
Z µ
Z
∂
∂
∂
~a × ∇f = ²ijk aj
f = −²ijk
aj f = f ²ijk
aj
Ii =
∂rk
∂rk
∂rk
i
(2.179)
~
Mit der Magnetisierung (magnetische Dipoldichte) M (~r) korrespondiert also
eine effektive Stromdichte
~ (~r)
~jM (~r) = c∇ × M
(2.180)
Diese Darstellung ist hier nur für eine Dipoldichte hergeleitet worden; wegen
∇~j = 0 ist sie aber für jede Stromverteilung im Prinzip möglich. Für den
Strom der freien Ladungsträger ist eine Darstellung gemäß Gl.2.180 aber
nicht sehr nützlich. Im allgemeinsten Fall lässt sich die Stromdichte ~j(~r) also
schreiben als
~ (~r)
~j(~r) = ~jf (~r0 ) + c∇ × M
(2.181)
(im stationären Fall). Im zeitabhängigen Fall kann man auch noch eine
Polarisationsstromdichte haben:
~ (~r, t) + ∂ P~ (~r, t).
~j(~r, t) = ~jf (~r, t) + c∇ × M
∂t
(2.182)
Einsetzen in die vierte Maxwellgleichung ergibt
~
~
~ − 1 ∂ E = 4π ~jf + 4π∇ × M
~ + 4π ∂ P
∇×B
c ∂t
c
c ∂t
53
(2.183)
~ =E
~ + 4π P~ auch noch das zweite
Wenn wir neben dem früher eingeführten D
Hilfsfeld
~ =B
~ − 4π M
~
H
(2.184)
einführen, so reduziert sich obiger Ausdruck zu
~
~ − 1 ∂ D = 4π ~jf .
∇×H
c ∂t
c
(2.185)
~ hat sich die Bezeichnung ”magnetisches Feld” eingebürgert
Für die Größe H
~ sondern B
~ die fundamentale magnetische Feldgröße ist).
(obwohl nicht H
Insgesamt findet man also für die makroskopischen Maxwellgleichungen
~ = 4πρf
∇D
(2.186)
~ =0
∇B
(2.187)
~
~ + 1 ∂B = 0
∇×E
(2.188)
c ∂t
~
~ − 1 ∂ D = 4π ~jf
∇×H
(2.189)
c ∂t
c
Diese Gleichungen bilden zusammen mit Material- oder Verknüpfungsgleichungen
~ = D(
~ E,
~ B),
~ H
~ = H(
~ E,
~ B)
~ ein lösbares System.
D
In der Magnetostatik gelten die Gleichungen
~ = 4π ~jf
∇×H
c
~ =0
∇B
(2.190)
Auf einer Oberfläche zwischen zwei Medien, auf der sich keine freien Ladungsträger
befinden, soll deshalb gelten:
Bn ist stetig; Htg ist stetig.
Die magnetische Suszeptibilität
Für einfache isotrope Materialien (mit der wichtigen Ausnahme der Ferro~ eine lineare Funktion von B:
~
magneten) ist M
~ = χm B
~
M
~ = (1 − 4πχm )B
~
H
(2.191)
~ aber nicht in B
~ sondern in H
~ ausgedrückt:
Üblicherweise wird M
~ = κH
~
M
~ = (1 + 4πκ)H
~ = µH
~
B
(2.192)
Die Größen κ und µ heißen magnetische Suszeptibilität bzw. Permeabilität.
Der mathematische Zusammenhang ist einfach:
κ=
χm
1 − 4πχm
µ=
54
1
1 − 4πχm
(2.193)
Die übliche Formulierung hat den Vorteil, dass magnetostatische Probleme
mit ~jf = 0 sich direkt auf elektrostatische Analoga abbilden lassen (einschließlich der Randbedingungen)
~ ↔H
~
E
~ ↔B
~
D
~
P~ ↔ M
² ↔ µ.
(2.194)
Der einzige Unterschied ist, dass µ, im Gegensatz zu ², sowohl größer als
auch kleiner als Eins sein kann. Materialien mit µ < 1 heißen diamagnetisch,
solche mit µ > 1 heißen paramagnetisch.
55
2.6
Die magnetische Energie
Die elektrostatische Energie einer Ladungsverteilung ist gleich der Energie,
die man aufbringen muss, um die Ladungen aus einer Vergleichskonfiguration, in der alle Punktladungen unendlich weit voneinander entfernt sind,
in die vorgeschreibene Konfiguration zu bringen. Dabei bewegen sich die
Ladungen zum Teil in Richtung der elektrischen Felder; somit ist der Beitrag
eines Teilchens zur elektrostatischen Energie als ein Wegintegral
Zr
Zt
~ (i)
Ui = −ei
0
0
~ (i) (~r0 , t0 )~v (t0 )dt0
E
0
E (~r , t )d~r = −ei
∞
(2.195)
t0
~ (i) das Feld der übrigen, festgehaltenen Ladungen ist
zu schreiben, wobei E
und ~r0 (t0 ) die Bahn entlang der das Teilchen mit der Ladung ei im Zeitintervall (t0 , t) aus dem Unendlichen zum Ort ~r gebracht wird.
Die magnetischen Beiträge zur Energie des Systems können nicht als die
Arbeit verstanden werden, die von den magnetischen Feldern geleistet wird.
Die Lorentzkraft
e~v
~ r)
F~L =
× B(~
(2.196)
c
steht immer senkrecht zur Geschwindigkeit des Teilchens und leistet daher
keine Arbeit. Andererseits wirken während des Einschaltens der für das Magnetfeld verantwortlichen Ströme elektrische Induktiosfelder, die sehr wohl Arbeit leisten können. Magnetische Energie ist letztendlich Arbeit, die von den
~ Feldes, geleistet
Induktionsfeldern, das heißt vom quellenfreien Anteil des Ewird. Sie ist also im Rahmen der Magnetostatik nicht wirklich befriedigend
zu behandeln.
Wir betrachten zuerst einen festen Stromkreis, in dem der Strom von Null
auf den Wert J hochgefahren wird. Der Strom J(t) erzeugt eine magnetische
~ r, t) und damit ein Induktionsfeld mit ∇ × E
~ = − 1 ∂ B~ . Die vom
Induktion B(~
c ∂t
Induktionsfeld geleistete Arbeit ist
dUm
= −I(t)
dt
I
ZZ
~ ~l = −I
Ed
C
~ 2O
~ =I
∇ × Ed
c
S
ZZ
~
∂B
~
d2 O
∂t
(2.197)
wobei S eine durch den Stromkreis C berandete Fläche ist. Einsetzen von
~ = ∇×A
~ erlaubt es, das Integral wieder auf ein Linienintegral zu reduzieren:
B
I
c
ZZ
S
~
∂B
~ =I
d2 O
∂t
c
ZZ
~
∂A
~ =I
∇×
d2 O
∂t
c
56
I
C
~
∂A
d~l
∂t
(2.198)
Dieser Ausdruck kann jetzt von einem einzelnen Stromkreis auf eine kontinuirliche Stromverteilung verallgemeinert werden
Z
Z
~ r, t)
~
dUm
1 ~
∂ A(~
1
3
~ ∂ A(~r, t) d3~r.
=
j(~r, t)
d ~r =
(∇ × B)
(2.199)
dt
c
∂t
4π
∂t
Bei der Herleitung der magnetischen Feldenergie ist ein Term in dUm /dt
weggelassen worden. Dieser beträgt (für ε = 1)
Z ~ ~
1
∂E ∂A 3
−
d ~r
(2.200)
4πc
∂t ∂t
Als erstes bemerken wir, dass der Term beliebig klein wird, wenn das Hochfahren
der Ströme beliebig langsam durchgeführt wird. Der Term kann aber zur stationären Feldenergie überhaupt keinen Beitrag liefern:
~ + 1 ∂ A~ ) = 0.
Die dritte Maxwellgleichung kann geschrieben werden als ∇ × (E
c ∂t
~ als auch A
~ divergenzfrei sind, bzw. gewählt
Weil in unserem Fall sowohl E
werden können, kann man den obigen Term schreiben als
Z ~
Z
1
∂E ~ 3
1 d
~ 2 d3~r.
Ed ~r =
|E|
(2.201)
4π
∂t
8π dt
~ konstant ist, und E
~ deshalb verWeil im Anfangs- wie im Endzustand B
schwindet, gibt der oben erwähnte Term nach Integration über t keinen
Beitrag zu Um .
Patielle Integration liefert (vgl. Gl. 2.178) für lokalisierte Ströme
· Z
¸
Z
Z
~
~
dUm
1
∂A
1
∂B
d 1
3
3
2 3
~
~
~
=
B(∇ ×
)d r =
B
dr=
B d ~r .
dt
4π
∂t
4π
∂t
dt 8π
(2.202)
~
Falls wir die magnetische Feldenergie für j := 0 gleich Null setzen, erhalten
wir also
Z
1
~ r)|2 d3~r
Um =
|B(~
(2.203)
8π
Der Ausdruck ist ganz analog zum Ausdruck für die elektrostatische Energie;
insbesondere spielt es keine Rolle, wie rasch oder langsam man den Strom
anwachsen lässt; die Energie hängt nur von der Endkonfiguration der Ströme
ab.
Wenn die Ströme sich nicht im Vakuum befinden, sondern es auch noch
magnetisierbare Substanzen gibt, so soll in der obigen Herleitung nur ~jf
~ substituiert werden. Dies führt zu
~j soll ∇ × H
auftreten und für 4π
c f
1
Um =
4π
Zt Z
~
~ r, t0 ) ∂ B(~r, t) dt0 d3~r
H(~
∂t
−∞
57
(2.204)
Für isotrope Materialien mit der Permeabilität µ führt dies zu
Z
1
~ r, t)B(~
~ r, t)d3~r
Um =
H(~
8π
(2.205)
Für reale Meaterialien, in denen die Magnetisierung sich nicht sofort dem
~ Feld anpassen kann, muss Gl.2.204 verwendet werden. In dem Fall ist
BUm zwar die von den Induktionsfeldern geleistete Arbeit; man braucht aber
eine seperate Überlegung, um festzustellen, ob diese Arbeit in der Feldenergie ”gespeichert” ist oder villeicht schon im magnetisierbaren Material in
Wärme umgesetzt worden ist. Solche Fragen sind allerdings Gegenstang der
Thermodynamik und sollen hier nicht weiter diskutiert werden.
Zwischenbemerkung über die elektrostatische Energie
Auch für die elektrostatische Energie in Anwesenheit von Dielektrika kann
man zu Gl.2.204 und Gl.2.205 analoge Ausdrücke herleiten. Die Änderung
der elektrostatischen Energie auf Grund einer infinitesimalen Änderung der
freien Ladungsträger beträgt
Z
Z
dUe
∂
∂ρf (~r, t)
1
3
~ 3~r =
φ (∇D)d
=
φ(~r, t)d ~r =
dt
∂t
4π
∂t
1
−
4π
Z
~
∂D
1
∇φ
d3~r =
∂t
4π
Z
~
~ ∂ D d3~r,
E
∂t
~ = εE)
~ zu
was für isotrope lineare Dielektrika (D
Z
1
~ r)E(~
~ r)d3~r
D(~
Ue =
8π
(2.206)
(2.207)
~ nicht instantan
führt. Auch hier gibt es Komplikationen, falls P~ dem Feld E
folgen kann.
Alternative Ausdrücke für die magnetische Energie im Vakuum
Für den für Ströme im Vakuum gültigen Ausdruck
Z
Z
1
1
2
3
~ (~r)d r =
~
~ 3r
B
B(∇
× A)d
(2.208)
Um =
8π
8π
kann man über eine partielle Integration (für eine auf einem endlichen Bereich
beschränkte Stromverteilung) den alternativen Ausdruck
Z
Z
1
1
3
~
~
~ r)d3~r
~j(~r)A(~
Um =
(∇ × B)Ad ~r =
(2.209)
8π
2c
58
~ als Funktion von ~j liefert
erhalten. Einsetzen des Ausdrucks für A
ZZ ~ ~ 0
1
j(~r)j(~r ) 3 3 0
Um = 2
d ~rd ~r .
2c
|~r − ~r0 |
(2.210)
Für eine auf N Stromkreise Ci mit Strömen Ji lokalisierte Stromverteilung
ergibt dies
I
N I
1 X
1X
Ii Ij ~ ~
Li,j Ii Ij
Um = 2
d
l
d
l
=
i
j
2c i,j=1 C1 C2 |~r − ~r0 |
2 i,j
(2.211)
wobei d~li ein Längenelement entlang dem i-ten Stromkreis ist. Die rein geometrischen Koeffizienten
I I
d~li d~lj
1
Lij = 2
(2.212)
c Ci C2 |~r − ~r0 |
heißen Induktivitätskoeffizienten. Offenbar gilt Lij = Lji . Die Größe Lii heißt
die Selbstinduktivität des i-ten Stromkreises, die Größe Lij heißt wechselseitige Induktivität der Stromkreise i und j.
Die Koeffizienten Lij geben auch den Zusammenhang zwischen den Strömen
Ii und dem Induktionsfluss φj durch den Stromkreis j. Letzterer ist definiert
als
ZZ
~ r)d2 O
~
φi =
B(~
(2.213)
Si
~ = 0).
für eine willkürlich durch Ci berandete Fläche (willkürlich wegen ∇B
Durch Spezialisierung von
Z
1
~ 3~r
~j Ad
Um =
(2.214)
2c
auf den Fall von N Stromkreisen erhält man
I
ZZ
X
1 X
1 X
~
~ = 1
~
~ 2O
Um =
Ii
Adl =
Ii
Bd
Ii φi
2c i
2c i
2c i
Ci
Si
(2.215)
und Vergleich mit dem oben erhaltenen Ausdruck erhält man
N
X
1
φi =
Lij Ij
c
j=1
(2.216)
(Genau betrachtet könnte man hier zu Lij noch eine willkürliche antisymmetrische Matrix addieren. Die Symmetrie von Lij lässt sich aber genauso
59
beweisen wie die Symmetrie von Cij ).
Magnetische Wechselwirkungsenergie
Wir teilen jetzt die Stromdichte ~j(~r) auf gemäß ~j(~r) = ~j0 (~r) + ~j1 (~r), wobei
~j0 (~r) die, festgehaltenen Erzeuger des ”äußeren Vektorpotentials” und ~j1 (~r)
die Stromverteilung in einem ”Testkörper” darstellen. Es gilt dann
Z
1
~0 + A
~ 1 )d3~r
Um =
(~j0 + ~j1 )(A
(2.217)
2c
~ 0 und A
~ 1 die von ~j0 bzw. ~j1 erzeugten Vektorpotentiale sind. Ausarwobei A
beiten dieses Ausdrucks liefert
Z
Z
Z
1
1
1
3
3
~ 0 d ~r +
~ 1 d ~r +
~ 0 d3~r
~j0 A
~j1 A
~j1 A
Um =
(2.218)
2c
2c
c
wobei wir die leicht beweisbare Identität
Z
Z
3
~
~ 1~j0 d3~r
~j1 A0 d ~r = A
(2.219)
benutzt haben. Der interessante Term in Gl.2.218 ist die Wechselwirkungsenergie
Z
1 ~ ~ 3
Um0 =
j1 A0 d ~r
(2.220)
c
Für eine lokalisierte Stromverteilung liegt es nahe, eine Multipolentwicklung
durchzuführen. Die etwas langwierige Rechnung kann ”kurzgeschlossen” werden, in dem man einsetzt
~ 1 (~r)
~j1 (~r) = c∇ × M
Man erhält so
Z
Um0 =
(2.221)
Z
~ 1 )A
~ 0 d3~r =
(∇ × M
oder
~ 1 (∇ × A
~ 0 )d3~r
M
(2.222)
Z
Um0 =
~ 1 (~r)B
~ 0 (~r)d3~r
M
(2.223)
Insbesondere erhält man für einen Punktdipol m
~ 1 in ~r
~ 0 (~r).
Um0 = m
~ 1B
(2.224)
Das Vorzeichen ist also genau das entgegengesetzte desjenigen im analogen
elektrostatischen Ausdruck
~ 0 (~r)
Ue0 = −~pE
60
(2.225)
Der Ausdruck (2.224) darf nicht dazu benutzt werden, die Kraft und das
~ 0 (~r) zu bestimmen.
Drehmoment auf den Dipol im vorgegebenen Magnetfeld B
Falls der Dipol verschoben oder gedreht wird, ändert sich nämlich der Fluss
~ 0 erzeugen. Um trotzdem den Strom
φ durch die Stromkreise, die das Feld B
~j0 aufrechtzuerhalten, muss Energie geleistet werden; auch diese Energie ist
in Um0 enthalten. Kraft und Drehmoment auf eine Stromverteilung in einem
vorgegebenen Feld berechnet man aus der Dichte der Lorentzkraft:
~k(~r) = 1~j1 (~r) × B
~ 0 (~r).
c
(2.226)
~ 1 ergibt das
Für ~j1 = c∇ × M
ki = ²ijk ²jlm (
∂
∂
∂
M1m )B0k = (
M1i )B0j − ( M1j )B0j
∂rl
∂rj
∂ri
(2.227)
Also für die Gesamtkraft:
Z
Z
3
~
~
~ 0) + M
~ 1 (∇B0i ))d3~r.
Ki = (B0 ∇M1i − B0i (∇M1 ))d ~r = (−M1i (∇B
(2.228)
Der erste Term verschwindet indentisch; der zweite liefert einen Punktdipol
Ki = m(∇B
~
0i )
also das genaue Analogon des elektrischen Ausdruckes.
Für das Drehmoment erhält man
Z
Z
1
3
~ 0 )d3~r
~ = ~r × ~k(~r)d ~r oder N
~ =
~r × (~j × B
N
c
Einsetzen der Identität ~a × (~b × ~c) = ~b(~a~c) − ~c(~a~b) liefert
Z
1
~
~ ~j − (~r~j)Bd
~ 3~r
N=
(~rB)
c
(2.229)
(2.230)
(2.231)
~ 0 - Feld lässt der erste Term sich genauso behandeln wie
Für ein homogenes B
~
der zweite Term in Gl.2.166. Das Ergebnis ist ~r/r3 → B(0):
~1 = m
~0
N
~ ×B
Im zweiten Term erscheint das Integral
Z
XZ
3
~
~rj(~r)d ~r =
ri ji (~r)d3~r,
i
61
(2.232)
(2.233)
das wegen der Identität
Z
ri jj + rj ji d3~r = 0
(2.234)
identisch verschwindet. Das gesamte Drehmoment ist also
~ =m
~ 0;
N
~B
(2.235)
dieser Ausdruck ist völlig analog zum Ausdruck
~ = p~ × E
~0
N
(2.236)
für das elektrische Analogon. Das Potentialfeld, aus dem sich die Kräfte und
Drehmomente im vorgegebenen Magnetfeld herleiten lassen, ist, wie man
auch allgemein zeigen kann,
Z
~ 1 (~r).B
~ 0 (~r)d3~r,
Vm = − M
(2.237)
also das Negative des Wechselwirkungsterms Um0 in der magnetischen Feldenergie.
Das unterschiedliche Vorzeichen der elektrischen und magnetischen Wechselwirkungsenergie trat auch schon in der Lagrangefunktion eines Teilchens
in elektrischen und magnetischen Feldern auf. Auf Seite 99 des Skriptums
Mechanik hatten wir gefunden
e ~
1
L = m~v 2 + ~v A.
2
c
(2.238)
Falls auch noch ein elektrostatisches Feld anwesend ist, so muss man wegen
L = T − V einen Term −eφ0 (~r) addieren:
1
e ~
L = m~v 2 + ~v A
0 − eφ0
2
c
(2.239)
In Kontinuumsschreibweise ergibt dies
Z
Z
1 ~ ~
3
L = Ekin +
j(~r)A0 (~r)d ~r − ρ(~r)φ0 (~r)d3~r = Ekin + Um0 − Ue0 (2.240)
c
Zur Klärung der Hintergründe gehen wir nochmals zum analogen elektrostatischen Problem zurück, und zwar zum im Zusammenhang mit dem Satz
von Thomson betrachteten System von N Leitern. Die elektrostatische Energie beträgt für dieses System
1X
Ue =
Qi Γij Qj .
(2.241)
2 ij
62
Die Matrix Γ ist eine rein geometrische Größe, die von der Form und der
relativen Lage der Leiter abhängt; diese seien mit den verallegemeinerten
Koordinaten Xk (k = 1, ..., M ) angedeutet. Die verallgemeinerte Kraft entlang der Koordinate Xk ist
¯
¯
X
X
¯
∂Γij
∂φi ¯¯
∂Ue ¯
Qi Qj
=−
Qi
(2.242)
Kk = −
=−
¯
∂Xk ¯Qk
∂Xk
∂Xk ¯
ij
i
Qk
wobei |Qk bedeuten soll, dass die Ableitungen bei konstanten Ladungen erfolgenPsollten; bei der letzten Umformung haben wir die Beziehung
φi = j Γij Qj benützt.
Die Größe Ue kann aber auch als Funktion der Potentiale aufgefasst werden:
Ue =
1X
φi Cij φj
2 ij
mit C = Γ−1
Die Ableitung von Ue nach Xk bei konstanten φa beträgt
¯
X ∂Cij
X ∂Cij
∂Ue ¯¯
Γil
φ
=
Γjm Ql Qm .
=
φ
j
i
∂Xk ¯φa
∂X
∂X
k
k
ij
ijlm
(2.243)
(2.244)
Jetzt nützen wir aus, dass Γ die Inverse von C ist
X ∂Cij
∂ X
∂Γjm
∂
(
Cij Γjm ) =
(
Γjm + Cij
)=
δim = 0
∂Xk j
∂X
∂X
∂X
k
k
k
j
(2.245)
Es gilt also
¯
X ∂Γlm
X
∂Ue ¯¯
∂Γjm
Q
Q
=
Ql
Qm
=
−
Γ
C
il
ij
l
m
∂Xk ¯φa
∂Xk
∂Xk
lm
ijlm
(2.246)
wobei wir die Symmetrie von C ausgenützt haben. Wir haben also letztendlich gefunden
¯
¯
¯
∂Ue ¯¯
∂Ue ¯¯
∂Ue ¯¯
=−
oder Kk =
(2.247)
∂Xk ¯φj
∂Xk ¯Qj
∂Xk ¯φj
Der unterschiedliche Energieaufwand ist natürlich die Energie, die benötigt
wird, um die Leiter trotz der Änderung der Geometrie auf demselben Potential zu halten durch Zuführung von Ladungen aus dem Unendlichen (φ = 0).
Diese Energie ist offenbar genau 2mal so groß wie die Energie, die für die
Änderung der Geometrie bei festen Ladungen nötig ist.
63
Kehren wir jetzt zurück zum magnetischen Fall mit N Stromkreisen. Die
magnetische Energie beträgt
Um =
1X
Ii Lij Ij .
2 ij
(2.248)
Wir können diese Energie aber auch in den Flüssen ausdrücken
X
φi = c
Lij Ij .
(2.249)
j
Der so erhaltene Ausdruck ist
1 X
Um = 2
φi Λij φj
c ij
mit
1
Λ = L−1
c2
(2.250)
Völlig analog zum elektrostatischen Fall kann man wieder herleiten
¯
¯
∂Um ¯¯
∂Um ¯¯
=−
(2.251)
∂Xk ¯φj
∂Xk ¯Ij
Das Potential, aus dem man die magnetischen Kräfte mittels der ”normalen”
Formel
∂Um
(2.252)
Kk = −
∂Xk
herleiten kann, ist also die magnetische Energie bei festgehaltenen Flüssen. In
diesem, nur für supraleitenden Stromkreisen realistischen Fall, brauchen die
Stromquellen tatsächlich keien Arbeit zu leisten. Falls wir dieselbe Änderung
der Geometrie bei festen Strömen durchführen wollen, so ist die für das
Konstanthalten der Ströme benötigte Energie offensichtlich genau 2mal der
Änderung der Feldenergie, was dann zum anomalen Vorzeichen führt. Auch
ein Vergleich der Herleitungen von Gl.2.202 und von dUe /dt in Gl2.206 zeigt,
dass die Flüsse in den magnetischen Formeln dort auftraten, wogegen die
Ströme die Rollen der Poteniale spielen.
Zum Schluss sei noch darauf hingewiesen, dass die Kräfte selbst natürlich
nicht davon abhängen, unter welchen Nebenbedingungen sie gemessen werden: Kräfte können durch Balanzieren gegen eine Feder, oder ein Gewicht,
gemessen werden, ohne dass eine tatsächliche Änderung der Koordinate auftritt.
64
3
3.1
Elektromagnetische Strahlung
Lösungen der freien Maxwellgleichung
In diesem Kapitel werden die zeitabhängigen Terme in den Maxwellgleichungen ernst genommen. Der einfachste Fall ist dann der Fall verschwindender
~j und ρ, oder der Fall eines homogenen Mediums mit verschwindendem ~jf
und ρf (wobei der Index f für ”frei” steht) und mit konstantem skalarem ε
und µ. Weil der letztere Fall formal den ersten einschließt, betachten wir die
freien Maxwellgleichungen
~ =0
ε∇E
(3.1)
~ =0
µ∇H
(3.2)
~
µ ∂H
=0
(3.3)
c ∂t
~
~ − ε ∂E = 0
∇×H
(3.4)
c ∂t
Wie schon in Absatz I.3 gezeigt wurde, erhält man Wellengleichungen durch
das Anwenden der Rotation auf die dritte und vierte Maxwellgleichung und
das Ausnützen der Identität
~+
∇×E
∇ × (∇ × ~c) = ∇(∇~c) − ∇2~c :
(3.5)
2~
~ − µ ∂ (∇ × H)
~ = −∇2 E
~ + µε ∂ E = 0
∇ × (∇ × E)
(3.6)
c ∂t
c2 ∂t2
2~
~ = −∇2 H
~ + µε ∂ H = 0
~ − ε ∂ (∇ × E)
(3.7)
∇ × (∇ × H)
c ∂t
c2 ∂t2
~ = 0 und ∇H
~ =0
Bei dieser Herleitung wurde auch noch die Bedingungen ∇E
~
~
verwendet. Jede Komponente von E und H gehorcht also der Wellengleichung
1 ∂ 2 ψ(~r, t)
c
∇2 ψ(~r, t) − 2
=0
v=√
(3.8)
2
v
∂t
εµ
deren Lösungen sich mit der Geschwindigkeit v fortpflanzende Wellen sind.
√
Im Vakuum gilt v = c; die Größe εµ heißt Brechungsindex und wird auch
mit n bezeichnet.
Spezielle Lösungen dieser Gleichung sind die ebenen Wellen. Wir setzen
zuerst an
~ r, t) = Re(E
~ ~ ei~k~r−iωt )
E(~
(3.9)
k
~ r, t) = Re(H
~ ~ ei~k~r−iωt )
H(~
k
65
(3.10)
~ ~ . Einsetzen in die Maxwell~ ~ und H
mit im allgemeinen komplexen Vektoren E
k
k
gleichungen ergibt
~k E
~~ = 0
(3.11)
k
~k H
~~ = 0
k
~k × E
~ ~ − µω H
~~ = 0
k
c k
~k × H
~~ = 0
~ ~ + εω E
k
c k
Als Beispiel der Herleitung diskutieren wir die erste Gleichung:
(3.12)
(3.13)
(3.14)
~ = Re(i~k E
~ ~ ei~k~r−iωt ) =
∇E
k
~ ~ ) cos(~k~r − ωt) − Re(~k E
~ ~ ) sin(~k~r − ωt) = 0
−Im(~k E
k
k
(3.15)
Diese Gleichung kann nur für alle ~r und t erfüllt sein, wenn Realteil und
~ ~ seperat verschwinden. Aus der Gl.3.13 oder Gl.3.14
Imaginärteil von ~k E
k
~ ~ bzw. H
~~:
erhält man durch Skalarmultiplikation mit E
k
k
~~ H
~
E
k ~k = 0
(3.16)
und durch Vektormultiplikation mit ~k
2
~k × (~k × E
~ ~ = − εµω E
~ ~ (3.17)
~ ~ ) = ~k(~k E
~ ~ ) − k2E
~ ~ = −k 2 E
~ ~ = µω ~k × H
k
k
k
k
k
k
c
c2
also die Beziehung
ω2 =
c2 k 2
n2
(3.18)
Für die weitere Diskussion legen wir die x-Achse entlang ~k. Aus den Gl.3.13
und 3.14 folgt dann (für ω > 0)
r
r
ck
ε
ε
H~kz =
E~ky =
E~ky
H~ky = −
E~
(3.19)
µω
µ
µ kz
~ ~ frei wählbar;
In unserem Ansatz sind also nur die zwei Komponenten von E
k
~ liegen damit fest.
die Komponenten von H
E~
Falls der Quotient E~ky eine reelle Zahl ist, welche als tan θ geschrieben werden
kz
~ Vektor zeigt immer entkann, so schwingen E~ky und E~kz in Phase und der Elang der Geraden in der y-z- Ebene, die einen Winkel θ mit der y-Achse ein~ Vektor zeigt immer entlang der dazu senkrechten Geraden in
schließt. Der Hder y-z- Ebene; die Welle heißt linear polarisiert. Ist das Verhältnis komplex,
66
z.B. tan θeiφ , so schwingen E~ky und E~kz mit verschiedener Phase; wie wir in
der Vorlesung Mechanik am Fall des isotropen harmonischen Oszillators gese~ Vektor eine Ellipse. Der H~ Vektor
hen haben (S.39), durchläuft dann der E◦
durchläuft ein um 90 gedrehte Ellipse mit demselben Achsenverhältnis. Die
Welle heißt dann elliptisch polarisiert. Der Spezialfall tan θ = 1, φ = ± π2
ergibt eine zirkular polarisierte Welle.
Die allgemeinste Lösung der freien Wellengleichungen ist also
Z
~
~ (+) ei~k~r−iωt + E
~ (−) ei~k~r+iωt )d3~r
E(~r, t) = (E
(3.20)
~k
~k
~ (+) und E
~ (−) zwei komplexe Vektoren sind, die nur den Bedingunwobei E
~k
~k
(±)
~
~
~ r, t), E
~ (±)∗ = E
~ (∓) untergen k E~k = 0, und wegen der Realität von E(~
~k
−~k
liegen. Letztere Bedingung kann hergeleitet werden durch die Verwendung
~ r, t) und Umbenennung der Indes komplex konjugierten der Gl.3.20 für E(~
~ r, t) schreibt man entsprechend
tegrationsvariablen von ~k in −~k. Für H(~
Z
~
~ (+) ei~k~r−iωt + H
~ (−) ei~k~r+iωt )d3~r
H(~r, t) = (H
(3.21)
~k
~k
mit
r
~ (+)
H
~k
~ (+)
E
~k
r
ε
~ (+)
=
k̂ × E
~k
µ
r
µ
~ (+)
=−
k̂ × H
~k
ε
~ (−)
H
~k
ε
~ (−)
k̂ × E
~k
µ
(3.22)
µ
~ (−)
k̂ × H
~k
ε
(3.23)
=−
r
~ (−)
E
~k
=
wobei k̂ der Einheitsvektor in der Richtung von ~k ist.
~ (+) und E
~ (−) folgen aus den Anfangswerten der Felder E
~
Die Koeffizienten E
~k
~k
~ Nach dem Fourierschen Satz gilt nämlich
und H.
Z
~ r, 0) =
E(~
Z
i~k~
r 3~
~~ e
E
k
~ r, 0) =
H(~
dk
~ ~ ei~k~r d3~k
H
k
(3.24)
~ r, 0)e−i~k~r d3~r
H(~
(3.25)
mit
~~ = 1
E
k
8π 3
Z
~ r, 0)e−i~k~r d3~r
E(~
~~ = 1
H
k
8π 3
Z
~ ~ und H
~ ~ lassen sich E
~ (+) und E
~ (−) bestimmen
Aus den so vorgegebenen E
~k
~k
k
k
mittels den Beziehungen
r
ε ~ (+) ~ (−)
(+)
(−)
~
~
~
~
E~k = E~k + E~k
k̂ × H~k = −
(E − E~k ),
(3.26)
µ ~k
67
die durch die Substitution von t = 0 in Gl.3.20/3.21 und den Beziehungen
~ (±) und H
~ (±) erhalten werden. Die Energie des elektromagnetiszwischen E
~k
~k
chen Strahlungsfeldes beträgt
Z
1
~ 2 (~r, t) + µH
~ 2 (~r, t))d3~r.
U=
(εE
(3.27)
8π
Die Auswertung des ersten Terms ergibt (für t = 0)
ZZZ
ε
~ (+)∗ + E
~ (−)∗ )(E
~ (+) + E
~ (−) )ei(~k−~k0 )~r d3~k 0 d3~kd3~r,
Ue =
(E
~k0
~k0
~k
~k
8π
was wegen
(3.28)
Z
~ ~0
ei(k−k )~r d3~r = 8π 3 δ(~k − ~k 0 )
(3.29)
geschrieben werden kann als
Z
Ue = επ
2
~ (+) + E
~ (−) |2 d3~k.
|E
~k0
~k0
(3.30)
Für den magnetischen Beitrag erhält man ebenso
Z
Z
(+)
(−)
2
2
3
2
~
~ | d ~k = επ
~ (+) + E
~ (−) |2 d3~k,
Um = µπ
|H
+H
|E
~k
~k
~k
~k
(3.31)
~ (±) und H
~ (±) benützt wurden. Die gesamte
wobei die Beziehungen zwischen E
~k
~k
Energie beträgt also
Z
2
~ (+) |2 + |E
~ (−) |2 d3~k.
(3.32)
U = 2επ
(|E
~k
~k
oder
1
1 ~~
~ H)
~
(εE 2 + µH 2 ) =
(D E + B
8π
8π
Die Energiedichte beträgt
U=
h
i
~
~
1 ∂D
∂u(~r, t)
~ + ∂ B H)
~ = c E(∇
~
~ − H(∇
~
~ .
=
(
E
× H)
× E)
∂t
4π ∂t
∂t
4π
(3.33)
(3.34)
Die Energie ist also aus Beiträgen der einzelnen räumlichen Fourierkomponenten zusammengesetzt. Für t 6= 0 substituiert man
~ (−) → E
~ (−) eiωt
E
~k
~k
~ (+) → E
~ (+) e−iωt
E
~k
~k
(3.35)
In den Ausdrücken für Ue und Um treten zeitabhängige Terme auf; der Ausdruck für U ist völlig zeitunabhängig. Weiter sind im Zeitmittel die Größen
68
Ue und Um einander gleich. In den elekromagnetischen Wellen wird also
ständig elektrische in magnetische Energie umgewandelt und umgekehrt,
genauso wie in Schwingungen einer Saite potentielle in kinetische Energie
umgewandelt wird. Die Gesamtenergie bleibt dabei selbstverständlich erhalten.
Man kann sich die Energieverhältnisse auch im Ortsraum ansehen. Für die
Änderung der lokalen Energiedichte erhält man durch Einsetzen der Maxwellgleichungen
=
∂ 1 ~2
~ 2 ) = c (E∇
~ ×H
~ − H∇
~ × E)
~
(εE + µH
∂t 8π
4π
(3.36)
c
∂
∂
c ∂
²ijk (Ei
Hk − Hi
Ek ) = −
(²jik Ei Hk )
4π
∂rj
∂rj
4π ∂rj
(3.37)
wobei im zweiten Term die Indizes i und k umbenannt wurden. Das Ergebnis
lässt sich also schreiben als
∂
~ r, t)
u(~r, t) = −∇S(~
∂t
(3.38)
wobei
~ r, t) = c E(~
~ r, t) × H(~
~ r, t)
S(~
(3.39)
4π
der sogenannte Poynting - Vektor ist, der den Energiestrom im Strahlungsfeld
darstellt.
In Anwesenheit einer freien Stromdichte ~jf (~r, t) erhält man
∂
~ r, t) − E
~ ~jf (~r, t)
u(~r, t) = −∇S(~
∂t
(3.40)
Der Zusatzterm entspricht der vom Feld geleisteten Arbeit und der obige
Satz (Poyntingscher Satz) ist als ein Spezialfall des Energieerhaltungssatz
anzusehen.
Neben der Energie trägt das Strahlungsfeld auch Impuls (und Drehimpuls,
aber dieser wird in dieser Vorlesung nicht betrachtet). Weil die Definition des
Feldimpulses in Medien einer gewissen Willkür unterliegt und zum Teil noch
kontroverst ist, beschränken wir uns bei der Betrachtung des Impuslsatzes auf
das Feld im Vakuum, d.h. auf die mikroskopischen Maxwellgleichungen. Der
vom Feld pro Volumselement übertragene Impuls ist gleich der Kraftdichte
"
#
~
1
1
∂
E
1
~k(~r) = ρE
~ E
~ + (∇ × B
~−
~ .
~ =
~ + ~j × B
(∇E)
)×B
(3.41)
c
4π
c ∂t
69
Verwendet man die Identität
~
~
~ × ∂ E = − ∂ (E
~ × B)
~ +E
~ × ∂ B = − ∂ (E
~ × B)
~ − cE
~ × (∇ × E)
~ (3.42)
B
∂t
∂t
∂t
∂t
erhält man
~k(~r) + 1 ∂ (E
~ × B)
~
4πc ∂t
i
1 h~
~ + B(∇
~ B)
~ −B
~ × (∇ × B)
~ −E
~ × (∇ × E)
~
E(∇E)
(3.43)
4π
~ B)
~ nur dazu dient, dem Auswobei der ohnehin verschwindende Term B(∇
druck ein etwas schöneres Aussehen zu geben. Wir identifizieren jetzt versuchsweise den Ausdruck
1 ~
~
~g =
E×B
(3.44)
4πc
mit der Impulsdichte des elektromagnetischen Feldes. Das ist nur dann
gerechtfertigt, wenn jede Komponente des Ausdrucks der rechten Seite in
Gl.3.43 als Divergenz eines Stromes dargestellt werden kann. In der Tat gilt
z.B.
¶
¶
µ
µ
h
i
∂Ey ∂Ex
∂Ex ∂Ez
~
~
~
~
~
E(∇E) − E × (∇ × E) = Ex ∇E−Ey
−
+Ez
−
∂x
∂y
∂z
∂x
x
µ
¶
∂ 1 2 1 2 1 2
∂
∂
=
Ex − Ey − Ez +
(Ex Ey ) + (Ex Ez )
(3.45)
∂x 2
2
2
∂y
∂z
=
also die Divergenz eines Vektors. Allgemein gilt
ki (~r) +
wobei
∂
∂
gi (~r) =
Tij
∂t
∂rj
·
¸
1
1
2
2
~
~
Tij =
Ei Ej + Bi Bj − δij (E + B )
4π
2
(3.46)
(3.47)
der Maxwellsche Spannungstensor genannt wird.
Die Impulsbilanzgleichung 3.46 sagt aus, dass das Strahlungsfeld neben Energie auch Impuls transportiert und deshalb auf Materie, die sie absorbiert
oder reflektiert einen Druck ausübt. Dieser Strahlungsdruck ist z.B. für das
Verständnis des Aufbaus von Sternen wesentlich. Für statistisch isotrope
Strahlungsfelder gilt im Mittel
1 ~ 2
Bi Bj = |B|
δij
3
1 ~ 2
δij
Ei Ej = |E|
3
70
(3.48)
also
1
Tij =
4π
µ
1 1
−
3 2
¶
~ 2 + |B|
~ 2 )δij = − 1 u.
(|E|
3
(3.49)
Der Strahlungsdruck eines isotropen Feldes ist also genau ein Drittel der
Energiedichte, eine Tatsache, die für die Theorie der Wärmestrahlung von
wesentlicher Bedeutung ist.
Dispersion
Bisher haben wir angenommen, dass die Polarisation P~ und die Magnetisierung
~ sich auch bei zeitlich veränderlichen Feldern instantan den Feldern E
~ und
M
~ anpassen. Es ist realistischer anzunehmen, dass die Ladungen innerhalb
B
von Atomen und Molekülen nur mit einer gewissen Verzögerung auf die Felder
reagieren; so würde z.B. für ein Elektron in einem Atom gelten
Zt
~ 0 )dt0
g(t − t0 )E(t
~r(t) = e
(3.50)
−∞
wobei g(t − t0 ) die Greensche Funktion des Elektrons darstellt. Eine solche
Greensche Funktion haben wir in der Vorlesung Mechanik für einen gedämpften
harmonischen Oszillator bestimmt. Für das Dipolmoment würde dann gelten
Zt
p~(t) = e
~ 0 )dt0
g(t − t0 )E(t
2
(3.51)
−∞
~
Insbesondere gilt für ein zeitlich harmonisch variierendes E-Feld
~
~ ω e−iωt
E(t)
=E
~ω
mit p~ω = α(ω)E
p~(t) = p~ω e−iωt
und
(3.52)
Z∞
g(τ )eiωt dτ
2
α(ω) = e
(3.53)
0
Aus α(ω) lässt sich (z.B. über die Clausius Mosotti - Beziehung) eine frequenzabhängige dielektrische Konstante ε(ω) bestimmen. Sowohl α(ω) als auch
ε(ω) sind i.a. komplexe Größen. Auf ähnliche Weise kann man auch eine frequenzabhängige magnetische Permeabilität µ(ω) einführen (in der Praxis ist
aber sowohl µ als auch µ(ω) sehr nahe bei Eins für die meisten Substanzen).
~ r, t) = Re(E
~ ω eikr−iωt ) führt auch für Medien mit frequenzDer Ansatz E(~
abhängigen ε(ω) und µ(ω) zum Ziel. Allerdings können für Frequenzen, bei
71
denen der Brechungsindex n(ω) =
ω in
p
ε(ω)µ(ω) komplex ist, die Größen ~k und
ω2
c2
nicht mehr beide reell sein. Wichtige Spezialfälle sind
k 2 = ε(ω)µ(ω)
(3.54)
1. ω reell, ~k komplex; z.B. (k + iκ)eˆx
Ex = Eω eikx−κx−iωt
(3.55)
Dies beschreibt eine gedämpfte Welle. Aus der Thermodynamik folgt,
dass für Materie im Gleichgewicht κ immer positiv sein muss. Negative
Werte von κ würden zu Verstärkung von elekromagnetischen Wellen
führen; dies tritt in Laser und Maser und gelegentlich im interstellaren
Raum auf. Das Abklingen der Welle impliziert, dass beim Durchgang
der Welle durch das Medium elektromagnetische Energie verloren gehen
~ r, t) und der Polarisationsstrom
muss. Der Grund dafür ist, dass E(~
∂ ~
~ ω ei~k~r−iωt )
P (~r, t) = Re(χ(ω)iω E
∂t
(3.56)
~ r, t). Deshalb leistet, auch gemitnicht mehr 90◦ außer Phase ist mit E(~
telt über eine Periode, das Feld Arbeit an dem für die Polarisation verantwortlichen Ladungsträgern, die letztendlich in Wärme umgesetzt
wird.
Der Fall 1 tritt auf im Strahlungsfeld harmonisch bewegter Quellen,
oder falls eine Welle aus dem Vakuum in ein Material eintritt (siehe
nächster Abschnitt für Einzelheiten). Insbesondere im letzten Fall
brauchen für isotrope Materialien die Vektoren ~k und ~κ nicht parallel
zu sein. Für Materialien im thermischen Gleichgewicht sind die Vorzeichen der Komponenten von ~κ aber immer so, dass die Welle beim
Durchlaufen des Mediums Energie an das Medium abgibt.
2. ~k reell; ω komplex
Dieser Fall tritt bei der Lösung von Anfangswertproblemen auf: nur die
~
eik~r mit reellem ~k bilden ein vollständiges Funktionensystem, nach dem
man bequem entwickeln kann. Für die Lösung braucht man ε(ω) und
µ(ω) für komplexe Werte von ω. Weil der Zusammenhang zwischen P~
~ kausal ist:
und E
Zt
P~ (~r, t) =
~ r, t0 )dt0 ,
Gp (~r; t − t0 )E(~
−∞
72
(3.57)
ist die Funktion χ(ω) und damit ε(ω) in die obere komplexe Halbebene
~ r, t) wohldefiniert.
analytisch fortsetzbar und für zeitlich abklingende E(~
Für Medien im Gleichgewicht treten bei der Lösung des Anfangswertproblems nur zeitlich abklingende Lösungen auf. In einem Laser hat
man auch instabile, exponentiell anwachsende Lösungen, die aus winzigen Feldfluktuationen zu makroskopischen Werten anwachsen können.
73
3.2
Wellen an Grenzflächen und in Hohlleitern
An einer Grenzfläche zwischen zwei Medien, die keine Oberflächenladung
oder Oberflächenstrom enthält, muss auf Grund der ersten zwei Maxwellgleichungen, auch in der Elektrodynamik, gelten:
Dn stetig
Bn stetig
Aus der dritten und vierten Maxwellgleichung folgt über eine Herleitung
Etg stetig
Htg stetig
(Die Beiträge der Zeitableitungen kann man beliebig klein machen durch die
Wahl einer beliebig ”engen” Schleife). Obige Stetigkeitsbedingungen müssen
an jedem Ort der Grenzfläche gültig sein.
In diesem Abschnitt beschäftigen wir uns nur mit ebenen Grenzflächen, auf
die eine ebene Welle aus einem Medium mit reellem Brechungsindex n1 auf
ein Medium mit Brechungsindex n2 einflällt. Für eine Grenzfläche in der x-yEbene variiert das einfallende Feld entlang der Oberfläche wie ei(kx x+ky y) . Zur
Erfüllung der Randbedingungen postulieren wir noch zwei weitere Wellen, die
dieselbe Abhängigkeit haben:
1. eine reflektierte Welle kx0 = kx , ky0 = ky , kz0 = −kz
q
n22 ω 2
00
00
00
− kx2 − ky2 mit
2. eine transmittierte Welle kx = kx , ky = ky , kz =
c2
ω=
c|~k|
n1
QQ
´´
~
Q k
0 ´
k~3́
´
Q
´
QQ
´
Q
´
Q
s α α0
Q
´
Q
´
Q´
C
C
C
C
C
α00CWC k~00
C
C
C
74
n2
n1
Der reflektierte Strahl erfüllt die Spiegelungsbedingung α = α0 , für reelles n2
gilt das Gesetz von Snellius:
n1 sin α = n2 sin α00
(3.58)
Im Falle n1 < n2 kann es vorkommen, dass dieses Kriterium ein sin α00 > 1
vorhersagt (bzw. dass für kz00 ein rein imaginärer Wert herauskommt). In
diesem Fall tritt im Medium n2 eine exponentiell abklingende oder evaneszente
Welle auf. Mit dieser Welle ist kein Energiestrom in das Medium hinein verbunden:
h
i
h
i
~ ~ ) × (ReH
~ ~ ) ∼ ReE
~ ~ × Re(~k × E
~~ )
Sz ∼ (ReE
(3.59)
k
k
k
k
z
wegen
z
~ ~ ) = ~k|| × ReE
~ ~ − ~κ × ImE
~~ ,
Re(~k × E
k
k
k
(3.60)
wobei ~κ nur eine z-Komponente hat, ergibt die Ausarbeitung des doppelten
Vektorprodukts
~ ~ ImE
~ ~ ) − ReE
~ ~ (ReE
~ ~ ~k|| − ImE
~ ~ ~κ)
Sz ∼ −κ(ReE
k
k
kz
k
k
(3.61)
~ ~ ImE
~ ~ ) − ReE
~ ~ Re(E
~ ~ ~k)
= −κ(ReE
k
k
kz
k
(3.62)
~ ~ ~k = 0; der erste Term verschwindet
Der zweite Term verschwindet wegen E
k
~ ~ und ImE
~ ~ einen Phasenunternach Mittelung über eine Periode, weil ReE
k
k
◦
schied von genau 90 haben:
h
i
~ ~ (~r, t)) = e−κz ReE
~ ~0 cos(~k||~r − ωt) − ImE
~ ~0 sin(~k||~r − ωt)
Re(E
(3.63)
k
k
k
h
i
~ ~ (~r, t)) = e−κz ReE
~ ~0 sin(~k||~r − ωt) − ImE
~ ~0 cos(~k||~r − ωt)
Im(E
(3.64)
k
k
k
Weil keine Energie ins Medium 2 hineinfließt, muss die Intensität des reflektierten Strahls gleich der Intensität des einfallenden Strahls sein.
Um die Intensitäten für reelle Werte von kz00 zu bestimmen, müssen die
Stetigkeitsbedingungen der Felder ausgenützt werden. Wir werden dies in
der Vorlesung nur für senkrechte Inzidenz durchführen, und für eine Welle
~ ~ in der x-Richtung. Für alle drei Wellen setzen wir dann ein E~ Feld
mit E
k
~ Feld in y-Richtung an; Stetigkeit der Tangenin der x-Richtung und ein H~ und H
~ liefert:
tialkomponenten von E
00
0
=0
− H0y
Hoy + Hoy
00
0
=0
− E0x
E0x + E0x
~ und H
~ ergibt
Einsetzen der Beziehung zwischen E
r
r
r
ε1
ε1 0
ε2 00
00
0
H0y =
E0x
H0y =
E0x
E
H0y = −
µ1
µ1
µ2 0x
75
(3.65)
(3.66)
Die Stetigkeitsbedingung für Htg ergibt also
r
ε2 µ1 00
0
E0x − Eox −
E =0
ε1 µ2 0x
0
00
Auflösen der zwei Beziehungen zwischen E0x , E0x
und E0x
ergibt
r
2
1−β
ε 2 µ1
00
0
E0x
=
E0x
E0x
=
E0x
β=
1+β
1+β
ε 1 µ2
(3.67)
(3.68)
Der Reflexionskoeffizient ist das Verhältnis der Energieströme in der reflektierten und in der einfallenden Welle:
R=
0 2
|E0x
|
(1 − β ∗ )(1 − β)
4Reβ
=
=1−
2
∗
|Eox |
(1 + β )(1 + β)
(1 − β ∗ )(1 + β)
(3.69)
Hierbei wurde verwendet, dass im Medium 1 ε1 und µ1 reell sind und damit
auch das Verhältnis
q zwischen E0x und H0y . Der Poynting Vektor ist also
ε1 ~ 2
proportional zu
|E| . Im Medium 2 trägt nur der Anteil von H0y der
µ1
in Phase ist mit E0x zum Energiestrom bei (vgl.
unsere Diskussion der
q
ε2 ~ 2
evaneszenten Welle); im Medium 2 gilt S ∼ Re µ2 |E| und für den Transmissionskoeffizienten erhält man
q
Re µε22 |E 00 |2
4Reβ
0x
T = q
=
=1−R
2
ε1 |E0x |
(1 − β ∗ )(1 − β)
(3.70)
µ1
√
Der Ausdruck für R nimmt für ε1 = µ1 = 1; µ2 reell und ε2 µ2 = n2 + iκ2
die vertraute Form
(n2 − µ2 )2 + κ22
R=
(3.71)
(n2 + µ2 )2 + κ22
an. Wir bemerken noch, dass für negative reelle Werte des Brechungsindex
(für ω = 0 nicht zulässig, aber für endliche ω durchaus) der Transmissionskoeffizient verschwindet; hier tritt auch für senkrechte Inzidenz Totalreflexion auf. Andererseits gibt es für Frequenzbereiche mit Re [ε(ω)µ(ω)] < −1
Oberflächenwellen, d.h. Wellen, die sich entlang der Oberfläche ausbreiten
und in beiden Medien exponentiell abklingen.
Wellen in Hohlleitern
Ein interessanter Grenzfall des obigen Problems ist der Fall einer Welle, die
~
auf einen idealen Leiter trifft. Innerhalb des Leiters muss das E-Feld
und
~
damit das H-Feld
verschwinden. An der Leiteroberfläche gilt deshalb
Etg = 0
Hn = 0
76
(3.72)
~ und H
~ können nicht stetig auf Null abDie sonstigen Komponenten von E
fallen, weil es Oberflächenladungen und Oberflächenströme geben kann. Wir
betrachten jetzt einen Wellenleiter mit Rechteckquerschnitt: 0 < x < X und
0 < y < Y , in dessen Inneren sich Vakuum befindet.
¡ ¡ ¡ ¡ ¡ ¡ ¡
¡ ¡ ¡ ¡ ¡ ¡ ¡
¡ 6
¡
¡
¡
Y
X
- ¡
¡¾
¡
¡
?
¡ ¡ ¡ ¡ ¡ ¡ ¡
¡ ¡ ¡ ¡ ¡ ¡ ¡
Es gilt also
Ey = Ez = Hx = 0
für x = 0, x = X
(3.73)
Ex = Ez = Hy = 0
für y = 0, y = Y
(3.74)
Für eine durch den Leiter laufende Welle setzen wir an
nπx
mπy ikz−iωt
cos
e
X
Y
(3.75)
nπx
mπy ikz−iωt
nπx
mπy ikz−iωt
0
Ey = β sin
cos
e
Hy = β cos
sin
e
X
Y
X
Y
(3.76)
nπx
mπy ikz−iωt
nπx
mπy
Ez = γ sin
sin
e
Hz = γ 0 cos
cos
eikz−iωt
X
Y
X
Y
(3.77)
mit m, n ∈ Z. Dieser Ansatz genügt den Randbedingungen automatisch.
~ = 0 und ∇H
~ =0
Die cos- Faktoren sind auch fast zwingend, wenn wir ∇E
erfüllen wollen. Weil weiters jede Fourier- Komponente des Ansatzes die
Wellengleichung im Vakuum erfüllen soll, muss gelten
Ex = α cos
nπx
mπy ikz−iωt
sin
e
X
Y
³ nπ ´2
X
+
Hx = α0 sin
³ mπ ´2
Y
+ k2 =
ω2
c2
(3.78)
Die Maxwellgleichungen führen zu Bedingungen zwischen den sechs Koeffizienten α, β, γ, α0 , β 0 , γ 0 . Insgesamt gibt es vier unabhängige Bedingungen,
d.h. zwei unabhängige Lösungen.
1. Wellen vom H- Typ (oder TE = transversal elektrische Wellen)
2
ω 0
ω 0
δ , β = nπ
δ , α0 = − nπ
kδ 0 , β 0 =
mit γ = 0, γ 0 = i(k 2 − ωc2 )δ 0 , α = − mπ
Y c
X c
X
mπ
0
− Y kδ . Wir sehen, dass für m = n = 0 die Lösung identisch verschwindet; falls nur eine dieser Zahlen ungleich Null ist, so hat man
77
sehr wohl eine Lösung. Für den Fall X > Y hat man also die Lösungen
mit reellem k ab der Grenzfrequenz
ωLH =
πc
X
(3.79)
2. Wellen vom E- Typ (TM = transversal magnetische Wellen)
2
ω
mit γ 0 = 0, γ = i(k 2 − ωc2 )δ, α = nπ
kδ, β = mπ
kδ, α0 = − mπ
δ, β 0 =
X
Y
Y c
nπ ω
δ. Jetzt stehen die Faktoren n und m bei ihrem cos statt bei ihrem
X c
sin und schon für entweder m oder n gleich Null verschwindet die ganze
Lösung. Die Grenzfrequenz ist jetzt
r
1
1
ωLE = πc
+
(3.80)
X2 Y 2
q
2
2
Ab jeder Grenzfrequenz ωmn = πc Xn 2 + m
erhält man eine (für n oder
Y2
m = 0) oder zwei zusätzliche Typen von Wellen, die sich im Wellenleiter
ausbreiten können.
Hohlraumresonatoren
Falls wir einen Wellenleiter auch noch in der z- Richtung zumachen, so
können im Inneren nur Linearkombinationen der oben konstruierten laufenden
Wellen mit k und −k existieren, die auch noch bei z = 0 und z = Z die
Randbedingungen erfüllen.
nπx
mπy
lπz
cos
cos
X
Y
Z
(3.81)
nπx
mπy
lπz
nπx
mπy
lπz
Ey = β sin
cos
sin
Hy = β 0 cos
sin
cos
X
Y
Z
X
Y
Z
(3.82)
nπx
mπy
lπz
nπx
mπy
lπz
sin
cos
Hz = γ 0 cos
cos
sin
Ez = γ sin
X
Y
Z
X
Y
Z
(3.83)
und es gibt nur die diskreten Frequenzen
r
m2
l2
n2
+
+
(3.84)
ωnml = πc
X2 Y 2 Z2
Ex = α cos
nπx
mπy
lπz
sin
sin
X
Y
Z
Hx = α0 sin
Es gibt wieder zwei Lösungen für den Fall, dass mindestens zwei Zahlen
n, m, l ungleich Null sind und eine Lösung, falls nur eine der Zahlen ungleich
Null ist.
78
3.3
Skalares und Vektorpotential
Wir betrachten jetzt die vollständigen mikroskopischen Maxwellgleichungen:
~ = 4πρ
∇E
(3.85)
~ =0
∇B
(3.86)
~ =−
∇×E
~
1 ∂B
c ∂t
~
~ = 4π ~j + 1 ∂ E
∇×B
c
c ∂t
Wegen der zweiten Gleichung kann man immer schreiben
~ =∇×A
~
B
Einsetzen in die dritte Gleichung liefert
Ã
!
~
1
∂
A
~+
∇× E
= 0,
c ∂t
(3.87)
(3.88)
(3.89)
(3.90)
also gibt es ein skalares Feld φ, so dass
~
~ = − 1 ∂ A − ∇φ.
E
c ∂t
(3.91)
Die Übereinkunft in der Notation mit dem elektrostatischen Potential ist
vorläufig zufällig. Einsetzen in die zwei übrigen Maxwellgleichungen liefert
∇2 φ +
1∂ ~
∇A = −4πρ
c ∂t
2~
~ + 1 ∂ A + 1 ∂ ∇φ = 4π ~j.
∇×∇×A
c2 ∂t2
c ∂t
c
(3.92)
(3.93)
~ und φ heißen Vektorpotential und skalares Potential. Sie sind
Die Größen A
nicht eindeutig bestimmt; die Gleichungen Gl.3.89 und Gl.3.91 sind invariant
unter der Transformation
φ0 = φ −
1 ∂f
c ∂t
~0 = A
~ + ∇f
A
(3.94)
mit einer beliebigen skalaren Funktion f (~r, t). Die Transformation (3.94)
heißt Eichtransformation, die Funktion f heißt Eichfunktion.
79
Es gibt zwei Arten von Eichungen, die zu einer Vereinfachung der Gleichun~ und φ führen. Die erste ist die schon eingeführte Coulomb-Eichung
gen für A
~
~ = g, so kann man durch Lösen
∇A = 0. Falls in irgendeiner Eichung gilt ∇A
2
der Gleichung ∇ f = −g eine Eichfunktion finden, die zur Coulomb-Eichung
führt:
~ 0 = ∇A
~ + ∇2 f = g − g = 0.
∇A
(3.95)
In der Coulomb-Eichung lauten die Gleichungen für die Potentiale
~
1 ∂ 2A
1∂
4π
= − ~j +
∇φ,
(3.96)
2
2
c ∂t
c
c ∂t
~ = ∇(∇A)
~ − ∇2 A
~ benutzt haben. Die erste
wobei wir die Formel ∇ × ∇ × A
Gleichung wird gelöst durch
Z
φ(~r0 , t) 3 0
φ(~r, t) =
d ~r + φ0 (~r, t),
(3.97)
|~r − ~r0 |
∇2 φ = −4πρ
~−
∇2 A
wobei φ0 (~r, t) eine Lösung der Laplace-Gleichung ∇2 φ0 = 0 ist. Einsetzen von
φ(~r, t) in die zweite Gleichung liefert eine inhomogene Wellengleichung, die
wir gleich näher betrachten werden. Die Zusatzbedingung für die Coulomb~ noch immer nicht ganz fest; wir können noch eine Umeichung
Eichung legt A
durchführen mit einer Eichfunktion, die ∇2 f = 0 genügt.
~ ist die Lorentz-Bedingung
Eine zweite nützliche Nebenbedingung für A
1 ∂φ
= 0.
(3.98)
c ∂t
Auch für diese Bedingung kann eine Eichfunktion leicht durch Lösen einer
Poissongleichung bestimmt werden. Die Lorentz-Bedingung führt zur En~ und φ:
tkopplung der Gleichungen für A
~+
∇A
~
1 ∂ 2φ
1 ∂ 2A
4π
2~
=
−4πρ
∇
A
−
= − ~j.
(3.99)
2
2
2
2
c ∂t
c ∂t
c
~ als auch φ einer inhomogenen Wellengleichung. Auch
Jetzt genügen sowohl A
die Lorentz-Bedingung legt die Potentiale noch nicht eindeutig fest: Es sind
noch Eichtransformationen zugelassen mit Eichfunktionen die der homogenen
Wellengleichung
1 ∂2f
(3.100)
∇2 f − 2 2 = 0
c ∂t
genügen, wie man durch Einsetzen leicht nachweist.
∇2 φ −
Die inhomogene Wellengleichung
¤ψ := ∇2 ψ −
1 ∂2ψ
= 4πρ
c2 ∂t2
80
(3.101)
hat die Lösungen
Z
ψret (~r, t) =
und
Z
ψadv (~r, t) =
0
r|
ρ(~r0 , t − |~r−~
) 3 0
c
d ~r
0
|~r − ~r |
(3.102)
0
r|
ρ(~r0 , t + |~r−~
) 3 0
c
d ~r
0
|~r − ~r |
(3.103)
Zum Beweis unterteilen wir die Integrale in ein Integral ψ1 über eine sehr
kleine Umgebung |~r0 − ~r| < ε vom Aufpunkt ~r und ein Integral ψ2 über
den übrigen Raum. In ψ1 können wir t ∓ 1c |~r − ~r0 | wegen der Kleinheit von
|~r − ~r0 | durch t ersetzen. Wir erhalten also dann den bekannten Fall der
Elektrostatik; es gilt also
∇2 ψ1 = −4πρ.
(3.104)
Weiters ist für nichtsinguläres ρ(~r) ψ1 selbst, und damit
zu machen; es gilt also auch in beliebig guter Näherung
∂ 2 ψ1
∂t2
beliebig klein
¤ψ1 = −4πρ.
(3.105)
Der Integrand in ψ2 hängt nur über r1 = |~r − ~r0 | von ~r ab. Für solche
Funktionen gilt
∇2 f (~r1 ) = ∇
~r1 ∂f
∂ 2f
2 ∂f
1 ∂2
= 2 +
=
r1 f (r1 )
r1 ∂r1
∂r1
r1 ∂r1
r1 ∂r12
Einsetzen mit f (r1 ) =
1
ρ(~r0 , t
r1
∓
Z
2
∇ ψ2 =
V0
r1
)
c
(r1 6= 0).
(3.106)
liefert
1 ∂2
r1
ρ(~r0 , t ∓ )d3~r1 .
2
r1 ∂r1
c
Weil r1 unter den Differentiationen nur in der Kombination t ∓
sieht man sofort, dass gelten muss
1 ∂ 2 ψ2
∇ ψ2 − 2
= 0.
c ∂t2
2
(3.107)
r1
c
auftritt,
(3.108)
Damit ist der Beweis der Korrektheit der retadierten und avancierten Lösungen
geliefert. Die Integration erstreckt sich über den sogenannten Lichtkegel, und
zwar für die retardierten Lösungen ψret über den Teil, der in der Vergangenheit liegt, und für die avancierten Lösungen ψadv über den Teil, der in der
Zukunft liegt.
81
t 6J

J

J

J
t0 − t = |~r−r~0 |
c
J

J

J

J q
J~

r
 J
J

J

J

|~
r−r~0 |
0
Jt − t = c

J

J

J

-
r~0
Für die meisten physikalischen Probleme ist ψret die relevante Lösung (Kausalität,
falls die Ladungen und Ströme als ”Ursache” für das Feld aufgefasst werden.)
Der Unterschied zwischen den retadierten Lösungen und den avancierten ist
eine Lösung der homogenen Wellengleichung. Welche von beiden Lösungen
(oder welche Linearkombination der beiden) man zu wählen hat, hängt also
letztendlich von den Randbedingungen für das Strahlungsfeld ab.
Die allgemeine Lösung der Potentialgleichungen in Lorentzeichung lautet also
Z
r0 |
) 3 0
ρ(~r0 , t − |~r−~
c
φ(~r, t) =
d ~r + φ0 (~r, t)
(3.109)
0
|~r − ~r |
Z
|~
r−~
r0 |
1 ~j(~r0 , t − c ) 3 0 ~
~
A(~r, t) =
d ~r + A0 (~r, t),
(3.110)
c
|~r − ~r0 |
~ r, t) Lösungen der freien Wellengleichungen sind, die
wobei φ0 (~r, t) und A(~
über die Lorentz-Bedingung miteinander zusammenhängen. Der homogene
Teil der obigen Ausdrücke kann noch etwas umgeschrieben werden
ZZ 0
φret (~r, t) =
Gret (~r − ~r0 , t − t0 )ρ(~r0 , t0 )d3~rdt
(3.111)
~ ret (~r, t) = 1
A
c
mit
ZZ
∞
0
Gret (~r − ~r0 , t − t0 )~j(~r0 , t0 )d3~rdt
(3.112)
∞
1 ³
r´
Gret (~r, t) = δ t −
r
c
82
(3.113)
die retardierte Greensche Funktion. Ganz analog führt man
1 ³
r´
Gadv (~r, t) = δ t +
,
r
c
(3.114)
die avancierte Greensche Funktion ein.
Für eine Punktladung, die sich entlang der Bahn ~r0 (t) bewegt, gilt, dass φret
~ ret im Punkt ~r bestimmt werden vom Schnittpunkt von ~r0 (t) mit dem
und A
rückwertigen Lichtkegel, dessen Spitze in ~r liegt, und von der Geschwindigkeit
~v (t) in diesem Punkt (Ein Teilchen, dessen Geschwindigkeit immer kleiner
als c ist, durchstößt den Lichtkegel nur einmal):
Z
φ(~r, t) = e
δ(t − t0 − 1c |~r − ~r0 (t0 )|) 0
dt
|~r − ~r0 (t0 )|
(3.115)
~ r, t).
und analog für A(~
t 6
¢
¢
A
A
¢
A ¢
r
A¢q ~
¢A
¢ A
¢
A
A
¢
r~0 (t)
Aq
A
¢
¢
A
¢
¢
A
¢
A
A
¢
¢
A
A
-
r
Bei der Auswertung des Integrals muss man bedenken, dass gilt
δ(f (t)) =
1
|f 0 (t0 )|
δ(t − t0 )
(3.116)
wenn t0 eine Nullstelle von f (t) ist. Für das Argument u(t) der δ- Funktion
gilt
~ 0)
~v (t0 ) ~r − ~r0 (t0 )
~v (t0 )R(t
du
=
−1
+
:=
−1
+
.
(3.117)
dt0
c |~r − ~r0 (t0 )|
R(t0 )c
83
~
Das Ergebnis ist also (für φ und analog für A)
φ(~r, t) = h
R−
e
~ v
R−~
c
i
t0 =t− R
c
"
~v
e
~ r, t) =
A(~
c R−
#
~v
R~
c
(3.118)
t0 =t− R
c
Diese Potentiale heißen Lienard-Wiechert-Potentiale. Es sind äußerst komplizierte Ausdrücke, weil für jeden Punkt (~r, t) zuerst der korrespondierende
~ t0 ) bestimmt werden muss.
Quellenpunkt (~r0 = ~r + R,
84
3.4
Strahlung einer lokalisierten Verteilung von Ladungen und Strömen
Wie in der Statik ist es auch in der Dynamik oft vorteilhaft, für das Feld einer
lokalisierten Verteilung von Ladungen und Strömen eine Multipolentwicklung
durchzuführen. Dabei stellt es sich als bequem heraus, zuerst bezüglich der
Zeit eine Fouriertransformation durchzuführen. Wir schreiben also
Z
ρ(~r, t) = ρω (~r)e−iωt dω
(3.119)
Z
φ(~r, t) =
φω (~r)e−iωt dω
(3.120)
~ r, t). Die Bestimmungsgleichungen für die Pound analog für ~j(~r, t) und A(~
tentiale lauten in der Lorentz-Eichung
∇2 φω + k 2 φω = −4πρω
(3.121)
4π ~
jω
c
(3.122)
~ ω + k2A
~ω = −
∇2 A
mit
ω
~ − iω φω = 0
und ∇A
c
c
Die Lösungen können geschrieben werden als
Z
φω = Gret
r − ~r0 )ρω (~r0 )d3~r0 + φ0ω (~r)
ω (~
k=
(3.123)
(3.124)
Z
1
~
~ 0 (~r)
Aω =
Gret
r − ~r0 )~jω (~r0 )d3~r0 + A
(3.125)
ω (~
ω
c
~ 0ω (~r) Lösungen der homogenen Gleichungen und Gret
Dabei sind φ0ω (~r) und A
ω
ist die Fouriertransformierte der retadierten Greenschen Funktion; es gilt z.B.
Z
1
ret
φret (t)eiωt dt
φω =
2π
ZZZ
1
Gret (~r − ~r0 , t − t0 )ρ(~r0 , t0 )eiωt dtd3~rdt0
=
2π
ZZZZ
1
0
Gret (~r − ~r0 , t − t0 )ρω0 (~r)eiωt−iωt dtd3~rdt0 dω 0
=
(3.126)
2π
1
Wenn wir jetzt (beachte das Fehlen des üblichen 2π
.)
Z
0
ret
0
Gω (~r − ~r ) = Gret (~r − ~r0 , t − t0 )ei(t−t ) d(t − t0 )
85
(3.127)
einführen und in Gl.3.126 die Integration über t in eine über t−t0 umwandeln,
so erhalten wir
ZZZ
1
0 0
ret
φω =
Gret
r − ~r0 )ρω0 (~r0 )ei(ω−ω )t d3~rdt0 dω 0
ω (~
2π
Z
ZZ
0 3
0
ret
0
r − ~r0 )ρω (~r0 )d3~r (3.128)
=
Gω (~r − ~r )ρω0 (~r)δ(ω − ω )d ~rdω = Gret
ω (~
Die explizite Form von Gret ist
Z
1
R
eikR
ret ~
Gω (R) =
δ(τ − )eiωτ dτ =
.
R
c
R
(3.129)
Dies ist der räumliche Anteil einer auslaufenden Kugelwelle; in R1 eikR−iωt sind
die Oberflächen konstanter Phase Kugeloberflächen (kR − ωt = cst), die sich
mit der Lichtgeschwindigkeit c = ωk vom Ursprung wegbewegen. Für die
avancierte Greensche Funktion erhält man
e−ikR
~
Gadv
ω (R) =
R
also eine einlaufende Kugelwelle.
Betrachten wir jetzt die retadierten Potentiale etwas näher:
Z ik|~r−~r0 |
e
ret
φω (~r) =
ρω (~r0 )d3~r0
|~r − ~r0 |
Z ik|~r−~r0 |
1
e
ret
~ (~r) =
~jω (~r0 )d3~r0
A
ω
c
|~r − ~r0 |
(3.130)
(3.131)
(3.132)
0
Falls kr0 << 1 gibt es eine Nahzone kr << 1, in der man den Faktor eik|~r−~r |
vernachlässigen kann; dort sind dann die Potentiale gleich den elektrostatischen und magnetostatischen Ausdrücken. Dagegen gilt im Fernfeld, kr >> 1,
dass man die ~r0 - Abhängigkeit des Nenners völlig vernachlässigen kann und
im Exponenten die Näherung
|~r − ~r0 | = r −
~r~r0
r
(3.133)
r
, so kann man schreiben
einsetzen. Falls wir noch einführen, dass ~k = k~
r
Z
eikr
eikr
~ 0
ret
φω (~r) '
ρω (~r0 )e−ik~r d3~r0 :=
ρ~
(3.134)
r
r k,ω
Z
eikr ~ 0 −i~k~r0 3 0
eikr ~
ret
~
Aω (~r) '
jω (~r )e
d ~r :=
j~
(3.135)
cr
cr k,ω
86
Die Amplitude der auslaufenden Welle in der Richtung r̂ ist also proportional zur Fouriertransformation der Ladungs- und Stromverteilung für einen
Wellenvektor mit Betrag k = ωc und Richtung r̂. (Wenigstens: Näherungsweise
~ ω (~r) und B
~ ω (~r):
im Fernfeld.) In derselben Näherung gilt für die Felder E
ikr
~
~ ω (~r) ' −∇φω (~r) − 1 ∂ Aω (~r, t) = e (−i~kρ~ + iω ~j~ )
E
kω
c
∂t
r
c2 kω
(3.136)
ikr
~ ω (~r) ' ∇ × A
~ ω (~r) = e i ~k × ~j~
B
(3.137)
kω
r c
~ ω lässt sich noch etwas vereinfachen durch Anwenden der
Der Ausdruck für E
Kontinuitätsgleichung
ωρ~kω = ~k~j~kω
(3.138)
und der Identität
~k × (~k × ~j) = ~k(~k~j) − k 2~j
Das Ergebnis ist
(3.139)
i~k~
r
~ ω (~r) ' − i ~k × (~k × ~j~ ) e
E
kω
c
r
(3.140)
~
ik~
r
~ ω (~r) ' i ~k × ~j~ e .
B
(3.141)
kω
c
r
~ ω und B
~ ω also senkrecht aufeinander und auf den AusIm Fernfeld stehen E
~
breitungsvektor k der Kugelwelle, die lokal wie eine ebene Welle ausschaut.
Intensitätsverteilung
Wir berechnen als Nächstes den Energiestrom (Poynting - Vektor) in Abhängigkeit
der Richtung r̂. Dabei muss man zwei Fälle unterscheiden:
1. harmonisch variierende Ströme
~j(~r, t) = Re(~jω (~r)e−iωt ).
(3.142)
~ r, t) = c Re(E
~ ω e−iωt ) × Re(B
~ ω e−iωt )
S(~
4π
(3.143)
Es gilt dann
Bei der Ausarbeitung von Re(fω e−iωt ) = 21 (fω e−iωt + fω∗ eiωt ) entstehen zeitunabhängige Terme und solche, die wie e±2iωt variieren. Bei
der Zeitmittlung über eine Periode (mit einem Querstrich angedeutet),
fallen letztere Terme weg und man erhält
i
c 1 h ~∗ ~
¯
∗
~
~
~
(Eω × Bω ) + (Eω × Bω )
(3.144)
S=
4π 4
87
~ω
also, nach Substitution unseres Ergebnisses für B
~¯ ' 1 |~k × ~j~ |2 ~r .
S
kω
8πc
r3
(3.145)
Dies ist ein Energiestrom pro Zeiteinheit und pro Flächeneinheit d2~r.
Für die Intensität dIω im Raumwinkel dΩ erhält man
dIω =
1 ~ ~ 2
|k × j~kω | dΩ
8πc
(3.146)
2. zeitlich begrenzte Ströme
Wir betrachten jetzt Größen f (t) und g(t) vom Typ
Z
Z
−iωt
f (t) = fω e
dω
g(t) = gω e−iωt dω
(3.147)
Es gilt nun offensichtlich
Z∞
ZZZ
0
fω gω∗ 0 e−iωt+iω t dωdω 0 dt0
f (t)g(t)dt =
−∞
ZZ
= 2π
Z
fω gω∗ 0 δ(ω
0
0
fω gω∗ 0 dω;
− ω )dωdω = 2π
(3.148)
(dies ist das Theorem von Fourier - Plancherel).
Wenn ~j(~r, t) und ~g (~r, t) von diesem Typ sind, so erhält man für die
insgesamt in Richtung r̂ emittierte Energie
Z∞
~ r, t)dt = c
S(~
4π
Z
~ r, t) × B(~
~ r, t)dt = c
E(~
2
Z
~ ω (~r) × B
~ ∗ (~r)dω
E
ω
−∞
(3.149)
also
Z∞
−∞
~ r, t)dt = 1 ~r
S(~
2c r3
Z∞
1 ~r
|~k × ~j~kω |2 dω =
c r3
−∞
Z∞
|~k × ~j~kω |2 dω
(3.150)
0
wobei wir verwendet haben, dass wegen der Realität von ~j(~r, t) gelten
muss ~jω∗ (~r) = ~j−ω (~r), also ~j~kω = ~j~k,−ω . Falls wir jetzt die insgesamt im
dE
Raumwinkel dΩ und im Frequenzbereich dω abgestrahlte Energie dω~kω
einführen über
Z∞
Z∞
dE~kω
~
r
~ r, t)dt =
r2 dΩ
S(~
dω,
(3.151)
r
dω
−∞
0
88
so erhalten wir
dζ~kω
1
= |~k × ~j~kω |2 dΩ
dω
c
(3.152)
oder auch
dζ~kω
1
= |~k × ~j~kω |2
(3.153)
dωdΩ
c
Die Fälle 1 und 2 sind physikalisch unterschiedlich. Im ersten Fall
wird stationär Strahlung einer genau festgelegten Frequenz emittiert;
im zweiten Fall hat man eine zeitlich begrenzte Emission, die über
ein mehr oder weniger breites Band von Frequenzen verteilt ist. Man
kann nicht von einem zum anderen Fall geraten durch Substitution
fω = fω0 δ(ω−ω0 ), weil man dann im Fourier - Plancherelschen Theorem
das Quadrat einer δ- Funktion erhält, welches nicht wohldefiniert ist.
Die Multipolentwicklung
Die für die Strahlungsemision bestimmende Größe ist
Z
~j~ = ~jω (~r)e−i~k~r d3~r.
kω
(3.154)
Wegen ~k~r << 1 (die Voraussetzung für sämtliche Überlegungen in diesem
Abschnitt) ist es sinnvoll, die Exponentialfunktion in diesem Integral zu
entwickeln: Das Verhalten von ~j~kω wird dann vom niedrigsten nichtverschwindenden Term dominiert werden. Wie schon im Kapitel über Elektrostatik und Magnetostatik gezeigt wurde, kann jede räumlich beschränkte
Stromverteilung geschrieben werden als Summe von Polarisations- und Magnetisierungsanteilen1 .
oder
~
~ (~r, t) + ∂ P (~r, t)
~j(~r, t) = c∇ × M
∂t
(3.155)
~ ω (~r) − iω P~ω (~r).
~jω (~r) = c∇ × M
(3.156)
Dabei ist P~ω (~r) aufzufassen als (vgl. Gl.2.110)
(1)
Piω (~r) = piω (~r) −
1 ∂ (2)
p (~r) + ...
2 ∂rj ijω
(3.157)
1
Diese Darstellung ist für den Fall, dass ~j(~r, t) ein einzelnes Atom oder Molekül
darstellt, natürlich nicht erlaubt. Die Ergebnisse sind trotzdem auch für den Fall gültig,
nur sehr langwieriger herzuleiten (siehe Jackson, Kap. 9)
89
wobei p(n) (~r) die elektrischen 2n -Poldichten darstellen. In ähnlicher Weise ist
~ ω (~r) aufzufassen als Summe einer magnetischen Dipoldichte und KorrekM
turterme, die höhere magnetische Multipoldichten enthalten.
Zum führenden Term in ~j~kω
Z
~j (0) = ~jω (~r)d3~r
(3.158)
~kω
trägt der Magnetisierungsanteil nicht bei, weil für diesen Anteil die Divergenz
verschwindet (S*)
Z
~j (0) = −iω P~ω (~r)d3~r = −iω~pω ,
(3.159)
~kω
wobei p~ω die Fouriertransformierte des gesamten elektrischen Dipolmoments
(0)
der Verteilung ist. Die von ~j~kω emittierte Strahlung heißt deshalb elektrische
~ ω und B
~ ω gilt
Dipolstrahlung. Für die Felder E



~
~ ω (~r) = ω ~k × p~ω eik~r
B
c
r

~
~ ω (~r) = −~k × (~k × p~ω ) eik~r 
E
r
el. Dipol
(3.160)
und für den Poynting Vektor eines harmonisch schwingenden Dipols erhält
man für den Fall, dass die Komponenten von p~ω in Phase schwingen
2
4
~¯ω = ω |~k × p~ω |2 ~r = ω |~pω |2 sin2 θ ~r
S
8πc
r3
8πc3
r3
(3.161)
wobei θ den Winkel zwischen p~ω und ~r darstellt.
Die gesamte abgestrahlte Leistung erhält man durch Integration der Radi~¯ω (sowieso die einzige nichtverschwindende Komponente)
alkomponente von S
über eine Kugel mit beliebigem Radius. Für ein im wesentlichen reelles p~ω
erhalten wir
ZZ
ω4
ω4
3
2
Itot =
sin
θdθdφ
=
|p
|
|pω |2
(3.162)
ω
8πc3
3c3
wobei wir benutzt haben
ZZ
Zπ
3
Z1
3
sin θdθdφ = 2π
sin θdθ = 2π
0
2
8π
(1 − µ2 )dµ = 2π(2 − ) =
.
3
3
−1
(3.163)
90
Die Gl.3.162, die hier nur für ein reelles p~ω hergeleitet wurde, gilt auch für
p~ω , deren Komponenten nicht die gleiche Phase haben.
In der nächsten Ordnung erhält man
Z
(1)
~ ω (~r) − iω P~ω (~r))d3~r
~j = −i ~k~r(c∇ × M
(3.164)
~kω
Der erste Term liefert nach partieller Integration
Z
Z
∂
(1,1)
3
(j~kω )j = −ic ki ri ²jkl
Mωl (~r)d ~r = ic ki ²jil Mωl (~r)d3~r,
∂rk
also
~j (1,1) = ic~k × m
~ ω,
~kω
(3.165)
(3.166)
wobei m
~ ω die Fouriertransformierte des gesamten magnetischen Dipolmo~ ω und B
~ω
ments der Verteilung darstellt. Einsetzen in den Ausdrücken für E
liefert

~
eik~r 
~
~
~
Bω (~r) = −k × (k × m
~ ω) r 
magn. Dipol
(3.167)

~
i
k~
r

~ ω (~r) = − ω (~k × m
E
~ ω) e r
c
wobei im letzten Ausdruck wieder die Formel für ~k × ~k ×~a verwendet wurde.
~ ω und B
~ ω verVerglichen mit dem elektrischen Dipol, sind die Rollen von E
tauscht. Für den Poynting Vektor erhält man
4
~r
~¯ = ω |m
S
~ ω |2 sin2 θ 3 .
3
8πc
r
(3.168)
Elektrische und magnetische Dipolstrahlung unterscheiden sich nur durch die
Polarisation.
R (1)
Für den zweiten Term in Gl.3.164 erhält man für ~rp~ω (~r)d3~r = 0 den
Ausdruck
Z
Z
1 ∂ (2)
1
(1,2)
(2)
3
(j~kω )i = −ω kj rj (−
pik (~r) + ...)d ~r = ωkj pij (~r)d3~r (3.169)
2 ∂rk
2
also
1
(1,2)
(j~kω )i = ωkj qijω
2
(3.170)
R (1)
wobei qijω dem Quadrupolmoment der Verteilung entspricht (falls ~rp~ω (~r)d3~r
nicht verschwindet liefert auch dieses Integral einen Beitrag zu Qω ; Jackson
verwendet eine Definition des Quadrupolmoments, die sich um einen Faktor 3
~ ω und B
~ ω sind
von der hier verwendeten unterscheidet). Die Ausdrücke für E
91
wieder einfach herzuschreiben. Wir betrachten hier nur noch den Ausdruck
für die abgestrahlte Leistung etwas näher:
~r
1 ω2
¯
~
Sω =
|²ijk kj kl qklω |2 3
8πc 4
r
(3.171)
Wir können ohne Einschränkung der Allgemeinheit annehmen, dass der Tensor Qω diagonal ist Qklω = Qk δkl . Der obige Ausdruck reduziert sich dann
zu
~¯ω =
r~rS
ω6
(sin2 θ cos2 θ sin2 φ|Qz − Qy |2 + sin2 θ cos2 θ cos2 φ|Qx − Qz |2
32πc5
+ sin4 θ sin2 φ cos2 φ|Qy − Qx |2 ).
(3.172)
Die Winkelverteilung kann also recht kompliziert aussehen. Der einfachste
Fall ist der gestreckte Quadrupol: Qx = Qy = − 12 Qz , wofür gilt
~¯ω =
r~rS
9ω 6
Q2 sin2 θ cos2 θ
128πc5 z
(3.173)
also eine zylindrisch symmetrische, kleeblattartige Richtungsverteilung.
Bei höheren Multipolmomenten kommen immer mehr Komponenten von k
ins Spiel, was zu immer schärferen Richteffekten führen kann. Allerdings ist
dafür notwendig, dass die Mulitpolentwicklung nicht ”zu stark” konvergiert,
d.h. dass man ein Antenne wählt, deren Dimension mit einer Wellenlänge
vergleichbar ist (für solche Verteilungen ist natürlich die direkte Auswertung
von ~j~kω der Multipolentwicklung vorzuziehen).
Bemerkung: Die in diesem Abschnitt berechneten Winkelverteilungen gelten nur für polarisationsunempfindliche Detektoren. Falls man vor dem De~ω
tektor einen Polarisator aufstellt, so muss man bei der Auswertung von S
~ ω und die (dazu
nur die vom Polarisator durchgelassene Komponente von E
~ ω berücksichtigen.
senkrechte) entsprechende Komponente von B
92
3.5
Streuung elektromagnetischer Strahlung
In diesem Abschnitt betrachten wir zuerst die Streuung elektromagnetischer
Strahlung an Objekten, die klein sind verglichen mit der Wellenläng des
Lichtes, z.B. an Atomen oder Molekülen. Im einfachsten Fall induziert das
einfallende Licht im Atom ein elektrisches Dipolmoment gemäß
~0
p~ω = α(ω)E
ω
(3.174)
~ 0 das elektrische Feld der einfallenden Lichtwelle darstellt. Das
wobei E
ω
Dipolmoment p~ω emittiert seinerseits elektromagnetische Strahlung nach den
im vorigen Abschnitt besprochenen Gesetzen. Insbesonder gilt für das gestreute
~
E-Feld
ikr
~ ω = −α(ω)~k × (~k × E
~ 0)e
E
(3.175)
ω
r
~
~ ω0
Für linear polarisiertes Licht liegt das gestreute E-Feld
in der Ebene durch E
senkrecht zu ~k. Die Intensität in der Richtung θ beträgt (pro Raumwinkeleinheit)
4
4
~ ω0 |2 sin2 θ
~¯ω = ω |~pω |2 sin2 θ = ω |α(ω)|2 |E
(3.176)
S
3
3
8πc
8πc
Der Poynting Vektor der einfallenden Strahlung hat den Betrag
~¯ω0 | = c |E
~ 0 |2
|S
8π ω
(3.177)
Wie in den Streuproblemen der Mechanik definiert man den differentiellen
Streuquerschnitt
~¯ω (θ, φ)
dσ
S
ω4
=
=
|α(ω)|2 sin2 θ
(3.178)
4
¯0
dΩ
c
~
|S ω |
Der gesamte Streuquerschnitt beträgt (vgl. Gl.3.161)
ZZ
dσ
8π ω 4
sin θdθdφ → σ =
|α(ω)|2 .
σ=
dΩ
3 c4
(3.179)
Für viele Moleküle hängt α(ω) nur relativ schwach von ω ab; die Frequenzabhängigkeit von σ wird dann vom Faktor ω 4 dominiert. Von Sonnenlicht werden also in der Atmosphäre vor allem die blauen und ultravioletten
Strahlen gestreut: hieraus erklärte Lord Rayleigh die blaue Farbe des Himmels, sowie die rote Farbe der untergehenden Sonne. Diese Erklärung setzt
allerdings voraus, dass die an verschiedenen Molekülen gestreuten Lichtwellen
nicht miteinander interferieren; man kann zeigen, dass dies für genügend
verdünnte Gase zutrifft.
93
Der oben erwähnte differentielle Wirkungsquerschnitt gilt für polarisiertes
Licht. Das Licht der Sonne ist bekanntlich nicht polarisiert, aber die zwei
Polarisationen werden in einem vorgegebenen Winkel mit unterschiedlichen
Intensitäten gestreut.
~k ´
´
´
-
k~0
´
]
J´3́
´J ~
´ ^E
ω
θ´
´ θ0
6
?
E~0
Die Polaristion in der Streuebene hat in ihrem Streuquerschnitt einen Faktor
sin2 θ = cos2 θ0 (siehe Skizze). Die Polarisation senkrecht zur Ebene der
Skizze hat θ = π2 und wird also maximal getstreut. Das Sonnenlicht ist
eine inkohärente Mischung der beiden Polarisationen und hat deshalb einen
Streuquerschnitt
dσ
ω4
1 + cos2 θ0
= 4 |α(ω)|2
dΩ
c
2
pro Molekül
(3.180)
Der Polarisationsgrad Π des gestreuten Lichts ist
Π(θ0 ) =
1 − cos2 θ0
1 + cos2 θ0
(3.181)
Die Vorzugspolaristion steht senkrecht zur Ebene durch die Sonne und die
Blickrichtung. In dieser Rechnung ist Mehrfachstreuung, sowie Streuung an
Staubpartikeln und Wassertröpfchen, Schneekristallen usw. vernachlässigt
worden. Für Teilchen, die groß sind gegenüber der Wellenlänge wird Licht
alle Frequenzen etwa gleich stark gestreut (die Reflexion an einer Ebene
hängt nur vom Brechungsindex ab und enthält keine weiteren ω - Faktoren).
Wolken sind deshalb weiß und der Himmel über Linz ist oft nicht allzu blau.
Streuung an freien Elektronen (Thomson - Streuung)
Für ein nichtrelativistisches Elektron gilt
~ 0 (~r0 , t),
m~r¨0 = eE
94
(3.182)
oder, für Auslenkungen klein gegenüber der Wellenlänge,
~ 0 (0, t),
m~r¨0 = eE
(3.183)
wenn wir den Ursprung in der mittleren Lage des Elektrons wählen. Die
Lösung für monochromatische Strahlung ist ~r0 (t) = ~r0ω e−iωt mit
~ 0ω
−mω 2~r0ω = eE
(3.184)
Das Dipolmoment relativ zum Ursprung ist p~ω = e~rω ; wir erhalten also einen
Sonderfall des schon behandelten Formalismus mit
α(ω) = −
e2
mω 2
(3.185)
Der differentielle Wirkungsquerschnitt für polarisiertes Licht ist
dσ
ω 4 e4
= 4 2 4 sin2 θ = a20 sin2 θ,
dΩ
c mω
(3.186)
2
e
−13
wobei a0 = mc
cm der schon in Gl.2.78 begegnete klassis2 = 2, 8.10
che Elektronenradius ist. Der Streuquerschnitt ist frequenzunabhängig; der
Gesamtquerschnitt ist
8π 2
σ=
a
(3.187)
3 0
Das Lorentzmodell eines Atoms; Strahlungsdämpfung
Nach Lorentz behandeln wir ein Elektron in einem Atom als ein harmonisch
~ 0 (~r, t) einer Lichtwelle
gebundenes Teilchen mit der Bewegungsgleichung im Feld E
~ 0 (~r, t) ' eE
~ 0 (~0, t)
m~r¨ + mω02~r = eE
(3.188)
wobei wir in der letzten Umformung angenommen haben, dass die Auslenkung
~r(t) klein gegenüber der Wellenlänge des Lichtes. Nach einer Fouriertransformation erhält man
~ 0ω
(3.189)
m(ω02 − ω 2 )~rω = eE
oder
p~ω = e~rω =
also
e2
~ 0ω ,
E
m(ω02 − ω 2 )
e2
α(ω) =
m(ω02 − ω 2 )
95
(3.190)
(3.191)
α(ω)
ω0
ω
~ 0 (~r, t) kann
Für ω = ω0 tritt eine Resonanz auf: Ein unendlich kleines E
schon zu einem unendlichen p~ω und damit zu einer endlichen Abstrahlung
führen. Schon aus Gründen der Energieerhaltung ist dies nicht akzeptabel.
Auch der Grund für den Fehler ist ersichtlich: Für starke Streuung darf für
das Feld am Ort des Elektrons nicht einfach nur das äußere Feld genommen
werden; auch die Rückwirkung des Streufeldes auf das strahlende Elektron
sollte berücksichtigt werden. Die präzise Behandlung wird sehr kompliziert;
es treten Divergenzen auf wie in der Theorie der elektrostatischen Selbstenergie des Elektrons. Wir werden diese Rechnung ”kurzschließen” über die
Annahme, dass die Strahlungsrückwirkung zu einem (wegen der Isotropie
skalaren) Dämpfungsterm in der Bewegungsgleichung führt:
~ 0 (~0, t)
m~r¨ + mγ~r˙ + mω02~r ' eE
Dies führt zu
~rω =
e
1
~ 0ω
E
2
m ω0 − ω 2 − iωγ
α(ω) =
e2
1
2
m ω0 − ω 2 − iωγ
(3.192)
(3.193)
(3.194)
Die Dämpfungskonstante γ bestimmen wir aus der Energieerhaltung: die von
der Reibungskraft F~ = −mγ~r˙ pro Zeiteinheit geleistete Arbeit soll gleich der
abgestrahlten Leistung sein. Die geleistete Arbeit pro Zeiteinheit ist
~ v = − 1 (F~ ∗~vω + F~ω~v ∗ ) = − 1 Re(F~ ∗~vω )
−F~
ω
ω
4 ω
2
96
(3.195)
0.12
0.1
|alpha|^2
0.08
0.06
0.04
0.02
0
0
1
2
3
omega
4
5
6
Dies soll der abgestrahlten Leistung
dIω =
ω4
e2 ω 2
2
|~
p
|
=
|~vω |2
ω
3c3
3c3
(3.196)
gleich sein. Für paralleles F~ω und ~vω liefert dies
2e2 ω02
2e2 ω 2
~
~vω ' −
~vω
Fω = −
3c3
3c3
(3.197)
(in der Nähe der Resonanz)
also
2e2 2 2a0 2 4πa0
γ=
ω =
ω =
ω0
(3.198)
3mc3 0
c 0
3λ0
wobei λ0 die Wellenlänge des Lichtes mit Frequenz ω0 ist und a0 der klassische
Elekronenradius. Für sichtbares Licht gilt γ << ω0 , also die Bewegung des
Elektrons ist nur leicht gedämpft (Für λ0 von der Ordnung a0 wäre sowieso
~ r, t) ' E(
~ ~0, t) unerlaubt gewesen). Das
die oben gemachte Dipolnäherung E(~
2
2
Ersetzen von ω durch ω0 in Gl.3.197 ist nicht nur eine Bequemlichkeitssache:
Belassen des Faktors ω 2 würde nach Fourierrücktransformation zu einer Bewegungsgleichung
... führen, in der die Strahlungsrückwirkung zu einem Term
proportional zu ~r führen würde:
mγ ...
~ 0 (~r, t).
(3.199)
− 2 ~r + m~r¨ + mω02~r = eE
ω0
Die Lösungen dieser Gleichung sind nicht länger durch die Anfangswerte
von ~r und ~r˙ eindeutig festgelegt; es gibt zusätzlich exponentiell anwachsende
Lösungen (runaway solutions), die offensichtlich unphysikalisch sind. In einer
97
genauen Theorie von Atom + Strahlungsfeld kann man in der Tat zeigen, dass
solche Lösungen nicht auftreten dürfen. Dies rechtfertigt im nachhinein das
Ersetzen von ω 2 durch ω02 , das diese Lösungen durch einen Trick eliminiert.
Zum Schluss unserer Betrachtungen schreiben wir noch den Ausdruck für
den differentiellen Streuquerschnitt eines Lorentz Atoms hin
dσ
ω4
= a20 2
|k̂ × ê0ω |2
(3.200)
dΩ
(ω0 − ω 2 )2 + ω 2 γ 2
wobei r̂ und êoω Einheitsvektoren in der Beobachtungsrichtung und in der
~ 0 sind. Für ω << ω0 erhält man den Ausdruck für
Richtung des Feldes E
e2
Rayleighstrahlung mit α(ω) = α(0) = mω
2 ; für ω >> ω0 erhält man den
0
Ausdruck für Thomson - Streuung an freien Elektronen.
Streuung an mehreren schwach streuenden Zentren; der Strukturfaktor
Zum Schluss dieses Abschnittes betrachten wir die Streuung von Licht an
einer Wolke von Atomen und Molekülen, mit einer zeitunabhängigen Dichte
n(~r). Die Wolke kann Abmessungen haben, die vergleichbar sind mit der
Wellenlänge des einfallenden Lichtes. Wir werden zur Vereinfachung des
Problems annehmen, dass jedes Atom für sich nur schwach streut und deshalb die Möglichkeit der Streuung des Lichtes an mehreren Atomen hintereinander vernachlässigbar ist. Ein Atom am Ort ~ri mit Polarisierbarkeit α(ω)
gibt im Punkt ~r in der Fernzone Anlass zu Streufeldern
ik|~
r−~
ri |
~ ωi (~r) ' −ei~k0~ri α(ω) e
~ 0ω )
E
(~k × ~k × E
|~r − ~ri |
eikr −i(~k−~k0 )~ri ~ ~ ~
e
(k × k × E0ω )
r
eikr −i(~k−~k0 )~ri ω ~ ~
' α(ω)
e
(k × E0ω )
r
c
' −α(ω)
(3.201)
~ ωi
B
(3.202)
¡
¡
¡
k~0
¡
¡
¡
¡
¡
¡
¡
¡
¡
¡
¡
¡
µ
¡
µ
¡
¡
¡
¡
¡
¡
¡
¡
µ
¡
µ
¡
¡
¡
¡
¡
r¡
¡~
k
r¡
r¡
¡
¡
¡
¡
r¡
r¡ θ0
-
98
~ ω und B
~ ω der verschiedenen Streuzentren
Wenn wir jetzt die Beiträge zu E
addieren, so erhalten wir, vergleichen mit den Ausdrücken für Einzelstreuung,
einen zusätzlichen Faktor
Z
0
~ ~
n~κ = n(~r0 )e−i(k−k0 )~r d3~r
(3.203)
Der Vektor ~κ = ~k0 − ~k heißt Streuvektor. Seine Länge hängt mit dem
Streuwinkel θ0 über
1
|~κ| = 2k sin θ0
(3.204)
2
zusammen.
>
½B
½
~k ½½
½
½
½
½
³
³
½
½
³³
B
Bk
³³ B
B
B
-BN
k~0
Für den Streuquerschnitt der gesamten Wolke aus punktförmigen Dipolstreuer erhalten wir letztendlich
µ ¶
µ ¶
dσ
dσ
2
= |n~κ |
= |n~κ |2 |α(ω)|2 k 4 sin2 θe
(3.205)
dΩ W
dΩ at
für polarisiertes Licht, oder
µ ¶
µ
¶
dσ
1 + cos2 θ0
2
2 4
= |n~κ | |α(ω)| k
dΩ W
2
(3.206)
für unpolarisiertes Licht. Der Vorfaktor
|n~κ |2 := S(~κ)
(3.207)
der die Modifikation der Richtungsverteilung der gestreuten Strahlung verglichen mit derjenigen der einzlenen Streuer angibt, heißt (statistischer) Strukturfaktor.
Beispiel 1: Eine Kugel
n(~r) = n0 θ(a − r)
99
(3.208)
Za Zπ Z2π
n~κ = n0
e
0
Za
= 4πn0
Z
0
i~κ~
r 2
r dr sin θdθdφ = 2πn0
eiκµr r2 dµdr =
0
·
¸
1
4πn0 1
a
2
sin(κr)r dr =
sin(κa) − cos(κa)
κr
κ
κ2
κ
(3.209)
0
Für κa << 1 erhält man n~κ '
teilchen. Für κa >> 1 gilt
n~κ ' −
4π
n a3
3 0
und die Kugel streut wie ein Punkt-
4πn0 a
πn0 a
cos(κa) ' 2 2 1 cos(κa)
2
κ
k sin 2 θ0
(3.210)
Der Strukturfaktor beträgt also
S(~κ) =
π 2 n20 a2
cos2 (κa)
4 1
4
k sin 2 θ0
(3.211)
Der Faktor k −4 fällt gegen k 4 im Streuquerschnitt des Einzelstreuers weg.
Das Streulicht von großen Streuern ist also weiß und stark vorwärts gerichtet.
Dies ”erklärt” die weiße Farbe von Nebel und Wolken (Allerdings ist dort die
Annahme schwacher Streuung nicht länger gerechtfertigt; die Faktoren k n
treten aber auch dann auf ähnliche Weise auf. Näheres über Streutheorie in
der Vorlesung Quantenmechanik).
Beispiel 2: periodische Strukturen
Für dreidimensionale (unendliche) periodische Strukturen (Kristalle) tritt
bei der Bildung von n~κ destruktive Interferenz auf, außer für Vektoren ~κ des
sogenannten reziproken Gitters, die definiert sind durch die Bedingung
~κ~ai = 2πni
(3.212)
~ai (i = 1, 2, 3) sind die drei Gittervektoren der Elementarzelle des Kristalls
und ni sind ganze Zahlen. Streuung tritt nur in ganz bestimmten Richtungen auf (Bragg - Peaks). Um die Kristallstruktur von ”echten” Kristallen zu
sehen, braucht man wegen |~κ| < 2k Strahlung genügend kurzer Wellenlänge
(Röntgen - Strahlung). Bragg - Streuung mit sichtbarem Licht kann man
an Superposition von Polystyrolkügelchen im Wasser, die sich für geschickt
gewählte Werte von Radius, Dichte und Ionenkonzentration spontan periodisch ordnen, beobachten.
100
4
4.1
Die spezielle Relativitätstheorie
Das Verhalten der Maxwellgleichungen unter Galilei
- Transformationen
Die klassische Mechanik ist invariant unter der Transformation zu einem
gleichförmig bewegten System:
~r0 = ~r − ~v0 t
~v 0 = ~v − ~v0
(4.1)
Es ist deshalb unmöglich, mittels mechanischer Experimente festzustellen, ob
das System, in dem der Experimentator sich befindet, sich bezüglich des ”absoluten Raumes” bewegt oder in Ruhe ist. Dies heißt das Relativitätsprinzip.
Es stellt sich jetzt heraus, dass die Maxwellgleichungen nicht invariant sind
unter der Transformation in Gl.4.1. Wir zeigen das an zwei Beispielen.
1. Lichtausbreitung
Die Maxwellgleichungen sagen voraus, dass das Licht sich in allen Richtungen
mit der Geschwindigkeit c ausbreitet. Nach Gl.4.1 kann dies allerdings nur in
einem einzelnen ausgezeichneten System der Fall sein. Andererseits lassen die
Maxwellgleichungen nicht zu, dass jede Lichtwelle mit der Geschwindigkeit c
bezüglich ihrer Quelle läuft: In den Lösungen der freien Maxwellgleichungen
im Vakuum ist nur eine einzelne Ausbreitungsgeschwindigkeit zulässig.
¡ ¡ ¡
¡ ¡ ¡ S2
l2
¡
¡ S0
¡
¡
¡
l1
¡
¡
¡
¡
¡
¡ S1
Det.
Eine Anordnung um nachzuprüfen, wie das Laborsystem sich bezüglich des
Vorzugsystems der Maxwellgleichungen bewegt, wurde von Michelson vorgeschlagen: Ein Lichtstrahl trifft auf einen Strahlteiler (halbdurchlässiger Spiegel)
S0 , der 45◦ zur Strahlrichtung geneigt ist. Die Teilstrahlen durchlaufen die
101
Strecken l1 und l2 bis zu festen Spiegeln S1 und S2 und werden dort zu
S0 zurückreflektiert. Im ruhenden System ist der Unterschied zwischen den
Laufzeiten
2l1 2l2
t1 − t2 =
−
(4.2)
c
c
Betrachten wir jetzt dieselbe Anordnung in einem System, das sich in der
Richtung S0 − S1 mit der Geschwindigkeit v bewegt. Auf dem Hinweg läuft
das Licht nach unserer Annahme 4.1 mit der Geschwindigkeit c − v, auf dem
Rückweg mit c + v. Die Laufzeit des ”waagrechten” Strahls ist also
t1 =
l1
l2
2l1
2l1
1
+
= ¡
2 ¢ :=
v
c−v c+v
c (1 − β 2 )
c 1 − c2
(4.3)
wobei wir die Abkürzung β = vc eingeführt haben. Der ”senkrechte” Strahl
hat in der für das Durchlaufen der Strecke 2l2 benötigten Zeit im Ruhesystem
auch noch den waagrechten Abstand vt2 zurückgelegt.
¡
¡
¡ ¡
¡
¡
¡ ¡
¤¤C
S1
¤ C
¤ C
C
¤
C
¤
l2
C
¤º¤
CW
¤
C
¤
C
¤¢
C ¢¢
¢
¤
¢
¤¾
-C ¢ S0 (t = t2 )
¢
¢C
vt2
¢
¢ C
¢
¢ C
C
S0 (t = t0 )
C
C
¡
¡
¡
¡
Det.
Es gilt also
ct2 =
oder
t2 =
q
4l22 + v 2 t22
2l2
1
p
.
c
1 − β2
102
(4.4)
(4.5)
Für den Laufzeitunterschied erhalten wir also
2l1 1
2l2
1
p
t1 − t2 =
−
2
c 1−β
c
1 − β2
(4.6)
Um jetzt das Interferenzmuster am Detektor zu zentrieren, sollten l1 und l2
so justiert werden, dass gilt t1 − t2 = 2πn
, wobei n ∈ N ist. Diese Justierung
ω
sollte dann aber verloren gehen, wenn wir die ganze Anordnung um 90◦
drehen. Dann sollten auch die Nenner in Gl.4.6 vertauscht werden und man
erhält
2l1
1
2l2 1
p
t1 − t2 =
−
(4.7)
2
c
c 1 − β2
1−β
was für allgemeines β nicht gleichzeitig ein ganzes Vielfaches von 2π
sein kann.
ω
Die Versuche von Michelson, und später von Michelson und Morley, waren so
ausgelegt, dass sich das Interferenzmuster bei Drehung der Anordnung auf
Grund der Umlaufgeschwindigkeiten der Erde um die Sonne merkbar hätte
verschieben müssen. Für einen bestimmten Tag wäre dies noch dadurch zu
erklären, dass sich die Geschwindigkeit derErde um die Sonne und diejenige
der Sonne bezüglich des absoluten Raums zufällig zu Null addieren. Diese
Erklärung würde aber implizieren, dass der Effekt ein halbes Jahr später
umso größer sein sollte. Auch das traf nicht ein. Ein verzweifelter Versuch,
dieses Nullergebnis zu erklären wurde von FitzGerald und Lorentz gemacht:
Sie nahmen an, dass die
p Abmessungen jedes Körpers in der Bewegungsrichtung um einen Faktor 1 − β 2 gestaucht werden. Zur Motivation, sicher bei
Lorentz, dienten Überlegungen über die Kraftwirkungen zwischen bewegten
Ladungen:
Die Felder einer gleichmäßig bewegten Ladungsverteilung Wir betrachten eine gleichmäßig bewegte Ladungsverteilung, gekennzeichnet durch
eine Ladungsdichte ρ(~r, t) und die zugehörige Stromdichte
~j(~r, t) = ~v ρ(~r, t).
(4.8)
In der Lorentzeichung gilt jetzt
¤φ = −4πρ
~
~ = ~v φ := βφ.
~ = −4πρ ~v → A
¤A
c
c
(4.9)
~ unverformt mit der Ladungsverteilung mitbeWeiter gilt, dass sich φ und A
wegen:
φ(~r, t) = φ(~r − ~v t, 0)
(4.10)
oder
∂φ
∂φ
+ ~v
=0
∂t
∂~r
103
(4.11)
~ - Feld gilt also
Für das E
µ
¶
~
1 ∂A
1 ~v ∂φ
~v ~v
~
E = −∇φ −
= −∇φ −
= −∇φ +
∇φ
c ∂t
c c ∂t
c c
~ - Feld
und für das B
µ
~ =∇×A
~ =∇×
B
~v
φ
c
¶
~v
~v
~
= − × ∇φ = × E
c
c
(4.12)
(4.13)
~ zu ~v parallel steht
Die letzte Umformung ist erlaubt, weil der Zusatzterm in E
c
und zum Vektorprodukt keinen Beitrag liefert. Die Bestimmungsgleichung
für φ lautet
Ã
!
µ
¶
~v~v
2
1
∂
2
¤φ = ∇2 − 2 2 φ = ∇2 − ∂c 2
φ = −4πρ
(4.14)
c ∂t
∂~
r∂~
r
oder in einem System mit ~v entlang der x- Achse:
·
¸
2
∂2
∂2
2 ∂
(1 − β ) 2 + 2 + 2 φ = −4πρ
∂x
∂y
∂z
Für β < 1 lässt sich die Lösung finden mittels der Transformation
p
y = y0
z = z0.
x = x0 1 − β 2
Es gilt dann
µ 2
¶
p
∂
∂2
∂2
0 0 0
0
+
+
1 − β 2, y0, z0)
φ(x
,
y
,
z
)
=
−4πρ(x
02
02
02
∂x
∂y
∂z
(4.15)
(4.16)
(4.17)
mit der Lösung
Z
0
0
0
φ(x , y , z ) =
p
ρ(ξ 0
p
1 − β 2 , η 0 , ζ 0 )dξ 0 dη 0 dζ 0
(x0 − ξ 0 )2 + (y 0 − η 0 )2 + (z 0 − ζ 0 )2
oder, in den ursprünglichen Koordinaten
Z
ρ(ξ, η, ζ)dξdηdζ
p
φ(x, y, z) =
2
(x − ξ) + (1 − β 2 ) [(y − η)2 + (z − ζ)2 ]
(Beachte, dass gilt dξ 0 = √ dξ
1−β 2
(4.18)
(4.19)
). Insbesondere findet man für eine Punkt-
ladung die sich für t = 0 im Ursprung befindet (ξ = η = ζ = 0):
φ(~r, 0) = p
e
x2 + (1 − β 2 )(y 2 + z 2 )
104
.
(4.20)
~ und B~ Feld sofort bestimmen. Wir
Aus diesem Ausdruck lassen sich E
beschränken uns auf die Betrachtung der Kraft auf eine mit Geschwindigkeit
~v mitbewegte Ladung e0 :
h
i
0 ~
0
~
~
~
~
~
~
K = e (E + ~v c × B) = −e (1 − β β)∇φ + β × (β × ∇φ)
= −e0 (1 − β 2 )∇φ,
(4.21)
~ β∇φ)
~
wobei wir benutzt haben β~ × (β~ × ∇φ) = β(
− β 2 ∇φ).
Die Kraft auf eine mitbewegte Ladung ist also herleitbar aus einem Konvektionspotential ψ = (1 − β 2 )φ. Dessen Äquipotentialflächen sind die Ellipsoiden
x2 + (1 − β 2 )(y 2 + z 2 ) = const.
(4.22)
³
1~
e0 ³³
k
³³
¢
¢
¢
-v
¢
e
Äquidistantfläche
Diese
Ellipsoiden sind also in der x-Richtung gestaucht um genau den Faktor
p
1 − β 2 , dem wir in der Kontraktionshypothese von Lorentz und FitzGerald begegneten. Die Idee von Lorenetz war jetzt, dass die Stauchung der
Äquipotentialoberflächen es den Atomen in z.B. einem Festkörper erlauben
würde, in der Richtung von ~v näher zusammenzurücken. Grundannahme
dabei war, dass die Kräfte, die die Kristallform bestimmen, letztendlich elektromagnetischer Natur sind. Wir werden auf die Argumentation nicht näher
eingehen; die obige Rechnung zeigt aber, dass die Kontraktionshypothese
keine reine ad-hoc Lösung war, sondern durchaus auch physikalischen Hintergrund hatte.
~ hat aber noch einige weitere Konsequenzen: Die
Der obige Ausdruck für K
Kraft zwischen zwei Teilchen ist nicht länger rein radial gerichtet. Die eröffnet
neue Möglichkeiten für Experimente, die die Geschwindigkeit eines Labors
bezüglich des absoluten Raums feststellen könnten:
1. Der Versuch von Trouton und Noble: Betrachte einen Stab, an
dessen Enden sich Ladungen befinden.
105
:
e0 »»»»»
r
»
ee0 > 0
»»
¤
¤
»»
»
9
¤
¤
¤
»
r
»
¤
»
»
»
»»»
9
:
»
»»
ee0 < 0
e
Auf diesem Stab würde nach den obigen Rechnungen ein Drehmoment
wirken, das bei gleichen Vorzeichen der Ladungen versuchen würde, den
Stab in die Richtung von ~v zu drehen, bei entgegengesetzten Vorzeichen
eine Ausrichtung senkrecht zu ~v bewirken würde. Der Versuch (mit
einem Kondensator an einem Torsionsfaden) lieferte ein Nullergebnis.
Erklärung laut Lorentz: Auch die mechanischen Spannungen, die die
Kondensatorplatten trotz der elektrostatischen Anziehung auseinander
halten, sind elektromagnetischer Natur und zeigen eine ähnliche Abweichung in einem bewegten System.
2. Als Gedankenexperiment könnte man versuchen, zwei Punktladungen aus einer Ruhelage heraus frei bewegen zu lassen. Im absoluten
~ = m~a die Bahnen auf einer gemeinsamen
Ruhesystem würden nach K
Geraden liegen; in bewegten Systemen sollten Abweichungen auftreten
und das Relativitätsprinzip wäre verletzt. Jetzt hilft keine Kontraktionshypothese mehr; man müsste, um das Relativitätsprinzip zu ret~ = m~a die skalare Größe Masse
ten vielmehr annehmen, dass auch in K
durch
p einen Tensor ersetzt wird, dessen xx-Komponente um einen Faktor 1 − β 2 größer wäre als die yy- und zz- Komponenten. Auch dies
ist nicht absurd, falls man annimmt, dass auch die Masse letztendlich
elektromagnetischer Natur ist; die Vermehrung von Zusatzhypothesen
verschönert die Theorie aber nicht.
Zusammenfassend lässt sich der Stand der Theorie um 1905 etwas wie folgt
charakterisieren:
Falls wir annehmen, dass die Maxwellgleichungen uneingeschrenkt richtig
sind und dass Transformationen zwischen zwei relativ zueinander bewegten
Systemen durch Galilei-Transformationen korrekt beschrieben werden (was
damals als selbstverständlich galt), so ist das Relativitätsprinzip auf der
Ebene der Grundgleichungen verletzt. Es gelingt aber nicht diese Verletztungen auch experimentell nachzuweisen, weil es immer eine Verschwörung
von einander gerade aufhebenden Effekten zu geben scheint.
106
Dieser Zustand war natürlich sehr unbefriedigend. Der naheliegende Ausweg
wäre, die Maxwellgleichungen so abzuändern, dass sie Galilei-invariant werden. Dies ist aber nicht befriedigend gelungen. Die von Einstein 1905
vorgeschlagene Lösung war eine Abänderung der Galilei-Transformation. Gegenüber
der neuen Transformation, die von Lorentz schon als eine Art mathematische Kuriosität eingeführt war, sind die Maxwellgleichungen offensichtlich
invariant. Das negative Ergebnis der Experimente von Michelson und Morley, Trouton und Noble usw. lässt sich jetzt zwanglos erklären. Allerdings
enthält die Lorentztransformation auch eine Transformation der Zeitvariable, deren physikalische Bedeutung verstanden werden muss. Weiters wird
auch eine Abänderung der Mechanik notwendig. Diese ist nämlich gegenüber
Galileitransformationen invariant, aber nicht gegenüber Lorentztransformationen. Einem Aspekt der benötigten Modifikationen (anisotrope Masse)
sind wir in der obigen Diskussion schon begegnet.
107
4.2
Die Postulate der speziellen Relativitätstheorie;
die Lorentztransformation
Einstein löste die Schwierigkeiten der Elektrodynamik bewegter Körper dadurch,
dass er das Reltivitätsprinzip als Postulat annahm:
1. Die Grundgleichungen der Physik sind dieselben in jedem Inertialsystem.
Als zweites Postulat nahm er die Gültigkeit der Maxwellgleichungen
in jedem Inertialsystem oder etwas schwächer:
2. Das Licht pflanzt sich im Vakuum in allen Inertialsystemen und in jede
Richtung mit der gleichen Geschwindigkeit c fort.
Um diese Postulate erfüllen zu können, erweist es sich als notwendig, beim
Übergang in ein bezüglich des Ausgangssystems gleichmäßig bewegtes System nicht nur die Raumkoordinaten, sondern auch die Zeit zu transfomieren:
(x, y, z, t) =⇒ (x0 , y 0 , z 0 , t0 )
(4.23)
Die gesuchte Transformation heißt Lorentztransformation. In der Transformation darf kein Punkt im Raum eine ausgezeichnete Rolle spielen; das geht
nur, wenn die Transformation linear ist. Wir betrachten zuerst den Fall,
dass die zwei Bezugssysteme sich gegeneinander mit einer Geschwindigkeit ~v
in x-Richung bewegen. Zur Zeit t = 0 sollen die Ursprünge zusammenfallen
und die Uhren werden synchronisiert:
x = y = z = t = 0 ⇐⇒ x0 = y 0 = z 0 = t0 = 0
(4.24)
Die Verknüpfungsgleichungen sind also homogen.
y0
y
k0
k
v
0
¡
x
0
0
¡
¡
¡
¡
¡
z0
z
108
-
x0
Die Bewegung des Ursprungs 00 des bewegten Systems wird definiert durch
x0 = 0 ⇐⇒ x = vt
(4.25)
x0 = γ(x − vt)
(4.26)
es muss also gelten
mit noch zu bestimmendem γ. Umgekehrt muss natürlich auch gelten (wegen
der Symmetrie der Anordnung)
x = γ(x0 + vt0 )
(4.27)
Betrachte jetzt einen Lichtimpuls der aus 0=0’ in t = t0 = 0 emittiert wird.
Zur Zeit t werde er in K im Punkte x = ct absorbiert. Dasselbe Absorptionsergebnis findet bezüglich K 0 im Punkt x0 zur Zeit t0 statt, wobei nach dem
zweiten Postulat wieder gelten muss x0 = ct0 . Es gilt also
ct0 = x0 = γ(x − vt) = γ(ct − vt) = γt(c − v)
(4.28)
ct = x = γ(x0 + vt0 ) = γ(ct0 + vt0 ) = γt0 (c + v)
(4.29)
bzw.
Multiplikation der beiden Gleichungen ergibt
1
c2 = γ 2 (c2 − v 2 ) ⇒ γ = q
1−
v2
c2
1
=p
1 − β2
(4.30)
Wir erhalten also
x0 + vt0
x= p
1 − β2
x − vt
x0 = p
1 − β2
(4.31)
Elimination von x0 bzw x aus den beiden Gleichungen ergibt
t − v2 x
t0 = p c
1 − β2
t0 + v2 x0
t= p c
1 − β2
(4.32)
Man überprüft leicht, dass gilt
x02 − c2 t02 =
¤
1 £
2
2
= x2 − c2 t2 .
(x
−
βct)
−
(ct
−
βx)
2
1−β
(4.33)
Bisher haben wir über das Verhalten von y und z unter der Transformation
noch keine Aussage gemacht. Um solche zu erhalten, benützen wir wieder
109
die Invarianz der Lichtgeschwindigkeit. Wird ein Punkt x,y,z zur Zeit t von
der aus ~r = 0 zur Zeit t = 0 ausgehenden Kugelwelle erreicht, so muss gelten
x2 + y 2 + z 2 − c 2 t 2 = 0 ⇒ y 2 + z 2 = c 2 t 2 − x2
(4.34)
Die Koordinaten für dasselbe Ereignis im Koordinatensystem K 0 müssen
natürlich derselben Bedingung genügen
x02 + y 02 + z 02 − c2 t02 = 0 ⇒ y 02 + z 02 = c2 t02 − x02 .
(4.35)
Es gilt also wegen der oben gezeigten Invarianz von c2 t2 − x2
y 02 + z 02 = y 2 + z 2
(4.36)
Die alten und neuen transversalen Koordinaten hängen also über eine Rotation zusammen; die einfachste Lösung ist, sie in den beiden Systemen identisch zu wählen:
y0 = y
z 0 = z.
(4.37)
In Matrixform ist der Zusammenhang der alten und neuen Koordinaten


 0 


√1
√β
0
0
−
2
2
x
x
1−β
1−β


 y0  
 y 
0
1 0
0
 0 =


(4.38)
 z 
 z  
0
0
1
0


ct0
ct
−√ β 2 0 0 √ 1 2
1−β
1−β
Diese Transformation kann als eine Drehung um einen ”imaginären” Winkel
ψ aufgefasst werden, d.h. wir können definiern
1
p
1 − β2
β
p
= sinh ψ
1 − β2
= cosh ψ
wodurch die Transformationsmatrix die Gestalt

cosh ψ 0 0 − sinh ψ

0
1 0
0


0
0 1
0
− sinh ψ 0 0 cosh ψ
annimmt.
110
(4.39)




(4.40)
u0 (x0 = 0)
@
@
u
@
@
@
s
@
£
£
£s
£
£
¡
¡
¡
¡
¡
£ ¡
³³ 0 0
s ³
£ ¡ ³³
x (u = 0)
@ £³
¡³³ s
³
@
£
³³¡
³
x
³
¡£ @
³
³
@
³
¡
£
³
@
¡ £
@
¡
£
@
¡
£
@
¡
£
@
¡
£
@
¡
£
@
Geometrisch heißt dies, dass die Einheitsintervalle auf der x- und u := ctAchse sich nicht, wie bei einer Rotation, in gleicher Richtung auf dem Kreis
x2 + u2 = 1 bewegen, sondern in entgegengesetzter Richtung auf den Hyperbelästen x2 − u2 = ±1. (Die x’ und u’-Achsen erhält man auch durch Lösen
der Gleichungen t0 = 0 bzw. x’=0).
Folgerungen aus der Lorentztransformation
a. Die Lorentzkontraktion: Betrachte einen im System K 0 ruhenden
Einheitsmaßstab. Die Koordinate der Endpunkte sind also durch die Gleichungen x01 = 0 und x02 = 1 (alle t) gegeben. Im ”ruhenden” System K
korrespondiert dies zu
p
(4.41)
x1 = vt
x2 = vt + 1 − β 2
Für einen Beobachter in K haben also
p die Enden des Maßstabes am für ihn
gleichen Zeitpunkt einen Abstand 1 − β 2 . Dies ist genau der Faktor, der
in der Lorentz-Fitzgerald Hypothese auftrat. Allerdings ist die Erklärung
ganz anders: Die Erklärung im vorherigen Abschnitt beruhte auf dem Verhalten der Maxwellgleichungen unter einer Galilei - Transformation; diese
Transformation beschreibt aber nach Einstein den Übergang zwischen zwei
zueinander bewegten Systemen nicht korrekt. In der Skizze erkennt man
auch die Symmetrie des Effektes: Auch die Weltlinie des Endes eines in K
ruhenden Maßstabes schneidet die x’- Achse (t0 = 0) links vom Punkt x’=1
b. Die Zeitdilitation: Betrachte eine in K 0 ruhende Uhr. Ihr Uhrzeiger
geht durch Null in t0 = t01 und t0 = t02 (am selben Ort x0 = x00 ). Im System
K wird der Abstand der zwei Ereignisse (x00 , t01 ) und (x00 , t02 ) gemessen als
t02 − t01
p
t2 − t1 =
;
1 − β2
(x01 = x02 )
(4.42)
der Zeitabstand erscheint also als verlängert (siehe Skizze für den Spezialfall
x00 = 0, t01 = 0). Auch hier ist der Effekt symmetrisch: Eine in K ruhende Uhr
111
erscheint einem Beobachter in K 0 genauso verlangsamt. Die Zeitdilitation ist
inzwischen wiederholt experimentell bestätigt worden.
Beispiel: µ- Mesonen werden von der kosmischen Strahlung in
etwa 10 km Höhe erzeugt. Ihre Geschwindigkeit ist etwa die
Lichtgeschwindigkeit, also ihre Flugzeit bis zur Erdoberfläche ist
3, 3.10−5 s. Die Lebensdauer eines µ- Mesons ist etwa 2.10−6 s; der
Fluss an senkrecht einfallenden Myonen wäre deshalb ohne Zeitdilitation um e−16,5 = 6, 83.10−8 abgeschwächt. In Wirklichkeit
p
beobachtet man kaum eine Schwächung: Der Faktor 1 − β 2
beträgt etwa 10−4 , wodurch der Abschwächungsfaktor nur noch
0,998 beträgt. Sehr genaue Messungen der Zeitdilitation gibt
es an in Speicherringen kreisenden Neutronen. Inzwischen ist
die Zeitdilitation auch mit normalen Cäsium - Uhren, von denen eine am Boden bleibt und zwei andere in Flugzeugen um
die Welt ostwärts bzw. westwärts umkreisen, gemessen worden.
Allerdings muss man dabei auch allgemein - relativistische Effekte
(Zeitverlangsamung in äußeren Potentialen, Effekte der Rotation)
berücksichtigen. Die von der Uhr registrierte Zeit ist dabei der sogenannten Eigenzeit gleichzusetzen, d.h. der Zeit in einem jeweils
mit der Uhr mitbewegten Koordinatensystem. Für ein infinitesimales Zeitelement dt ist das entsprechende Element der Eigenzeit
dτ gegeben durch
r
v(t)2
dτ = dt 1 − 2
(4.43)
c
oder
µ
¶
|~v (t)|2
2
2
2 2
c dτ = c dt 1 −
= c2 dt2 − dx2 − dy 2 − dz 2 , (4.44)
c2
wobei die Definition
dxi
(4.45)
dt
verwendet wurde. Weil das Intervall ds2 = c2 dt2 − dx2 − dy 2 − dz 2
dür jedes Inertialsystem dasselbe ist, erhält auch jeder Beobachter
für die Eigenzeit dτ denselben Wert.
Das Zwillingsparadoxon: Ein Raumfahrer fliegt mit einer Geschwindigkeit
v = 21 c nach einem 5 Lichtjahre entfernten Stern und zurück. Für
einen ruhenden Beobachter dauert die Reise 10 × 2 = 20a.
q Die
3
=
Eigenzeit des Raumfahrers dagegen ist um einen Faktor
4
0, 866 kürzer: für ihn sind nur 17, 32a vergangen. Am Ende seines
vi =
112
Abenteuers ist er also um 2 Jahre und 8 Monate jünger als ein
etwaiger zurückgebliebener Zwillingbruder. Hierbei sind Effekte
der Beschleunigungsphasen nicht berücksichtigt; diese können nur
aus der allgemeinen Relativitätstheorie berechnet werden. Sie
werden aber erwartungsgemäß von der insgesamt zurückgelegten
Streckt unabhängig sein und deshalb den oben errechneten Effekt nie aufheben können. Beachte, dass die Situation der beiden Brüder, anders als in den vorherigen Beispielen, nicht symmetrisch ist: Nur der zuhause gebliebene Bruder sitzt (näherungsweise)
in einem Inertialsystem!
c. Absolute Zukunft und Vergangenheit; der Lichtkegel: In den
obigen Diskussionen ist schon enthalten, dass dem Begriff der Gleichzeitigkeit in der Relativitätstheorie keine absolute Bedeutung zukommt. Zwei
an verschiedenen Orten x01 und x02 im System K 0 aufgestellte Uhren zeigen
im System K eine Gangunterschied
t2 − t1 =
t02 − t01 + cv2 (x02 − x01 )
v x0 − x01
p
=⇒ 2 p2
c
1 − β2
1 − β2
(4.46)
für t02 = t01 . Ob zwei räumlich getrennte Ereignisse gleichzeitig sind, hängt
also vom Koordinatensystem ab. Dagegen hat das Vorzeichen der Invariante
s212 = c2 (t2 − t1 )2 − |~r2 − ~r1 |2
(4.47)
schon eine absolute Bedeutung. Es gibt drei Möglichkeiten:
1. s212 > 0: Der Intervall heißt zeitartig. Lorentztransformationen mit
v < c können das Vorzeichen nicht ändern. Wohl gibt es eine Transformation, die für die zwei Ereignisse dieselben Ortskoordinaten liefert.
Das Ereignis (~r2 , t2 ) liegt bezüglich (~r1 , t1 ) in der absoluten Zukunft
oder in der absoluten Vergangenheit
2. s12 < 0: Der Intervall heißt raumartig. Das Vorzeichen von
t02 − t01 kann zu Null gemacht werden; zwischen den Ereignissen (~r1 , t1 )
und (~r2 , tr ) kann kein Signal mit Licht- oder Unterlichtgeschwindigkeit
laufen. (~r2 , t2 ) liegt bezüglich (~r1 , t1 ) im absoluten Anderswo.
3. s12 = 0. Die Ereignisse können durch ein Lichtsignal verknüpft werden.
Jedes Ereignis liegt auf dem Lichtkegel des anderen. Falls die Ereignisse
nicht zusammenfallen, kann man sie durch Lorentztransformation mit
|~v | < c weder am selben Ort noch zur selben Zeit stattfinden lassen.
113
In der Skizze sind die Verhältnisse 3- dimensional skizziert. Für das Getrenntbleiben von Zukunft und Vergangenheit ist es wesentlich, die Existenz von
Überlichgeschwindigkeiten auszuschließen. Einführen solcher Geschwindigkeiten
führt sofort zu in der Science Fiction Literatur beliebten Paradoxa, wie das
Grundthema des Films ”Zurück in die Zukunft”
1. Ein Jüngling wird aus dem Punkt 0 auf der Erde mit Überlichtgeschwindigkeit
zu einem rasch bewegten Raumschiff transportiert und trifft dort im Punkt
P an.
2. Er wird sofort zur Erde zurückgeschossen, gleichfalls mit v > c (aber: mit
positiver Neigung zur Achse t0 = const, also subjektiv in die Zukunft)
3. Er kommt dort in einem Punkt Q an, der früher liegt als 0 und begegnet
seiner Mutter als jungem Mädchen.
Im Abschnitt ”relativistische Mechanik” werden wir leider finden, dass Beschleunigung auf Überlichtgeschwindigkeiten mit endlichem Energieaufwand nicht
möglich ist.
d. Transformation der Geschwindigkeiten: Betrachte ein Teilchen, das
sich im System K mit der Geschwindigkeit ~v = (vx , vy , vz ) bewegt. Es gilt
also
dri
vi =
(4.48)
dt
Im System K 0 sind die Koordinaten des Teilchens bekanntlich
x − vt
x =p
1 − β2
0
0
y =y
t − cv2 x
t =p
1 − β2
0
0
z =z
Die Geschwindigkeit in K 0 ist definiert als
dr0
,
dt
(4.49)
also insbesondere
√vx −v
0
0
dt
vx − v
dx
dx
1−β 2
vx0 = 0 =
= 1− v vx =
0
dt
dt dt
1 − vvc2x
√ c2
(4.50)
1−β 2
und
vy0
p
vy 1 − β 2
dy 0
= 0 =
dt
1 − vvc2x
(4.51)
p
vz 1 − β 2
=
1 − vvc2x
(4.52)
bzw.
vz0
Für den Spezialfall vy = vz = 0 gilt auch vy0 = vz0 = 0 aber im allgemeinen
werden auch die Transversialkomponenten von ~v durch die Transformation
geändert.
114
Ein zweiter wichtiger Spezialfall tritt für den Fall, dass ~v die Geschwindigkeit
eines Lichtimpulses |~v | = c2 ist auf. Es gilt dann
µ
vx02 +vy02 +vz02 −c2
µ
=
=
1
1 − vvc2x
¶2 ·
2
(vx − v) + (1 − β
2
)(vy2
+
vz2 )
¸
³
vvx ´2
−c 1− 2
c
2
¶2 ·
¸
v 2 vx2
1
2
2
2
2
2
2
vx − 2vvx + v + (1 − β )(vy + vz ) − c + 2vvx − 2
1 − vvc2x
c
¶
µ
¤
£ 2
1
(4.53)
(vx + vy2 + vz2 )(1 − β 2 ) − c2 (1 − β 2 ) = 0
=
vvx
1 − c2
also auch |~v 0 | hat den Betrag c; die Transformation ändert nur die Richtung
der Geschwindigkeit. Als Beispiel betrachten wir die Aberration des Sternlichtes für einen Stern in einer Richtung senkrecht zur Erdbahn. Bezüglich
der Sonne hat dessen Licht eine Geschwindigkeit ~v = −cêz . Bezüglich der
Erde gilt
p
p
vx0 = −v
vy0 = 0
vz0 = vz 1 − β 2 = −c 1 − β 2
(4.54)
tan α =
vx0
β
p
=
vz0
1 − β2
(4.55)
Sternlicht
k 0 ' Erde
k ' Sonne
z0
z
£°£
Sternlicht
£
£
£
?
£
£°
£
£
£
£
£
£
£
Teleskop
x0
x
Weil die Umlaufgeschwindigkeit der Erde etwas 30 km/s beträgt, erhält man
α ' β ' 10−4 , was etwa 20 Bogensekunden entspricht. Im Laufe des Jahres
beschreibt ein Stern am Pol der Ellipsen am Himmel also einen Kreis mit
Radius 20”.
Eine zweite Anwendung ist der Fizeauscher Mitführungsversuch. Ein Lichtimpuls bewege sich in einer mit der Geschwindigkeit ±v parallel zum Licht
strömenden Flüssigkeit. Bezüglich der Flüssigkeit ist die Geschwindigkeit
115
des Lichtimpulses bekanntlich u =
sion). Im Laborsystem gilt also
c
n
(Unter Vernachlässigung der Disper-
µ
¶
±v
c
1
±v 1− 2
u =
v '
1 ± cn
n
n
0
Der Faktor 1 −
1
n2
c
n
(v << c)
(4.56)
heißt Mitführungskoeffizient.
Ströhmungsrohr
¡
¡
¡
v
-
@
@
@
¡
¡
¡
Strahlteiler
Quelle
¡
¡
¡
¡
¡
¾
¡
¡
¡
−v
¡
Det.
In der skizzierten Versuchsanordnung würde man also einen Laufzeitunterschied
¶
¸
µ
·
1
1
1 n2
(4.57)
− c
' 2lv 1 − 2
l c
n
c2
− v(1 − n−2 )
+ (1 − n−2 )
n
n
erwarten, wie auch experimentell bestätigt wurde.
116
4.3
Vierervektoren und Tensoren; Relativistische Mechanik
In diesem Abschnitt befassen wir uns mit dem Verhalten verschiedener physikalischer Größen unter Lorentztransformationen. Dies ist vor allem wichtig, wenn
wir die Newtonsche Mechanik so abändern wollen, dass sie unter Lorentztransformationen, statt wie bisher unter Galileitransformationen invariant
ist. Insbesondere werden wir versuchen, für die Beschreibung physikalischer
Phänomene Größen mit möglichst einfachem Verhalten unter Lorentztransformationen auszuwählen.
Das Beispiel der zu entwickelnden Theorie ist die Vektorrechnung und Vektoranalysis. Falls ein Naturgesetz in Vektorschreibweise formuliert ist, so
ist seine Invarianz unter Drehungen des Bezugssystems unmittelbar evident
(Allerdings muss natürlich verifiziert werden, dass Größen, die als Vektoren
geschrieben werden, sich auch tatsächlich wie Vektoren unter Drehungen
verhalten; das Einführen eines Formalismus beweist an und für sich keine
Naturgesetze!). Ich möchte in diesem Zusammenhang zwei Aspekte der Vektorrechnung hervorheben:
1. Der Transformationscharakter sämtlicher Größen unter Drehungen (bis
auf Skalare, die sich überhaupt nicht ändern) wird auf das Verhalten
des Ortsvektors ~r reduziert: Ein Vektor ist ein Satz dreier Größen, die
sich wie die Komponenten von ~r transformieren:
fi0 = Dij fj
falls gilt ri0 = Dij rj
(4.58)
ein Tensor zweiter Stufe verhält sich wie das dyadische Produkt (oder
Tensorprodukt) eines Ortsvektors mit sich selbst
Tij0 = Dik Djl Tkl
(4.59)
und so weiter für Tensoren höherer Stufe.
2. Es gibt ein unter Drehungen invariantes Skalarprodukt
~g = fi gi
f~
(4.60)
dessen Invarianz aus einer speziellen Symmetrieeigenschaften der Drehmatrizen erfolgt; die Gespiegelte ist gleich der Inversen:
−1
−1
Dij
= Dji ⇒ fi0 gi0 = Dij Dik fj gk = fj Dji
Dik gk = fj gj .
(4.61)
Das Skalarprodukt kann verwendet werden, um aus Tensoren oder
Paaren von Tensoren und/oder Vektoren Tensoren niedrigerer Stufe
zu bilden; so ist die Spur Tii eines Tensors zweiter Stufe ein Skalar und
das Skalarprodukt f~T = fi Tij ein Vektor.
117
In der Relativitätstheorie ist die Ausgangsgröße nicht der Ortsvektor, sondern
der Vierervektor, der die Raum- und Zeitkoordinaten eines Ereignis festlegt.
Wir wählen dafür die Notation
xµ = (x0 , x1 , x2 , x3 ) := (ct, x, y, z).
(4.62)
(Die Gründe für die Hochstellung der Indizes werden später klar.)
Unter Lorentztransformation verhält sich dieser Vierervektor wie
x0µ = Λµν xν
(4.63)
wobei Λµν die konstruierte Matrix (Gl.4.38) der Lorentztransformation darstellt.
Die invariante Länge
s2 = c2 t2 − x2 − y 2 − z 2
(4.64)
kann geschrieben werden als
s2 = xµ gµν xν
(4.65)

1 0
0
0
 0 −1 0
0 

g=
 0 0 −1 0 
0 0
0 −1
(4.66)
wobei gµν die 4 × 4 Matrix

darstellt. Die Invarianz dieses Ausdrucks folgt aus
x0µ gµν x0ν = xµ Λκµ gκλ Λλν xν = xµ gµν xν ,
(4.67)
λκµ gκλ Λλν = gµν
(4.68)
also
wie man leicht durch ausschreiben der relevanten Komponenten von Λ leicht
nachweist:
µ
¶µ
¶µ
¶
cosh ψ − sinh ψ
1 0
cosh ψ − sinh ψ
− sinh ψ cosh ψ
0 −1
− sinh ψ cosh ψ
µ
¶µ
¶
cosh ψ − sinh ψ
cosh ψ − sinh ψ
=
− sinh ψ cosh ψ
sinh ψ − cosh ψ
µ
¶ µ
¶
cosh2 ψ − sinh2 ψ
0
1 0
=
=
(4.69)
0 −1
0
sinh2 ψ − cosh2 ψ
Ein zweites Beispiel einer skalaren Größe (neben der Länge eines Vierervektors oder des Skalarprodukts f µ gµν hν zweier Vierervektoren) ist die Phase
118
einer elektromagnetischen Welle. Die Aussage ”Die Welle hat in (ct, ~r) ein
Maximum oder einen Knoten” sollte eine vom Bezugssystem unabhängige
Bedeutung haben. Deshalb müsste der Ausdruck
φ(~r, t) = ~k~r − ωt
(4.70)
der offensichtlich linear ist in den Komponenten xµ als das Skalarprodukt
des Vierervektors xµ mit einem Wellenvierervektor k µ aufzufassen sein. Man
prüft leich nach, dass gilt
ω
mit k = ( , kx , ky , kz ).
c
φ(~r, t) = −k µ gµν xν
(4.71)
Der Vierervektor k µ hat also als räumliche Komponenten die Komponenten
des gewöhnlichen Wellenvektors ~k und als zeitliche Komponente den Betrag
2
von ~k. Die Viererlänge k µ gµν k ν = ωc2 − |~k 2 | erweist sich deshalb als Null.
Das Verhalten der k µ unter Lorentztransformationen ist jetzt auch klar: die
Komponenten k µ transformieren wie die xµ :
k 0µ = Λµν k ν
(4.72)
also insbesondere
v
kx
ω0
1
ω
=p
− pc
2
c
1−β c
1 − β2
kx0
kx − vω
c2
=p
1 − β2
ky0 = ky
kz0 = kz
(4.73)
Der erste Ausdruck beschreibt eine Änderung der Frequenz der Welle; für
β << 1 erhält man den klassischen Ausdruck für den Dopplereffekt:
³
v|| ´
0
ω =ω 1−
(4.74)
c
Der volle Ausdruck erhält Korrekturen dazu; insbesondere tritt auch für rein
transversale Geschwindigkeiten eine Frequenzverschiebung auf (transversaler
Dopplereffekt). Die Transformationsregeln für die räumlichen Komponenten
von k µ zeigen, dass neben der Längenänderung von ~k auch noch eine Drehung
auftritt. Dies ist nichts anderes als die schon in Gl.4.53-4.55 begegnete Aberration.
Ein weiteres Beispiel eines Vierervektors ist die Vierergeschwindigkeit, d.h.
die Ableitung des Vektors xµ nach der Eigenzeit des bewegenden Teilchens
(Die normale Geschwindigkeit hat, wie im vorhergehenden Abschnitt gezeigt,
ein ziemlich kompliziertes Transformationsverhalten). Aus Gl4.43 folgt
1
d
d
=p
dτ
1 − β 2 (τ ) dt
119
(4.75)
Man erhält also für die Komponenten der Vierergeschwindigkeit uµ :
1
(u0 , u1 , u2 , u3 ) = p
1 − β 2 (τ )
(c, vx , vy , vz ).
(4.76)
Das invariante Längenquadrat dieses Vierervektors hat offensichtlich den universellen Wert uµ gµν uν = c2 .
Nochmaliges Differenzieren von uµ nach der Eigenzeit liefert die Viererbeschleunigung
d µ
aµ =
u .
(4.77)
dτ
Es liegt also nahe, als relativistische Verallgemeinerung des zweiten Newtonschen Gesetzes zu postulieren
m0 aµ = K µ ,
(4.78)
wobei m0 eine invariante Masse ist und K µ ein Vierervektor, dessen räumliche
Komponenten für niedrige Geschwindigkeiten (streng: im momentanen Ruhesystem des Teilchens) die vertraute Newtonsche Kraft liefern. Die Gl.4.78
wurde zuerst von Minkowski vorgeschlagen und die Größe K µ heißt deshalb
Minkowski Kraft. Die räumlichen Komponenten von Gl.4.78 können mit Hilfe
der soeben benutzen Beziehung zwischen t und τ umgeschrieben werden:
~
K
d
~v
p
=p
1 − β 2 dt 1 − β 2
1 − β2
p
mit
m0
~ :=
K
p
1 − β 2 (Kx , Ky , Kz ).
(4.79)
(4.80)
~ hat im Ruhesystem des Teilchens und für nicht zu große BeschleDie Größe K
unigungen die Eigenschaften der Newtonschen Kraft. Die nullte Komponente
von K µ folgt aus der Bedingung, dass die Viererlänge von uµ den konstanten
Wert c hat. Dies bedeutet
also
d µ
(u gµν uν ) = 2K µ gµν uν = 0
dτ
(4.81)
~v
~v
K 0c
K~
K~
0
p
p
=⇒
K
=
=
.
1 − β2
1 − β2
c 1 − β2
(4.82)
~
Im nichtrelativistischen Grenzfall reduziert sich K 0 auf die von der Kraft K
erbrachte Arbeit; diese muss wegen der Energieerhaltung gleich der Zunahme
120
der kinetischen Energie des Teilchens sein, genauso wie die Kraft selber gleich der Änderung des Impulses des Teilchens sein muss. Die Minkowskische
Bewegungsgleichung liefert also eine Zusammenfassung und zugleich eine relativistische Verallgemeinerung der Erhaltungssätze für Energie und Impuls:
d
m0 c2
~ v.
= K~
=p
2
dt
1−β
d m0~v
~
p
=K
dt 1 − β 2
Die Identifikation von √m0 c
2
1−β 2
(4.83)
mit der kinetischen Energie erfolgt durch Tay-
lorentwicklung:
1
m c2
1
p 0
= m0 c2 (1 + β 2 + ...) = m0 c2 + m0 v 2 + ...
2
2
1 − β2
(4.84)
Der Zusatzterm m0 c2 ist eine eher unbedeutende additive Konstante solange
das Teilchen seine Identität nicht ändert. Bei chemischen Reaktionen und
sonstigen Stoßprozessen sowie bei radioaktiven Zerfällen wird der Term aber
wichtig. In der klassischen Mechanik ist bei Stößen die Summe der Teichenimpulse immer eine erhaltene Größe, die Summe der kinetischen Energien
dagegen nur bei elastischen Stößen, in denen sich die innere Energie der
Teilchen nicht ändert. In einer relativistischen Theorie ist ein solcher Unterschied aber nicht möglich: Die vier Komponenten des Viererimpulses
1
pµ = m0 uµ = p
1 − β2
(m0 c, m0~v )
(4.85)
können durch Lorentztransformationen miteinander vermischt werden. Falls
in einem Stoßprozess die Summe der räumlichen Komponenten der Viererimpulse der beteiligten Teilchen erhalten ist, so muss dies auch mit der Summe
der zeitlichen Komponenten der Fall sein. Im nichtrelativistischen Grenzfall
bedeutet dies, dass eine Änderung der gesamten kinetischen Energie durch
eine Änderung des Massenterms ausgeglichen werden muss:
X
X
∆(
m0i vi2 ) + ∆(
m0i c2 ) = 0.
(4.86)
i
i
Einer Änderung der inneren Energie eines Teilchens entspricht also eine
Änderung der Ruhemasse gemäß
∆Eint = (∆m0 )c2 .
(4.87)
Dies ist die berühmte Äquivalenz von Masse und Energie.
Zum Schluss betrachten wir noch den Impulsvektor im momentanen Ruhesystem des Teilchens. Dort verschwinden seine räumlichen Komponenten;
121
der Vektor hat die Gestalt
pµ = (m0 c, 0, 0, 0).
(4.88)
Für Teilchen mit der Ruhemasse m0 = 0 würde dies das Verschwinden des
gesamten Ausdrucks bedeuten (im Ruhesystem und wegen der Linearität
der Lorentztransformation deshalb in jedem System). Es gibt aber einen
Ausweg: Für ein Teilchen mit einer Geschwindigkeit vom Betrag c ist eine
Transformation in das Ruhesystem nicht möchlich:
Teilchen mit Ruhemasse Null haben immer |~v | = c.
Andererseits können Teilchen mit endlicher Ruhemasse die Lichtgeschwindigkeit
nie erreichen: Die Teilchenenergie
m0 c2
E=p
1 − β2
(4.89)
divergiert offensichtlich für β → 1. Die Aufnahme einer endlichen Menge Energie kann also nie ein Teilchen auf Lichtgeschwindigkeit bringen (geschweige
denn auf Überlichtgeschwindigkeit)
Kovariante und Kontravariante Vektoren.
Die in Gl.4.70 diskutierte Phase ist ein Beispiel eines skalaren Feldes; d.h.
einer Größe, die für jeden Punkt des Raum - Zeit Kontinuums einen skalaren
Wert annimmt. In der normalen Vektorananlysis erhält man aus einem
skalaren Feld ein Vektorfeld durch Bildung des Gradienten. Der Vierergradient
∂φ
∂µ φ :=
= gµν k ν
(4.90)
∂xµ
ist aber offensichtlich kein Vierervektor vom soeben betrachteten Typ; es gilt
vielmehr
∂µ0 φ = gµν Λνλ k λ = (Λ−1 )νµ gνλ k λ = (Λ−1 )νµ ∂ν φ
(4.91)
Dabei ist Λνµ die Matrix der Lorentztransformation, die in unserer jetzigen
Notation die Gestalt

 

γ
−γβ 0 0
cosh ψ − sinh ψ 0 0
 −γβ


γ
0 0 
 =  − sinh ψ cosh ψ 0 0 
Λ=
(4.92)
 0
0
1 0  
0
0
1 0 
0
0
0 1
0
0
0 1
hat. Die in Gl.4.91 benützte Identität gµν Λνλ = (Λ−1 )νµ gνλ erhält man aus
dem schon bekannten
(4.93)
Λκµ gκλ Λλν = gµν
122
durch Matrixmultiplikation von links mit (Λ−1 )µρ . Die Transformationseigenschaft (4.91) kann auch direkt aus der Definition des Vierergradienten hergeleitet
werden. Aus der Definition der Lorentztransformation
x0µ = Λµν xν
(4.94)
∂x0µ
∂xν
(4.95)
folgt sofort
Λµν =
und für die inverse Transformation
(Λ−1 )µν =
∂xµ
.
∂x0ν
(4.96)
Auswertung von ∂µ0 φ über die Kettenregel ergibt jetzt
∂µ0 φ =
∂φ ∂xν
∂φ
=
= (Λ−1 )νµ ∂ν φ.
∂x0µ
∂xν ∂x0µ
(4.97)
Wir haben also offensichtlich zwei Arten von Vektoren: solche die mit Λµν
transformieren und solche, die mit (Λ−1 )µν transformieren. Vekoren vom ersten Typ (d.h. der Sorte xµ ) heißen kontravariant und werden mit hochgestelltem Index geschrieben; Vektoren vom zweiten Typ (d.h. der Sorte ∂µ φ)
heißen kovariant und werden mit niedergestelltem Index geschrieben. Aus
einem kontravarianten Vektor k µ kann man den dazugehörigen kovarianten
Vektor kµ durch Matrixmultiplikation mit gµν bilden: kµ = gµν k ν . Weil gµν
sein eigenes Inverses ist gilt auch
k µ = g µν kν
(4.98)
wobei g µν vorläufig als eine alternative Schreibweise für gµν aufzufassen ist.
Tensoren
Analog zum gewöhnlichen Vektorformalismus definiert man einen Tensor nter Stufe als ein in einem gewissen Bezugssystem definiertes Gebilde mit
4n Komponenten, die unter Lorentztransformationen wie das direkte Produkt (auch Tensorprodukt oder dyadisches Produkt genannt) von n Vektoren transformieren. Weil es zwei Arten von Vektoren gibt, gibt es (2n + 1)
Typen von Tensoren n-ter Stufe. Wir werden uns im Folgenden vorwiegend
mit Tensoren zweiter Stufe befassen. Es gibt davon 3 Typen:
1. Kontravariante Tensoren T µν , die transformieren wie k µ hν
2. Kovariante Tensoren Tµν , die transformieren wie kµ hν
123
3. Gemischte Tensoren T µ ν , die transformieren wie k µ hν oder Tµ ν , die
transformieren wie kµ hν
T 0µν = Λµκ Λνλ T κλ
T 0µ
ν
= Λµκ (Λ−1 )λν T κ
0
Tµν
= (Λ−1 )κµ (Λ−1 )νλ Tκλ
Tµ0
λ
ν
= (Λ−1 )κµ Λνλ Tκ
(4.99)
λ
(4.100)
Die Spur Tµµ eines gemischten Tensors transformiert offensichtlich wie ein
Skalar, wie aus der obigen Formel sofort einsichtlich ist:
Λµκ (Λ−1 )λµ = δκλ
(4.101)
Bemerkung 1: Die Transformationsmatrizen Λµν sind trotz ihrer Erscheinung keine Tensoren, weil sie nicht in einem bestimmten System definiert sind,
sondern Größen in verschiedenen Bezugssystemen miteinander verknüpfen!
(Genauso sind Drehmatrizen in der Vektorrechnung keine Tensoren.)
Bemerkung 2: Der metrische Tensor gµν ist sehr wohl ein richtiger Tensor, jedoch einer der in jedem Bezugssystem denselben Wert hat. Die schon
einige Male benutzte Beziehung Λκµ Λλν gκλ = gµν entspricht genau dem Transformationsverhalten eines kovarianten Tensors. Weil (Λ−1 genauso wie Λ
eine Lorentztransformation ist (nur mit dem anderen Vorzeichen von v) gilt
genauso
(Λ−1 )µκ (Λ1 )νλ g κλ = g µν
(4.102)
also die Matrix g (die Diagonalmatrix mit Elementen 1,-1,-1,-1) ist auch als
kontravarianter Tensor aufzufassen.
Skalare Multiplikation, Verjüngung
Weil der metrische Tensor gµν (oder g µν ) einen kontravarianten Vektor in
seinen kovarianten Zwilling umwandelt (oder umgekehrt), kann man das
Skalarprodukt zweier kontravarianter Vektroren auch schreiben als
(f, h) := f µ gµν hν = f µ hν = fµ hν .
(4.103)
Die Summation über einen Index, der einmal als oberer und einmal als unterer Index vorkommt, ergibt also in diesem Fall (wie bei der Spurbildung
eines gemischten Tensors) einen Skalar. Dies ist auch aus den Transformationseigenschaften ersichtlich: mit dem oberen Index ist eine Λ- Matrix
assoziiert, mit dem unteren eine Λ−1 - Matrix und mit der Summe das Matrixprodukt dieser beiden, also die Einheitsmatrix. Allgemein bildet man aus
einem gemischten Tensor (m + 2)-ter Stufe einen Tensor m-ter Stufe durch
Summation über einen Index, der einmal als oberer und einmal als unterer
Index vorkommt. Dieser Prozess heißt Verjüngung oder Kontraktion.
124
Die Summation über eine Zahl, die zweimal als oberer oder zweimal als unterer Index vorkommt, liefert hingegen keine Größe mit vernünftigem Transformationscharakter. Einschränkung der Einsteinkonvention: Wir werden
deshalb ab jetzt (Nachprüfung des Skriptums erweist: eigentlich schon ab
Anfang dieses Abschnittes) die Einsteinsche Konvention nur gelten lassen
für Indizes, die einmal als oberer und einmal als unterer Index vorkommen.
Schlussbemerkung: Die drei Gestalten des metrischen Tensors. Man prüft
leicht nach: g µκ g νλ gλκ = g µν ; g µκ gκν = δνµ (die 4-dimensionale Einheitsmatrix). Die Einheitsmatrix bildet also mit g µν und gµν einen Tensor - Drilling.
125
4.4
Relativistische Elektrodynamik
Die spezielle Relativitätstheorie wurde eingeführt, um eine Rahmentheorie zu schaffen, innerhalb derer sowohl das Relativitätsprinzip als auch die
Maxwellgleichungen streng gültig sein können. Allerdings haben wir dies bis
jetzt nur für einen Aspekt der Maxwellgleichungen, die Konstanz der Lichtgeschwindigkeit, auch wirklich nachgewiesen. In diesem Abschnitt werden
wir die Invarianz der vollständigen Maxwellgleichungen nachweisen. Dabei
werden wir zugleich auch die elektromagnetischen Größen in Vierervektoren
und Vierertensoren ausdrücken, damit ihr Transformationsverhalten einfach
zu ermitteln ist.
Als Ausgangspunkt betrachten wir die Quellen des elektromagnetischen Feldes,
die Ladungen und Ströme. Wir schlagen vor, diese zu einem Viererstrom 2
J µ = (cρ, jx , jy , jz )
(4.104)
zusammenfassen. Dessen Viererdivergenz
∂ρ
+ ∇~j
∂t
∂µ J µ =
(4.105)
verschwindet wegen der Kontinuitätsgleichung. Für eine Vektordichte mit
verschwindender Viererdivergenz ist das Integral über den Raum nicht nur
in der Zeit erhalten, sondern auch ein Lorentzskalar.
v = −v1 + v2
t0 = t0
©
©
H
HH ©© AAU
©
© HH
j 6
©© v2 H
t=0
©
HH
¢
¢
¢
6
¢
¢
©
v1 ¢® ©©
©
©©
©©
AAU
Um dies zu zeigen, verwenden wir den 4-dimensionalen Gaußschen Satz:
Z
Z
µ 4
∂µ A d x =
Aµ d3 Sµ
(4.106)
V
S
und wählen für V ein Volumen begrenzt durch die Hyperebenen t = 0 (im
Laborsystem) und t = t00 (in irgendeinem Inertialsystem) und eine räumliche
2
Eigentlich ist j µ (x) kein Vierervektor, sondern eine sogenannte Vektordichte; der Unterschied ist aber für unsere Zwecke unwichtig.
126
Begrenzung außerhalb des Gebietes wo J µ (x) von Null verschiedene Werte
annimmt. Die Normalen auf die Hyperebenen zeigen entlang den jeweiligen
Zeitrichtungen; falls Aµ wie ein Vierervektor transformiert gilt also
Z
Z
0
3
(4.107)
A (0, ~r)c ~r = A00 (t00 , ~r0 )d3~r0
d.h. das Raumintegral von A0 (t, ~r) ist nicht nur unabhängig von t0 , sondern
auch vom Bezugssystem.
Als Nächstes betrachten wir die Potentialgleichungen (in Lorentzeichung)
~=−
¤A
4π ~
j
c
¤φ = −4πρ
(4.108)
Der Operator ¤ ist ein skalarer Operator:
1 ∂2
¤ = ∇ − 2 2 = −∂µ g µν ∂ν = −∂µ ∂ µ
c ∂t
2
(4.109)
~ einführen, wofür gilt
Wir können also einen Vierervektor φν = (φ, A)
∂µ ∂ µ φ ν =
4π ν
J
c
(4.110)
Das Viererpotential erfüllt zusätzlich die Nebenbedingung
~+
∇A
1 ∂φ
=0
c ∂t
oder ∂µ φµ = 0
(4.111)
Diese zwei Ausdrücke fassen die gesamten Maxwellgleichungen zusammen in
einer offensichtlich Lorentz - invarianten Form.
~ wird aus A
~ und φ abgeleitet über
Das elektrische Feld E
~
~ = − 1 ∂ A − ∇φ
E
c ∂t
(4.112)
∂φi
∂φ0
−
= −(∂0 φi + ∂i φ0 ) = −(∂ 0 φi − ∂ i φ0 )
∂x0
∂xi
(4.113)
also
Ei = −
wobei wir bei der letzten Umformung die Indizes der Differentialoperatoren
~ erhält man
mittels g µν angehoben haben. Für die Komponenten von B
ähnliche Ausdrücke; so gilt für die Komponente Bx :
~ x = ∂y Az − ∂z Ay = ∂2 φ3 − ∂3 φ2 = −(∂ 2 φ3 − ∂ 3 φ2 ). (4.114)
Bx = (∇ × A)
127
Die elektrischen und magnetischen Felder kann man also zusammenfassen in
einem antisymmetrischen kontravarianten Tensor zweiter Stufe


0 −Ex −Ey −Ez
 Ex
0
−Bz By 

F µν = ∂µφν − ∂ ν φµ = 
(4.115)
 Ey Bz
0
−Bx 
Ez −By Bx
0
~ und B
~ sofort abgelesen
Jetzt können die Transformationseigenschaften von E
werden. Sie folgen aus
F 0µν = Λµκ Λνλ F κλ
(4.116)
also für die einzelnen Komponenten (nach einigem Rechnen)
Ex0 = Ex
Bx0 = Bx
Ey0 = γ(Ey − βBz ) By0 = γ(By + βEz )
Ez0 = γ(Ez + βBy ) Bz0 = γ(Bz − βEy )
(4.117)
(4.118)
(4.119)
(4.120)
~ → B;
~
An diesen Formeln sieht man, dass man nach der Substitution E
~
~
~
~ also
B → −E eine gleichartige Struktur erreicht; man kann aus E und B
einen zweiten kontravarianten Tensor bilden, den dualen Tensor


0 −Bx −By −Bz
 Bx
0
Ez −Ey 

(4.121)
F̃ µν = 
 By −Ez
0
Ex 
Bz Ey −Ex
0
Mit Hilfe von F µν und F̃ µν lassen sich auch die Maxwellgleichungen sehr
kompakt schreiben. Der Ausdruck
(
~ = 4πρ
4π
∇E
(ν = 0)
∂µ F µν =
J ν =⇒
(4.122)
~
~ − 1 ∂ E = 4π ~j
c
∇×B
(ν
=
1,
2,
3)
c ∂t
c
(
∂µ F̃ µν = 0 =⇒
~ =0
∇B
~+
∇×E
~
1 ∂B
c ∂t
(ν = 0)
=0
(= 1, 2, 3)
(4.123)
Weiters liest man aus Gl.4.119 die Existenz zweier Lorentz - Skalare ab:
~2 − B
~ 2 = 1 F µν Fνµ
E
2
(4.124)
~B
~ = 1 F µν F̃νµ
E
4
(4.125)
128
Zum Schluss dieses Abschnittes betrachten wir noch die Lorentzkraft
~ = e(E
~ + ~v × B).
~ In diesem Abschnitt erkennt man die räumlichen KompoK
c
nenten des Skalarprodukts zwischen F µν und der kovaranten Teilchengeschwindigkeit
uµ = γ(c, −~v ).
(4.126)
Der Faktor γ, der zuerst zuviel erscheint, entfällt, falls wir zur zugehörigen
Minkowski - Kraft übergehen
e
K µ = F µν uν
c
(4.127)
Die Nullkomponente ergibt erwartungsgemäß
K0 =
γ ~
eE~v
c
(4.128)
also bis auf den Faktor γ die vom Feld geleistete Arbeit, wie in Gl.4.82 Das
Magnetfeld liefert bekanntlich zur geleisteten Arbeit keinen Beitrag.
129
4.5
Die Lorentzgruppe
Bisher haben wir uns nur mit Lorentztransformationen beschäftigt, für die
die Relativgeschwindigkeit der beiden Systeme entlang der x-Achse liegt.
Solange nur zwei Systeme im Spiel sind, ist dies selbstverständlich erlaubt.
Falls wir aber z.B. die momentanen Ruhesysteme für ein Teilchen diskutieren wollen, das sich entlang einer gekrümmten Bahn bewegt, so reicht
diese einfache Beschreibung nicht mehr aus. Als Erstes werden wir daher die
Lorentztransformation für eine willkürliche Richtung von ~v bestimmen. Die
Verallgemeinerung von
ct0 = γ(ct − βx)
x0 = γ(x − βct)
y0 = y
z0 = z
(4.129)
lautet in Dreiervektornotation (x0 , ~x)
~ x)
x00 = γ(x0 − β~
~x0 = ~x + (γ + 1)
~ xβ)
~
β(~
~ 0
− γ βx
2
β
(4.130)
(Der zweite Term in ~x0 enthält die Projektion von ~x auf den Geschwindigkeitsvektor β~ = ~vc ; der Term verschwindet also für die Komponenten von ~x0 senkrecht
~ xβ)
~
zu β~ und gibt (γ − 1)x|| für die Komponente x|| = β(~
). Die Matrix für die
β2
durch 4.130 vermittelte Transformation ist


γ
−γβ1
−γβ2
−β3
γ−1
 −γβ 1 + γ−1 β 2 γ−1 β β
ββ 
1

β2 1
β2 1 2
β2 1 3 
~
Λ(β) = 
(4.131)

γ−1
γ−1 2
γ−1
ββ
1 + β 2 β2
ββ
 −γβ2
β2 1 2
β2 2 3 
γ−1
−γβ3 γ−1
ββ
ββ
1 + γ−1
β2
β2 1 3
β2 2 3
β2 3
Die so erhaltene Matrix ist für jeden Vektor β~ symmetrisch. Weiters ist die
~ invariant, wie man z.B. durch
invariante Länge s2 = x20 − |~x|2 unter Λ(β)
direkte Substitution beweisen kann. Ein eleganterer Beweis erfolt, falls man
in Gl.4.131 in der Form
~ = I − βγK + (γ − 1)K 2 = (I − K 2 ) − sinh ψK + cosh ψK 2 (4.132)
Λ(β)
β̂
β̂
β̂
β̂
β̂
schreibt, mit der bekannten Parametrisierung βγ = sinh ψ, γ = cosh ψ, und

 2


β
0
0
0
0 −β1 −β2 −β3

1 
0
0 
β12 β1 β2 β1 β3 

 −β1 0
 ; K2 = 1  0
Kβ̂ =
0
0  β̂ β 2  0 β1 β2 β22 β2 β3 
|β|  −β2 0
0 β1 β3 β2 β3 β32
−β3 0
0
0
(4.133)
130
Man sieht leicht, dass gilt Kβ̂3 = Kβ̂ ; alle höheren geraden Potenzen sind
gleich Kβ̂2 , alle ungeraden Potenzen sind gleich Kβ̂ . Der obige Ausdruck für
~ geht also nach Substitution der Potenzreihen für sinh ψ und cosh ψ in
Λ(β)
die Potenzreihen für die Marixfunktion exp(−ψKβ̂ ) über:
Λ(β) = e−ψKβ̂
(4.134)
d
~
~ = Λ(β)(−K
~
~
Λ(β)gΛ(
β)
β̂ g − gKβ̂ )Λ(β) = 0
dψ
(4.135)
und man sieht sofort
wegen des Verschwindens des Ausdrucks in eckigen Klammern. Weil Λ(0) = 0
ist also Λ̃gΛ gleich g und damit auch
s02 = xΛ̃gΛx = xgx = s2
(4.136)
wobei x für den Vierervektor (x0 , ~x) steht.
Die Lorentztranformationen sind allerdings nicht die allgemeinsten linearen
Transformationen unter denen s2 invariant ist. Ein weiteres Beispiel sind die
räumlichen Drehungen; diese lassen x02 und ~x2 einzeln invariant, also auch
deren Differenz. Für eine räumliche Drehung kann man die Parametrisierung
Dω~ = e−ωSω̂
einführen mit

0 0
0
0
1  0 0 −ω3 ω2 
;
Sω̂ = 
0 −ω1 
ω  0 ω3
0 −ω2 ω1
0

0
0
0
0
2
2

1
0 ω1 − ω
ω1 ω2
ω1 ω3
Sω̂2 = 2 
2
2

0 ω1 ω2
ω2 − ω
ω2 ω3
ω
0 ω1 ω3
ω2 ω3
ω32 − ω 2
(4.137)





(4.138)
und, wie man relativ leicht sieht,
Sω̂3 = −Sω̂
(4.139)
Dω̂ = I − Sω̂2 − sin ωSω̂ − cos ωSω̂ .
(4.140)
also
Man erkennt auch die bekannte Eigenschaft der Drehmatrizen
−1
D−ω
= D̃ω~
~ := (Dω
~)
131
(4.141)
in diesen Ausdrücken leicht wieder. Wir suchen jetzt die allgemeinste reelle
Transformation, die s2 invariant lässt und stetig mit der Identität verbunden
werden kann. Die Matrix ist also Element einer stetigen Klasse invertierbarer
Matrizen A(λ) mit A(0) = I. Weil eine invertierbare Matrix keine Eigenwerte Null haben darf, sind die Eigenwerte von A(λ) für alle Werte von λ
ungleich Null; weil sie für λ → 0 nach Eins gehen müssen, sind sie daher alle
positiv und A lässt sich schreiben als
A = eL .
(4.142)
Jetzt muss gelten ÃgA = g, also Ãg = gA−1 .
Wegen g 2 = 1 muss auch gelten g Ãg = A−1 = e−L
Andererseits gilt egL̃g = 1 + g L̃g + 12 g L̃2 g + ... = g Ãg
Die Matrizen gLg und −L müssen deshalb identisch sein. Ausarbeiten dieser
Bedingungen ergibt, dass L die Gestalt


0
L01
L02 L03
 L01
0
L12 L13 

L=
(4.143)
 L02 −L12
0
L23 
L03 −L13 −L23 0
haben muss. L ist also die Summe einer infinitesimalen Lorentztransformation vom Typ Kβ̂ und einer infinitesimalen Drehung vom Typ Sω̂ . Weiters
gilt Sp(L) = 0, also
det A = eSp(L) = 1.
(4.144)
Um die allgemeinste Matrix A zu finden, die s2 invariant lässt müssen wir
noch zulassen, dass die hier gefundenen Matrizen noch mit denen der Raumspiegelung


1 0
0
0
 0 −1 0
0 

Π~x = 
(4.145)
 0 0 −1 0 
0 0
0 −1
oder der Zeitspiegelung

−1
 0
Π0 = 
 0
0
0
1
0
0
0
0
1
0

0
0 

0 
1
(4.146)
multipliziert werden dürfen oder auch mit beiden oder keiner der beiden.
Spin-Bahn Kopplung und Thomaspräzession
132
Als Anwendung des in den letzten zwei Abschnitten behandelten Formalismus betrachten wir einen relativistischen Effekt aus der Atomphysik, die
Spin-Bahn Kopplung. Nach Uhlenbeck und Goudsmit (1926) besitzt das
Elektron einen intrinsischen Drehimpuls ~s und damit ein assoziertes magnetisches Moment
ge
~µ =
~s
(4.147)
2mc
wobei g bis auf winzige Korrekturen den Wert g = 2 hat. In einem Magnet~ 0 empfindet ein magnetisches Moment bekanntlich ein Drehmoment
feld B
~ = ~µ × B
~ 0.
N
(4.148)
Das assozierte Potential beträgt
~ 0.
U = −~µB
(4.149)
~ 0 durch das Magnetfeld im RuhIn der Relativitätstheorie soll allerdings B
esystems des Elektrons ersetzt werden. Weil im Atom auch ein elektrisches
~ herrscht, erhalten wir also nach Anwendung der TransformationsFeld E
~
formeln (Gl.4.121) (in niedrigster Ordnung in β)
~ 0 = ~µ × (B
~ 0 − ~v × E)
~
N
c
~ 0 − ~v × E).
~
U 0 = −~µ(B
c
(4.150)
~ von einem zentralsymmetrischen elektrostatischen Potential hergeleitet
Weil E
ge~s
werden kann, gilt (mit ~µ = 2mc
)
~ = − 1 ~r dV =⇒ U 0 = ge ~sB
~ + g (~sL)
~ 1 dV
E
2
2
e r dr
2mc
2m c
r dr
(4.151)
~ = m~v × ~r der Bahndrehimpuls des Elektrons ist. Der Effekt kann
wobei L
tatsächlich gemessen werden; man findet dann allerdings nur etwa die Hälfte
~
des Terms mit ~sL.
Dieser Effekt wurde von Thomas erklärt. Er machte darauf aufmerksam,
dass das Elektron im Laufe seiner Umdrehung des Kerns dauernd senkrecht
zu seiner Geschwindigkeit beschleunigt wird. Um ein Ruhesystem des Elektrons zu bleiben müssen also dauernd Lorentztransformationen um zueinander senkrechte Achsen ausgeführt werden. Das Produkt zweier solcher Transformationen ist aber selbst keine reine Lorentztransformation mehr, sondern
das Produkt einer Lorentztransformation und einer Rotation. Falls wir für
t = 0 die Geschwindigkeit entlang der x-Achse und die Beschleunigung entlang der y-Achse wählen, so erhalten wir für den Zusammenhang zwischen
133
x0 (im Ruhesystem für t = 0) und x im Laborsystem:


γ
−βγ 0 0
 −βγ
γ
0 0 
x
x0 = 
 0
0
1 0 
0
0
0 1
(4.152)
(bis zu linearen
und für x00 im Ruhesystem zu Zeit t + ∆τ mit ∆β = a∆t
c
Termen in ∆β)


γ
−βγ −∆βγ 0
γ−1
 −βγ
γ
∆β 0 
β
x
x00 = 
(4.153)
γ−1
 −∆βγ
∆β
1
0 
β
0
0
0
1
Elimination von x liefert:


1
0
−γ∆β 0
γ−1

0
1
∆β 0 
β
 x0
x00 = 

 −γ∆β − γ−1 ∆β
1
0
β
0
0
0
1
(4.154)
d.h. eine infinitesimale Lorentztransformation über ∆βêy und eine Drehung
um
γ−1
βγ 2 a
βaêz
∆Ω = −
∆βêz = −
êz dt ' −
dt
(4.155)
β
1+γ c
2c
2
wobei wir β 2 = γ γ−1
benutzt haben und nur die niedrigste Ordnung in
2
β beibehalten haben. Das Ruhesystem des Elektrons rotiert also mit der
Winkelgeschwindigkeit
ω
~T = −
βaêz
~v × ~r 1 dV
1 ~ 1 dV
=−
= − 2 2L
2
2c
2emc r dr
2m c r dr
(4.156)
Diese Rotation heißt Thomaspräzession. Um im momentanen Ruhesystem
des Elektrons zu bleiben müssen wir also nicht nur die Richtung des Geschwindigkeit
andauernd justieren, sondern auch noch die Thomaspräzission mitmachen.
Auch die Präzission des Spins erhält man dadurch einen Zusatzterm:
µ ¶
ge ~ ~v
ds
~ + ~s × ω
(B − × E)
~T
(4.157)
= ~s ×
dt Lab
2mc
c
und für die Wechselwirkungsenergie erhält man letztendlich
U 00 =
ge ~
g
~ 1 dV + ~s~ωT
~sB +
(~sL)
2
2
2mc
2m c
r dr
134
(4.158)
oder durch Einsetzen von Gl.4.156
U 00 =
ge ~
g − 1 ~ 1 dV
~sB +
(~sL)
,
2mc
2m2 c2
r dt
(4.159)
womit die Halbierung des Spin-Bahn Kopplungsterms erklärt ist.
Der Präzissionseffekt tritt nicht nur für elektrisch geladene Teilchen auf; auch
ein Gyroskop in einer Erdumlaufbahn müsste den Effekt zeigen. Zur Berechnung braucht man aber die relativistische Verallgemeinerung der Newtonschon Gravitationsgesetze, d.h. die allgemeine Relativitätstheorie. Das Experiment ist technisch schwierig und könnte den Verzögerungen im amerikanischen Raumfahrtsprogramm zum Opfer fallen. Die Thomaspräzession wurde
zuerst richtig beschrieben durch relativistische quantenmechanische Theorie des Elektrons (Diracgleichung). Die oben skizzierte klassische Erklärung
durch Thomas erfolgte erst nacher.
135