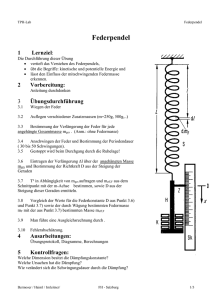
Federpendel Einführung Das Federpendel

www.SchulLV.de
Basiswissen > Mechanische Schwingungen > Federpendel
Federpendel
Skript PLUS
Einführung
Wärst du mutig genug für einen
Bungee-Sprung? Oder hast du gar
schon einen gemacht?
Wenn ja, hast du dir auch schon
einmal
Gedanken
über
die
physikalischen Gegebenheiten einer
solchen Freizeitgestaltung gemacht?
Wieso wirst du nach einer Weile
abgebremst und was sorgt dafür,
dass alle Springer wieder heil am
Boden ankommen? Springt man in
den Abgrund, so fliegt man erst
einmal eine Weile um schließlich vom
Bungee-Seil
abgefangen
und
gebremst zu werden. Dieses Bremsen
resultiert aus der Dehnung des Seils
und der damit zusammenhängenden
rücktreibenden Kraft. Diese sorgt
ebenfalls dafür, dass du im unteren
Umkehrpunkt wieder nach oben
geschleudert wirst.
Abb. 1: Bungee-Jumping.
Du fliegst danach also wieder nach oben, bis zum oberen Umkehrpunkt, wo dich die Erdanziehung
dann wieder nach unten fliegen lässt. Bei einem Bungee-Sprung vollführt dein ganzer Körper also
eine Schwingung. Diese lässt sich im Prinzip mit einem physikalischen Federpendel vergleichen. Im
folgenden Abschnitt werden dir also die nötigen Formeln als Werkzeuge gegeben, damit du vor dem
nächsten Bungee-Sprung berechnen könntest, wie der Sprung abläuft und ob alles gut gehen wird.
Das Federpendel
Das sogenannte Federpendel umfasst eine im Schwerefeld der Erde aufgehängte Feder, an deren
www.SchulLV.de
1 von 7
unterem Ende ein Gewicht befestigt wird. Vor dem Befestigen des Gewichts hängt die Feder noch
entspannt an ihrer Aufhängung und nach dem Befestigen verlängert sie sich auf Grund der
Erdanziehungskraft, je nach Masse des Gewichts, um eine bestimmte Strecke.
Abb. 2.
Normalerweise, wenn keine Kraft außer der Gewichtskraft auf diese Feder wirkt, verweilt sie in der
Gleichgewichtslage und führt keine Schwingung aus. Wenn du nun allerdings die an der Feder
befestigte Masse aus der Gleichgewichtslage auslenkst, indem du entweder die Masse anhebst oder
an ihr nach unten ziehst, und sie anschließend loslässt, so vollführt sie eine harmonische
Schwingung um die Gleichgewichtslage.
Abb. 3.
Aus der Formel der harmonischen Schwingung des Einheitskreises folgt für den Ort s(t) und durch
Ableiten mit der Produktregel, die Geschwindigkeit v(t) und die Beschleunigung a(t) des Gewichts:
ṡ (t)
s̈ (t)
=
v̇ (t)
=
=
⋅
⋅ ⋅
− ⋅ ⋅
− ⋅
− ⋅ ⋅
s(t)
=
ŝ
v(t)
=
ω
a(t)
a(t)
⋅
=
sin(ωt + φ )
ŝ
ω
=
ω
2
cos(ωt + φ )
ŝ
2
0
0
sin(ωt + φ )
0
s(t)
Mit dem 2. Newtonschen Axiom folgt also für die elastische Kraft:
www.SchulLV.de
F (t) = m
a(t) =
m
2
s(t)
2 von 7
⋅
F (t) = m
a(t) =
− ⋅ ⋅
m
ω
2
s(t)
⏟
konstant
Diese Kraft entsteht dadurch, dass die Feder gerne wieder in ihre ursprüngliche Gestalt zurück
kehren würde. Wie du erkennen kannst, ist der Betrag dieser elastischen, rücktreibenden Kraft
proportional zur Auslenkung. Dies führt zu einer harmonischen Schwingung. Der konstante Teil der
Gleichung wird als sogenannte Federkonstante D definiert:
m
⋅
ω
2
= D
Es ergibt sich daher das Hooksche Gesetz:
FFeder =
Δs
− ⋅
D
Δs
beschreibt hierbei gerade die Verlängerung der Feder aus ihrer ursprünglichen Gestalt. Stellst du
das Hooksche Gesetz nach D um, kannst du erkennen, was du dir konkret unter einer
Federkonstanten vorstellen kannst:
D =
−
F
Δs
Die Federkonstante bezeichnet also gerade die Kraft, die aufgewendet werden muss, um die Feder
eine bestimmte Strecke aus ihrer ursprünglichen Gestalt zu verformen. Je größer also die
Federkonstante ist, desto schwerer ist es, die Feder zu verformen. Sie ist also ein Maß für die Härte
der Feder.
Den Betrag der Federkonstante kann man hierbei rechnerisch bestimmen, indem man ein
Massenstück an die Feder hängt. Zu Beginn, nach dem Anhängen des Gewichts, sorgt die
Gewichtskraft dafür, dass sich die Feder verlängert. Dies geschieht bis zu dem Zeitpunkt, zu dem
sich ein Gleichgewicht einstellt und die auf die Feder wirkende Gewichtskraft genauso groß ist wie
die Spannkraft der Feder nach oben. Eine Feder der Länge l verlängert sich also gerade um die
Strecke s :
www.SchulLV.de
3 von 7
Abb. 4.
Beachte hierbei, dass wir uns zur Vereinfachung die Masse des Gewichtes in seinem Schwerpunkt
konzentriert vorstellen. Andernfalls würden die Rechnungen deutlich komplizierter ausfallen. In dieser
Gleichgewichtslage sind die beiden auf die Feder wirkenden Kräfte der Gravitation FG und der
Spannung der Feder FFeder gleich groß. Es gilt also:
m
⋅
FG
=
g
=
− ⋅
FFeder
D
s
Die Gravitationsbeschleunigung g kann hierbei als allgemeine Beschleunigung
werden und wir erhalten eine Differentialgleichung zweiten Grades:
m
m
⋅
⋅
a(t)
=
¨
s(t)
=
¨
s(t)
=
− ⋅
− ⋅
− ⋅
D
s
D
s
a(t)
geschrieben
D
s
m
Die Lösung dieser Differentialgleichung ist:
s(t) = ŝ
⋅
sin(ωt + φ )
0
Hierbei beschreibt ŝ die Amplitude, also gerade die heruntergezogene oder gehobene Strecke aus
der Gleichgewichtslage, der daraus erfolgenden harmonischen Schwingung. Mit der allgemeinen
Definition der Kreisfrequenz
umgeformt nach ω :
2π
ω =
und der Definition der Federkonstanten
T
=
T
www.SchulLV.de
⋅
ω
2
= D
folgt
⎯⎯⎯⎯
D
2π
ω =
m
√m
4 von 7
Hiermit ergibt sich für die Periodendauer T :
⎯⎯⎯⎯
D
2π
=
√m
T
⎯⎯⎯⎯
D
T
=
1
√m
2π
T
−
=
⋅
2π
⎯⎯⎯⎯
m
√D
Darüber hinaus solltest du das schwingende Federpendel in einem geeigneten Koordinatensystem
verorten, indem du zum Beispiel Abstünde vom Boden oder einer Tischplatte aus bestimmst. Dies
kann hilfreich sein, wenn du erklüren sollst, wo sich die schwingende Masse befindet. Ebenfalls lohnt
sich die Überlegung bei welcher Elongation sich die Masse bei Schwingungsbeginn befindet. Es
lüsst sich also dadurch der Phasenwinkel φ berechnen, wenn der Startpunkt s(0) = s 0 bekannt ist.
Es folgt dann gerade:
s(0)
⋅
=
sin(ω
=
sin(φ )
0 + φ )
0
0
Diese Betrachtung kann häufig hilfreich sein. Da
π
sin(x +
) = cos(x)
2
gilt, lässt sich ein Nullphasenwinkel
φ
0
von
π
nämlich dahingehend umformen, dass sich die
2
Lösungsformel in der Differentialgleichung zu Folgendem vereinfacht:
s(t)
=
=
s(t)
=
ŝ
ŝ
ŝ
⋅
⋅
⋅
sin(ω
sin(ω
cos(ω
⋅
⋅
⋅
t + φ )
0
π
t +
)
2
t)
Immer also, wenn die Schwingung aus einem der beiden Umkehrpunkte beginnt, kannst du zur
Einfachheit den Kosinus verwenden.
Energiebetrachtung
Bei der harmonischen Schwingung einer Feder kommt Energie in verschiedenen Formen vor.
Dadurch, dass es Momente gibt, wo die schwingende Masse an der Feder in Ruhe ist, gibt es
Momente in denen die Energie nicht mehr in kinetischer Form vorliegen kann. Dies besagt die Formel
der kinetischen Energie:
1
Ekin =
⋅ ⋅
m
2
v
2
Ist die Geschwindigkeit Null, so muss also zwingend auch die kinetische Energie Null sein. Allerdings
www.SchulLV.de
5 von 7
besagt der Energieerhaltungssatz, dass Energie nicht einfach erzeugt oder vernichtet, sondern nur
umgewandelt werden kann. Daher stellt sich die Frage, in was für einer Form die Energie noch
vorliegen kann? Da sich die Feder im Umkehrpunkt am stärksten wieder in ihren ursprünglichen
Zustand zurück bewegen will, ist hier die Spannung der Feder am größten. Diese Spannung ist eine
Form der potentiellen Energie und wird auch als Spannenergie bezeichnet.
Die Umwandlung der Energie erfolgt also folgendermaßen:
Abb. 5.
Wie du erkennen kannst, ist es möglich über den Energieerhaltungssatz die maximale
Geschwindigkeit der Masse zu bestimmen. Doch für solch eine Betrachtung ist erst einmal eine
Formel für die Spannenergie nötig. Diese erhältst du gerade durch das Kraft-Verlängerung-Schaubild
(F-s-Schaubild):
Abb. 6.
www.SchulLV.de
6 von 7
Die Kraft F steigt hier laut Hookschem Gesetz proportional zur Verlängerung s der Feder, wobei D
die Steigung definiert. Da die zugehörige Energie die Fläche unter der Kurve beschreibt, ist die
Spannenergie auch dadurch deutbar, dass die Fläche gerade ESpann = 12 F s ist. Setzt du in
diese Gleichung das Hooksche Gesetz FFeder
= D
1
ESpann =
⋅
s
⋅ ⋅
ein, erhältst du für die Spannenergie:
⋅ ⋅
D
2
s
2
Bildnachweise [nach oben]
[1] http://commons.wikimedia.org/wiki/File:Bungeejump_begin_Scheveningen_31_mei_2004.JPG – Ellywa,
CC BY-SA.
[2] © 2015 – SchulLV.
[3] © 2015 – SchulLV.
[4] © 2015 – SchulLV.
[5] © 2015 – SchulLV.
[6] © 2015 – SchulLV.
www.SchulLV.de
7 von 7