ELEKTROMAGNETISCHE SCHWINGUNGEN

Kapitel 9
ELEKTROMAGNETISCHE
SCHWINGUNGEN
9.1
Freie Schwingung
Ein Schwingkreis besteht aus einer Kombination eines Kondensators und einer
Induktivität. Der Kondensator C wird periodisch aufgeladen und entladen. Im
Gegenzug dafür wird das Magnetfeld in einer Induktivität L abgebaut und wieder aufgebaut. Ein mechanisches Analogon zum elektrischen Schwingkreis ist
der harmonische Oszillator.
Die potentielle Energie
der Masse M entspricht
der Feldenergie im Kondensator
!
" # $
!
1
Wel = CU 2
2
Die kinetischen Energie
der Masse M entspricht
der magnetischen Feldenergie
Wmag =
% &'
!
!
" # $
% &'
1 2
LI
2
Berücksichtigt man den endlichen Widerstand R der Leiter im Schwingkreis, hat
man auch ein Analogon zum Reibungsverlust des Federoszillators. Für diesen
hatten wir mit der rücktreibenden Kraft Fx = −D x und der geschwindigkeitsabhängigen Reibungskraft −αẋ die Bewegungsgleichung
mẍ + αẋ + D x = 0
(9.1)
Dem zeitlichen Verlauf des Stromes in einem Schwingkreis entspricht die Amplitude der Schwingung eines gedämpften harmonischen Oszillators.
81
Für die Spannungen im Schwingkreis gilt
LI˙ + RI +
$ %!
! "#
Q
=0
C
Die Ableitung nach der Zeit ergibt mit Q̇ = I
I
LI¨ + RI˙ +
=0
C
&
!
'( )
Mit dem Ansatz I = Aeλt , wobei A und λ komplex sein können, erhalten wir
die quadratische Gleichung
R
1
λ+
=0
L
LC
mit den Lösungen
!
R2
1
R
−
λ1,2 = −
±
= −α ± β
2L
4L2
LC
Somit ist die allgemeine Lösung
λ2 +
(9.2)
(9.3)
I = A1 e−(α−β)t + A2 e−(α+β)t
Für den Fall R2 < 4L/C ist β imaginär.
So erhalten wir mit dem Ansatz β = iω
und α = R/(2L) als allgemeine Lösung
"
#
I = e−αt A1 e+iωt + A2 e−iωt
(9.4)
!
#! !
"
!
Mit A1,2 = a ± ib ist eine reelle Lösung
I
$ "
#
"
#%
= e−αt a e+iωt + e−iωt + ib e+iωt + e−iωt
= |A|e−αt cos (ωt + ϕ)
√
wobei |A| = 2 a2 + b2 und tan ϕ = b/a ist. Die Anfangsbedingungen bestimmen
die Konstanten |A| und ϕ. Die Eigenfrequenz des freien Schwingkreises ist
!
1
R2
ω=
−
(9.5)
LC
4L2
Im ungedämpften Fall (R = 0) ergibt sich die sogenannte Thomson Gleichung
ω0 = √
1
LC
(9.6)
Für R2 > 4L/C wird β rell und der Strom fällt monoton ab (Kriechfall). Für
den Fall R2 = 4L/C ist β = 0. Auch hier hat der Strom keinen Nulldurchgang
(aperiodischer Grenzfall).
Die Eigenfrequenz erhöht sich, wenn L und C kleiner werden.
9.2
Erzwungene Schwingung
Legt man von aussen eine periodische Spannung U = U0 cos ωt an (wobei
ω frei wählbar ist, unabhängig von der Definition in (9.5)), ergibt sich eine erzwungene gedämpfte Schwingung, mit dem typischen Verhaltens eines
Resonanzkreises. Die Summe aus äußerer Spannung und Induktionspannung muss gleich sein
dem Spannungsabfall an R und C:
U + Uind
=
+RI +
!
Q
C
I
= LI¨ + RI˙ +
C
U̇
$ %!
! "#
&
Mit dem komplexen Ansatz
!
&
'( )
!
U = U0 eiωt und I = I0 ei(ωt−ϕ)
"#$
gilt
iωU =
&
1
−Lω 2 + iωR +
C
'
! "# $
I
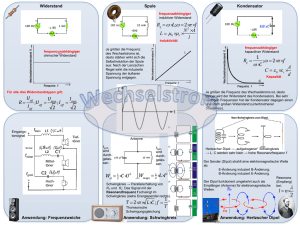
Der komplexe Widerstand definiert sich als
&
'
U
1
Z=
= R + i ωL −
I
ωC
und die Impedanz |Z|
(
&
'2
1
2
|Z| = R + ωL −
ωC
wobei Z = |Z| · e
iϕ
4
3
«Z« 2
R
R
R
1
0
0
1
ist.
2
ZsZ0
2
1
0
3
4
)
In den Bildern wurde die Einheit von R in der Einheiten von L/C gewählt.
Bei großen Werten von ω ist die Steigung gleich ωL. Komplexe Widerstände
werden übersichtlich als Vektoren in der komplexen Ebene dargestellt.
Ss2
4
1s«Z«
-.
! $
%& '# (
# !
M
!
0
2
0
R
R
Ss2
0
1
Der zeitabhängige Strom wird damit
I=
0.3
0.03
1
"
)* +! ,
R
R
3
U0
cos (ωt − ϕ)
|Z|
wobei
2
ZsZ0
3
tan ϕ =
4
0.5
ωL −
Im{Z}
=
Re{Z}
R
1
1.5
ZsZ0
1
ωC
.3
.03
2
(9.7)
Der Strom wird maximal, wenn die Thomson Bedingung ωL−1/(ωC) = 0 erfüllt
ist, also ω = ω0 . In diesem Fall ist der Phasenwinkel ϕ = 0, und der Strom ist
in Phase mit der angelegten Wechselspannung. Die Resonanzkurve verbreitert
sich mit steigendem
√ Widerstand R. Geht R → 0, dann wird I unendlich bei der
Frequenz ω0 = 1/ LC. Der Widerstand R verbraucht die Leistung
U02 cos2 ωt
R
|Z|2
16
12
P!
P = I2 R =
Da der Mittelwert $cos ωt% = 1/2
ist, beträgt die mittlere Leistung
2
$P % =
R
R
8
.3
.03
4
R
1
2 R2 + [ωL − 1/(ωC)]2
U02
0
0
1
2
ZsZ0
3
4
«UC « s U0
Erfolgt die externe Einkopplung wie in der Abbildung auf Seite 83 oben, spricht
man von einem Serienschwingkreis. Am Kondensator liegt die Spannung
*
Idt
Q
4
=
UC =
C * C
3
R .03
U0 eiωt dt
=
R .3
ZC
R .6
2
U0 eiωt
I
=
=
iω Z C
iωC
1
mit |UC | = U0 /(|Z|ωC) gleich dem Betrag der
0
Amplitude. Das Maximum der Spannungsreso0
1
2
ZsZ0
nanz verschiebt sich bei steigender Dämpfung (
Wert von R) nach
√ Werten unter der Resonanzfrequenz ω0 = 1/ LC.
Wegen 1i = −i = e−i π/2 besteht zwischen der Spannung am Kondensator und
dem Strom im Schwingkreis eine Phasenverschiebung von −π/2 = −90o .
Im
M
M
UC
Im
Im
M
900
0
U0
Re
i M
I0 e
M
0
90
UC
U0
I0 Re
Ss2
UC
M
U0
Re
I0
Der Resonanzfall kann auch in einem Parallelschwingkreis beobachtet werden. Von aussen wird eine Wechselspannung an den Kondensator angelegt. Die
periodische Änderung des Magnetfeldes in der Induktivität wird über eine Sekundärspule beobachtet.
9.3
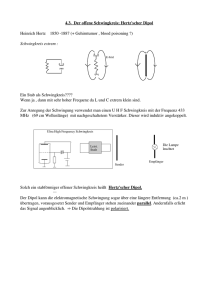
Offener Schwingkreis
Wie macht man die Induktivität und die Kapazität kleiner? Zum Beispiel in
einem kontinuierlichen Übergang, in dem man zuerst die Spule durch einen
Drahtbügel ersetzt, und in Folge das Drahtende als die Kapazität interpretiert.
Damit entsteht der klassische Hertz’sche Dipol.
!
!
!
!
"
"
"
"
Ein Hertzscher Dipol ist ein linearer oszillierender Dipol, dessen Enden abwechselnd positiv und negativ aufgeladen werden. Seine Eigenfrequenz wird
durch Länge des Dipol bestimmt. Speisen wir in die Mitte des Antennenstabes
(bei z = 0) eine Wechselspannung ein, so fließt der Strom
I(z, t) = I0 (z) sinωt
(9.8)
Die Bedingung, dass der Strom am Antennenende eine Nullstelle zeigt
1
I(z = ± ') = 0
2
(9.9)
verursacht das Resonanzverhalten der Antenne. Resonanz tritt auf, wenn die
Dipollänge ein Vielfaches der halben Wellenlänge ist: ' = nλ/2. Dabei ist die
Wellenlänge über die Phasengeschwindigkeit c des elektromagnetischen Signales mit der Frequenz verknüpft, ω = 2πν = 2πc/λ. Legt man den periodischen
Strom unter Resonanz bei z = 0 bei der niedrigsten Resonanz (n = 1) an den
Dipol an, dann ergeben sich für den räumlichen Verlauf von Strom und Spannung
I0 (z)
U0 (z)
πz
'
πz
= U0 sin
'
= I0 cos
! "# "$%&
)
Die sich ausbildende Stehwelle ist
mit Glühlampen in der Dipolleitung nachweisbar. Hell erscheint
eine Lampe, wenn der Spannungsabfall an ihr (der Strom) groß ist.
! "# "'
'
*! +
!'*! +
$"# "! "%"&
! "# "( $%&
Beispiel für Antennenresonanz: Wir nehmen die Länge ' = 6 cm, damit ist
'=
λ
1 c
=
2
2 ν
→
ν=
3 · 1010
= 2.5 GHz
2·6
Bei hoher Frequenz ist die Schwingung im Hertz’schen Dipol stark
gedämpft, allerdings nicht durch den Ohmschen Widerstand, sondern durch Abstrahlung einer elektromagnetischen Welle.
Um die Abstrahlung zu verstehen, untersuchen wir zuerst die Ausbreitung eines
elektrischen Pulses entlang einer Lecherleitung:
!
"# $ % & & ' & ( "
Eine Lecherleitung sind zwei lange, parallele Leiter mit einer Stromquelle an
einem Ende. Wir machen Momentaufnahmen der (idealisierten) Potentialverteilung entlang des Leiters als Funktion der Zeit,
!
A) bei Anlegen einer
Gleichspannung
!
B) bei Anlegen eines
Spannungsstoßes
!
! ) *+
C) bei Anlegen einer
Wechselspannung
Im Fall C) (zeitlich periodischer Vorgang) ergibt sich ein auch räumlich periodischer Vorgang, eine Welle,und zwar nur deshalb, weil die Ausbreitungsgeschwindigkeit endlich ist. Heinrich Hertz hatte 1898 beobachtet, dass sich
elektrische Störungen mit endlicher Geschwindigkeit ausbreiten (für parallele
Drähte im Vakuum gilt v ∼
= c).
Aus einer Lecherleitung können wir durch
Aufbiegen eine Dipolantenne gestalten.
Die Entstehung des zeitlich und räumlich periodischen Feldes können wir uns
so vorstellen:
Angenommen die Schwingungsfrequenz beträgt 100 M Hz ( 2.5 GHz), dann
ändert sich die Polarität alle 5 ns (200 ps). Um instantan ein stationäres elektrisches Feld entsprechend der Polarität des Dipols auszubilden, müßte sich
das Feld in 5 ns (200 ps) bis ins Unendliche ausbreiten und dann wieder verschwinden, wenn der Dipol umpolt. Das Feld breitet sich aber maximal mit
)
der Lichtgeschwindigkeit c aus. Das E-Feld
kann nicht Schritt halten mit der
zeitlichen Änderung des Dipolmomentes an der Antenne. Die Folge davon ist,
dass die Feldlinien nicht mehr zum Dipol zurückkehren. Sie lösen sich ab und
wandern als geschlossene Wirbelfelder in den Raum. Analoges gilt für die
magnetischen Felder, die durch den Dipolstrom erzeugt werden.
!
!
"
!
"
!
"
"
!#$ #%
&#$ #%
!
!
!
&#$ #' () *
&#$ #' (+ *
&#$ #, () *
In einem Experiment gelingt der Nachweis der Felder über eine Glimmlampe oder Glühlampe mit unterschiedlich geformten Empfangsantennen:
)
Dipolantenne Das periodisch sich ändernde EFeld regt Elektronen zum Mitschwingen an
(erzwingt also einen Wechselstrom mit der
Frequenz des elektrischen Feldes). Die Lampe
leuchtet an den Orten maximaler elektrischer
Feldstärke. Mit dieser Anordnung läßt sich die
) als parastarke Richtungsabhängigkeit von E
lell zur Dipolachse zeigen.
)
Drahtschleife Das periodisch sich ändernde B-Feld
induziert in der Schleife einen Wechselstrom
und die Lampe leuchtet an den Orten maximaler magnetischer Feldstärke. Auch mit dieser Anordnung läßt sich die starke Richtungs) als senkrecht zur Dipoabhängigkeit von B
lachse zeigen. Damit wird der Beweis geführt,
) und B
) senkrecht zueinander stehen.
dass E
!
!
Das Hertz’sche Gitter ist eine Anordnung von parallelen Metalldrähten im
Abstand kleiner als die Wellenlänge. Das Gitter ist
• undurchlässig (wie eine Metallwand), wenn die Gitterdrähte parallel zur
Dipolachse liegen.
• durchlässig für eine Stellung der Gitterdrähte senkrecht zur Dipolachse
(keine Ströme fließen in den Gitterdrähten).
• Steht das Gitter unter einem Winkel α relativ zur Orientierung der Dipolachse, wird Strahlung mit einer Polarisation senkrecht zu den Gitterdrähten durch das Hertz’sche Gitter durchgelassen (allerdings mit verminderter Intensität, I ∝ cos2 α )
9.4
Retardierung
Zur Verdeutlichung der zeitlichen Entwicklung
des elektromagnetischen Feldes untersuchen wir
zuerst das Vektorpotential einer stationären
Stromverteilung
+ )
j()r2 )
) r1 ) = µ0
dV2
(9.10)
A()
4π 2 r12
#
!
"
$
% !
&
%
Jetzt betrachten wir eine zeitlich veränderliche Stromdichte und berücksichten
die Zeit, die das Feld braucht, um sich von 2 nach 1 auszubreiten: Diese Zeit,
die sogenannte Retardierung ist ∆t = r12 /c. Für eine nicht-stationäre Stromverteilung müssen wir also schreiben:
) r1 , t) = µ0
A()
4π
+ )
j()r2 , t − r12 /c)
dV2
r12
2
(9.11)
Wenn der Aufpunkt (1) weit weg liegt von der Dipolantenne, dann gilt für alle
Punkte aus der Antenne r12 ≈ r = const. Fließt die Ladungsdichte ρ mit der
Geschwindigkeit vz entlang der z-Achse ergibt sich das Vektorpotential
+
) r1 , t) = µ0 êz
vz ρ()r2 , t − r/c) dV2
A()
(9.12)
4πr r
9.5
Hertz’scher Dipol
) der Hertz’schen Dipolantenne zur Zeit t"
Das elektrische Dipolmoment P
) ")
P(t
= Q )z (t" )
= Q z0 sin ωt" êz
(9.13)
= p(t" ) êz
beschreibt die Oszillation der Elektronen gegenüber der festen positiven Ladung
der Ionenrümpfe, wobei Q die Gesamtladung der beweglichen Ladungsträger in
der Antenne ist. Mit der Beziehung für die retardierte Zeit
t" = t−r/c
(9.14)
ist
d
p (t" ) = Qż = Qvz =
dt
+
ρvz dV2
(9.15)
Damit gilt für nach Gl.(9.12) für das Vektorfeld in der Umgebung des Dipols
) 1 , t) =
A(r
=
µ0
4π
µ0
4π
êz d ,
rp t−
r dt
c
êz
"
ṗ (t )
r
(9.16)
Das Vektorpotential ist proportional zur ersten zeitlichen Ableitung des Dipol) ∝ ṗ. Mit
momentes A
ω (t − r/c) = ωt −
2π
r = ωt − )k · )r
λ
(9.17)
wird
,
) 1 , t) = µ0 êz Qz0 ω cos ωt − )k · )r
(9.18)
A(r
4π r
Die Interpretation dieser Gleichung ist, dass ein sich zeitlich änderndes Dipolmoment ein sich zeitlich änderndes Vektorpotential erzeugt, das sich mit Lichtgeschwindigkeit im Raum ausbreitet. Auf Grund der 1/r Abhängigkeit ist die
Form dieser Gleichung gleich der einer Kugelwelle (wir hatten die Annahme gemacht, dass r12 ) z0 ).
) = {0, 0, Az } und
Liegt die Dipolachse entlang der z-Richtung ist dann ist A
)
)
)
wegen B = ∇ × A ergibt sich
.
/
∂Az
∂Az
)
(9.19)
B= +
,−
,0
∂y
∂x
)
Das B-Feld
liegt also in der x−y-Ebene. Wir überlegen uns die x-Komponente
des B-Feldes und berücksichtigen, dass sowohl 1/r als auch ṗ(t" ) (und zwar
wegen der retardierten Zeit) von y abhängen.
0
1
∂ 1 1 ∂
µ0
"
"
ṗ(t ) ·
+ ·
ṗ(t )
Bx = +
(9.20)
4π
∂y r
r ∂y
Wenn wir die Antenne in den Ursprung des Koordinatensystems setzen ist r2 =
x2 +y 2 +z 2 . Wir verwenden die Substitution t" = t−r/c und erhalten ṗ = ∂p/∂t" ,
sowie ∂t" /∂r = −1/c und ∂r/∂y = y/r. Damit ist
∂ ṗ
∂ ṗ ∂t" ∂r
1 y
= "·
·
= −p̈
∂y
∂t ∂r ∂y
c r
(9.21)
Berücksichten wir auch noch den ersten Term in Gleichung 9.20
y
∂ 1
=− 3
∂y r
r
(9.22)
dann erhalten wir für Bx und analog für By
µ0 , y
y Bx = −
ṗ 3 + p̈ 2
4π , r
cr x
x
µ0
ṗ 3 + p̈ 2
By = +
(9.23)
4π
r
cr
also Terme, die sowohl von der ersten, als auch von der zweiten zeitlichen Ableitung des Dipolmomentes abhängen (die zweite Ableitung erscheint über die
räumlich Ableitung der retardierten Zeit).
Der erste Term in Gl.9.23 fällt schneller mit dem Abstand ab als der zweite,
also dominiert der zweite Term in der Fernzone des Dipols. Nach Umrechung auf
Polarkoordinaten ist der Betrag der magnetischen Feldstärke in der Fernzone
|B(r, ϑ, t)| =
µ0
1 sin ϑ
p̈(t" )
4π
c r
(9.24)
Analog ergibt sich (|B| = |E|/c) der Betrag der elektrischen Feldstärke als
|E(r, ϑ, t)| =
sin ϑ
µ0
p̈(t" )
4π
r
(9.25)
Die Strahlungleistung berechnet sich aus der Energiedichte beider Felder
wem =
#
1 " 2
-0 E + c2 B 2 = -0 E 2
2
(9.26)
als die Energiestromdichte
sem = c wem = c -0 E 2
(9.27)
Die Abstrahlung erfolgt bevorzugt senkrecht zur Dipolachse, also E 2 ∝ sin2 ϑ.
!
!
!
!
#$ #%! &
#
"
$ %
&! '
"
Aus der periodischen Zeitabhängigkeit in Gl.(9.13) ergibt sich für die Frequenzabhängigkeit von
ṗ ∝ ω
und
p̈ ∝ ω 2
(9.28)
2
Die gesamte vom schwingenden Dipol abgestrahlte Leistung ist Pem = sem dS,
mit dem Flächenelement dS = r2 sinϑ dϑ dϕ. Im Mittel beträgt die abgestrahlte
Leistung
$Pem % =
µ0
Q2 ω 4 z02
12πc
(9.29)
Sie steigt mit ω 4 an, Aus diesem Grund ist die Strahlungsdämpfung bei hohen Frequenzen besonders hoch.
Unter Verwendung von Gleichung (9.13) sehen wir, dass die Feldamplituden in (9.24) und (9.25) proportional sind zu z̈, also zur Beschleunigung der
Ladungsträger. Die abgestrahlte Leistung ist demnach proportional zum Quadrat der Beschleunigung. Dies gilt nicht nur für harmonische Bewegungen, sondern auch für beliebige Beschleunigungsvorgänge, z.B. beim scharfen Abbremsen
bzw. bei der Ablenkung schneller Elektronen in einem Metall (Röntgenanode,
Röntgenbremsstrahlung) oder bei der Zentripetalbeschleunigung schneller
Elektronen in einem Speicherring (Synchrotronstrahlung). Zur Bestimmung
der Richtungsverteilung der Abstrahlung einer beschleunigten Ladung bei hohen Geschwindigkeiten müssen relativistische Effekte berücksichtigt werden.