Loesung Nachklausur_WT_WS0506

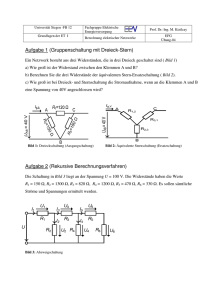
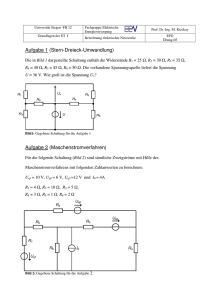
Musterlösung Klausur Wechselstromtechnik WS0506 vom 23.03.2006
Bitte beachten Sie, dass in den Berechnungen zugunsten reduzierter Schreibarbeit die
Dimensionen nicht mitgeführt werden und nur die Endergebnisse mit der Dimension versehen
sind. Allerdings sind gegebene Werte falls nötig immer auf die Standardgrößen umzuformen,
also z.B. F statt µF, H statt mH, Ω statt kΩ, V statt kV, etc.
Aufgabe 1:
a)
Durch Anwendung der Formel für den komplexen Spannungsteiler ergibt sich die gesuchte
Spannung zu:
R + jωL
jωRC − ω 2 LC
U2 =
U1 =
U1
2
1
ω
ω
+
−
1
j
RC
LC
+ R + j ωL
jωC
j ⋅ 314 ⋅ 10 ⋅ 100 ⋅ 10 − 314 ⋅ 0,01 ⋅ 100 ⋅ 10
⋅ 230V
1 + j ⋅ 314 ⋅ 10 ⋅ 100 ⋅ 10 −6 − 314 2 ⋅ 0,01 ⋅ 100 ⋅ 10 −6
− 0,0493 + j ⋅ 0,314
=
⋅ 230V ⋅ e j 45° = 73,01V ⋅ e j 80 , 65°
0,951 + j ⋅ 0,314
−6
=
−6
2
6
b)
Um die Formel gemäß Skript Seite 31 zur Umwandlung einer Reihendarstellung in einer
Parallelschaltung anwenden zu können, muss in einem ersten Schritt die gegebene Schaltung
in die Reihenschaltung eines reellen und eines imaginären Anteils umgeformt werden. Dies
geschieht einfach durch Berechnung der komplexen Impedanz Z der Schaltung, die zugleich,
aufgeteilt in Real- und Imaginärteil, die gesuchten Komponenten in Reihendarstellung liefern.
RR
jXR
2
Z
Es gilt daher für Z bzw. RR und XR:
1
1 ⎞
⎛
+ R + j ωL = R + j ⋅ ⎜ ω L −
⎟
j ωC
ωC ⎠
⎝
1
⎛
⎞
= 10 + j ⋅ ⎜1,57 −
⎟
314 ⋅ 100 ⋅ 10 −6 ⎠
⎝
= (10 − j ⋅ 30,28)Ω = RR + j ⋅ X R
Z=
Es folgt:
RR = 10Ω
X R = −30,28Ω
2
Auf der Grundlage dieser Werte ist es nun möglich, die eigentlich gesuchte parallele
Darstellung zu berechnen. Es gilt (s. Skript S. 32):
RR + X R 100 + 30,28 2
=
= 101,7Ω
RP =
RR
10
2
2
RR + X R
100 + 30,28
= j
= − j 33,58Ω
XR
− 30,28
2
jX P = j
2
2
3
Die gesuchte Kapazität CP ergibt sich schließlich zu:
− j 33,58Ω = − j
CP =
1
ωC P
1
1
1
=
= 1,054 ⋅ 10 4 F
ω ⋅ 33,58 314 ⋅ 33,58
Offensichtlich stellt jXP wie gewünscht eine kapazitive Reaktanz dar. Anhand der Formel
erkennt man, dass das Vorzeichen von XR direkt das Vorzeichen von XP bestimmt, denn der
Zähler ist aufgrund der Quadrate immer positiv. Daher ist die Bedingung dafür, dass die
originale Schaltung durch eine Parallelschatung aus RP und CP darstellbar ist die, dass die
Induktivität nicht zu groß ist und damit die gesamte originale Reihenschaltung kapazitiven
Charakter besitzt.
2
c)
Die symbolische Methode der Wechselstromtechnik beschreibt das Verhalten einer elektrischen
Schaltung für die Anregung mit sinusförmigen Wechselspannungen fester (Netz-)Frequenz ω.
Für eine solche feste Frequenz ω genügt eine einzige komplexe Impedanz Z, um eine beliebig
komplexe lineare Schaltung aus R, L und C zu beschreiben.
4
Das dynamische Einschwingverhalten eines solchen Systems dagegen ist von der zugrunde
liegenden Differentialgleichung höherer Ordnung des Systems abhängig, so dass im gegeben
Beispiel die einfache Parallelschaltung aus Widerstand und Kondensator (Dgl. 1. Ordnung)
nicht das Schwingungsverhalten des Reihenschwingkreises (Dgl. 2. Ordnung) abbilden kann.
Aufgabe 2: (20 Punkte)
a)
Solange die in der Abbildung ergänzten Kapazitäten der Leitungen gegen Erde klein sind
(kleine Ausdehnung des Netzes), sind die Ströme im Vergleich zu den Nennströmen klein und
die Sicherung werden nicht ansprechen.
2
Erst bei ausgedehnten Netzes könnte der Fehlerstrom über den Erdschluss möglicherweise
hinreichend groß werden. Allerdings darf man sich für eine sichere Auslösung der Sicherung
nicht verlassen. Im Gegenteil werden isolierte Sternpunkte oft bei kleineren Netzen eingesetzt,
wenn man im einphasigen Erdschluss die Verfügbarkeit des Netzes erhalten möchte. In diesem 2
Fall darf der Fehlerstrom schon aus Sicherheitsgründen (Spannungstrichter) nicht so groß sein,
dass die Sicherungen auslösen.
U1
U2
N
U3
S1
Z1
S2
Z2
M
S3
Z3
b)
Bei symmetrischen Spannungen und Lasten liegen die Sternpunkte N und M auf identischem
Potential.
Durch den Erdschluss kommt es zur Verschiebung des Sternpunktes N, denn die Erde erhält
das Potential der Spannung U3. Damit ergibt sich für den Sternpunkt N (und damit bei
Symmetrie auch M) das Potential relativ zur Erde von –U3.
c)
Vorteile:
- Einfach und preiswert, da keine weitere Gerätetechnik nötig
- Verbraucher können im Fehlerfall weiter betrieben werden
Nachteile:
- Je nach Netzgröße gefährliche Spannungstrichter an der Fehlerstelle
- Netzschutz / Sicherungen werden i.a. nicht ausgelöst
- Mögliche Beeinflussung von Fernmeldanlagen
4
4
d)
Durch eine niederohmige Erdung (Widerstand R) des Sternpunktes N entsteht über den
Erdschluss ein niederohmiger Kurzschluss der Spannung U3 und damit ein entsprechend hoher
Fehlerstrom, der von Sicherung S3 sicher erkannt und zur allphasigen Abschaltung genutzt
werden kann:
U1
N
R
e)
U2
U3
S1
Z1
S2
Z2
M
S3
Z3
3
Bei gelöschtem Betrieb wird der Sternpunkt N über eine einstellbare Spule geerdet. Die
Induktivität dieser Spule wird dabei auf die Leitungskapazitäten so eingestellt, dass sich in
Parallelresonanz die Leitungskapazität und die Erdungsinduktivität gerade kompensieren und
damit der Fehlerstrom nahezu 0 wird.
Allerdings kann die Spule nur auf eine Frequenz, die Netz-Betriebsfrequenz ωN, eingestellt
werden. Dies führt dazu, dass Oberwellen n⋅ωN (z.B. durch Leistungselektronik / Stromrichter /
Umrichter) nahezu unkompensiert über den Erdschluss fließen können (analog dem Fall des
isolierten Sternpunktes). Entsprechend große Ströme können fließen, zumal die für die den
Stromfluss verantwortlichen Leitungskapazitäten mit wachsender Frequenz eine geringere
Reaktanz besitzen und der Fehlerstrom deshalb ansteigt.
5
Aufgabe 3: (24 Punkte)
a)
Die Spanungsquelle samt Innenwiderstand ist in eine Stromquelle umzuwandeln. Hierzu ist die
Spannungsquelle kurzzuschließen und hieraus der Kurzschlußstrom zu ermitteln:
Ri
2
Ik
U0
Es gilt daher für den Kurzschlussstrom:
Ik =
U 0 230V
=
= 230 A
Ri
1Ω
2
Der Innenwiderstand der Spannungsquelle wird unverändert in die Stromquelle übernommen.
Man erhält schließlich das folgende Schaltbild, bei dem die Spannungsquelle in einen
Stromquelle überführt wurde:
R1
jX1
R3
Ik
2
Ri
R2
jX2
b)
Zur Berechnung der Schaltung mit dem Knotenspannungsverfahren sind im nächsten Schritt
alle Impedanzen in Admittanzen umzurechnen. Es ergibt sich das folgende Schaltbild:
G1
jY1
2
G3
Gi
Ik
G2
jY2
mit:
Gi = 1 / Ri = 1 S
G1 = 1 / R1 = 1 S
G2 = 1 / R2 = 2 S
G3 = 1 / R3 = 4 S
Y1 = 1 / X1 = 1 S
Y2 = 1 / X2 = 2 S
Zur Anwendung des Knotenspannungsverfahrens ist nun ein Bezugsknoten mit Potential 0 und
die Bezugspfeile der anderen Spannungen festzulegen.
K3
G1
jY1
G3
Ik
U3
K1
Gi
U1
K2
G2
U2
4
jY2
Bezugsknoten ϕ=0 (willkürliche Wahl)
Damit sind die Voraussetzungen geschaffen, das zur Berechnung der Knotenspannung
notwendige Gleichungssystem aufzustellen:
− G3
⎛ G2 + G3 + jY1
⎜
G1 + G3 + jY2
− G3
⎜
⎜
− jY1
− G1
⎝
− jY1
⎞ ⎛U 1 ⎞ ⎛ 0 ⎞
⎟ ⎜ ⎟ ⎜ ⎟
− G1
⎟ ⋅ ⎜U 2 ⎟ = ⎜ 0 ⎟
G1 + Gi + jY1 ⎟⎠ ⎜⎝ U 3 ⎟⎠ ⎜⎝ I k ⎟⎠
4
Einsetzen der Werte liefert schließlich:
−4
− j ⎞ ⎛U 1 ⎞ ⎛ 0 ⎞
⎛6 + j
⎟
⎟ ⎜ ⎟ ⎜
⎜
4
5
2
1
0
j
U
=
⋅
−
+
−
⎟
⎟ ⎜ 2⎟ ⎜
⎜
⎜
⎟
⎜
⎟
⎜ −j
2 + j ⎠ ⎝ U 3 ⎠ ⎝ 230 ⎟⎠
−1
⎝
2
Ergänzung (nicht Bestandteil der Klausuraufgabe):
Das Gleichungssystem kann man nur mühsam manuell lösen, deshalb hier die Lösung, die man
z.B. mit MATLAB ermitteln kann:
⎞
⎛ U 1 ⎞ ⎛ 31,39V ⋅ e
⎟
⎜ ⎟ ⎜
− j 41, 45
=
U
45
,
52
V
e
⋅
2
⎟
⎜ ⎟ ⎜
⎜ U ⎟ ⎜ 121,3V ⋅ e − j 26 , 47 ⎟
⎝ 3⎠ ⎝
⎠
− j 13 , 06
c)
1. Möglichkeit:
Um die Methode ohne weitere Änderung anwenden zu können führt man für jede
Spannungsquelle von 0 verschiedene Innenwiderstände Ri ein, die klein sind gegenüber den
Beträgen der übrigen Impedanzen und somit die Berechnung nur unwesentlich beeinflussen,
aber dennoch die Lösbarkeit sicherstellen. Dies ist ein Näherungsansatz, der aber für alle
praktischen Belange hinreichend genau ist.
2. Möglichkeit
Spannungsquellen werden nicht in Stromquellen umgewandelt, vielmehr wird ein reduziertes
Gleichungssystem betrachtet. Dieses enthält diejenigen Zeilen nicht, die zur Berechnung der
Spannungen der Knoten dienen, die über die Spannungsquellen miteinander verbunden sind.
3
3
Die 2. Möglichkeit erfordert zwar keine Näherungslösung wie Möglichkeit 1, jedoch erfordert
eine Vorab-Analyse der Schaltung und ist nicht so einfach in ein mathematisches Programm
umzusetzen. Aus diesem Grunde verwenden viele Programme zur Schaltungsanalyse die 1.
Möglichkeit.
Aufgabe 4: (16 Punkte)
a)
Werden zwei Verbraucher an einem Trenntransformator angeschlossen, so kann es zu einem
gefährlichen Zustand kommen, wenn die Gehäuse jeweils mit einem der beiden
Versorgungsleitungen L1 bzw. L2 Kontakt kommen (hier durch die schwarzen Punkte
gekennzeichnet). Zwischen den Gehäusen leigt dann die volle Sekundärspannung des Trafos
an. Eine gleichzeitige Berührung beider Gehäuse stellt eine zweipolige Berührung dar, die
Schutzwirkung des Trenntrafos ist nicht mehr vorhanden.
3
L1
3
V1
L2
b)
V2
Wird die Verbindung des Gehäuses zum (vermeintlichen) PEN Leiter im Verbraucher
durchgeführt, so hängt es von der Orientierung des Steckers in der Dose ab, ob das Gehäuse
tatsächlich mit dem PEN und damit mit Erde verbunden wird (in der Abbildung fette
durchgezogene Linien zwischen Dose und Stecker).
Wird der Strecker dagegen verdreht (strichlierte Verbindung) erhält das „geerdete“ Gehäuse
Kontakt mit L1, was tödlich enden kann.
Dose
3
Stecker
L1
3
PEN
c)
Wie bei der einphasigen FI-Schutzschaltung muss auch im dreiphasigen Fall der FISchutzschalter überprüfen, ob der über die drei Phasen gelieferte Strom zum Verbraucher
wieder vollständig über den Neutralleiter zurückfließt oder ob ein Teil des Stroms anderweitig
(z.B. über einen Erdschluss) abfließt. Die Summe aller Ströme durch den FI-Schalter muss also
gleich 0 sein. Entsprechend muss der FI-Schutzschalter in alle 4 Leiter eingeschleift werden:
Z1
U1
N
Z2
U2
M
4
FI
U3
Z3
Aufgabe 5:
a)
Zur Berechnung per Superposition wird die Aufgabe in mehrere Teilaufgaben zerlegt. In jeder
Teilaufgabe werden alle Strom- bzw. Spannungsquellen bis auf eine einzige entfernt bzw.
kurzgeschlossen. Die verbleibende Schaltung wird mit den bekannten Methoden der
Schaltungsanalyse bearbeitet. Die Gesamtlösung ergibt sich schließlich aus der Summe der
Teillösungen.
In der vorliegenden Aufgabe existieren 2 Spannungsquellen, so dass die Berechnung des
gesuchten Stroms IR in zwei Teilberechnungen zerlegt werden muss.
1. Teilschaltung (Spannungsquelle U2 entfernt und Teilstrom IR1 eingeführt):
U1
IR1
C
1
R
Der Maschenumlauf liefert:
⎛
1 ⎞
U 1 = I R1 ⎜⎜ R +
⎟
jωC ⎟⎠
⎝
U1
j ωC
I R1 =
=
U1
1
1
+
j
ω
RC
R+
jω C
2
2. Teilschaltung (Spannungsquelle U1 entfernt und Teilstrom IR2 eingeführt):
U2
IR2
C
R
1
Der Maschenumlauf liefert:
⎛
1 ⎞
U 2 + I R 2 ⎜⎜ R +
⎟⎟ = 0
j
ω
C
⎝
⎠
U2
j ωC
I R2 = −
=−
U2
1
1
+
j
ω
RC
R+
j ωC
2
Der Gesamtstrom berechnet sich damit zu:
jωC
jωC
jω C
U1 −
U 2 = (U 1 − U 2 )
1 + jωRC
1 + jωRC
1 + jωRC
j ωC
jω C
S = 230V (1 + j )
S
= 230V (e j 0 − e − j 90° )
1 + jωRC
1 + jωRC
I R = I R1 + I R 2 =
= 230V ⋅ (1 + j ) ⋅ e
= 230 ⋅ 2 ⋅
= 230 ⋅ 2 ⋅
j arctan (1 )
jω C
⋅
1 + jωRC
j arctan
0
⋅ ⎛⎜ e
⋅ e − j arctan ωRC ⎞⎟ S
⎝
⎠
ωC
ωC
j 45°
j ( 90° − arctan 0 , 0628 )
⋅
e
⋅
e
A
2
2
1 + (ωRC )
4
0,0314
A ⋅ e j ( 45°+90°−3, 59° )
1,002
= 10,19 A ⋅ e j131, 4°
b)
IR
UC
- U2
U1 – U2
6
ϕ
UR
U1
U2
c)
Die Leistung kann direkt aus dem Betrag des Stroms IR und Widerstand R berechnet werden.
Es ergibt sich:
P = I R ⋅ R = (10,19 A) ⋅ 2Ω = 207,7W
2
2
4