Zahlenfolgen

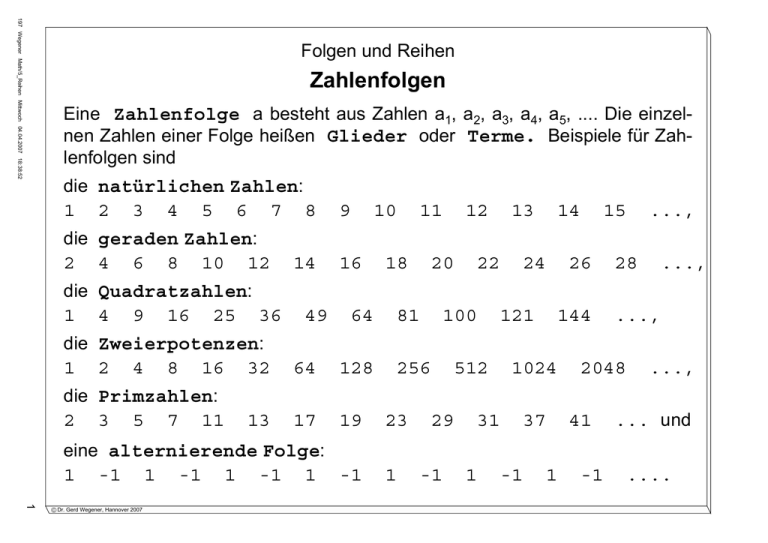
197 Wegener Math/5_Reihen Mittwoch 04.04.2007 18:38:52
Folgen und Reihen
Zahlenfolgen
Eine Zahlenfolge a besteht aus Zahlen a1, a2, a3, a4, a5, .... Die einzelnen Zahlen einer Folge heißen Glieder oder Terme. Beispiele für Zahlenfolgen sind
die natürlichen Zahlen:
1
die
2
die
1
die
1
die
2
2 3 4 5 6 7 8
geraden Zahlen:
4 6 8 10 12 14
Quadratzahlen:
4 9 16 25 36 49
Zweierpotenzen:
2 4 8 16 32 64
Primzahlen:
3 5 7 11 13 17
9
10
16
11
18
64
12
20
81
128
22
23
-1
1
14
24
100
256
19
13
26
121
512
29
144
1024
31
15
37
...,
28
...,
2048
41
...,
...,
... und
eine alternierende Folge:
1
-1
1
© Dr. Gerd Wegener, Hannover 2007
1
-1
1
-1
1
-1
1
-1
1
-1
....
Folgen und Reihen
Zahlenfolgen
Formal gesehen ist eine Zahlenfolge f eine Zuordnung der Menge IN der natürlichen Zahlen zu einer anderen Zahlenmenge A:
f: n → an mit n ∈ IN und an ∈ A ⊂ IR
Zahlenfolgen aus rationalen Zahlen sind z.B.
1
0
1
1
1
3
5
-
-
1
1
1
1
7
9
11
7
13
8
9
1
8
1
120
720
-
1
2
4
5
6
2
1
3
1
5
1
6
7
2
6
24
-
1
1
15
17
-
1
1
21
13
14
9
10
11
19
12
10
12
13
1
11
1
5040
40320
1
1
1
1
1
1
1
√2
√3
2
√5
√ 2·3
√7
1
π
1
π2
© Dr. Gerd Wegener, Hannover 2007
1
π3
1
π4
1
π5
1
π6
1
π7
1
362880
3628800
... und
1
π8
... und
1
Zahlenfolgen aus irrationalen Zahlen sind z.B.
1
...,
1
π9
....
...
2
Folgen und Reihen
Zahlenfolgen
Häufig gelingt es, eine Formel für jedes Glied an einer Zahlenfolge a anzugeben. Diese lautet
für die natürlichen Zahlen:
an = n,
für die geraden Zahlen:
an = 2·n,
für die Quadratzahlen:
an = n 2,
für die Zweierpotenzen:
an = 2 n
für die alternierende Folge 1 -1 1 -1 ...:
an = -1n+1.
und
Für die Primzahlen hat bisher niemand eine Formel gefunden und es ist
ziemlich sicher, dass es keine gibt.
© Dr. Gerd Wegener, Hannover 2007
3
Folgen und Reihen
Zahlenfolgen
Auch für die angegebenen Folgen aus rationalen und irrationalen Zahlen lassen sich Formeln notieren:
an =
an =
an =
-1n-1
2·n - 1
n-1
n
1
n!
→ 0
= 1 → 0
1
n
an =
→ 1
an =
1
√n
1
π
n-1
→ 0
→ 0
(n! = 1·2·3·4·5·...·n, sprich: n-Fakultät,
es wird festgelegt, dass 0! = 1 gilt.)
Alle diese Folgen streben für wachsendes n einem Grenzwert zu.
© Dr. Gerd Wegener, Hannover 2007
4
Folgen und Reihen
Monoton steigende und fallende Folgen
Ist jedes Glied an einer Folge (größer) größer oder gleich bzw. (kleiner) kleiner oder gleich seinem Vorgänger an-1, so heißt diese Folge (streng)
monoton steigend bzw. fallend.
Ist die Differenz zweier aufeinanderfolgender Glieder einer Zahlenfolge konstant, so spricht man von einer arithmetischen Folge. Die Folge der geraden Zahlen
2
4
6
8
10
12
14
16
18
20
2
2
2
2
2
2
2
2
2
ist z.B. eine streng monoton steigende arithmetische Folge.
© Dr. Gerd Wegener, Hannover 2007
22
2
...
2
5
Folgen und Reihen
Arithmetische Folgen
Die Quadratzahlen haben keine konstante Differenz,
1
4
3
9
5
16
7
25
9
36
11
49
13
64
15
81
17
100
19
...
21
2
2
2
2
2
2
2
2
2
2
aber die Differenz der Differenzen ist konstant. So eine Folge heißt dann
arithmetische Folge zweiter Ordnung. Dritter, vierter, fünfter, etc.
Ordnung bedeutet dann, dass die dritte, vierte, fünfte, etc. Differenzenfolge
konstant ist.
© Dr. Gerd Wegener, Hannover 2007
6
Folgen und Reihen
Geometrische Folgen
Ein Zahlenfolge heißt
geometrische Folge, wenn der Quotient
q=an+1/an zweier aufeinanderfolgender Glieder konstant ist.
Die Zweierpotenzen stellen eine geometrische Folge dar
1
2
4
8
16
32
64
128
256
512
...
2
2
2
2
2
2
2
2
2
2
aber auch die angegebene alternierende Folge
1
-1
1
-1
1
-1
1
-1
1
-1
...
-1
-1
-1
-1
-1
-1
-1
-1
-1
© Dr. Gerd Wegener, Hannover 2007
7
Folgen und Reihen
Grenzwerte von Folgen
Eine Zahl a∈IR heißt Grenzwert einer Folge a1, a2, a3, ..., wenn
es zu jeder reellen Zahl ε>0 ein n∈IN gibt, so dass gilt
⏐a - an⏐ < ε
Der Begriff Grenzwert kann auch noch anders definiert werden: Zu jeder reellen Zahl ε>0 gibt es ein N∈IN, so dass für alle m,n∈IN mit m,n≥N gilt
⏐am - an⏐ < ε
Der Vorteil dieser vom Mathematiker Augustin-Louis Cauchy (1789-1857) eingeführten Definition ist, dass man den Grenzwert nicht angeben muss. Es
muss nur sicher sein, dass alle weiter "hinten" stehenden Terme beliebig
dicht beieinander stehen.
Arithmetische Folgen mit einer Differenz verschieden von Null haben keinen
Grenzwert. Geometrische Folgen, für deren Quotient q gilt
0 < |q| < 1,
haben den Grenzwert 0. Eine solche Folge wird
8
© Dr. Gerd Wegener, Hannover 2007
Nullfolge
genannt.
Folgen und Reihen
Summen von Folgen
Eine Summe von n Gliedern einer arithmetischen Folge (erster Ordnung)
lässt sich folgendermaßen berechnen (d=ai+1-ai):
n
∑ ai
= a1 + a2 + a3 + ... + an
i=1
= a1 + (d+a1) + (2·d+a1) + ... + (n·d+a1)
= n·a1 + d + 2·d + ... + n·d
n
= n·a1 + d·∑ i
i=1
= n·a1 + d·
n·(n+1)
= n·(a1 + d·
© Dr. Gerd Wegener, Hannover 2007
2
n+1
2
)
9
Folgen und Reihen
Summen von Folgen
Eine Summe von n Gliedern einer geometrischen Folge lässt sich folgendermaßen berechnen (q=ai+1/ai):
n
∑ ai
= a1 + a2 + a3 + ... + an
i=1
2
= a1 + (q·a1) + (q ·a1) + ... + (q
= a1 · (1+q+q2+...+qn-1)
= a1 ·
2
1-q
1-q
n-1
Es gilt: (1+q+q +...+q
© Dr. Gerd Wegener, Hannover 2007
n
n
)·(1-q)=1-q
n-1
·a1)
10
Folgen und Reihen
Reihen
Zu jeder Folge lässt sich ihre Summenfolge bilden. Eine unendliche Summe der Glieder einer Zahlenfolge heißt Reihe. Wenn eine Reihe eine reelle Zahl als Grenzwert hat, bezeichnet man diese als konvergent, andernfalls, wenn die Reihe also über alle Genzen wächst, nennt man sie diver-
gent.
Beispiele für Reihen:
∞
n-1
∑ 2·n-1
-1
= 1 -
i=1
1
3
+
1
5
-
1
7
+
1
9
-
1
11
+
1
13
- ... + ... =
π
4
Diese Reihe ist unter dem Namen Leibnizsche Reihe bekannt geworden (Gottfried Wilhelm Leibniz (1646-1716)). Er geschrieb dazu: "Deus numeri impari gaudet!" ("Gott erfreut sich der ungeraden Zahlen!").
© Dr. Gerd Wegener, Hannover 2007
11
Folgen und Reihen
Reihen
Weitere Beispiele:
∞
∑i
1
= 1 +
i=1
1
2
+
1
3
+
1
+
4
1
5
+
1
6
+
1
+ ... = ∞
7
Diese Reihe wird Harmonische Reihe genannt. Sie ist divergent. Konvergent dagegen ist:
∞
∑i
1
2
= 1 +
i=1
© Dr. Gerd Wegener, Hannover 2007
1
4
+
1
9
+
1
16
+
1
25
+
1
36
+
1
49
+ ... ≈ 1.645
12
Folgen und Reihen
Grenzwerte
Geometrische Reihen von Folgen mit einem Quotienten |q|<1 sind konvergent. Ihr Grenzwert lässt sich mit Hilfe der Summenformel berechnen:
n
lim
Δx→0
∑ ai = lim a1·
Δx→0
i=1
1-qn
1-q
= a 1·
1
1-q
n
Der Grenzwert von q
für |q|<1 ist 0.
Die Reihe aus der Folge der reziproken Zweierpotenzen lässt sich z.B. mit
Hilfe dieser Formel berechnen:
∞
lim
Δx→0
∑2
1
i
i=0
© Dr. Gerd Wegener, Hannover 2007
= 1·
1
1-1/2
= 2
13