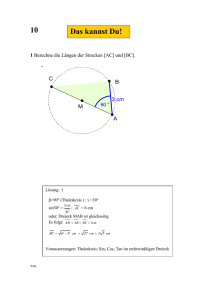
A 2.0 Die nebenstehende Zeichnung zeigt ein Schrägbild der
Werbung

Aufgabe A 2 Haupttermin S A 2.0 Die nebenstehende Zeichnung zeigt ein Schrägbild der Pyramide ABCS, deren Grundfläche das gleichseitige Dreieck ABC ist. Der Fußpunkt T der Pyramidenhöhe [ST] teilt die Dreieckshöhe [MB] des gleichseitigen Dreiecks ABC im Verhältnis MT : TB 1: 2 . Es gilt: MB 6 cm ; SBM 65 . In der Zeichnung gilt: 1 q ; 45 ; [MB] liegt auf der Schrägbildachse. 2 Runden Sie im Folgenden auf zwei Stellen nach dem Komma. C M B T A A 2.1 Berechnen Sie die Länge der Strecke [ST] . [Ergebnis: ST 8,58 cm ] 1P A 2.2 Punkte Pn liegen auf der Strecke [BS] . Die Winkel BMPn haben das Maß mit [0; 76,88] . Die Punkte Pn sind zusammen mit den Punkten A und C die Eckpunkte von gleichschenkligen Dreiecken APn C mit der Basis [AC] . Zeichnen Sie das Dreieck AP1C für 20 in das Schrägbild zu 2.0 ein. 1P A 2.3 Zeigen Sie durch Rechnung, dass für die Länge der Strecken [MPn ] in Abhängig5, 44 keit von gilt: MPn () cm . sin 65 2P Seite - 2 - Aufgabe A 2 Haupttermin A 2.4 Unter den Dreiecken APn C hat das Dreieck AP2 C den minimalen Flächeninhalt. Berechnen Sie den Flächeninhalt des Dreiecks AP2 C . 2P A 2.5 Die Punkte Pn sind für ]0; 76,88] Spitzen von Pyramiden ABCPn mit den Höhen [Pn Fn ], deren Fußpunkte Fn auf [MB] liegen. Für das Volumen der Pyrami1 de ABCP3 gilt: VABCP3 VABCS . Bestimmen Sie das zugehörige Winkelmaß . 2 3P Seite - 3 - A 2.0 Die nebenstehende Zeichnung zeigt ein Schrägbild der Pyramide ABCS, deren Grundfläche das gleichseitige Dreieck ABC ist. Der Fußpunkt T der Pyramidenhöhe [ST ] teilt die Dreieckshöhe [ MB] des gleichseitigen Dreiecks ABC im Verhältnis MT : TB = 1 : 2. Es gilt: MB = 6 cm; ^SBM = 65◦ . In der Zeichnung gilt: q = 21 ; ω = 45◦ ; [ MB] liegt auf der Schrägbildachse. Runden Sie im Folgenden auf zwei Stellen nach dem Komma. S × × P1 C × M ϕ × × T × B × A A 2.1 Berechnen Sie die Länge der Strecke [ST ]. [Ergebnis: ST = 8,58 cm] Gegebene Maÿe in der Zeichnung farbig markieren und geeignetes Dreieck (am besten rechtwinklig) suchen. S × TB = 2 3 · MB ST TB ST = TB · tan ^SBM = 4 cm · tan 65◦ = 8,58 cm tan ^SBM = ⇔ C M × × × T × A × B A 2.2 Punkte Pn liegen auf der Strecke [ BS]. Die Winkel BMPn haben das Maß ϕ mit ϕ ∈ [0◦ ; 76,88◦ ]. Die Punkte Pn sind zusammen mit den Punkten A und C die Eckpunkte von gleichschenkligen Dreiecken APn C mit der Basis [ AC ]. Zeichnen Sie das Dreieck AP1 C für ϕ = 20◦ in das Schrägbild zu 2.0 ein S × Unbedingt den Winkel ϕ und den zweiten Schenkel, [ MP1 ], auch einzeichnen, da dies für spätere Auf- also gaben entscheidend ist. × P1 C × M ϕ × × T × B × A A 2.3 Zeigen Sie durch Rechnung, dass für die Länge der Strecken [ MPn ] in Abhängigkeit von ϕ gilt: 5,44 MPn ( ϕ) = cm sin ( ϕ + 65◦ ) Geeignetes Dreieck suchen und gegebene Gröÿen markieren. Man sieht, dass der Kongruenzsatz WSW erfüllt ist. Daher erst das fehlende Winkelmaÿ über S die Innenwinkelsumme bestimmen. Es bietet sich an, das Winkalmaÿ in der Form 180◦ − ( ϕ + 65◦ ) zu bestimmen und, mit Blick auf das angegebene × Ergebnis, anschlieÿend über die Supplementbeziehung zu vereinfachen. ^ MPn B = 180◦ − (^ BMPn + ^ Pn BM) = 180◦ − ( ϕ + 65◦ ) = ϕ + 65◦ Sinussatz aufstellen: 180◦ − ( ϕ + 65◦ ) P1 C ϕ 65◦ B T MPn sin ^ Pn BM = × × M × A × × ⇔ MPn = ⇒ MPn = × = MB ^ MPn B MB · sin ^ Pn BM sin ^ MPn B 6 cm · sin 65◦ sin ( ϕ + 65◦ ) 5,44 cm sin ( ϕ + 65◦ ) A 2.4 Unter den Dreiecken APn C hat das Dreieck AP2 C den minimalen Flächeninhalt. Berechnen Sie den Flächeninhalt des Dreiecks AP2 C. S Das Dreieck APn C hat genau dann den minimalen Flächeninhalt, wenn die Länge der Strecke [ MPn ] minimal ist. Die Länge der Strecke [ MPn ] ist genau dann minimal, wenn [ MPn ]⊥[ BS ] × gilt. MPn minimal für ^ MP2 B = 90◦ × C ϕ 180◦ − 65◦ − ϕ = 90◦ ⇔ − ϕ = −25◦ ⇔ ϕ = 25◦ P1 × M 65◦ × × × T B AC über Satz des Pythagoras berechnen: × A AB ⇔ AC ⇒ ⇔ ⇔ ⇒ A AP2 C = = 1 2 1 2 2 2 2 = AM + MB !2 AC 2 = + MB 2 2 AC + (6 cm)2 4 2 · AC = 36 cm2 2 AC = 48 cm2 AC = 6,93 cm AC 3 4 2 2 = · AC · MPn · 6,93 cm · 5,44 cm = 18,85 cm2 sin (25◦ + 65◦ ) A 2.5 Die Punkte Pn sind für ϕ ∈ [0◦ ; 76,88◦ ] Spitzen von Pyramiden ABCPn mit den Höhen [ Pn Fn ], deren 1 Fußpunkte Fn auf [ MB] liegen. Für das Volumen der Pyramide ABCP gilt: VABCP3 = · VABCS . 2 Bestimmen Sie das zugehörige Winkelmaß ϕ. S Höhe × [ Pn Fn ] und Höhenfuÿpunkt F1 einzeichnen. Hier bietet es sich an, mit der gegebenen Formel für das Verhältnis der Volumina zu beginnen. VABCP3 ⇔ × P1 C ϕ × M × × × T B F1 1 3 = · A ABC · P3 F3 = 1 2 1 2 1 2 1 2 · VABCS · 13 · A ABC · ST ⇔ P3 F3 = · ST ⇒ P3 F3 = ⇔ P3 F3 = 4,29 cm · 8,58 cm × A Geeignetes Dreieck suchen, um die Länge der Strecke [ P3 F3 ] in Abhängigkeit von ϕ darzustellen: Dreieck sin (25◦ + 65◦ ) vorkommt, wäre die Gleichung für uns nicht lösbar. Also brauchen wir eine weitere, konkrete, Streckenlänge im Dreieck MF3 P3 : MF3 . Diese erhalten wir über den Tangens des Winkels ^SBM im Dreieck BP3 F3 : MF3 P3 . Da hier momentan aber sowohl tan ^SBM = ⇔ sin ϕ als auch P3 F3 F3 B F3 B · tan ^SBM = P3 F3 P3 F3 tan ^SBM 4,29 cm ⇒ F3 B = = 2 cm tan 65◦ MF3 = MB − F3 B = 6 cm − 2 cm = 4 cm ⇔ F3 B = P3 F3 MF3 4,29 cm = 4 cm ϕ = 47◦ tan ^ F3 MP3 = ⇒