LernaufgabenimMU2009_druck - math

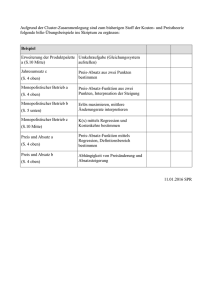
Lernaufgaben im
Mathematikunterricht
Gliederung
1. Einstieg: Den Blick schärfen für das Lernpotential von Aufgaben
2. Sind nicht alle Aufgaben immer auch Lernaufgaben?
3. Modelle zur Analyse und Konstruktion von Aufgaben: Zieltypisierung
4. Kann mit offenen Aufgaben mehr und besser gelernt werden?
5. Wege zur Aufgabenkonstruktion: Schwierigkeitsparameter, Aufgabenvariation
Prof. Dr. Regina Bruder
Technische Universität Darmstadt
Ausblick:
Qualitätskriterien für Lern- und Testaufgaben
Oldenburg, 23.09.2009
1. Den Blick schärfen für das Lernpotential von Aufgaben
1. Den Blick schärfen für das Lernpotential von Aufgaben
Aufgabe 1:
Aufgabenstellung:
Vergleichen Sie die folgenden Aufgaben paarweise
Miteinander.
Worin unterscheiden sich die Aufgaben?
Welche Gemeinsamkeiten besitzen die Aufgaben?
Aufgabe 2:
Am 15. Februar 1969 gelang es 34 Personen, sich gleichzeitig in einen VW-Käfer zu "setzen".
a) Wie groß wurde das zusätzliche Gewicht für den Käfer?
b) Wie viel Platz muss in einem VW-Käfer sein, damit man darin überhaupt so viele Menschen
unterbringen kann? Wie könnte man vorgehen, um das Volumen eines durchschnittlich großen
Menschen anzugeben? Überlege welche Genauigkeit dafür erforderlich ist.
Aufgabe 3:
23. September 2009 | Fachbereich Mathematik | AG Didaktik | Prof. Dr. R. Bruder und C. Collet | 3
Didaktische Funktion einer
Aufgabe und potentielle Lernziele
Aufgaben können Funktionen auf mehreren Ebenen übernehmen:
Aufgaben zur Erarbeitung oder Überprüfung intelligenten Wissens
(Begriffe, Sätze, Verfahren/Strategien, Anwendungsfelder)
Aufgaben zur Gewinnung oder Feststellung von
Handlungskompetenzen (Erkennen, Beschreiben, Verknüpfen,
Anwenden, Begründen)
Aufgaben zur Entwicklung und Beschreibung von
Metakompetenzen (Mathematikbild, Selbsteinschätzung,
Interpretieren von Zusammenhängen)
Aufgaben unterscheiden sich…
nach äußerlichen Merkmalen (viel oder wenig Text, mit oder ohne
Bildern…)
nach inneren Merkmalen (Aufgabentypen: offen/geschlossen,
Schwierigkeitsmerkmale wie Komplexität,
Art der erforderlichen Schülertätigkeiten
nach übergreifenden Merkmalen wie didaktische Einsatzmöglichkeiten
der Aufgabe, mögliche Lösungsstrategien…
Gliederung
Zielstellung des Workshops:
1. Einstieg: Den Blick schärfen für das Lernpotential von Aufgaben
2. Sind nicht alle Aufgaben immer auch Lernaufgaben?
3. Modelle zur Analyse und Konstruktion von Aufgaben: Zieltypisierung
- Kennen lernen von Modellen
zur Analyse und Entwicklung
von Lernaufgaben
aus unterschiedlichen Blickwinkeln
4. Kann mit offenen Aufgaben mehr und besser gelernt werden?
5. Wege zur Aufgabenkonstruktion: Schwierigkeitsparameter, Aufgabenvariation
Ausblick:
Qualitätskriterien für Lern- und Testaufgaben
2. Sind nicht alle Aufgaben immer auch
Lernaufgaben?
Lernsituation versus Testsituation (Klassenarbeit):
Was ist eigentlich eine Aufgabe?
• alle Testaufgaben einer Klassenarbeit sollten sich auch als
Lernaufgaben eignen (Chance zur Kommunikation im Unterricht)
Eine Aufgabe ist eine Aufforderung zum Lernhandeln.
und lässt sich beschreiben durch eine Anfangssituation, eine
Endsituation und geeignete Transformationen von der Anfangsin die Endsituation
• nicht alle Lernaufgaben eignen sich auch als Testaufgaben
(Bsp.: offene Modellierungsaufgaben: Wie lange dauert ein
Wasserwechsel im Schwimmbad?
Warum ist nicht jede Lernaufgabe für den Unterricht auch als
Testaufgabe geeignet ?
Phasen mathematischen Modellierens als Rahmen
schulischen Lernens von Mathematik
Mathematisches
Modell
Mathematik
Mathematische
Ergebnisse
3
4
2
1 situiertes
Strukturieren
Lernsituation versus Testsituation (Klassenarbeit):
• alle Testaufgaben einer Klassenarbeit sollten sich auch als
Lernaufgaben eignen (Chance der Kommunikation im Unterricht)
2 Mathematisieren
• nicht alle Lernaufgaben eignen sich auch als Testaufgaben
3 Verarbeiten – mit
math. Werkzeugen
umgehen
(Bsp.: offene Modellierungsaufgaben: Wie lange dauert ein
Wasserwechsel im Schwimmbad?
Realität
4 Interpretieren
5 Validieren
Realmodell
5
1
• MC-Formate eignen sich nur unter besonderen Bedingungen zur
Diagnose und Förderung (Erkennen typischer Fehler und
Fehlvorstellungen)
Reale
Ergebnisse
Realsituation
Im Herbstsemester 1989 wählten in Stockholm 13246
Lernende den wirtschaftlichen Vertiefungszweig und 12511
Lernende den technischen Zweig.
Beispiele für MC-Aufgaben:
(1) Insgesamt wählten 10388 Mädchen den wirtschaftlichen
und technischen Zweig.
(2) 5430 Jungen wählten den wirtschaftlichen Zweig.
Wie viele Mädchen wählten den technischen Zweig?
Ausreichend Information für eine Lösung erhält man
a) in (1) aber nicht in (2)
b) in (2) aber nicht in (1)
c) in (1) zusammen mit (2)
d) in (1) und (2) jede für sich alleine
e) gar nicht durch beide Aussagen.
Beispiel für eine Testaufgabe, die auch
Lernaufgabe sein kann
Jörg und seine Freundin Susi fahren zum Sommerschlussverkauf in die Stadt. Sie
gehen in das Einkaufszentrum und schlendern durch die Geschäfte.
a) Susi findet eine Hose, deren ursprünglicher Preis von 50 € auf 40 € gesenkt
wurde. Wie groß ist die Ersparnis?
5% 10%
20%
30% 40%
b) Jörg kauft für Susi eine Sonnenbrille. Ihr Preis wurde um 40 % gesenkt und
kostet jetzt nur noch 15 €. Wie teuer war sie ursprünglich?
c) Jörg möchte eine Mütze kaufen, deren Preis um 30% reduziert ist. Wegen eines
Farbfehlers kann er den Preis um zusätzliche 20% herunterhandeln. Wie viel
Prozent gegenüber dem ursprünglichen Preis wird er an der Kasse insgesamt
sparen?
d) Susi liest auf einem Werbeplakat ihres Mobilfunkanbieters, dass die Kosten für
SMS um ein Drittel gesenkt werden. Susi freut sich: „Jetzt kann ich für denselben
Betrag ein Drittel mehr SMS als bislang verschicken!“ Jörg widerspricht: „Das
sind sogar zwei Drittel mehr!“
Wer hat Recht? (Begründe deine Entscheidung)
Beispiel Klasse 5
Lena stellt Martin ein Zahlenrätsel: „Denke dir eine Zahl. Addiere nun 1 und
multipliziere das Ergebnis mit 5. Subtrahiere jetzt 4 von der letzten Zahl.
Wenn du mir nun das Ergebnis sagst, sage ich dir, welche Zahl du dir
gedacht hast!“
a) Martin denkt sich die Zahl 6. Welches Ergebnis bekommt er heraus?
-----------------b) Nun denkt sich Martin eine neue Zahl. Sein Ergebnis lautet jetzt 76.
Welche Zahl hat er sich gedacht?
-----------------c) Beschreibe, wie Lena aus Martins Ergebnis immer seine gedachte Zahl
erhält.
23. September 2009 | Fachbereich Mathematik | AG Didaktik | Prof. Dr. R. Bruder und C. Collet | 15.
Gliederung
1. Einstieg: Den Blick schärfen für das Lernpotential von Aufgaben
3. Modelle zur Analyse und Konstruktion von
Lernaufgaben: Zieltypisierung
Welche Aufgabentypen sind grundsätzlich notwendig für nachhaltiges
Lernen ?
2. Sind nicht alle Aufgaben immer auch Lernaufgaben?
3. Modelle zur Analyse und Konstruktion von Aufgaben: Zieltypisierung
4. Kann mit offenen Aufgaben mehr und besser gelernt werden?
Aufgabenkonzept nach Zieltypen
5. Wege zur Aufgabenkonstruktion: Schwierigkeitsparameter, Aufgabenvariation
Ausblick:
Qualitätskriterien für Lern- und Testaufgaben
Gege- TransforGesuchbenes mationen
tes
----------------------------------------------------------------------X
X
X
gelöste Aufgabe ( stimmt das?)
X
X
einfache Bestimmungsaufgabe
Aufgabentypisierung für nachhaltiges Lernen
Gegebenes
Transformationen
Gesuchtes
-----------------------------------------------------------------------
-
X
X
einfache Umkehraufgabe
X
-
X
Beweisaufgabe, Spielstrategie
X
-
-
X
schwere Bestimmungsaufgabe
schwierige Umkehraufgabe
-
X
-
Aufforderung, eine Aufgabe zu
erfinden
(-)
-
(-)
offene Problemsituation
Aufgabentypisierung für nachhaltiges Lernen
Gegebenes
Transformationen
Gesuchtes
X
-
einfache Bestimmungsaufgabe (Ausführen)
Informationen in einer vorgegebenen Weise sammeln
bzw. verarbeiten, ein gegebenes Verfahren anwenden…
X
x
gelöste Aufgabe, Beispiel, Muster;
ein Verfahren vorführen Schritt für Schritt;
Variationen: Gelöste Aufgabe gegeben - stimmt das?
Aufgabentypisierung für nachhaltiges Lernen
Gegebenes
----------------------------------------------------------------------X
X
Transfor- Gesuchmationen tes
----------------------------------------------------------------------X
X
X
gelöste Aufgabe, Muster ( stimmt das?)
X
-
X
X
X
einfache Bestimmungsaufgabe
einfache Umkehraufgabe
X
-
X
Beweisaufgabe, Argumentationsketten aufbauen,
Spielstrategie bzw. Methode finden
Rätsel aufklären – wie funktioniert das?
Ursachen für Phänomene finden – Hypothesen bilden
Ein Beispiel nach bestimmten Kriterien auswählen
-
X
X
einfache Umkehraufgabe (Verstehen, Reflexion ! )
Die Anfangssituation einer Verfahrensanwendung
rekonstruieren.
Schwieriger (--x):
Die möglichen Kriterien rekonstruieren, nach denen
Beispiele von Mitschülern ausgewählt wurden.
Aufgabentypisierung für nachhaltiges Lernen
Gegebenes
Transfor- Gesuchmationen tes
Aufgabentypisierung für nachhaltiges Lernen
Gegebenes
Transfor- Gesuchmationen tes
-----------------------------------------------------------------------
-----------------------------------------------------------------------
X
X
-
(-)
schwere Bestimmungsaufgabe
Etwas entwickeln und gestalten ohne explizit gegebene
Vorbilder;
Informationen vergleichen, einordnen bzw. beurteilen
ohne vorgegebene Maßstäbe
Neue Lösungswege finden (geeignet für
Einstiegsaufgaben in ein neues Thema)
-
(-)
schwere Bestimmungsaufgabe
Aufgabentypisierung erzeugt Problembewusstsein:
Zieltransparenz:
Ist der Weg das eigentliche Ziel der Aufgabe – oder das Ergebnis von
zentraler Bedeutung – oder beides?
FERMI-Aufgaben (Motivationsproblem!)
-
-
(X)
schwierige Umkehraufgabe
Projekt mit klarem Ziel;
Rekonstruktion ohne Vorbilder oder Muster
Ebenen der Lernanforderungen und ggf. Mehrwert des Arbeitsaufwands
klären: Fachliche Lerninhalte versus Werkzeugkompetenz
Aufgabentypisierung für nachhaltiges Lernen
Gegebenes
Aufgabentypisierung für nachhaltiges Lernen
Transfor- Gesuchmationen tes
Gegebenes
Transfor- Gesuchmationen tes
----------------------------------------------------------------------X
X
X
gelöste Aufgabe, Muster ( stimmt das?)
X
X
einfache Bestimmungsaufgabe
X
X
einfache Umkehraufgabe
X
X
Beweisaufgabe, Spielstrategie bzw. Methode finden
----------------------------------------------------------------------X
X
X
gelöste Aufgabe, Muster ( stimmt das?)
X
X
einfache Bestimmungsaufgabe
X
X
einfache Umkehraufgabe
X
X
Beweisaufgabe, Spielstrategie bzw. Methode finden
X
-
-
X
schwere Bestimmungsaufgabe
schwierige Umkehraufgabe
X
-
-
X
schwere Bestimmungsaufgabe
schwierige Umkehraufgabe
-
X
-
Aufforderung, eine Aufgabe zu erfinden bzw. eine
Beispielanwendung zu beschreiben
-
X
-
Aufforderung, eine Aufgabe zu erfinden
(-)
-
(-)
Verständnisfördernd, wenn eigene Beispiele für einen Sachverhalt gesucht
werden
Selbst entwickelte (Lern- oder Test-)Aufgaben von Schülern zur Bearbeitung
anbieten.
offene Problemsituation
„Echte“ Modellbildungen – reale Fragestellungen
(Qualitätsbrille: Weg und Ziel sind relevant)
Einstiegsaufgabe für ein neues Thema bzw. einen
Projektauftrag
Erste und vertiefende Übung zu Nullstellenberechnungen von linearen Funktionen
Wähle mindestens fünf der folgenden Aufgaben aus und löse sie (Zeitrahmen 20 min) vorgesehen.
-------------------------------------------------------------------------------------------------------------1. Gesucht ist jeweils die Nullstelle der folgenden linearen Funktionen:
f(x) = x – 5,
These:
Nachhaltiges Lernen erfordert eine Orientierung an den 8 Zieltypen.
Umsetzung
als Leitfaden und Konstruktionsheuristik beim
Aufbau von Selbstlerneinheiten, Stationenlernen, Expertenpuzzle bzw.
bei der Bereitstellung von Lernvoraussetzungen
(vielseitige kognitive Aktivierung)
a)
(x x -)
b)
(- x x)
c)
(x x -)
d)
(x - -)
e)
((-) – (-))
proportionale Zuordnung? Begründe.
d) Für 24 Schüler rechnet Frank einen Preis von 1140€ aus.
Maike meint, dass die Gruppe noch günstiger fahren kann.
Hat Maike recht? Begründe.
e) Die Fährgesellschaft will eine Blockkarte für 50 Personen
einführen. Was wäre ein angemessener Preis?
2. Zeichne eine lineare Funktion mit einer Nullstelle bei x = - 3
Umkehrung (-, x, x)
3. Was kann eine Nullstelle einer linearen Funktion praktisch bedeuten?
(x,-,-)
------------------------------------------------------------------------------------------------------------4. Gib die Gleichungen zweier linearer Funktionen an,
(
,
,
x
)
die bei x = 4 ihre Nullstelle haben.
5. Notiere die Gleichung einer linearen Funktion, die keine Nullstelle hat.
(-,-,x)
6. Überlege Dir einen Sachverhalt, der mit Hilfe einer linearen Funktion
beschrieben werden kann, welche bei P(1;0) eine Nullstelle hat. ( - , x, - )
-----------------------------------------------------------------------------------------------------------7. Warum können lineare Funktionen nie mehr als eine Nullstelle haben? ( x , - , x )
Ein Lernaufgabenarrangement für
nachhaltiges Lernen
c) Handelt es sich bei der Preistabelle um eine
Quelle: Jordan, Uni Kassel 2004
Grundaufgabe (x, x, -)
f(x) = mx + b und gib dazu evtl. notwendige Bedingungen für m, x und b an! ( (x) , - , - )
Aufgaben mit aufsteigender Komplexität und Offenheit:
a) Welchen Preis hat eine Gruppe von 4 Personen
zu zahlen?
b) Wie viele Karten bekommt man für 300€ ?
f(x) = - 5x – 2,5
8. Finde einen Ausdruck zur Bestimmung der Nullstelle für eine beliebige lineare Funktion:
als prozessbegleitende Testelemente zur Unterstützung von
Einübung, Verständnissicherung und Selbsteinschätzung
An der Anlegestelle einer großen Fähre steht:
Karte
1 Person
50€
Blockkarte 8 Personen
380€
Blockkarte 20 Personen
900€
f(x) = 2x + 6
Grundaufgaben
Abwandlungen von Grundaufgaben
(Umkehraufgaben: offen bzgl. Lösungsweg oder/und Resultat,
verschiedene Lösungswege frei stellen, prüfen und sichern
Verständnis)
Erweiterungen von Grundaufgaben (Inhalte aus früheren
Stoffgebieten einbeziehen – Verfügbarkeit von Grundlagen sichern)
Komplexe Aufgaben mit Standard- und Problemcharakter
(Wahlmöglichkeiten)
Problemsituationen (offen bzgl. der Fragestellungen,
binnenleistungsdifferenzierend, Wahlmöglichkeiten)
Ein solches Aufgabenset für Lernsituationen bildet wesentliche
Lerntätigkeiten ab, ermöglicht Vernetzung, bietet individuelle Freiräume
und erfordert methodische Variabilität des Lernangebotes.
- Ist meist zu umfangreich für Leistungserhebungen!
4. Kann mit offenen Aufgaben mehr und besser
gelernt werden?
Unterschiedliche Lösungswege
Bewusstmachen von Strategien – Müller-Mufflig-Aufgabe
Offen heisst Ergebnisvielfalt oder unterschiedliche Lösungswege oder
beides z.B. in einer Modellierungsaufgabe
Offen heisst nicht unstrukturiert und ziellos!! (best. kognitive Stile haben
Schwierigkeiten mit zu vielen Wahloptionen)
Offene Aufgaben sind ein notwendiger Teil einer nachhaltigen
Lernumgebung
Überwiegen offene Aufgaben, dann unterstützen sie eher leistungsstarke
Lernende, fördern aber lernschwache Schüler zu wenig
Ergebnisoffen:
Unterschiedliche Lösungswege
Bewusstmachen von Strategien – Müller-Mufflig-Aufgabe
Informative Figur
Systematisches Probieren mit Hilfe einer Tabelle
14
12
12
10
10
8
8
6
6
4
4
2
2
Arbeiten mit Invarianten und Gleichungen
0 0.5 1
1.5 2
2.5 3
3.5 4
Hinterherlaufen
Mathematisches
Modell
40
Tankinhalt in l
Weg in km
14
0 0.5 1
Zeit in h
1.5 2
2.5 3
30
Mathematik
4
2
Realität
20
Realmodell
10
3.5 4
Mathematische
Ergebnisse
3
5
1
Reale
Ergebnisse
Realsituation
Entgegengehen
0
08:00
10:00
12:00
Was haben die beiden Bewegungen gemeinsam?
14:00
16:00
18:00
Uhrzeit
Familie Schnell fährt mit dem Auto in den Urlaub.
Das Diagramm zeigt, wie viel Benzin sich zu jedem Zeitpunkt der Reise
im Tank befindet.
Was bleibt gleich?
Beschreibe mögliche Ereignisse auf der Reise von 8:00 bis 18:00 Uhr.
23. September 2009 | Fachbereich Mathematik | AG Didaktik | Prof. Dr. Regina Bruder und C. Collet | 33
Unterschiedliche Lösungswege und Strategien
Unterschiedliche Lösungswege
Kerzen
Zwei Kerzen brennen mit unterschiedlichen
Geschwindigkeiten ab: Kerze A ist 36cm lang und brennt
mit 3cm pro Stunde ab, Kerze B ist 10cm lang und
brennt mit 1cm pro Stunde ab. Wann sind beide Kerzen
gleich lang?
Beispiel eines Testitems: „Kino“
Mike stellt ein Kino - Rätsel: „Nur ein Fünftel der Plätze sind von
Erwachsenen belegt. 10 Plätze mehr werden von Jungen
eingenommen. Außerdem sind 30 Mädchen hier. 20 Plätze sind frei.
Wie viele Sitze hat das Kino?“
Lösung mithilfe einer informativen Figur
Weitere Heurismen:
Gleichung
Kerze A: y=36-3x
Invarianzprinzip
Gleichsetzen !
Informative Figur
Überprüfung des Ergebnisses mit
der realen Situation
Gleichung
Kerze B: y=10-1x
23. September 2009 | Fachbereich Mathematik | AG Didaktik | Prof. Dr. Regina Bruder und C. Collet | 35
Weitere Lösungsmöglichkeiten:
Tabelle in Verbindung mit systematischem Probieren
23. September 2009 | Fachbereich Mathematik | AG Didaktik | Prof. Dr. R. Bruder und C. Collet | 36
5. Wege zur Aufgabenkonstruktion
Zwischenstand:
Potenzialanalyse von Aufgaben nach
- Handlungsziel: 8 Zieltypen bzw. Aufgabenset
- Schülertätigkeiten (Grundhandlungen, Kompetenzen im
Modellierungskeislauf…)
Vertiefung
- Schwierigkeit: drei Anforderungsniveaus aus den Standards,
(F,K,B,A)-Modell oder die drei Orientierungslevel
Was macht eine Aufgabe schwer?
Zieltypisierung - auch mit Beachtung der Komplexität reicht noch nicht aus! Deshalb: Vertiefte Analyse des
Anforderungsniveaus von Aufgaben:
Das Anforderungsniveau einer Aufgabe bezogen auf eine
Lerngruppe zu einem bestimmten Testzeitpunkt wird durch
4 Parameter bestimmt:
Formalisierungsgrad F
Komplexitätsgrad K
Bekanntheitsgrad B
Ausführungsaufwand A
Aufgabenvariation
Individuell verschieden, aber doch insgesamt schwieriger wird es
insbesondere dann,
wenn eine Aufgabe nicht verstanden wurde oder gar die Bereitschaft
fehlt, sich auf die Aufgabe einzulassen,
wenn ein Sachverhalt erst mathematisiert werden muss, um ihn
bearbeiten zu können und geeignete Mathematisierungsmuster nicht
unmittelbar verfügbar sind,
Formalisierungsgrad
• wenn mögliche Lösungswege mehrere Teilschritte umfassen, die
Anforderungen also komplexer werden und
Komplexitätsgrad
•
•
wenn die notwendigen Grundvorstellungen für die Anwendung
mathematischer Operationen und für die Interpretation der Ergebnisse nicht
ausgebildet sind, also Fehlvorstellungen eine erfolgreiche
Aufgabenbearbeitung verhindern. Ausführungsaufwand
wenn Basiswissen fehlt, nicht verfügbar und nicht vernetzt ist
Initialaufgabe:
Berechne das Volumen eines 10cm hohen Zylinders mit dem
Durchmesser von 12cm!
Variationsmöglichkeit – Wackeln: geringfügig ändern
Berechne das Volumen eines Zylinders mit der Höhe von 6dm und
einem Radius von 6cm!
Variationsmöglichkeit – Ersetzen: analogisieren
Welches Volumen hat ein Quader mit den Maßen a=3cm, b=4cm und c=5cm?
Variationsmöglichkeit – Rahmen wechseln: Kontext ändern
Ist es möglich, dass ein Quader ein Volumen von 270cm3 besitzt bei einer
Gesamtkantenlänge von 80cm, wenn alle Kantenlängen natürliche Zahlen sind?
23. September 2009 | Fachbereich Mathematik | AG Didaktik | Prof. Dr. R. Bruder und C. Collet | 40
Kategoriensystem
Fachlicher Hintergrund: Fachliche Angemessenheit und perspektivische Dimension,
Korrektheit von Musterlösungen, Sachliche Angemessenheit der Aufgabenstellung
Zieltransparenz: Klarheit der Aufgabenstellung und des Erwartungshorizontes
Motivation: Altersangemessenheit der Aufgabenstellung und des Kontextes
Ausgangsniveau: Erfassen und Berücksichtigen des Ausgangsniveaus
(Diagnoseelement), Wiederholungsangebote zum Schließen von Lücken, Unterstützung
zum Verständnis des Sachverhalts
Binnendifferenzierung: Individueller Übungsbedarf (Schwierigkeitsgrade,
Zusatzaufgaben, Wahlmöglichkeiten), Offene Aufgaben,
Angemessene Sozialformen, unterschiedliche Erkenntnisebenen
Kognitive Aktivierung: Inhaltliche Vernetzungen, Variation der Zieltypen, möglicher
Heurismeneinsatz, Variation und Vielfalt an Lerntätigkeiten
Unterstützung der Selbstregulation: Zeitplanung, Strategien, Lösungsweg, Methoden,
Korrektheit der Lösung
Einsatz technischer Hilfsmittel
Konzeptbezug: Problemlösen, Selbstregulation, Basiskönnen, Rechnereinsatz etc.;
Orientierungslevel
Vielen Dank für Ihre Aufmerksamkeit!
Online-Fortbildungen von Mathematik-Lehrkräften
www.prolehre.de
Arbeitsprodukte der Lehrkräfte
www.problemloesenlernen.de
Aufgabendatenbank madaba
www.madaba.de
Kontakt:
Mathematikwettbewerbe:
[email protected]
http://www.mathe-kaenguru.de/
[email protected]
http://www.mathematik-wettbewerb.de/
Anmeldeadresse: [email protected]
23. September 2009 | Fachbereich Mathematik | AG Didaktik | Prof. Dr. Regina
R. Bruder
Bruder
und C.
und
Collet
C. Collet
| 42 | 42