Wahrscheinlichkeit3 – Binomialverteilung/Bernoulli

Wahrscheinlichkeit3 – Binomialverteilung/Bernoulli-Formel
Aufgaben
Lösen Sie A1 und A2 sowohl mit der Bernoulli-Formel als auch mit dem TR(BV), die anderen
Aufgaben lösen sie mit dem TR(BV).
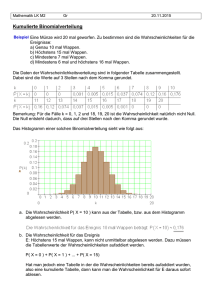
A1 Eine Familie hat 6 Kinder. Die Wahrscheinlichkeit ein Mädchen zu gebären
betrage p = 0,5.
Berechnen Sie die Wahrscheinlichkeit dafür, das unter den 6 Kindern
0, 1, 2, 3, 4, 5, 6 Mädchen sind und zeichnen Sie das
Säulendiagramm/Histogramm der Wahrscheinlichkeitsverteilung.
Bestimmen Sie die Wahrscheinlichkeit folgender Ereignisse:
A: Genau die Hälfte der Kinder sind Mädchen.
B: Höchstens die Hälfte der Kinder sind Mädchen.
C: Mindestens die Hälfte der Kinder sind Mädchen.
A2 Eine Münze wird 5 mal geworfen. p sei 0,5.
a) Bestimmen Sie die Wahrscheinlichkeitsverteilung der Zufallsvariablen
X: Anzahl der Wappen.
b) Mit welcher Wahrscheinlichkeit wirft man
(1) höchstens 3 mal Wappen?
(2) weniger als 3 mal Wappen?
(3) mindestens 1 mal Wappen?
(4) mehr als einmal Wappen?
A3 Eine Münze wird 20 mal geworfen.
a) Zeichnen Sie das Säulendiagramm der Binomialverteilung.
b) Zu bestimmen sind die Wahrscheinlichkeit für die Ereignisse:
(1) Genau 10 mal Wappen.
(2) Höchstens 15 mal Wappen.
(3) Mindestens 7 mal Wappen.
(4) Mindestens 6 und höchstens 16 mal Wappen.
A4 Ein Multiple- Choice- Test besteht aus 50 Aufgaben mit jeweils 5 Antworten, von
denen nur jeweils eine richtig ist.
Mit welcher Wahrscheinlichkeit kann man durch bloßes Raten folgende Anzahl
von Aufgaben richtig beantworten?
a) Mehr als 20 Aufgaben.
b) Mindestens 10 und höchstens 20 Aufgaben.
c) Weniger als 10 Aufgaben.
d) Genau 15 Aufgaben.
Die Trefferwahrscheinlichkeit pro Aufgabe ist 1/5 = 0,2.
Wahrscheinlichkeit3-Binomialverteilung/Bernoulli-Formel
Seite 1
Berechnen Sie für A5, A6 und A7 auch den Erwartungswert und die Standardabweichung.
A5 n  20 und p  0,5
a) Die Anzahl der Erfolge beträgt höchstens 12
b) Die Anzahl der Erfolge beträgt mindestens 10
c) Die Anzahl der Erfolge beträgt genau 11
d) Die Anzahl der Erfolge liegt zwischen 7 und 13
A6
1
6
Die Anzahl der Erfolge beträgt genau 10
Die Anzahl der Erfolge beträgt mindestens 11
Die Anzahl der Erfolge liegt zwischen 6 und 14
Die Anzahl der Erfolge beträgt höchstens 8
n  60 und p 
a)
b)
c)
d)
A7 n  100 und p  0,1
a) Die Anzahl der Erfolge beträgt genau 10
b) Die Anzahl der Erfolge beträgt mindestens 9
c) Die Anzahl der Erfolge liegt zwischen 5 und 15
d) Die Anzahl der Erfolge beträgt höchstens 12
A8 Bestimmen Sie die 95%- Umgebung vom Erwartungswert.
a) n  150 und p  0,28
b) n  250 und p  0,7
Wahrscheinlichkeit3-Binomialverteilung/Bernoulli-Formel
Seite 2
Lösungen
A1
Berechnung mit Bernoulli-Formel
Das Problem kann als 6- stufiger Bernoulli- Versuch betrachtet werden
mit n = 6 und p = 0,5. Gesucht ist P(X = k) für k = 0, 1, 2, 3, 4, 5, 6
n
n k
P  X  k      pk  1  p 
k 
6  1 
P  X  0      
0  2 
6  1 
P  X  1      
 1  2 
3
3
3
6
1
1
 1
 1
    1    1

 0,015625
64 64
2
2
3
6
1
6
 1
 1
   6   6

 0,09375
64 64
2
2
6  1 
P  X  2      
 2  2 
3
1 15
 1
 1
    15     15 

 0,234375
64 64
2
2
6  1 
P  X  3      
3  2 
3
654  1
1
 1
  
    20 
 0,3125
3  2 1  2 
64
2
3
1 15
 1
 1
    15     15 

 0,234375
64 64
2
2
3
1
6
 1
 1
   6   6

 0,09375
64 64
2
2
3
1
1
 1
 1
    1    1

 0,015625
64 64
2
2
6  1
P  X  4      
4  2 
6  1 
P  X  5      
5  2 
6  1 
P  X  6      
6  2 
3
6
3
6
3
6
3
6
3
6
Histogramm der Binomialverteilungverteilung
0.4
0.35
0.3
0.25
P ( k)
0.2
0.15
0.1
0.05
1
0
1
2
3
4
5
6
7
k
Wahrscheinlichkeit3-Binomialverteilung/Bernoulli-Formel
Seite 3
A1
P  A   P  X  3   0,3125
ist die Wahrscheinlichkeit dafür, dass unter den 6 Kindern genau drei Mädchen
sind.
P B   P  X  3   P  X  0   P  X  1  P  X  2   P  X  3 
1
6 15 20 42 21





 0,65625
64 64 64 64 64 32
ist die Wahrscheinlichkeit dafür, dass unter den 6 Kindern höchstens drei
Mädchen sind.

P C  P  X  3   P  X  3   P  X  4   P  X  5   P  X  6 
20 15 6
1
42 21





 0,65625
64 64 64 64 64 32
ist die Wahrscheinlichkeit dafür, dass unter den 6 Kindern mindestens drei
Mädchen sind.

A2
Berechnung mit Bernoulli-Formel
Das Problem kann als 5- stufiger Bernoulli- Versuch betrachtet werden
mit n = 5 und p = 0,5.
a) Gesucht ist P(X = k) für k = 0, 1, 2, 3, 4, 5
k PX  k
0
 1
 
2
1
 1
 
2
5  1 
0   
0  2 
1
5  1 
  
 1  2 
5  1 
2   
 2  2 
2
5  1 
3   
3  2 
3
5 0
5 1
 1
 
2
52
 1
 
2
5 3
4
5  1  1
4     
4  2   2 
5  1 
5   
5  2 
5
5
1
1
 1
 1 1    5 
32
2
2
 1
 
2
4
5

5  1  1
1
5
 1
    5   5 5 
1 2 2
32
2
2

54  1

2  1  2 

543  1

3  2  1  2 

5432  1  1
1
5
 1
     5   5 5 
4  3  2 1  2   2 
32
2
2

5  4  3  2 1  1 

5  4  3  2  1  2 
54
2
3
3
2
5
1 10
 1
 1
    10     10  5 
32
2
2
2
4
5 5
5
1 10
 1
 1
    10     10  5 
32
2
2
2
1
5
5
0
5
1
1
 1
 1
    1    1  1 5 
32
2
2
2
Wahrscheinlichkeit3-Binomialverteilung/Bernoulli-Formel
Seite 4
A2
b) (1) Höchstens 3 mal Wappen bedeutet:
1
5 10 10 26
P  X  3 




 0,8125
32 32 32 32 32
(2) Weniger als 3 mal Wappen bedeutet:
1
5 10 16
P  X  3 



 0,5
32 32 32 32
(3) Mindestens 1 mal Wappen bedeutet:
5 10 10 5
1
31
P  X  1 





 0,96875
32 32 32 32 32 32
(4) Mehr als 1 mal Wappen bedeutet:
10 10 5
1 26
P  X  1 




 0,8125
32 32 32 32 32
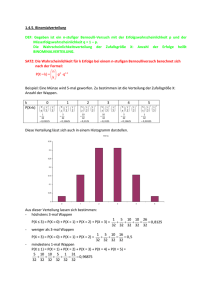
A3
a)
Säulendiagramm der Binomialverteilung für n = 20 und p = 0,5
0.2
0.18
0.16
0.14
0.12
P ( k) 0.1
0.08
0.06
0.04
0.02
0 1 2 3 4 5 6 7 8 9 10 1112 131415 1617 181920
k
b) (1) Die Wahrscheinlichkeit P(X = 10) kann aus der Tabelle,
bzw. aus dem Diagramm abgelesen werden.
Die Wahrscheinlichkeit für das Ereignis 10 mal Wappen beträgt:
P  X  10   0,176
b) (2) Höchstens 15 mal bedeutet P  X  15   0,994
b) (3) Mindestens 7 mal bedeutet:
P  X  7   P  X  20   P  X  6   1  0,058  0,942
b) (4) Mindestens 6 mal und höchstens 16 mal bedeutet
P  6,7,...16   P  X  16   P  X  5   0,999  0,021  0,978
Wahrscheinlichkeit3-Binomialverteilung/Bernoulli-Formel
Seite 5
A4
a) P  X  21  P  X  50   P  X  20   1  1  0
Die Wahrscheinlichkeit durch bloßes Raten mehr als 20 Aufgaben richtig zu
beantworten ist kleiner als 0,001 (0,1%).
b) P 10  k  20   P  X  20   P  X  9   1 0,444  0,565
Die Wahrscheinlichkeit durch bloßes Raten mindestens 10 und höchstens 20
Aufgaben richtig zu beantworten ist 0,565 (56,5%).
c) P  X  9   0,444 direkt aus der Tabelle ablesbar.
Die Wahrscheinlichkeit durch bloßes Raten weniger als 10 Aufgaben richtig
zu beantworten ist 0,444 (44,4%).
d) P  X  15   P  X  15   P  X  14   0,969  0,939  0,03
Die Wahrscheinlichkeit durch bloßes Raten genau 15 Aufgaben richtig zu
beantworten ist 0,03 (3%).
A5 n  20 und p  0,5    10 ;   5  2,236
a) P  X  12  0,868
b) P  X  10   0,588
c) P  X  11  0,160
d) P  8  X  12  0,736
A6
1
50
   10 ;  
 2,887
6
6
a) P  X  10   0,137
b) P  X  11  0,417
c) P  7  X  13   0,777
d) P  X  8   0,312
n  60 und p 
A7 n  100 und p  0,1    10 ;   9  3,00
a) P  X  10   0,132
b) P  X  9   0,679
c) P  6  X  14   0,869
d) P  X  12  0,802
Wahrscheinlichkeit3-Binomialverteilung/Bernoulli-Formel
Seite 6
A8
p  0,28
a) n  150
  n  p  150  0,28  42
  n  p 1  p   42  0,72  30,24  5,499  3
95%  Umgebung : [...{ ?...42...? }...]
z  1,96
r  z    1,96  5,499  10,778
  r  42  10,778  31,22
  r  42  10,778  52,78
b) n  250
p  0,7
  n  p  250  0,7  175
  n  p 1  p   175  0,3  52,5  7,246  3
95%  Umgebung : [...{ ?...175...? }...]
z  1,96
r  z    1,96  7,246  14,2
  r  175  14,2  160,8
  r  175  14,2  189,2
Wahrscheinlichkeit3-Binomialverteilung/Bernoulli-Formel
Seite 7