12 Differentialrechnung und Integralrechnung
Werbung

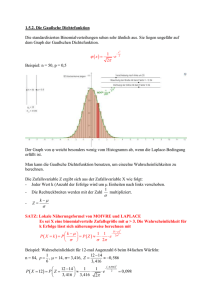
2 Differentialrechnung und Integralrechnung 12 Differentialrechnung und Integralrechnung 12.1 Differenzen- und Differentialquotient Differenzenquotient: mittlere Änderung pro Einheit, Steigung der Sekante durch die Punkte ( x0 | f (x0 ) ) Δy f (x1 ) − f (x0 ) und ( x1 | f (x1 ) ): ___ Δx = _________ . x − x 1 0 Differentialquotient: Grenzwert des Differenzenquotienten f ( x0 + h ) − f (x0 ) dy Δy f (x) − f (x0 ) ____________ y′= f ′ (x0) = ___ = lim ___ = lim ________ = lim . dx Δx x − x h Δx → 0 x → x0 0 h → 0 Eine Funktion ist differenzierbar in x0 , wenn der Differentialquotient f ′(x0 ) existiert, also der ­Grenzwert des Differenzenquotienten. 12.2 Ableitungen Funktion Ableitung n n − 1 Funktion Ableitung y = arcsin x 1 _ y′ = ______ √ 1 − x2 y = x y′ = n · x y = ex y′ = ex y = arccos x y = ax y′ = ax · ln a y = arctan x 1 y′ = _____ 2 y = ln x y′ = __1 y = sinh x y′ = cosh x y = lg x 1 y′ = _____ x · ln 10 y = cosh x y′ = − sinh x y = sin x y′ = cos x y = tanh x 1 y′ = ______ 2 y = cos x y′ = − sin x y = tan x 1 y′ = 1 + tan2 x = _____ 2 x 1 _ y′ = − ______ √ 1 − x2 1 + x cosh x cos x 12.3 Ableitungsregeln (1) f, g differenzierbar, k ∊ ℝ 1 Additive Konstante f = konst ⇒ f ′ = 0 Quotientenregel 1) Summenregel ( f ± g)′ = f ′ ± g′ Reziprokenregel 1) Faktorregel (k · f)′ = k · f ′ Kettenregel 2) Produktregel ( f · g)′ = f ′ · g + f · g′ ) g (x) ≠ 0 f ′ · g – f · g′ ( __ gf )′ = ________ g g′ ( __ 1g )′ = – __g 2 2 y = y ( z (x) ) ⇒ y′ = y′ (z) · z′ (x) dy dy dz oder __ = __ · __ 2 ) Voraussetzung: f in a und g in f (a) differenzierbar 1 1 (2) Ableitung der Umkehrfunktion f * an der Stelle y = f (x): ( f *)′ (y) = _______ = ____ f ′ ( f * (y) ) f ′ (x) dx dz dx Differentialrechnung und Integralrechnung 12.4 Graphenuntersuchung (1)Der Definitionsbereich (auch Definitionsmenge) ist die Menge an Zahlen, der wir eine bestimmte Zahl aus dem Wertebereich (auch Zielbereich) zuordnen. (2) Verhalten an den Rändern der Definitionsmenge: lim f (x) bzw. lim f (x), falls r Randstelle oder Definitionslücke, Untersuchung von lim f (x), x → +∞ x → –∞ (Stelle, an der f (r) nicht definiert ist) ist. x → r (3) Nullstellen f (xN ) = 0 Nullstellen findet man durch Zerlegen des Funktionsterms in Faktoren: f (x) = f1 (x) · f2 (x) (vgl. auch Linearfaktorzerlegung) (4) Symmetrie Achsensymmetrie: zur y-Achse zu x = a Punktsymmetrie: zum Ursprung zu S (a | b) S (a b) x=a f (– x) = f (x) f (a – x) = f (a + x) f (– x) = – f (x) f (a + x) + f (a – x) = 2 b Für ganzrationale Funktionen gilt: Treten nur Potenzen von x auf mit – geraden Exponenten, so liegt Achsensymmetrie zur y-Achse vor. – ungeraden Exponenten, so liegt Punktsymmetrie zum Ursprung vor. (5) Monotonie, Extrempunkte Monotonieintervalle sind bestimmt durch die Extrempunkte von f und die Definitionslücken (vgl. Monotoniesätze S. 37) f' > 0 Extremstellen liegen vor, falls: f ′(xE ) = 0 und f ′ hat Vorzeichenwechsel in x E oder: f ′ (xE) = 0 und f ″ (xE ) > 0 (lokales Minimum) oder: f ′ (xE) = 0 und f ″ (xE ) < 0 (lokales Maximum) f' < 0 f' < 0 f' > 0 f' > 0 xE f ' (xE) = 0 f' > 0 f' < 0 f' < 0 f' < 0 f' > 0 xE f ' (xE) = 0 3 4 Numerische Methoden 14 Numerische Methoden 14.1 Näherungsweises Berechnen von Nullstellen Sekantenverfahren (Regula falsi) y f (x1) < 0 Tangentenverfahren (Newton) y f (x2) < 0 f xn + 1 x1 x0 x x2 x – x f (x2 ) – f (x1 ) x xn f (x ) f ′ (xn ) 2 1 x0 = x1 – f (x1 ) _________ n , n ∊ 핅 x n + 1 = xn – _____ Falls f (x0 ) > 0, setze x2 : = x0 , Falls f (x0 ) < 0, setze x 1 : = x0 . Allgemeines Iterationsverfahren (1) Suche a, b so, dass f (a), f (b) verschiedene Vorzeichen haben. (2) Forme f (x) = 0 um: x = g (x) (3)Die rekursiv definierte Folge x n + 1 = g (xn ) konvergiert gegen die Nullstelle, falls g′ stetig auf [a; b] und |g′ (x)| < 1. y=x y y=x y g g x0 x x2 x4 x3 x1 – 1 < g′ (x) < 0 x0 x 1 x2 x 0 < g′ (x) < 1 14.2 Integrale Trapezsummenregel Zerlegung von [a; b] in n gleichbreite Teilintervalle. Ersetzen des Graphen von f durch einen Streckenzug liefert: y f b b – a · f (a) + 2 f (x ) + 2 f (x ) + … + 2 f (x ) + f (b) = T ∫ f (x) dx ≈ ____ ) n 1 2 n – 1 2 n ( a Fehlerabschätzung: b f ″ (ϑ) · (b – a) f (x) dx – Tn = – __________ ∫ mit 12 n2 a 3 ϑ ∊ [a; b] b n – 1 a i = 0 b – a ∑ f (xi + 0,5 ) Mittelpunkts- oder Tangentenformel: ∫ f (x) dx ≈ ____ 2 n a x1 x2 x3 … xn − 1 b x Numerische Methoden Simpson’sche Regel Zerlegung von [a; b] in eine gerade Anzahl n gleichbreiter Teilintervalle. Ersetzen des Graphen von f durch Parabelstücke liefert: b b – a · f (a) + 4 f (x ) + 2 f (x ) + 4 f (x ) + 2 f (x ) + … + 4 f (x ) + f (b) = S ∫ f (x) dx ≈ ____ ) n 1 2 3 4 n – 1 3 n ( a b Fehlerabschätzung: f (ϑ) · (b – a) ∫ mit f (x) dx – Sn = – ___________ 180 n4 (4) 5 a ϑ ∊ [a; b] Kepler’sche Fassregel Sonderfall der Simpson’schen Regel (2 Teilintervalle, Graph durch Parabel ersetzt): b ( ( b – a ∫ f (x) dx ≈ ____ f (a) + 4 f ____ a + b + f (b) 2 6 a ) ) 14.3 Fehlerrechnung |Δx |: Messunsicherheit oder absoluter Maximalfehler, x0: gemessener Wert, x: wahrer Wert Messwerte Absoluter Fehler: |x 0 − x | ± |Δx| | | Relative Messunsicherheit oder relativer Maximalfehler: ___ Δx x 0 Absoluter Fehler: Δy = f ′ (x) · Δx y = f (x) | Δy | f ′ (x) f (x) Relativer Fehler: ___ y = ____ · Δx Lineares Fehlerfortpflanzungsgesetz: Δzmax = |f x (x0 , y0 ) · Δx| + |fy (x0 , y0 ) · Δy| bei den Grundrechnungsarten: z = x + y oder z = x − y ⇒ Δzm ax = |Δx| + |Δy| z = f (x, y) | | | | Δy Δzmax x z = x · y oder z = __xy ⇒ _____ = ___ Δx + ___ , z0 = x0 · y0 oder z0 = __0 x y y z 0 0 0 0 14.4 Methode der kleinesten Quadrate Gegeben sind die Messpunkte P 1 (x1 | y1 ), P2 (x2 | y2 ), …, Pn (xn | yn). Eine Funktion, mit der man die Mess­ punkte annähern will, ist festzulegen f (x; a, b, …). a, b, … sind die Parameter der Funktion und daher gesucht, indem man den Fehler minimiert (Extremwertaufgabe). n ∂ g ∂ g g (a, b, …) = ∑ [yi − f (xi ; a, b, …)]2 = Min! ⇒ ___ = 0, ___ = 0, … i = 0 ∂ a ∂ b Spezialfall: Annäherung durch eine Gerade (siehe Regressionsgerade) 5 6 Wahrscheinlichkeitsrechnung 16.1 Diskrete Verteilung Binomialverteilung Zufallsversuch: Bernoulli-Versuch Aus einer Gesamtheit wird n-mal mit Zurücklegen gezogen. Man unterscheidet nur (die Ausprägungen) Erfolg bzw. Misserfolg. Die Wahrscheinlichkeiten für einen Erfolg (p) bzw. für einen Misserfolg (q = 1 – p) sind auf jeder Stufe gleich. Zufallsgröße X: Anzahl der Erfolge beim n-stufigen Bernoulli-Versuch mit q = 1 – p. k = 0, 1, …, n µ = n · p σ2 = n · p · q P (X = k) = ( n ) · pk qn – k k Zusammenhang mit dem Binomischen Lehrsatz: n pn 1 = (q + p)n = ( n0 ) qn + ( n1 ) p qn – 1 + ( n2 ) p2 qn – 2 + … + ( ____ n – 1 ) – 1 q + ( nn ) pn = P (X = 0) + P (X = 1) + P (X = 2) + … + P (X = n – 1) + P (X = n) Die Poisson-Verteilung ist eine Annäherung für die Binomialverteilung für große n (≥ 100) und kleine p (≤ 0,1): μk P (X = k) ≈ __ · e–µ , k ∊ 핅, µ = n · p, σ 2 ≈ µ k! Rekursive Berechnung: P (X = 0) = e– µ µ P (X = k) = __ · P (X = k – 1), k = 1, 2, … , n k Geometrische Verteilung Zufallsgröße X: Anzahl der Stufen bis zum ersten Eintreten eines Erfolges mit p: Wahrscheinlichkeit des Ereignisses und q = 1 – p. q 1 ; σ 2 = __ P (X = k) = p · qk – 1, k ∊ ℕ*, µ = __ 2 p p Gleichverteilung Zufallsgröße X nimmt die Werte 1, 2, …, m mit gleicher Wahrscheinlichkeit an: 2 1 , µ = _____ m + 1 m – 1 P (X = k) = __ , σ2 = _____ 2 12 m Hypergeometrische Verteilung Zufallsversuch: Aus einer Gesamtheit vom Umfang N wird eine Stichprobe vom Umfang n gezogen (d. h. nacheinander ohne Zurücklegen oder mit einem Griff). In der Gesamtheit sind zwei Merkmalsausprägungen vom Umfang K bzw. N – K. Zufallsgröße X: Anzahl der Merkmalsträger 1. Art in der Stichprobe ( k ) ( n – k ) K N – K , k = 0, 1, …, n, µ = n · p, σ = n · p · (1 – p) _____ N – n P (X = k) = ________ N N – 1 ( n ) K wobei p = __ N N > 10 Approximation durch die Binomialverteilung, falls __ n Wahrscheinlichkeitsrechnung 16.2 Stetige Zufallsvariable Wahrscheinlichkeit dafür, dass eine stetige Zufallsgröße X einen Wert aus dem Intervall B = [x1, x2 ] ­annimmt: x2 P(x1 ≤ X ≤ x2 ) = ∫ f (x) dx = F (x2 ) − F (x1 ) x1 Normalverteilung N (μ, σ2 ) Normalverteilte Zufallsgröße X mit Erwartungswert µ und Standardabweichung σ: X ist eine stetige Zufallsgröße mit der Dichtefunktion ( ) x – μ 2 – __21 ____ σ 1_ f (x) = _____ · e σ √ 2 π Gauss’sche Dichtefunktion (Dichtefunktion der Standard-Normalverteilung): j (z) 0,4 2 z __ 1 · e– 2 _ φ (z) = ____ √ 2 π Gauss’sche Integralfunktion z Φ (z) = ∫ φ (t) dt 0,1 – ∞ –3 –2 1 –1 2 3 z Standardisierte Normalverteilung N (0, 1) Wird die Normalverteilung N (μ, σ2 ) zentriert auf μ = 0, σ 2 = 1, so ergibt sich die Standard-Normal­ verteilung N (0, 1) (Gauss’sche Dichtefunktion), die von der Tabelle im Anhang abgelesen werden kann. 2 x __ 1 · e− 2 , und somit für die Verteilungs_ Für die Wahrscheinlichkeitsdichtefunktion ergibt sich: φ (x) = ____ √ 2 π x funktion: t __ 1 _ ∫ e− 2 dt Φ (x) = P (X ≤ x) = ____ √ 2 π – ∞ Transformationsformel 2 x − μ z = ____ σ Verteilung von Stichprobenmittelwerte Ein Zufallsversuch mit der Zufallsgröße X werde n-mal durchgeführt. x = E (X) = E (X i ) und σx2 = V (X) = V (X i ) Xi sei die Zufallsgröße der i-ten Stufe mit µ __ _ 1 (X + … + X ) gilt: √ n -Gesetz: Für das Stichprobenmittel X = __ i n __ _ __ __ __ n _ √ ) = µX = √ V ( X = E ( X ) = E (X) = µX , σ X __ σx __ _ . n1 V (X) = ___ √ n Nach Zentralem Grenzwertsatz ist X annähernd __ normalverteilt, wenn n hinreichend groß. Dann sind Wahrscheinlichkeitsaussagen über X möglich, z. B. ( | __ | σ √ n ) x _ P X ≈ 0,95 (vgl. S. 30) – µx ≤ 1,96 ___ 7