3 Folgen - TUM

Ferienkurs Analysis I für Physiker
WS15/16
Tag 1
Florian Häse
Florian Kandzia
21.03.2016
Inhaltsverzeichnis
1 Die komplexen Zahlen C
1.1 Definition und Rechenregeln . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 Komplexe Zahlenebene und Polardarstellung . . . . . . . . . . . . . . . . . . . . . . . . .
2
2
3
2 Vollständige Induktion
4
3 Folgen
3.1 Definitionen . . . . . . . . . . . . .
3.2 Konvergenzkriterien . . . . . . . .
3.3 Häufungspunkte . . . . . . . . . .
3.4 Cauchyfolgen . . . . . . . . . . . .
3.5 Konvergenz in metrischen Räumen
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
5
6
7
8
8
1. Die komplexen Zahlen C
1
1 Die komplexen Zahlen C
Bei der Lösung physikalischer Probleme tauchen immer wieder Gleichungen der Form
z 2 = −1
(1)
auf, welche nicht lösbar sind in R. Es ist daher nötig den Körper der reellen Zahlen zu erweitern, um
Gleichungen diesen Typs lösen zu können.
1.1 Definition und Rechenregeln
Zur Lösung von Problemen der Gestalt von Gleichung (1) definiert man sich
i2 = −1
(2)
als eine mögliche Lösung. Eine beliebige komplexe Zahl z kann somit über ein Zahlenpaar (x, y) ∈ R × R
definiert werden.
z = x + iy
(3)
wobei x = Re(z) und y = Im(z) den Realteil, bzw. den Imaginärteil der komplexen Zahl bilden.
Definition 1.1 (Addition in C)
Die Addition von zwei komplexen Zahlen z1 und z2 ist folgendermaßen definiert:
z1 + z2 = x1 + x2 + i(y1 + y2 )
(4)
Die Addition geschieht also komponentenweise.
Definition 1.2 (Multiplikation in C)
Die Multiplikation geschieht ebenfalls komponentenweise. (Beachte: i2 = −1)
z1 ∗ z2 = (x1 + iy1 )(x2 + iy2 )
= x1 x2 − y1 y2 + i(x1 y2 + x2 y1 )
(5)
Definition 1.3 (C ist ein Körper)
Mit der Addition (Def. 1.1) und Multiplikation (Def. 1.2) bildet die Menge der komplexen Zahlen
einen Körper. Dieser Körper wird mit C bezeichnet. Gleichungen vom Typ (1) besitzen in ihm zwei
Lösungen.
Definition 1.4 (imaginäre Einheit)
Die Lösung i aus Gleichung (2) heißt imaginäre Einheit. Sie ist definiert als
i :=(0, 1)
(6)
2
i =(−1, 0)
(7)
z = x − iy
(8)
Definition 1.5 (Konjugation)
Für z = x + iy, (x, y ∈ R) definiert man
das Komplex-Konjugierte von z.
Seite 2
1. Die komplexen Zahlen C
1
Rechenregeln:
1. z1 + z2 = z1 + z2
2. z1 · z2 = z1 · z2
3. z + z = 2 Re z
4. z − z = 2 Im z
5. z = z genau dann, wenn z ∈ R
6. z · z = x2 + y 2 , ist reell und ≥ 0
Definition 1.6 (Betrag)
Der Betrag einer komplexen Zahl z, ist definiert als
|z| :=
√
zz =
p
x2 + y 2
(9)
und ist immer positiv (oder gleich 0).
Rechenregeln:
1. |z| > 0 für z 6= 0 und |z| = |z|
2. |Re z| ≤ |z|
3. |Im z| ≤ |z|
4. |z1 · z2 | = |z1 | · |z2 |
5. |z1 + z2 | ≤ |z1 | + |z2 | Dreiecksungleichung
Für komplexe Zahlen ohne Imaginärteil (also rein reelle z) stimmen die oben aufgeführten Rechenregeln
mit den Rechenregeln von R überein.
1.2 Komplexe Zahlenebene und Polardarstellung
Komplexe Zahlen können als Vektoren einer Ebene (Re,Im) aufgefasst und mit dem R2 identifiziert
werden. Analog zu Vektoren im R2 , lässt sich eine von Null verschiedene komplexe Zahl z ∈ C, z 6= 0
eindeutig durch Betrag r = |z| und Phase φ = arg(z) ∈ [−π, π] darstellen.
iφ
mit e
z = r cos(φ) + ir sin(φ)
(10)
z = reiφ
(11)
= cos(φ) + i sin(φ) folgt:
Definition 1.7 (n-te komplexe Wurzel) Für n ∈ N und w ∈ C heißt z n-te komplexe Wurzel
von w, wenn z n = w gilt. Die Abbildung
p
√
i arg(z)/2
: C → C, z 7→ 2 |z|e
(12)
heißt (Hauptzweig der) komplexe Quadratwurzel.
Seite 3
2. Vollständige Induktion
2
Example 1.1 (Rechenbeispiele)
1. Umwandeln in kartesische Darstellungen:
a)
3 + 5i
(3 + 5i)(3 + 7i)
9 − 35 + i(15 + 21)
13
18
=
=
=− +i
3 − 7i
9 + 49
58
29
29
b)
√
π
√
1
3
= 4 (cos (π/6) + i sin (π/6)) = 4
+i
= 2 3 + 2i
4 exp i
6
2
2
c)
π i = exp(i ln(π)) = cos(ln(π)) + i sin(ln(π))
2. Betragsbildung:
a)
√
r
3 + 5i 13
18
169
324
493
3 − 7i = − 29 + i 29 = 841 + 841 = 29
2 Vollständige Induktion
Mit der vollständigen Induktion lässt sich eine Folge von Aussagen A(n), n ∈ N belegen, basierend auf
der Annahme, dass eine beliebige Aussage A(n) der Folge wahr ist und daraufhin die folgenden Aussage
A(n + 1) auch stimmen muss.
Definition 2.1 (Vollständige Induktion - Vorgehensweise)
Grundannahme Alle Aussagen A(n) sind richtig, wenn man den Induktionsanfang und den Induktionsschluss beweisen kann.
Induktionsanfang Der Induktionsanfang ist die erste Aussage A(1), die gelten soll. Diese bildet die
Basis, auf der die anderen Aussagen aufbauen. Ihre Aussage muss explizit gezeigt (verifiziert)
werden. In einzelnen Fällen ist es nötig, für den Induktionsanfang eine von der ersten Aussage verschiedene Aussage zu wählen (z.B. A(2) ). In einem solchen Fall müssen alle davor
vorangehenden Aussagen separat gezeigt werden.
Induktionsvoraussetzung (auch Induktionsannahme) In der Induktionsvoraussetzung geht man davon aus, dass alle Aussagen bis einschließlich zur Aussage A(n), n ∈ N gelten.
Induktionsschluss Im Induktionsschluss wird gezeigt, dass die Aussage A(n+1) wahr ist. Dazu wird
die aus der Induktionsvoraussetzung als geltend angenommene Aussage A(n) verwendet.
Seite 4
3. Folgen
3
Example 2.1 (Summenformel)
Für jede natürliche Zahl n gilt:
A(n) : 1 + 2 + 3 + · · · + n =
1
n(n + 1)
2
Induktionsanfang A(1) : 1 = 21 1(1 + 1) ist richtig.
Induktionsschluss Schluss von A(n) → A(n + 1)
1 + 2 + 3 + · · · + n + (n + 1) =
1
1
n(n + 1) + (n + 1) = (n + 1)(n + 2)
2
2
{z
}
| {z }
|
A(n)
A(n+1)
Example 2.2 Bernoulli Ungleichung Für alle x ∈ R mit x ≥ −1 und alle n ∈ N gilt:
(1 + x)n ≥ 1 + nx
Induktionsanfang A(1): Für n = 1 gilt
(1 + x)1 = 1 + x ≥ 1 + 1 · x,
sodass die Behauptung gilt.
Induktionsschluss Schluss von A(n) → A(n + 1). Es gelte
(1 + x)n ≥ 1 + nx
Wir betrachten nun
(1 + x)n+1 = (1 + x)(1 + x)n = (1 + x)n + x(1 + x)n
≥ 1 + nx + x(1 + nx) = 1 + x + nx + nx2 = 1 + (1 + n)x + nx2 ≥ 1 + (n + 1)x,
und haben damit die Behauptung gezeigt.
3 Folgen
Unter einer Folge von reellen Zahlen versteht man eine durchnummerierte Menge an Zahlen a1 , a2 , ..., an .
Im vorangegangenen Abschnitt haben wir gesehen, dass R ein Unterkörper von C ist. Wir betrachten
daher den allgemeineren Fall von komplexen Folgen. Folgen haben bestimmte Eigenschaften und es gelten
gewisse Regeln zum Rechnen mit Folgen, die im Folgenden erläutert werden.
3.1 Definitionen
Definition 3.1 (Folgen)
Eine Abbildung f : N → C, n 7→ an heißt (komplexe) Folge.
(an ) heißt reelle Folge, wenn gilt: f : N → R, n 7→ an .
Man schreibt:
(an )n∈N oder (an )n oder (an )
Definition 3.2 (Konvergenz)
Eine Folge (an )n∈N heißt konvergent gegen den Grenzwert/Limes a ∈ C, wenn gilt:
∀ > 0, ∃ N ∈ N : ∀ n > N : |an − a| < Seite 5
(13)
3. Folgen
3
Man schreibt dann:
lim an = a oder auch an → a für n → ∞.
n→∞
Konvergiert eine Folge gegen a = 0, so heißt sie Nullfolge.
Eine Folge (an )n∈N heißt uneigentlich/bestimmt konvergent gegen + (−)∞ wenn gilt:
∀ K > 0 ∃ NK ∈ N : ∀ n ≥ NK : an ≥ K (an ≤ −K)
(14)
Man schreibt:
lim an = + (−)∞ oder auch an → + (−)∞ für n → ∞.
n→∞
Im Konvergenzfall ist der Grenzwert einer Folge eindeutig bestimmt.
Existiert kein solches a, dann heißt die Folge divergent.
Achtung: Eine (uneigentlich) konvergente Folge reeler Zahlen konvergiert, aufgefasst als komplexe Folge
auch. Umgekehrt gilt dies nicht!
Rechenregeln für Folgen:
(an ) und (bn ) seien konvergente Folgen in R oder in C mit den Grenzwerten a und b.
Dann gilt:
1. (an ) + (bn ) → a + b
2. (an ) · (bn ) → a · b
3. Sei b 6= 0, so sind fast alle (bn ) 6= 0 und es gilt:
(an )
n→∞ (bn )
4. Spezialfall: Gilt lim
(an )
(bn )
→
a
b
= 1 so heißen die Folgen asymptotisch gleich.
Mit diesen Regeln kann man in vielen Fällen die Bestimmung von Grenzwerten von Folgen auf einfache
und bekannte Fälle zurückführen.
Rechenregeln für Folgen:
Sei (an ) eine konvergente komplexe Folge mit (an ) → a.
Dann gilt:
1. |(an )| → |a|
2. an → a
3. Re(an ) → Re a
4. Im(an ) → Im a
5. lim(an ) = lim Re(an ) + i lim Im(an )
3.2 Konvergenzkriterien
Die Konvergenz einer Folge kann an Hand bestimmter Eigenschaften geprüft werden, den sogenannten
Konvergenzkriterien.
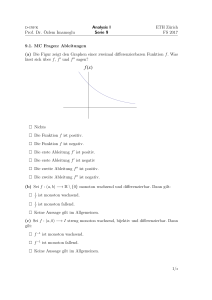
Definition 3.3 (Monotonie)
Eine reelle Folge (an )n∈N heißt
1.
monoton wachsend wenn an+1 ≥ an ∀n ∈ N
2. streng monoton wachsend wenn an+1 > an ∀n ∈ N
3.
monoton fallend wenn an+1 ≤ an ∀n ∈ N
4. streng monoton fallend wenn an+1 < an ∀n ∈ N
5. monoton, falls sie (streng) monoton wachsend oder (streng) monoton fallend ist.
Seite 6
3. Folgen
3
Es gibt Folgen, die sich nicht monoton verhalten, zum Beispiel alternierende Folgen. Sie können zwischen
mehreren sog. Häufungspunkten hin und her springen.
Definition 3.4 (Beschränktheit)
Eine reelle Folge (an )n∈N heißt
1. nach oben beschränkt wenn ∃ p ∈ R : p ≥ an ∀ n ∈ N
2. nach unten beschränkt wenn ∃ q ∈ R : q ≤ an ∀ n ∈ N
3.
beschränkt wenn ∃ p, q ∈ R : q ≤ an ≤ p ∀ n ∈ N
Aus Def. 3.2 bis 3.4 folgt:
Jede beschränkte, monoton wachsende (fallende) Folge (an ) konvergiert:
1. Ist (an ) monoton wachsend, so gilt: lim an = sup an
n→∞
2. Ist (an ) monoton fallend, so gilt: lim an = inf an
n→∞
Die Folgeglieder jeder nach oben beschränkten, monoton wachsenden reellen Folge befinden sich unterhalb
der Schranke p. Da die Folge jedoch monoton wachsend ist, werden die Folgeglieder mit wachsendem n
immer weiter in Richtung der Schranke getrieben und „eingequetscht“. Die Folge konvergiert also.
Aus Def. 3.3 und 3.4 folgt:
Ist eine reelle Folge (an )n∈N nach oben (unten) unbeschränkt und monoton wachsend (fallend), so gilt:
lim an = +∞ (−∞)
n→∞
(15)
Definition 3.5 (Einschließungskriterium)
Seien (an )n∈N , (bn )n∈N und (xn )n∈N reelle Folgen. Es gelte:
1. (an ) und (bn ) seien konvergent mit:
lim an = lim bn = a
n→∞
n→∞
(16)
2. an ≥ xn ≥ bn für fast alle n ∈ N
dann konvergiert (xn )n∈N ebenfalls gegen a.
3.3 Häufungspunkte
Ein schwächerer Begriff als der Grenzwert einer Folge ist der des Häufungspunktes. Das bedeutet es müssen für n → ∞ nicht alle Folgenglieder in der Nähe des (Grenz-)Wertes liegen, sondern nur unendlich
viele Folgenglieder müssen sich um den (Häufungs-)Punkt „anhäufen“. Zur Bestimmung von Häufungspunkten ist es nützlich nicht die komplette Folge (an ) zu betrachten, sondern lediglich einen gewissen
Teil davon. Dazu definiert man sich zunächst Teilfolgen.
Definition 3.6 (Teilfolge)
Sei (an )n∈N eine komplexe Folge und (nk )k∈N eine streng monoton wachsende Folge natürlicher
Zahlen ( nk ∈ N ∀k ∈ N), dann heißt (ank )k∈N Teilfolge von (an )n∈N
Jede Teilfolge einer konvergenten Folge konvergiert gegen den selben Grenzwert, wie die gesamte Folge.
Seite 7
3. Folgen
3
Definition 3.7 (Häufungspunkt)
h ∈ C ist ein Häufungspunkt(-wert) der Folge (an ), wenn jede Umgebung K (h) von h unendlich
viele Folgeglieder an enthält, d.h. wenn gilt:
∀ > 0 : |h − an | < für unendlich viele n ∈ N
(17)
D.h. h ∈ C ist ein Häufungswert der Folge (an ) genau dann, wenn h der Grenzwert (mindestens) einer
Teilfolge (ank ) ist. Ist h der Grenzwert aller Teilfolgen (ank ), so ist h der Grenzwert der Folge an .
Definition 3.8 (Bolzano-Weierstraß I)
Jede beschränkte Folge komplexer Zahlen besitzt einen Häufungspunkt. Jede beschränkte, reelle Folge
(an )n∈N besitzt eine größten Häufungswert h∗ und einen kleinsten Häufungswert h∗ ; ∀ > 0 gilt:
Limes superior
an < h∗ + für fast alle n
lim sup an := lim sup{ak |k ≥ n} = h∗
n→∞
Limes inferior
an > h∗ − für fast alle n
n→∞
lim inf an := lim inf{ak |k ≥ n} = h∗
n→∞
n→∞
(18)
(19)
Definition 3.9 (Bolzano-Weierstraß II)
Jede beschränkte Folge komplexer Zahlen besitzt eine konvergente Teilfolge (und somit mindestens
einen Häufungspunkt).
3.4 Cauchyfolgen
Als alternative Definition von Konvergenz sei hier noch das Konvergenzkriterium von Cauchy angegeben.
Es charakterisiert im Unterschied zur oben angeführten Definition die Konvergenz von Folgen ohne den
Bezug zu einem Limes.
Definition 3.10 (Konvergenzkriterium von Cauchy und Cauchyfolge)
Eine Folge (an ) komplexer Zahlen konvergiert genau dann, wenn gilt:
∀ > 0, ∃N ∈ N : ∀n, m > N : |an − am | < (20)
Eine Folge (an ) komplexer Zahlen heißt Cauchyfolge, wenn gilt:
∀ > 0, ∃N ∈ N : ∀n, m > N : |an − am | < (21)
Eine komplexe Folge konvergiert also genau dann, wenn sie eine Cauchyfolge ist.
3.5 Konvergenz in metrischen Räumen
Definition 3.11 (metrischer Raum mit Metrik)
Ein Paar (M, d) bestehend aus einer Menge M und einer Abbildung d : M × M → R+
0 heißt
metrischer Raum mit Metrik d, wenn gilt:
1. positiv definiert ∀x, y ∈ M : d(x, y) ≥ 0
2. Nichtdegeneriertheit: ∀x, y ∈ M : d(x, y) = 0 ⇔ x = y
3. Symmetrie: ∀x, y ∈ M : d(x, y) = d(y, x)
4. Dreiecksungleichung: ∀x, y, z ∈ M : d(x, z) ≤ d(x, y) + d(y, z)
Die Menge U (x) = {y ∈ M | d(x, y) < } für x ∈ M heißt -Umgebung von x.
Seite 8