Mathematik für Informatiker II

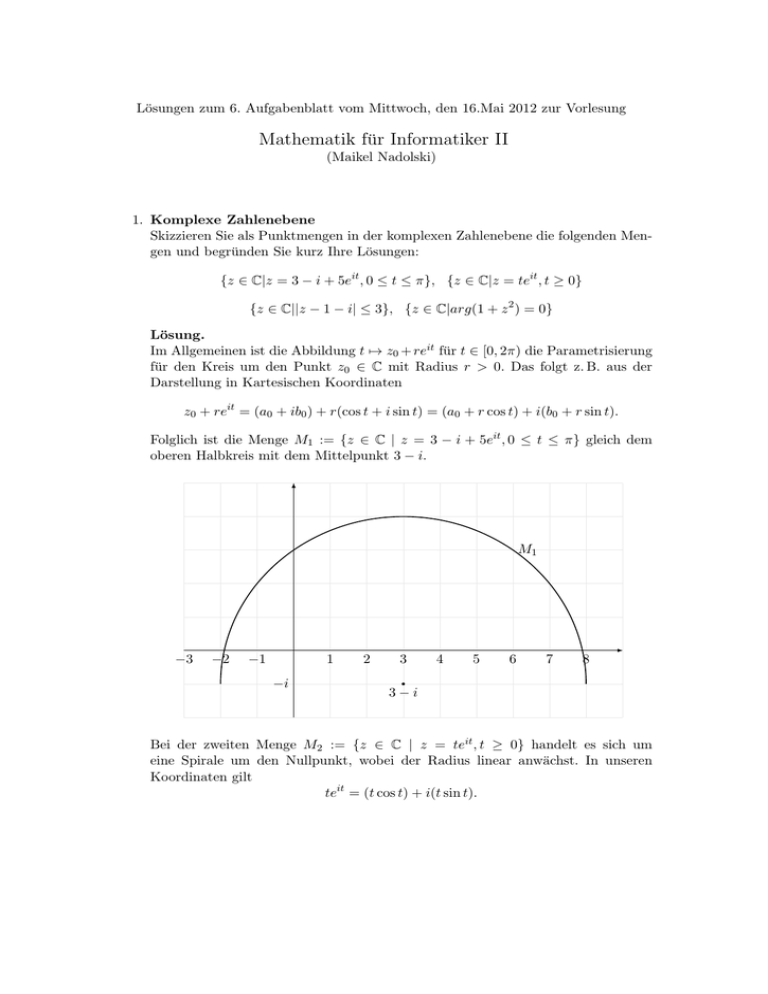
Lösungen zum 6. Aufgabenblatt vom Mittwoch, den 16.Mai 2012 zur Vorlesung
Mathematik für Informatiker II
(Maikel Nadolski)
1. Komplexe Zahlenebene
Skizzieren Sie als Punktmengen in der komplexen Zahlenebene die folgenden Mengen und begründen Sie kurz Ihre Lösungen:
{z ∈ C|z = 3 − i + 5eit , 0 ≤ t ≤ π}, {z ∈ C|z = teit , t ≥ 0}
{z ∈ C||z − 1 − i| ≤ 3}, {z ∈ C|arg(1 + z 2 ) = 0}
Lösung.
Im Allgemeinen ist die Abbildung t 7→ z0 + reit für t ∈ [0, 2π) die Parametrisierung
für den Kreis um den Punkt z0 ∈ C mit Radius r > 0. Das folgt z. B. aus der
Darstellung in Kartesischen Koordinaten
z0 + reit = (a0 + ib0 ) + r(cos t + i sin t) = (a0 + r cos t) + i(b0 + r sin t).
Folglich ist die Menge M1 := {z ∈ C | z = 3 − i + 5eit , 0 ≤ t ≤ π} gleich dem
oberen Halbkreis mit dem Mittelpunkt 3 − i.
M1
−3
−2
−1
1
−i
2
3
4
5
6
7
8
3−i
Bei der zweiten Menge M2 := {z ∈ C | z = teit , t ≥ 0} handelt es sich um
eine Spirale um den Nullpunkt, wobei der Radius linear anwächst. In unseren
Koordinaten gilt
teit = (t cos t) + i(t sin t).
teit
0
2π
4π
6π
In der dritten Menge M3 := {z ∈ C | |z − (1 + i)| ≤ 3} sind alle Punkte z ∈ C
enthalten, sodass der Abstand zum Punkt i + 1 kleinergleich 3 ist. Die eingegraute
Menge mit Rand illustriert uns die Menge M3 .
4
3
M3
2
1
−2
−1
1+i
1
2
3
4
−1
−2
Die letzte Menge M4 := {z ∈ C|arg(1 + z 2 ) = 0} besteht aus allen komplexen
Zahlen z, sodass 1 + z 2 eine positive reelle Zahl ist. Sei a > 0 eine solche reele Zahl.
√
Dann muss die Gleichung 1 + z 2 = a gelten, also z = a − 1.
√ Falls a > 1 gilt, so
gibt es zwei reele Lösungen. Ist nun 0 < a < 1 so sind z = ±i 1 − a die Lösungen
der Gleichung. M4 ist also die Vereinigung der ganzen reelen Achse mit dem Stück
(−i, i).
i
M4
−i
2. Überlagertes
Gegeben seien zwei gleichfrequente harmonische Schwingungen der Form
uk (t) = ck cos(ωt + φk ),
k = 1, 2
Gesucht ist deren Überlagerung u(t) = u1 (t) + u2 (t) in der Form u(t) = A cos(ωt +
φ), mit Amplitude A und Phase φ. Zur Lösung werden die beiden Schwingungen
als Realteile der entsprechenden komplexen Schwingungen interpretiert:
uk (t) = Re(ck ei(ωt+φk ) )
Danach wird im Komplexen die Summe der komplexen Schwingungen gebildet und
davon der Realteil ist die gesuchte Schwingung.
Berechnen Sie die Überlagerung von 10 sin(πt+π/10) und 5 cos(πt+π/6). Rechnen
Sie in der Kosinusdarstellung! Stellen Sie die 3 Kurven in geeigneter Form grafisch
dar.
Hinweis: Sie können zum Bsp. MAPLE an einem Institutsrechner benutzen, sollten
aber die einzelnen Schritte auch hinreichend dokumentieren.
Lösung.
Es gilt zunächst 10 sin(πt + π/10) = 10 cos(πt − 6π/10). Gesucht ist also
4
1
10 cos πt − π + 5 cos πt + π .
10
6
Dies fassen wir als Realteil einer entsprechenden Addition von komplexen Zahlen
auf.
4
1
4
1
Re 10eiπt−i 10 π + 5eiπt+i 6 π = Re 5eiπt 2e−i 10 π + ei 6 π .
Dem Computer entnehmen wir, dass
2 cos(−4π/10) + cos(π/6) + i(2 sin(−4π/10) + sin(π/6)) ∼ 1.484 − i1.402
gilt. Wir erhalten
4
1
Re 5eiπt 2e−i 10 π + ei 6 π
∼ Re 5eiπt (1.484 − i1.402)
∼ Re 5eiπt · 2.04 · e−i·0.757
= Re 10.25 · ei(πt−0.757)
= 10.25 · cos(πt − 0.757).
Anbei finden sich dann Plots dieser Aufgabe.
3. Rechnen im Komplexen
Bestimmen Sie jeweils alle komplexen Lösungen für die Gleichung
p(x) = 4x4 + 4x3 − 7x2 + x − 2 = 0
als auch für Gleichung
q(x) = x6 + 1 =
√
3i
Lösung.
Wir raten zunächst für das Polynom p die Nullstelle x0 = 1 und erhalten mithilfe
des Hornerschemas
4
1
4
4
−7
1
−2
4
8
1
2
8
1
2
0
und folglich gilt p(x) = (x − 1)(4x3 + 8x2 + x + 2). Nun können wir eine weitere
Nullstelle x1 = −2 leicht raten und erhalten ferner
4
−2
4
8
1
2
−8
0
−2
0
1
0
und somit die Darstellung p(x) = (x − 1)(x + 2)(4x2 + 1). 4x2 + 1 hat die beiden
Nullstellen x2 = 2i und x3 = − 2i . Alle komplexen Nullstellen von p sind somit
x0 = 1,
x1 = −2,
i
x2 = ,
2
i
x3 = − .
2
√
Nullstellen von q sind
die
sechsten
Wurzeln
von
z
=
−1
+
i
3. Es gilt |z| = 2 und
√
arg(z) = arctan(− 3) + π = 2π
.
Folglich
sind
die
sechsten
Wurzeln
durch
3
z0 =
z1 =
z2 =
z3 =
z4 =
z5 =
√
√
√
√
√
√
2π
2e 18
8π
2e 18
2e
14π
18
2e
20π
18
2e
26π
18
2e
36π
18
4. Trigonometrisches
Beweisen Sie mittels vollständiger Induktion, dass für n > 0 und sin α 6= 0 gilt:
cos α + cos 3α + . . . + cos(2n − 1)α =
sin(2nα)
2 sin α
Lösung.
Wir benutzen in dieser Aufgabe die Additionstheoreme
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
und
cos(α + β) = cos(α) cos(β) − sin(α) sin(β).
Weiterhin werden wir auch die Identität 1 = sin2 (α) + cos2 (α) verwenden.
Für n = 1 formt sich die Aussage zu cos(α) = 2sin(2α)
sin(α) und dies ist nach dem
Additionstheorem für den Sinus wahr. Sei die Aussage nun für ein n ∈ N wahr.
Wir zeigen sie für n + 1. Es gilt
sin(2(n + 1)α) = sin(2nα) cos(2α) + cos(2nα) sin(2α)
= sin(2nα) cos2 (α) − sin2 (α) + 2 cos(2nα) cos(α) sin(α)
= sin(2nα) − 2 sin(2nα) sin(α) sin(α) + 2 cos(2nα) cos(α)(sin(α)
= sin(2nα) + 2 sin(α) cos(2nα) cos(α) − sin(2nα) sin(α)
= sin(2nα) + 2 sin(α) cos((2n + 1)α).
Nach Induktionsvoraussetzung gilt
sin(2nα) = 2 sin(α)(cos(α) + . . . + cos((2n − 1)α))
und damit folgt die Aussage
sin(2(n + 1)α) = 2 sin(α) cos(α) + . . . + cos((2n − 1)α) + cos((2(n + 1) − 1)α) ,
was zu zeigen war.
t
10 sin(πt +
π
10 )
5 cos(πt + π6 )
10 sin(πt +
π
10 )
+ 5 cos(πt + π6 )
Abbildung 1: Die Plots zu Aufgabe 2