Übungsbeispiele samt Lösungen - HS

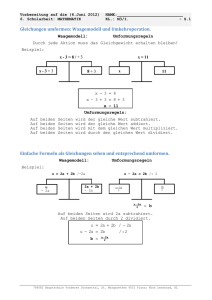
2012
Vorübungen auf die 6. M-Schularbeit
KL, KV
Ich habe mich bemüht, dir möglichst wieder
früh Unterlagen zur Verfügung zu stellen, die
Pfingstferien klopfen an die Türe, …
HS Pians
St. Margarethen
Alles Gute!
Vorbereitung auf die
NAME:
6. Schularbeit aus MATHEMATIK
KL.: M3/I.
- S.2
Mi, 6. 6. 2012
1)
Berechne die Unbekannte n nach dem Umkehrmodell und führe die
Probe durch!
3 € n - 8,1 + 2,1 € n + 5,3 = 2,2 € n + 55,5 + 1,3 € n + 9,7
Welche Zahl erfüllt die gegebene Gleichung?
Verwende das Waagemodell und führe die Probe durch!
9,1x - 8,2 - 10,3 - 6,4x = 2,5x
Löse folgende Gleichung mit einer Umkehroperation und führe die
Probe durch!
1
4
2y •
‚
3
4
• y
2) – 4) Angaben aus den Lösungen entnehmen!
5)
Folgende Gleichung ist nach dem Waagemodell zu lösen und mit einer
Probe zu kontrollieren.
2y •
1
4
‚
3
4
6)
Die Masse eines Quaders wird mit der Formel
m = G € h € • (Masse = Grundfläche € Höhe € Dichte) berechnet.
Berechne aus dieser Formel G!
7)
Der Umfang eines gleichschenkeligen Dreiecks
ist mit u = 2 € a + c gegeben.
Berechne c zunächst mit Variablen und setze
dann für u 156 cm und für a 32 cm ein!
C
a
A
a
c
B
8) 7A1.12-E / 010-m
0 1 2
Aus den gegebenen Strecken ergibt sich die angegebene Formel:
a
b
c
d
e
a + b + c + d = e
Berechne aus dieser Gleichung die Strecke (a + b)!
Gib zwei Lösungswege an!
1. Lösungsweg:
2. Lösungsweg:
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
NAME:
6. Schularbeit aus MATHEMATIK
KL.: M3/I.
Mi, 6. 6. 2012
9)
Forme die Gleichung nach den gewünschten Größen um!
A = B + k € s
B = ?
- S.3
s = ?
10)
Aus folgender Formel sind die gewünschten Größen zu berechnen.
S ‚ rg € Q
r = ?
g = ?
Q = ?
11)
Forme die Gleichung nach den gewünschten Größen um!
K €p€ m
100 € 12
Z ‚
p = ?
K = ?
12)
O = 2G + M ist die allgemeine Oberflächenformel für
einen Quader.
Gib eine Formel für h an, wenn die Variablen aus
der gegebenen Skizze Gültigkeit haben!
h
a
a
13)
Wie heißt die Zahl, wenn folgende Bedingungen gelten? Das 3-fache
einer Zahl, vermehrt um das 5-fache dieser Zahl, ergibt 168.
Löse mit einer Gleichung und kontrolliere das Ergebnis!
14)
D
C
„
ƒ
ƒ
„
A
B
In einem Parallelogramm soll der Winkel „ um
30° größer sein als der Winkel ƒ.
Ermittle die Größe der Winkel mit einer
Gleichung und kontrolliere die Ergebnisse!
15)
Bei der „SCHULOLYMPIADE” nahmen 305 Kinder teil. Es waren um
15 Knaben mehr als Mädchen. Berechne wie viele Mädchen und Knaben
an der „SCHULOLYMPIADE” teilgenommen haben!
16)
D
C
„
ƒ
ƒ
„
A
In einem Parallelogramm soll der Winkel „
doppelt so groß sein wie ƒ.
Berechne die Größe der Winkel!
B
17)
Addiert man zum Doppelten einer Zahl die Zahl 24, so erhält man
die Differenz vom 8fachen der Ausgangszahl und 6. Ermittle diese
Zahl mit einer Gleichung und führe die Probe durch!
18) 7A1.14-S / 016-m
0 1 2
Gegeben ist ein gleichschenkeliges Dreieck.
Berechne die Seitenlängen, wenn der Umfang mit
176 cm gegeben ist und ein Schenkel 3,5-mal so lang
wie die Basis sein soll!
Das Ergebnis ist mit einer Probe zu kontrollieren.
C
a
A
a
c
B
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
NAME:
6. Schularbeit aus MATHEMATIK
KL.: M3/I.
- S.4
Mi, 6. 6. 2012
19)
Addiert man zum Doppelten einer Zahl die Zahl 32, so erhält man
die Differenz vom 8fachen der Ausgangszahl und 4.
Wie heißt diese Zahl? Probe!
20)
D
C
„
ƒ
A
ƒ
In einem Parallelogramm soll der Winkel ƒ um
30° kleiner sein als „. Berechne ƒ und „!
„
B
21)
Die Summe dreier Zahlen beträgt 288. Berechne die Summanden mit
einer Gleichung, wenn der 1. Summand halb so groß sein soll wie
der zweite und der 3. Summand 3-mal so groß wie der 1. Summand
sein soll. Vergiss nicht die Lösung zu kontrollieren!
22)
Herr Maurer kauft eine Bohrmaschine, einen passenden Koffer und
bezahlt dafür 189 €.
Die Bohrmaschine kostet 13-mal so viel wie der Koffer.
Was kostet die Bohrmaschine ohne Koffer?
23)
In der 3. C (28 Kinder) wurde der/die Klassensprecher/in gewählt.
Barbara erhielt um 7 Stimmen mehr als Martin und um 2 Stimmen
weniger als Robert.
Berechne, wie viele Stimmen Barbara, Martin und Robert erhielten!.
24)
Bestimme den Wert für y und führe die Probe durch!
2 € (4y + 2) = 13 - y
25)
Löse die Gleichung und führe die Probe durch!
2 € (2x - 4) - 4 = 2 € (x + 1)
26)
Finde eine Lösung für die Gleichung! Vergiss nicht auf die
Kontrolle!
(2a + 3) € (2a - 3) + 4 = 4a € (a - 2) + 11
27)
Löse die Gleichung und führe die Probe durch!
14 - [ 4y - 8 - 3 € (y + 3)] = 4 € (3y - 2)
28)
Löse die Gleichung und führe die Probe durch!
(-2a + 8)(2a - 7) = 4 + 27a - 4a²
29)
Löse die Gleichung und führe die Probe durch!
(3m - 2)² - 72 = (3m + 2)²
30)
Berechne die Unbekannte und führe die Probe durch!
3(5x + 12) + 5(4x - 50) = -12(3x - 32) + 4(5x + 16) + 1
31)
Welche Zahl kann für a eingesetzt werden? (Probe nicht vergessen!)
(a - 1)² + (a - 2)² = (a - 3)² + (a - 4)²
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
NAME:
6. Schularbeit aus MATHEMATIK
KL.: M3/I.
- S.5
Mi, 6. 6. 2012
32)
Überprüfe die Lösung durch Einsetzen in die gegebene Gleichung!
a•4 a
‚
3
4
33)
Wenn man zur Zahl a, die um 6 größere Zahl addiert, so erhält
man 38. Welche Zahl kann man für a einsetzen? Probe!
34)
Karins Großmutter ist 76 Jahre alt. Karin ist 16 Jahre alt. Mit
wie vielen Jahren wird die Großmutter 4-mal so alt wie Karin sein?
35)
In einem gleichschenkeligen Dreieck ist ein Basiswinkel doppelt so
groß, wie der Winkel, der der Basis gegenüberliegt. Berechne die
Winkel von diesem gleichschenkeligen Dreieck!
36)
Markus und sein Vater sind zusammen 52 Jahre alt. In 16 Jahren
wird sein Vater doppelt so alt wie Markus sein. Wie alt ist Markus
jetzt?
37)
Das 6fache einer um 4 verminderten Zahl ist gleich dem 2fachen der
um 10 vergrößerten Zahl? Wie heißt diese Zahl? Kontrolliere!
38)
Gegeben sind 2 Quadrate. Die Seite des kleineren Quadrates ist um
4 cm kürzer und hat einen um 72 cm² kleineren Flächeninhalt.
Berechne die Seitenlängen beider Quadrate!
39)
Drücke aus der gegebenen Formel die angegebene Unbekannte aus!
Netto = Brutto - Tara
N = B - T
a) B = ?
b) T = ?
40)
Wie lautet aus der Umfangsformel des gleichseitigen Dreiecks
u = 3s die Seite s?
41)
Aus der gegebenen Formel ist die angegebene Unbekannte anzugeben!
Weg = Zeit . Geschwindigkeit: s = t . v
a) v = ?
b) t = ?
42)
Drücke die angegebene Variable in der Formel aus!
F = 4 . a . g
g = ?
43)
Berechne die angegebenen Variablen aus den gegebenen Formeln!
a) Fläche des
Trapezes:
a • c
A ‚ 2 .h
h = ?
a = ?
c = ?
b) einfache Zinsen
für Monate:
K . p . m
Z ‚ 100 . 12
K = ?
p = ?
m = ?
c) Volumen eines
rechtw. dreiseitigen Prismas:
a . b
V ‚ 2 .h
a = ?
b = ?
h = ?
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
NAME:
6. Schularbeit aus MATHEMATIK
KL.: M3/I.
- S.6
Mi, 6. 6. 2012
44)
Berechne die angegebene Variable aus der gegebenen Formel!
2 T
b) L ‚ ba . M … c3
a) R ‚ S … 3
a = 9; c = 15; L = 31; M = 28;
R = 105; S = 135;
b = ?
T = ?
45)
Die angegebene Variable ist aus der Formel zu berechnen!
d ‚ 3f 2…e g
g ‚ ?
46)
Wie ändert sich der Umfang eines Rechtecks, wenn die Länge um
24 vergrößert und die Breite um 14 verkleinert wird?
47)
Den Umfang eines Quadrates berechnet man mit u(s) = 4 . s. Wie
ändert sich der Umfang, wenn man s verdoppelt?
48)
Wie ändert sich der Flächeninhalt eines Rechtecks, wenn man
a) die Seite a um 5 vergrößert?
b) die Seite b um 7 verkleinert?
49)
Wie ändert sich der Umfang des gleichseitigen Dreiecks, wenn s
um 7 vergrößert wird?
50)
Wie ändert sich in einem gleichschenkligen Dreieck der Winkel †,
wenn man den Basiswinkel ƒ um 12° verkleinert?
51)
Zeichne das Netz einer quadratischen Pyramide mit folgenden
Angaben!
a = 3 cm
s = 3,6 cm
52)
Von
die
a
hg
einer quadratischen Pyramide kennt man die Grundkante a und
Höhe der Dreiecksfläche hg. Zeichne das Netz der Pyramide!
= 3,5 cm
= 4,2 cm
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
NAME:
6. Schularbeit aus MATHEMATIK
KL.: M3/I.
- S.7
Mi, 6. 6. 2012
53)
Gegeben ist eine rechteckige Pyramide mit den Grundkanten a,b und
der Seitenkante s.
Zeichne das Netz der Pyramide in Form eines Sternes!
a = 3,8 cm
b = 25 mm
s = 0,34 dm
54)
Kreuze die Netze an, aus denen man Pyramiden erzeugen kann!
55)
Konstruiere das Netz einer regelmäßigen dreiseitigen Pyramide mit
der Grundkante a = 28 mm und der Seitenkante s = 35 mm!
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
NAME:
6. Schularbeit aus MATHEMATIK
KL.: M3/I.
Mi, 6. 6. 2012
56)
Zeichne das Netz einer regelmäßigen sechseitigen Pyramide!
a = 2 cm
s = 25 mm
- S.8
57)
Berechne die Oberfläche einer quadratischen Pyramide!
Skizziere das Netz der Pyramide!
a
= 12 cm
ha
=
8 cm
58)
Zeichne die quadratische Pyramide im Schrägriß!
Verzerrungsverhältnis v ‚ 23
Verzerrungswinkel ƒ ‚ 30‡
a = 2,7 cm
h = 3,5 cm
59)
Die Cheopspyramide ist die größte Pyramide von Gizeh.
Eine Seite der quadratischen Grundfläche ist 230 m lang, die Höhe
eines Seitendreieckes beträgt 187 m.
Berechne die Mantelfläche dieser größten Pyramide!
60)
Gegeben ist eine Pyramidemit rechteckigerGrundfläche.
Zeichne eine Skizze der Oberflächeund berechnesie!
a = 3,2 cm
b = 1,8 cm
ha = 1,5 cm
hb =
2 cm
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
NAME:
6. Schularbeit aus MATHEMATIK
KL.: M3/I.
Mi, 6. 6. 2012
61)
Gegeben ist eine regelmäßige dreiseitige Pyramide.
Fertige eine Skizze der Oberfläche an und berechne sie!
a = 6,4 cm
ha = 5,5 cm
hs = 7,1 cm
- S.9
62)
Berechne die Oberfläche einer regelmäßigen
sechsseitigen Pyramide und fertige eine
Skizze an!
A = 5,6 m
ha = 19 m
Fertige eine maßstäbliche Zeichnung der
Grundfläche an!
Entnimm daraus die Höhe hg eines
gleichseitigen Dreiecks der Grundfläche!
63)
Wie groß ist das Volumen folgender Pyramide mit rechteckiger
Grundfläche?
a = 18 cm
b = 13,1 cm
h = 9 cm
64)
Eine Pyramide mit rechteckiger Grundfläche hat eine Körperhöhe von
9,7 cm.
Berechne das Volumen dieses Körpers!
a = 6,8 cm
b = 4,5 cm
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
NAME:
6. Schularbeit aus MATHEMATIK
KL.: M3/I.
- S.10
Mi, 6. 6. 2012
65)
Berechne das Volumen nebenstehender Figur!
Auf der Grund- und Deckfläche des Prismas befindet sich jeweils
eine Pyramide, die die gleiche Höhe wie das Prisma besitzt.
a = 13,5 cm
b = 1,7 dm
h = 21,5 cm
66)
Ein Briefbeschwerer aus Marmor hat die Form einer regelmäßigen
quadratischen Pyramide.
Wie schwer ist diese Pyramide, wenn Marmor eine Dichte von 2,6 t/m3
hat?
a = 81 mm
h = 75 mm
67)
Von einer quadratischen Pyramide kennt man das Volumen und die
Körperhöhe. Berechne die Größe der Grundfläche!
h = 18 cm
V = 864 cm3
68)
Von einer quadratischen Pyramide kennt man die Grundkante a und
das Volumen V. Berechne die Körperhöhe h!
a = 5,7 cm
V = 68,229 cm3
69)
Berechne die Grundkante a einer Pyramide mit rechteckiger
Grundfläche, wenn das Volumen 2184 cm3, die Grundkante b = 13 cm
und die Körperhöhe h = 24 cm betragen!
70)
Eine quadratische Pyramide aus Sandstein (Dichte ˆ = 2,3 kg/dm³)
hat ein Gewicht von 0,8 kg.
Wie hoch ist sie, wenn die Grundkante 11,5 cm misst?
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
6. Schularbeit aus MATHEMATIK
Mi, 6. 6. 2012
L Ö S U N G E N
1)
9x … 8 … 10 … 6x ‚
3x … 18 ‚
x … 18 ‚
x ‚
2x
2x / … 2x
0 / •18
18
NAME:
KL.: M3/I.
- S.11
Pr.: 9 € 18 … 8 … 10 … 6 € 18 ‚ 2 € 18
162 … 18 … 108 ‚ 36
36 ‚ 36
2)
3 € n … 8,1 • 2,1 € n • 5,3 ‚
5,1 € n … 2,8 ‚
1,6 € n … 2,8 ‚
1,6 € n ‚
n ‚
2,2 € n • 55,5 • 1,3 € n • 9,7
3,5 € n • 65,2
65,2
68
42,5
Probe:
3 € 42,5 … 8,1 • 2,1 € 42,5 • 5,3 ‚ 2,2 € 42,5 • 55,5 • 1,3 € 42,5 • 9,7
127,5 … 8,1 • 89,25 • 5,3 ‚ 93,5 • 55,5 • 55,25 • 9,7
213,95 ‚ 213,95
3)
9,1x … 8,2 … 10,3 … 6,4x =
2,7x … 18,5 =
0,2x … 18,5 =
0,2x =
x =
2,5x
2,5x / … 2,5x
0
/ • 18,5
18,5 /: 0,2
92,5
Probe:
9,1 € 92,5 … 8,2 … 10,3 … 6,4 € 92,5 ‚ 2,5 € 92,5
841,75 … 8,2 … 10,3 … 592 ‚ 231,25
231,25 ‚ 231,25
4)
‚
3
4
• y
2y ‚
2
4
• y
y ‚
2
4
‚
2y •
1
4
1
2
Pr.:
2€
1
2
•
1
4
‚
3
4
1 •
1
4
‚
5
4
5
4
‚
5
4
•
2
4
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
6. Schularbeit aus MATHEMATIK
Mi, 6. 6. 2012
5)
2y •
1
4
‚
3
4
/ …
NAME:
KL.: M3/I.
- S.12
Pr.: 2 €
1
4
2y ‚ 24 / € 4
8y ‚ 2 /: 8
y ‚ 28 ‚ 14
Einfachere Lösung:
2y muss 24 sein ==>
y ‚
1
4
•
1
4
‚
3
4
2
4
•
1
4
‚
3
4
3
4
‚
3
4
1
4
6)
m = G € h € ˆ / : (h € ˆ)
m
‚ G
h€ •
7)
156 … 64 ‚ c
u ‚ 2 € a • c/… 2 € a
92 ‚ c
u … 2€ a ‚ c
Die Seite c ist 92 cm lang.
8)
1. Lösungsweg:
2. Lösungsweg:
a + b + c + d = e /-(c+d)
a + b = e - (c + d)
a + b + c + d = e /-c-d
a + b = e - c - d
9)
A ‚ B • k€s/ …B
A … B ‚ k€s
/: k
A ‚ B • k € s/ …k €s
A … k € s ‚ B
A … B
k
‚ s
10)
S ‚
r
g
€ Q /€g
S € g ‚ r € Q /: Q
S€g
Q
S ‚
r
g
€ Q /€g
S ‚
S € g ‚ r € Q /: S
‚ r
g ‚
r
g
€ Q /€g
S € g ‚ r € Q /: r
r€Q
S
S€g
r
‚ Q
11)
Z ‚
K€p€m
100 € 12
/ € 1200
1200 € Z ‚ K € p € m /:( K € m )
1200 € Z
K €m
‚ p
Z ‚
K€p€m
100 € 12
/ € 1200
1200 € Z ‚ K € p € m /:( p € m )
1200 € Z
p€ m
‚ K
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
6. Schularbeit aus MATHEMATIK
Mi, 6. 6. 2012
12)
NAME:
KL.: M3/I.
- S.13
O ‚ 2G • M
O ‚ 2 € a² • 4 € a € h / … 2 € a²
O … 2 € a² ‚ 4 € a € h
/:(4 € a)
G = a € a = a²
M = a € h € 4
O … 2 € a²
4€a
‚ h
13)
3 € x • 5 € x ‚ 168
8 € x ‚ 168
x ‚ 21
Pr.: 3 € 21 • 5 € 21 ‚ 168
63 • 105 ‚ 168
168 ‚ 168
Die Zahl heißt 21.
14)
x • ( x • 30 ) • x • ( x • 30 )
4 € x • 60
4€ x
x
ƒ = x
„ = x + 30
‚
‚
‚
‚
360
360
300
75
75°
105°
180° € 2 = 360°
Der Winkel Alpha hat 75° und der Winkel Beta hat 105°.
15)
x • 15 • x
2x • 15
2x
x
Knaben: x + 15
Mädchen:
x
K + M
305
‚
‚
‚
‚
305
305
290
145
305
- 145
160
Es nahmen 145 Mädchen und 160 Knaben an der „SCHULOLYMPIADE” teil.
16)
x • 2 € x • x • 2 € x ‚ 360
6 € x ‚ 360
x ‚ 60
ƒ = x
„ = 2 € x
60° € 2 = 120°
Der Winkel Alpha hat 60° und der Winkel Beta hat 120°.
17)
2 € x • 24
24
30
5
‚
‚
‚
‚
8€ x … 6
6€ x … 6
6€ x
x
Pr.:
2 € 5 • 24 ‚ 8 € 5 … 6
10 • 24 ‚ 40 … 6
34 ‚ 34
Die Zahl heißt 5.
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
6. Schularbeit aus MATHEMATIK
Mi, 6. 6. 2012
18)
NAME:
KL.: M3/I.
- S.14
x • 3,5 € x • 3,5 € x ‚ 176
8 € x ‚ 176
x ‚ 22
c = x
a = 3,5 € x
u = 176
Pr.:
22
77
77
176
Die Basis ist 22 cm und ein Schenkel ist 77 cm lang.
19)
2 € x • 32
32
36
6
‚
‚
‚
‚
8€ x … 4
6€ x … 4
6€ x
x
Pr.:
2 € 6 • 32 ‚ 8 € 6 … 4
12 • 32 ‚ 48 … 4
44 ‚ 44
Die Zahl heißt 6.
20)
ƒ = „ - 30
„ = ƒ + 30
ƒ + „
ƒ + ƒ + 30
2ƒ
‚
=
=
=
=
105
- 30
75
180
180
150
75
ƒ + „ = 180
75 + „ = 180
ƒ = 105
Der Winkel Alpha hat 75° und der Winkel Beta hat 105°.
21)
1. Summand:
2. Summand:
3. Summand:
Summe:
x
2
x
2
x
€3
288
• x • 3 €
x
2
Pr.: 48
96
144
288
‚ 288
x • 2 € x • 3 € x ‚ 576
6 € x ‚ 576
x ‚ 96
x
2
Die Summanden heißen 48, 96 und 144.
22)
Bohrmaschine: 13 € x
Koffer:
x
Zusammen:
189
13 € x • x ‚ 189
14 € x ‚ 189
x ‚ 13,5
175,5
+ 13,5
189,0
Die Bohrmaschine kostet 175,5 €.
23)
Barbara:
x + 7
Martin:
x
Robert: (x + 7) + 2
Insgesamt:
28
x • 7 • x • x • 9
3 € x • 16
3€ x
x
‚
‚
‚
‚
28
28
12
4
Robert erhielt 13, Barbara erhielt 11 und Martin erhielt
4 Stimmen.
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
11
4
13
28
Vorbereitung auf die
6. Schularbeit aus MATHEMATIK
Mi, 6. 6. 2012
24)
NAME:
KL.: M3/I.
2 € ( 4y • 2 ) ‚ 1 3 … y
8y • 4 ‚ 1 3 … y
9y • 4 ‚ 1 3
9y ‚ 9
- S.15
Pr.: 2 € ( 4 € 1 • 2 ) ‚ 13 … 1
2 € ( 4 • 2 ) ‚ 12
2 € 6 ‚ 12
12 ‚ 12
y ‚ 1
25)
2 € ( 2x … 4 ) … 4 ‚ 2 € ( x • 1 )
4x … 8 … 4 ‚ 2x • 2
4x … 1 2 ‚ 2x • 2
2x … 1 2 ‚ 2
2x ‚ 1 4
x ‚ 7
Pr.: 2 € ( 2 € 7 … 4 ) … 4 ‚ 2 € ( 7 • 1 )
2 € ( 14 … 4 ) … 4 ‚ 2 € ( 8 )
2 € ( 10 ) … 4 ‚ 16
20 … 4 ‚ 16
16 ‚ 16
26)
( 2a • 3 ) € ( 2a … 3 ) • 4 ‚ 4a € ( a … 2 ) • 11
4a² • 6a … 6a … 9 • 4 ‚ 4a² … 8a • 11
4a² … 5 ‚ 4a² … 8a • 11
… 5 ‚ … 8a • 11
8a … 5 ‚ 11
8a ‚ 16
a‚2
Probe:
( 2 € 2 • 3 ) € ( 2 € 2 … 3 ) • 4 ‚ 4 € 2 € ( 2 … 2 ) • 11
7 € 1 • 4 ‚ 8 € 0 • 11
11 ‚ 11
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
6. Schularbeit aus MATHEMATIK
Mi, 6. 6. 2012
27)
14 … [4y … 8 … 3 € (y • 3)]
14 … [4y … 8 … 3y … 9]
14 … 4y • 8 • 3y • 9
… y • 31
… 13y • 31
… 13y
y
Probe:
‚
‚
‚
‚
‚
‚
‚
NAME:
KL.: M3/I.
- S.16
4 € (3y … 2)
12y … 8
12y … 8
12y … 8
…8
…39
3
14 … [ 4 € 3 … 8 … 3 € ( 3 • 3 )] ‚
14 … [ 12 … 8 … 3 € ( 6 )] ‚
14 … [ 12 … 8 … 18 ] ‚
14 … [ … 14 ] ‚
14 • 14 ‚
28 ‚
4 € (3 € 3 … 2)
4 € (9 … 2)
4 € (7)
28
28
28
28)
( … 2a • 8 )( 2a … 7 ) ‚ 4 • 27a … 4a²
… 4a² • 16a • 14a … 56 ‚ 4 • 27a … 4a²
30a … 56 ‚ 27a • 4
3a … 56 ‚ 4
3a ‚ 60
a ‚ 20
Probe:
[( … 2 ) € 20 • 8 ][ 2 € 20 … 7 ] ‚
[ … 40 • 8 ][ 40 … 7 ] ‚
[ … 32 ][ 33 ] ‚
… 1056 ‚
4 • 27 € 20 … 4 € 20²
4 • 540 … 4 € 400
4 • 540 … 1600
… 1056
29)
Pr.: [ 3 € ( … 3 ) … 2 ]² … 72 ‚ [ 3 € ( … 3 ) • 2 ]²
( 3m … 2 )² … 72 ‚ ( 3m • 2 )²
[ … 9 … 2 ]² … 72 ‚ [ … 9 • 2 ]²
9m² … 12m • 4 … 72 ‚ 9m² • 12m • 4
[ … 11 ]² … 72 ‚ [ … 7 ]²
… 12m … 68 ‚ 12m • 4
121 … 72 ‚ 49
… 24m … 68 ‚ 4
49 ‚ 49
… 24m ‚ 72
m ‚…3
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
6. Schularbeit aus MATHEMATIK
Mi, 6. 6. 2012
30)
NAME:
KL.: M3/I.
- S.17
3 ( 5x • 12 ) • 5 ( 4x … 50 ) ‚ … 12( 3x … 32 ) • 4( 5x • 16 ) • 1
15x • 36 • 20x … 250 ‚ … 36x • 384 • 20x • 64 • 1
35x … 214 ‚ … 16x • 449
51x … 214 ‚ 449
51x ‚ 663
x ‚ 13
3( 5 € 13 • 12 ) • 5( 4 € 13 … 50 ) ‚ … 12( 3 € 13 … 32 ) • 4( 5 € 13 • 16 ) • 1
3( 65 • 12 ) • 5( 52 … 50 ) ‚ … 12( 39 … 32 ) • 4( 65 • 16 ) • 1
3( 77 ) • 5( 2 ) ‚ … 12( 7 ) • 4( 81 ) • 1
231 • 10 ‚ … 84 • 324 • 1
241 ‚ 241
Pr.:
31)
( a … 1 )² • ( a … 2 )² ‚ ( a … 3 )² • ( a … 4 )²
a² … 2a • 1 • a² … 4a • 4 ‚ a² … 6a • 9 • a² … 8a • 16
2a² … 6a • 5 ‚ 2a² … 14a • 25
… 6a • 5 ‚ … 14a • 25
8a • 5 ‚ 25
8a ‚ 20
a ‚ 2,5
( 2,5 … 1 )² • ( 2,5 … 2 )² ‚ ( 2,5 … 3 )² • ( 2,5 … 4)²
1,5² • 0,5² ‚ ( … 0,5 )² • ( … 1,5 )²
2,25 • 0,25 ‚ 0,25 • 2,25
2,50 ‚ 2,50
Probe:
32)
a•4
3
4a • 16
a • 16
a
a
4
‚ 3a
‚0
‚ … 16
‚
Pr.: … 16 • 4 … 16
‚
3
4
… 12
3
‚…4
…4‚ …4
33)
a • a • 6 ‚ 38
2a • 6 ‚ 38
2a ‚ 32
a ‚ 16
Für a kann man die Zahl 16 einsetzen.
Pr.:
16 + 16 + 6 = 38
38 = 38
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
6. Schularbeit aus MATHEMATIK
Mi, 6. 6. 2012
34)
Großmutter
76
77
78
79
80
Karin
16
17
18
19
20
NAME:
KL.: M3/I.
- S.18
76 • x ‚ ( 16 • x ) € 4
76 • x ‚ 64 • 4x
76 ‚ 64 • 3x
12 ‚ 3x
4‚x
Großm.: 76 + x
Karin: (16 + x) € 4
Mit 80 Jahren ist die Großmutter 4-mal so alt wie Karin.
35)
180 ‡ ‚ 2† • 2† • †
180 ‡ ‚ 5†
36 ‡ ‚ „
2„ ‚ 72 ‡
C
†
2†
2†
A
B
Die Basiswinkel sind je 72° und der Winkel,
der der Basis gegenüberliegt, hat 36°.
36)
Jahre
Markus:
x
Vater: 52 - x
in 16 Jahren
x + 16
52 - x + 16
Markus ist jetzt 12 Jahre alt.
( x • 16 ) € 2
2x • 32
3x • 32
3x
x
‚
‚
‚
‚
‚
52 … x • 16
68 … x
68
36
12
37)
6 € ( x … 4) ‚
6x … 24 ‚
4x … 24 ‚
4x ‚
x ‚
2 € ( x • 10 )
2x • 20
20
44
11
Pr.: 6 € (11 … 4) ‚ 2 € (11 • 10)
6 € 7 ‚ 2 € 21
42 ‚ 42
Diese Zahl heißt 11.
38)
Agroß = s²
s
A
s-4
s
klein
um 72 cm² größer
= (s-4)€(s-4) =
s² … 72 ‚
… 72 ‚
0 ‚
8s ‚
s ‚
s² - 8s + 16
sgroß = 11 cm
sklein = 7 cm
Die Quadratseiten sind 11 cm bzw. 7 cm lang.
39)
a) B = N + T
b) T = B - N
s-4
40)
s ‚
s² … 8 s • 16
… 8 s • 16
… 8 s • 88
88
11
u
3
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
6. Schularbeit aus MATHEMATIK
Mi, 6. 6. 2012
41)
a) v ‚ ts
42)
g ‚ 4Fa
43)
a)h ‚
a ‚
c ‚
2. A
(a • c)
2. A
h
2. A
h
NAME:
KL.: M3/I.
- S.19
s
v
b) t ‚
b) K ‚
Z . 100 . 12
p . m
c) a ‚
2. V
b . h
… c
p ‚
Z . 100 . 12
K . m
b ‚
2. V
a . h
… a
m ‚
Z . 100 . 12
K . p
h ‚
2. V
a . b
44)
a) T ‚
3 (S … R)
2
3 (135 … 105)
2
b) b ‚
T ‚
T = 45
b ‚
a. M
L •
c
3
9 . 28
31 •
15
3
b = 7
45)
d . (3f … g) ‚ 2e
3f … g ‚
2e
d
g ‚ 3f …
2e
d
46)
u = 2 . (a + b)
u([a+24],[b-14]) = 2 . ([a + 24] + [b - 14])
= 2 . (a + 24 + b - 14)
= 2 . (a + b + 10)
= 2a + 2b + 20
Der Umfang vergrößert sich um 20.
47)
u(s) = 4 . s
u(2s) = 4 . (2s)
= 8 . s
Der Umfang verdoppelt sich.
48)
a)
A(a,b) = a . b
A([a+5], b ) = (a + 5) . b
= ab + 5b
Der Flächeninhalt vergrößert sich um 5b.
b)
A(a,b) = a . b
A(a,[b-7]) = a . (b - 7)
= ab - 7a
Der Flächeninhalt verkleinert sich um 7a.
49)
u(s) = 3 . s
u(s+7) = 3 . (s + 7)
u(s+7) = 3s + 21
u(s+7) = u(s) + 21
Der Umfang vergrößert sich um 21.
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
6. Schularbeit aus MATHEMATIK
Mi, 6. 6. 2012
50)
180° = 2ƒ + †
= 2.(ƒ - 12) + († + 24)
† wird um 24° größer.
51)
Lösungsvorschlag:
NAME:
KL.: M3/I.
- S.20
52) Lösung zu 7G5.02-E / 002-e
Lösungsvorschlag:
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
6. Schularbeit aus MATHEMATIK
Mi, 6. 6. 2012
53)
Lösungsvorschlag:
NAME:
KL.: M3/I.
- S.21
54)
55)
Lösungsvorschlag:
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die
6. Schularbeit aus MATHEMATIK
Mi, 6. 6. 2012
56)
Lösungsvorschlag:
NAME:
KL.: M3/I.
- S.22
VIEL GLÜCK!
Abpfiff!
Köck Leonhard
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL