Gleichungen umformen: Waagemodell und Umkehroperation

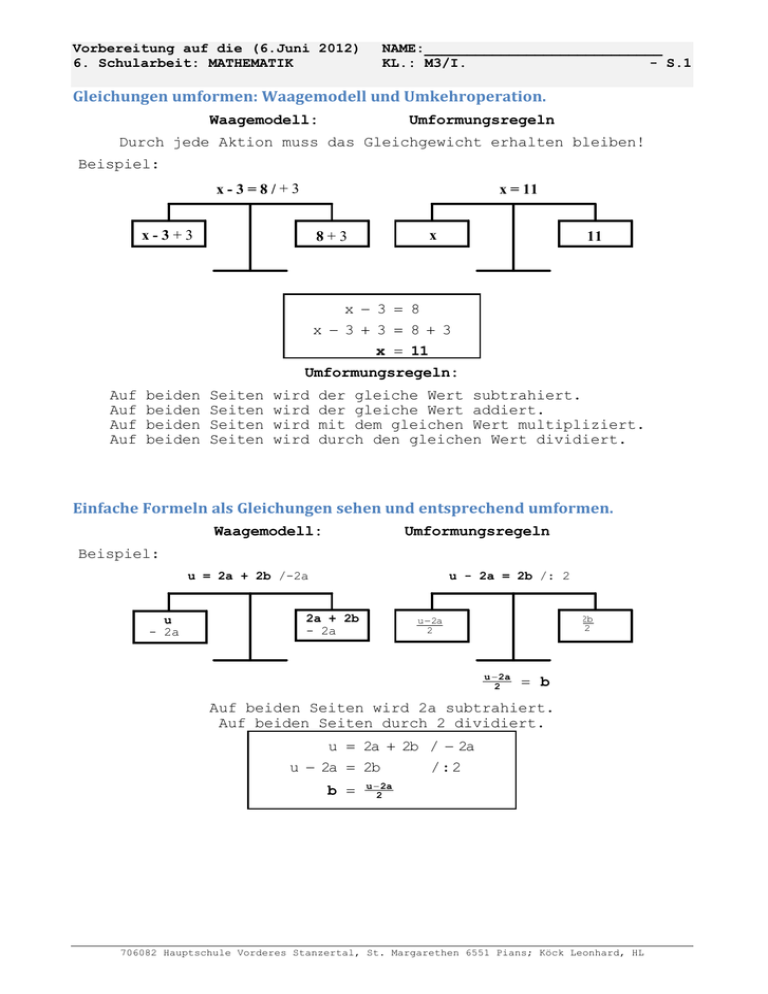
Vorbereitung auf die (6.Juni 2012)
6. Schularbeit: MATHEMATIK
NAME:____________________________
KL.: M3/I.
- S.1
Gleichungen umformen: Waagemodell und Umkehroperation.
Waagemodell:
Umformungsregeln
Durch jede Aktion muss das Gleichgewicht erhalten bleiben!
Beispiel:
x-3=8/+3
x = 11
x-3+3
x
8+3
11
x € 3 • 8
x € 3 ‚ 3 • 8 ‚ 3
x • 11
Umformungsregeln:
Auf
Auf
Auf
Auf
beiden
beiden
beiden
beiden
Seiten
Seiten
Seiten
Seiten
wird
wird
wird
wird
der gleiche Wert subtrahiert.
der gleiche Wert addiert.
mit dem gleichen Wert multipliziert.
durch den gleichen Wert dividiert.
Einfache Formeln als Gleichungen sehen und entsprechend umformen.
Waagemodell:
Umformungsregeln
Beispiel:
u = 2a + 2b /-2a
u
- 2a
u - 2a = 2b /: 2
2a + 2b
- 2a
2b
2
u €2a
2
u € 2a
2
• b
Auf beiden Seiten wird 2a subtrahiert.
Auf beiden Seiten durch 2 dividiert.
u • 2a ‚ 2b / € 2a
u € 2a • 2b
/: 2
b •
u € 2a
2
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die (6.Juni 2012)
6. Schularbeit: MATHEMATIK
NAME:____________________________
KL.: M3/I.
- S.2
Zu Textaufgaben Gleichungen anschreiben und lösen.
Ziel ist es, einen mathematischen Sachverhalt durch eine Gleichung
auszudrücken.
Die gesuchte Zahl bzw. der gesuchte Wert wird mit einer Variablen
(einem Platzhalter) belegt.
Beispiel:
In einem Parallelogramm soll der Winkel ƒ um 12° größer sein als
der Winkel „. Ermittle die Größe der Winkel mit einer Gleichung
und kontrolliere diese Berechnungen!
Die Innenwinkelsumme eines Vierecks ist 360°.
C
D
„
ƒ
ƒ
A
„
„ = ƒ - 12
„ = 96 -12
„ = 84
B
ƒ ‚ ( ƒ € 12 ) ‚ ƒ ‚ ( ƒ € 12 ) • 360
4 … ƒ € 24 • 360 / ‚ 24
4 … ƒ • 384 / : 4
ƒ • 96
Kontrolle:
360 = 2 . 96 + 2 . 84
360 = 192 + 168
360 = 360
w. A.
Antwort: Der Winkel ƒ hat 96° und der Winkel „ hat 84°.
Die Variable in einer Gleichung muss nicht immer x heißen.
Gleichungen mit Klammertermen lösen.
2 . (13 - b) =
26 - 2b =
26 + 6b =
6b =
b =
8 . (7 - b)
1)
56 - 8b
/ + 8b
56
/ - 26
30
/ : 6 2)
5
Jede Seite vereinfachen,
wobei die Vorrangregeln
eingehalten werden müssen.
So lange Umformen bis
„Ordnung” herrscht!
d. h. Auf einer Seite steht
die Variable und auf der
anderen Seite ihr Zahlenwert.
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die (6.Juni 2012)
6. Schularbeit: MATHEMATIK
NAME:____________________________
KL.: M3/I.
- S.3
Textaufgaben lösen, die zu Gleichungen mit verschiedenen Rechenoperationen
führen.
Für eine Party werden 60 Flaschen Apfelsaft und Orangensaft um
606 € gekauft.
Eine Flasche Apfelsaft kostete 8,50 €, Orangensaft 10,90 €.
Wie viel Faschen jeder Sorte werden gekauft?
Anz. d. Fl. Preis pro Fl.
Gesamtpr.
Apfelsaft
x
8,50
x … 8,50
Orangensaft
60 - x
10,90
(60 - x)…10,90
606
x … 8,5 ‚ (60 € x) … 10,9 •
8,5x ‚ 654 € 10,9x •
€ 2,4x ‚ 654 •
48 •
20 •
20 Flaschen Apfelsaft
606
Pr obe:
606
20 Fl. Apfels. ••••† 8,50 … 20 • 170,00
606
40 Fl. Orangens. •† 10,90 … 40 • 436,00
24
,x
60 Flaschen für insgesamt ••† 606,00
x
und 40 Flaschen Orangensaft wurden gekauft.
Umformen von Formeln.
Wende die Umformungsregeln für Gleichungen an!
Für das Umformen von Gleichungen kann man das Modell der
Umkehroperationen oder das Waagemodell verwenden.
Waagemodell:
Umformungsregeln
Beispiel:
A •
A
A
c … hc
2
/ …2
2A = c . hc /: c
c . hc
2A
c
hc
1) Beide Seiten mit gleichem Faktor multiplizieren.
2) Beide Seiten durch gleichen Divisor dividieren.
3) Auf beiden Seiten den gleichen Wert (Term) addieren.
4) Auf beiden Seiten den gleichen Wert (Term) subtrahieren.
Angeben, wie sich das Verändern einer Größe in einer Formel auf das Ergebnis
auswirkt.
Beachte, in welchem Teil der Formel eine Größe verändert wird.
Versuche mit konkreten, einfachen Zahlenbeispielen die
allgemeine Gesetzmäßigkeit herauszufinden.
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die (6.Juni 2012)
6. Schularbeit: MATHEMATIK
NAME:____________________________
KL.: M3/I.
- S.4
Netze von Pyramiden mit verschiedenen Grundflächen zeichnen
Das Netz einer Pyramide besteht aus der Grundfläche und dem
Mantel.
s
S
s
S
a
s
h
a
ha
a
a
a
a
s
a
h
a
b
b
a
ha
hb
b
a
b
a
a
Konstruktionsweg:
1) Grundfläche konstruieren.
2) Gleichschenkeliges Seitenflächendreieck (a, ha) an die
Grundfläche anfügen. (Spitze mit S bezeichnen)
3) Kreisbogen mit Radius s und Mittelpunkt S.
4) Grundflächenkanten als Sehnen auf dem Kreisbogen abtragen,
Mantelflächen „erzeugen”.
Die Oberfläche von Pyramiden berechnen Anfertigen von Skizzen
Die Oberfläche besteht aus Grundfläche + Mantel.
Mantel = Summe der Seitenflächen
Oberfläche = Grundfläche + Mantel
O • G ‚ M
quadratische Pyramide
rechteckige Pyramide
a
a
a
a
a
h
a
a
b
a
ha
b
a
hb
h
ha
b
a
a
b
a
a… ha
2
a… ha
2
b … hb
2
M • 4…
M • 2 … a … ha
M • 2…
‚ 2…
M • a … ha ‚ b … hb
O • a2 ‚ 2 … a … ha
O • a … b ‚ a … ha ‚ b … h b
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die (6.Juni 2012)
6. Schularbeit: MATHEMATIK
NAME:____________________________
KL.: M3/I.
- S.5
Das Volumen von Pyramiden berechnen
Der Inhalt einer quadratischen Pyramide mit der Grundflächenkante a und der
Körperhöhe a, wird in einen Würfel mit gleicher Grundfläche gefüllt. Dieser
Vorgang kann genau dreimal durchgeführt werden.
Daraus folgt, dass das Volumen dieser Pyramide genau ein Drittel des
Würfelvolumens ist.
h
a
a
Grundfläche mal Höhe
3
Grundflächenhöhe € Körperhöhe
Volumen•
h
b
a
Tipp: Skizziere die Grundfläche mit ihrem Umkreismittelpunkt U im
Schrägriss. (Nicht in allen regelmäßigen Vierecken ist U
gleichzeitig der Diagonalenschnittpunkt!)
Dieser Punkt ist der Fußpunkt der Körperhöhe in geraden
Pyramiden. Die Körperhöhe steht normal auf der Grundfläche.
Skizzen sollten nicht zu klein sein und sorgfältig beschriftet
werden.
Grundfläche:
Quadrat: G = a²
‡G
•
2
d
2
Volumen:
ˆ
Rechteck: G = a … b
2
gleichseitiges Dreieck:
G • a …4 3
2
Sechseck:
G • 6 … a …4 3
V •
a2 …h
3
V •
a… b … h
3
V •
a2 … 3
4
V • 6…
…
h
3
a2 … 3
4
…
h
3
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL
Vorbereitung auf die (6.Juni 2012)
6. Schularbeit: MATHEMATIK
NAME:____________________________
KL.: M3/I.
- S.6
Umkehraufgaben zur Volumensberechnung von Prismen und Pyramiden
Eine Frage kann bei der Lösung von Umkehraufgaben den Lösungsweg
„starten”: Kommt in der Angabe ein Wert vor, der ursprünglich mit
einer Formel berechnet werden musste?
Diese Formel ist der Ausgangspunkt. Durch Umformen erhält man
eine neue Formel, um die fehlende Größe berechnen zu können.
Beispiel:
Gegeben ist das Volumen eines Quaders; seine Höhe und die
Seitenkante a der Grundfläche. Berechne die fehlende Seitenkante!
Lösungsweg:
1) Aus dem Volumen kann die Grundfläche
V • G … h
/: h
errechnet werden.
G • Vh
2) Aus der Grundfläche wird die fehlende
G • a … b /: a
Seitenkante errechnet.
b • Ga
Prismen:
Pyramiden:
Volumen •
Volumen • Grundfläche … Höhe
V • G … h
Berechnung der Grundfläche:
V • G … h
/: h
G •
V
h
Berechne der Höhe:
V • G … h
h •
V
G
/: G
V •
Grundfläche… Höhe
3
G …h
3
Berechnung der Grundfläche
V • G3… h
/ …3
3 … V • G … h /: h
G • 3h… V
Berechnung der Höhe:
V • G3… h
/ …3
3 … V • G … h /: G
h •
3… V
G
…ich wünsche dir das Allerbeste …
KL, KV
706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL