10.2.1 Statistik des Uranzerfalls ****** 1 Motivation 2

V100201
Statistik des Uranzerfalls
10.2.1 Statistik des Uranzerfalls
******
1 Motivation
Der radioaktive Zerfall von Uran wird mit einem Lautsprecher hörbar gemacht. Dies macht
deutlich, dass der Zeitpunkt eines Zerfalls nicht vorherbestimmt ist, sondern nur durch ein
statistisches Zerfallsgesetz beschrieben werden kann.
2 Experiment
Abbildung 1: Versuchsanordnung zur Statistik des Uranzerfalls“
”
2.1 Experimenteller Aufbau
Die Versuchsanordnung ist in Abb. 1 zu sehen. Ein Stück Uranerz wird in die Nähe eines GeigerMüller-Zählrohrs gebracht. Die vom Zählrohr ausgehenden elektronischen Impulse werden auf
ein en Philips-Scaler gegeben, welcher die einzelnen Zerfallssignale in fünf nebeneinander angebrachten Dekadenzählern anzeigt: Der ganz rechts stehende Dekadenzähler zählt die einzelnen
Impulse und gibt beim erreichen von zehn Impulsen einen Impuls an den von ihm linksstehenden
Zähler weiter, so dass damit insgesamt eine fünfstellige Dezimalzahl angezeigt wird.
Der Ausgang des Philips-Scalers kann bei hohen Zählraten untersetzt werden, diese untersetzten
Signale werden auf einen Scaler MFZG gegeben, welcher die Ereignisse mit Ziffern anzeigt,
und bei dem man eine Messzeit einstellen kann. Dasselbe Signal wird auf eine sogenannte
Knatterbox gegeben, die bei jedem Signal ein knatterndes Geräusch von sich gibt.
2.2 Einstellen der Betriebsspannung
Mit einer scheibenförmigen 137 Cs-Eichquelle kann die Einstellung geprüft werden: Man bringt
die Eichquelle auf ca. 10 cm Abstand vom Zählrohr und sollte dann ein heftiges Knattern hören.
Falls kein Knattern hörbar wäre, sollte man die Quelle entfernen und die Hochspannung des
Zählrohrs langsam erhöhen, bis eine Rate von ca. 5 s−1 erreicht ist.
Physikdepartement ETH Zürich
1
V100201
Statistik des Uranzerfalls
Falls dies nicht funktioniert, sollte man die Hochspannung wieder herunterfahren, eventuell unter
den Anfangswert.
Im Zweifelsfall sollte ein anderes Zählrohr verwendet werden.
2.3 Messung
• Zuerst sollte man ohne Untersetzung der Rate messen (Ausgang an blauer Succobox).
• Danach das Erz näher an das Zählrohr stellen und Anschluss am Drehschalter verwenden.
• Untersetzung am Drehschalter wählen: Das Knattern wird regelmässiger bei stärkerer Untersetzung.
• Messzeit ∆t = 10 s wählen. Zum Zurücksetzen der Anzeige Knopf 0“ drücken, neue
”
Messung mit Knopf 1“ starten.
”
• Bei konstanten Messbedingungen mehrfach messen und eine Häufigkeitsverteilung der dabei erzielten Messwerte erstellen (Poissonverteilung).
3 Theorie
3.1 Zerfallsgesetz
Der Zerfall eines Teilchens gehorcht einem exponentiellen Zerfallsgesetz. Die Anzahl Zerfälle dN
in einem Teilchenensemble mit N = N (t) während der Zeit dt ist proportional zur Anzahl N
der Teilchen, die noch nicht zerfallen sind:
⇒
dN = −λN dt
(1)
−λt
(2)
N (t) = N0 e
Dabei bedeuten λ die Zerfallskonstante und N0 die Anzahl Teilchen zur Zeit t = 0.
Die mittlere Lebensdauer τ , die im Allgemeinen in der Teilchenphysik verwendet wird, beträgt
τ=
1
λ
(3)
In der Kernphysik ist es dagegen üblich, die Halbwertszeit τ1/2 zu verwenden:
τ1/2 =
ln 2
= τ ln 2
λ
(4)
3.2 Binomialverteilung
Ein Versuch bestehe aus der einfachen Zerlegung
E = A + Ā
(5)
und P (Ā) = 1 − p = q
(6)
mit den Wahrscheinlichkeiten
P (A) = p
In unserem Fall bedeutet A, dass ein Zerfall eintritt und Ā das Gegenteil dazu.
Physikdepartement ETH Zürich
2
Physik II, Prof. W. Fetscher, FS 2008
1
V100201
300
103 Wpn (k)
150
Statistik des Uranzerfalls
103 Wpn (k)
n = 10
p = 0,4
n = 30
p = 0,4
200
100
100
50
0
0
5
k
0
10
0
5
10
15
20
25
k
30
Abbildung6.1:
2: Binomialverteilung.
Abbildung
Binomialverteilung.
Das Zeitintervall, während dessen gemessen wird, muss so klein sein, dass die Wahrscheinlichkeit
für mehr als einen Zerfall vernachlässigbar klein ist. Es werden nun n unabhängige Versuche
durchgeführt. Durchschnittlich tritt dabei das Ereignis A µ = pn ∈ R mal ein. Damit ist die
Wahrscheinlichkeit p, dass A eintritt, gegeben durch:
0≤p=
µ
<1
n
(7)
Bei einer Wiederholung dieses Experiments werden k Zerfälle gemessen. Gesucht ist damit die
Wahrscheinlichkeitsdichte Wpn (k)1 , dass bei n Versuchen A genau k mal eintritt.
Dazu nehmen wir zunächst an, dass genau bei den ersten k Versuchen A eintritt und bei den
restlichen Versuchen Ā. Die Wahrscheinlichkeit P dafür ist
P =
k
Y
i=1
pi
n
Y
(1 − p)j = pk (1 − p)n−k
(8)
j=k+1
Nun gibt es nk verschiedene Kombinationen, bei denen genau k mal der Wert A eintritt. Damit
erhalten wir für die gesuchte Wahrscheinlichkeit die Binomialverteilung:
n k
n
Wp (k) =
p (1 − p)n−k
(9)
k
bzw.
Wµn (k)
n
µ k
µ n−k
=
1−
k
n
n
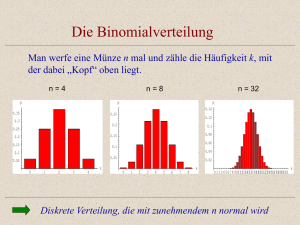
Abb. 2 zeigt zwei Binomialverteilungen mit p = 0,4 und n = 10 bzw. n = 30.
Physikdepartement ETH Zürich
1
Man beachte, dass µ eine beliebige positive reelle Zahl ist, k dagegen eine natürliche Zahl sein muss!
3
(10)
Physik II, Prof. W. Fetscher, FS 2008
1
V100201
103 P (k, λ)
Statistik des Uranzerfalls
103 P (k, λ)
200
λ = 4,0
100
λ = 12,0
100
50
0
0
5
k
10
0
0
5
10
15
20
25
k
30
Abbildung6.1:
3: Poissonverteilung.
Abbildung
Poissonverteilung.
3.3 Poissonverteilung
Wir verwenden nun von die soeben gefundene Binomialverteilung, um die Häufigkeitsverteilung
der Zerfälle in einem vorgegeben, beliebig langen, Zeitintervall ∆t zu berechnen. Da die Zeit
eine kontinuierliche Variable ist, werden wir den Grenzübergang n → ∞ durchführen, verlangen
dabei aber, dass gleichzeitig p → 0 geht derart, dass der Erwartungswert µ = np konstant bleibt.
Wµn (k)
µ k
n
µ n−k
=
1−
k
n
n
k
n!
µ
µ n µ −k
=
· k · 1−
· 1−
k!(n − k)! n
n
n
k (n − k + 1) µ
µ −k
n (n − 1)
=
·
···
·
· 1−
n
n
n
k! |
{zn }
|
{z
}
→1
→1
µ n
· 1−
(n → ∞)
| {zn }
(11)
(12)
(13)
→e−µ
Dies ist die gesuchte Poissonverteilung:
P (k, µ) =
µk −µ
·e
k!
Abb. 3 zeigt zwei Poissonverteilungen mit µ = 4,0 bzw. µ = 12,0.
Physikdepartement ETH Zürich
4
(14)
V100201
Statistik des Uranzerfalls
Man beachte den wichtigen Unterschied zwischen Binomial- und Poissonverteilung: Bei der
Binomialverteilung kann k nur einen Wert aus dem Bereich [0, . . . , n] annehmen, während der
Definitionsbereich bei der Poissonverteilung [0, . . . , ∞) ist. Beiden Verteilungen gemeinsam ist,
dass sie Wahrscheinlichkeitsdichten darstellen, wie man leicht beim Betrachten der Abbn. 2 und
3 einsehen kann. Bei jedem Wert von k wird die Wahrscheinlichkeit durch die farbig markierte
Fläche dargestellt, die ein Produkt der Abszissen- mit der Ordinatenbreite ist.
3.4 Momente der Poissonverteilung
Die Poissonverteilung ist auf 1 normiert:
∞
X
∞
X
µk
P (k, µ) =
k=0
k=0
−µ
=e
k!
· e−µ
∞
X
µk
k!
k=0
−µ µ
=e
∞
X
e =1
P (k, µ) = 1
(15)
k=0
Der Erwartungswert E(k) ist gleich
E(k) =
∞
X
k=0
=
∞
µk −µ X µk −µ
·e =
k
·e
k·
k!
k!
k=1
∞
X
µ · µk−1
j=1
(k − 1)!
⇒
−µ
·e
=µ
∞
X
µj
j=0
j!
· e−µ
(16)
E(k) = µ
Der Erwartungswert E(k 2 ) berechnet sich entsprechend:
2
∞
X
∞
X
µk−1
· e−µ
k!
(k − 1)!
k=1
k=1


∞
∞


j
j
X
X
µ
µ
=µ
(j + 1) · e−µ = µ
j
· e−µ + 1


j!
j!
E(k ) =
k
k
2µ
−µ
·e
=µ
j=0
k·
j=0
⇒
E(k 2 ) = µ(µ + 1)
Mit den Gln. (16) und (17) lässt sich die Varianz der Verteilung berechnen:
σ 2 (k) = E(k 2 ) − E(k)2 = µ(µ + 1) − µ2
Physikdepartement ETH Zürich
5
(17)
V100201
Statistik des Uranzerfalls
⇒
σ 2 (k) = µ
(18)
Zuletzt berechnen wir noch die Schiefe der Verteilung:
µ3 = E (k − E(k))3 = µ
Die Schiefe ist damit gleich
⇒
γ=
µ3
µ
= 3/2 = µ−1/2
3
σ
µ
Die Poissonverteilung wird demnach umso symmetrischer, je grösser µ ist.
√
Für genügend grosse µ kann man also µ als Messfehler annehmen.
Physikdepartement ETH Zürich
6
(19)